为了满足不同空间任务需求,对各种型号的卫星、深空探测器、空间站等航天器推进系统性能的要求不断提高。作为空间推进技术的一种,电推进技术得到了前所未有的应用与发展[1~3]。近年来各国均加强了对微型空间推进系统的研发,以用于微纳卫星的主推进系统,或是执行各类卫星的精确姿轨控任务等[4]。例如电子回旋共振离子推力器(ECRIT)已被日本用作探索小行星的深空探测器“隼鸟”号的主推进系统,推力器的推力系数为92%,比冲为3200s,最大推力为8mN,发射后推进剂利用率达到87%[5, 6]。深空探测和地球轨道卫星的姿态保持、轨道控制等任务中,通常要求推进系统具有高比冲、长寿命以及无污染等特点[7]。在本文中,电子回旋共振等离子体推力器(ECRPT)是一类准中性电推进装置,具有ECR源的高电离性能以及无需中和器的特点,电子和离子在磁喷管中同时加速喷出[8],其寿命长、比冲高、结构简单、可靠性高,适用于深空探测等长时间空间飞行任务[3, 9, 10]。
美国、法国和日本在ECRPT的研究工作中取得了一定的成果。美国NASA马歇尔太空飞行中心(MSFC)针对ECRPT进行了实验研究,结果表明推进工质经由电子回旋共振的方式吸收微波能量,产生高密度等离子体,在羽流中的等离子体密度达到1013~1016m-3数量级,离子速度达到20~30km/s[11]。法国航空航天局(ONERA)针对ECRPT采用氙气作为推进气体,研究了质量流量和微波功率对离子电流和离子能量分布的影响,在微波功率为50 W时获得质量利用效率达45%和离子能量达350eV[12]。日本京都大学对ECRPT进行了粒子模拟,采用蒙特卡罗碰撞算法的二维轴对称粒子模型对ECRPT进行数值模拟,数值计算在微波频率为4GHz和磁感应强度为1430G下进行,结果表明磁场能有效地约束等离子体中的电子,并且离子通过空间静电场作用加速喷出,也验证了在放电腔室区域电子回旋共振效应,电子数密度最高可达到1016m-3量级[13]。
已有的文献报道表明,目前尚未开展不同工质气体、微波功率、工作气压条件对ECRPT放电影响的研究,因此本文采用漂移-扩散流体模拟方法[9],根据所设计的推力器基本结构,通过改变推进剂气体种类、工作压强和微波功率范围,仿真模拟了微波等离子体放电过程,分析不同工作条件下放电腔内电子数密度、电子温度以及碰撞功率损耗的分布规律,为ECRPT的研究与设计提供理论指导。
2 ECRPT工作原理和系统结构 2.1 工作原理ECRPT通过电子回旋共振吸收微波功率而产生高密度等离子体,并且通过磁喷管加速喷出而产生推力[14]。根据已报道的研究结果,推进剂的利用效率高达45%,离子能量高达350eV,该推力器具有较高的比冲,其能够显著降低推进工质的重量,增加有效载荷[15]。
ECRPT工作过程中,通过在放电腔室中的电子直接轰击工质气体产生等离子体,离子沿着磁场运动,在此过程中,其被空间静电场加速喷出[16]。在磁场作用下,电子将沿磁感线做旋转运动,在磁场强度最低处,电子沿磁感线方向的运动速度最高。在磁场强度最高的磁体表面,电子沿磁感线的方向运动,在速度达到零后发生方向反转,于是电子在磁场约束下沿磁感线作往复回旋运动。
在电子回旋共振放电技术中,当磁场中的电子回旋频率等于波动角频率ωce时发生基本共振。这种共振机制使等离子体可以高效吸收微波能量[17]。合理设计磁场分布,则会使得在等离子体中的某个区域,微波电磁场的波动角频率和电子回旋频率相等,即ωce=eB/m。电子的旋转相位和微波相位相同时,微波和作回旋运动的电子之间发生共振作用,此时微波电场对作回旋运动的电子的作用可等效为一个恒定电场对作直线运动电子的作用,于是电子在磁场和微波电场的共同作用下不断获得加速,持续从微波场中获得能量,最后成为高能电子。而在其它位置处,如果上述两个条件有一个不能满足,那么电子或者得到微波电场的加速,或者被减速,其获能效率要低于ECR面上的电子。因而在ECR面上的电子为高能电子,这类高能电子在一定的气体压强范围内通过与中性粒子(原子以及分子)发生碰撞,导致气体激发和电离形成高密度等离子体。
2.2 系统结构目前ECRPT系统结构组成主要包括微波能量输入系统、微波传输系统、工质供应系统、激发天线、磁场系统、放电腔室及磁喷管[18]。微波能量输入系统主要提供特定频率(如2.45GHz,4.2GHz等)的电磁波,并通过微波传输系统将能量传递给激发天线。其中微波传输系统采用同轴电缆进行能量传递,同轴电缆中传输的微波主模式是TEM波。推进工质通常使用氩气、氙气等,也可根据实际使用条件的不同,选用相应的实验工质气体。激发天线、磁场系统、放电腔室和磁喷管是整个系统的核心部件,对于其设计的结果直接影响到ECRPT的综合性能,磁场系统为ECRPT提供了电子回旋共振面所需的磁感应强度,同时磁场系统所形成的发散磁场一并起到磁喷管的作用,激发天线与放电腔室在一定程度上决定等离子体是否能够有效形成。
在磁化的等离子体中,电子沿着磁感线旋转,其电子回旋频率fce定义为
| $ {f_{{\rm{ce}}}} = \frac{{eB}}{{2{\rm{ \mathit{ π} }}{\mathit{m}_{\rm{e}}}}} $ | (1) |
式中B是磁感应强度,e是单位电荷,me是电子质量。
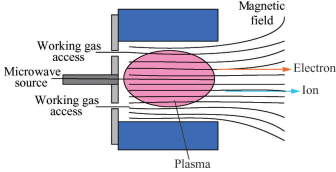
对于微波源频率2.45GHz或者4.2GHz,通过应用式(1)计算得到ECR面的形成需满足磁感应强度为875G或者1500G。如图 1为ECRPT原理示意图。
|
Fig. 1 ECRPT schematic diagram |
本文采用基于流体扩散模型研究了不同工质下推力器放电腔室中的电子数密度、电子温度、功率碰撞损失以及不同压强、不同功率条件下放电腔室的电子数密度和功率碰撞损失,为探究推力器的性能参数提供了参考。
3.1 漂移扩散模型计算的基础是描述电子在电场中传输的漂移扩散过程。漂移扩散方程包含反应/对流-扩散方程,分别用于电子密度和电子能量密度。
本文中使用漂移扩散模型模拟了电子数密度和电子能量密度,并且通过将电子能量密度除以电子数密度来计算平均电子能量。对于电子数密度求解的方程式
| $ \frac{\partial }{{\partial t}}\left( {{n_{\rm{e}}}} \right) + \nabla {\mathit{\Gamma }_{\rm{e}}} = {R_{\rm{e}}} $ | (2) |
| $ {\mathit{\Gamma }_{\rm{e}}} =-\left( {{\mu _{\rm{e}}} \cdot E} \right){n_{\rm{e}}}-{D_{\rm{e}}} \cdot \nabla {n_{\rm{e}}} $ | (3) |
式中ne表示电子数密度(1/m3),Re是电子速率表达式(1/m3·s)),μe为电子迁移率(m2/ (v·s)),E是电场(V/m),De是电子扩散率,(μe·E)ne表示由于电场的作用而形成的电子迁移,De·
电子能量密度求解方程
| $ \frac{\partial }{{\partial t}}\left( {{n_\varepsilon }} \right) + \nabla {\mathit{\Gamma }_{\rm{e}}} + E \cdot {\mathit{\Gamma }_{\rm{e}}} = {R_\varepsilon } $ | (4) |
| $ {\mathit{\Gamma }_{\rm{e}}} =-\left( {{\mu _{\rm{e}}} \cdot E} \right){n_\varepsilon }-{D_\varepsilon } \cdot \nabla {n_{\rm{e}}} $ | (5) |
式中nε表示电子能密度(V/m3),Rε表示由于非弹性碰撞引起的能量损失/增益(V/(m3·s)),με表示电子能量迁移率(m2 /(v·s)),E表示电场(V/m),Dε表示电子能量扩散系数(m2/s)。下标ε是指电子能量。式(4)中的E·Γe表示由外部电场引起的电子的加热。
对于麦克斯韦电子能量分布函数,以下关系成立
| $ {D_{\rm{e}}} = {\mu _{\rm{e}}}{T_{\rm{e}}}, {\mu _\varepsilon } = \left( {\frac{5}{3}} \right){n_{\rm{e}}}, {D_\varepsilon } = {\mu _\varepsilon }{T_{\rm{e}}} $ | (6) |
式中Te表示电子温度。因此,考虑到电子迁移率,可以计算所需的其他传输性能。电子温度可以表示为平均电子能的函数,其定义为
| $ \dot \varepsilon = \frac{{{n_\varepsilon }}}{{{n_{\rm{e}}}}}, {T_{\rm{e}}} = \left( {\frac{2}{3}} \right)\dot \varepsilon $ | (7) |
电磁场的分析方法主要是依据对微分形式的麦克斯韦方程组的求解,对于一般的时变场,其微分形式的麦克斯韦方程组可写成
| $ \nabla \times E + \frac{{\nabla B}}{{\nabla t}} = 0 $ | (8) |
| $ \nabla \times H-\frac{{\nabla D}}{{\nabla t}} = J $ | (9) |
| $ \nabla \cdot D = \rho $ | (10) |
| $ \nabla \cdot B = 0 $ | (11) |
式中E是电场强度,D是电通量密度, H是磁场强度,B是磁通量密度,J是电流密度,B是电荷密度。另一个基本方程式连续性方程为
| $ \nabla J =-\frac{{\partial \rho }}{{\partial t}} $ | (12) |
其表示电荷守恒。
在静磁场的情况下,式(8)、式(9)和式(12)可写成
| $ \nabla \times E = 0 $ | (13) |
| $ \nabla \times H = J $ | (14) |
| $ \nabla \cdot J = 0 $ | (15) |
静电场的标量势由式(9)和式(12)得。E表示成
| $ E =-\nabla \mathit{\Phi } $ | (16) |
将式(15)代入式(9),应用式(8)得到Φ的二阶微分方程即泊松(Poisson)方程
| $ -\nabla \left( {\varepsilon \cdot \nabla \mathit{\Phi }} \right) = \rho $ | (17) |
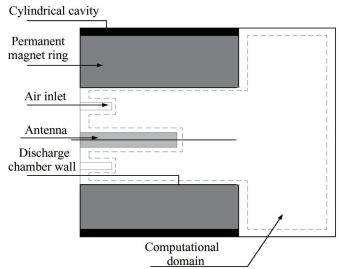
如图 2所示,为微波电磁场物理模型。除了永磁环作为磁路系统外,微波电磁场的物理模型主要有同轴传输电缆、激发天线和放电腔。其计算域由激发天线和放电腔室壁面围绕而成。
|
Fig. 2 Microwave magnetic field physical model |
通过改变包括微波输入功率、放电腔室内气压以及不同工质气体对等离子体参数的影响计算微波电磁场的分布,其中微波的传输模态为TEM模。
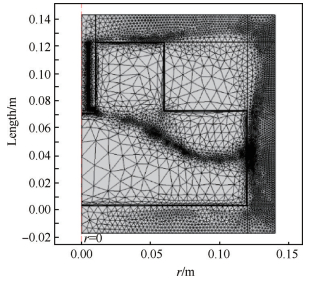
3.3.2 微波电磁场的有限元模型(a) 计算域:对于微波电磁场分析,其计算域包括激发天线和放电腔室。与静磁场的建模结构类似如图 3所示。
|
Fig. 3 Grid model of microwave electromagnetic field |
(b) 网格划分:为了研究ECRPT放电腔室内的电子回旋共振效应,需对微波电磁场网格划分进行细化,在2.45GHz的入射微波频率下,所对应的电子回旋共振效应所需的磁感应强度为875G,因此在该处进行网格细化,如图 3所示。其中三角形单元数为10679、四边形单元数为642、边单元数为694以及顶点单元数为26。
(c) 边界条件:同轴端口的边界条件用于驱动激发电磁波。对于电子,忽略反射作用,通过二次热发射得到电子流量的边界条件。
| $ -n \cdot {\mathit{\Gamma }_{\rm{e}}} = \left( {\frac{1}{2}{v_{{\rm{e, th}}}}{n_{\rm{e}}}} \right) $ | (18) |
电子能量流量表达式
| $ -n \cdot {\mathit{\Gamma }_{\rm{e}}} = \left( {\frac{5}{6}{v_{{\rm{e, th}}}}{n_{\rm{e}}}} \right) $ | (19) |
对于重粒子在壁上的损失是由于表面反应和双极场的迁移
| $ \begin{array}{l} - n \cdot {j_{\rm{k}}} = {M_{\rm{ \mathit{ ω} }}}{R_{\rm{k}}} + {M_{\rm{ \mathit{ ω} }}}{c_k}Z{\mu _{\rm{k}}} \cdot \\ \left[{\left( {{A^{-1}} \cdot E} \right) \cdot n} \right]\left[{\left( {{Z_{\rm{k}}}{\mu _{\rm{k}}}\left( {{A^{-1}} \cdot E} \right) \cdot n} \right)} \right] \end{array} $ | (20) |
腔壁接地。
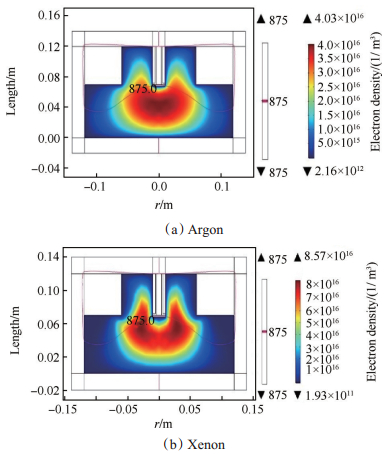
4 模拟结果与分析 4.1 不同工质气体对ECRPT放电的影响对于不同工质气体,其物理特性不同,在其他条件相同的情形下,放电结果会有区别。本文比较了微波入射功率为10W,压强为1Pa条件下,计算域中即放电腔室中电子数密度、电子温度、碰撞功率损耗的不同分布,模拟结果如图 4、图 5和图 6所示,等值线为875G的ECR面。
|
Fig. 4 Distribution of electron density |
|
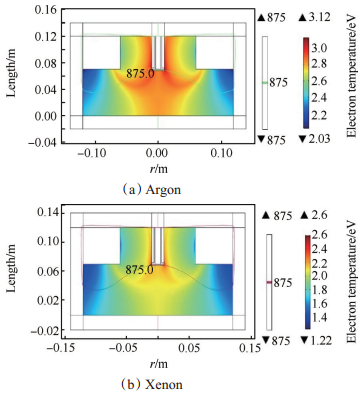
Fig. 5 Distribution of electron temperature |
|
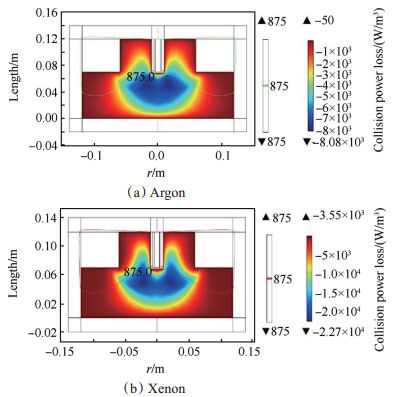
Fig. 6 Distribution of collision power loss |
从图 4、图 5及图 6中可以看出,在相同条件下,氩气和氙气的电子数密度都能达到1016m-3数量级,中心区域的电子数密度最大,由于电子回旋共振效应使得电子数密度最大的位置均靠近磁感应强度为875G的等值线,且氩气的电子数密度高于氙气;氩气和氙气在放电腔室内沿着激发天线和磁感应强度为875G的等值线处均有最大的电子温度,且氩气的电子温度高于氙气;氩气和氙气的碰撞功率损耗分别在-103J和-104J,氙气的碰撞功率损耗低于氩气。这是由于氙气的电离能低于氩气的电离能,因而氙气更容易电离,其电子与中性粒子之间的碰撞更加剧烈,高能电子数目比较多,碰撞功率损耗越小。由于磁场的作用,电子会绕着磁力线做回旋运动,伴随着入射微波功率形成电子回旋共振效应,则在磁感应强度为875G的等值线上存在大量的高能电子,此区域会与大量中性粒子碰撞,从而产生大量等离子体,故在中心区域和靠近磁感应强度为875G的等值线上处电子数密度较高、电子温度较大、碰撞功率损耗较小。从而可以确定采用氙气作为ECRPT的工质气体能够获得更大的推力及更高的比冲。
4.2 不同气体压强对ECRPT放电的影响压强对于放电的影响表现在粒子之间的碰撞频率,因此,不同压强对于等离子体放电具有重要影响。本文模拟了微波入射功率为10W,计算域温度为300K,工质气体为氩气,压强分别为1Pa,2Pa,5Pa及10Pa条件下,放电腔室中氩气电子数密度、电子温度和碰撞功率损耗分布情况,模拟结果分别如图 7,图 8和图 9所示。
|
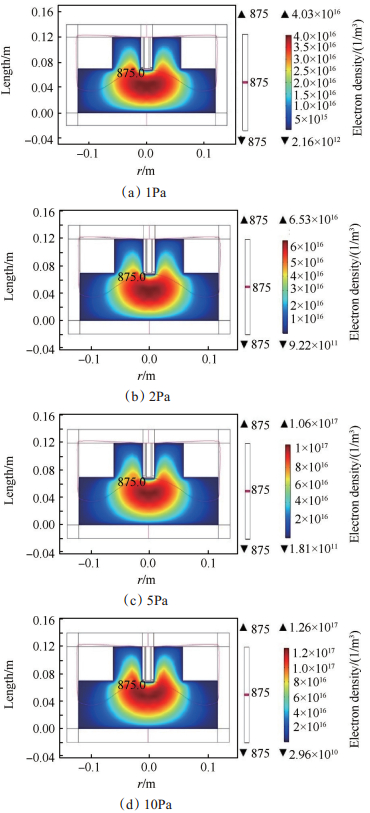
Fig. 7 Distribution of electron density at different pressures |
|
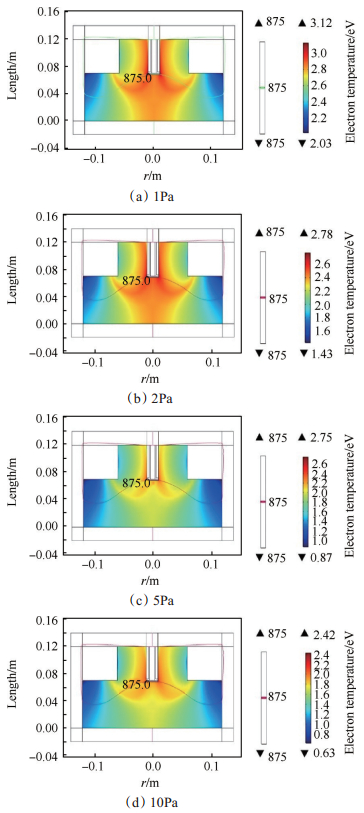
Fig. 8 Electron temperature distribution at different pressures |
|
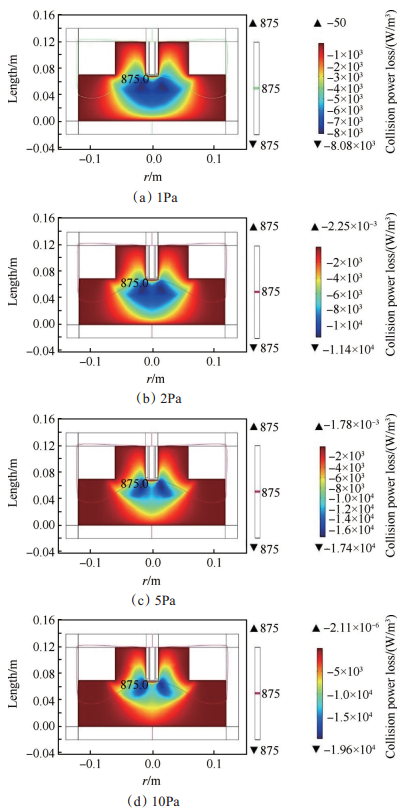
Fig. 9 Collision power loss distribution at different pressure |
从图 7,图 8及图 9中可以看出,相同条件下,在压强由1~10Pa范围内间断性变化,随着气体的压强增大,电子数密度增大,电子温度降低,碰撞功率损耗增大。说明压强对粒子之间的碰撞具有较大影响,压强增高,电子与中性粒子之间的碰撞越剧烈,随之电离程度也增大,高能电子数目越多,碰撞损耗功率增大。在图 7中随着压强越高电子数密度越集中在中心区域和磁感应强度为875G的等值线处,说明压强越高使得电子与中性粒子的碰撞更剧烈,产生的等离子体密度越高,并且伴随着磁场而产生的电子回旋共振效应使得大量电子被约束在该区域;在图 8中随着压强的增高电子温度明显降低,但电子温度峰值区域未改变,呈现一定范围性减小,说明压强的增高使得电子与中性粒子碰撞更剧烈,使得电离程度提高,故电子温度减小;在图 9中随着压强的增高碰撞功率损耗有所增加,增加的幅度不是很大,但碰撞功率损耗的区域有明显变化,说明压强增高,在磁感应强度为875G的等值线上高能电子明显增多,使得此处的碰撞功率损耗减小,并且范围更加集中在电子回旋共振线上,即磁感应强度为875G等值线。因此,对于ECRPT放电需要控制和调节工质气体的流量,从而改变放电腔室的压强,以获得更高密度的等离子体。
4.3 不同微波功率对ECRPT放电的影响入射微波功率是工质气体电离能量的来源,并且对于ECRPT而言微波入射功率频率是影响电子回旋共振效应的主要参数,本文中所采用的入射微波频率为2.45GHz,对应电子回旋共振效应所需的磁感应强度为875G,因此入射微波功率对于ECRPT放电具有重要影响。本文模拟了压强为1Pa,计算域温度为300K,工质气体为氩气,入射微波功率分别为10W,15W,20W和25W条件下,放电腔室内电子数密度、碰撞功率损耗的分布情况,模拟结果分别如图 10和图 11。
|
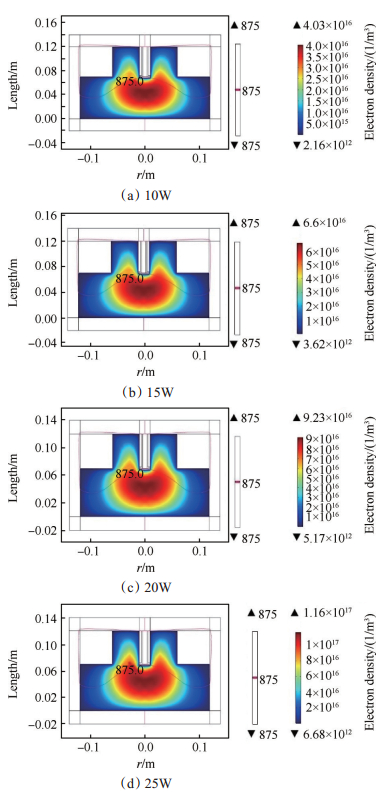
Fig. 10 Electron density distribution under different microwave power conditions |
|
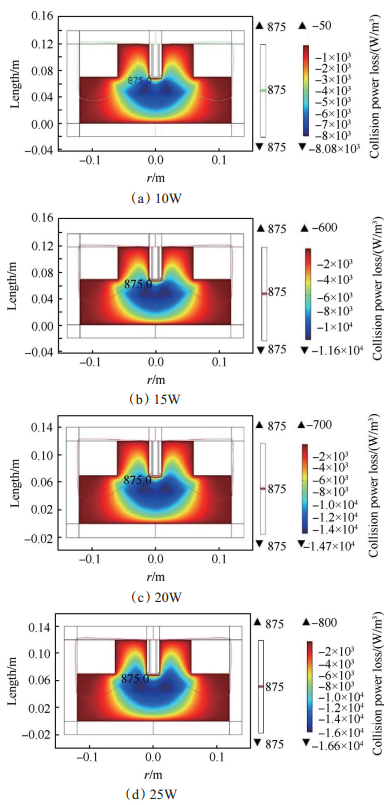
Fig. 11 Distribution of power loss under different microwave power |
从图 10和图 11可得出,相同物理条件下,入射微波功率在10~25W内间断性变化,入射微波功率增大,电子数密度增高,碰撞功率损耗增大。其原因在于入射微波功率通过同轴电缆传输到放电腔室,在放电腔室中入射微波功率通过激发天线将其能量传递给电子,电子与中性粒子碰撞产生等离子体,且由于电子回旋共振效应高能电子数增多使得等离子体密度更高,入射微波功率越大,电子获得的能量就越多,与中性粒子碰撞后使得更多中性粒子电离,故电离之后产生更多的电子,电子数密度也随之增大。碰撞功率损耗随着入射微波功率的增加略有增大,碰撞功率损耗的分布没有明显变化,高能电子越多,碰撞功率损耗越小。因此,对于ECRPT入射微波功率的变化对于该推力器具有重要的影响,合适的入射微波功率有助于提高该推力器的效率。
5 结论(1) 本文通过分别改变工质气体种类、计算域内压强、入射微波功率,模拟仿真获得ECRPT放电腔室内电子数密度、电子温度和碰撞功率损耗的分布特性及规律。数值模拟结果表明,以上物理参数对于电子回旋共振等离子体放电具有重要意义。
(2) 通过模拟结果发现,在微波入射功率为10W、压强为1Pa条件下,氙气的最大电子数密度8.57×1016/m3,数量级为氩气的4.03×1016/m3的两倍;氙气的最大碰撞功率损耗为-2.27×104W/m3,高于氩气的-8.808×103 W/m3,说明氙气的电离效果要优于氩气,更容易获得较高的电子数密度,氙气的电离能相对较低,发生电离的中性粒子数更多,因此电子回旋共振效应获得的等离子体密度较高。
(3) 在微波功率为10W、工质气体为氩气条件下,通过改变计算域内压强,模拟结果表明随着压强的增大,最大电子数密度从4×1016/m3上升到1.26×1017/m3数量级;最大功率碰撞功率损失从-8.08×103 W/m3上升到-1.96×104W/m3;电子温度不断减小,说明增大计算域内压强能够使电子与中性粒子之间的碰撞加剧。
(4) 在工作压强为1 Pa、工质气体为氩气条件下,模拟结果表明随着入射微波功率的增大,最大电子数密度从4.03×1016/m3增大到1.16×1017/m3数量级;碰撞功率损耗随着入射微波功率的增大而增大,说明增大入射微波功率,中性粒子的电离程度获得显著提高。通过以上模拟结果可明显看出,在电子回旋共振线即磁感应强度为875G等值线上,电子数密度最大和碰撞功率损耗最小,验证了电子回旋共振效应对等离子体产生的重要作用。
综合以上各影响因素,在未来ECRPT的实际应用中,可以通过使用氙气,适当增大推力器腔内压强以及入射微波功率,使其具有最佳的推力、比冲和工作效率。
| [1] |
Gollor M, Weinberg S, Boss M, et al.Electric Propulsion Electronics Activities in Europe[C].Hartford: AIAA/ASME/SAE/ASEE Joint Propulsion Conference & amp; Exhibit, 2013.
(  0) 0) |
| [2] |
Tverdokhlebov S, Semenkin A, Garkusha V, et al.Overview of Electric Propulsion Activities in Russia[C].Fort Lauderdale: 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, 2004.
(  0) 0) |
| [3] |
陈茂林, 毛根旺, 夏广庆, 等. 电子回旋共振离子推力器栅极光学系统的PIC/MCC模拟[J]. 推进技术, 2012, 33(1): 150-154. (CHEN Mao-lin, MAO Gen-wang, XIA Guang-qing, et al. PIC/MCC Simulation of Gate Optical System for Electron Cyclotron Resonance Ion Thruster[J]. Journal of Propulsion Technology, 2012, 33(1): 150-154.)
(  0) 0) |
| [4] |
汤明杰, 杨涓, 金逸舟, 等. 微型电子回旋共振离子推力器离子源结构优化实验研究[J]. 物理学报, 2015, 64(21): 319-325. (  0) 0) |
| [5] |
Kuninaka H, Nishiyama K, Funaki I, et al. Powered Flight of Electron Cyclotron Resonance Ion Engines on Hayabusa Explorer[J]. Journal of Propulsion and Power, 2007, 23(3): 544-551. DOI:10.2514/1.25434
(  0) 0) |
| [6] |
Funaki I, Kuninaka H, Toki K. Plasma Characterization of a 10cm Diameter Microwave Discharge Ion Thruster[J]. Journal of Propulsion and Power, 2004, 20(4): 718-727. DOI:10.2514/1.11379
(  0) 0) |
| [7] |
成玉国, 夏广庆, 韩亚杰. 发散磁场中等离子体加速和推进性能数值研究[J]. 推进技术, 2017, 38(8): 1914-1920. (CHENG Yu-guo, XIA Guang-qing, HAN Ya-jie. Numerical Investigation on Plasma Acceleration Process and Propulsion Performance on Divergence Magnetic Field[J]. Journal of Propulsion Technology, 2017, 38(8): 1914-1920.)
(  0) 0) |
| [8] |
Jarrige J, Elias D, Packan D.Measurement of Ion Acceleration in the Magnetic Nozzle of an Ecr Plasma Thruster[R].Space Propulsion-2014-2980896.
(  0) 0) |
| [9] |
杨涓, 石峰, 杨铁链, 等. 电子回旋共振离子推力器放电室等离子体数值模拟[J]. 物理学报, 2010, 59(12): 8701-8706. DOI:10.7498/aps.59.8701 (  0) 0) |
| [10] |
罗立涛, 杨涓, 金逸舟, 等. ECR中和器改进试验研究[J]. 中国空间科学技术, 2016, 36(1): 35-42. (  0) 0) |
| [11] |
Brainerd J, Reisz A.Electron Cyclotron Resonance Propulsion[C].Nashville: AIAA/ASME/SAE/ASEE Joint Propulsion Conference & amp; Exhibit, 2013.
(  0) 0) |
| [12] |
Jarrige J, Elias P Q, Cannat F, et al.Performance Comparison of an ECR Plasma Thruster using Argon and Xenon as Propellant Gas[C].Washington: IEPC, 2013: 63–71.
(  0) 0) |
| [13] |
Ueno K, Mori D, Takao Y, et al.Particle- in-Cell Simulation of a Micro ECR Plasma Thruster[C].Honolulu: APS Meeting, 2015.
(  0) 0) |
| [14] |
Cannat F, Lafleur T, Jarrige J, et al. Optimization of a Coaxial Electron Cyclotron Resonance Plasma Thruster with an Analytical Model[J]. Physics of Plasmas, 2015, 22(5).
(  0) 0) |
| [15] |
Jarrige J, Elias P Q, Packan D, et al.Characterization of a Coaxial ECR Plasma Thruster[C].San Diego: AIAA Plasma dynamics and Lasers Conference, 2013.
(  0) 0) |
| [16] |
Meg & íamac & ías A, Cort & ázar O D, Vizca & ín-odejuli & án A. Influence of Microwave Driver Coupling Design on Plasma Density at Testbench for Ion Sources Plasma Studies, a 2.45GHz Electron Cyclotron Resonance Plasma Reactor[J]. Review of Scientific Instruments.
(  0) 0) |
| [17] |
Ganguli A, Tarey R, Arora N, et al. Development and Studies on a Compact Electron Cyclotron Resonance Plasma Source[J]. Plasma Sources Science and Technology, 2016, 25(2).
(  0) 0) |
| [18] |
陈兆权, 王冬雪, 夏广庆, 等. 微波放电等离子体点火与助燃研究进展[J]. 固体火箭技术, 2014, 37(1): 63-67. (  0) 0) |
 2018, Vol. 39
2018, Vol. 39


