栅极是离子推力器的核心部组件之一,栅极所组成的静电场离子引出结构又称为离子光学系统,其主要功能是聚焦并加速引出放电室工质气体电离后产生的离子,作为离子推力器的推力源[1]。鉴定离子光学系统的一个重要指标是引出离子束流密度均匀性,一般用束流平直度来表征。如果束流平直度较差,则离子推力器中心区域束流密度偏高,而边缘区域束流密度偏低,造成栅极中心区域溅射腐蚀和热变形加剧,边缘区域离子光学聚焦效果差,影响离子推力器的性能和可靠性。
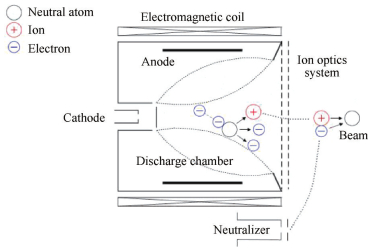
为了减小离子对栅极的溅射腐蚀,研究者提出三栅级设计方案,即增加减速栅保护加速栅,并通过试验证明三栅结构抑制离子欠聚焦现象,减缓了离子对加速栅的溅射腐蚀,但是下游径向电场增强使得离子推力器发散角增大,且对束流平直度没有改善[2],此外,三栅设计引入结构可靠性降低的问题。对于双栅结构常规方法是通过调节放电室构型及磁场布局来提高原初电子区域矩形度[3, 4],从而改善束流均匀性,适用于环切场离子推力器。对于发散场离子推力器而言,如图 1所示,该方法提高束流均匀性只能提高到一定程度,存在瓶颈。从离子光学系统的设计角度来提高束流均匀性,可以对上述常规方法进行补充,是一种新颖的技术途径。
|
Fig. 1 Schematic of divergent magnetic field thruster |
目前双栅离子光学系统普遍通过增加加速栅拱高,进行补偿设计,来提高束流均匀性[5],但是该方法势必要增加束流发散角,导致有效束径降低。因此有研究者提出栅极孔径与放电室等离子体参数相匹配变化的设想,即在栅极不同区域采用电化学腐蚀工艺加工不同直径的栅孔,现已成功应用于LKJ-1B-10和LKJ-1B-15发散场离子源,束流平直度提升了75%[6]。2007年英国Qinetiq公司的Wallace和Corbett将离子源栅极设计经验引入T6发散场离子推力器研发中,提出变孔径栅极设计方案,改善了束流均匀性,其较高的束流平直度是使T6推力器在地面6056h寿命考核试验中栅极最大腐蚀深度仅为0.033mm的主要原因[7]。研究表明发散场离子推力器采用变孔径栅极设计,可有效弥补其放电室结构带来的较低束流均匀性。
粒子云网格法(PIC)和蒙特卡洛碰撞(MCC)结合的方法(PIC/MCC)是一种自洽的数值模拟计算方法,充分考虑了离子和中性原子碰撞造成的影响,前期研究者做了大量工作[8~10],和试验数据有较高的符合度,是一种成熟可靠的栅极设计方案评估手段。本文针对10cm发散场离子推力器(兰州空间技术物理研究所针对无拖曳飞行航天器的阻尼补偿任务自主研制)现有栅极设计进行优化改进,建立变孔径栅极模型,采用PIC/MCC数值计算方法分析了各分区的离子引出电势和离子密度分布,并将现有设计模拟结果与实测值进行了对比,验证了方法的正确性,同时通过对比分析鞍点电势、聚焦点位置、束径、发散角和束流平直度,论证了变孔径优化方案的合理性。
2 变孔径栅极方案设计10cm离子推力器采用小孔离子光学系统双栅设计,其中屏栅孔径ds是共比参数,直接决定了离子引出过程中的离子透明度,受到引出束离子特性和栅极的力学特性所约束,是确定离子光学系统几何参数的关键尺寸[1]。引入栅孔的离子数与栅孔上游的放电室等离子体密度ni有关,到达离子鞘的离子流密度为
| $ {J_i} = e{n_i}{v_i} $ | (1) |
鞘层发射的离子受空间电荷效应作用遵守Child-Langmuir定律,且由离子鞘发射的离子流通过栅孔形成束离子流受到限制[10]。其中与栅极尺寸相关的损失因子ε=exp(-2ts/ds),其他参数如Clausing系数、几何透明度等可不考虑。如果双栅间距lg,加速电压不变,则单孔束流Ib与ni,Te,ε和ds几个参数的关系为
| $ {I_{\rm{b}}}\infty {n_i}\sqrt {{T_{\rm{e}}}} {\rm{exp}}\left( { - \frac{{2{t_{\rm{s}}}}}{{{d_{\rm{s}}}}}} \right){d_{\rm{s}}}^2 $ | (2) |
由于ni和Te分布沿径向不均匀,束流均匀性受到限制。因此,采用变孔径栅极设计方案:屏栅分区域变孔径,加速栅孔径保持不变。该设计旨在人为降低离子光学系统中心区域引出束流密度,提高边缘区域引出束流密度。同时,避免引出欠聚焦和过聚焦现象[11, 12],使束流均匀性得到提高,从而有效提升离子推力器的性能。此外,栅极中心区域引出的束流密度减小,可有效缓解加速栅极在中心区域遭受离子轰击过于集中而导致过早失效的问题。
式(2)建立了屏栅孔径匹配等离子体浓度和电子温度设计的关系,具体方法是使屏栅孔径与等离子体浓度和电子温度分布相匹配,将屏栅分成中心圆和几个同心圆环,然后计算出各区域等离子体密度和温度的相对均值,屏栅上不同径向位置的孔径选取按照该位置的ni和Te来确定,则可利用不同的孔径抽取相同的束流密度,达到改善束流均匀性的目的。
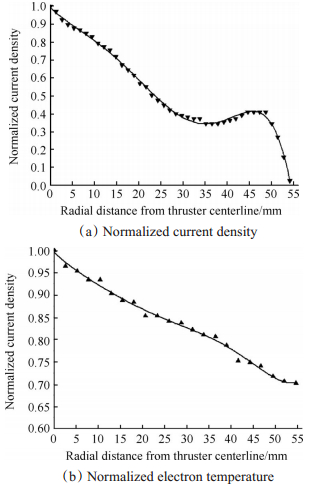
对离子推力器展开了Langmuir探针测量屏栅上游等离子体密度和电子温度试验,归一化之后的结果分别如图 2(a)和(b)所示,可以发现:等离子体密度在离推力器轴线0~30mm内基本呈线性减小变化,30~45mm基本呈水平波动变化,45~55mm又呈线性下降趋势;而电子温度整体在3.1~4.5eV内基本呈线性下降趋势。根据该试验结果和式(2)开展变孔径设计,由于束流存在一定发散角,不同区域的子束流有部分交叉,所以不能分得过细,此处将屏栅分成四个区域,具体方案设计如表 1所示。
|
Fig. 2 Calibration curve for normalized current density and electron temperature |
|
|
Table 1 Optimization of the optics system by varying aperture diameters |
10cm离子推力器双栅厚度均为0.5mm,各有约2000个按六角阵列排布的圆孔,栅间距为0.9mm。在数值模拟计算过程中为了避免庞大计算量,没有必要对整个栅极进行模拟,可以直接从栅极设计区域选择能包含栅极所有信息的最小单元进行数值建模即可。同时,由于栅孔具备轴对称性,因此采用二维建模同样可以表征三维引出过程[12]。
为了对比验证变孔径栅极方案设计的有效性,将原有设计也分为相同的4个分区。计算区域的选取如图 3所示,各包含1/2屏栅孔和相应1/2加速栅孔。计算区域上下边界均为对称边界,该计算模型经过多次对称拼接后,可组合成整个栅面,因此该模型包含了栅极所有信息。

|
Fig. 3 PIC/MCC calculation regions for partitioned ion optics system |
各分区计算区域均选取一个栅孔的中心线作为计算区域的下边界,垂直方向上取孔间距的1/2处为上边界,计算区域的左边界位于放电室内,右边界位于加速栅下游。
图 4为边界条件示意图。其中,边界条件可以分为两类:(a)电场边界条件:左边界为放电室鞘层等离子体,电势取屏栅电势Vs与等离子体悬浮电势Vp之和;上下边界和右边界均取Neumann边界[11],即∂

|
Fig. 4 Schematic of boundary conditions |
利用PIC/MCC方法求解离子光学系统引出束流问题时,时间步长和空间步长的选取是非常重要的,应遵循等离子体基本特性的稳定性条件,选取不当将会直接影响到模拟结果的准确性。
任何电荷密度的扰动都会造成等离子体振荡,该振荡频率ωp是等离子体的固有属性[13]。时间步长Δt的选取和ωp存在直接关系
| $ \Delta t \le \frac{1}{{{\omega _{\rm{p}}}}} = \sqrt {\frac{{4{{\rm{ \mathsf{ π} }}^2}{\varepsilon _0}{m_e}}}{{{e^2}{n_i}}}} $ | (3) |
为了方便使用差分方法求解,并保证计算精确度,将计算区域划分为了大量正交等距网格,空间步长,即网格尺度h不大于上游等离子体的德拜长度λD[14]
| $ h \le {\lambda _{\rm{D}}} = \sqrt {\frac{{{\varepsilon _0}k{T_{\rm{e}}}}}{{{n_i}{e^2}}}} $ | (4) |
将4个分区鞘层等离子体密度ni和电子温度Te带入式(3)和式(4)中,可得到各分区步长参考值,如表 2所示。
|
|
Table 2 Result of calculation for step size |
其中,4个分区中最大ωp为4.65GHz,为了缩短计算时间,将计算时间步长选取为0.2ns。同样,4个分区中最小λD为0.029mm,为了简化处理,将屏栅和加速栅边界与设置网格重合,综合考虑将等距网格尺寸取为0.025mm。
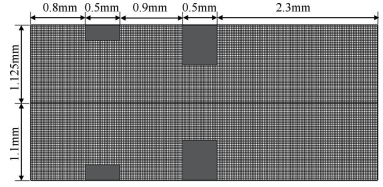
孔间距取经典值lcc = ds + 0.3mm[6],变孔径设计lcc = 2.25mm,原有设计lcc = 2.2mm。因此,将计算区域划分为200×45(变孔径设计)+200×44(原设计)个正交等距网格,如图 5所示。其中,鞘层厚度约为10倍的德拜长度[6],左边界选取至少包含整个等离子体鞘层,文中取0.8mm。加速栅下游到右边界的距离取决于下游离子回流到栅极的有效路径长度[15],文中取2.3mm。
|
Fig. 5 Schematic of mesh generation |
离子光学系统引出束流过程中受放电室内磁场影响很小,可以将其忽略,因此可直接用静电场的Poisson方程来描述离子引出过程
| $ \frac{{{\partial ^2}\phi }}{{{\partial ^2}r}} + \frac{1}{r}\frac{{\partial \phi }}{{\partial r}} + \frac{{{\partial ^2}\phi }}{{{\partial ^2}z}} = - \frac{{e\left( {{n_{\rm{i}}} - {n_{\rm{e}}}} \right)}}{{{\varepsilon _0}}} $ | (5) |
式(5)常见的解法为五点差分格式法[16]求解,解得(j,k)节点处的电势为
| $ \begin{array}{l} {\phi _{j,k}} = \frac{1}{4}\left[ {\left( {1 + \frac{h}{{2r}}} \right){\phi _{j,k + 1}} + \left( {1 - \frac{h}{{2r}}} \right){\phi _{j,\mathit{k} - 1}} + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {{\phi _{j - 1,k}} + {\phi _{j + 1,k}} + {h^2}\frac{{e\left( {{n_{\rm{i}}} - {n_{\rm{e}}}} \right)}}{{{\varepsilon _0}}}} \right] \end{array} $ | (6) |
采用电荷位置权重法将离子所带电荷(忽略双荷离子)分配到离子所在网格内的四个网格节点上,利用该方法对计算域内的所有离子所带电荷进行权重,并对其进行累加,即可得到节点(j,k)处的总离子电荷量Qi,总电荷量除以该节点代表的体积和电子电荷e就可得到该节点位置处的离子密度ni。电子视为服从Boltzmann分布的热流体,电子密度ne为
| $ {n_{\rm{e}}} = {n_{{\rm{e,rp}}}}{\rm{exp}}\left( {\frac{{\phi - {\phi _{{\rm{rp}}}}}}{{{T_{{\rm{e,rp}}}}}}} \right) $ | (7) |
式中ne, rp,ϕrp和Te, rp分别代表参考点离子密度、电势和电子温度,对于加速栅上游区域,参考点为左边界;对于加速栅下游,参考点为右边界。根据该方法计算,下游电势能自洽求出,可以避免人为选取中和面造成的误差[12]。将ni和ne带入式(6)采用SOR迭代法即可求得相应电势ϕj, k,进而可计算出网格节点处的电场强度E = -
数值模拟计算中,不考虑双荷氙离子,离子进入计算区域是通过每个时间步从左边界进入一定数量的离子来实现,当每个时间步中进入离子数目等于右边界和栅极吸收的总离子数相等时,认为该时间步达到稳态。每个时间步从左边界进入计算区域的离子数[17]为
| $ N = {n_{\rm{i}}}{\left( {\frac{{k{T_{\rm{e}}}}}{{{m_{\rm{i}}}}}} \right)^{\frac{1}{2}}}{\rm{exp}}\left( { - \frac{1}{2}} \right){\rm{ \mathsf{ π} }}{\mathit{R}^2}\Delta t $ | (8) |
该时间步进入的离子初始位置在z-r坐标系中可表示为
| $ \begin{array}{l} z = 0\\ r = R\sqrt {rand} \end{array} $ | (9) |
式中rand为0~1之间的随机数,即初始位置为左边界上,径向位置随机分布,总体上保证离子沿径向均匀分布。左边界进入离子初始速度取Bohm速度
| $ {v_0} = \sqrt {\frac{{k{T_{\rm{e}}}}}{{{m_{\rm{i}}}}}} $ | (10) |
离子进入计算区域后,在静电场力F = Ee = midv/dt的作用下加速,离子的位置坐标可表示为
| $ \begin{array}{l} {z_{i + 1}} = {z_i} + \left( {{v_{zi}} + \frac{{{E_{\rm{z}}}e}}{{{m_i}}}\Delta t} \right)\Delta t\\ {r_{i + 1}} = {r_i} + \left( {{v_{ri}} + \frac{{{E_{\rm{r}}}e}}{{{m_i}}}\Delta t} \right)\Delta t \end{array} $ | (11) |
根据式(6)可求出划分网格节点上的轴向、径向电场,文中离子具体位置的电场采用最近邻电场插值法,带入式(11)中即可求出离子位置分布。
离子光学系统引出离子束流过程中,离子除了在静电场作用下的加速运动外,还会与中性原子发生碰撞。文中采用MCC方法来模拟该碰撞过程,在一个时间步Δt内,某离子与所处空间位置上中性原子发生碰撞的概率为
| $ {P_i} = 1 - {\rm{exp}}\left( { - \sigma {n_{\rm{n}}}{v_{\rm{n}}}\Delta t} \right) $ | (12) |
式中nn为中性原子数密度,vn为中性原子速度,σ为碰撞截面。σ与离子和中性原子之间的相对速度Δv相关,采用半经验公式[18]计算
| $ {\sigma ^{\frac{1}{2}}} = - {k_1}{\rm{ln}}\Delta v + {k_2} $ | (13) |
式中k1和k2为常数,k1=0.8821,k2=15.1262。数值计算中随机产生一个0~1的随机数,当该随机数小于Pi时,认为离子与所处位置上的中性原子发生碰撞。
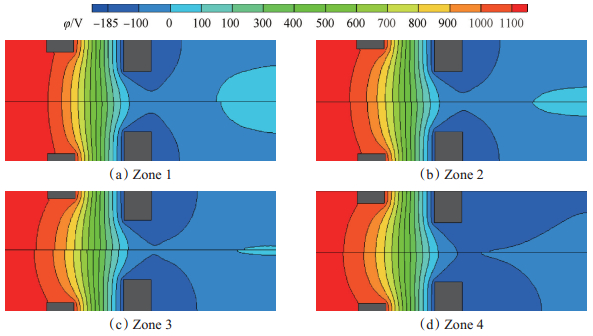
4 计算结果与讨论 4.1 电势分布PIC/MCC数值计算电势分布仿真结果如图 6所示,其中(a)~(d)分别对应分区1~4。从图中可以发现:相对原有栅极,变孔径设计使得电势分布发生了变化,尤其是屏栅上游和加速栅下游区域。其中分区1屏栅下游等势线左移;分区2加速栅上游等势线左移,加速栅下游等势线右移;分区3整个计算区域等势线右移;分区4屏栅上游和加速栅下游等势线右移。分区1和分区2轴向电场强度变小;分区3和分区4轴向电场强度增大。
|
Fig. 6 Potential distribution |
轴线上电势最小值位于加速栅下游附近区域,这个电势通常称之为“鞍点电势”,该电势要明显高于加速栅电位,这是由于离子束的空间电荷效应引起的。同时,该电势直接决定了电子的反流率[19]。鞍点电势结果如表 3所示,现有栅极设计鞍点电势实测值为-86V,模拟计算为-89.4V,符合性较好,证明了模型的正确性。变孔径栅极设计中心区域鞍点电势位置左移,边缘区域右移,鞍点电势绝对值降低1.8V,阻止电子反流能力得到提高。
|
|
Table 3 Result of saddle-point location and potential on-axis |
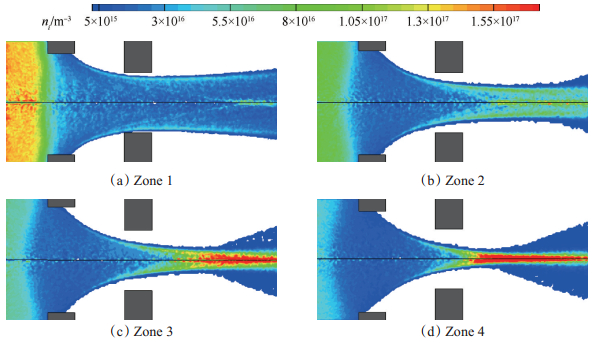
PIC/MCC数值计算离子密度分布仿真结果如图 7所示,其中(a)~(d)分别对应分区1~4。从图中可以发现:相对原有栅极,变孔径设计使得离子密度分布发生了变化,尤其是离子光学聚焦点位置。其中分区1聚焦点左移;分区2聚焦点基本不变;分区3和分区4聚焦点右移。分区1和分区2离子束径变小;分区3和分区4离子束径增大,且发散角变小。离子引出过程未发生过聚焦和欠聚焦现象,这与变孔径设计的初衷相符。
|
Fig. 7 Ion density distribution |
右边界吸收的离子所带电荷累积即为相应的半孔束电流Ihb,统计结果如表 4所示。
|
|
Table 4 Statistical result of half-beamlet current |
对应的束流密度Jb计算公式为
| $ {J_{\rm{b}}} = \frac{{{I_{{\rm{hb}}}}}}{{\frac{{\sqrt 3 }}{4}{l_{{\rm{cc}}}}^2}} $ | (14) |
变孔径设计使得分区1束流密度降低27.8%,分区2降低10.2%,分区3提高15.2%,分区4提高32.9%。束流平直度F,最大推力Tmax[2],屏栅寿命Tsg[20]分别定义为
| $ F = \frac{{{I_{\rm{B}}}}}{{{J_{{\rm{bmax}}}}{\rm{ \mathsf{ π} }}{\mathit{r}_{\rm{b}}}^2}} = \frac{{2{\rm{ \mathsf{ π} }}\int_0^{{r_b}} {{J_{\rm{b}}}r{\rm{d}}\mathit{r}} }}{{{J_{{\rm{bmax}}}}{\rm{ \mathsf{ π} }}{\mathit{r}_{\rm{b}}}^2}} $ | (15) |
| $ {T_{{\rm{max}}}} = \frac{8}{9}{\varepsilon _0}\gamma {T_{\rm{s}}}{A_{\rm{g}}}\sqrt {\frac{{{V_{\rm{s}}}}}{{{V_{\rm{T}}}}}} \frac{{{V_{\rm{T}}}^2}}{{{{\left( {{L_{\rm{g}}} + {t_{\rm{s}}}} \right)}^2} + {d_{\rm{s}}}^2/4}} $ | (16) |
| $ {T_{{\rm{sg}}}} = \frac{{{t_{\rm{s}}}{\varphi _{\rm{i}}}Fe\rho {A_{\rm{b}}}\left( {1 - {\varphi _{\rm{s}}}} \right)\left( {1 + {f_{\rm{d}}}R_ + ^{ + + }} \right)}}{{{I_{\rm{B}}}{m_{\rm{g}}}\left( {1 - {\varphi _i}} \right)\left( {{Y_ + } + \frac{{{f_{\rm{d}}}}}{2}R_ + ^{ + + }{Y_{ + + }}} \right)}} $ | (17) |
尽管变孔径栅极设计使得积分总束流IB降低了5.8%,但是束流平直度由原来的0.41(实测值为0.38)提升至0.57,相应发散角变小,有效束径增加。从计算结果来看,束流降低是由于变孔径设计导致屏栅透明度变化引起的,随之放电损耗增加5.8%,最大推力降低2.8%,电效率降低1.1%;束流平直度的改善,使得屏栅预估寿命提升了40.9%。显然,该方案并没有显著降低离子推力器的主要性能参数,但是栅极离子光学聚焦引出性能和可靠性得到了有效提升,从工程应用角度出发,该变孔径栅极优化设计方案合理可行。
5 结论通过采用PIC/MCC数值方法模拟了10cm发散场离子推力器变孔径栅极方案离子引出特性,与现有设计对比分析了栅极工作特性,获得如下结论:
(1) 本模型计算出10cm离子推力器鞍点电势为-89.4V,束流平直度为0.41,对应试验实测值分别为-86V和0.38,符合性较好,证明了该数值模型的正确性。
(2) 变孔径栅极设计中心区域轴向电场强度变小,边缘区域增大。中心区域鞍点电势位置内移,边缘区域位置外移,鞍点电势绝对值降低1.8V,阻止电子反流能力得到提高,降低电子反流带来的失效风险。
(3) 变孔径栅极设计中心区域离子聚焦点内移,束流密度降低,离子束径变小;边缘区域聚焦点外移,束流密度提高,束径增大,且发散角变小。证明了变孔径优化方案的合理性。
(4) 尽管变孔径设计使得积分总束流降低了5.8%,但是束流平直度由原来的0.41提升至0.57,可有效提高离子推力器的性能和可靠性。
| [1] |
Goebel D M, Katz I. Fundamentals of Electric Propulsion: Ion and Hall Thruster[M]. USA: John Wiley & Sons, Inc., 2008.
(  0) 0) |
| [2] |
陈茂林, 夏广庆, 杨正岩, 等. 离子推力器三栅极系统的3维PIC仿真[J]. 高电压技术, 2014, 40(10): 3012-3017. (  0) 0) |
| [3] |
于达仁, 刘辉, 丁永杰, 等. 空间电推进原理[M]. 哈尔滨: 哈尔滨工业大学出版社, 2014.
(  0) 0) |
| [4] |
Wirz R, Goebel D. Effects of Magnetic Field Topography on Ion Thruster Discharge Performance[J]. Plasma Sources Science and Technology, 2008, 17(3).
(  0) 0) |
| [5] |
郑茂繁, 江豪成. 改善离子推力器束流均匀性的方法[J]. 推进技术, 2011, 32(6): 762-765. (ZHENG Mao-fan, JIANG Hao-cheng. Method of Improving Beam Current Profile for Ion Thruster[J]. Journal of Propulsion Technology, 2011, 32(6): 762-765.)
(  0) 0) |
| [6] |
刘金声. 离子束技术与应用[M]. 北京: 国防工业出版社, 1995.
(  0) 0) |
| [7] |
Wallace N C, Corbett M. Optimisation and Assessment of the Total Impulse Capability of the T6 Ion Thruster[R]. IEPC-2007-231.
(  0) 0) |
| [8] |
ZHONG Lingwei, LIU Yu, WEN Zheng, et al. Numerical Simulation of Ion Extraction Through Ion Thruster Optics[J]. Plasma Science and Technology, 2010, 12(1): 103-108. DOI:10.1088/1009-0630/12/1/22
(  0) 0) |
| [9] |
SUN Anbang, MAO Genwang, YANG Juan, et al. Particle Simulation of Three-Grid ECR Ion Thruster Optics and Erosion Prediction[J]. Plasma Science and Technology, 2010, 12(2): 240-247. DOI:10.1088/1009-0630/12/2/21
(  0) 0) |
| [10] |
Farnell C C. Performance and Lifetime Simulation of Ion Thruster Optics[D]. Colorado: Colorado State University, 2007.
(  0) 0) |
| [11] |
Martinez R A, Buttweiler M S, Williams J D, et al. Evaluation of Sub-Scale NEXIS Ion Optics and Strategies for Performing Accelerated Wear Testing[R]. AIAA 2004-3814.
(  0) 0) |
| [12] |
Kafafy R, Wang J. A HG-IFE-PIC Simulation Model for Ion Thruster Optics Plasma Flow[R]. AIAA 2005-4789.
(  0) 0) |
| [13] |
迈克尔A力伯曼, 阿伦J里登伯格.等离子体放电原理与材料处理[M].蒲以康译.北京: 科学出版社, 2007.
(  0) 0) |
| [14] |
Wang J, Cao Y, Kafafy R, et al. Ion Impingement Limits of Sub-Scale Ion Optics: Comparison of Simulation and Experiment[R]. AIAA 2006-4999.
(  0) 0) |
| [15] |
Miller J S, Pullins S H, Levandier D J, et al. Xenon Charge Exchange Cross Sections for Electrostatic Thruster Models[J]. Journal of Applied Physics, 2002, 91(3): 984-991. DOI:10.1063/1.1426246
(  0) 0) |
| [16] |
李荣华. 偏微分方程数值解法[M]. 北京: 高等教育出版社, 2007.
(  0) 0) |
| [17] |
Okawa Y, Takegahara H, Tachibana T. Numerical Analysis of Ion Beam Extraction Phenomena in an Ion Thruster[R]. IEPC-01-97.
(  0) 0) |
| [18] |
Rapp D, Francis W E. Charge Exchange Between Gaseous Ion and Atoms[J]. Journal of Chemical Physics, 1962, 37(11): 2631-2645. DOI:10.1063/1.1733066
(  0) 0) |
| [19] |
贾艳辉, 张天平, 郑茂繁, 等. 离子推力器栅极系统电子反流阈值的数值分析[J]. 推进技术, 2012, 33(6): 991-996. (JIA Yan-hui, ZHANG Tian-ping, ZHENG Mao-fan, et al. Numerical Analysis for Electron Backstreaming Accelerator Grid Limited Voltage for 20cm Xe Ion Thruster Grid System[J]. Journal of Propulsion Technology, 2012, 33(6): 991-996.)
(  0) 0) |
| [20] |
Brophy J R, Garner C E, Polk J E, et al. The Ion Propulsion System on NASA's Space Technology 4/Champollion Comet Rendezvous Mission[R]. AIAA 99-2856.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

