2. 南京航空航天大学 能源与动力学院 江苏省航空动力系统重点实验室,江苏 南京 210016;
3. 南京航空航天大学 机械结构力学及控制国家重点实验室,江苏 南京 210016
2. Jiangsu Province Key Laboratory of Aerospace Power System, College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;
3. State Key Laboratory of Mechanics and Control Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
不断地提高推重比、降低耗油率已成为航空发动机发展的大势所趋。而提高航空发动机推重比最有效的两种方式是减轻航空发动机结构件重量和增加涡轮前进口温度。目前推重比为12~15的航空发动机正在被加速研制中,其涡轮前进口平均温度已达到1800℃,传统的高温合金材料已经难以满足要求。陶瓷基复合材料(CMCs)具有高比模量、高比强度、耐高温、耐腐蚀等特点,能在高温环境下长时间有效的工作,因此,被广泛用于航空发动机热端防护领域[1~3]。GE将CMCs应用到多个发动机部件中,使得发动机的耐久性得到很大的提升。此外,Rolls-Royce将CMCs应用于高压涡轮叶片以及外罩部件,试验结果显示叶片重量减少了50%[4],发动机的效率得到很大的提升。
了解陶瓷基复合材料的损伤模式是材料结构设计的基础。目前探究陶瓷基复合材料损伤失效的方法有CDM[5~6]和细观力学方法[7~10]。细观力学方法是研究材料内部损伤与宏观力学性能之间的关系的方法,目前逐渐受到广泛的关注。细观力学的难点之一是细观力学参数的确定。细观力学参数主要包含纤维、基体和界面等组分材料的相关参数。目前纳米压痕技术是测量纤维、基体弹性模量的主要方法[11]。然而,由于陶瓷基复合材料内部的不均匀性,纳米压痕技术的测量结果存在很大的分散性。对于界面参数,目前的测量方法有直接法和间接法。直接法有纤维推入、拔出等[12~14]。这些方法对试件和实验设备的要求较高。间接法是根据陶瓷基复合材料的迟滞行为,利用加卸载迟滞环的面积估计界面摩擦力[15~18]。该方法需要标准的迟滞环,而实验结果一般存在偏差。此外,该方法没有考虑卸载过程存在的裂纹闭合等现象[19],界面参数识别结果的准确性有待评估。因此,陶瓷基复合材料细观力学参数的确定需要进一步的探究。
CMCs在单向加载过程中,当加载应力小于基体初始开裂应力,材料的应力应变曲线表现为线性特征。随着载荷的继续增加,材料发生基体开裂、界面脱粘、界面滑移等损伤模式,应力应变曲线表现出非线性特征[20]。当加载应力大于界面完全滑移对应的应力,随着载荷的继续增加,只有纤维继续承载。因此,材料的应力应变曲线出现第二个线段性。CMCs拉伸曲线包含细观力学参数的信息。因此,可以通过拉伸实验曲线确定材料的细观力学参数,其典型的拉伸曲线如图 1所示。
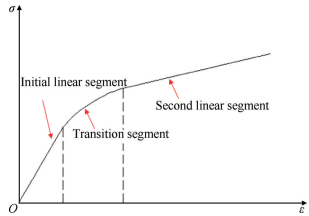
|
Fig. 1 Typical tensile curve of CMCs |
剪滞模型[21]可用于描述单向材料基体开裂以及纤维沿基体滑动等细观力学行为。因此,本文基于剪滞模型建立陶瓷基复合材料轴向拉伸过程中宏观应力应变行为与细观力学参数之间的关系。并对SiC/SiC单向陶瓷基复合材料进行单向拉伸实验,得到材料的拉伸实验曲线。将剪滞模型与实验曲线结合,进行细观力学参数的识别。具体步骤如下:首先利用实验曲线第二线性段的信息识别纤维弹性模量和界面摩擦力。然后通过实验曲线初始线性段的信息识别基体弹性模量。其次利用实验曲线的非线性段的信息确定基体开裂参数。最后将识别的细观力学参数带入剪滞模型,预测材料的拉伸应力应变曲线,并与实验结果进行比较。
2 实验材料及方法本文使用的SiC/SiC单向陶瓷基复合材料是由中科院金属研究所提供。采用电子拉伸实验机(WDW-100)对单向陶瓷基复合材料进行单向拉伸实验,直至材料最终断裂失效。电子引伸计(YYU-5/25)用来测量单向陶瓷基复合材料的应变。实验装置如图 2所示。

|
Fig. 2 Equipment of uniaxial tensile experiment of UD-CMCs of SiC/SiC |
不同加载应力下的裂纹分布可通过裂纹实时监测技术得到。实验设备由显微镜和加载装置组成,如图所示3所示。

|
Fig. 3 Equipment of real-time crack detection experiment |
本文采用包含单个纤维束和基体的陶瓷基复合材料进行实验和理论研究。该材料是单向陶瓷基复合材料的一种。由于其结构比较简单,因此便于理论研究。本文采用剪滞模型模拟单向陶瓷基复合材料单向拉伸过程,并提出如下假设:材料加载过程中,不考虑纤维失效。
基于剪滞模型,建立理论应力应变与细观参数之间函数关系。
3.1 初始线性段当加载应力小于基体初始开裂应力,材料内部不存在微观损伤。因此,CMCs的应力应变曲线表现为线性特征。材料的应变可表示为
| $ \varepsilon = \frac{\sigma }{{{E_{\rm{c}}}}} $ | (1) |
其中Ec为复合材料等效弹性模量,即为拉伸曲线的初始斜率。Ec的理论表达式可用混合率公式表示为如下形式
| $ {E_{\rm{c}}} = {E_{\rm{f}}}{v_{\rm{f}}} + {E_{\rm{m}}}{v_{\rm{m}}} $ | (2) |
式中Ef,Em分别表示纤维、基体的弹性模量,vf,vm分别表示纤维、基体的体积分数。若纤维弹性模量已知,则基体等效弹性模量可通过式(2)确定。
3.2 中间过渡段当加载应力大于基体初始开裂应力,材料发生基体开裂、界面脱粘和界面滑移等损伤行为。材料的应力应变曲线表现为非线性特征。基于剪滞模型,界面区域可分为脱粘区域和粘结区域,如图 4所示。则纤维沿x轴的应力分布如公(3)所示。
| $ {\sigma _{\rm{f}}} = \left\{ \begin{array}{l} \frac{\sigma }{{b{v_{\rm{f}}}}}-{\rm{tan}}{\theta _x}, \;\;\;x \in \left( {\left. {0, d} \right]} \right.\\ {\sigma _{{\rm{f0}}}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x \in \left( {\left. {d, L/2} \right]} \right. \end{array} \right. $ | (3) |
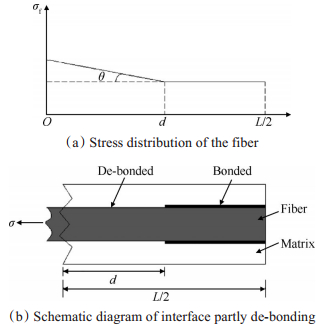
|
Fig. 4 Interface partly de-bonding under uniaxial tension |
其中
| $ \varepsilon = \int_0^{L/2} {\frac{{{\sigma _{\rm{f}}}{\rm{d}}\mathit{x}}}{{{E_{\rm{f}}}\left( {L/2} \right)}} + {\varepsilon _{{\rm{th}}}}} $ | (4) |
式中εth为热残余应变。
当加载应力大于基体开裂应力,随着应力的增加,新的裂纹在已产生的裂纹之间产生。对于脆性失效的材料,基体缺陷可采用Weibull分布模型描述[22, 23],则任意加载应力下基体裂纹平均间距为
| $ L = {L_{{\rm{sat}}}}/\left[{1-{\rm{exp}}\left( {-{{\left( {\frac{\sigma }{{{b_0}}}} \right)}^m}} \right)} \right] $ | (5) |
式中m, b0分别表示Weibull模量和Weibull基体开裂特征强度。通过对实验曲线过渡段的拟合可以确定m, b0的数值。Lsat为饱和裂纹间距,可通过实验观察得到。
3.3 第二线性段当加载应力大于界面完全滑移对应的应力时,界面完全滑移。纤维应力沿x轴分布如图 5所示,其表达式为
| $ {\sigma _{\rm{f}}} = \frac{\sigma }{{{v_{\rm{f}}}}}-{\rm{tan}}\theta \mathit{x, }\;\;\;\mathit{x} \in \left( {\left. {0, L/2} \right]} \right. $ | (6) |
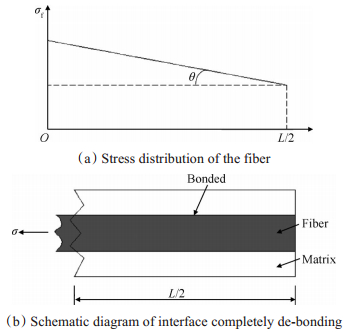
|
Fig. 5 Interface completely de-bonding under uniaxial tension |
材料的应变可表示为
| $ \varepsilon = \int_0^{L/2} {\frac{{{\sigma _{\rm{f}}}{\rm{d}}\mathit{x}}}{{{E_{\rm{f}}}\left( {L/2} \right)}} = \frac{{\frac{\sigma }{{{v_{\rm{f}}}}}-\frac{1}{2}{{\left( {\frac{L}{2}} \right)}^2}{\rm{tan}}\theta }}{{{E_{\rm{f}}}\frac{L}{2}}}} + {\varepsilon _{{\rm{th}}}} $ | (7) |
将式(7)进行适当变化,如式(8)所示
| $ \sigma = {E_{\rm{f}}}{v_{\rm{f}}}\varepsilon + {E_{\rm{f}}}{v_f}\left( {\frac{{L{\rm{tan}}\theta }}{{4{E_{\rm{f}}}}}-{\varepsilon _{{\rm{th}}}}} \right) $ | (8) |
从式(8)可以看出,第二阶段的应力与应变成线性关系,其斜率和截距的表达式分别为Efvf和
基于单向陶瓷基复合材料单向拉伸实验曲线的参数识别流程图如图 6所示。
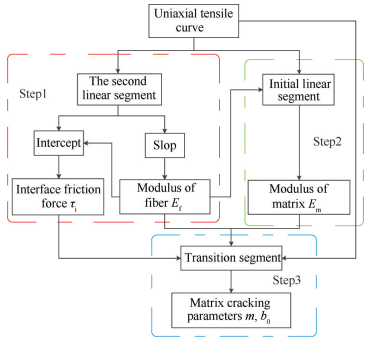
|
Fig. 6 Flowchart of parameter identification based on tensile curve of UD-CMCs |
参数识别的具体步骤:首先获得单向陶瓷基复合材料的轴向拉伸实验曲线。然后,计算实验曲线第二个线性段的斜率和截距。将第二个线性段斜率的理论值与实验值进行比较,识别出纤维弹性模量,并将其带入第二个线性段的截距表达式。将第二个线性段截距的理论值与实验值进行比较,识别出界面摩擦力。其次,计算实验曲线初始线性段的斜率。将识别的纤维弹性模量带入初始线性段斜率的表达式中,并将理论值与实验值进行比较,识别出基体弹性模量。最后,将已经识别的细观力学参数带入剪滞模型。对过渡段实验曲线进行拟合来确定基体Weibull参数和Weibull基体开裂特征强度。
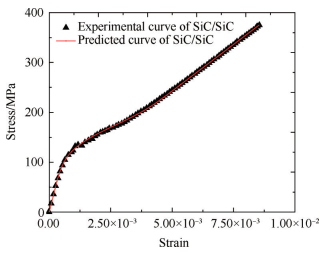
4 结果与讨论 4.1 实验结果SiC/SiC单向陶瓷基复合材料轴向拉伸实验曲线如图 7所示。将拉伸实验曲线带入图 6的参数识别流程图中进行材料细观力学参数的识别。细观力学参数的识别结果如表 1所示。将表 1中的参数带入剪滞模型,则单向陶瓷基复合材料拉伸应力应变预测曲线如图 7所示。从图 7中可以发现,预测结果与实验吻合很好,说明本文细观力学参数的识别方法是可行的。
|
Fig. 7 Comparison between the predicted stress-strain curve and tensile experimental curve of UD-CMCs of SiC/SiC |
|
|
Table 1 Identified results of micromechanical parameters of UD-CMCs of SiC/SiC |
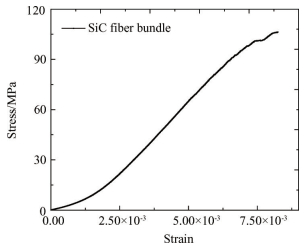
采用另一种方法测量纤维弹性模量,即将纤维束弹性模量等效为纤维弹性模量。纤维束弹性模量采用如下方法确定:采用电子拉伸实验机(WDW-100)对纤维束进行单向拉伸实验,实验装置如图 8所示。并获得纤维束轴向拉伸实验曲线,如图 9所示。对实验曲线的线性段进行拟合确定纤维束弹性模量。该方法测量的纤维弹性模量为Ef=170.0GPa,与基于本文识别方法确定的纤维弹性模量进行比较。两种方法测量结果偏差小于5%,说明本文提出的纤维弹性模量的识别方法是可行的。

|
Fig. 8 Equipment of tensile experiment of the fiber bundle |
|
Fig. 9 Tensile experimental curve of the fiber bundle |
基于单向陶瓷基复合材料轴向拉伸曲线,本文提出材料细观力学参数的识别方法,并得出以下结论:
(1) 典型的单向SiC/SiC陶瓷基复合材料轴向拉伸曲线存在两个明显的线性段。第一个线性段对应材料没有发生微观损伤,第二个线性段对应纤维/基体界面完全滑移。
(2) 基于本文方法识别的细观力学参数有纤维和基体弹性模量、界面摩擦力和基体开裂参数。将识别的细观力学参数带入剪滞模型,并预测材料的拉伸应力应变曲线。预测结果与实验吻合很好,说明本文提出的方法是合理的。
(3) 采用纤维束拉伸实验测量纤维的弹性模量,并将测量结果与基于本文方法的识别结果进行对比。两种方法测量结果偏差小于5%。
| [1] |
李志永, 郑日恒, 李立翰, 等. 冲压发动机C/SiC喷管承压失效研究[J]. 推进技术, 2013, 34(4): 545-550. (LI Zhi-yong, ZHENG Ri-heng, LI Li-han, et al. Investigation on Pressure Failure of C/SiC Nozzle in Ramjet[J]. Journal of Propulsion Technology, 2013, 34(4): 545-550.)
(  0) 0) |
| [2] |
张杰, 魏鑫, 郑力铭, 等. C/SiC复合材料在空气中的氧化烧蚀[J]. 推进技术, 2008, 29(4): 488-493. (ZHANG Jie, WEI Xin, ZHENG Li-ming, et al. Oxidation and Ablation of C/SiC Composites in Air[J]. Journal of Propulsion Technology, 2008, 29(4): 488-493. DOI:10.3321/j.issn:1001-4055.2008.04.019)
(  0) 0) |
| [3] |
邱海鹏, 陈明伟, 谢巍杰. SiC/SiC陶瓷基复合材料研究及应用[J]. 航空制造技术, 2015, 483(14): 94-97. (  0) 0) |
| [4] |
Sun Z, Shao H, Chen X, et al. Analysis of Residual Performance of UD-CMC in Oxidation Atmosphere Based on a Notch-Like Oxidation Model[J]. Applied Composite Materials, 2016, 23(5): 1079-1098. DOI:10.1007/s10443-016-9500-9
(  0) 0) |
| [5] |
Gao X, Li L, Song Y. A temperature-Dependent Constitutive Model for Fiber-Reinforced Ceramic Matrix Composites and Structural Stress Analysis[J]. International Journal of Damage Mechanics, 2014, 23(4): 507-522. DOI:10.1177/1056789513500296
(  0) 0) |
| [6] |
Iannucci L. Progressive Failure Modelling of Woven Carbon Composite under Impact[J]. International Journal of Impact Engineering, 2006, 32(6): 1013-1043. DOI:10.1016/j.ijimpeng.2004.08.006
(  0) 0) |
| [7] |
Pailler F, Lamon J. Micromechanics Based Model of Fatigue Oxidation for Ceramic Matrix Composites[J]. Composites Science & Technology, 2005, 65(3): 369-374.
(  0) 0) |
| [8] |
Min J B, Xue D, Shi Y. Micromechanics Modeling for Fatigue Damage Analysis Designed for Fabric Reinforced Ceramic Matrix Composites[J]. Composite Structures, 2014, 111(1): 213-223.
(  0) 0) |
| [9] |
Allen D H, Foulk J W, Helms K, et al. A Model for Predicting the Effect of Environmental Degradation on Damage Evolution of Metal-Matrix Composites[J]. Astm Special Technical Publication, 1997(1315): 17.
(  0) 0) |
| [10] |
Poh L, Della C, Ying S, et al. Micromechanics Model for Predicting Effective Elastic Moduli of Porous Ceramic Matrices with Randomly Oriented Carbon Nanotube Reinforcements[J]. Aip Advances, 2015, 2(9): 38.
(  0) 0) |
| [11] |
Zhao S, Zhou X, Yu J. Effect of Heat Ttreatment on the Mechanical Properties of PIP–SiC/SiC Composites Fabricated with a Consolidation Process[J]. Ceramics International, 2014, 40(3): 3879-3885. DOI:10.1016/j.ceramint.2013.08.029
(  0) 0) |
| [12] |
Sahin M, etinarslan C S, Akata H E. Effect of Surface Roughness on Friction Coefficients During Upsetting Processes for Different Materials[J]. Materials & Design, 2007, 28(2): 633-640.
(  0) 0) |
| [13] |
Kuntz M, Grathwohl G. Advanced Evaluation of Push-In Data for the Assessment of Fiber Reinforced Ceramic Matrix Composites[J]. Advanced Engineering Materials, 2001, 3(6): 371-379. DOI:10.1002/(ISSN)1527-2648
(  0) 0) |
| [14] |
Chandra N, Ghonem H. Interfacial Mechanics of Push-Out Tests: Theory and Experiments[J]. Composites Part A, 2001, 32(3-4): 575-584. DOI:10.1016/S1359-835X(00)00051-8
(  0) 0) |
| [15] |
Solti J P, Mall S, Robertson D D. Modeling Damage in Unidirectional Ceramic-Matrix Composites[J]. Composites Science & Technology, 1995, 54(1): 55-66.
(  0) 0) |
| [16] |
Fantozzi G, Reynaud P. Mechanical Hysteresis in Ceramic Matrix Composites[J]. Materials Science & Engineering A, 2009, 521–522(10): 18-23.
(  0) 0) |
| [17] |
Li L, Song Y, Sun Y. Estimate Interface Shear Stress of Unidirectional C/SiC Ceramic Matrix Composites from Hysteresis Loops[J]. Applied Composite Materials, 2013, 20(4): 693-707. DOI:10.1007/s10443-012-9297-0
(  0) 0) |
| [18] |
Li L, Song Y. Estimate Interface Frictional Coefficient of Ceramic Matrix Composites from Hysteresis Loops[J]. Journal of Composite Materials, 2011, 45(9): 989-1006. DOI:10.1177/0021998310381437
(  0) 0) |
| [19] |
Zhang S, Gao X, Dong H, et al. Effects of Gradual Matrix Crack Closure on the Constitutive Behavior of SiC/SiC Composites Upon Unloading[J]. Ceramics International, 2016, 43(2): 1839-1842.
(  0) 0) |
| [20] |
Aveston J. Single and Multiple Fracture[J]. Properties of Fiber Composites, 1971(1).
(  0) 0) |
| [21] |
Zhang S, Gao X, Chen J, et al. Strength Model of the Matrix Element in SiC/SiC Composites[J]. Materials & Design, 2016, 101: 66-71.
(  0) 0) |
| [22] |
Lissart N, Lamon J. Damage and Failure in Ceramic Matrix Minicomposites: Experimental Study and Model[J]. Acta Materialia, 1997, 45(3): 1025-1044. DOI:10.1016/S1359-6454(96)00224-8
(  0) 0) |
| [23] |
Chateau C, Gélébart L, Bornert M, et al. Modeling of Damage in Unidirectional Ceramic Matrix Composites and Multi-Scale Experimental Validation on Third Generation SiC/SiC Minicomposites[J]. Journal of the Mechanics & Physics of Solids, 2014, 63(1): 298-319.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


