随着实验测量技术的发展,人们对航空发动机内部复杂流动的认识经历了从一维到三维,从无粘到有粘,从定常到非定常的过程,相应地航空发动机的设计体系也从最初的一维体系发展到了现如今较为成熟的三维定常设计体系,目前进一步向全三维非定常阶段发展。因此,对相应的内部流场的精细化测量提出了越来越高的要求。目前,常见的流场测试手段,如皮托管、PIV以及LDV等,存在着诸如干扰流场、测试精度不够、近壁区域反光难以测量、数据处理困难等问题。相较而言,热线风速仪对被测流场干扰小,空间分辨率高,响应时间短,在流动测量中得到广泛应用,特别是用于测量湍流和低流速场合[1]。但是由于标定设备的限制,目前热线风速仪仅适用于常温下的流场测试,而在高温、高压等非标定工况下则会出现较大误差,严重限制了其广泛应用。
热线风速仪的基本测速原理是根据King公式[2],将通过探头中热丝的电流Iw与流体速度U建立起一一对应的关系,通过测量电流Iw而实现流速的测量。
热线风速仪依其工作方式可分为恒流、恒温两种类型,本文以恒温型热线风速仪单丝热线为例,热线温度Iw即热线电阻Rw保持恒定。热线风速仪在使用前均需进行标定,目前,标准标定设备仅限于常温、常压工况,当待测流场的温度、压力与常温、常压存在较大差异时,将会导致极大的测试误差。从King公式中可以看出,影响Iw与U对应关系的两个因素分别为流体热线之间的温度差以及流体物性参数。温度、压力变化所导致的流体物性参数变化会使得上述所建立的Iw与U函数关系发生重大改变,进而引起测试结果的极大误差。
鉴于此,目前对于热线风速仪非标定工况下应用的修正方法主要有两种,一种是只考虑流体与热线之间的温差变化的修正方法。
Bearman[3]根据对King公式中常数系数随温度变化的分析,在不考虑物性参数变化的情况下,提出了针对不可压流体的温度修正函数关系式。实验表明,这种修正方法在温度变化小于10℃的情况下较为准确,温度变化较大时误差仍然较大。
文献[4, 5]根据对强迫对流的分析,在不考虑物性参数变化的情况下,提出了温度修正函数关系式。该公式受到了广泛的认可,并被应用于X探头的矫正以及湍流的测量[6, 7]。但Kostka等[8]进行了实验验证,结果表明,使用该公式进行的修正误差仍然较大。
Bearman和Bremhorst提出的温度修正公式都是只考虑了流体与热线之间温度差的变化,通过实验皆证明了其不能较好地修正流体温度变化对输出电压的影响。
Abdel-Rahman等[9]通过分析由温度引起的物性参数变化导致努赛尔数变化的程度,讨论了物性参数变化对换热结果的影响,说明物性参数变化对输出信号的影响较大,忽略物性参数变化影响是不合理的。
第二种修正方法是同时考虑了物性参数变化的影响。
据此,邓康耀[10]通过确定零流速时热线风速仪输出电压,提出了一种温度修正函数关系式。经实验证明,这种修正方法同样是在温度变化较小的情况下较为准确。究其原因,该公式虽然考虑了流体热线之间的温度差以及物性变化引起的误差,但并没有考虑其引起的强迫对流误差,因此温度变化较大时修正误差较大。
梁雄耀[11]通过对强迫对流以及支架导热的分析,结合支架温度的经验公式,在考虑物性参数变化的情况下,提出了修正函数关系式。该修正方法虽然考虑了物性变化的影响,相对第一种方法在高温时使得修正精度有所提升,但由于忽略了自然对流和辐射换热的影响,并且支架导热的半经验公式引入也会导致一定误差,因此总体而言高温时的修正精度并不理想。
张万路[12]通过对强迫对流的分析,在考虑物性参数变化的情况下,提出了温度修正函数关系式。张万路在对公式的推导中,采用的是在相同输出电流下,修正不同温度流体的速度值,其基本修正思路是采用比例修正的方法。由于是用不同流速下的强迫对流换热量对比,而忽略了不同流速下自然对流、辐射换热和支架导热等变化引起的强迫对流换热量占比变化的影响,且并未考虑压力变化对测试的影响,因此尚存在一定误差。
近几年,虽然热线风速仪被广泛应用在航空、低温、风洞流场、微风速等测量领域,但非标定工况下的修正方法并无太大进展,相关研究多集中在对标定方法的数学模型以及实验设备的改进上。其中在航空设备上,对于换热的研究比较充分[13, 14],但是对于流动的研究较少,并且大部分都是采用恒温、恒压或者不进行修正的方法进行测试、分析[15~17]。在高、低温测量领域则采用设计精确温度控制设备来进行标定[18~21]。在风洞流场和微风速测量方面,则采用设计高精度实验装置,通过改良数学模型结合实际标定的方式进行测试分析[22~27]。但造价昂贵的标定设备,加之极为繁琐的标定过程,耗费较多物力及时间,严重限制了其应用。
综上所述,对热线风速仪非标定工况下应用的修正方法目前多侧重于温度影响因素的单一修正,即仅限于热丝和流体间温度差变化修正或者仅考虑对热丝强迫对流影响的比例修正,而忽略了流体物性参数变化、热丝自然对流、辐射换热、支架导热等综合因素影响,同时对于对物性参数有着重要影响的压力条件尚缺乏考虑。基于此,本文在考虑流体物性参数变化的基础上,综合分析了热丝强迫对流、自然对流、辐射换热、支架导热等影响因素,结合压力条件的影响,建立了非标定工况下热线风速仪应用的温度、压力综合修正方法,并给出了修正关系式。
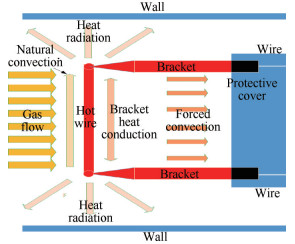
2 修正关系式的推导 2.1 热力学模型依据传热学原理,热线风速仪探头的热丝与流体之间主要存在四种换热形式,分别为强迫对流、自然对流、辐射换热以及与支架间的导热,如图 1所示。
|
Fig. 1 Four types of heat transfer |
依据能量守恒及传热分析,建立其总体能量方程
| ${E^2}/{R_{\rm{w}}} = {Q_{{\rm{fc}}}} + {Q_{\rm{n}}} + {Q_{\rm{r}}} + {Q_{\rm{c}}} $ | (1) |
式中Qfc为强迫对流换热量,Qn为自然对流换热量,Qr为热辐射换热量,Qc为支架导热换热量,E为热丝电压,Rw为热丝电阻。针对四种换热形式,下面将分别开展分析。
(1)强迫对流:依据希尔帕特公式[28],结合努赛尔数定义[29]以及牛顿冷却公式,可得探头热丝强迫对流换热量为
| ${Q_{{\rm{fc}}}} = \frac{{CR{e^n}P{r^{1/3}}\cdot\mathit{\lambda }}}{d} \cdot S \cdot \left( {{T_{\rm{w}}} - {T_{\rm{f}}}} \right) $ | (2) |
式中Re为雷诺数,Pr为普朗特数,λ为气体导热系数,S为热线表面积,d为热丝直径,Tf为来流温度,C,n为与雷诺数有关的常数系数。
当被测流体实际工况与热线标定工况不同时,将其强迫对流换热量作比可得
| $\begin{array}{*{20}{l}} {\frac{{{Q_{{\rm{fc}}2}}}}{{{Q_{{\rm{fc}}1}}}} = \frac{{{C_2}}}{{{C_1}}}{{\left( {U \cdot d} \right)}^{n - m}}\cdot{\upsilon _1}^m\cdot{\upsilon _2}^{ - n}\cdot}\\ {\;\;\;\;\;\;\;\;\;\;{{\left( {\frac{{P{r_2}}}{{P{r_1}}}} \right)}^{1/3}}\cdot\left( {\frac{{{\lambda _2}}}{{{\lambda _1}}}} \right)\cdot\left( {\frac{{{T_{\rm{w}}} - {T_{{\rm{f}}2}}}}{{{T_{\rm{w}}} - {T_{{\rm{f}}1}}}}} \right)} \end{array} $ | (3) |
式中n,m为与雷诺数有关的常数系数,n为实际条件下常数系数,m为标定条件下常数系数,下标1为标定条件下参数;2为实测条件下参数。
式中运动粘度υ,普朗特数Pr,导热系数λ等各参数均为温度的函数,在标准大气条件下皆可通过查表获得,非标准大气条件下可经过相应公式换算获得[30],定性温度取平均温度
(2)自然对流:由于篇幅所限,本文以竖放热丝模型为例,热丝横放时只是换热表达式不同[29],并不影响最终结果。
依据Muller公式[31],结合努赛尔数定义以及牛顿冷却公式,可得探头热丝自然对流换热量为
| ${Q_{\rm{n}}} = \frac{{{{(G{r_{\rm{d}}}\cdot Pr)}^{0.11}}\cdot\lambda }}{L}\cdot S\cdot\left( {{T_{\rm{w}}} - {T_{\rm{f}}}} \right) $ | (4) |
式中Grd为格拉晓夫数,L为热丝长度。
(3)辐射换热:依据内包物体的辐射传热公式,由于外界表面积远远大于热丝表面积,钨丝可视为黑体,黑度ε取1,所以本文采用的内包物体辐射换热公式可简化为
| ${Q_{\rm{r}}} = S\cdot\sigma \cdot\left( {{T_{\rm{w}}}^4 - {T_{\rm{f}}}^4} \right) $ | (5) |
式中σ为黑体辐射常数。
(4)支架导热:依据傅里叶定律导热公式,热丝横截面温度分布均匀条件下的导热可表示为
| ${Q_{\rm{c}}} = \frac{{{\rm{ \mathit{ π} }}\cdot{d^2}}}{2}\cdot{\lambda _{\rm{w}}}\cdot\left( {\frac{{{\rm{d}}T}}{{{\rm{d}}x}}} \right) $ | (6) |
以热丝为研究对象,其沿轴向自中心向一端与支架交点处的轴向导热为
| ${Q_{{\rm{E}}1}} = {\lambda _{\rm{w}}}\cdot{S_{\rm{w}}}\cdot\frac{{{T_{\rm{w}}} - T}}{{L/2}} $ | (7) |
式中T为热丝与支架交点处温度,Sw为热丝横截面面积,λw为热丝导热系数。
以热丝支架为研究对象,其沿轴向自与热丝交点至支架根部的导热为
| ${Q_{{\rm{E}}2}} = {\lambda _{\rm{s}}}\cdot{S_{\rm{s}}}\cdot\frac{{T - {T_{\rm{f}}}}}{{{L_{\rm{s}}}}} $ | (8) |
式中Ss为支架横截面面积,λs为支架导热系数,Ls为支架长度。
可认为QE1=QE2,将上述两个公式联立,得
| ${\lambda _{\rm{w}}}\cdot{S_{\rm{w}}}\cdot\frac{{{T_{\rm{w}}} - T}}{{L/2}} = {\lambda _{\rm{s}}}\cdot{S_{\rm{s}}}\cdot\frac{{T - {T_{\rm{f}}}}}{{{L_{\rm{s}}}}} $ | (9) |
依据该公式,可求得热丝与支架交点处温度T,进而求得支架导热量Qc。以热丝温度Tw=523K,来流温度Tf=283K,293K,303K,313K,323K,333K为例,计算求得热丝与支架交点处温度如表 1所示。其与来流温度差在4K左右,与梁雄耀的实验研究结果[11]相一致,表明该分析为合理的。
|
|
Table 1 Temperature at the intersection of the hot wire and the bracket(K) |
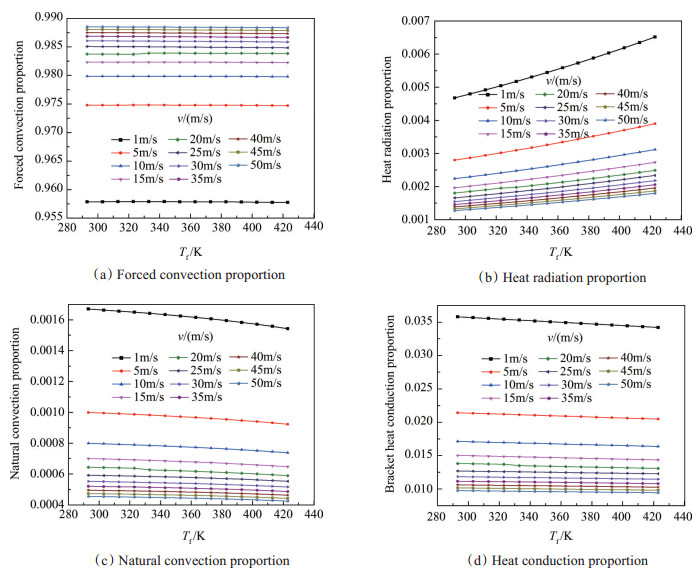
基于上述换热分析,计算了标准大气压下相同热丝表面温度、不同流速下,热丝与流体之间四种换热形式换热量占总换热量的比值随来流温度的变化情况,如图 2所示。从中可以看出:
|
Fig. 2 Proportion of heat transfer changes with temperatures |
(1)相同工况下,热丝的换热以强迫对流为主,其占总换热量的比例在95%~99%,该比例随着速度的增大而增大。
(2)相同来流速度下,来流温度的变化对强迫对流换热量的占比几乎不产生影响,即不同的来流温度下,热丝总换热量的比值与其强迫对流换热量的比值基本相等,误差小于0.02%。
基于上述规律,本文建立了热线风速仪在非标定工况下应用的温度修正方法。具体步骤如下
| $\frac{{{E_2}^2/{R_{\rm{W}}}}}{{{E_1}^2/{R_{\rm{W}}}}} = \frac{{{Q_{{\rm{fc}}2}}}}{{{Q_{{\rm{fc}}1}}}} $ | (10) |
将公式(3)代入公式(10)可得热线风速仪的温度修正公式
| $\begin{array}{*{20}{l}} {\frac{{{E_2}^2}}{{{E_1}^2}} = \frac{{{C_2}}}{{{C_1}}}{{\left( {U\cdot d} \right)}^{n - m}}\cdot{\upsilon _1}^m\cdot{\upsilon _2}^{ - n}\cdot}\\ {\;\;\;\;\;\;\;\;\;\;{{\left( {\frac{{P{r_2}}}{{P{r_1}}}} \right)}^{1/3}}\cdot\left( {\frac{{{\lambda _2}}}{{{\lambda _1}}}} \right)\cdot\left( {\frac{{{T_{\rm{w}}} - {T_{{\rm{f}}2}}}}{{{T_{\rm{w}}} - {T_{{\rm{f}}1}}}}} \right)} \end{array} $ | (11) |
Kays William等推荐的空气物性参数随温度变化的关系式[30]如下
| $\frac{{P{r_2}}}{{P{r_1}}} = 1, \frac{{{\lambda _2}}}{{{\lambda _1}}} = {\left( {\frac{{{T_2}}}{{{T_1}}}} \right)^{0.85}}, \frac{{{\upsilon _2}}}{{{\upsilon _1}}} = {\left( {\frac{{{T_2}}}{{{T_1}}}} \right)^{1.7}} $ | (12) |
空气温度取定性温度则
| $\frac{{P{r_2}}}{{P{r_1}}} = 1, \frac{{{\lambda _2}}}{{{\lambda _1}}} = {\left( {\frac{{{T_{\rm{w}}} + {T_{{\rm{f}}2}}}}{{{T_{\rm{w}}} + {T_{{\rm{f}}1}}}}} \right)^{0.85}}, \frac{{{\upsilon _2}}}{{{\upsilon _1}}} = {\left( {\frac{{{T_{\rm{w}}} + {T_{{\rm{f}}2}}}}{{{T_{\rm{w}}} + {T_{{\rm{f}}1}}}}} \right)^{1.7}} $ | (13) |
将公式(13)代入(11),整理后可得热线风速仪非标定工况下应用时的温度修正关系式,如下所示
| $\frac{{{E_2}^2}}{{{E_1}^2}} = {\left( {\frac{{{T_{\rm{w}}} + {T_{{\rm{f}}2}}}}{{{T_{\rm{w}}} + {T_{{\rm{f}}1}}}}} \right)^{ - 1.7n}}\cdot{\left( {\frac{{{T_{\rm{w}}} + {T_{{\rm{f}}2}}}}{{{T_{\rm{w}}} + {T_{{\rm{f}}1}}}}} \right)^{0.85}}\cdot\left( {\frac{{{T_{\rm{w}}} - {T_{{\rm{f}}2}}}}{{{T_{\rm{w}}} - {T_{{\rm{f}}1}}}}} \right) $ | (14) |
至此完成了综合考虑物性变化以及强迫对流、自然对流、辐射换热、支架导热等因素的非标定工况应用温度修正。具体应用时:固定来流速度U以及热丝温度Tw,通过标定温度Tf1,对应的热丝两端电压E1以及待测来流温度Tf2,依据式(14)可求得待测来流温度为Tf2时对应的热丝两端电压E2;改变来流速度,通过多组计算建立新的即修正后的U-E2曲线。与以往温度修正方法不同的是,在综合考虑自然对流、辐射换热、支架导热等影响后发现,不同来流速度下的强迫对流占比是不同的,因此通过固定速度修正电压的方法要更为合理。
2.3 压力影响修正文献[22, 23, 27]对恒温型热线风速仪测量可压缩流体的校准方法进行了研究。在热线风速仪的实际应用中尤其是进行高速流体测试时,压力对热线风速仪输出信号的影响较为突出。究其原因,压力变化会导致流体粘度变化,从而影响热线风速仪的输出信号。因此对热线风速仪进行压力修正是十分必要的。
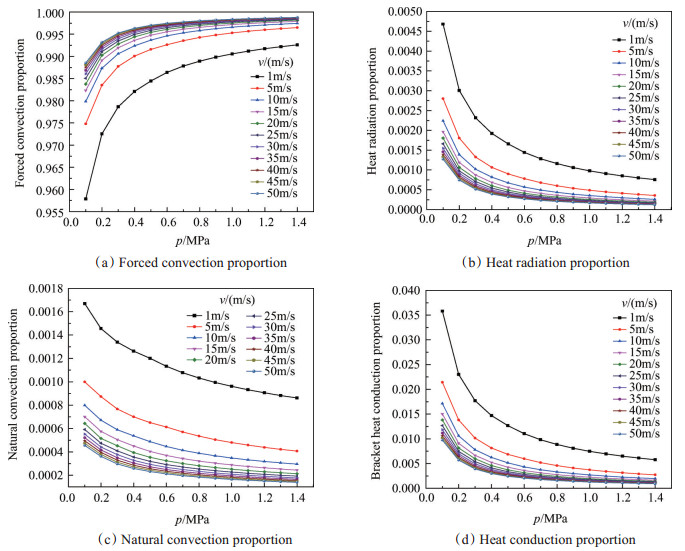
基于换热分析,计算了常温、相同热丝表面温度条件下,热丝与流体之间四种换热形式换热量占总换热量的比值随来流压力的变化情况,如图 3所示。从中可以看出:
|
Fig. 3 Proportion of heat transfer changes with pressures |
(1)相同工况下,热丝的换热同样以强迫对流为主导,其占总换热量的比例一般在95%以上,该比例随着速度的增大而增大。
(2)相同来流速度下,来流压力的变化会对强迫对流换热量的占比产生较大影响,即不同压力下,热丝总换热量的比值与其强迫对流换热量的比值不相等,误差可达3%以上。
基于上述规律,本文建立了热线风速仪在非标定工况下应用的压力修正方法,该方法为需要确定修正系数ξ的比例修正方法。具体步骤如下:
根据热丝与流体间强迫对流与总换热量之间关系可得以下等式
| $\frac{{{Q_{{\rm{fc}}2}}}}{{{Q_{{\rm{fc}}1}}}} = \frac{{{\xi _2}\cdot{E_2}^2/{R_{\rm{w}}}}}{{{\xi _1}\cdot{E_1}^2/{R_{\rm{w}}}}} $ | (15) |
| $\frac{{{E_2}^2}}{{{E_1}^2}} = \frac{{{\xi _1}\cdot{Q_{{\rm{fc}}2}}}}{{{\xi _2}\cdot{Q_{{\rm{fc}}1}}}} = \xi \cdot\frac{{{Q_{{\rm{fc}}2}}}}{{{Q_{{\rm{fc}}1}}}} $ | (16) |
定义修正系数
| $\xi = \frac{{{Q_{{\rm{fc}}1}}/\left( {{Q_{{\rm{fc}}1}} + {Q_{{\rm{n}}1}} + {Q_{{\rm{r}}1}} + {Q_{{\rm{c}}1}}} \right)}}{{{Q_{{\rm{fc}}2}}/\left( {{Q_{{\rm{fc}}2}} + {Q_{{\rm{n}}2}} + {Q_{{\rm{r}}2}} + {Q_{{\rm{c}}2}}} \right)}} $ | (17) |
式中ξ1,ξ2分别为标定条件和实际条件下热丝的强迫对流换热量占总换热量的比值。
由田立楠[32]对气体加压时导热系数变化的研究,以及通过查看物性参数表可知,在较大压力变化范围内导热系数几乎不随压力变化。文献[30]推荐了流体的变物性模型:采用定常普朗特数,密度与动力粘度的乘积也为一常数。可通过理想气体定律计算密度,而后根据ρ2·υ=常数,计算出运动粘度。
依据以上讨论以及公式(12),在气体压力、温度变化时可得
| $\frac{{P{r_2}}}{{P{r_1}}} = 1, \frac{{{\lambda _2}}}{{{\lambda _1}}} = {\left( {\frac{{{T_2}}}{{{T_1}}}} \right)^{0.85}}, \frac{{{\upsilon _2}}}{{{\upsilon _1}}} = {\left( {\frac{{{p_1}}}{{{p_2}}}} \right)^2}\cdot{\left( {\frac{{{T_2}}}{{{T_1}}}} \right)^2} $ | (18) |
所以温度不变时
| $\frac{{P{r_2}}}{{P{r_1}}} = 1, \frac{{{\lambda _2}}}{{{\lambda _1}}} = 1, \frac{{{\upsilon _2}}}{{{\upsilon _1}}} = {\left( {\frac{{{p_1}}}{{{p_2}}}} \right)^2} $ | (19) |
由公式(3),(16),(19)可得热线风速仪的压力修正公式
| $\frac{{{E_2}^2}}{{{E_1}^2}} = \xi \cdot\frac{{{C_2}}}{{{C_1}}}\cdot{\left( {U\cdot d} \right)^{n - m}}\cdot{\upsilon _1}^{m - n}\cdot\left( {\frac{{{p_1}}}{{{p_2}}}} \right.{)^{ - 2n}}\cdot\left( {\frac{{{T_{\rm{w}}} - {T_{{\rm{f}}2}}}}{{{T_{\rm{w}}} - {T_{{\rm{f}}1}}}}} \right) $ | (20) |
由于压力变化对于气体流过热线的雷诺数影响较大,因此公式(20)中与雷诺数有关的常系数C,n,m不能消掉,需根据标定与实际工况下的雷诺数确定其值。
从温度的影响修正中可知,强迫对流换热量的占比与来流温度无关,仅与来流速度、压力有关。为便于应用,可将修正系数ξ的计算数据利用Origin软件进行拟合,可得拟合公式。
2.4 温度、压力影响综合修正对于温度、压力均为非标定状态的情况,不但物性参数随压力和温度发生了改变,而且压力的变化使强迫对流换热量的占比也发生了改变,需要确定修正系数。基于以上对温度、压力单一修正方法中的讨论,当温度、压力同时变化时,将公式(18)中的温度取定性温度即可获得温度、压力同时修正时的物性参数公式,如下所示
| $\frac{{P{r_2}}}{{P{r_1}}} = 1, \frac{{{\lambda _2}}}{{{\lambda _1}}} = {\left( {\frac{{{T_{\rm{w}}} + {T_{{\rm{f}}2}}}}{{{T_{\rm{w}}} + {T_{{\rm{f}}1}}}}} \right)^{0.85}}, \frac{{{\upsilon _2}}}{{{\upsilon _1}}} = {\left( {\frac{{{p_1}}}{{{p_2}}}} \right)^2}\cdot{\left( {\frac{{{T_{\rm{w}}} + {T_{{\rm{f}}2}}}}{{{T_{\rm{w}}} + {T_{{\rm{f}}1}}}}} \right)^2} $ | (21) |
由公式(3),(16),(21)可得温度、压力影响的综合修正公式
| $\begin{array}{*{20}{l}} {\frac{{{E_2}^2}}{{{E_1}^2}} = \xi \cdot\frac{{{C_2}}}{{{C_1}}}\cdot{{\left( {U\cdot d} \right)}^{n - m}}\cdot{\upsilon _1}^{m - n}\cdot{{\left( {\frac{{{T_{\rm{w}}} + {T_{{\rm{f}}2}}}}{{{T_{\rm{w}}} + {T_{{\rm{f}}1}}}}} \right)}^{ - 2n}}\cdot}\\ {\;\;\;\;\;\;\;\;\;\;{{\left( {\frac{{{T_{\rm{w}}} + {T_{{\rm{f}}2}}}}{{{T_{\rm{w}}} + {T_{{\rm{f}}1}}}}} \right)}^{0.85}}\cdot{{\left( {\frac{{{p_1}}}{{{p_2}}}} \right)}^{ - 2n}}\cdot\left( {\frac{{{T_{\rm{w}}} - {T_{{\rm{f}}2}}}}{{{T_{\rm{w}}} - {T_{{\rm{f}}1}}}}} \right)} \end{array} $ | (22) |
至此完成了综合考虑物性变化以及强迫对流、自然对流、辐射换热、支架导热等因素的非标定工况应用压力修正以及温度、压力综合修正。具体应用时,采用与温度修正相同的方式,依据式(20),(22)建立新的即修正后的U-E2曲线。不同的是计算过程中要获得标定工况下的运动粘度,并通过速度进行雷诺数的计算,以确定希尔帕特公式中的常系数C,n,m。
由于该修正方法是根据压力、温度变化的影响,对热线风速仪的输出电压进行修正,可以得到相应测试条件下的电压-速度真实曲线。因此,采用本修正方法在提高测试精度的同时,并不影响热线风速仪在脉动方面的测量。
3 修正方法验证 3.1 修正方法误差分析公式(22)为温度、压力影响的综合修正公式。试验时温度一般由热电偶测量,以采用T型铜-康铜热电偶为例,标定后其测温误差为±0.3K;压力由Kulite压力传感器测量,测压误差为±0.5%FS。
以来流温度473K,压力0.4MPa,速度220m/s计算,此时热线风速仪的修正输出电压相对误差为
| $\frac{{{\rm{\Delta }}E}}{E} = \sqrt {{{\left( {\frac{{\partial E}}{{\partial T}}} \right)}^2}{{\left( {\frac{{{\rm{\Delta }}T}}{E}} \right)}^2} + {{\left( {\frac{{\partial E}}{{\partial p}}} \right)}^2}{{\left( {\frac{{{\rm{\Delta }}p}}{E}} \right)}^2}} = 0.4{\rm{\% }} $ | (23) |
杜钰锋等[22]进行了可压缩流体恒温热线风速仪校准方法的研究,校准原始数据以及通过本文提出的修正方法修正后的输出电压如表 2所示。表中p0与T0分别为总压和总温,计算中需换算为静压和静温,同时以p0=101.9359kPa,T0=302.6136K为标定工况。热线温度取标准使用温度523K,低于此温度,计算误差均小于表中误差。
|
|
Table 2 Comparison of the raw and reduction data |
实际工况中热线风速仪输出电压的真实值与修正值对比如表 2所示。从中可以看出,在实验工况范围内,平均误差0.68%,最大误差2.2%。表明本文所采用的修正方法是可行且具有较高修正精度的。
4 结论通过本文研究,得到如下结论:
(1)热线风速仪热丝在不同来流速度下的强迫对流换热量占总换热量比例是不同的,而在同一来流速度下,强迫对流占比几乎不随温度变化而变化,但随压力变化较大,即热丝总换热量的比值与其强迫对流换热量的比值不相等,误差可达3%以上。
(2)给出了一种新的适用于非标准工况的热线风速仪测试修正方法及修正公式。与公开文献数据进行了比对,平均误差0.68%,最大误差2.2%。证明该修正方法具有较高精度。
| [1] |
盛森芝, 沈熊, 舒炜. 流速测量技术[M]. 北京: 北京大学出版社, 1987.
(  0) 0) |
| [2] |
李敏毅, 甘妙昌, 马思龙.热线风速仪测量原理简介[C].杭州: 压力计量服务和测试技术研讨会, 2003.
(  0) 0) |
| [3] |
Bearman P W. Correction for the Effect of Ambient Temperature Drift on Hot-Wire Measurements in Compressible Flow[J]. DISA Information, 1971(11): 25-30.
(  0) 0) |
| [4] |
Bremhorst K. Effect of Fluid Temperature on Hot-Wire Anemometers and an Improve Method of Temperature Compensation and Linearisation Without Use of Small Signal Sensitivities[J]. Journal of Physics E: Scientific Instruments, 1985, 18(1): 44-49. DOI:10.1088/0022-3735/18/1/013
(  0) 0) |
| [5] |
Lekakis I C, Adrian R J, Jones B G. Measurement of Velocity Vectors with Orthogonal and Non-Orthogonal Triple-Sensor Probes[J]. Experiments in Fluids, 1989, 7(4): 228-240. DOI:10.1007/BF00198002
(  0) 0) |
| [6] |
John J, Schobeiri T. A Simple and Accurate Method of Calibrating X-Probes[J]. Journal of Fluids Engineering, 1993, 115(1): 148-152. DOI:10.1115/1.2910098
(  0) 0) |
| [7] |
Lenoms G, Dracos T. A New Calibration and Data Reduction Method for Turbulence Measurement by Multihotwire Probes[J]. Experiments in Fluids, 1995, 18(5): 319-328. DOI:10.1007/BF00211387
(  0) 0) |
| [8] |
Kostka M, Vasanta Ram V. On the Effects of Fluid Temperature on Hot Wire Characteristics[J]. Experiments in Fluids, 1992, 13(23): 155-162.
(  0) 0) |
| [9] |
Abdel-Rahman A, Tropea C, Slawson P. On Temperature Compensation in Hot-Wire Anemometry[J]. Journal of Physics E: Scientific Instruments, 2000, 20(3): 315-319.
(  0) 0) |
| [10] |
邓康耀.可变几何涡轮增压和排气管系二维不稳定流场研究[D].上海: 上海交通大学, 1991.
(  0) 0) |
| [11] |
梁雄耀. 热线风速仪输出信号的温度和压力修正[J]. 重庆交通学院学报, 1993, 12(1): 80-88. (  0) 0) |
| [12] |
张万路. 热线风速仪在线测量的修正模型[J]. 计量技术, 2004(5): 27-28. DOI:10.3969/j.issn.1000-0771.2004.05.010 (  0) 0) |
| [13] |
马超, 黄名海, 葛冰, 等. 高温风洞中空冷涡轮叶片冷却特性的实验研究[J]. 推进技术, 2016, 37(3): 496-503. (MA Chao, HUANG Ming-hai, GE Bing, et al. Experimental Investigation of Cooling Performance of Air-Cooled Turbine Blade in a High-Temperature Wind Tunnel[J]. Journal of Propulsion Technology, 2016, 37(3): 496-503.)
(  0) 0) |
| [14] |
朱惠人, 向安定, 许都纯, 等. 涡轮叶片表面气膜冷却效率的实验研究[J]. 推进技术, 2003, 24(6): 528-531. (ZHU Hui-ren, XIANG An-ding, XU Du-chun, et al. An Experimental Investigation of Film Cooling Effectiveness on the Surface of Turbine Blade[J]. Journal of Propulsion Technology, 2003, 24(6): 528-531. DOI:10.3321/j.issn:1001-4055.2003.06.013)
(  0) 0) |
| [15] |
Chaluvadi V S P, Kalfas A I, Hodson H P. Vortex Transport and Blade Interactions in High Pressure Turbines[J]. Journal of Turbomachinery, 2004, 126(3): 395-405. DOI:10.1115/1.1773849
(  0) 0) |
| [16] |
高丽敏, 席光, 王尚锦, 等. 用热线风速仪测量叶轮后叶片扩压器流场[J]. 工程热物理学报, 2005, 26(4): 599-601. DOI:10.3321/j.issn:0253-231X.2005.04.018 (  0) 0) |
| [17] |
魏宽, 陶智, 邓宏武, 等. 旋转状态下方形通道内部流场特性热线实验[J]. 航空动力学报, 2016, 31(11): 2635-2640. (  0) 0) |
| [18] |
Quix H, Quest J, Brzek C. Hot-Wire Measurements in Cryogenic Environment[C]. Orlando: 49th US AIAA Aerospace Science Meeting, 2011.
(  0) 0) |
| [19] |
Struk P M, Rigby D L, Venkatara K. A Thermal Analysis of a Hot-Wire Probe for Icing Applications[C]. US: 6th AIAA Atmospheric and Space Environments Conference, 2014.
(  0) 0) |
| [20] |
王鑫, 杨颖, 马云驰, 等. 应用热线风速仪对熔喷流场的温度速度同步测量方法[J]. 实验流体力学, 2016, 30(1): 91-96. (  0) 0) |
| [21] |
王仑, 周远, 侯宇葵. 热线风速仪低温测速的初步研究[J]. 真空与低温, 2001, 7(2): 89-91. DOI:10.3969/j.issn.1006-7086.2001.02.007 (  0) 0) |
| [22] |
杜钰锋, 林俊, 马护生, 等. 可压缩流体恒温热线风速仪校准方法[J]. 航空动力学报, 2017, 38(6). (  0) 0) |
| [23] |
论立勇, 陈厚磊, 蔡京辉. 高压交变流动下热线风速仪标定方法研究[J]. 实验流体力学, 2010, 24(3): 87-91. DOI:10.3969/j.issn.1672-9897.2010.03.018 (  0) 0) |
| [24] |
姚惠元, 刘国政, 孙楠, 等. 恒温热线风速仪的一种新型校准方法[J]. 现代电子技术, 2013, 36(23): 110-112. DOI:10.3969/j.issn.1004-373X.2013.23.031 (  0) 0) |
| [25] |
陈曦, 沙奕卓, 吕文华. 热线流速仪在风洞流场测试中的应用[J]. 仪器仪表学报, 2011, 32(12): 356-360. (  0) 0) |
| [26] |
李鹏, 崔骊水, 李金海, 等. 热线风速仪微风速下的校准实验研究[J]. 计量技术, 2016(9): 3-7. DOI:10.3969/j.issn.1000-0771.2016.09.01 (  0) 0) |
| [27] |
韦青燕, 张天宏. 高超声速热线热膜风速仪研究综述及分析[J]. 测试技术学报, 2012, 26(2): 142-149. DOI:10.3969/j.issn.1671-7449.2012.02.010 (  0) 0) |
| [28] |
Hilpert R. Heat Transfer from Cylinders[J]. Forsch Geb Ingenieurwes, 1933(4): 215-224.
(  0) 0) |
| [29] |
李友荣. 高等传热学[M]. 北京: 科学出版社, 2013.
(  0) 0) |
| [30] |
Kays William, Crawford Michael, Weigand Bernhar著.对流传热与传质[M].赵镇南译.北京: 高等教育出版社, 2007.
(  0) 0) |
| [31] |
侯亚丽, 汪建文, 刘志刚. 微细长竖圆柱外侧的自然对流换热[J]. 制冷学报, 2013, 34(2): 60-65. DOI:10.3969/j.issn.0253-4339.2013.02.060 (  0) 0) |
| [32] |
田立楠. 纯气体混合气体及液体导热系数的计算[J]. 氮肥设计, 1996, 34(4): 19-22. (  0) 0) |
 2018, Vol. 39
2018, Vol. 39


