为了大幅度提高涡轮负荷,涡轮气动设计广泛采用跨声速设计;同时燃气涡轮发动机进口温度越来越高,受材料许用温度的限制,有效的涡轮叶片冷却设计越来越重要[1, 2]。而涡轮叶栅通道内为复杂的三维流动,会出现转捩、二次流,激波及附面层相互干扰等现象[3, 4]。刘聪等[5]对跨声速涡轮导叶的数值研究表明,激波诱导边界层分离和转捩,换热系数会有大幅度变化。因此,准确预测转捩位置和叶片表面对流换热系数分布对设计高效的冷却方案具有重要意义。
叶栅通道内的流动转捩会严重影响叶片表面对流换热系数,工程常用的转捩预测方法主要有:经验关联方法[6]、以eN为代表的线性稳定性方法、基于间歇因子的预测方法[7],以及Menter和Langtry等发展的
董平等[16, 17]、李涛等[18]采用
基于上述问题,本文主要参考零压力梯度时自由流湍流度衰减率实验结果,给出了一种快速估算来流粘性比的方法,避免多次试算的繁复。通过在入口处设置合适的粘性比来控制湍流度衰减,确保叶栅前缘具有准确的湍流度和期望的衰减率。并对MARK Ⅱ与VKI涡轮叶栅通道在亚、跨声速下的流动换热情况进行了算例验证,结果表明,按本文方法设置入口粘性比能很好地改善
间歇因子输运方程[10]为
| $\frac{{\partial \left( {\rho \gamma } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {U_{{\rm j}}}\gamma } \right)}}{{\partial {x_{{\rm j}}}}} = {P_{{\rm \mathsf{ γ} }}} - {E_{{\rm \mathsf{ γ} }}} + \frac{\partial }{{\partial {x_{{\rm j}}}}}\left[ {\left( {\mu + \frac{{{\mu _{{\rm t}}}}}{{{\sigma _{{\rm f}}}}}} \right)\frac{{\partial \gamma }}{{\partial {x_{{\rm j}}}}}} \right]$ | (1) |
其中,转捩源项
| ${P_{{\rm \mathsf{ γ} }}} = {F_{{{\rm length}}}}{c_{{{\rm a}}1}}\rho S{\left[ {\gamma {F_{{{\rm onset}}}}} \right]^{0.5}}\left( {1 - {c_{{{\rm e}}1}}\gamma } \right)$ | (2) |
| ${E_{{\rm \mathsf{ γ} }}} = {c_{{{\rm a}}2}}\rho \mathit{\Omega }\gamma {F_{{{\rm turb}}}}\left( {{c_{{{\rm e}}2}}\gamma - 1} \right)$ | (3) |
| ${F_{{{\rm onset}}}} = {{\rm max}}\left( {{F_{{{\rm onset}}2}} - {F_{{{\rm onset}}3}}, 0} \right)$ | (4) |
| ${F_{{{\rm turb}}}} = {{{\rm e}}^{ - {{\left( {{R_{{\rm T}}}/4} \right)}^4}}}, {R_{{\rm T}}} = \rho k/\mu \omega $ | (5) |
| ${F_{{{\rm onset}}1}} = R{e_{{\rm v}}}/\left( {2.193R{e_{\theta {{\rm c}}}}} \right), {{\rm }}R{e_{{\rm v}}} = \rho {y^2}S/\mu $ | (6) |
| ${F_{{{\rm onset}}2}} = {{\rm min}}\left( {{{\rm max}}\left( {{F_{{{\rm onset}}1}}, F_{{{\rm onset}}1}^4} \right), 2.0} \right)$ | (7) |
| ${F_{{{\rm onset}}3}} = {{\rm max}}\left( {1 - {{\left( {{R_{{\rm T}}}/2.5} \right)}^3}, 0} \right)$ | (8) |
式中Flength为控制转捩区长度的关键参数;Reθc为间歇函数在边界层内第一次开始增大的临界雷诺数。Flength和Reθc都是当地转捩动量厚度雷诺数
当地转捩动量厚度雷诺数
| $ \begin{array}{*{20}{l}} {\frac{{\partial \left( {\rho \tilde R{e_{\theta {{\rm t}}}}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {U_{{\rm j}}}\tilde R{e_{\theta {{\rm t}}}}} \right)}}{{\partial {x_{{\rm j}}}}} = }\\ {{P_{\theta {{\rm t}}}} + \frac{\partial }{{\partial {x_j}}}\left[ {{\sigma _{\theta {{\rm t}}}}\left( {\mu + \frac{{{\mu _{{\rm t}}}}}{{{\sigma _{{\rm f}}}}}} \right)\frac{{\partial \tilde R{e_{\theta {{\rm t}}}}}}{{\partial {x_{{\rm j}}}}}} \right]} \end{array} $ | (9) |
式中,源项
| $ {P_{\theta {{\rm t}}}} = {c_{\theta {{\rm t}}}}\frac{\rho }{{{t_{{\rm s}}}}}\left( {R{e_{\theta {{\rm t}}}} - \tilde R{e_{\theta {{\rm t}}}}} \right)\left( {1.0 - {F_{\theta {{\rm t}}}}} \right) $ | (10) |
这里ts是为了协调量纲而存在的时间参数。混合函数Fθt用来控制
转捩动量厚度雷诺数Reθt直接影响着转捩过程,它是自由流湍流强度Tu,流向压力梯度参数λθ的关联函数;Reθt采用Langtry[10]给出的形式
| $ \begin{array}{*{20}{l}} {R{e_{\theta {{\rm t}}}} = \left[ {1173.51 - 589.428Tu + \frac{{0.2196}}{{T{u^2}}}} \right]F\left( {{\lambda _\theta }} \right), }\\ {Tu \le 1.3} \end{array} $ | (11) |
| $ R{e_{\theta {{\rm t}}}} = 331.50{\left[ {Tu - 0.5658} \right]^{ - 0.671}}F\left( {{\lambda _\theta }} \right), Tu > 1.3 $ | (12) |
式中F(λθ)代表压力梯度的影响。
转捩模型耦合于SST湍流模型中,通过间歇因子γ作用于湍动能方程的生成项和耗散项来模拟转捩过程,即
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {U_{{\rm j}}}k} \right)}}{{\partial {x_{{\rm j}}}}} = \overline {{P_{{\rm \mathsf{ γ} }}}} - \overline {{E_{{\rm \mathsf{ γ} }}}} + \frac{\partial }{{\partial {x_{{\rm j}}}}}\left[ {\left( {\mu + \frac{{{\mu _{{\rm t}}}}}{{{\sigma _{{\rm k}}}}}} \right)\frac{{\partial k}}{{\partial {x_{{\rm j}}}}}} \right] $ | (13) |
| $ \overline {{P_{{\rm \mathsf{ γ} }}}} = {\gamma _{{{\rm eff}}}}{P_{{\rm k}}}\;\;\overline {{E_{{\rm \mathsf{ γ} }}}} = {{\rm min}}\left( {{{\rm max}}\left( {{\gamma _{{{\rm eff}}}}, 0.1} \right), 1.0} \right){D_{{\rm k}}} $ |
式中Pk和Dk是原来k-ω SST湍流模型的生成项和耗散项;对ω输运方程不做任何修改。
3 自由流湍流度控制由上节可知,转捩模型中转捩动量厚度雷诺数Reθt强烈依赖于当地自由流湍流度Tu。研究发现[22],在数值模拟中,入口湍流度沿程会迅速衰减,且衰减速度取决于进口粘性比;进口粘性比越大,湍流衰减越慢;但是过大的入口粘性比则会影响壁面摩阻。因此,在数值模拟中需指定进口自由流湍流度并给定合理的入口粘性比,以保证叶栅前缘附近具有合理的湍流度水平和期望的衰减率。然而在实验中一般只测量来流的湍流强度,很少测量湍流长度尺度[23],所以难以确定入口的湍流粘性比。
采用SST模型描述湍流,在匀速运动参考系上观察,湍流度强度随时间的衰减率为
| $\frac{{{{\rm d}}k}}{{{{\rm d}}t}} = - {\beta ^{{\rm *}}}\omega k, \frac{{{{\rm d}}\omega }}{{{{\rm d}}t}} = - \beta {\omega ^2}$ |
初始时入口处t=0, k=kinlet, ω=ωinlet
求解上式可以得到自由流中的湍动能衰减公式
| $k = {k_{{{\rm inlet}}}}{\left( {1 + {\omega _{{{\rm inlet}}}}\beta t} \right)^{ - \frac{{{\beta ^{{\rm *}}}}}{\beta }}}$ | (14) |
式中β=0.09, β*=0.0828。
在静止参考系中,湍流度变化是定常的,湍流强度从入口处的值沿流向不断衰减。将时间尺度用空间尺度替换,即t=X/V,X为流向距离,V为流动速度;涡粘性μt=ρk/ω,引入粘性比RT=μt/μ=ρk/ωμ;湍流度
| $Tu = {\left( {Tu_{{{\rm inlet}}}^2{{\left[ {1 + \frac{{3\rho Vx\beta Tu_{{{\rm inlet}}}^2}}{{2\mu \left( {{\mu _{{\rm t}}}/\mu } \right)}}} \right]}^{ - \frac{{{\beta ^{{\rm *}}}}}{\beta }}}} \right)^{0.5}}$ | (15) |
则入口粘性比为
| ${R_{{\rm T}}}_{{{\rm inlet}}} = 1.5\beta \frac{{\rho {V_{{{\rm inlet}}}}x}}{\mu }\frac{{Tu_{{{\rm inlet}}}^2}}{{{{\left( {Tu/T{u_{{{\rm inlet}}}}} \right)}^{ - 2\beta /{\beta ^{{\rm *}}}}} - 1}}$ | (16) |
为了高效地获得合理的入口粘性比,提高计算效率,本文参考零压力梯度时自由流湍流强度的衰减规律[23],给出了入口粘性比的计算方法,具体方法如下。
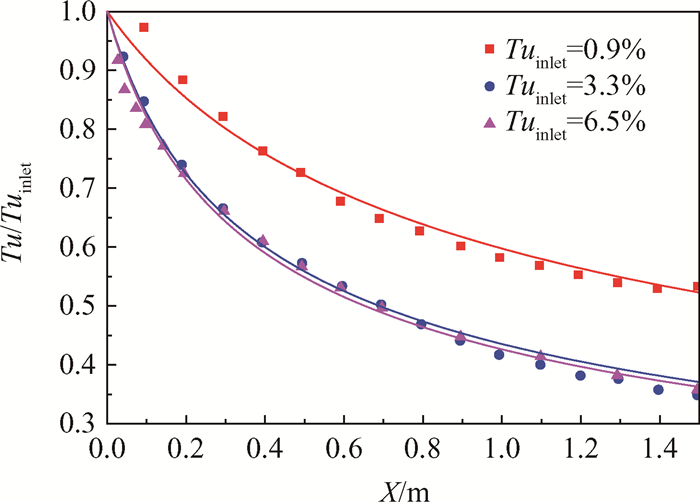
图 1为不同入口湍流度下相对湍流度Tu/Tuinlet沿流向距离分布的实验点[22]及其拟合曲线。由图可知,随着流向距离增大,湍流衰减趋于平缓; 在入口湍流度较低(Tuinlet=0.9%)时,与中高入口湍流度之间的衰减程度相差较大,且入口湍流度越大,相对湍流度沿流向衰减越快;在入口湍流度较高时(Tuinlet > 3.3%),不同入口湍流度下的相对湍流度沿流向衰减程度基本相同。在涡轮叶栅数值模拟中,可由确定的入口与涡轮叶栅前缘之间距离X1和入口湍流度Tuinlet,依据图 1来估算出对应X1处的前缘湍流度TuLE及其与入口湍流度Tuinlet之比,代入到公式(16)中可得到所需要的入口粘性比RT inlet。
|
Fig. 1 Free-stream turbulence intensity decay curve[23] |
本文采用商业软件ANSYS CFX,针对两个典型的涡轮叶栅MARK Ⅱ和VKI模型,选用
计算中,在入口处分别给定
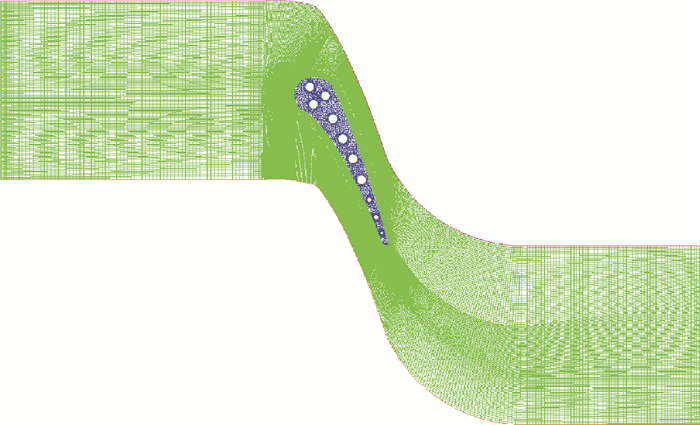
表 1和图 2分别为Mark Ⅱ叶型的主要几何参数和计算网格,详细叶型数据和冷却通道数据可参见文献[24]。叶栅流道内采用结构化网格,网格数量约为332万,在叶栅壁面附近加密网格,壁面网格最小尺度为5.0 × 10-7m,保证y+ < 1,网格法向增长率为1.1;固体叶栅部分采用非结构化网格,网格数量为26万。计算工况如表 2所示,各冷气通道平均温度和换热系数参见文献[24]。
|
|
Table 1 Geometry parameters of MARK Ⅱ |
|
Fig. 2 Computational mesh of MARK Ⅱ |
|
|
Table 2 MARK Ⅱ boundary conditions |
在数值模拟中采用
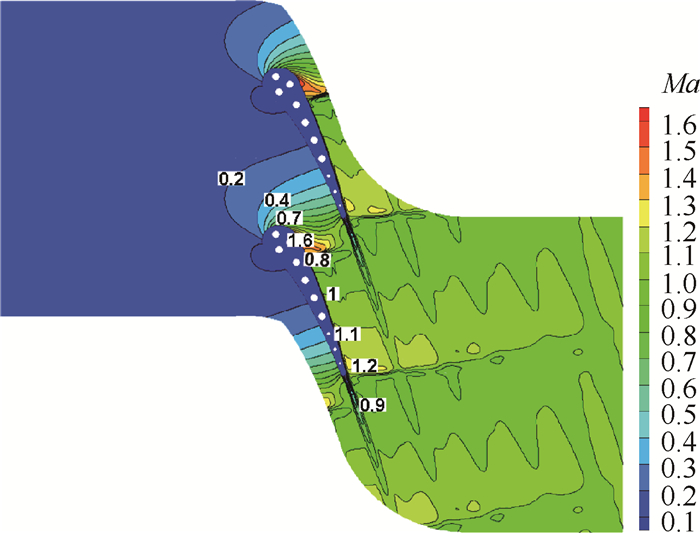
图 3给出了跨声速5411工况下涡轮叶栅通道马赫数分布云图。此时在流道中出现了局部超声速区域,在吸力面X/L=0.43位置产生一道较强的激波,同时尾缘处形成一对斜激波,激波与激波相互干涉以及激波与边界层的相互干扰,使流动变得更加复杂。
|
Fig. 3 Mach number distribution (5411) |
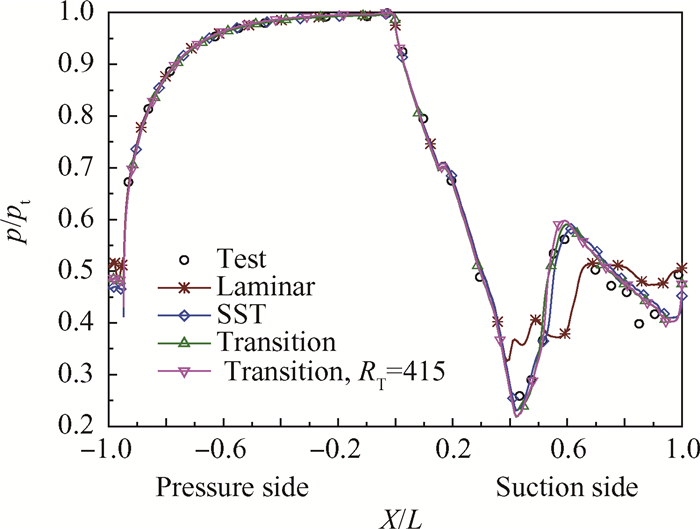
图 4给出了Mark Ⅱ涡轮叶栅5411工况下涡轮叶栅表面无量纲压力分布,其中p表示叶栅表面压力,pt表示进口总压,X/L表示轴向位置与轴向弦长之比。可以看出,除层流模型外,数值模拟的压力分布与试验值吻合得较好。由于在吸力面0.43倍轴向弦长处产生了激波,激波后压力骤增,产生较强的逆压梯度,引起层流边界层分离,从图 5的吸力面局部流线图中可以看到分离泡的存在;层流分离触发流动转捩,使得吸力面上对流换热系数突增。
|
Fig. 4 Pressure distribution (5411) |

|
Fig. 5 Streamline near the transitional point(Transition RT inlet=415) |
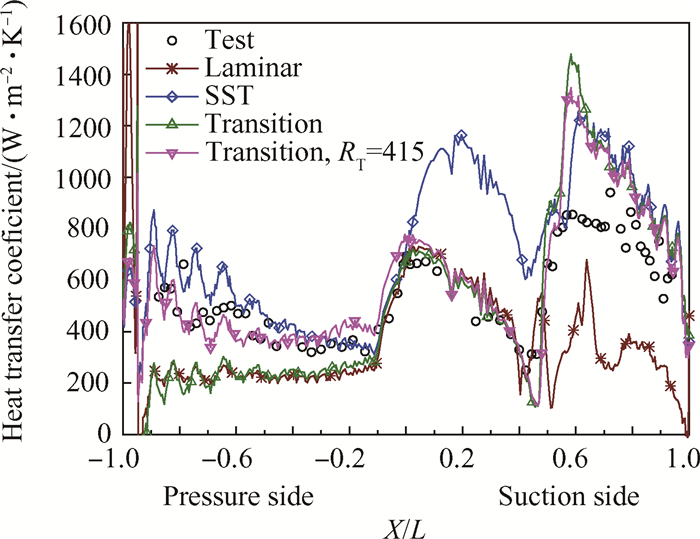
图 6为Mark Ⅱ叶片5411工况下叶片表面对流换热系数分布。叶片表面对流换热系数由下式计算
|
Fig. 6 Heat transfer coefficient distribution (5411) |
| $h = {q_{{\rm w}}}/\left( {T_1^* - {T_{{\rm w}}}} \right)$ | (17) |
式中qw为壁面热流密度;T1*为叶栅进口总温;Tw为叶栅壁面温度。
由图 6可知,对于跨声速工况5411,在压力面,边界层对自由流湍流强度敏感,当转捩模型采用缺省进口粘性比时(RT 1=65),此时入口湍流度会迅速衰减,叶片前缘湍流度大大低于入口湍流度,预测的换热系数远低于实验值,与层流结果相近;当设定合理进口粘性比(RT inlet=415)后,使入口到前缘位置具有合适的湍流度衰减率,此时叶栅压力面为完全湍流流动,转捩模型的换热结果与实验值吻合得较好,相对于缺省粘性比情况,对于压力面大部分区域相对误差减小约30%;SST湍流模型的结果稍高于实验值。在吸力面,转捩模型能较好地获得转捩点位置;在转捩点之前,转捩模型计算结果与实验值相吻合,而完全湍流模型SST结果偏大;在转捩点之后,层流模型的换热结果偏低,转捩模型结果与SST模型结果基本相同,均出现了一较大的峰值,过高估计了对流换热系数。这可能是由于此处产生了较强的激波,实际流动压缩性效应显著,而转捩模型本身未考虑流体压缩效应,高估了边界层内的湍动能,从而引起较大误差。对于这种情况进行流动可压缩性修正,可显著减小吸力面传热系数数值计算误差[25]。总体来看,在
VKI叶型的主要几何参数和计算网格如表 3和图 7所示,详细叶型数据可参见文献[26]。采用结构化网格,流道内网格数量约为156万。在叶栅壁面加密网格,壁面第一层厚度为7.0 × 10-7m,y+ < 1.3,网格法向增长率为1.1。计算工况如表 4所示,MUR 241和MUR 247分别为出口跨声速、亚声速。
|
|
Table 3 Geometry parameters of VKI |

|
Fig. 7 Computational mesh of VKI |
|
|
Table 4 VKI boundary conditions |
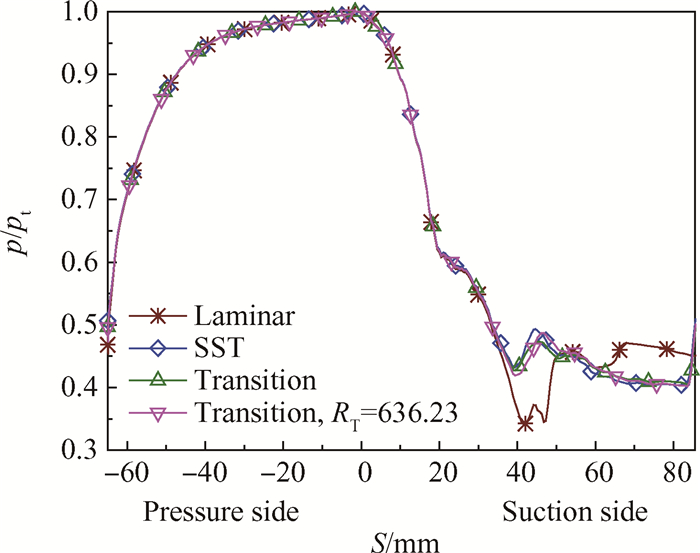
图 8和图 9分别为工况MUR 241下,涡轮叶栅表面压力分布与外换热系数分布图。由图 8可知,除层流模型之外,其它模型得到的压力分布基本相同;在吸力面中部出现弱激波,此时逆压梯度较小,未发生边界层分离。
|
Fig. 8 Pressure distribution(MUR241) |
|
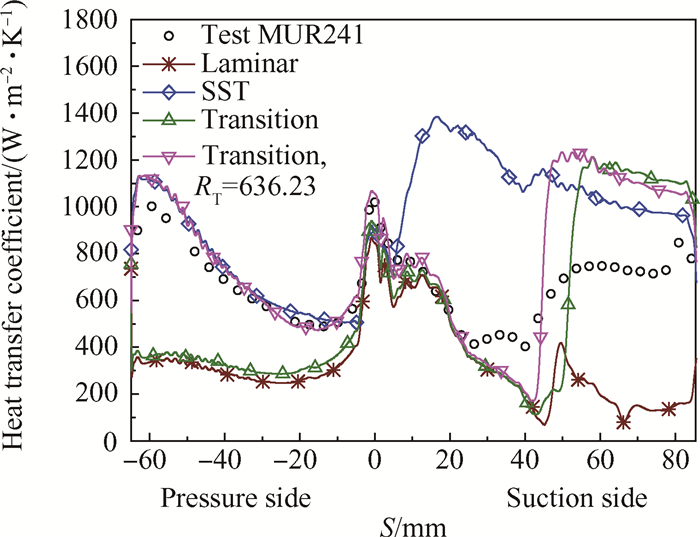
Fig. 9 Heat transfer coefficient distribution(MUR241) |
由图 9可知,工况MUR241下各模型换热结果与实验的对比情况与Mark Ⅱ的跨声速工况5411结果基本类似。在压力面,采用缺省入口粘性比(RT 1=60)时转捩模型预测的换热系数远低于实验值,在压力面大部分区域,相对误差高达50%,与层流模型的结果相当;而当合理设置入口粘性比(RT inlet=636.23)后,整个压力面的对流换热系数与实验值符合得较好,相对误差最大约7%;在此区域,SST完全湍流模型也得到较好的换热结果。而在吸力面,转捩模型能较准确地获得转捩点位置;从滞止点到转捩点之前,层流模型和转捩模型的结果均与试验值符合得较好,给定合理入口粘性比时转捩模型预测结果与实验最为接近。在转捩点之后,层流模型预测的对流换热系数过低;而转捩模型与SST模型一样,均高估了对流换热系数。
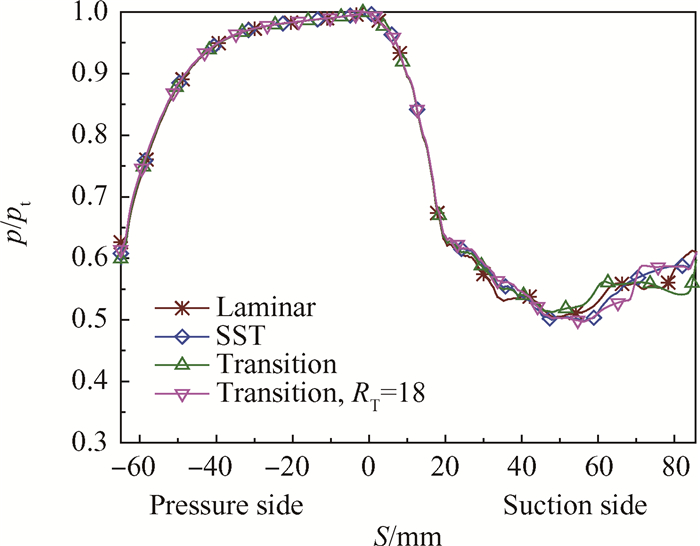
在工况MUR247下,VKI叶片表面压力分布如图 10所示。同MUR 241工况类似,几种湍流模型模拟的压力分布基本相同。转捩模型模拟结果显示在叶栅吸力面中部喉道附近达到声速,但并未产生激波。图 11是转捩位置附近局部流线,在靠近吸力面尾缘位置产生了流动分离,引起转捩。
|
Fig. 10 Pressure distribution (MUR247) |

|
Fig. 11 Streamline near the transitional point(Transition RT inlet=18) |
图 12为工况MUR 247下的对流换热系数分布。由图可知,对于SST湍流模型,除前缘区外均高估了对流换热水平,层流模型则在吸力面转捩点之后低估了对流换热水平。对于转捩模型,在压力面,由于入口自由流湍流度较低,流动保持层流,采用缺省入口粘性比(RT 1 =10)和设置合理入口粘性比(RT inlet=18)时的换热结果均与试验值相符。而在吸力面,采用缺省入口粘性比使得入口湍流度衰减过大,转捩之后换热结果远低于实验值;当设置合理的入口粘性比时,换热结果与试验值基本相符。

|
Fig. 12 Heat transfer coefficient distribution (MUR247) |
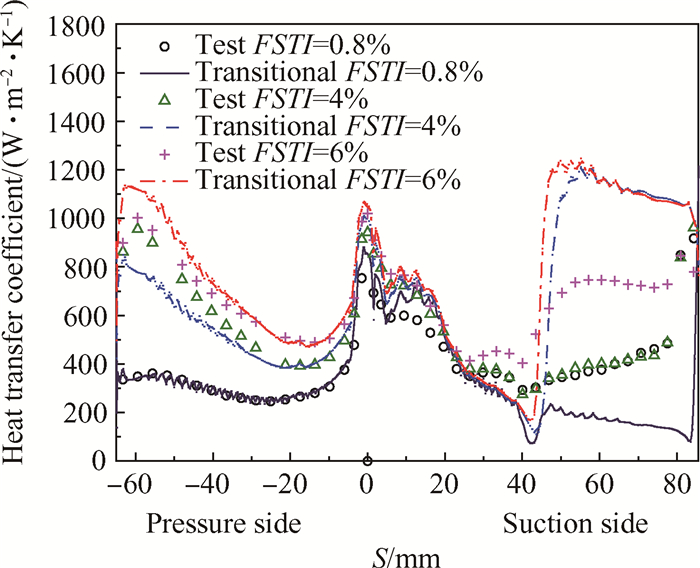
本文还采用给定入口粘性比的转捩模型,对比了VKI叶栅在出口亚声速、超声速时不同入口湍流度下的叶栅表面换热系数分布,如图 13和图 14所示。其中,试验值参见文献[26],图中FSTI表示入口来流湍流度。由图可知,叶栅压力面的换热模拟结果与实验值均符合得较好,在来流湍流度较低时,压力面保持层流流动;来流湍流度较高时,压力面为湍流流动。
|
Fig. 13 Heat transfer coefficient distribution (Ma=1.09) |
|
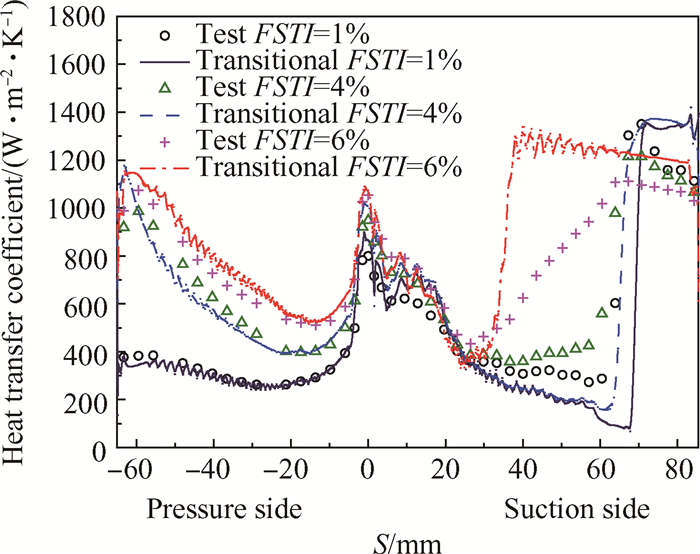
Fig. 14 Heat transfer coefficient distribution (Ma=0.92) |
在吸力面,对于出口超声速工况,吸力面中弦附近产生弱激波,激波与边界层相互作用,使流动变得更加复杂。在转捩点之前流动处于层流,换热模拟结果与实验值较为符合,转捩点之后的换热结果与实验值偏差较大。对于高湍流度情况,激波之后触发转捩,转捩模型高估了对流换热系数。对于低湍流度工况,在吸力面中弦附近的微弱激波不足以触发转捩,流动保持层流,直至靠近尾缘处产生流动转捩,换热增强[10],此时模拟的换热结果与试验值有较大差异。对于中等湍流度,计算值接近于高湍流度的结果,激波后发生转捩,而实验值接近于低湍流度结果,激波后未发生转捩,这是由于压缩性对转捩有一定抑制作用。表明此时流动可压缩性效应显著,需进一步考虑流动可压缩性修正[11]。
如图 14,对于出口亚声速工况,流动在喉道截面达到声速,在此之后,由于通道扩张,流动减速,无激波产生。在吸力面转捩点之前,换热系数的模拟结果与试验值基本符合;在中低入口湍流度时,转捩点位置较试验值稍有延后,转捩之后的换热系数与试验值相差不大;而在高入口湍流度时,转捩点相对出口超声速工况有所提前(图 13),在S=26.45mm处(喉道之前)发生转捩,其转捩区的范围相对实验结果明显偏窄,换热系数相对实验值偏高。
5 结论通过研究,得到如下结论:
(1)当采用本文方法对
(2)在本文的中等雷诺数范围,对于涡轮叶栅压力面,当较低入口湍流度时,流动保持层流;较高入口湍流度时,流动为完全湍流,采用合理入口粘性比时,压力面换热系数模拟值与试验值符合得较好,与缺省粘性比情况相比,传热系数计算相对误差降低30%以上。
(3)在本文的中等雷诺数范围,对涡轮叶栅吸力面,当出口亚声速、无激波产生时,中低湍流度时在近叶栅尾缘处发生转捩,换热强化;在高湍流度时计算模型能够较好地获得转捩位置,但转捩宽度偏窄,转捩后换热系数偏高。当出口超声速时叶栅通道内有弱激波,较高入口湍流度时,激波引发转捩,换热增强;设置合理粘性比的转捩模型能较准确地预测叶栅前缘至吸力面转捩点的换热情况;转捩点之后转捩模型高估了对流换热系数。表明流动可压缩性显著,需进一步考虑流动可压缩性修正。
| [1] |
曾军, 向传国, 程信华. 跨声速涡轮叶栅三维流场的数值模拟[J]. 航空动力学报, 2007, 22(11): 1915-1920. DOI:10.3969/j.issn.1000-8055.2007.11.023 (  0) 0) |
| [2] |
卿雄杰, 潘炳华, 曾军. 涡轮叶片外换热计算程序对比研究[J]. 航空动力学报, 2010, 25(4): 741-747. (  0) 0) |
| [3] |
Goldstein R J, Spores R A. Turbulent Transport on the Endwall in the Region Between Adjacent Turbine Blades[J]. Journal of Heat Transfer, 1988, 110(4  0) 0) |
| [4] |
Giel P W, Boyle R J, Bunker R S, et al. Measurements and Predictions of Heat Transfer on Rotor Blades in a Transonic Turbine Cascade[J]. Journal of Turbomachinery, 2004, 126(1): 623-638.
(  0) 0) |
| [5] |
刘聪, 朱惠人, 许卫疆, 等. 跨声速涡轮导叶吸力面换热特性数值研究[J]. 推进技术, 2015, 36(7): 1046-1053. (LIU Cong, ZHU Hui-ren, XU Wei-jiang, et al. Numerical Study for Heat Transfer Characteristics on Suction Side of Transonic Nozzle Guide Vane[J]. Journal of Propulsion Technology, 2015, 36(7): 1046-1053.)
(  0) 0) |
| [6] |
Abughannam B J, Shaw R. Natural Transition of Boundary Layers-the Effects of Turbulence, Pressure Gradient, and Flow History[J]. Journal of Mechanical Engineering Science, 1980, 22(5): 213-228. DOI:10.1243/JMES_JOUR_1980_022_043_02
(  0) 0) |
| [7] |
Suzen Y B, Huang P G. Modeling of Flow Transition Using an Intermittency Transport Equation[J]. Journal of Fluids Engineering, 2000, 122(2): 273-284.
(  0) 0) |
| [8] |
Menter F R, Langtry R B, Likki S R, et al. A Correlation Based Transition Model Using Local Variables Part 1-Model Formulation[R]. ASME-GT 2004-53452. http://ci.nii.ac.jp/lognavi?name=crossref&id=info:doi/10.1115/1.2184352
(  0) 0) |
| [9] |
Langtry R B, Menter F R, Likki S R, et al. A Correlation-Based Transition Model Using Local Variables—Part Ⅱ: Test Cases and Industrial Applications[R]. ASME-GT 2004-53454.
(  0) 0) |
| [10] |
Langtry R B, Menter F R. Correlation-Based Transition Modeling for Unstructured Parallelized Computational Fluid Dynamics Codes[J]. AIAA Journal, 2012, 47(12): 2894-2906.
(  0) 0) |
| [11] |
张晓东, 高正红. 关于补充Langtry的转捩模型经验修正式的数值探讨[J]. 应用数学和力学, 2010, 31(5): 544-552. DOI:10.3879/j.issn.1000-0887.2010.05.005 (  0) 0) |
| [12] |
Tomac M, Pettersson K, Rizzi A. Calibration and Verification of a γ-Reθt Transition Prediction Method for Airfoil Computations[R]. AIAA 2013-0407.
(  0) 0) |
| [13] |
郑赟, 李虹杨, 刘大响. γ-Reθ转捩模型在高超声速下的应用及分析[J]. 推进技术, 2014, 35(3): 296-304. (ZHENG Yun, LI Hong-yang, LIU Da-xiang. Application and Analysis of γ-ReθTransition Model in Hypersonic Flow[J]. Journal of Propulsion Technology, 2014, 35(3): 296-304.)
(  0) 0) |
| [14] |
王刚, 刘毅, 王光秋, 等. 采用γ-Reθt模型的转捩流动计算分析[J]. 航空学报, 2014, 35(1): 70-79. (  0) 0) |
| [15] |
陈立立, 郭正. 基于γ-Reθt转捩模型的低雷诺数翼型数值分析[J]. 航空学报, 2016, 37(4): 1114-1126. (  0) 0) |
| [16] |
董平, 黄洪雁, 冯国泰. 高压燃气涡轮径向内冷叶片气热耦合的数值分析[J]. 航空动力学报, 2008, 23(2): 201-207. (  0) 0) |
| [17] |
董平.航空发动机气冷涡轮叶片的气热耦合数值研究[D].哈尔滨: 哈尔滨工业大学, 2009: 69-83. http://cdmd.cnki.com.cn/Article/CDMD-10213-2010031090.htm
(  0) 0) |
| [18] |
李涛, 边昕, 冯宇, 等. 基于Gama-Theta转捩模型的气冷涡轮气热耦合研究[J]. 推进技术, 2014, 35(7): 932-940. (LI Tao, BIAN Xin, FENG Yu, et al. Conjugate Heat Transfer Simulation of Air-Cooled Turbine Based on Gamma-Theta Transition Model[J]. Journal of Propulsion Technology, 2014, 35(7): 932-940.)
(  0) 0) |
| [19] |
曾军, 卿雄杰. 涡轮叶栅流动和传热耦合计算[J]. 航空动力学报, 2009, 24(6): 1204-1210. (  0) 0) |
| [20] |
孟德虹, 张玉伦, 王光学, 等. γ-Reθ转捩模型在二维低速问题中的应用[J]. 航空学报, 2011, 32(5): 792-801. (  0) 0) |
| [21] |
张玉伦, 王光学, 孟德虹, 等. γ-Reθ转捩模型的标定研究[J]. 空气动力学学报, 2011, 29(3): 295-301. DOI:10.3969/j.issn.0258-1825.2011.03.006 (  0) 0) |
| [22] |
Spalart P R, Rumsey C L. Effective Inflow Conditions for Turbulence Models in Aerodynamic Calculations[J]. AIAA Journal, 2007, 45(10): 2544-2553. DOI:10.2514/1.29373
(  0) 0) |
| [23] |
Menter F R, Smirnov P E, Liu T, et al. A One-Equation Local Correlation-Based Transition Model[J]. Flow, Turbulence and Combustion, 2015, 95(4): 583-619.
(  0) 0) |
| [24] |
Hylton L D, Mihelc M S, Turner E R, et al. Analytical and Experimental Evaluation of the Heat Distribution over the Surfaces of Turbine Vanes[R]. NASA CR168015, 1983.
(  0) 0) |
| [25] |
刘丽平, 郭隽.转捩模型在跨音速涡轮叶栅中的压缩修正[C].北京: 第十九届燃烧与传热传质学术交流会, 2017.
(  0) 0) |
| [26] |
Arts T, Lambert de Rouvroit M, Rutherford A W. Aero-Thermal Investigation of a Highly Loaded Transonic Linear Turbine Guide Vane Cascade. A Test Case for Inviscid and Viscous Flow Computations[R]. VKI for Fluid Dynamics, TN 174, 1990.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


