管道中的激波串自激振荡是指来流条件和反压都保持不变的情况下,激波串仍在某一平衡位置附近前后振荡的现象。早在1947年,Weise[1]通过纹影照片发现激波串前后振荡的现象,激波串的每道激波所处的位置随时间在不断变化。1974年Ikui等[2]首次实验研究了等截面直管道中激波串自激振荡现象,实验发现激波串中各激波以相同的形式振荡。Ikui等在文章中提到,随着上游自由来流马赫数增大,激波振荡的振幅随之增大,第一道激波的振幅小于随后的激波。Sugiyama等[3]重复了Ikui的实验,指出沿管道壁面边界层变化会改变第一道和第二道激波之间的气动喉道大小,从而使第一道激波以一定频率振动,且第一道激波与隔离段出口之间的气柱振动决定此第一道激波振动的频率。Robinet等[4]数值计算扩压段的激波串振荡,结果表明边界层产生的分离包使激波后平均速度增大,同时,可以用无粘的准一维稳定理论来预测自激振荡,边界层引起的横向波不是扩压器中激波振荡的主要原因。Sajben等[5]实验研究了混压式进气道结尾激波振动特性,研究表明逆压力梯度诱导的激波会使气流分离,而流动分离是结尾激波振荡的主要原因。谭慧俊等[6, 7]数值模拟了弯曲等截面管道中的激波串特性,并用实验方法对三维轴对称进气道内隔离段的激波串进行了初步研究,研究表明,管道弯曲对流动的对称性有明显的影响,管道弯曲能有效抑制出口压力变化导致的出口界面马赫数大幅度波动。Su等[8]数值模拟反压对隔离段激波串振荡的影响,研究表明,激波串前缘点处的压力振幅最大。当壁面某点静压达到最大值时,对应时刻的激波串头激波在最上游位置,当静压达到最小值时,激波串头激波在最下游位置;反压的脉动频率和幅度都对激波串的前缘位置有较大影响;反压越大,引起不起动的激波移动到上游越快。Hsieh等[9]发现通道的长高比对激波串的振荡频率有影响。田旭昂等[10]实验研究了Ma5风洞中斜激波串的流动结构和动态特性,发现及激波串前移过程中的两种状态。熊冰等[11、12]研究了隔离段内激波串的迟滞特性和受迫振荡特性,发现隔离段的扩张比对激波串的迟滞反压范围和迟滞量都有影响,激波串受迫振荡含两种形式。
针对激波串自激振荡现象的机理,许多研究人员做出了自己的解释,Ikui等[2]认为来流的湍流波动造成激波串的振荡。Yamane等[13, 14]实验研究了管路长度对激波串的影响,推测激波串的振荡是由于来自于下游伪激波的压力扰动。Hiromu等[15]认为激波串轴向方向的振荡是由伪激波区域内边界层振荡造成的。Sugiyama等[3]认为振荡的原因在于激波串头激波根部的边界层分离运动。Tan等[16]研究了高超声速进气道隔离段内背景激波对激波串的影响,研究认为,隔离段预先存在逆压力梯度是造成激波串振荡的重要原因。Li等[17]对二元超声速进气道进行了实验研究,认为上游产生的压缩波/激波在节流段的反射是出现激波振荡的重要原因。直至目前,研究人员对于激波串自激振荡的形成机理还没得出统一结论。
相比于直扩张段,弯曲扩张段内部的流动更加复杂,主要表现在:弯曲扩张段内部激波串更长,非对称性更明显;在壁面离心力作用下,激波附面层作用更易产生气流分离;弯曲扩张段上下壁面压差更大,更易产生激波串振荡现象。而扩张段内的流动特性对进气道的气动性能有直接影响,因此,对于弯曲扩张段激波串振荡现象开展的研究具有重要意义。本文主要采用定常和非定常数值模拟方法研究弯曲扩张段内部的激波串振荡特性。
2 物理模型及计算方法 2.1 弯曲扩张段的设计当进气道喉道与出口截面中心不在同一高度上时,扩张段进出口存在偏心距,因此中心线的形状在带偏距的进气道设计中极为重要,为了减小转弯损失和分离,转弯应尽量缓和。本文研究的扩张段中心线采用S弯形,中心线变化规律和面积变化规律都采用前缓后急,S弯的中心线方程和面积变化方程由文献[18]给出。本课题组在先前的研究中已得出此种亚声速扩张段设计方法能够满足超声速弯曲扩张段的设计要求。
进气道模型如图 1所示,进气道设计马赫数Ma=3.3,飞行高度20km。进气道前体外压缩角为

|
Fig. 1 Model of inlet |
本文采用Fluent软件对不同反压下的进气道进行了定常与非定常数值计算,非定常计算是在各反压定常计算得到的基础流场上进行的。湍流模型采用k-ω Shear Stress Transform(k-ω SST)模型,粘性系数采用Sutherland公式计算。无粘对流通量离散使用Roe Flux-Difference Splitting(Roe-FDS)格式离散,对流项采用二阶迎风格式。计算的边界条件有:压力远场,压力出口,无滑移固壁等。计算网格约为17.6万,壁面网格进行加密,保证壁面y+为1.0左右,非定常计算时间步长取10μs,单个时间步长内迭代150步,采用隐式时间离散方法求解。计算过程中监测方程残差,喉道马赫数,喉道及出口质量流量。计算收敛准则为:各项残差下降到0.001以下。计算的来流参数均取自20km高空,来流马赫数Ma=3.3,静压
为了验证本文采用的定常数值仿真方法的可信度,利用文献[19]中的进气道型面和实验数据进行了算例验证。实验来流条件:自由来流马赫数2.41,来流总压540kPa,总温305K,隔离段长度为79.3mm,出口为通流状态。
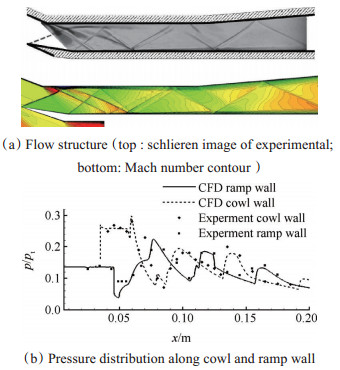
图 2给出了仿真与实验结果的对比。由图 2(a)可见本文采用的数值方法能清晰展现隔离段内复杂的斜激波与膨胀波波系,流场结构与实验结果基本吻合。图 2(b)对比了仿真与实验测得的壁面压力分布,可见计算的壁面沿程压力分布与实验结果基本吻合,说明本文采用k-ω SST模型进行计算研究是可行的。
|
Fig. 2 Comparisons of computed and experimental results |
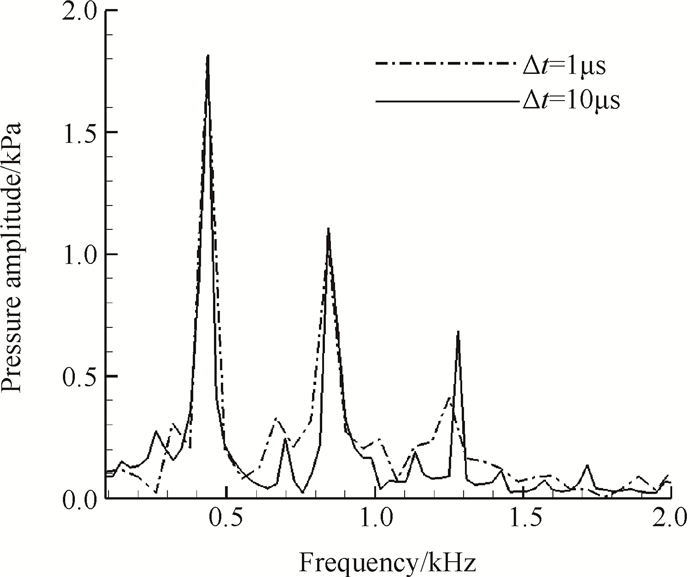
为了验证本文非定常计算所使用的时间步长的独立性,选取了1μs和10μs两个时间步长,对反压为19
|
Fig. 3 FFT results of total pressure of inlet exit for using different time step size |
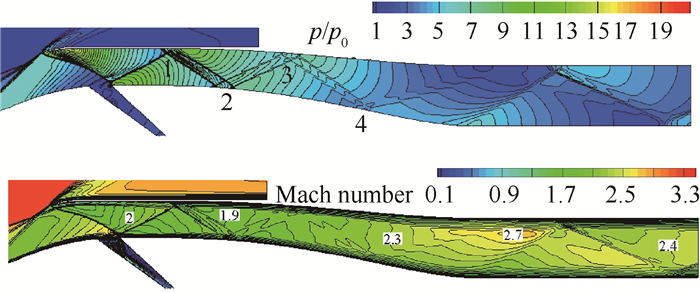
图 4为通流状态下进气道的压力和马赫数云图。进入进气道内收缩段的气流在泄流槽的作用下,下壁面大部分附面层被排除,而唇罩壁面气流的附面层经过长距离发展后,形成了较厚的附面层。唇口斜激波经喉道等直段反射后,与上壁面的附面层相互作用,诱发分离。超声速气流进过分离包,形成了两道几乎平行的激波,即分离激波和再附激波。两道激波在扩张段上下壁面反射三次后进入后方等直段。由壁面压力分布图可以看出,扩张段的上下壁面压力都存在两次由于反射激波造成的压升。为分析方便,将激波反射位置分别定义为反射位置1,2,3,4,如图 4所示。
|
Fig. 4 Pressure and Mach number contour of unthrottled flow |
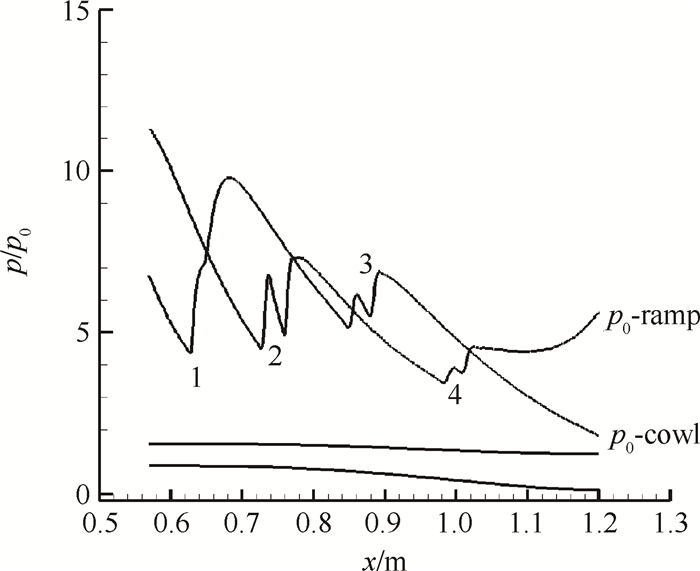
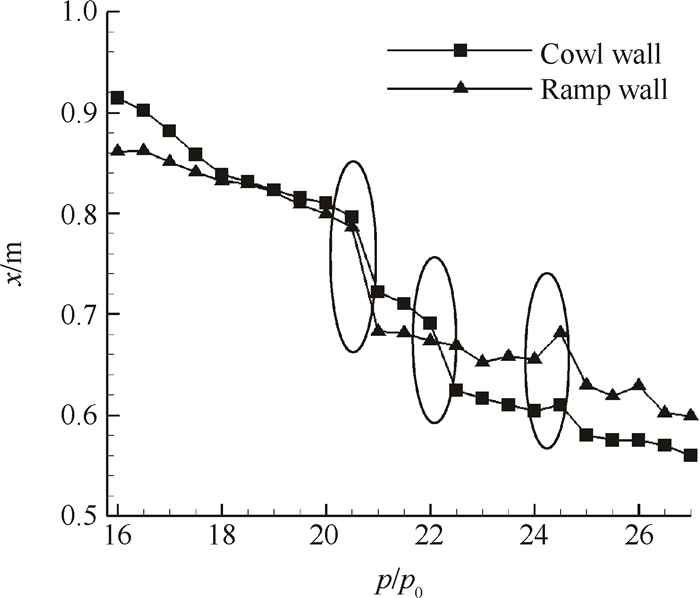
图 6是定常计算下扩张段内激波串前缘点位置随反压变化曲线,纵坐标为激波串前缘点位置与扩张段入口之间的距离。由图可看出,激波串在上下壁面的前缘点位置总体上是随着反压上升逐渐向上游移动的。反压为22.5
|
Fig. 5 Pressure distribution along diffuser wall |
|
Fig. 6 Position of leading point of shock train varying with backpressure in the diffuser |
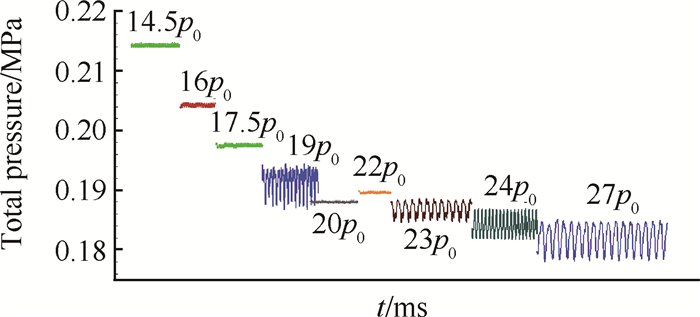
使用非定常数值模拟方法,研究各反压下扩张段内部的流场结构和振荡特性。图 7给出几种反压下进气道出口的总压振荡图,可见随反压增大激波串的大幅振荡和小幅振荡交错出现。根据出口总压的振荡幅度,可将反压增大过程中所呈现的流场结构分为4个过程。
|
Fig. 7 Total pressure of inlet exit variation with time at different backpressure |
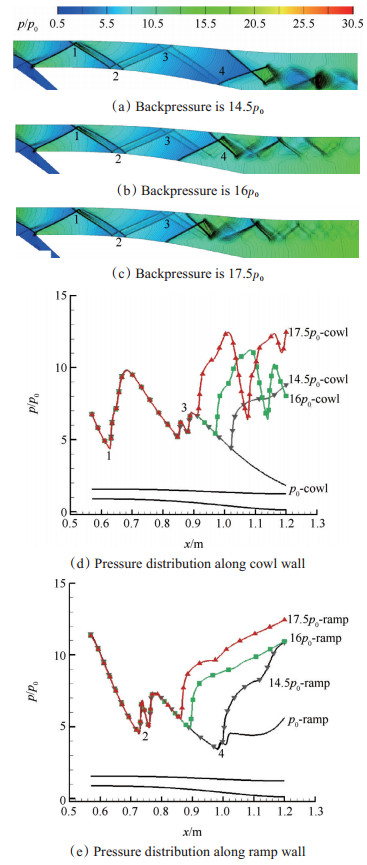
过程1:扩张段上壁面激波串前缘点在反射位置3之后,下壁面激波串前缘点在反射位置2,4之间,代表性的反压有14.5
|
Fig. 8 Stage 1, pressure contours of diffuser and pressure distribution along diffuser wall |
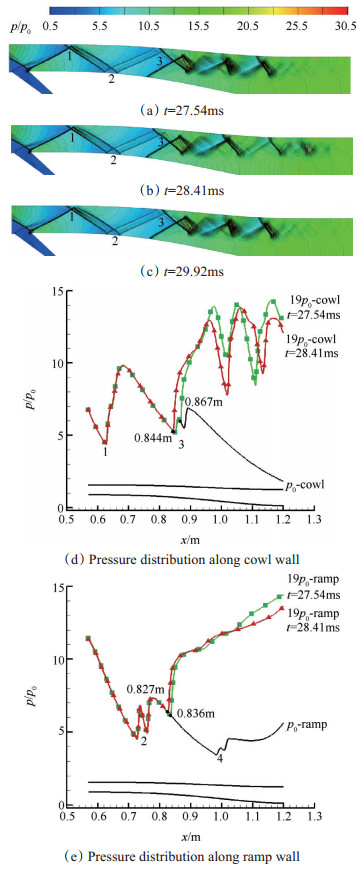
过程2:继续增大反压,流场由稳定状态变为不稳定,上壁面激波串前缘点在反射位置3的两束反射激波之间来回振荡,此时反压为19
|
Fig. 9 Stage 2, pressure contours of diffuser and pressure distribution along diffuser wall when backpressure is 19p0 |
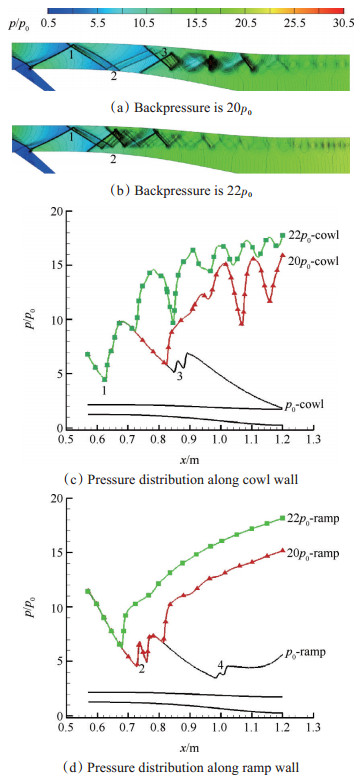
过程3:在这一过程,激波振荡由上阶段的大幅度振荡回归稳定,上壁面激波串前缘点位于反射位置1,3之间,代表性的反压有20
|
Fig. 10 Stage 3, pressure contours of diffuser and pressure distribution along diffuser wall |
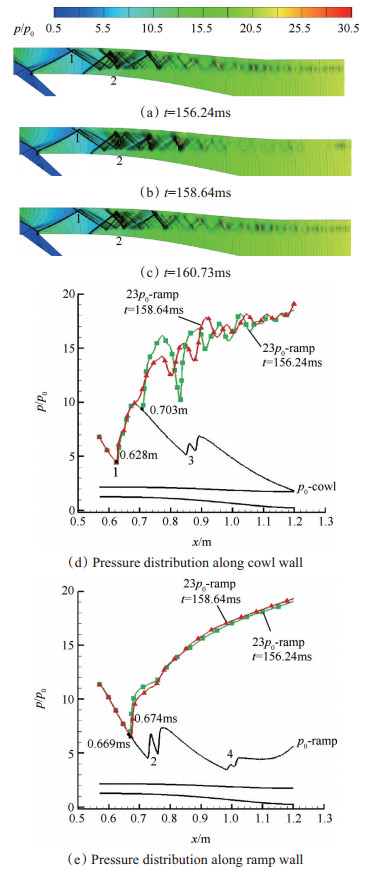
过程4:反压继续上升,上壁面激波串前缘点继续前移。由图 11中压力云图可以看出,反压为23
|
Fig. 11 Stage 4, pressure contours of diffuser and pressure distribution along diffuser wall when backpressure is 23p0 |
|
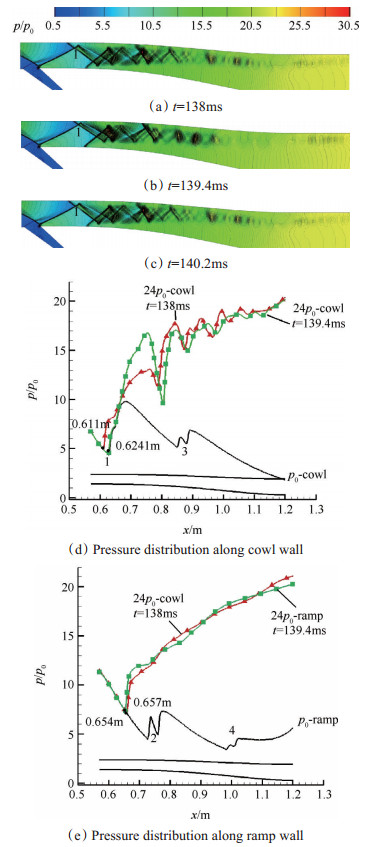
Fig. 12 Stage 4, pressure contours of diffuser and pressure distribution along diffuser wall when backpressure is 24p0 |
|
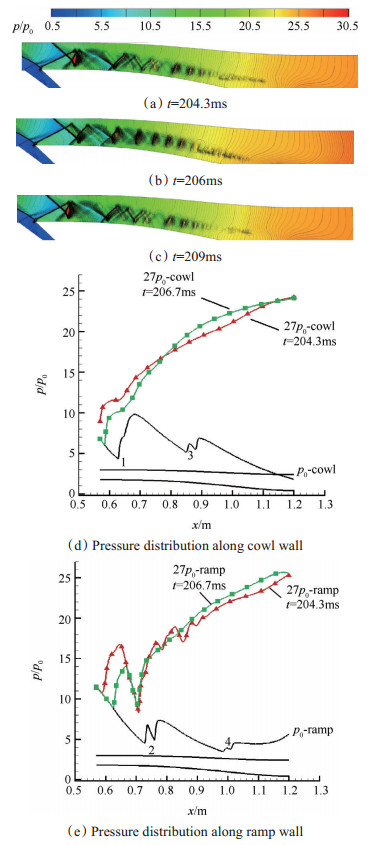
Fig. 13 Stage 4, pressure contours of diffuser and pressure distribution along diffuser wall when backpressure is 27p0 |
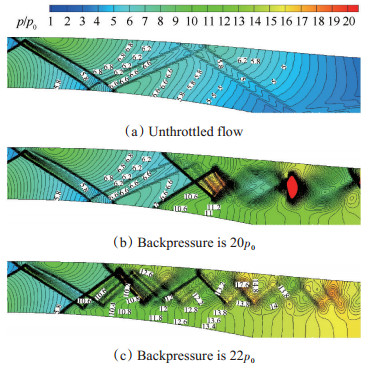
通过分析反压增大过程中扩张段内部四种流场结构,可知扩张段内的激波串结构随反压增大发生了由对称→非对称→对称→非对称的演化。结合各反压下扩张段内压力云图及壁面压力图,可知当激波串头激波与背景激波相交时,激波串出现小幅振荡,当激波串前缘点的位置处在扩张段上(凹)壁面存在逆压力梯度区域时,即背景激波反射点位置,或进气道处于临界工作状态,激波串会发生大幅振荡。
同时在计算过程中发现,下(凸)壁面激波串前缘点不会在激波反射位置2,4两处发生大幅振荡,而是缓慢越过两反射位置。出现这种现象主要是因为:激波反射位置2和4所处的壁面为凸曲面,壁面产生的微弱膨胀波束有助于气流加速,下壁面附近产生顺压力梯度区域,且等压线方向与下侧头激波方向基本一致,如图 14所示。当激波串头激波靠近两激波反射位置时,下侧头激波受到的阻力很小,会缓慢越过这两个反射位置,而不发生振荡,这也是激波串对称与不对称交错出现的原因。由此可以推断,壁面弯曲方式是激波串发生大幅自激振荡的影响因素。
|
Fig. 14 Pressure contour of diffuser |
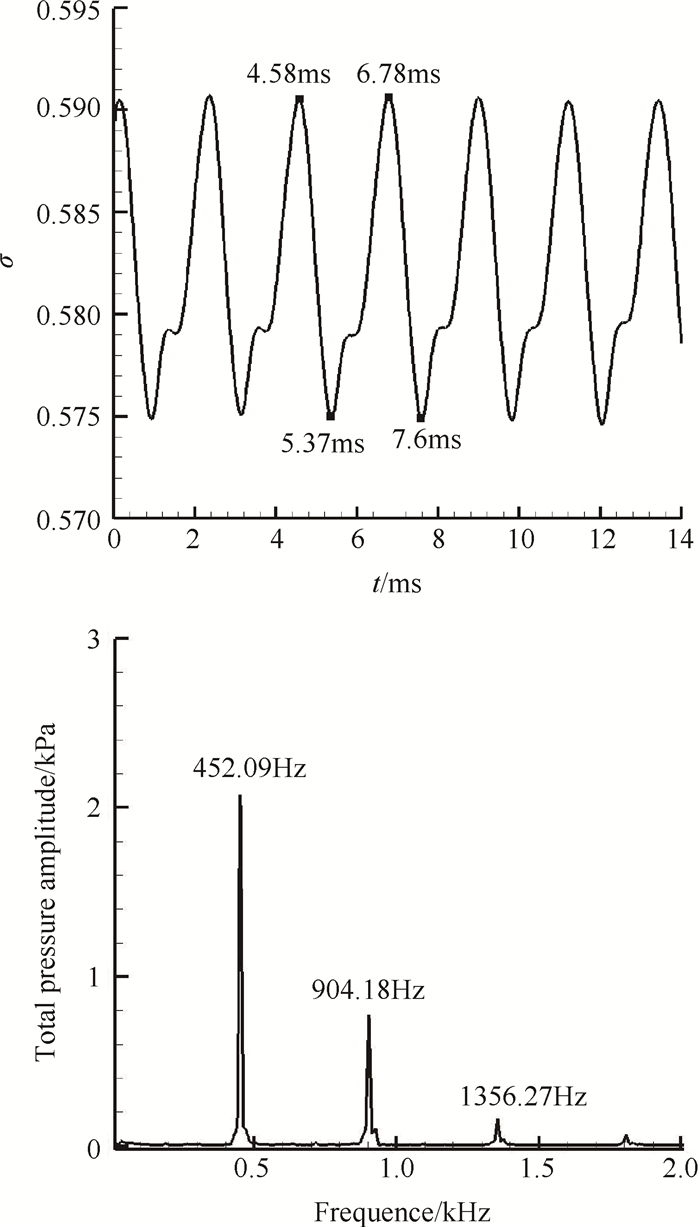
Sugiyama等[3]指出激波串振荡的原因在于激波串头激波根部的边界层分离运动,本节为了解激波串振荡和流动分离之间的联系,选择反压为24p0状态作为研究对象,计算得到进气道出口总压恢复系数和流量振荡曲线如图 15,16所示。该反压下由于扩张段内存在分离包,分离包一边从主流中卷携质量,一边结构脱落,流向下游边界层[20],两者之差造成监测面处的流量和总压恢复系数变化。
|
Fig. 15 Total pressure recovery coefficient oscillation curve of inlet exit and the FFT result as backpressure is 24p0 |
|
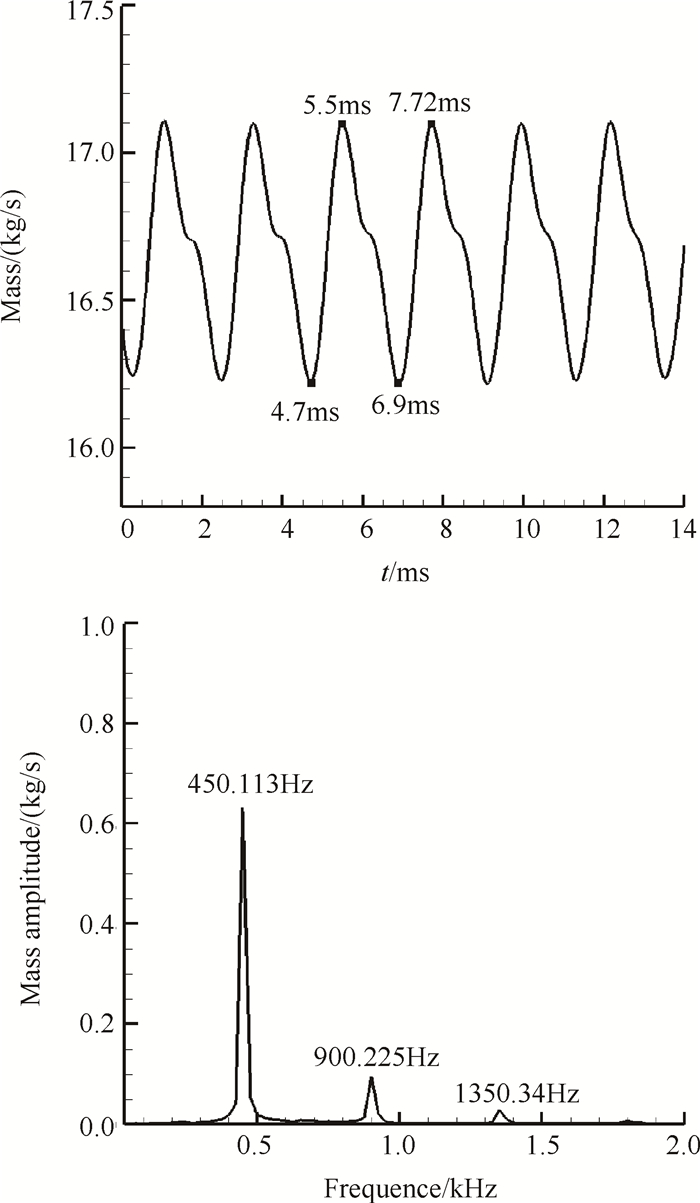
Fig. 16 Mass oscillation curve of inlet exit and the FFT result when backpressure is 24p0 |
图 15,16还给出了该反压下进气道出口的总压及流量随时间振荡的FFT分析,由FFT分析图可知,激波串振荡与分离包振荡的三个主频率几乎是相等的,说明激波串振荡和分离包运动有很强的相关性。由振荡曲线可知,t=5.37ms总压恢复系数最小,t=5.5ms流量才达到最大值,出口总压恢复数和流量存在相位差。
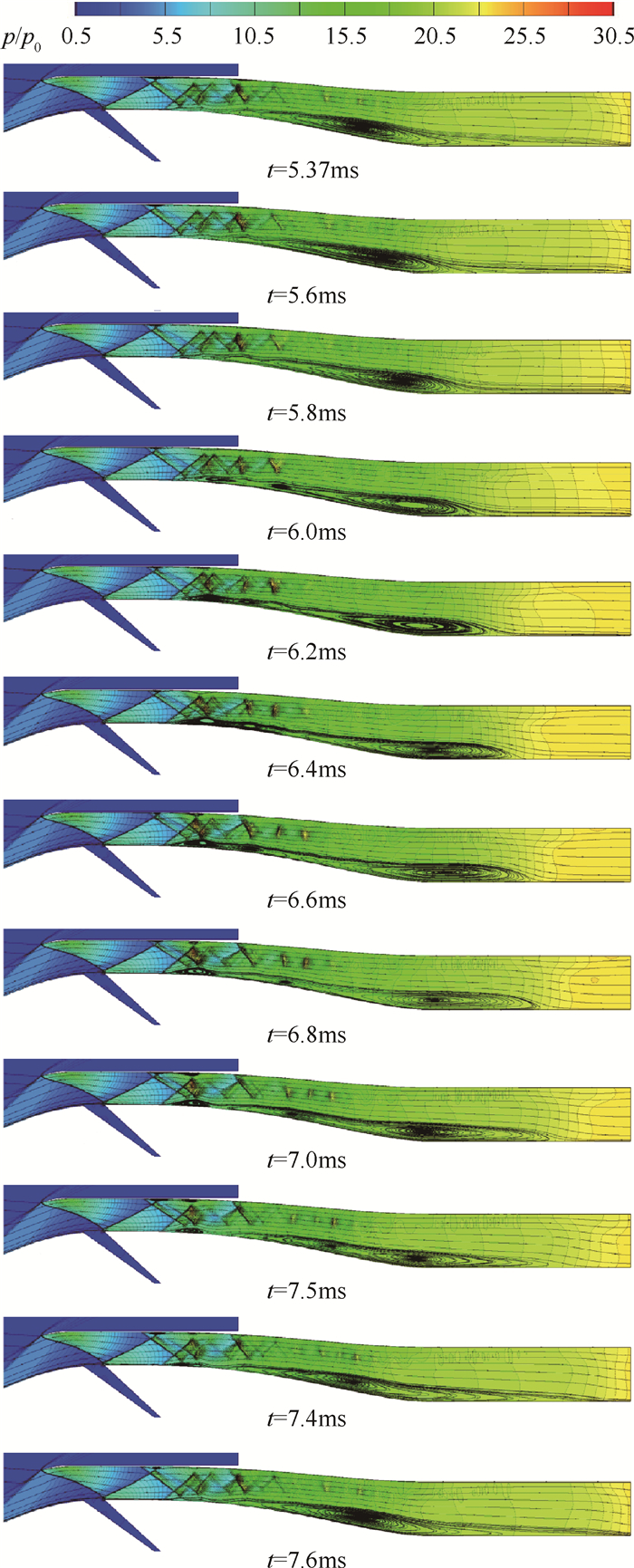
图 17为一个振荡周期内扩张段内部流线和压力分布图。可见分离包恰似一个弹簧,完成一个周期的伸缩变化,且可以发现分离包从最大缩小到最小所用时间要大于其从最小扩张到最大所用的时间(t=5.37ms时分离包最大,t=6.6ms时分离包最小)。这是因为当分离包最大时,分离区主要集中在下壁面型线的拐点处,气流再附点位置最为靠后,主流过渡较为平缓。当来流扰动增加,迫使分离包收缩时,气流再附点前移,此时流道面积在再附点位置突然增大,由于分离包自身很难维持这种流道面积的突变,所以一旦这种扰动减弱,分离包就会迅速扩张,回到较为稳定的下壁面拐点处,再附点也会向下游移动,主流道变得缓和。
|
Fig. 17 Streamline and pressure contours of the diffuser at one circle of oscillation when backpressure is 24p0 |
结合图 15,16,17,可知当t=5.37ms时,进气道出口总压恢复系数达到最小值,此时扩张段内部的分离区最大,出口流量接近最大值;而当t=6.78ms时,总压恢复系数达到最大值,分离区缩小至最小,出口流量接近最小值。出口总压恢复系数与流量的这种相反的变化关系主要是由于分离包变化所引起,当出口流量最小时,分离包最小,分离包内卷入较少的低能流,进入下游的主要为高能流,故此时总压恢复最大,反之亦然。
3.5 频域分析对各反压下计算得到的进气道出口总压进行快速傅里叶变换,得出了各反压下振荡频率及幅值,如表 1所示。
|
|
Table 1 Basic frequency and total pressure amplitude of inlet exit at different backpressure |
由表可知:扩张段内激波串自激振荡可以分为两种形式,一种是反压较低时,如14
对于激波串自激振荡频率,许多学者给出了预测公式。Hankey等[21]发现亚声速扩压段内部激波振荡现象的反馈机制,提出用波的传播理论预测振荡频率。按照作者的理论,本文通道可看作是一个入口为开口端,出口为闭口端的模型,计算频率公式为
| $ f=\left( 2n+1 \right)\frac{c\left( 1-{{\left( Ma \right)}^{2}} \right)}{4L} $ | (1) |
L=1.03m,为扩压段长度和后方等直段长度之和,反压为24
通过对二元超声速进气道进行数值模拟,对比不同反压下弯曲扩张段内的激波串振荡特性,可以得出以下结论:
(1)反压逐渐增大过程中,进气道所呈现出的流场结构和激波串振荡现象可以分为四个过程,激波串的结构发生了由对称→非对称→对称→非对称的演化,激波串振荡现象发生了由稳定→振荡→稳定→振荡的演化。
(2)当反压使激波串的头激波位于弯曲扩张段凹壁面背景激波反射位置附近或使进气道处于近临界工作状态时,激波串发生大幅低频振荡,振动频率为200~500Hz,其它反压下发生小幅高频振荡,振动频率大于900Hz,壁面形状和背景激波的逆压力梯度是激波串大幅自激振荡的影响因素。
(3)在激波串一个振荡周期内,进气道出口流量接近最小值时,总压恢复系数到达最大值,反之亦然。扩张段内部激波串振荡和分离包运动有很强的相关性。
| [1] |
Weise A. The Separation of Flow Due to Compressibility Shock[R]. NACA TM 1152, 1947.
(  0) 0) |
| [2] |
Ikui T, Matsuo K, Nagai M, et al. Oscillation Phenomena of Pseudo-Shock Waves[J]. Bulletin of the JSME, 1974, 17(112): 1278-1285. DOI:10.1299/jsme1958.17.1278
(  0) 0) |
| [3] |
Sugiyama H, Takeda H, Zhang J, et al. Locations and Oscillation Phenomena of Pseudo-Shock Waves in a Straight Rectangular Duct[J]. JSME International Journal, 1988, 31(1): 9-15.
(  0) 0) |
| [4] |
Robinet J C, Casalis G. Shock Oscillation in Diffuser Modeled by a Selective Noise Amplification[J]. AIAA Journal, 1999, 37(4): 453-459. DOI:10.2514/2.755
(  0) 0) |
| [5] |
Sajben M, Donovan J F, Morris M J. Experimental Investigation of Terminal Shock Sensors for Mixed-Compression Inlets[J]. Journal of Propulsion and Power, 1992, 8(1): 168-174. DOI:10.2514/3.23457
(  0) 0) |
| [6] |
谭慧俊, 郭荣伟. 二维弯曲等截面管道中的激波串特性研究[J]. 航空学报, 2006, 27(6): 1039-1045. DOI:10.3321/j.issn:1000-6893.2006.06.010 (  0) 0) |
| [7] |
Huijun Tan, Shu Sun. Preliminary Study of Shock Train in a Curved Variable-Section Diffuser[J]. Journal of Propulsion and Power, 2008, 24(2): 246-252.
(  0) 0) |
| [8] |
Su Weiyi, Zhang Kunyuan. Back-Pressure Effects on the Hypersonic Inlet-Isolator Pseudoshock Motions[J]. Journal of Propulsion and Power, 2013, 29(6): 1391-1399. DOI:10.2514/1.B34803
(  0) 0) |
| [9] |
Hsieh T, Wardlaw A B, Coakley T. Ramjet Diffuser Flowfield Response to Large-Amplitude Combustor Pressure Oscillations[J]. Journal of Propulsion and Power, 1987, 3(5): 472-477. DOI:10.2514/3.23013
(  0) 0) |
| [10] |
田旭昂, 王成鹏, 程克明. Ma5斜激波串动态特性实验研究[J]. 推进技术, 2014, 35(8): 1030-1039. (TIAN Xu-ang, WANG Cheng-peng, CHENG Ke-ming. Experimental Investigation of Dynamic Characteristics of Oblique Shock Train in Mach 5 Flow[J]. Journal of Propulsion Technology, 2014, 35(8): 1030-1039.)
(  0) 0) |
| [11] |
熊冰, 范晓樯, 王振国. 中心偏置隔离段内激波串迟滞特性研究[J]. 推进技术, 2016, 37(5): 864-870. (XIONG Bing, FAN Xiao-qiang, WANG Zhen-guo. Hysteresis Characteristics of Shock Train in Deflected Center-Line Isolator[J]. Journal of Propulsion Technology, 2016, 37(5): 864-870.)
(  0) 0) |
| [12] |
熊冰, 王振国, 范晓樯, 等. 隔离段内正激波串受迫振荡特性研究[J]. 推进技术, 2017, 38(1): 1-7. (XIONG Bing, WANG Zhen-guo, FAN Xiao-qiang, et al. Characteristics of Forced Normal Shock-Train Oscillation in Isolator[J]. Journal of Propulsion Technology, 2017, 38(1): 1-7.)
(  0) 0) |
| [13] |
Yamane R, Kondo E, Tomita Y, et al. Vibration of Pseudo-Shock in Straight Duct, 1st Report, Fluctuation of Static Pressure[J]. Transaction of the JSME B, 1984, 27(229): 1385-1392. DOI:10.1299/jsme1958.27.1385
(  0) 0) |
| [14] |
Yamane R, Takahashi M, Saito H. Vabration of Pseudo-Shock in Straight Duct, 2nd Report. Correlation of Static Pressure Fluctuation[J]. JSME International Journal, 1984, 27(229): 1393-1398. DOI:10.1299/jsme1958.27.1393
(  0) 0) |
| [15] |
Hiromu, Sugiyama, Ryojiro, et al. Study on Shock Wave and Turbulent Boundary Layer Interactions in a Square Duct at Mach 2 and 4[J]. Journal of Thermol Science, 2000, 15(1): 37-42.
(  0) 0) |
| [16] |
Tan Huijun, Sun Shu, Huang Hexia. Behavior of Shock Trains in a Hypersonic Inlet/Isolator Model with Complex Background Waves[J]. Experiments in Fluids, 2012, 53(6): 1647-1661. DOI:10.1007/s00348-012-1386-1
(  0) 0) |
| [17] |
Li Zhufei, Gao Wenzhi, Jiang Hongliang, et al. Unsteady Behaviors of a Hypersonic Inlet Caused by Throttling in Shock Tunnel[J]. AIAA Journal, 2013, 51(10): 2485-2492. DOI:10.2514/1.J052384
(  0) 0) |
| [18] |
Lee C, Boedicker C. Subsonic Diffuser Design and Performance for Advanced Fighter Aircraft[C]. Colorado: Aircraft Design Systems and Operations Meeting, 1985.
(  0) 0) |
| [19] |
Reinartz B U, Herrman C D, Ballmann J. Aerodynamic Performance Analysis of a Hypersonic Inlet Isolator Using Computation and Experiment[J]. Journal of Propulsion and Power, 2003, 19(5): 868-875. DOI:10.2514/2.6177
(  0) 0) |
| [20] |
Piponniau S, Dussauge J P, Debieve J F, et al. Simple Model for Low Frequency Unsteadiness in Shock-Induced Separation[J]. Journal of Fluid Mechanics, 2009, 629: 87-108. DOI:10.1017/S0022112009006417
(  0) 0) |
| [21] |
Hankey W L, Shang J S. Analysis of Self-Excited Oscillations in Fluid Flow[R]. AIAA 80-1346.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


