2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
进气系统是为压气机供气的重要装置。进气系统应尽量减少气流的流动损失,避免出现气流局部降速和分离,出口流场要尽量均匀,无周向旋绕。Williams指出,进气周向不均引起的畸变会使得压气机性能下降较为明显[1]。
对于双轴压气机实验平台,进气系统形式受制于平台驱动方案。美、俄等国在研制这类平台时大都采取的是稳定性较高的动力对置方案——驱动系统分别从实验平台两端传动[2]。这种驱动方案导致进气系统只能采用径向进气方式。径向进气系统设计准则不成熟,较难保证供气品质,因此其设计是研制此类实验平台的重点和难点。
径向进气系统主要包括进气道与进气蜗壳。进气道一般为圆形截面的弯管或者直管,进气蜗壳结构及内部流动则较为复杂。
Flathers等对进气蜗壳出口截面的10个周向位置采用三孔探针进行测量,并首次使用考虑粘性作用的三维CFD技术模拟进气蜗壳的流动情况[3]。CFD技术的引入让学者们认识到进气蜗壳内部流动十分复杂:气流从蜗壳单侧进入后难以在周向上均匀分布;在气流从径向折转为轴向时,气流易在径向上存在不均。然而对于进气蜗壳的设计依然停留在简单的一维无粘方法。学者们研究重点集中在如何改进蜗壳的结构以提升蜗壳的出口气流品质。
Simone等对进气蜗壳结构改进的研究结果很细致且很有启发性[4]。Simone等认为气流进入蜗壳后,分为两大部分:有一部分直接从顶部进入环形通道,另外部分沿着周向旋转再进入环形通道,在旋转过程中伴随着漩涡产生。前者比例通常大于后者,导致蜗壳出口不均并存在一定的气流角。基于这种分析,他们对蜗壳结构进行改进。方法是在不同周向位置前后移动唇边的位置,以控制周向各处的进气面积。最后得到的改进结构中,蜗壳顶部的唇边位置向前移动以减小进气面积,蜗壳底部则相反。
在进气蜗壳内加入导流叶片是改善蜗壳内部流动、提升出口气流品质的重要手段。导流叶片能够帮助气流从径向折转为轴向,同时也改变蜗壳在周向上的阻力,有利于气流在周向均匀分布。Kim等对某进气蜗壳内的导流叶片安装角进行优化[5]。原结构中导流叶片存在较大攻角使得叶背处发生分离,经过对叶片调整优化后,导流叶片攻角减少,蜗壳出口气流角降低,均匀性提高。Simone等研究了叶片数目对出口气动参数分布的影响[4],研究结果表明叶片数目增多能够减少出口气流角,提升气流均匀性,但同时也会带来蜗壳内流动损失的增加。
相比于进气蜗壳,学者们对进气道的研究较少。Koch等的研究结果表明,当进气道破坏整个进气系统的对称性时,它将对进气蜗壳出口分布产生不利影响[6]。Engeda等研究了含有弯头的进气道对压气机性能的影响,结果显示弯头中加入导流叶片能够有效抑制弯头结构产生的二次流,从而使压气机的进气畸变减弱[7]。
在国内,王锐等研究了进气蜗壳内部的流动受下游离心叶轮的影响[8]。韩凤翚、谭佳健等对某进气蜗壳进出口及内部展开细致的测量[9]。陈宗华等以级等熵效率为优化目标,采用神经网络方法对某进气蜗壳的子午型线进行改进[10]。经优化后,轮盖侧及子午侧型线均向流动区域偏移,级效率在设计流量点提高了1.26%。
综上,进气系统设计准则不成熟,出口气流品质难以保证。为改善蜗壳内部流动、提升蜗壳出口气流品质,学者们多采用导流叶片的手段,然而对于导流叶片的调整是一个基于模拟结果反复试错修正的过程,有时还存在导流叶片变工况时难以导流的问题,故这种方法易用性较差。因此在改善蜗壳流动方面还缺乏较为简单有效的方法。
本文作者已从以国内首台双轴压气机实验平台的研制需求出发,得出了一种新颖高效的径向进气系统设计方案。该系统新颖之处是在流道折转处布置蜂窝整流器来改善气流流动。蜂窝整流器由于其多孔平行通道的结构不仅能够均流和消除气流脉动,还可以起到导向作用。然而,蜂窝器一般被布置在直管段[11, 12],其导向作用体现的并不明显。将其布置在进气系统中需均流及导向的位置,利用其气动特性改善流动,是值得研究和探讨的新颖方案。
本文在之前的研究基础上[13]对蜂窝器在进气道内的布置位置进行了探讨,并展开了对该进气系统在小流量工况下的实验研究,以考察数值方法的准确性及设计方案的先进性。
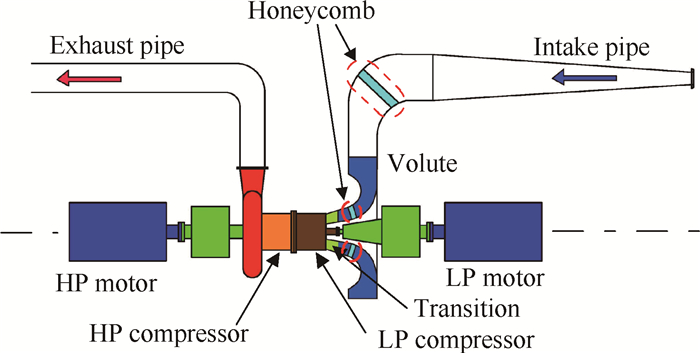
2 设计方案图 1为双轴压气机实验平台的整体布置。实验平台采用动力对置的驱动方案,即高、低压级电机(蓝色)及齿轮箱(绿色)分别位于实验段两端。受驱动方案的限制,进气系统需采用径向进气方式。
|
Fig. 1 Scheme of test rig |
进气系统主要包括进气道、进气蜗壳和过渡段。为减少平台的侧向尺寸,进气道折转90°与进气蜗壳的一侧相连。进气蜗壳在设计上存在诸多物理限制因素。轴向上受制于齿轮箱的延伸轴长度,径向上受制于实验平台的中心高。另外,蜗壳中心需要穿轴,为避免干涉蜗壳内侧的型线也受到限制。过渡段用来连接实验件与进气蜗壳,由于在实验平台试车的实验件有多个,它们进口尺寸各异,因此需要分别设计多个过渡段来与不同的实验件匹配。
综上,该进气系统需在有限空间内完成气流的折转(进气道及蜗壳内两次折转)与分配(单侧局部进气转为全周进气),同时在全流量范围内(0~20kg/s)保证较高供气品质。
经过多轮设计和优化满足要求的完整的径向进气系统。在进气道及蜗壳气流折转角度较大的位置处布置有蜂窝器来改善流动,其具体位置参见图 1中红圈处。以下针对蜂窝器在进气道的位置讨论和分析,并对蜗壳方案进行简介。模拟计算方法在文献[13]中进行了详细介绍。
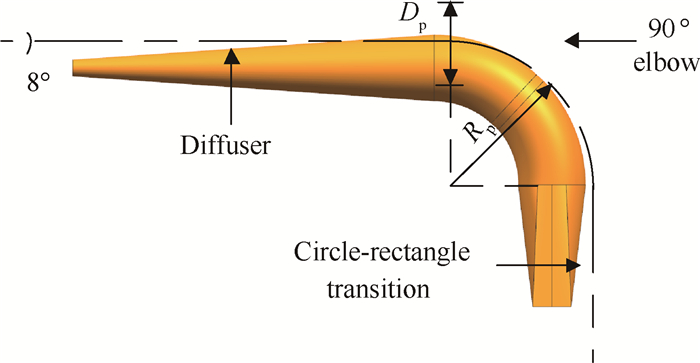
2.1 进气道方案进气道由扩张段、90°弯头和圆变方转接段组成。在一定轴向长度及侧向空间限制下,扩张角选取较大会引起流动分离,较小则使得扩张段过长压缩下游弯头折转半径。弯头处的曲率半径
|
Fig. 2 Intake pipe scheme (Case origin) |
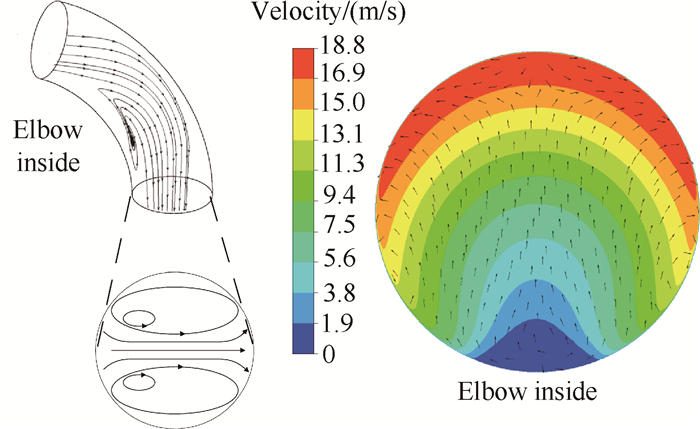
以20kg/s为分析工况,该工况点是进气系统的最大流量点。图 3显示气流在进气道的流动情况。从流线图可以看出,气流在弯头内侧发生明显的流动分离。在弯头处,由于流动折转产生的离心力诱导气流从内侧运动至外侧,受到外侧壁面的阻碍气流最后分为两股沿着壁面返至内侧,在弯头出口截面处的对涡结构被称之为迪恩涡(Dean vortex),截面速度分布呈现“C”型(见速度云图)[15]。这种二次流叠加至主流的结果是大量受到壁面剪切作用的低能流体被输运至弯头内侧,聚集的低能流体导致弯头内侧较易发生流动分离。在进气道出口处,气流角在弯头内侧较大。
|
Fig. 3 Flow condition at elbow |
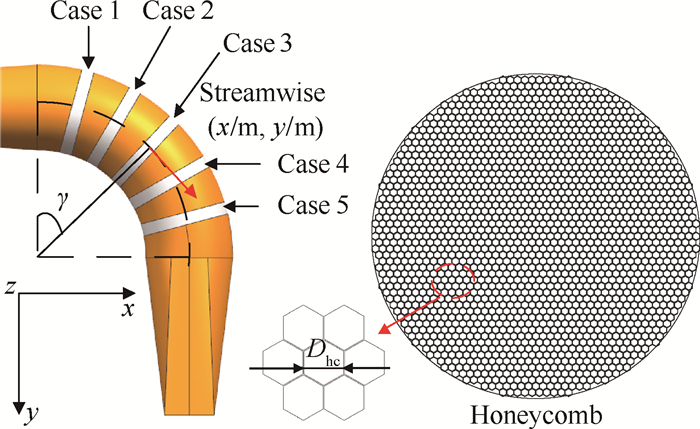
从以上分析可知,在进气道的弯头处,气流由于折转较为剧烈在弯头内侧发生流动分离,流动较为紊乱。为改善气流在弯头处的流动,考虑在其中加入蜂窝器。在弯头折转处布置蜂窝器,目的是为调整气流方向,帮助气流折转。本文分别在弯头处的5个位置布置圆柱形蜂窝器,对比各方案下的计算结果,以选取较佳的布置位置。蜂窝器长度为200mm。表 1为蜂窝器位置及流向。图 4为蜂窝器各方案的示意,γ为蜂窝器在弯头处的位置角度,蜂窝器单元内接圆直径
|
|
Table 1 Modified schemes of intake pipe |
|
Fig. 4 Modified schemes with honeycomb of intake pipe |
用进气道出口截面的气流角来考察改进方案的导流效果。气流角定义为
| $ {\alpha _{\rm{s}}} = {\rm{atan}}\left( {\sqrt {V_x^2 + V_z^2} /{V_y}} \right) $ | (1) |
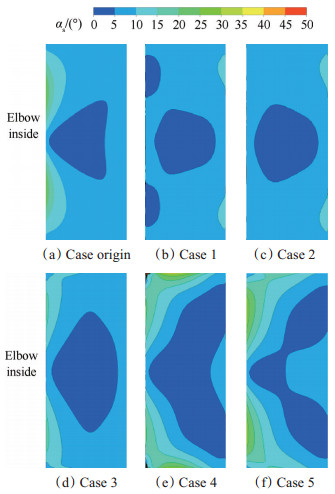
图 5为进气道出口截面的气流角,图 5(a)为原始方案,图 5(b)~(f)为蜂窝器方案。蜂窝器的加入显著的改变了出口截面气流角分布。当蜂窝器布置在弯头前半部及中部(15°,30°,45°)时,气流角整体分布较好,当蜂窝器布置在弯头后半部(60°,75°)时,气流角整体分布明显较差。在Case 1~3中,大部分区域的气流角均在10°以内,壁面附近的气流角稍大。而在Case 4~5中,弯头内侧的壁面附近区域气流角较大。
|
Fig. 5 Outlet flow angle at exit of intake pipe |
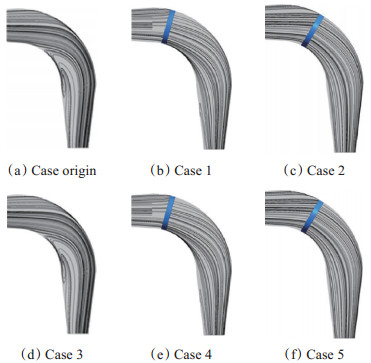
图 6为各种情况下弯头处的流线。蜂窝器与分离点的相对位置是关系到蜂窝器能否发挥改善作用的关键。可以观察到,在Case origin中流动分离基本在弯头内侧约45°位置开始发生,卷起的分离漩涡占据了流道内侧区域,造成出口截面内侧处气流角较大。在Case 1~3中,位于弯头中部15°,30°,45°处的蜂窝器起到较好的导流效果,流线大致按照弯头流道的形状折转,弯头内侧的流动分离受到抑制,分离区域消失。在Case 5中,蜂窝器位于弯头的后半部,此时蜂窝器上游、弯头内侧的气流已经发生流动分离,即使经过蜂窝器的导向整流,下游的流动情况依旧较为恶劣。
|
Fig. 6 Streamline at elbow |
综上分析,将蜂窝器布置在弯头前半部或中部,流动分离原本开始发生的位置上游或附近时,弯头内侧的流动分离将会受到抑制,进气道出口气流角分布有所改善;将蜂窝器放置于弯头后半部时,流动分离依然会发生,进气道出口气流角分布更为恶化。综合考虑导流效果以及安装的便易性,选取Case 3方案为进气道的较优方案。
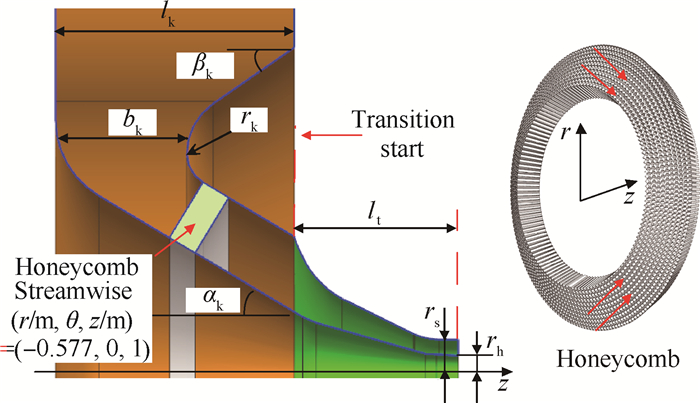
2.3 蜗壳方案图 7为蜗壳子午面的中剖面及蜂窝器的示意图。中剖面结构参数如表 2所示。表 2中,
|
Fig. 7 Volute within honeycomb inside |
|
|
Table 2 Geometrical parameters of volute |
为考察进气系统的性能、验证设计方案的先进性,对进气系统的出口处气动参数分布进行测量。采用的实验件为某双轴结构的离心压气机低压级。
3.1 测量工具及测量位置测量流场的主要工具是五孔探针,共有三支。图 8显示了探针五个探孔的位置。五孔探针在使用前须经过校准风洞的标定。在风洞中,将探针固定在五自由度位移机构上,通过改变探针相对来流的角度以及来流马赫数来获取探针的校准系数。

|
Fig. 8 Probe holes |
对于各校准设备的精度,大气压力计为±20Pa,位移机构为0.005°,风洞总压为±0.05%。各校准系数如下
| $ {p_{{\rm{ave}}}} = \left( {{p_1} + {p_3} + {p_4} + {p_5}} \right)/4 $ | (2) |
| $ {K_{\rm{ \mathsf{ α} }}} = \left( {{p_1} - {p_3}} \right)/{p_{{\rm{ave}}}} $ | (3) |
| $ {K_{\rm{ \mathsf{ β} }}} = \left( {{p_4} - {p_5}} \right)/{p_{{\rm{ave}}}} $ | (4) |
| $ {K_{\rm{M}}} = \left( {{p_2} - {p_{{\rm{ave}}}}} \right)/{p_2} $ | (5) |
| $ {K_{\rm{t}}} = ({p^{\rm{*}}} - p{}_2^{})/\left( {{p_2} - {p_{{\rm{ave}}}}} \right) $ | (6) |
| $ {K_{\rm{q}}} = \left( {{p^{\rm{*}}} - p} \right)/\left( {{p_2} - {p_{{\rm{ave}}}}} \right) $ | (7) |
式中
|
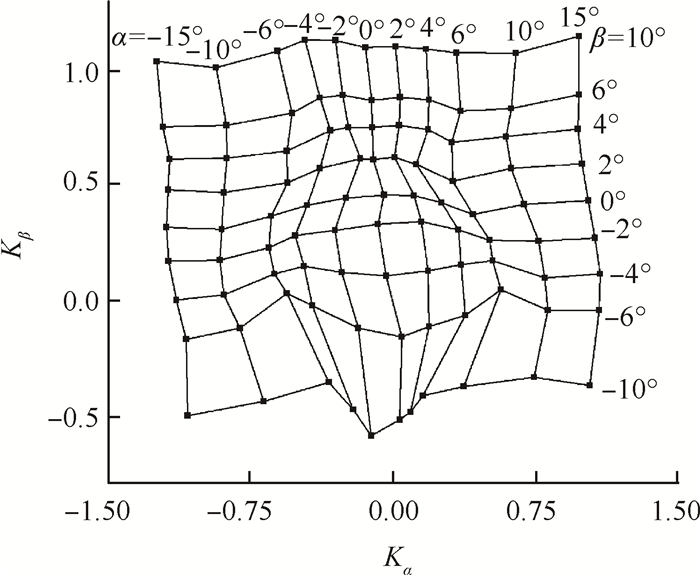
Fig. 9 Calibration coefficients of five hole |
通过标定数据,拟合出五孔压力与气流的偏航角α,俯仰角β,总压系数
| $ \begin{array}{l} A = C_1^{} + C_2^{}{K_\alpha } + C_3^{}{K_{\rm{ \mathsf{ β} }}} + C_4^{}{K_{\rm{M}}} + C_5^{}K_{\rm{ \mathsf{ α} }}^2 + \\ \;\;\;\;\;\;C_6^{}K_{\rm{ \mathsf{ β} }}^2 + C_7^{}K_{\rm{M}}^2 + C_8^{}{K_{\rm{ \mathsf{ α} }}}{K_{\rm{ \mathsf{ β} }}} + C_9^{}{K_{\rm{ \mathsf{ α} }}}{K_{\rm{M}}} + \\ \;\;\;\;\;\;C_{10}^{}{K_{\rm{ \mathsf{ β} }}}{K_{\rm{M}}} + C_{11}^{}K_{\rm{ \mathsf{ α} }}^3 + C_{12}^{}K_{\rm{ \mathsf{ β} }}^3 + C_{13}^{}K_{\rm{M}}^3 + \\ \;\;\;\;\;\;C_{14}^{}K_{\rm{ \mathsf{ α} }}^2{K_{\rm{ \mathsf{ β} }}} + C_{15}^{}{K_{\rm{ \mathsf{ α} }}}K_{\rm{ \mathsf{ β} }}^2 + C_{16}^{}{K_{\rm{ \mathsf{ α} }}}{K_{\rm{M}}} + \\ \;\;\;\;\;\;C_{17}^{}{K_{\rm{ \mathsf{ α} }}}K_{\rm{M}}^2 + C_{18}^{}K_{\rm{ \mathsf{ β} }}^2{K_{\rm{M}}} + C_{19}^{}{K_{\rm{ \mathsf{ β} }}}K_{\rm{M}}^2 + C_{20}^{}{K_{\rm{ \mathsf{ α} }}}{K_{\rm{ \mathsf{ β} }}}{K_{\rm{M}}} \end{array} $ | (8) |
拟合值与风洞的测量值之间存在误差表示为
| $ \sigma \left( A \right)=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}{{{({{A}_{\text{exp}}}-{{A}_{\text{fit}}})}^{2}}}} $ | (9) |
三支探针的拟合误差如表 3所示。
|
|
Table 3 Error of fitting |
考虑到探针安装座的加工便易性及实验件的结构限制,测量的位置选择在过渡段上,具体如图 10及图 11。探针杆身方向与过渡段外侧壁面的法线方向相同,垂直于杆身的探头在流道内所对的方向与流向有一定的偏差。在周向上,过渡段上每隔18°加工有一个探针安装座(除在90°及270°位置外);在展向上,探针的探头位于流道的中部位置。图 11中标示出了五孔探针的偏航角及俯仰角的定义。

|
Fig. 10 Pictures of real test rig |

|
Fig. 11 Measurement positions at transition |
测量中记录的数据包括进气系统的流量、大气温度和五孔探针在周向各个位置的压力数据。测量时调整转速保证进气系统的折合流量为3.00kg/s。进气系统的折合流量计算公式为
| $ {m_{{\rm{cor}}}} = {m_{\rm{a}}}\sqrt {\frac{{T_{\rm{a}}^{\rm{*}}}}{{288}}} \frac{{101325}}{{p_{\rm{a}}^{\rm{*}}}} $ | (10) |
式中
除五孔探针外,实验还采用总压探针对气流总压进行复测以验证五孔探针测量结果。另外,实验还对外壁面静压进行测量。上述两种方法测量精度分别为0.2%与0.3%。
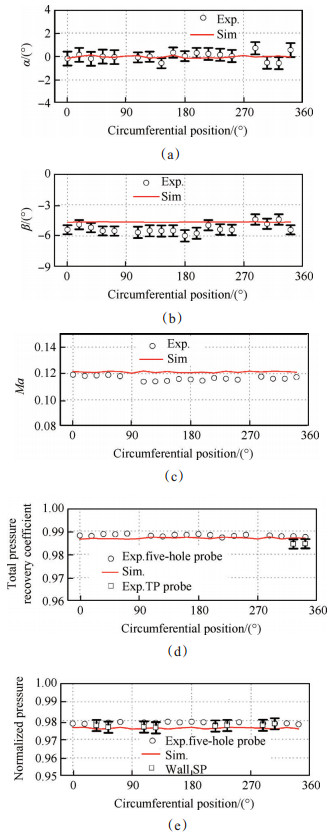
3.2 测量结果图 12展示了测量结果与模拟计算结果的对比。在测量结果中,使用总压恢复系数表示总压,对静压通过大气压力进行归一化处理。俯仰角与偏航角加入了拟合误差带,总压探针及壁面静压结果加入了测量误差带。文献[13]已对模拟计算方法详细介绍。
|
Fig. 12 Experimental and simulation results |
从图 12可以看出,各气动参数沿周向十分均匀。反映气流周向偏转的偏航角测量值在整个周向上最大值不超过2°,这表明气流的周向运动十分微弱,也从侧面反映了气动参数在周向的均匀性,计算结果与测量值相差不大。
在进气道内,布置的蜂窝器所起的抑制分离作用能为下游的蜗壳提供较好的来流。在蜗壳内,蜂窝器的流阻特性能够起到分配来流的作用,在亚音速环境下气流对于流阻的自适应特性提高了气流在周向上的均匀性。另外,当气流通过蜂窝器时,由于蜂窝器的导向作用,气流的周向运动进一步被抑制。因此,在过渡段处的气流沿周向十分均匀。
由于过渡段流道的内外侧壁面不平行,与外侧壁面垂直的探针会与主流方向存在一定的夹角,计算结果显示当地气流与探针方向的俯仰角为4.25°左右,测量值相比计算结果幅值稍微偏大。
对于气流的马赫数、静压,计算值与测量值均相差不大。气流总压恢复系数大于98.3%,计算值略小于实验结果,这可能是由于计算时采用的多孔介质模型中选取的阻力参数偏大以及加工精度引起的实际模型与计算模型的差异。五孔探针与总压探针两种方法的测量值接近,这证明了五孔探针测量结果较为可信。壁面静压稍微低于气流静压,说明气流沿展向变化不大。
4 结论本文对双轴压气机实验平台的径向进气系统进行数值及实验研究,得到以下结论:
(1)在弯头的前半部及中部加入蜂窝器能够更好地抑制弯头处的流动分离。
(2)实验结果表明小流量工况下在测量位置处,气流在周向上的偏航角小于2°,俯仰角在-4.5°左右,总静压及马赫数均较为均匀。总压恢复系数大于98.3%。实验结果与模拟结果吻合较好,验证了数值研究方法的可信度和可靠性,同时也证明该进气系统的先进性。
| [1] |
Williams D D. Review of Current Knowledge on Engine Response to Distorted Inlet Flow Conditions[R]. AGARD CP-400, 1986.
(  0) 0) |
| [2] |
管前列. 国外双轴压气机实验技术[J]. 推进技术, 1996, 17(2): 88-92. (GUAN Qian-lie. Test Technique of Dual-Spool Compressor System Abroad[J]. Journal of Propulsion Technology, 1996, 17(2): 88-92. DOI:10.3321/j.issn:1001-4055.1996.02.021)
(  0) 0) |
| [3] |
Flathers M, Bache G E, Rainsberger R. An Experimental and Computational Investigation of Flow in a Radial Inlet of an Industrial Pipeline Centrifugal Compressor[R]. ASME 94-GT-134.
(  0) 0) |
| [4] |
Simone P, Vittorio M. Analysis and Design Outlines of Centrifugal Compressor Inlet Volutes[R]. ASME 2000-GT-0464.
(  0) 0) |
| [5] |
Kim Y, Koch J. Design and Numerical Investigation of Advanced Radial Inlet for a Centrifugal Compressor Stage[R]. IMECE 2004-60538 https://www.netl.doe.gov/File%20Library/Research/Oil-Gas/41643_ASME_full_draft_radial_inlet.pdf
(  0) 0) |
| [6] |
Koch J M, Chow P N, Hutchinson B R, et al. Experimental and Computational Study of a Radial Compressor Inlet[R]. ASME 95-GT-082.
(  0) 0) |
| [7] |
Engeda A, Kim Y, Aungier R, et al. The Inlet Flow Structure of a Centrifugal Compressor Stage and Its Influence on the Compressor Performance[J]. Journal of Fluids Engineering, 2003, 125(5): 779-785. DOI:10.1115/1.1601255
(  0) 0) |
| [8] |
王锐, 祁大同, 王学军, 等. 离心压缩机径向吸气室内部流动的数值研究[J]. 流体机械, 2008, 36(6): 19-24. DOI:10.3969/j.issn.1005-0329.2008.06.005 (  0) 0) |
| [9] |
Han F, Qi D, Tan J, et al. Experimental and Numerical Investigation of the Flow Field in the Radial Inlet of a Centrifugal Compressor[R]. ASME 2012-GT-69353.
(  0) 0) |
| [10] |
陈宗华, 谷传纲, 舒信伟. 基于CFD技术的离心压缩机径向进气室结构形状优化设计[J]. 机械工程学报, 2010, 46(14): 124-129. (  0) 0) |
| [11] |
刘子娟. 主动控制湍流模拟风洞系统设计[D]. 上海: 上海交通大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10248-1013021436.htm
(  0) 0) |
| [12] |
蒋啸, 张启璆. 风量测量用整流器的实验研究[J]. 中国电机工程学报, 2006, 26(14): 104-108. DOI:10.3321/j.issn:0258-8013.2006.14.019 (  0) 0) |
| [13] |
邵冬, 孙志刚, 吴世勋, 等. 一种新颖径向进气系统的研究[J]. 推进技术, 2017, 38(12). (SHAO Dong, SUN Zhi-gang, WU Shi-xun, et al. Investigation on a Novel Radial Air Intake System[J]. Journal of Propulsion Technology, 2017, 38(12).)
(  0) 0) |
| [14] |
Kim J, Yadav M, Kim S. Characteristics of Secondary Flow Induced by 90-Degree Elbow in Turbulent Pipe Flow[J]. Engineering Applications of Computational Fluid Mechanics, 2014, 8(2): 229-239. DOI:10.1080/19942060.2014.11015509
(  0) 0) |
| [15] |
Dean W R, Hurst J M. Note on the Motion of Fluid in a Curved Pipe[J]. Mathematika, 1959, 6(1): 77-85. DOI:10.1112/S0025579300001947
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


