2. 辽宁省重点实验室-船舶安全与污染控制技术研究中心, 辽宁 大连 116026;
3. 大连海事大学 航海学院, 辽宁 大连 116026
2. Key Laboratory of Liaoning Province-Ship Security and Pollution Prevention Technology Research Center, Dalian 116026, China;
3. Department of Navigation, Dalian Maritime University, Dalian 116026, China
海洋环境流场包括波浪、水流对船舶推进性能具有极其重要的影响, 当前关于环境流场对船舶推进性能的研究大多基于物理船池实验, 但物理船池实验及测试设备造价、维护管理成本高, 实验周期长, 实验过程中船舶及推进器周围流场很难做到实时全方位监测, 通常会忽略某些重要的流场细微变化[1~3], 基于此, 越来越多学者建立了船舶数值波浪水池, 为船舶推进技术及船舶水动力计算的发展提供了精确有效的数值平台。而其中造波技术及消波技术是建立船舶数值波浪水池的关键, 当前主要的造波方法有仿物理造波方法及域内源项造波方法, 前者包括推板造波方法和摇板造波方法[4~6], 以及由推板造波方法衍生的设置速度入口造波方法[7, 8], 域内源造波方法主要包括以下几方面: (1)设置造波区域速度和压力造波方法[9]; (2)动量源造波方法(也称解析松弛造波方法)[10, 11]; (3)质量源造波方法(包括线源及域源造波法)[12, 13], 主要的消波技术有阻尼消波及解析松弛消波法。在进行船舶推进及水动力计算时绝大多数都是基于以上造波消波方法建立的纯波浪工况船舶数值波浪水池进行。然而在船舶实际航行过程中, 波浪和水流总是同时存在[14], 忽略水流作用而用纯波浪理论和模型来计算会带来很大误差[15], 因此需建立波流工况船舶数值波流水池。近年来关于波流相互作用数值研究已经获得广泛关注, 诸多学者从缓坡方程、Boussinesq方程及N-S方程开展了大量数值研究。其中基于Boussinesq方程进行波流相互作用研究发展最为成熟, Boussinesq方程包含了频率频散和非线性低阶效应, 它能讨论能量在频率间的转换和每个单波形的变化, 以及波包在浅水区变形等, Boussinesq方程只能应用于相对浅水深区域且不考虑水的粘性作用, 求解结果不能同时直接提供波模式及水流状态[16~18]。基于N-S方程的波流相互作用数值研究近年也得到了发展, 其中, 吴永胜等[19]从N-S方程推导并建立了波浪水流相互作用数学模型, 但模型求解涉及耦合模型方程较多、波浪复波数求解和模型边界条件复杂等因素使得模型计算非常烦琐; 秦楠等, 吴梓鑫等[20, 21]基于商业软件FLUENT结合设置速度入口方法及解析松弛消波技术实现波流相互作用模拟, 所建立的模型数值耗散大, 计算波高沿程损失非常大。当前基于N-S方程进行波流相互作用数值模拟还较少, 现有的模型存在数值耗散问题。
本文基于雷诺平均不可压缩粘性流N-S方程(RANS方程), 结合相函数方法(VOF方法)和质量源造波方法成功构建恒定水深黏性流船舶数值波流水池。通过在水池两端设定稳定入口速度实现水池区域均匀流的生成, 同时在水池中间指定区域内添加质量源生成目标波, 为了消除边界处反射波的影响并同时维持边界处流速不变从而保证水池计算区域平均水深恒定, 在靠近水池两端大于一倍波长计算区域内设置了动量源消波器。基于该模型分析了不同工况下波面与速度分布情况, 并与理论结果进行了对比验证, 结果表明数值结果与理论结果吻合良好, 表明建立的恒定水深黏性流船舶数值波流水池可以进行波流耦合研究, 并进一步分析了水流对波浪参数的影响。
2 数学模型 2.1 控制方程和边界条件可以采用以速度和压力为变量的连续性方程和雷诺平均N-S方程(RANS方程)来描述由波流相互作用引起的不可压缩流体运动过程
| $\frac{{\partial \left( {{u_i}} \right)}}{{\partial {x_i}}} = {S_{\rm{m}}}$ | (1) |
| $\begin{array}{*{20}{l}} {\frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left( {\mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \right) - }\\ {\frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left( { - \rho \overline {u_i^{\rm{'}}u_j^{\rm{'}}} } \right) + \rho {g_i} + {S_i}} \end{array}$ | (2) |
式中xi(i = 1, 2)分别为笛卡尔坐标系中的x, y方向坐标, ui(i = 1, 2)为流体运动速度分量, ρ为流体密度, p为流体压力, μ是流体动力黏性系数, g为重力加速度, 在x2方向值为-9.81, Sm为附加质量源项, Si为附加动量源项,
| $ - \rho \overline {u_i^{\rm{'}}u_j^{\rm{'}}} = {\mu _{\rm{t}}}\left[ {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right] - \frac{2}{3}\rho {\delta _{ij}}k$ | (3) |
式中μt是湍流粘度, k是湍动能项,
| $\begin{array}{*{20}{l}} {\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \rho k\left( {\frac{{\partial {u_i}}}{{\partial {x_i}}}} \right) = }\\ {\frac{\partial }{{\partial {x_i}}}\left( {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_i}}}} \right) + {G_k} - \rho \varepsilon } \end{array}$ | (4) |
| $\begin{array}{*{20}{l}} {\frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \rho \varepsilon \left( {\frac{{\partial {u_i}}}{{\partial {x_i}}}} \right) = }\\ {\frac{{\partial \varepsilon }}{{\partial {x_i}}}\left( {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_i}}}} \right) + \frac{{{C_{1\varepsilon }}\varepsilon }}{k}{G_k} - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}} \end{array}$ | (5) |
式中C1ε = 1.44, C2ε = 1.92, σk = 1, σε = 1.3。
2.2 造波及消波船舶数值波流水池最关键的技术是造波技术和消波技术。质量源造波技术最早由Pengzhi Lin[22]等提出, 基本原理是在计算域内设置一脉动源, 具体源项表达式推导见文献[23], 在源两边同时产生传播方向相反两列波, 源项函数表达式如下
| ${S_{\rm{m}}} = 2c\eta /A$ | (6) |
式中A为指定添加源项区域面积, c为目标波浪波速, η为目标波波面。
在进行波流相互作用数值模拟时, 需要考虑消除入射波的反射对实验区域影响, 因此需设置消波段, 常用的阻尼消波法无法保证水池平均水深不变, 本文采用解析松弛消波法消除波浪反射影响同时维持计算域内平均水深值恒定。解析松弛方法也叫动量源方法, 最早是由Madsen等提出[24], 基本原理是对源项区域内每一网格节点流速及压强在每一时刻进行更新, 使该区域内水质点流速及压强值在每一时刻都更新为初始时刻水平均匀流流速值, 具体更新规则如下
| ${u_{iM}} = C{u_{iJ}} + \left( {1 - C} \right){U_i}$ | (7) |
式中下标M代表在指定区域内对物理量的修正, 下标J代表前一时间步计算值, Ui为水流速值, 本文只考虑水平均匀流, 因此Ui=0(i=2), C = C (x)为与空间位置有关的光滑过渡加权函数, 在前端消波区内满足: Cxmin = 0, Cxmax = 1, 在尾端消波区内满足: Cxmin = 1, Cxmax = 0。
将式(7)代入式(2), 对比不添加源项的离散后方程可得尾端消除反射波区中附加动量源项表达式为
| $\begin{array}{*{20}{l}} {{S_i} = \left( {1 - C} \right)\left( {\frac{{\partial {p_J}}}{{\partial {x_i}}} - \rho \frac{{{u_{iJ}} - {U_i}}}{{{\rm{\Delta }}t}}} \right) + }\\ {\rho \left( {1 - {C^2}} \right)\left[ {{u_{iJ}}\frac{{\partial {u_{iJ}}}}{{\partial {x_i}}}} \right] - \rho C\left( {1 - C} \right){U_i}{u_{iJ}}} \end{array}$ | (8) |
采用Volume of fluid(VOF)模型追踪水波自由面, 其基本思想是通过构造相体积分数函数α来追踪每个控制体内流体流量, 并根据其函数值和导数值构造自由面位置及形状。α是时间点和空间点的标量函数, 其定义为单元内某相流体所占体积与该单元总体积之比。若该标量函数值为1, 表示单元内全部为该相流体; 若该标量函数值为0, 表示单元内没有该相流体; 若该标量函数值介于0到1之间, 则该单元为交界面单元。相体积分数函数需满足如下方程
| $\frac{{\partial {\alpha _q}}}{{\partial t}} + \frac{{\partial \left( {{u_i}{\alpha _q}} \right)}}{{\partial {x_i}}} = 0$ | (9) |
| $\mathop \sum \nolimits {\alpha _q} = 1$ | (10) |
对于船舶数值波流水池, 只有气液两相, q=1表示第一相为空气, q=2表示第二相为水, VOF模型内物性参数的离散格式采用显式, 并且设置COURANT数为0.25来减小数值误差。
3 数值计算与模型验证 3.1 数值计算数值波流水池模型如图 1所示, 该水池仿哈尔滨工程大学多功能水池主尺度建模, 通过对其进行合理简化后选取数值水池长度范围为(-100 ~ 100m), 总高11m, 水池静水深h = 10m。通过使用FLUENT前处理软件Gambit进行建模和网格划分, 前人研究指出, 使用FLUENT进行波浪数值模拟时, 网格应该满足一定要求(波长方向网格单元格长度L/20 ~ L/50范围内, 波面附近网格高度在H/5 ~ H/10范围内), 因此网格划分后单元格长Δx = 0.1m, y方向使用非均匀网格, 自由液面附近网格单元高Δy = 0.01m, 总的网格单元数为120万。其中EF为静水面, 上部为空气, 下部为水。Ⅰ为造波源区域, Ⅱ为工作区, Ⅲ为消波区。水池顶部设置为压力入口边界, 底部设置为无滑移不可穿透固壁边界, 左右两端面设置为速度入口边界条件, 指定水深以下为水相入口和出口并且设置水平均匀流U, 造波源产生的波浪分别向左和向右传播, 当其向左传播时与来流逆向而向右传播时与来流同向, 因此位于造波源左边计算区域(-100~0m)处于波流逆向工况而位于造波源右边计算区域(0~100m)处于波流同向工况。控制方程采用有限体积法进行离散, 压力离散采用Body Force Weight, 压力速度耦合采用PISO算法, VOF模型中的自由面采用几何重构法, 动量方程中瞬态项离散采用二阶隐式, 对流项和扩散项离散都采用一阶迎风格式。每次迭代的收敛判定标准为10-3, 初始时刻自由面上部分水相体积分数为0, 自由面以下水相体积分数为1, 同时初始化流场u1 = U, u2 = 0, 压力为静水压力分布。所有模拟计算都是基于工作站(双至强E5-2640V3处理器)进行并行计算完成。

|
Fig. 1 Sketch of ship viscous numerical wave and current tank with constant water depth |
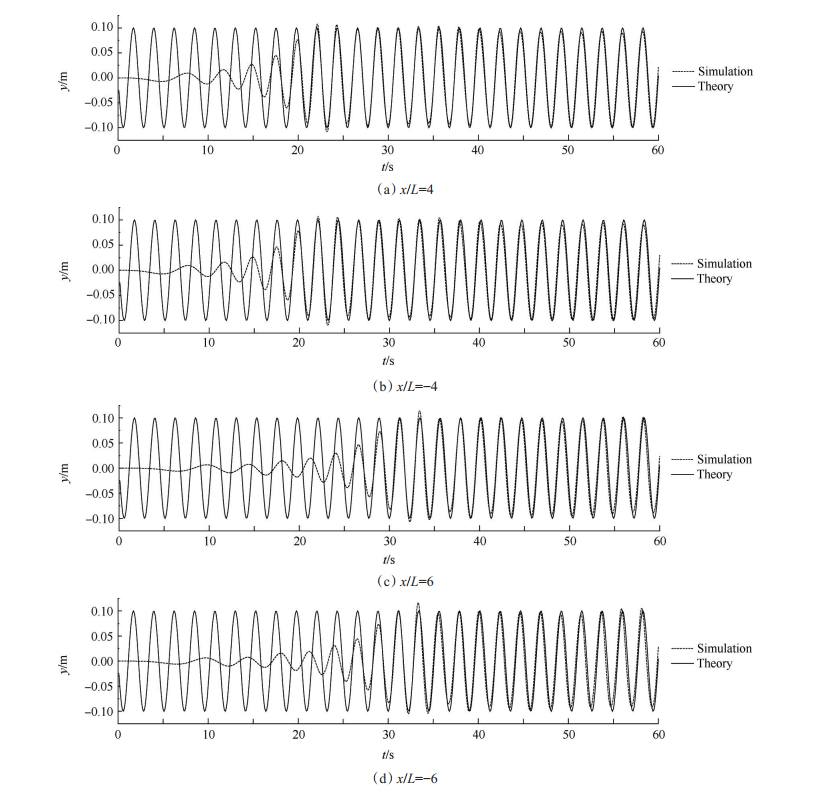
选取目标波长为8m, 波高为0.2m, 水流速度U = 0.1m/s。在水池不同位置(x = ±32m(x/L = ±4), x = ±48m(x/L = ±6))设置波高监测仪, 记录波面时间历程, 其结果如图 2和图 3所示。
|
Fig. 2 Comparison of simulated and analytical time series of water surface profile in wave-alone case |
|
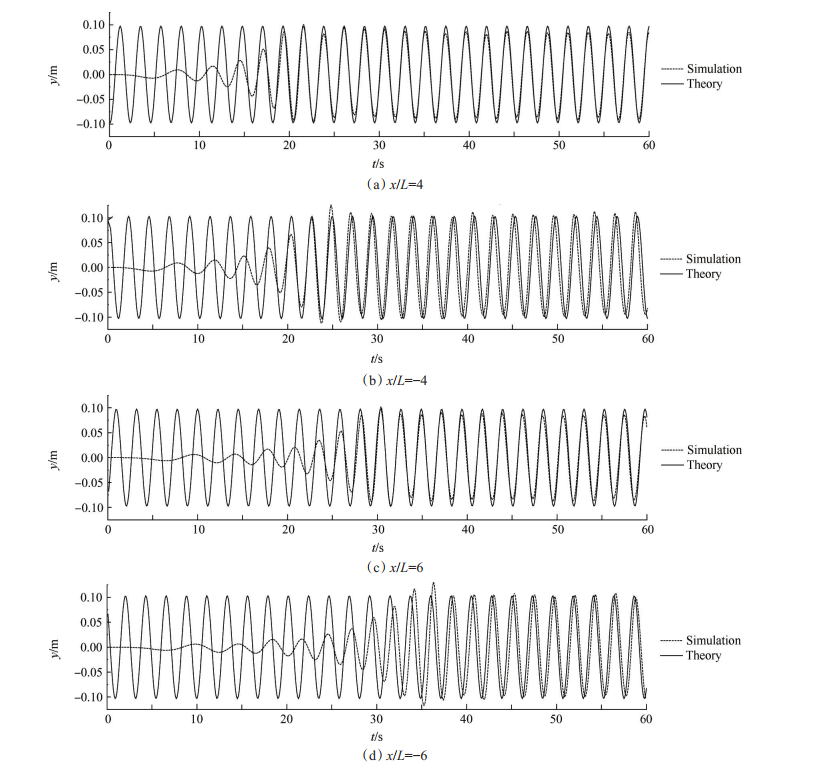
Fig. 3 Comparison of simulated and analytical water surface profile in wave-alone case |
图 2给出了纯波浪工况下不同站点位置波面位移时间序列数值解解与解析解的比较, 可以发现模拟结果与解析解基本吻合。图 3给出了波流工况下不同站点位置波面位移时间序列数值解解与解析解的比较, 其中解析解的计算基于文献[25]所提出公式给出:
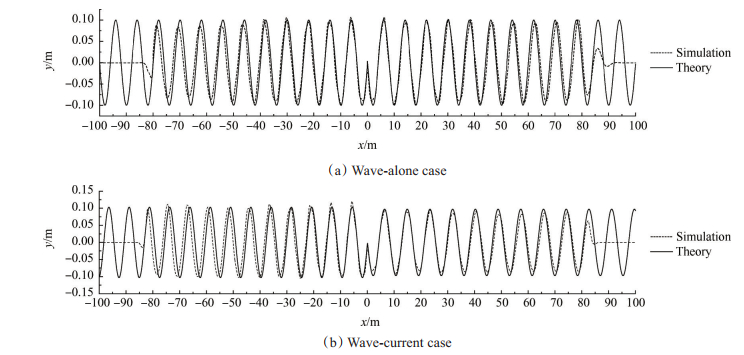
图 4给出了不同工况下模拟的波面瞬态图与理论值的比较, 可以看到数值结果与理论结果非常吻合且解析松弛消波效果良好。同时分析波面包络线可以发现, 对于纯波浪情况(图(a)), 整个计算域内生成的波幅基本一致, 衰减很小, 说明建立的波流水池在模拟纯波浪工况时可以生成准确稳定性良好的目标波。对于波流工况(图(b)), 波浪向左端传播(波流逆向)时波幅增加, 波长减小, 波浪向右端传播时波幅减小(波流同向), 波长增大, 符合多普勒效应, 进一步说明建立的波流水槽可以进行波流相互作用研究, 为将来进行船舶在波流相互作用下受力分析和运动响应研究提供数值实验平台。
|
Fig. 4 Comparison between simulated and theoretical free surface elevation for wave-alone and wave-current cases |
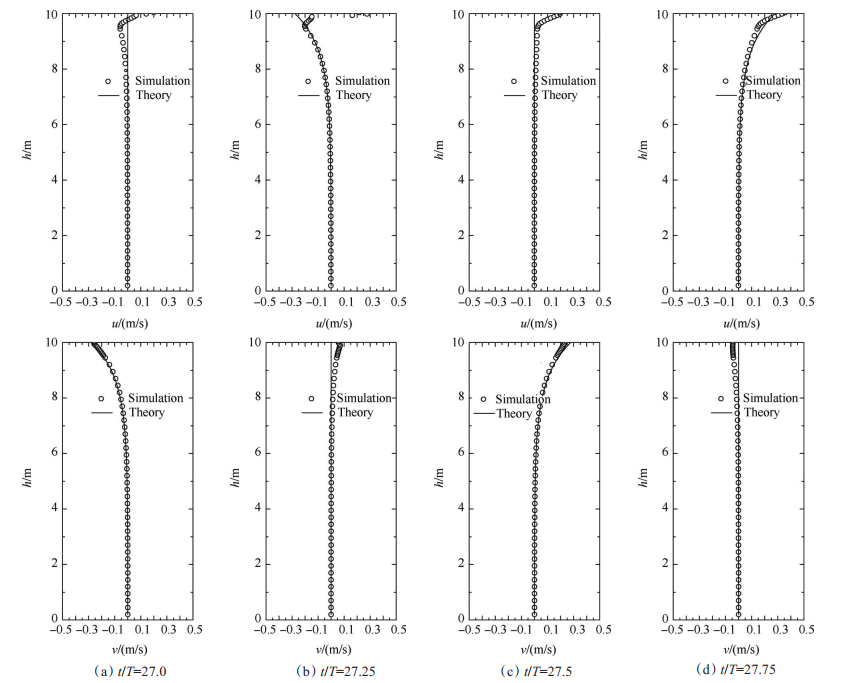
波面运动及水流速度对波浪水质点速度影响关系, 对于纯波浪工况, 对比了模拟计算的水平方向u及垂直方向波浪水质点速度v沿水深分布的数值解和相应的解析解, 对比结果如图 5所示。从图 5可以看到, 数值解与理论解吻合得非常良好, 进一步表明所建立的模型能够精确地模拟规则波。同时通过分析可以发现波浪水质点速度沿水深分布情况受波面运动影响非常大。由图中的垂直方向分布情况可以看到, 当监测站点趋于中位波面时波浪水质点速度垂直分量的绝对值在水深方向逐渐增大(图 5中的t/T = 27.0和t/T = 27.5)。由图中的速度水平方向分布情况可以看到, 当监测站点趋于波峰或波谷时波浪水质点速度水平分量的绝对值在水深方向逐渐增大(图 5中的t/T = 27.25和t/T = 27.75)。
|
Fig. 5 Comparison of simulated and theoretical velocity profiles at location x=32m for wave-only cases |
波流工况下波面运动及水流速度对波浪水质点速度的影响, 由于目前还没有关于波流相互作用下波浪水质点速度分布理论解, 波流工况下的水质点速度由线性叠加原理即下式计算得到
| $\left\{ {\begin{array}{*{20}{l}} {u = U + \frac{{gAk{\rm{'}}}}{\omega }\frac{{chk{\rm{'}}y}}{{chk{\rm{'}}h}}{\rm{sin}}\left( {k{\rm{'}}x - \omega t} \right)}\\ {v = \frac{{gAk{\rm{'}}}}{\omega }\frac{{shk{\rm{'}}y}}{{chk{\rm{'}}h}}{\rm{cos}}\left( {k{\rm{'}}x - \omega t} \right)} \end{array}} \right.$ | (11) |
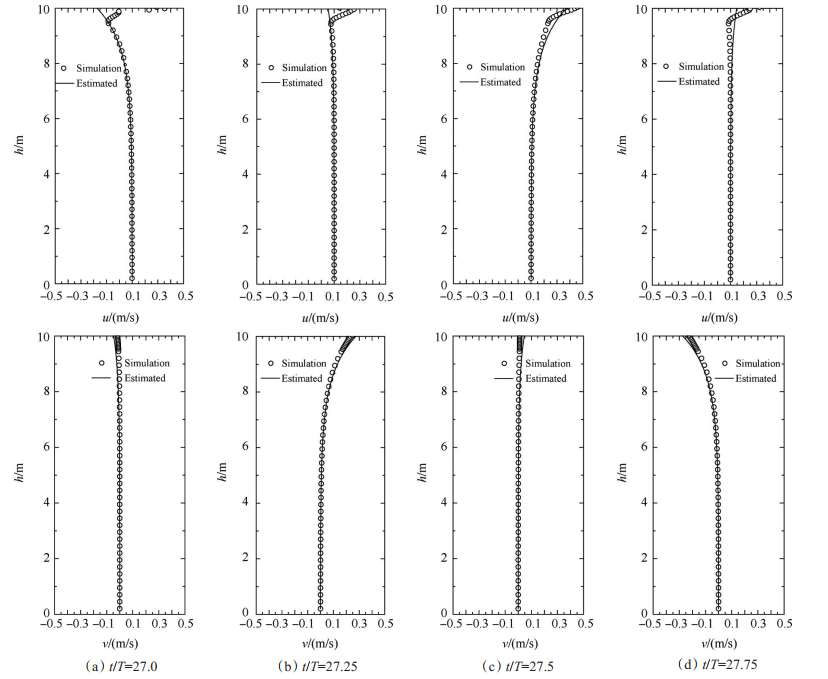
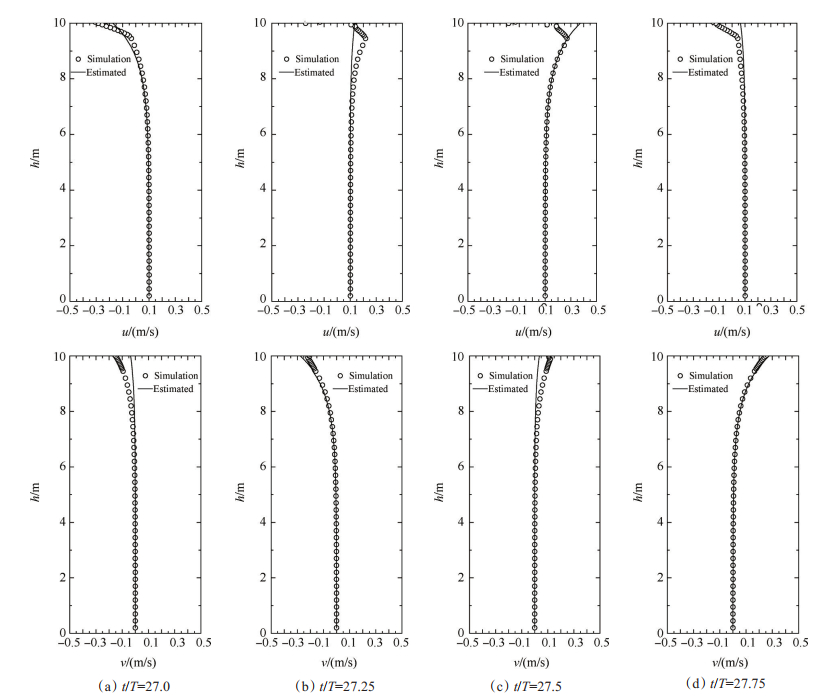
对比结果如图 6和图 7所示。可以看到模拟的结果与采用线性叠加原理估算的预估值基本吻合良好, 水面附近结果误差相对较大, 主要原因是数据统计过程中产生的误差以及波面附近线性求解所带来的误差。对比图 5, 图 6和图 7可以发现波流工况下波浪水质速度同时受水流速度及波面运动的影响。
|
Fig. 6 Comparison of simulated and estimated velocity profiles for wave with following current(x=32m) |
|
Fig. 7 Comparison of simulated and estimated velocity profiles for wave with opposing current(x=-32m) |
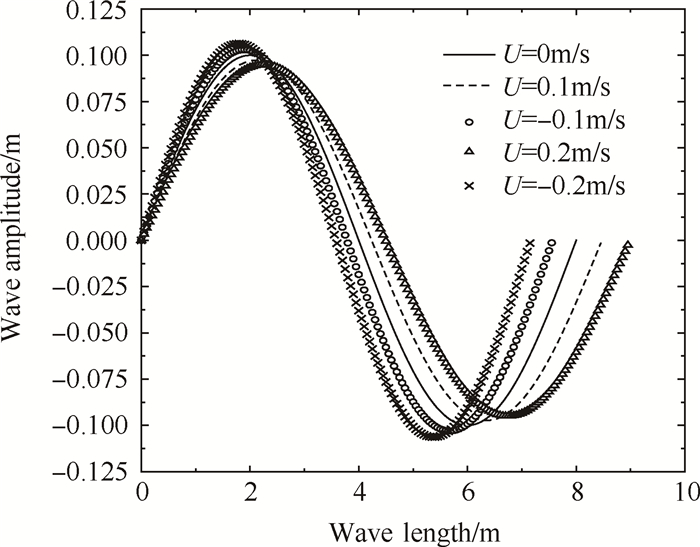
接下来结合以上案例并增加水流速度至u = 0.2m/s进行水流速度对波浪参数影响的定量分析。在计算时间t/T = 27时刻分别对计算区域x = 3 ~ 8L(纯波浪工况和波流同向工况)和x = -8 ~ -3L(波流逆向工况)内波面进行平均处理, 处理结果如图 8所示。从图中可以更明显看到波流同向使得波长增大而波幅减小, 波浪非线性作用减弱, 波流逆向使得波长减小而波幅增大, 波浪非线性作用增强。当水流速度为u = 0.1m/s时, 波流同向工况下波幅减小了2.68%而波长增大了5.94%, 波流逆向工况下波幅增大了2.99%而波长减小了5.31%;当水流速度增大为u = 0.2m/s时, 波流同向工况下波幅减小了5.04%而波长增大了12.2%, 波流逆向工况下波幅增大了6.32%而波长减小了10.31%。
|
Fig. 8 Effects of currents on the water surface profile |
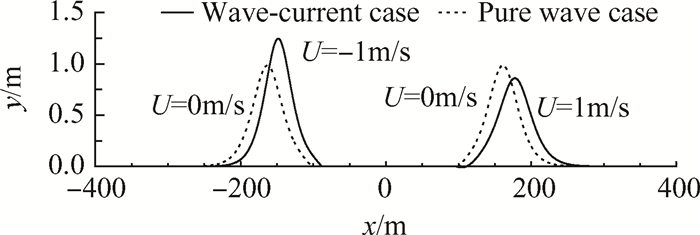
我国南海波高浪大, 时常出现其他海区所不常见的恶劣海况-波高很大的单峰波即孤立波, 具有极强的非线性, 不能用传统的线性理论进行处理, 特别是砰击和上浪等强非线性载荷使得船舶及其他海工平台发生结构破损事件。本文建立的模型可以用来分析孤立波与水流相互作用过程。数值模拟时, 水槽长800m(-400 ~ 400m), 最大水深10m, 静水深8m, 波高选定为1m, 水流速度为0m/s和±1m/s。对整个计算区域使用均匀网格:Δx = 0.2m, Δy = 4mm(93.1MB, 包含100万矩形网格单元)。图 9显示了在模拟时间t = 27s时波流工况及纯波浪工况下的波形图, 可以看到模拟的波流逆向工况下的波高(1.25m)比纯波浪工况下的波高(1m)增大了25%, 波流同向工况下的波高(0.86m)比纯波浪工况下的波高减少了14%。因此逆向流对波高的改变要比同向流大得多, 这也是为什么逆向流存在时孤立波对结构物的破坏作用要增大很多。同时分析波峰位置可以发现, 逆向工况时峰值出现在x=-147m而纯波浪工况峰值出现在x=-162m, 同向工况时峰值出现在x=178m而纯波浪工况峰值出现在x=162m, 表明逆向流减少了孤立波传播速度而同向流增加了其传播速度。
|
Fig. 9 Comparison of the simulated water free surface elevation for wave-current case and wave-only case |
通过本文研究, 得到以下结论:
(1) 本文数值结果与理论结果吻合良好, 表明所建立的水池模型具有较好的准确性。
(2) 波流相互作用时, 顺流加快波浪传播, 逆流减慢波浪传播; 波流同向时的波峰变小波长增大, 波浪非线性作用减弱, 而波流逆向增大波峰且减小了波长, 波浪非线性作用增强。
(3) 逆向流减少了孤立波传播速度而同向流增加了其传播速度, 逆向流对波高的改变要比同向流大得多, 逆向流存在时孤立波对结构物的破坏作用要增大很多。
| [1] |
王洋, 曹璞钰, 印刚, 等. 非均匀进流下喷水推进泵的内流特性和载荷分布[J]. 推进技术, 2017, 38(1): 69-75. (WANG Yang, CAO Pu-yu, YIN Gang, et al. Flow Feature and Blade Loading of a Water-Jet Pump under Non-Uniform Suction Flow[J]. Journal of Propulsion Technology, 2017, 38(1): 69-75.)
(  0) 0) |
| [2] |
楼云锋, 李昊. 考虑结构响应及轴线形状的防浪堤抗波浪冲击数值模拟研究[J]. 工程力学, 2015, 32(2): 241-249. (  0) 0) |
| [3] |
舒敏骅, 陈科, 尤云祥, 等. 外部轴向激励作用下螺旋桨轴承力非定常变化特性数值研究[J]. 推进技术, 2017, 38(4): 721-731. (SHU Min-hua, CHEN Ke, YOU Yun-xiang, et al. Numerical Study on Unsteady Variation Characteristics for Bearing Forces of a Propeller with External Axial-Excitation[J]. Journal of Propulsion Technology, 2017, 38(4): 721-731.)
(  0) 0) |
| [4] |
吴乘胜, 朱德祥, 顾民. 数值波浪水池及顶浪中船舶水动力计算[J]. 船舶力学, 2008, 12(2): 168-179. (  0) 0) |
| [5] |
Hong Xiao, Wenrui Huang, Jianhua Tao. Numerical Modeling of Wave-Current Forces Acting on Horizontal Cylinder of Marine Structures by VOF Method[J]. Ocean Engineering, 2013, 67: 58-67. DOI:10.1016/j.oceaneng.2013.01.027
(  0) 0) |
| [6] |
董志, 詹杰民. 基于VOF方法的数值波浪水池以及造波、消波方法研究[J]. 水动力学研究与进展(A辑), 2009, 24(1): 15-21. (  0) 0) |
| [7] |
Chen L F, Zang J, Hillis A J. Numerical Investigation of Wave-Structure Interaction Using OpenFOAM[J]. Ocean Engineering, 2014, 88: 91-109. DOI:10.1016/j.oceaneng.2014.06.003
(  0) 0) |
| [8] |
方昭昭, 朱仁传, 缪国平. 基于数值波浪水池的波浪中船舶水动力计算[J]. 水动力学研究与进展(A辑), 2012, 27(5): 515-524. (  0) 0) |
| [9] |
封星, 吴宛青. 二维数值波浪水槽在FLUENT中的实现[J]. 大连海事大学学报, 2010, 36(3): 94-96. (  0) 0) |
| [10] |
唐耀, 邹早建. 二维黏性流数值波浪水池的开发与验证[J]. 水动力学研究与进展(A辑), 2013, 28(5): 15-21. (  0) 0) |
| [11] |
Chen Yenlung, Shih-Chun Hsiao. Generation of 3D Water Waves Using Mass Source Wavemaker Applied to Navier-Stokes Model[J]. Coastal Engineering, 2016, 109: 76-95. DOI:10.1016/j.coastaleng.2015.11.011
(  0) 0) |
| [12] |
Zhang J S, Zhang Y, Jeng D S. Numerical Simulation of Wave-Current Interaction Using a RANS Solver[J]. Ocean Engineering, 2014, 75: 157-164. DOI:10.1016/j.oceaneng.2013.10.014
(  0) 0) |
| [13] |
宁德志, 陈丽芬, 田宏光. 波流混合作用的完全非线性数值水池模型[J]. 哈尔滨工程大学学报, 2010, 31(11): 1450-1455. (  0) 0) |
| [14] |
唐恺, 朱仁传, 缪国平. 波浪中浮体运动的时域混合格林函数法[J]. 上海交通大学学报, 2014, 48(4): 508-514. (  0) 0) |
| [15] |
Anbarsooz M, PassandidehFard M, Moghiman M. Fully Nonlinear Viscous Wave Generation in Numerical Wave Tanks[J]. Ocean Engineering, 2013, 59: 73-85. DOI:10.1016/j.oceaneng.2012.11.011
(  0) 0) |
| [16] |
Azhen Kang, Pengzhi Lin, Yi Jiat Lee. Numerical Simulation of Wave Interaction with Vertical Circular Cylinders of Different Submergences Using Immersed Boundary Method[J]. Computers & Fluids, 2015, 106: 41-53.
(  0) 0) |
| [17] |
Zhongbo Liu, Kezhao Fang. Two-Layer Boussinesq Models for Coastal Water Waves[J]. Wave Motion, 2015, 57: 88-111. DOI:10.1016/j.wavemoti.2015.03.006
(  0) 0) |
| [18] |
Junwoo Choi, James Kirby T. Boussinesq Modeling of Long Shore Currents in the Sandy Duck Experiment under Directional Random Wave Conditions[J]. Coastal Engineering, 2015, 101: 17-34. DOI:10.1016/j.coastaleng.2015.04.005
(  0) 0) |
| [19] |
吴永胜, 练继建, 王兆印, 等. 波浪-水流相互作用模型[J]. 水利学报, 2002(4): 13-17. (  0) 0) |
| [20] |
秦楠, 鲁传敬. 数值波流水池构造方法研究[J]. 水动力学研究与进展(A辑), 2013, 28(3): 349-356. (  0) 0) |
| [21] |
吴梓鑫, 朱仁庆, 缪志刚. 波流数值水池模拟研究[J]. 江苏科技大学学报(自然科学版), 2015(1): 10-15. (  0) 0) |
| [22] |
Pengzhi Lin, Philip L, Liu F, et al. Internal Wave-Maker for Navier-Stokes Equations Models[J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 1999, 125(4): 207-214. DOI:10.1061/(ASCE)0733-950X(1999)125:4(207)
(  0) 0) |
| [23] |
Wei G, Kirby J T, Sinha A. Generation of Waves in Boussinesq Models Using a Source Function Method[J]. Coastal Engineering, 1999, 36: 271-299. DOI:10.1016/S0378-3839(99)00009-5
(  0) 0) |
| [24] |
Madsen P A, Bingham H B, Liu H. A New Boussinesq Method for Fully Nonlinear Waves from Shallow to Deep Water[J]. Journal of Fluid Mechanical, 2003, 462: 1-30.
(  0) 0) |
| [25] |
邹志利. 水波理论及其应用[M]. 北京: 科学出版社, 2005.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


