2. 西安航天动力研究所 液体火箭发动机技术重点实验室,陕西 西安 710100
2. Science and Technology on Liquid Rocket Engine Laboratory, Xi'an Aerospace Propulsion Institute, Xi'an 710100, China
对于诸如航天器类重要、复杂的工程结构,其研制过程对结构动态分析结果的准确性提出了极为苛刻的要求,当前迫切需要提高计算精度与效率,数学建模分析是结构动力分析中最关键的一环[1]。由于工程结构的日益大型复杂化,要建立复杂结构高精度的动力学模型并进行准确、高效的计算分析,这本身就是一件非常困难的工作。如大型火箭二级整机由相同的四机并联组成,四台发动机共用一个机架,每台发动机主要是由推力室、燃气发生器、涡轮泵系统、气/液管路、自动器、贮箱和高压气瓶等组件高度集成的大型复杂、多尺度多维度动态系统,其结构动力学特性非常复杂,对发动机进行精细化动力学设计是当前研究的一项重要任务,如何在保证结果精度的前提下提高分析效率至关重要。
目前,结构有限元(FE)分析法、子结构法已成为解决结构动力问题的主要方法之一。FE方法采取由零件、部件到整机的有限元建模思想,对原始复杂的物理模型进行合理的简化,以尽量准确模拟发动机的刚度和质量分布为建模总原则,使动力学模型既简单又能反映其动态特性,从而建立完整的有限元模型;然而,整体FE法在处理大型复杂结构问题时效率偏低,有时可能会失效。子结构法以Rayleigh-Ritz法为理论基础,在20世纪60年代,由Hurty W C和Gladwell G M L提出,Craig R R,Bampton M C C等对Hurty W C的方法作了改进与完善,该方法在提高分析效率和精度方面优势显著,目前已成为解决复杂工程结构动力学问题的有效方法;根据界面性质,子结构法分为约束子结构法、自由子结构法和混合子结构法;向树红、邱吉宝等[2, 3]对子结构方法的最新研究进展进行了详细介绍,总结了运载火箭结构动力学研究精确模态综合法的一些新技术;Wang等、徐庆红、杜飞平等[4~6]将子结构模态综合法应用于火箭、卫星的动力学分析中,对航天器的结构动力学建模技术、动态响应分析及动态试验仿真技术等进行了研究;但是传统(单级)动力子结构法在获取各子结构间组装关系及各子结构模态信息时有很多不足,导致求解复杂结构动特性的精度与效率得不到保证。
多重多级子结构方法由Zhong等[7]提出,利用多重多级子结构技术求解大型复杂结构动力特性[8~12];Ragnarsson等,Kim等和Boo等[13~15]提出了基于模态综合法的AMLS法,采用多重划分方式以减少接口自由度。多重动态子结构法除具有传统FE法、子结构法的优点外,还有采取分层与装配策略、思路更加清晰;避免重复建模,试验与计算高效结合,建模效率进一步提高;重设计或模型修正时仅对需要修改的部分做调整,增大了灵活性;最大限度减小求解规模,分析效率更高;分析结果不受子结构划分、调用方式的影响,更适合于结构之间的耦合分析等。另外,相比多重多级子结构方法,多重动态子结构法在分析大型复杂结构动态特性与动态响应问题时性能更加优越。
本文针对大型复杂结构动力分析中存在的问题,提出了适合于解决该问题的多重动态子结构法。详细推导与说明了多重多级动态子结构理论,介绍了运用该理论对大型复杂结构进行动力分析的工程实现方法,开展了该方法在某大型四机并联液体火箭发动机动力分析中的应用研究,并对方法的可行性与有效性进行了评价。
2 多重动态子结构理论多重动态子结构技术是C-B法对接坐标主模态缩减法的多级应用。其主要思想是:首先,依据子结构分层策略及划分原则对具有层次性及分解性的多层次大系统进行“嵌套”分割,将结构划分成若干子结构(定义为一级子结构);再将一级子结构分成更小的子结构(二级子结构),依次可划分成三,…,J级更小的子结构,直到问题方便求解;最后将各子结构逐级组集成系统级模型。在求解过程中,采用由后向前、从低级到高级逐级减缩子结构,上层子结构间的界面节点成为下层子结构的内部节点而被凝聚掉;通过子结构内部自由度、子结构间界面自由度缩聚,最终系统模型的自由度数会最大程度得到缩减,使装配后的特征方程矩阵维度大大降低,进而可综合出系统的动态特性。该方法可实现子结构的镜像、旋转、平移或多层次调用等操作,能更好地处理大型复杂结构的建模分析问题。
2.1 子结构模型缩聚设线性结构动力学方程为
| $ \mathit{\boldsymbol{M}}\ddot u + \mathit{\boldsymbol{C}}\dot u + \mathit{\boldsymbol{K}}u = f + R $ | (1) |
式中M,C,K为质量、阻尼及刚度阵,u为位移,f为外力,R为界面力。将式(1)简化为无阻尼自由振动方程,并按内部自由度(D集)与界面自由度(A集)进行分块
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_{dd}}}&{{\mathit{\boldsymbol{M}}_{da}}}\\ {{\mathit{\boldsymbol{M}}_{ad}}}&{{\mathit{\boldsymbol{M}}_{aa}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\ddot u}}_d}}\\ {{\mathit{\boldsymbol{\ddot u}}_a}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_{dd}}}&{{\mathit{\boldsymbol{K}}_{da}}}\\ {{\mathit{\boldsymbol{K}}_{ad}}}&{{\mathit{\boldsymbol{K}}_{aa}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{u}}_d}}\\ {{\mathit{\boldsymbol{u}}_a}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} 0\\ {{\mathit{\boldsymbol{R}}_a}} \end{array}} \right] $ | (2) |
式中ud,ua为内部、外部位移。d,a为内部、界面自由度,d∈D,a∈A。总内部位移
| $ {\mathit{\boldsymbol{u}}_d} = \mathit{\boldsymbol{u}}_d^{{\rm{free}}} + \mathit{\boldsymbol{u}}_d^{{\rm{fixed}}} = {\mathit{\boldsymbol{G}}_{da}}{\mathit{\boldsymbol{u}}_a} + \mathit{\boldsymbol{u}}_d^{{\rm{fixed}}} $ | (3) |
式中udfree,udfixed为自由、固定界面位移,Gda为变换阵。进行固定边界缩聚时,
| $ {\mathit{\boldsymbol{M}}_{dd}}{\mathit{\boldsymbol{\ddot u}}_d} + {\mathit{\boldsymbol{K}}_{dd}}{\mathit{\boldsymbol{u}}_d} = 0 $ | (4) |
其特征方程为
| $ {\mathit{\boldsymbol{K}}_{dd}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_N} = {\mathit{\boldsymbol{\lambda }}_N}{\mathit{\boldsymbol{M}}_{dd}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_N} $ | (5) |
式中ΦN为特征向量阵,λN为特征值阵,N=1, 2, …, d。令ΛN= diag(ωN2),认为ΦN已正则化
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{M}}_{QQ}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_N}{\mathit{\boldsymbol{M}}_{dd}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_N} = {\mathit{\boldsymbol{I}}_N}}\\ {{\mathit{\boldsymbol{K}}_{QQ}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_N}{\mathit{\boldsymbol{K}}_{dd}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_N} = {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_N}} \end{array}} \right. $ | (6) |
释放固定界面自由度,用固定界面模态基向量把udfixed变换到模态空间,代入式(3)得
| $ {\mathit{\boldsymbol{u}}_d} = - \mathit{\boldsymbol{K}}_{dd}^{ - 1}{\mathit{\boldsymbol{K}}_{da}}{\mathit{\boldsymbol{u}}_a} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_N}{\mathit{\boldsymbol{p}}_N} $ | (7) |
由固定边界模态与约束模态构成广义坐标,有
| $ \mathit{\boldsymbol{u}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{u}}_d}}\\ {{\mathit{\boldsymbol{u}}_a}} \end{array}} \right] = \mathit{\boldsymbol{ \boldsymbol{\varPhi} p}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_N}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_C}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{p}}_N}}\\ {{\mathit{\boldsymbol{p}}_c}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_N}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_a}}\\ 0&{{\mathit{\boldsymbol{I}}_a}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{p}}_N}}\\ {{\mathit{\boldsymbol{u}}_a}} \end{array}} \right] $ | (8) |
式中pN为模态坐标向量,ΦN为固定界面主模态,Φa为约束模态,Φa=-Kdd-1KdaIa。只保留前k阶主模态Φk(k≪N),主模态截断准则要求模态数目应能保证动态响应计算模态截断后的正确性,建议模态频率值应为动态响应关心最高频率的2~3倍,即选取所关心频率3倍以内的子结构主模态[16]。这样就能大幅度缩减子结构模型自由度,有
| $ \mathit{\boldsymbol{u}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_a}}\\ 0&{{\mathit{\boldsymbol{I}}_a}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{p}}_k}}\\ {{\mathit{\boldsymbol{u}}_a}} \end{array}} \right] = \mathit{\boldsymbol{T}}\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{p}}_k}}\\ {{\mathit{\boldsymbol{u}}_a}} \end{array}} \right] $ | (9) |
式中T为广义动力缩聚变换阵。将质量归一化,根据主模态的正交性,将式(2)由物理坐标变换到模态空间,建立子结构在模态坐标下的动力学方程
| $ \mathit{\boldsymbol{\tilde M\ddot p}} + \mathit{\boldsymbol{\tilde Kp}} = \mathit{\boldsymbol{\tilde F}} $ | (10) |
式中
将各子结构的动力学方程写成式(10)的形式,认为这些方程是相互独立的,根据各子结构的界面位移协调(ua(i)=ua)和力平衡(
对于具有m个子结构的单级系统,其在广义坐标q下的特征方程为
| $ \left( {{{\mathit{\boldsymbol{\tilde K}}}^{\rm{*}}} - \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}{{\mathit{\boldsymbol{\tilde M}}}^{\rm{*}}}} \right)\mathit{\boldsymbol{q}} = 0 $ | (11) |
式中
对于具有J重子结构的系统,保留Φv低阶对接坐标V主模态(对界面对接坐标动力缩聚),将广义坐标q下末级子结构的运动方程代入系统运动方程,可得降阶的系统广义坐标下运动方程
| $ \left( {{{\mathit{\boldsymbol{\tilde K}}}^{\rm{*}}} - \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} {{\mathit{\boldsymbol{\tilde M}}}^{\rm{*}}}} \right)\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{q}}_k}}\\ {{\mathit{\boldsymbol{q}}_v}} \end{array}} \right] = 0 $ | (12) |
其中
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;{{\mathit{\boldsymbol{\tilde K}}}^{\rm{*}}} = \left[ {\begin{array}{*{20}{c}} {{\rm{diag}}\left( {^{\left( \mathit{i} \right)}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{kk}}} \right)}&0\\ 0&{{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{vv}}} \end{array}} \right], \\ {{\mathit{\boldsymbol{\tilde M}}}^{\rm{*}}} = \left[ {\begin{array}{*{20}{c}} {^{\left( 1 \right)}{\mathit{\boldsymbol{I}}_{kk}}}&{}&{}&{}&{}\\ {}& \ddots &{}&{}&{}\\ {}&{}&{^{\left( i \right)}{\mathit{\boldsymbol{I}}_{kk}}}&{}&{}\\ {}&{}&{}& \ddots &{}\\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} {{_v^{\rm{T}}}^{\left( 1 \right)}}{{\mathit{\boldsymbol{\tilde M}}}_{ad}}}& \cdots &{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} {{_v^{\rm{T}}}^{\left( i \right)}}{{\mathit{\boldsymbol{\tilde M}}}_{ad}}}& \cdots &{{\mathit{\boldsymbol{I}}_{aa}}} \end{array}} \right], \end{array} $ |
主坐标
| $ \left\{ {\begin{array}{*{20}{l}} {{}_{}^{\left( i \right)}{\mathit{\boldsymbol{u}}_a} = {}_{}^{\left( i \right)}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_v}{}_{}^{\left( i \right)}{\mathit{\boldsymbol{p}}_v}}\\ {{}_{}^{\left( i \right)}{\mathit{\boldsymbol{u}}_d} = {}_{}^{\left( i \right)}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{dk}}{}_{}^{\left( i \right)}{\mathit{\boldsymbol{p}}_k} + {\mathit{\boldsymbol{\varphi }}_{da}}{}_{}^{\left( i \right)}{\mathit{\boldsymbol{p}}_v}} \end{array}} \right. $ | (13) |
第J重子结构的无阻尼自由振动方程为
| $ \left( {\mathit{\boldsymbol{\tilde K}}_J^{\rm{*}} - \mathit{\boldsymbol{ \boldsymbol{\varLambda} \tilde M}}_J^{\rm{*}}} \right){\mathit{\boldsymbol{p}}_J} = 0 $ | (14) |
式中
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\; \mathit{\boldsymbol{\tilde K}}_J^{\rm{*}} = \left[ {\begin{array}{*{20}{c}} {{\rm{diag}}\left( {\mathit{\boldsymbol{\tilde K}}_i^{J - 1}} \right)}&0\\ 0&{\mathit{\boldsymbol{\tilde K}}_v^{J - 1}} \end{array}} \right]\\ \mathit{\boldsymbol{\tilde M}}_J^{\rm{*}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde M}}_1^{J - 1}}&{}&{}&{}&{\mathit{\boldsymbol{\tilde M}}_{1c}^{J - 1}}\\ {}& \ddots &{}&{}& \vdots \\ {}&{}&{\mathit{\boldsymbol{\tilde M}}_i^{J - 1}}&{}&{\mathit{\boldsymbol{\tilde M}}_{ic}^{J - 1}}\\ {}&{}&{}& \ddots&\vdots \\ {\mathit{\boldsymbol{\tilde M}}_{c1}^{J - 1}}& \cdots &{\mathit{\boldsymbol{\tilde M}}_{ci}^{J - 1}}& \cdots &{\mathit{\boldsymbol{\tilde M}}_v^{J - 1}} \end{array}} \right] \end{array} $ |
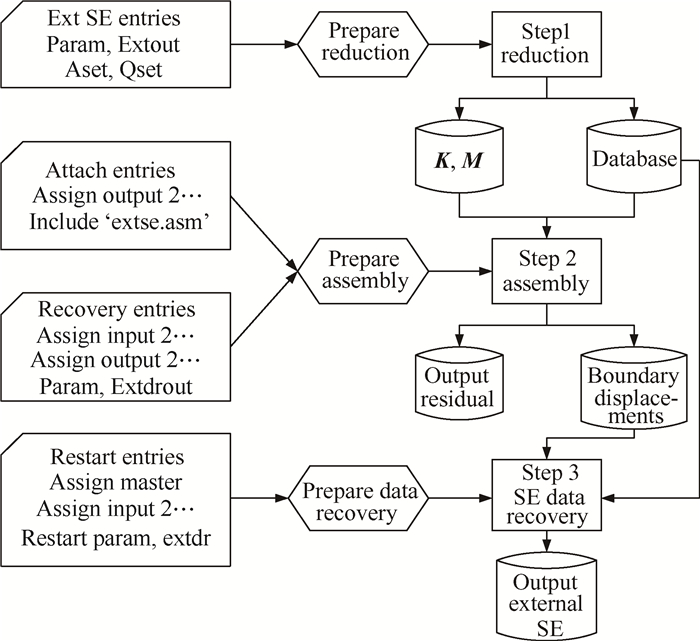
运用多重动态子结构理论对大型复杂工程结构进行动力分析,在MSC Nastran软件中借助于多级超单元技术实现。由于外部超单元相比原始、映像超单元具有更高的应用价值,故其得到了更广泛的应用。多级外部超单元的分析过程分外部超单元生成、模型组集及数据恢复三部分(见图 1,图 2),下面对软件实现方法以及使用技巧进行详细说明。整个工程实现过程的模型缩聚、模型组集、求解及数据恢复是以多重动态子结构的子结构模型缩聚、模型综合、求解及数据恢复理论为基础。
|
Fig. 1 Schematic of 3-step external superelement process |
|
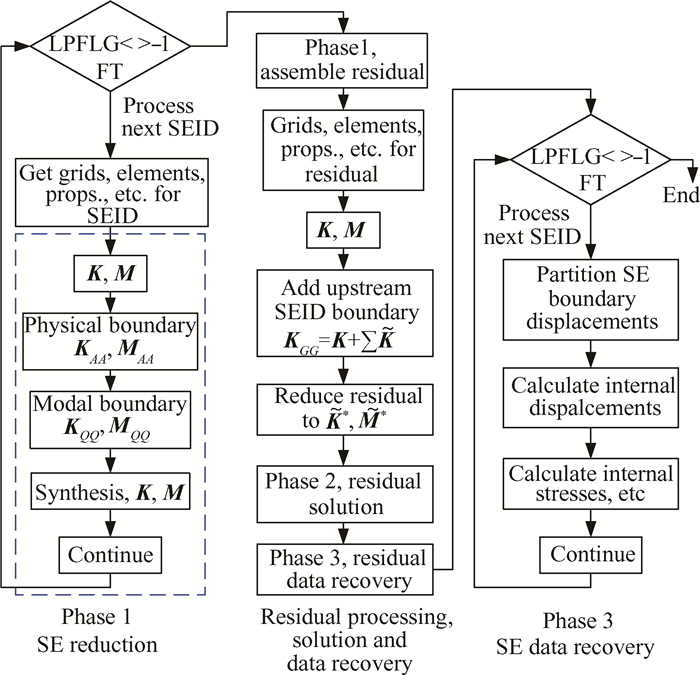
Fig. 2 Flowchart for dynamic superelement processing |
外部超单元包括质量矩阵、刚度矩阵及转换矩阵等,以提取模态信息。采用PARAM,AUTOQSET,YES命令定义广义节点SPOINTs和广义自由度QSETi;定义界面节点(固定界面ASETi,自由界面BNDFREEi);定义模型骨架Plotel。情况控制卡(Case Control)中的Extseout命令用于控制生成超单元矩阵,以及后续模型装配中以Part命令读入的外部超单元需要的输入数据。
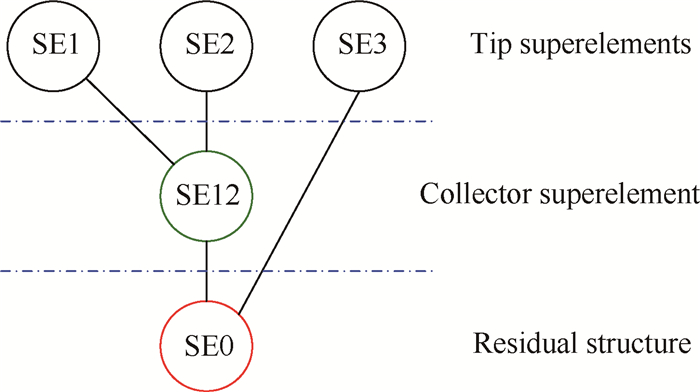
3.2 模型组集模型装配是将外部超单元与本体结构或超单元之间的连接过程。多级超单元的创建方法与单级超单元相同,只需在创建过程中将上一级超单元装配后求解。图 3给出了多级超单元体系结构示意。末端超单元(Tip Superelement)SE1,SE2经二次缩聚后得缩聚超单元(Collector Superelement)SE12,SE12和SE3超单元再与主体模型(Residual Structure,SEID=0)进行连接。装配时,首先界面节点位置应保持一致,否则需要调整模型。如果外部超单元模型位置需要调整,在主模型的Main Bulk Section中采用Seloc命令,对超单元模型进行平移、旋转使之调整到所需要的位置。如果界面节点位置一致,则不需进行任何改动,*.asm文件中Seconct将超单元和本体结构在一定误差间距内的两个界面节点自动对接。
|
Fig. 3 Multilevel superelement tree |
将装配好的主体模型递交计算,在求解完成后,采取重启动方法,进行超单元的数据恢复。恢复过程与多级缩聚相反,以从顶至底的顺序,由凝聚解计算结构所有自由度的完整解。先获得子结构各节点位移,再计算应力、应变和能量等各种所需的物理量。
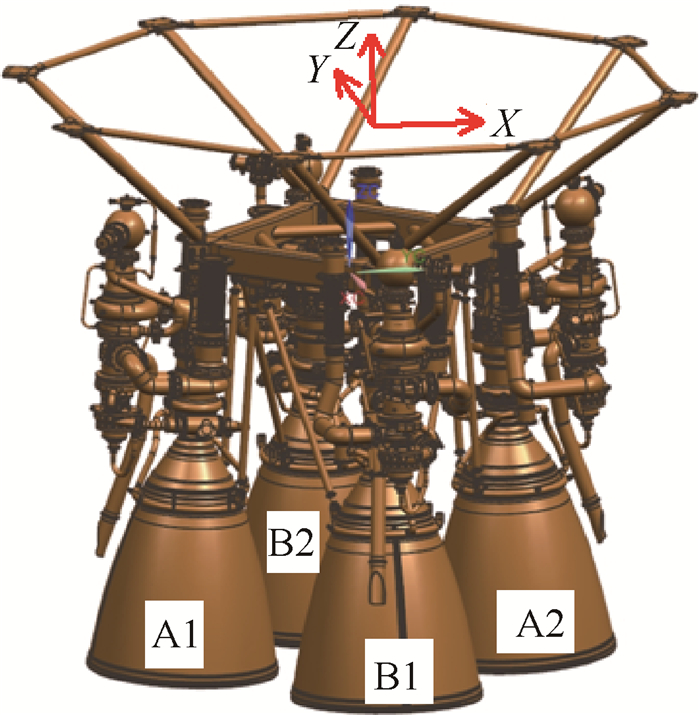
4 应用实例大型火箭二级整机由四台相同的单机并联组成,四台发动机共用一个机架,每台发动机结构高度集成,如图 4所示,其整体建模及动力分析难度极大。
|
Fig. 4 A second-stage rocket engine |
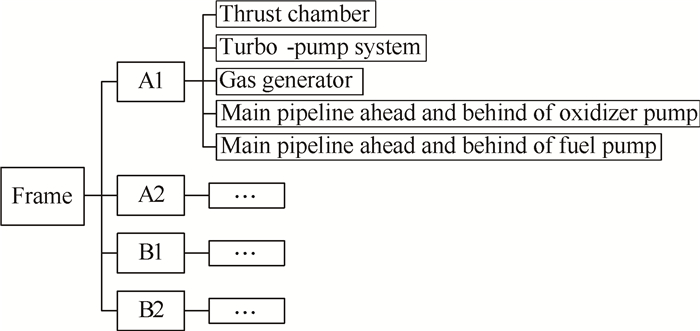
本例采用多重动力子结构技术,对发动机结构进行动力学特性分析。考虑到子结构划分对计算精度、效率的影响,精度主要受模型准确性、模态截断误差及求解累积误差等的影响,随着子结构调用层次的增多,计算过程中的误差不受调用方式的影响,从量级上大幅度缩减整体结构的自由度而不改变问题的本质,可以精确计算出结构的模态;同时,子结构数增加,可更大程度减小求解模型规模,提高计算效率,但模型处理、数据管理的工作量也随之增加;另外,在子结构划分完成后,建议残余结构的规模一般不超过整体模型自由度的10%为宜。因此,本文按实际结构几何形状和装配边界条件等子结构划分原则[1]进行子结构划分,其中,Ⅰ级子结构包括机架及A1,A2,B1,B2分机共5个子结构;Ⅱ级子结构为A1,A2,B1及B2分机,每个分机均包括推力室、涡轮泵系统、燃气发生器、氧化剂泵前后主管路、燃料泵前后主管路共7个子结构,如图 5所示。
|
Fig. 5 Tree-like composition of the multilevel substructures |
分别建立了机架、推力室、涡轮泵、燃气发生器、主要管路、摇摆软管、伺服摇摆机构、集中质量、连接和非结构质量等典型组部件的FE模型[17],装配得单机FE模型。对单机进行固定约束正则模态分析,得到单机子结构的模态。
对比分析仿真与模态测试结果后发现(见表 1),计算前四阶模态频率相对误差高达10%,模型精度偏低,需对初始有限元模型进行修正。本文运用灵敏度分析与优化算法进行模型修正。将模型参数分为确定性参数与不确定性参数,确定性参数与实际比较相符,而造成误差的主要原因是建模中某些连接的不确定性,只需对不确定参数进行修改。通过灵敏度分析发现,推力室与机架连接位置的轴承(弱)刚度为发动机低阶模态的最敏感参数;进一步细化轴承部分模型,使用多点约束RBE2或RBE3连接内圈节点与中心点,同样使用多点约束连外圈节点与重合位置上的另一个中心点,然后在两个中心点处建立CBUSH单元,CBUSH单元可以设置轴承在各平动和转动方向上的刚度。以该弱连接部位刚度为设计变量,构造联合使用模态频率及模态振型为目标函数,进行单机有限元模型修正。
|
|
Table 1 Comparison of simulation results with experimental values before and after the model updating of the single engine |
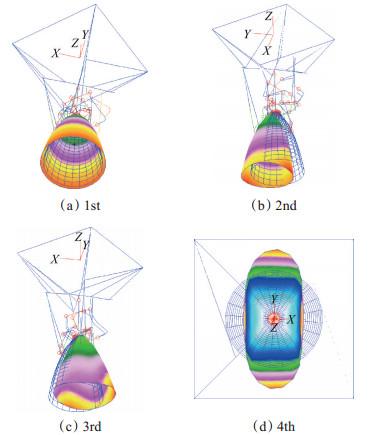
经模型修正后,仿真、试验频率误差小于1.2%,每个子结构数学模型能准确反映实际结构的动力学特性,模型准确性满足工程设计要求。模型修正后的计算振型如图 6所示。
|
Fig. 6 Simulation mode shapes of the single engine |
在对单机进行准确模态分析的基础上,根据四机并联发动机的实际物理作用关系,将单机扩展到四机并联状态,在模态域进行子结构综合,对并联发动机进行固定界面模态综合分析。
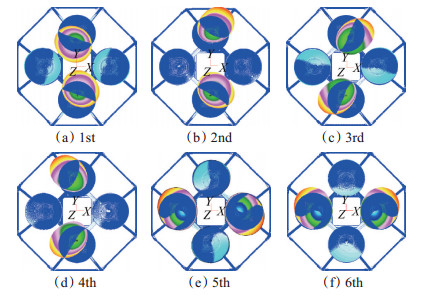
图 7为预示振型,表 2给出了仿真预示、模态测试结果对比。仿真前六阶模态频率与试验值的误差在5%以内,且预示模态振型和试验结果基本一致,说明了在低频范围内预示结果具有较高的精度,满足NASA,ECSS的有效性评价标准。
|
Fig. 7 Mode shapes of the four parallel connected engines |
|
|
Table 2 Comparison of simulation and test results of the four parallel connected engines |
整机前四阶模态为B1,B2单机在X或Y方向上的相对摆动,这主要由对固定发动机的约束相对较弱所引起。第五、六阶模态为A1,A2单机的相对扭摆,这主要受摇摆发动机伺服机构的影响。前六阶模态为两固定、两摇摆发动机的相对运动,整机的三维空间模态十分丰富,并可能会出现横、扭运动相互耦合,从而构成一个复杂的模态族。分析振型斜率(结构在固有振动频率下相对振型变化率,即振型和相对转角沿着飞行器总体轴线的相对变化量)发现,斜率最大位置位于摇摆十字轴附近,说明该处为整体刚度最弱位置,单机一阶弯曲、扭转模态对该位置非常敏感。发动机的第一阶模态为9.5Hz,且低阶模态均为发动机的横向摆动,发动机与箭体纵向模态耦合振动的可能性较小。
另外,对比采用多重动态子结构法、整体FE方法进行模态分析发现,前者模型自由度数仅为后者的3‰,从而大大降低了求解规模,提高了分析效率。
5 结论(1) 针对在大型复杂结构动力学精细化设计中的突出问题,提出了多重动力子结构法,详细论述了多重多级动态子结构基础理论,给出了采用该方法进行动力建模分析的工程实现技术途径。
(2) 此动力分析技术已成功应用于我国某大型运载火箭四机并联发动机的结构动力学预示中,算例验证了方法的有效性与灵活性。该分析技术可实现前六阶仿真、试验模态频率相对误差小于5%,模态振型相关性MAC值大于0.9,分析结果精度满足工程应用要求;相比传统子结构法、整体FE法,采用多重动力子结构方法可在保证分析精度的同时,极大提高了求解效率。
(3) 运用多重多级动态子结构方法来研究大型、超大型复杂结构低阶模态振动问题是有效的,并在分析效率、精度等方面优势显著,该方法为超大型复杂结构动态响应分析及动力学优化设计奠定了基础。
| [1] |
邱吉宝, 向树红, 张正平. 结构动力学及其在航天工程中的应用[M]. 合肥: 中国科学技术大学出版社, 2015.
(  0) 0) |
| [2] |
向树红, 邱吉宝, 王大钧. 模态分析与动态子结构方法新进展[J]. 力学进展, 2004, 34(3): 289-303. DOI:10.6052/1000-0992-2004-3-J2003-090 (  0) 0) |
| [3] |
邱吉宝, 王建民, 谭志勇. 运载火箭结构动力分析的一些新技术[J]. 导弹与航天运载技术, 2001, 250(2): 29-34. (  0) 0) |
| [4] |
Wang J M, Qiu J B. Simulation Techniques for the Modal Test of a Large Strap-on Launch Vehicle[C]. Beijing: Proc. CD-ROM of the 6th World Congress on Computational Mechanics, Tsinghua University Press & Springer-Verlag, 2004.
(  0) 0) |
| [5] |
徐庆红, 王明宇, 胡炜. 星箭动力学分析中多动力子结构模型综合研究[J]. 导弹与航天运载技术, 2015, 340(4): 46-49. (  0) 0) |
| [6] |
杜飞平, 谭永华, 陈建华. 基于子结构试验建模综合的火箭发动机结构动力分析[J]. 推进技术, 2015, 36(10): 1547-1553. (DU Fei-ping, TAN Yong-hua, CHEN Jian-hua. Structural Dynamic Analysis of Rocket Engine Based on Synthetic Technology for Substructure Test Model[J]. Journal of Propulsion Technology, 2015, 36(10): 1547-1553.)
(  0) 0) |
| [7] |
Zhong W X, Lin J H, Qiu C H. Computational Structural Mechanics and Optimal Control the Simulation of Substructural Chain Theory to Linear Quadratic Optimal Control Problems[J]. International Journal of Numerical Methods in Engineering, 1992(33): 197-211.
(  0) 0) |
| [8] |
Yang Y S, Hsien S H, Asce M. Improving Parallel Substructuring Efficiency by Using a Multilevel Approach[J]. Journal of Computing in Civil Engineering, 2012, 26(4): 457-464. DOI:10.1061/(ASCE)CP.1943-5487.0000142
(  0) 0) |
| [9] |
Zhao R, Yu K P. An Efficient Transient Analysis Method for Linear Time-Varying Structures Based on Multi-level Substructuring Method[J]. Computers and Structures, 2015(146): 76-90.
(  0) 0) |
| [10] |
贺尔铭, 杨智春. 高等结构动力学[M]. 西安: 西北工业大学出版社, 2016.
(  0) 0) |
| [11] |
Valsamos G, Sikelis K, Natsiavas S. Stochastic Dynamics and Fatigue Analysis of Large-Scale Mechanical Models Using Multilevel Substructuring[J]. Journal of Multi-Body Dynamics, 2012, 226(4): 343-358.
(  0) 0) |
| [12] |
Frank Blömeling. Multi-Level Substructuring Combined with Model Order Reduction Methods[J]. Linear Algebra and Its Applications, 2012, 436: 3864-3882. DOI:10.1016/j.laa.2011.02.040
(  0) 0) |
| [13] |
Ragnarsson P, Gaal T Van. Fast Approximation of Synthesized Frequency Response Functions with Automated Multi-Level Substructuring[J]. Finite Elements in Analysis and Design, 2011(47): 195-199.
(  0) 0) |
| [14] |
Kim Jin-Gyun, Boo Seung-Hwan. An Enhanced AMLS Method and Its Performance[J]. Computer Methods in Applied Mechanics and Engineering, 2015(287): 90-111.
(  0) 0) |
| [15] |
Boo Seung-Hwan, Kim Jin-Gyun, Lee Phill-Seung. Error Estimation for the Automated Multi-Level Substructuring Method[J]. International Journal for Numerical Methods in Engineering, 2016, 106: 927-950. DOI:10.1002/nme.v106.11
(  0) 0) |
| [16] |
Geng Z. Component-Based and Parametric Reduced-Order Modeling Methods for Vibration Analysis of Complex Structures[D]. Ann Aobor: The University of Michigan, 2005.
(  0) 0) |
| [17] |
杜大华, 贺尔铭, 薛杰, 等. 大推力液体火箭发动机启动冲击响应特性研究[J]. 西北工业大学学报, 2016, 34(6): 982-989. (  0) 0) |
 2018, Vol. 39
2018, Vol. 39


