2. 北京精密机电控制设备研究所,北京 100076
2. Beijing Research Institute of Precise Mechanical and Electronic Control Equipment, Beijing 100076, China
行星滚柱丝杠是一种通过螺纹啮合进行运动传递的高精度传动机构,它能适应高速、重载及高频的工作环境,因此在航空、航天等领域具有广泛应用。行星滚柱丝杠结构中存在大量非标准螺纹的啮合,导致动力学建模困难。提高行星滚柱丝杠的动力学模型精度对提高伺服系统动态响应速度以及稳定性具有重要意义[1~4]。
国内外对于行星滚柱丝杠展开了大量研究。针对其运动特性,Matthew等建立了行星滚柱丝杠的运动模型,并对行星滚柱丝杠工作过程中出现的相对滑移进行了分析,并得到运动误差随螺母运动位移以及螺母与滚柱之间相对滑移速度的变化关系,对研究行星滚柱丝杠传动效率的研究具有重要作用[5]。Aurégan等[6]进行了不同润滑条件下的行星滚柱丝杠摩擦特性试验,得出结论行星滚柱丝杠的滑动率和滚动速度都与润滑效果有直接关系。对于行星滚柱丝杠静刚度展开的研究主要有,Folly等建立了一种新的计算行星滚柱丝杠静态力分布以及行星滚柱丝杠轴向刚度的研究方法,并通过有限元模型对该方法进行了验证[7, 8]。Matthew等针对行星滚柱丝杠的结构特点首先建立了其静刚度模型,该模型不需要行星滚柱丝杠模型进行简化,提高了行星滚柱丝杠刚度模型的精度[9]。国内许多学者对行星滚柱丝杠的轴向刚度[10, 11],运动特性[12, 13],以及啮合机理[14, 15]进行了仿真研究。
动力学特性是评价行星滚柱丝杠综合性能的一个重要指标。目前,国内外对于行星滚柱丝杠动力学研究多着重通过商业有限元软件进行分析。Matthew等建立了行星滚柱丝杠的动力学方程,考虑了摩擦以及滚柱滑移等因素,得到了滑移速度与丝杠螺距以及螺纹接触角之间的关系,对行星滚柱丝杠的设计有指导意义,但所建立的方程相对复杂,不利于行星滚柱丝杠模型动力学特性的快速计算[16]。国内学者马尚军等通过有限元软件对行星滚柱丝杠的动态特性和弹性变形进行了分析,从仿真结果中可以看出滚柱的转速会影响丝杠的运动特性,合理增大螺旋升角和接触角有利于提高行星滚柱丝杠副的传动精度[17, 18]。岳琳琳等使用有限元软件对行星滚柱丝杠进行了模态分析,得到了行星滚柱丝杠的前六阶固有频率及最大变形,但仿真计算量大,耗时长,不利于舵机位移控制系统的建模及响应分析[19]。
螺纹之间的啮合刚度是影响行星滚柱丝杠刚度模型的重要因素。为简化行星滚柱丝杠动力学模型并提高其精度,本文建立了单个螺纹的啮合刚度,并将各个螺纹的啮合刚度进行合并和化简得到行星滚柱丝杠系统的支承刚度,使用有限元方法建立了考虑螺纹啮合刚度的行星滚柱丝杠动力学模型,仿真分析了螺纹接触角和滚柱半径对行星滚柱丝杠固有频率的影响,并通过行星滚柱丝杠的固有频率试验对仿真结果进行了验证。
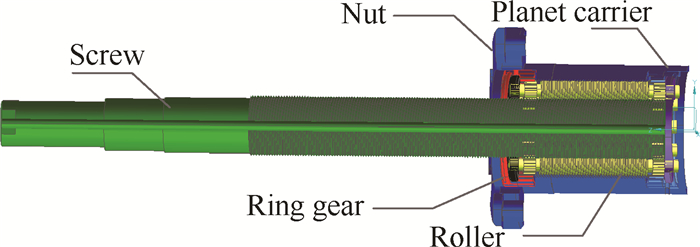
2 行星滚柱丝杠动力学建模行星滚柱丝杠副主要由丝杠、滚柱、螺母、内齿圈以及行星架组成。行星滚柱丝杠的工作原理是行星传动原理,工作过程中丝杠由电机驱动发生旋转,丝杠与滚柱发生接触,滚柱围绕自身轴线发生旋转,同时也围绕丝杠轴线公转并沿丝杠轴向方向进行直线运动;螺母在滚柱的带动下沿着丝杠的轴向方向直线运动。行星滚柱丝杠结构示意图,如图 1所示。
|
Fig. 1 Structure of planetary roller screw |
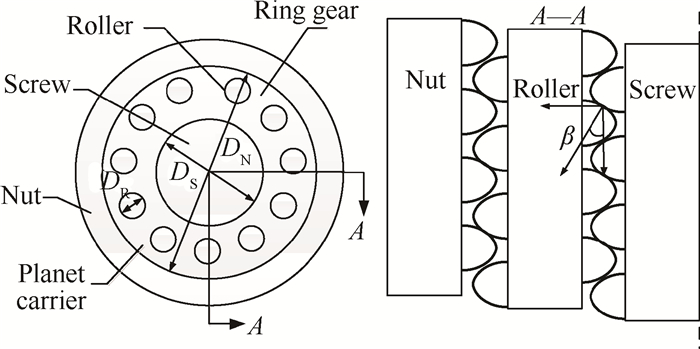
在行星滚柱丝杠工作过程中,螺母承受负载,丝杠下方的滚柱提供支承。行星滚柱丝杠整体的刚度主要包括:体刚度、螺纹刚度和接触刚度。体刚度和螺纹刚度是轴向方向的,而接触刚度是垂直于接触面方向的。由于整个行星滚柱丝杠中存在大量的螺纹接触,会使得行星滚柱丝杠系统的动力学模型比较复杂,需要对其动力学模型进行简化,螺纹接触模型的示意图如图 2所示,DR为滚柱直径,DS为丝杠直径,DN为螺母直径,β为接触两物体的接触角。
|
Fig. 2 Force of thread contact |
在无轴承支撑条件下,行星滚柱丝杠竖直方向的支承刚度由行星滚柱丝杠中各螺纹接触刚度的竖直方向分量组成。由赫兹接触理论得到两个接触螺纹的曲面接触的变形公式[20]
| $ {\delta _{\rm{H}}} = {\left( {\frac{{9{p^2}}}{{16{E^{{\rm{*}}2}}{R_{{\rm{Ei}}}}}}} \right)^{\frac{1}{3}}}{\rm{cos}}\beta {F_2} $ | (1) |
式中E*为当量弹性模量,其表达式为
| $ \frac{1}{{{E^{\rm{*}}}}} = \frac{1}{{{E_1}}} + \frac{1}{{{E_2}}} $ | (2) |
式(1)中REi为接触曲面的等效曲率半径
| $ {R_{{\rm{Ei}}}} = \frac{1}{2}{\left( {AB} \right)^{ - \frac{1}{2}}} $ | (3) |
式(3)中A和B为接触曲面主轴长度
| $ A + B = \frac{1}{2}\left( {\frac{1}{{R'}} + \frac{1}{{R''}}} \right) = \frac{1}{2}\left( {\frac{1}{{{{R'}_1}}} + \frac{1}{{{{R''}_2}}} + \frac{1}{{{{R'}_2}}} + \frac{1}{{{{R''}_2}}}} \right) $ | (4) |
| $ B - A = \frac{1}{2}{\left\{ {\begin{array}{*{20}{l}} {{{\left( {\frac{1}{{{{R'}_1}}} - \frac{1}{{{{R''}_1}}}} \right)}^2} + {{\left( {\frac{1}{{{{R'}_2}}} - \frac{1}{{{{R''}_2}}}} \right)}^2} + }\\ {2\left( {\frac{1}{{{{R'}_1}}} - \frac{1}{{{{R''}_1}}}} \right)\left( {\frac{1}{{{{R'}_2}}} - \frac{1}{{{{R''}_2}}}} \right){\rm{cos}}2\gamma } \end{array}} \right\}^{\frac{1}{2}}} $ | (5) |
式中p为接触面所受压力;E1,E2为两接触面各自的弹性模量;α为螺纹升角;β为接触角;F2为Hertz接触中的位移修正因子;R'1和R"1分别为一个接触物体的两个主曲率半径;R'2和R"2分别为另一个接触物体的两个主曲率半径;γ是两曲率半径夹角。
滚柱和丝杠之间的接触刚度模型为
| $ {K_{{\rm{HS}}}} = \frac{F}{{{\delta _{\rm{S}}}}} $ | (6) |
式中F是作用于丝杠和滚柱上的力;KHS是丝杠和滚柱之间的接触刚度;δS是滚柱和丝杠之间的接触变形。
由于行星滚柱丝杠内部存在大量螺纹接触,并且结构比较复杂,为方便快速计算需要对行星滚柱丝杠进行简化。滚柱螺纹的接触刚度由两部分组成,滚柱与丝杠之间的螺纹接触刚度KHS和滚柱与螺母之间的螺纹接触刚度KHN。同一螺纹的两个接触刚度KHS和KHN需要串联在一起,而不同的滚柱之间的接触刚度模型是并联的。同一滚柱螺纹所承受的接触刚度模型公式为
| $ {K_{\rm{H}}} = \frac{{{K_{{\rm{HS}}}}{K_{{\rm{HN}}}}}}{{{K_{{\rm{HS}}}} + {K_{{\rm{HN}}}}}} $ | (7) |
从接触变形的公式中可以看出,接触刚度是非线性的,螺纹接触角度以及滚柱半径的变化都会导致行星滚柱丝杠整体支承刚度发生变化。
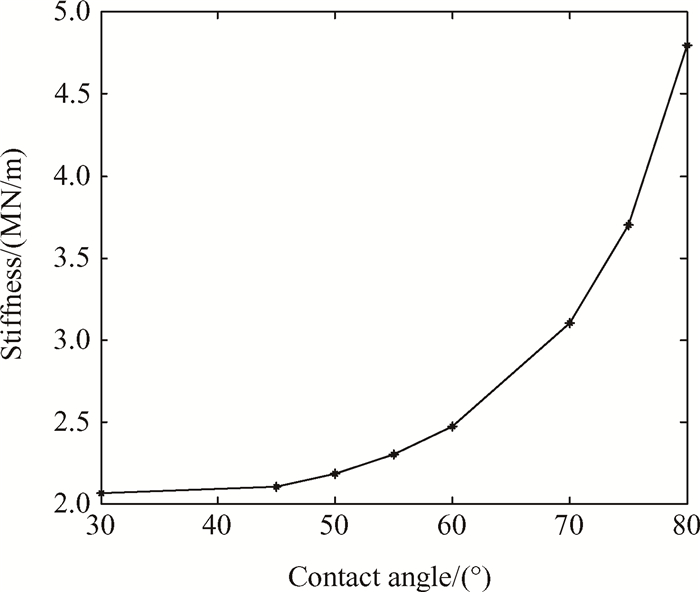
图 3所示为同一圈螺纹上的总接触刚度随接触角度变化趋势图。从图 3中可以看出接触刚度随接触角度增加而增加,而且接触刚度增加的速度随接触角增加而加快。
|
Fig. 3 Effects of contact angle on PRS axial stiffness |
本文使用的行星滚柱丝杠模型的结构参数如表 1所示。
|
|
Table 1 Parameters of PRS |
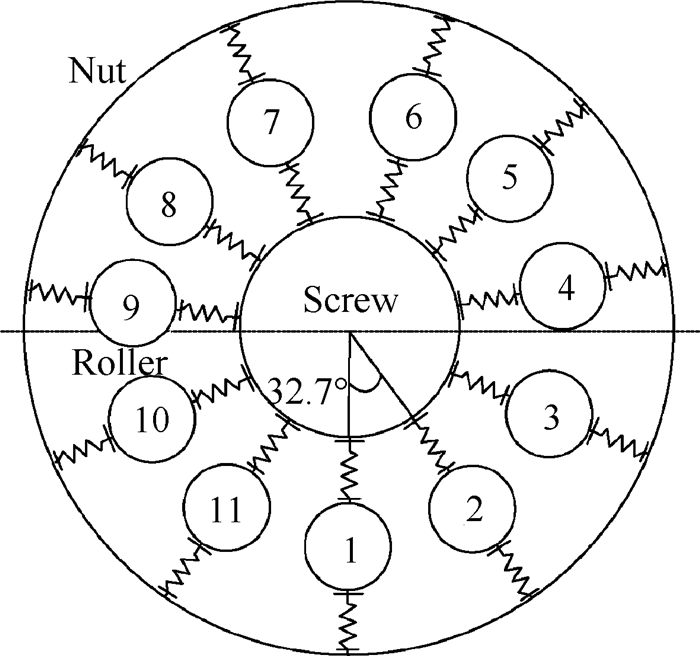
本文所建立的模型是有一个滚柱处在丝杠正下方,滚柱分布示意图如图 4所示。对行星滚柱丝杠进行等效简化,将滚柱等效成只承受压力不承受拉力的特殊弹簧结构,将弹簧受压力产生的变形转化为竖直方向的变形,从而得到整个行星滚柱丝杠系统的支承刚度。本文分析所使用的行星滚柱丝杠有11个滚柱,两个滚柱之间夹角为32.7°,每个滚柱的变形在竖直方向的分量以及支承刚度的表达式如下所示
| $ \left\{ {\begin{array}{*{20}{l}} {{\delta _1} = \delta {\rm{cos}}\left( {\frac{{2{\rm{ \mathsf{ π} }}}}{{11}} \times 2} \right)}\\ {{K_{{\rm{H}}1}} = \frac{F}{{{\delta _1}}}} \end{array}} \right. $ | (8) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\delta _2} = \delta {\rm{cos}}\left( {\frac{{2{\rm{ \mathsf{ π} }}}}{{11}}} \right)}\\ {{K_{{\rm{H}}2}} = \frac{F}{{{\delta _2}}}} \end{array}} \right. $ | (9) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\delta _3} = \delta }\\ {{K_{{\rm{H}}3}} = \frac{F}{{{\delta _3}}}} \end{array}} \right. $ | (10) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\delta _4} = \delta {\rm{cos}}\left( {\frac{{2{\rm{ \mathsf{ π} }}}}{{11}}} \right)}\\ {{K_{{\rm{H}}4}} = \frac{F}{{{\delta _4}}}} \end{array}} \right. $ | (11) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\delta _5} = \delta {\rm{cos}}\left( {\frac{{2{\rm{ \mathsf{ π} }}}}{{11}} \times 2} \right)}\\ {{K_{{\rm{H}}5}} = \frac{F}{{{\delta _5}}}} \end{array}} \right. $ | (12) |
| $ K = {K_{{\rm{H}}1}} + {K_{{\rm{H}}2}} + {K_{{\rm{H}}3}} + {K_{{\rm{H}}4}} + {K_{{\rm{H}}5}} $ | (13) |
|
Fig. 4 Roller distribution of simplified PRS |
式中δ为每根滚柱的变形;δ1为第一根滚柱变形在竖直方向的分量;KH1是滚柱1在竖直方向的刚度;K是行星滚柱丝杠整体的支承刚度;F是作用于滚柱上的力。
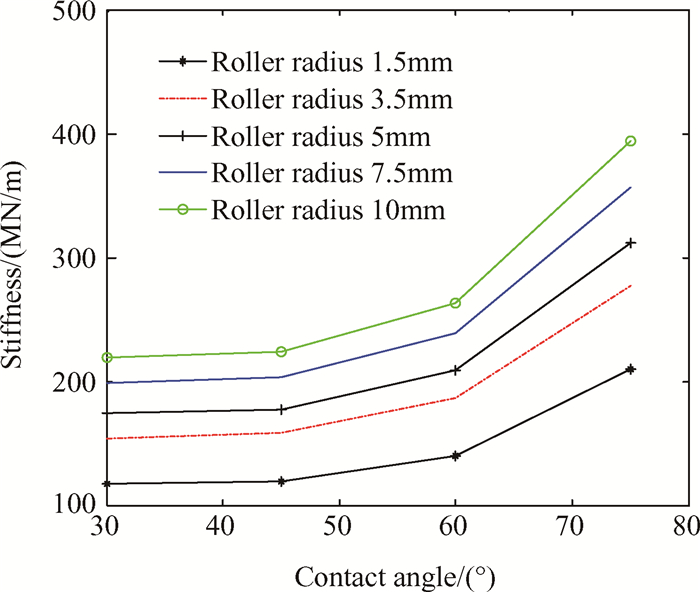
图 5所示为不同滚柱半径下,行星滚柱丝杠整体支承刚度随接触角度的变化趋势。从图 5中可以看出支承刚度随接触角增加而增大,而且增加的速度会加快。
|
Fig. 5 Effects of contact angle on PRS supporting stiffness |
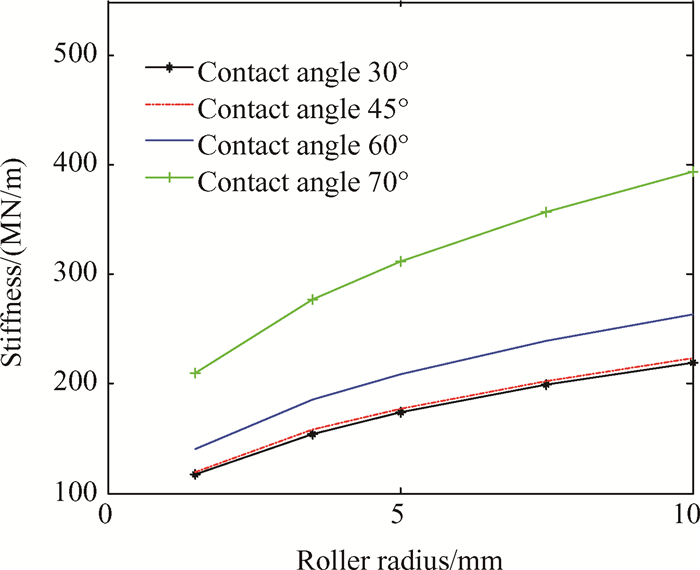
图 6所示为不同的接触角下,支承刚度随滚柱半径的变化趋势图。从图 6中可以看出支承刚度随滚柱半径增加而增加,增加的速度会降低。各个接触角条件下的支承刚度分别趋近于各自的极限值。滚柱半径会影响支承刚度的原因是滚柱半径的选择会影响到滚柱螺纹形状的设计[11],滚柱的螺纹外形圆弧半径公式为
|
Fig. 6 Effects of roller radius on PRS bracing stiffness |
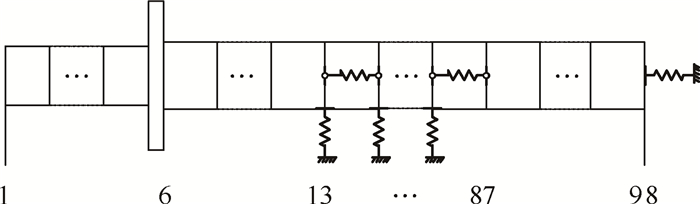
行星滚柱丝杠简化后的模型可以简化为一个圆柱梁,将滚柱的每一个螺纹都简化为支承刚度和附加质量,行星滚柱丝杠简化并离散后的示意图如图 7所示。
|
Fig. 7 Simplified model of PRS |
由于行星滚柱丝杠模型丝杠螺距为2mm的5头螺纹,因此中间有螺纹接触部分离散单元的长度为0.4mm,整个行星滚柱丝杠离散成97个单元、75个弹簧单元以及75个附加质量单元,其中在13~87节点位置要添加弹簧单元和附加质量单元,同时为保证仿真结果与试验结果的一致性,在节点6和节点98位置添加了附加质量单元,代表试验装置中的预载装置。由于行星滚柱丝杠的动力学方程
| $ \left[ \mathit{\boldsymbol{M}} \right]\left\{ {\ddot u} \right\} + \left[ \mathit{\boldsymbol{C}} \right]\left\{ {\dot u} \right\} + \left[ \mathit{\boldsymbol{K}} \right]\left\{ u \right\} = \left\{ Q \right\} $ | (14) |
根据行星滚柱丝杠离散方法得到行星滚柱丝杠的质量矩阵和刚度矩阵[M]490×490和[K]490×490,{u}490×1为系统的位移,由两个方向的弯曲位移、轴向位移和两个方向的弯曲角度组成,
忽略阻尼,得到行星滚柱丝杠系统的无阻尼自由振动微分方程的矩阵形式为
| $ \left[ \mathit{\boldsymbol{M}} \right]\left\{ {\ddot u} \right\} + \left[ \mathit{\boldsymbol{K}} \right]\left\{ u \right\} = 0 $ | (15) |
响应的频率行列式为
| $ \left( {K - {\omega ^2}M} \right)\varphi = 0 $ | (16) |
式(16)的非零解,即为行星滚柱丝杠系统的固有频率。
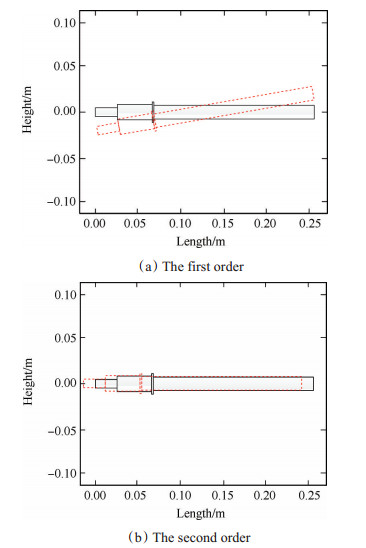
3 行星滚柱丝杠动力学模型验证 3.1 行星滚柱丝杠固有频率特性仿真根据所建立的行星滚柱丝杠的动力学模型,对行星滚柱丝杠的第一阶和第二阶固有频率进行仿真计算,得到行星滚柱丝杠前两阶固有频率及其振型,如图 8所示。
|
Fig. 8 Mode shapes of various orders of PRS |
从振型图中可以看出,仿真计算的第一阶模态振型为绕中间支点的摆动,行星滚柱丝杠轴向和径向都发生较大位移,如图 8(a)所示;第二阶模态振型为轴向平动,图 8(b)中y轴所示为行星滚柱丝杠的轴向位移,可以看出丝杠发生较大的轴向平动。通过动力学特性仿真计算得到行星滚柱丝杠模型的一阶固有频率为182Hz,二阶固有频率为781Hz。
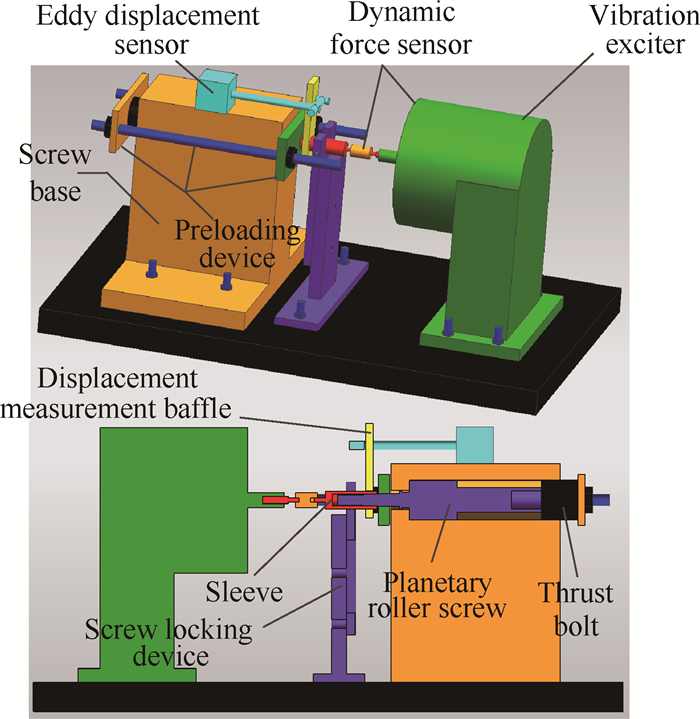
3.2 行星滚柱丝杠动态特性试验为验证行星滚柱丝杠动力学模型的准确性,搭建了行星滚柱丝杠动刚度特性试验台,试验台的原理示意图如图 9所示。
|
Fig. 9 Experiment schematic diagram |
行星滚柱丝杠动力学特性试验台主要由激振器、行星滚柱丝杠及基座、动态力传感器、位移传感器、预载装置、丝杠止动装置、止推大螺柱和数据采集分析系统组成。使用激振器施加正弦力激励,对行星滚柱丝杠进行正弦扫描。行星滚柱丝杠放置在丝杠基座中,丝杠基座的材料是Q235碳素结构钢,行星滚柱丝杠试验件的螺纹接触角为45°。丝杠止动装置用来防止丝杠旋转;止推大螺柱直径为54mm,长度为50mm,作用是防止丝杠发生轴向运动。行星滚柱丝杠动力学特性试验台如图 10所示。

|
Fig. 10 Dynamic experimental test setup of PRS |
试验中使用的传感器参数如表 2所示,试验台主要部件的结构参数如表 3所示。
|
|
Table 2 Parameters of sensors |
|
|
Table 3 Parameters of dynamic experiment device |
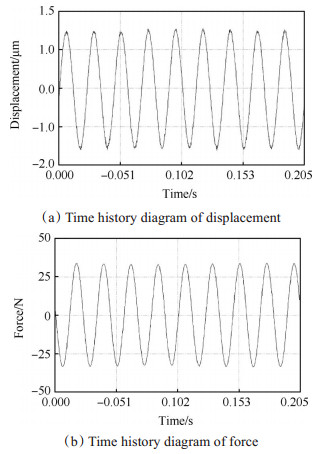
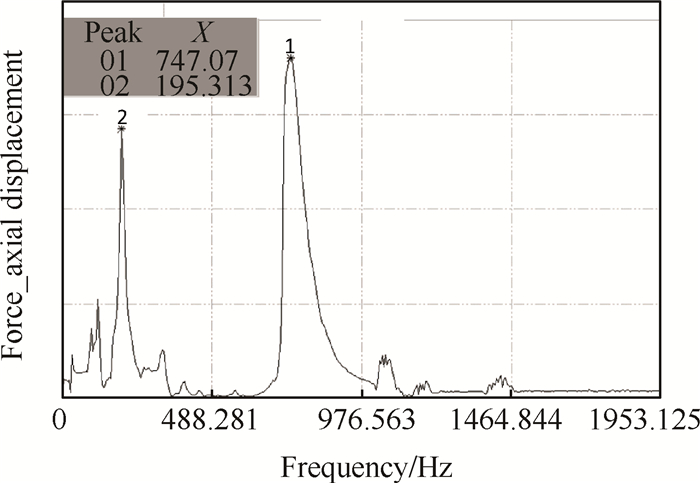
图 11(a)和图 11(b)分别为进行行星滚柱丝杠动力学特性试验时,丝杠产生的位移和激振器产生激振力的时间历程图,从图 11(b)中可以看出激振器对行星滚柱丝杠施加正弦激振力。图 12为动力学特性试验的幅频特性曲线,从图 12中可以看出在195Hz和747Hz两个频率下,行星滚柱丝杠振动明显,得到行星滚柱丝杠的前两阶固有频率。
|
Fig. 11 Output of two sensors |
|
Fig. 12 Amplitude frequency characteristic curve of PRS dynamic experiment |
试验中施加正弦激振力,改变激励频率,得到所施加的激振力与行星滚柱丝杠变形的关系,通过频响分析,可以得到行星滚柱丝杠的前两阶固有频率。由于行星滚柱丝杠是通过螺纹进行力的传递,而螺纹啮合面本身是一个圆斜面,因此在激振器施加轴向激振力的同时也会产生横向激振力,丝杠会产生轴向和径向两个方向的位移。通过试验测得行星滚柱丝杠的第一、二阶固有频率分别为195Hz和747Hz。试验结果与仿真计算结果的误差分别为6.7%和4.3%。由于试验台的连接存在间隙等非线性因素,会导致试验结果与仿真结果之间存在误差。试验结果证明了本文所建立的行星滚柱丝杠动力学模型的准确性。
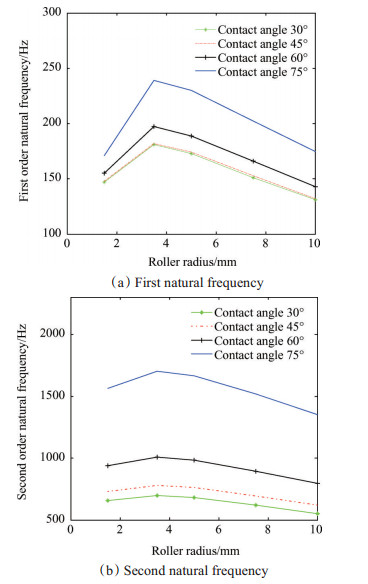
4 行星滚柱丝杠动力学特性仿真由于接触角和滚柱半径会对支承刚度带来影响,因此也会对行星滚柱丝杠副的固有频率带来影响。图 13(a)和图 13(b)为滚柱半径对行星滚柱丝杠的第一、二阶固有频率的影响图。在行星滚柱丝杠整体长度不变的条件下,行星滚柱丝在滚柱半径为3.5mm附近有最大的第一、二阶固有频率。这是因为半径的变化引起行星滚柱丝杠的支承刚度发生变化,同时又引起了丝杠的质量、转动惯量、附加质量以及附加转动惯量等参数的变化,从而影响行星滚柱丝杠的固有频率,适当的选择滚柱半径能有效提高行星滚柱丝杠的固有频率。
|
Fig. 13 Effects of roller radius on PRS natural frequencies |
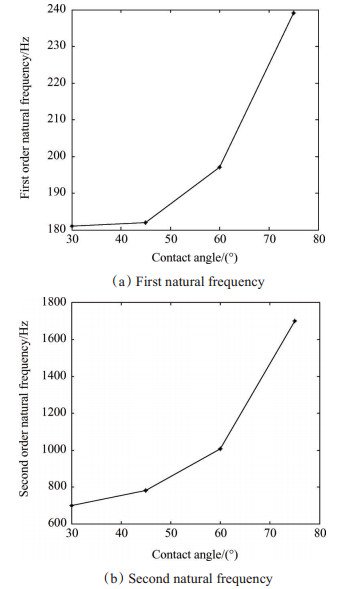
图 14(a)和图 14(b)为行星滚柱丝杠螺纹接触角对行星滚柱丝杠的第一、二阶固有频率的影响图,图 14(a)和图 14(b)中所使用的仿真模型是滚柱直径为3.5mm的行星滚柱丝杠模型。可以看出随着接触角的增加,行星滚柱丝杠的第一、二阶固有频率都会增加,而且增加的速度也会变快,合理地提高螺纹接触角能够有效提高行星滚柱丝杠的固有频率。
|
Fig. 14 Effects of contact angle on PRS natural frequencies |
本文首先建立了考虑螺纹啮合的行星滚柱丝杠动力学模型,搭建了行星滚柱丝杠动力学特性试验台,对建立的行星滚柱丝杠动力学模型进行验证,得到了结论如下:
(1) 螺纹接触角和滚柱半径对行星滚柱丝杠啮合刚度的影响较大,合理地增大螺纹接触角和滚柱半径会增大螺纹的啮合刚度。
(2) 对所建立的简化动力学模型进行仿真研究并搭建试验台进行验证,得到行星滚柱丝杠第一、二阶固有频率为182Hz和781Hz;试验结果与仿真结果的相对误差都小于6.7%,验证了本文所建立模型的准确性。
(3) 通过对行星滚柱丝杠动力学模型的仿真分析,可以看出接触角的增加会使行星滚柱丝杠的前两阶固有频率增加;滚柱半径在3.5mm附近时行星滚柱丝杠的第一、二阶固有频率最大。从仿真结果中看出,增大螺纹接触角以及适当的选择滚柱半径,可以提高行星滚柱丝杠的固有频率,使其工作范围低于其第一、二阶固有频率,防止行星滚柱丝杠发生共振。
| [1] |
Yehezkely E, Karpel M. Nonlinear Flutter Analysis of Missiles with Pneumatic Fin Actuators[J]. Journal of Guidance Control and Dynamics, 1996, 19(3): 664-670. DOI:10.2514/3.21672
(  0) 0) |
| [2] |
张仁嘉, 吴志刚, 杨超. 电动伺服舵系统动力学建模及颤振分析[J]. 北京航空航天大学学报, 2016, 7(42): 1368-1376. (  0) 0) |
| [3] |
Tselishchev A S, Zharov I S. Elastic Elements in Roller-Screw Mechanisms[J]. Russian Engineering Research, 2008, 28(11): 1040-1043. DOI:10.3103/S1068798X08110026
(  0) 0) |
| [4] |
李强, 张绞龙, 周军, 等. 行星滚柱丝杠传动机构非线性建模与仿真[J]. 西北工业大学学报, 2015, 10(33): 739-743. (  0) 0) |
| [5] |
Matthew H J, Steven A V. Kinematics of Roller Migration in the Planetary Roller Screw Mechanism[J]. Journal of Mechanical Design, 2015, 134(6).
(  0) 0) |
| [6] |
Aurégan G, Fridrici V, Kapsa Ph, et al. Experimental Simulation of Rolling-Sliding Contact for Application to Planetary Roller Screw Mechanism[J]. Wear, 2015(332-333): 1176-1184.
(  0) 0) |
| [7] |
Folly A, Alain D, Michel C, et al. Static Load Distribution and Axial Stiffness in a Planetary Roller Screw Mechanism[J]. Journal of Mechanical Design, 2016, 138(1).
(  0) 0) |
| [8] |
Folly A, Alain D, Michel C, et al. Static Analysis of an Inverted Planetary Roller Screw Mechanism[J]. Journal of Mechanisms and Robotics, 2016(8).
(  0) 0) |
| [9] |
Matthew H J, Steven A. Stiffness of Roller Screw Mechanism by the Direct Method[J]. Mechanics Based Design of Structures and Machines, 2014, 42(1): 17-34. DOI:10.1080/15397734.2013.839385
(  0) 0) |
| [10] |
靳谦忠, 杨家军, 孙健利. 滚珠丝杠副和行星式滚柱丝杠副静刚度的比较研究[J]. 机械科学与技术, 1999, 18(2): 230-232. (  0) 0) |
| [11] |
杨家军, 韦振兴, 朱继生, 等. 行星滚柱丝杠副载荷分布及刚度计算[J]. 华中科技大学学报, 2011, 39(4): 1-4. (  0) 0) |
| [12] |
马尚军, 刘更, 佟瑞庭, 等. 考虑节圆偏移的反向式行星滚柱丝杠副运动学分析[J]. 中国机械工程, 2014, 6(25): 1421-1426. (  0) 0) |
| [13] |
马尚军, 刘更, 付晓军, 等. 考虑弹性变形的行星滚柱丝杠副滚花特性[J]. 东南大学学报, 2015, 45(3): 461-468. DOI:10.3969/j.issn.1001-0505.2015.03.009 (  0) 0) |
| [14] |
付晓军, 刘更, 马尚军, 等. 行星滚柱丝杠副螺旋曲面啮合机理研究[J]. 机械工程师学报, 2016, 52(3): 26-33. (  0) 0) |
| [15] |
付晓军, 刘更, 马尚军, 等. 考虑零件偏斜的行星滚柱丝杠副啮合特性研究[J]. 机械工程学报, 2017, 53(3): 25-33. (  0) 0) |
| [16] |
Matthew H J, Steven A, Lasky Ty A. Dynamics of the Planetary Roller Screw Mechanism[J]. Journal of Mechanisms and Robotics, 2015, 8(1).
(  0) 0) |
| [17] |
马尚君, 刘更, 周建星, 等. 行星滚柱丝杠副运转过程动态特性分析[J]. 振动与冲击, 2013, 32(3): 167-171. (  0) 0) |
| [18] |
马尚军, 刘更, 佟瑞庭, 等. 行星滚柱丝杠副轴向弹性变形的有限元分析[J]. 机械传动, 2012, 36(7): 79-81. (  0) 0) |
| [19] |
岳琳琳, 王卫英, 胡宝根, 等. 基于有限元仿真的行星滚柱丝杠动态特性分析[J]. 机械工程与自动化, 2014, 183(2). (  0) 0) |
| [20] |
Johnson K. Contact Mechanics[M]. 徐秉业, 罗学富, 刘信声, 译. 北京: 高等教育出版社, 1992.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


