双模态超燃冲压发动机燃烧室内部流场结构复杂,存在激波串与附面层相互作用、流动分离再附等复杂的物理现象,为发动机的性能分析带来挑战。三维数值仿真虽然能够对这些复杂的物理现象提供详细的流场信息,但计算过程耗时耗力;而一维分析方法计算量小,可以通过合适的计算模型获得较高精度的计算结果[1, 2],因而被广泛应用于燃烧室性能评估[3~6]。
目前,超燃燃烧室一维分析方法主要分为两类:(1)基于掺混和化学反应经验公式,获得燃烧室沿程释热分布,从而来计算其他一维流动参数。该方法需要采用合适的激波串模型,进而计算获得较为准确的压力、马赫数的分布[7]。(2)基于实验获得的壁面压力分布和芯流面积拟合来计算其他一维流动参数。本文选用的是第二种方法,根据核心流再附的经验性假设,将超燃燃烧室内的流动分为芯流和分离区两部分,其中芯流反映了燃烧室内核心区流体的流动情况,可用于燃烧室的性能分析,其流动参数主要采用一维欧拉方法求解[8]。从William Heiser等[9]的一维分析结果可以看出,在燃烧室入口气体流速为Ma=2的工况下,回流区截面积与燃烧室几何截面积之比可高达25%。计算过程中如果直接将燃烧室截面积带入一维模型,会使流动分离再附过程的计算结果出现较大偏差[10],因此需要对芯流面积进行有效的评估。William Heiser等[9]给出了芯流面积的经验性公式,但公式中的经验常数变化范围较大,难以根据实际情况给出合理数值;文献[9, 11, 12]根据等压燃烧假设,将燃烧室分为三段:绝热压缩段由气体动力学公式计算芯流面积,等压燃烧段通过差值或拟合的方式获得芯流面积,膨胀释热段由多变过程关系式“PAn=常数”计算芯流面积,但发动机实际工作过程中,燃料的释热过程难以维持等压过程[13],多变关系式也难以满足任意工况的壁面压力数据[9];张鹏[14]、程柳维[15]等放弃等压燃烧假设,通过确定释热起始点和芯流再附点位置,通过拟合的方式获得芯流面积,但释热点与再附点位置是根据实验经验确定的,在一定程度上存在人的主观因素。
研究表明,为获得流动分离再附过程中的芯流面积,给出某个变量的变化规律是一个比较好的方法[14]。因此,本文基于实验获得的壁面压力数据,引入燃烧室释热分布模型,对芯流面积进行求解。求解过程中,放弃了选取再附点的方法,认为燃料释热过程满足瑞利概率密度分布,释热模型中的经验常数由燃烧室构型参数和壁面压力反算获得,在一定程度上降低了人为干扰因素,提高了该模型的通用性。
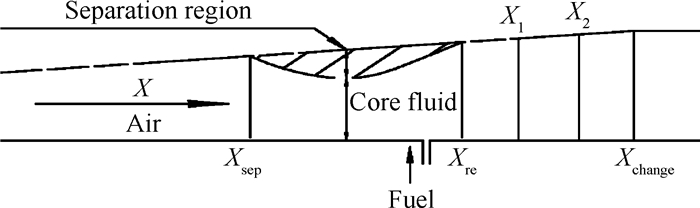
2 物理模型和计算方法在超燃冲压发动机燃烧室工作过程中,由于燃料喷注、释热等因素,导致燃烧室内的流动过程存在逆压力梯度,出现回流区,使流动分为芯流和分离区两部分,如图 1所示。在
|
Fig. 1 Flow in the supersonic combustion |
本文的研究基于定常流动假设,考虑芯流面积变化、摩擦、释热、加质的影响,构建了一维流动分析模型,控制方程组如下
状态方程
| $ \frac{{{\rm{d}}\rho }}{\rho } + \frac{{{\rm{d}}T}}{T} = \frac{{{\rm{d}}p}}{p} $ | (1) |
连续性方程
| $ \frac{{{\rm{d}}\rho }}{\rho } + \frac{{{\rm{d}}V}}{V} + \frac{{{\rm{d}}{A_{\rm{c}}}}}{{{A_{\rm{c}}}}} = \frac{{{\rm{d}}\dot m}}{{\dot m}} $ | (2) |
动量方程方程
| $ kM{a^2}\frac{{{\rm{d}}V}}{V} = - E - F - \frac{{{\rm{d}}p}}{p} $ | (3) |
速度/马赫数方程
| $ \frac{{2{\rm{d}}Ma}}{{Ma}} + \frac{{{\rm{d}}T}}{T} = \frac{{2{\rm{d}}V}}{V} $ | (4) |
总温方程
| $ \frac{{{\rm{d}}{T_{\rm{t}}}}}{{{T_{\rm{t}}}}} = \frac{{{\rm{d}}T}}{T} + \frac{{\left( {k - 1} \right)M{a^2}}}{{1 + \frac{{\left( {k - 1} \right)}}{2}M{a^2}}}\frac{{{\rm{d}}p}}{p} $ | (5) |
式中p,
由公式(1)~(5)可得到Ma和芯流面积Ac的一维微分方程
| $ \begin{array}{*{20}{l}} {\frac{{{\rm{d}}Ma}}{{Ma}} = - \left( {1 + \frac{{k - 1}}{2}M{a^2}} \right) \times }\\ {\left( {\frac{1}{{kM{a^2}}}\frac{{{\rm{d}}p}}{p} + \frac{1}{2}\frac{{{\rm{d}}{T_{\rm{t}}}}}{{{T_{\rm{t}}}}}} \right) - E' - F''} \end{array} $ | (6) |
| $ \begin{array}{*{20}{l}} {\frac{{{\rm{d}}{A_{\rm{c}}}}}{{{A_{\rm{c}}}}} = \left( {\frac{1}{{kM{a^2}}} - \frac{1}{k}} \right)\frac{{{\rm{d}}p}}{p} + }\\ {\left( {1 + \frac{{k - 1}}{2}M{a^2}} \right)\frac{{{\rm{d}}{T_{\rm{t}}}}}{{{T_{\rm{t}}}}} - E'' - F''} \end{array} $ | (7) |
式中E',E"为摩擦项,F',F"为添质项。可以看出,马赫数是总温和壁面压力的函数,而芯流面积是马赫数、总温、壁面压力的函数。可以看出,在其他参数不变的情况下,释热越快,总温抬升越快,对应芯流面积增加得也就越快,因此选取合适的释热分布模型,即可通过四阶Runge-Kutta法计算得到燃烧室芯流面积变化情况。
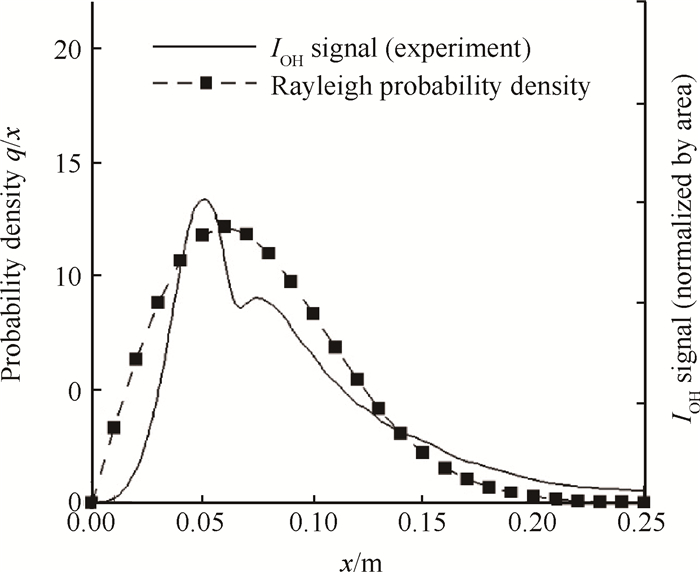
2.2 释热分布模型William Heiser等[9]曾采用总温分布函数来描述燃烧室内的释热过程,但该模型的释热分布曲线为单调递减函数,释热最快的位置发生在释热起始点,这一结论与实际情况存在较大差异;近年来,本课题组[17]通过瑞利概率密度分布来描述燃烧室内的释热分布情况,获得了较好的计算结果。图 2给出了瑞利概率密度分布曲线和Micka等[18]通过实验获得的OH基团的分布。可以看出,二者的曲线具有较好的相似性,而OH基团的分布则反映了燃烧室内释热分布情况,故采该模型具有一定的可行性。
|
Fig. 2 Rayleigh probability density distribution and OH distribution in scramjet combustor |
采用瑞利概率密度描述燃烧室释热分布的具体关系式为
| $ q\left( x \right) = \frac{{\left( x \right)}}{{{\mu ^2}}} \times {{\rm{e}}^{ - \left( {\frac{{{x^2}}}{{2{\mu ^2}}}} \right)}} $ | (8) |
| $ \frac{{{\rm{d}}Q\left( x \right)}}{{{\rm{d}}x}} = {\dot m_{{\rm{fuel}}}}q\left( x \right){E_{\rm{u}}}{\eta _{\rm{c}}} $ | (9) |
式(8)为瑞利概率密度函数,μ和ηc为经验常数,μ为反应释热分布形态的唯一参数,ηc为燃烧效率;式(9)为释热分布函数,Q(x)为燃料释热量,
| $ {T_{\rm{t}}}\left( x \right) = \left\{ \begin{array}{l} {T_{t, {\rm{in}}}} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {x \le {x_0}} \right)\\ {T_{{\rm{t}}, {\rm{in}}}} + \frac{{Q\left( {x - {x_0}} \right)}}{{{c_p}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;(x > {x_0}) \end{array} \right. $ | (10) |
| $ Q\left( x \right) = {m_{{\rm{fuel}}}}{E_{\rm{u}}}{\eta _{\rm{c}}}\left( {1 - {{\rm{e}}^{ - \left( {\frac{{{x^2}}}{{2{\mu ^2}}}} \right)}}} \right) $ | (11) |
式中x0为释热起始位置;Tt, in为燃烧室入口总温,cp为定压比热容。
2.3 计算方法将式(10)代入式(6)、(7)中,即可对燃烧室芯流马赫数、芯流面积进行求解,经验常数μ,ηc取不同数值时,可得到不同的芯流面积分布。因此,选取适合的经验常数μ,ηc,即可得到适应实际工况的释热分布,从而求解芯流面积。
在超燃燃烧室芯流完成再附过程后,忽略附面层等因素的影响,可以认为芯流面积等于燃烧室的截面积,如图 1所示。因此,在再附点xre后选取x1,x2两个截面作为参考截面,令x1,x2处计算得到的芯流面积Ac与参考截面的燃烧室截面积A0相等,即可通过迭代计算获得适用当前工况的常数μ,ηc值;同时,流动再附后分离区消失,芯流面积等于燃烧室截面积,因此在x>x2段令Ac=A0,芯流马赫数Ma为
| $ \begin{array}{*{20}{l}} {\frac{{{\rm{d}}Ma}}{{Ma}} = \frac{1}{2}[\left( { - \frac{E}{{kM{a^2}}}} \right) + \left( {\frac{{{\rm{d}}\dot m}}{{\dot m}} - \frac{F}{{kM{a^2}}}} \right) - }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 + \frac{1}{{kM{a^2}}}} \right)\frac{{{\rm{d}}p}}{p} - \frac{{{\rm{d}}{A_0}}}{{{A_0}}}]} \end{array} $ | (12) |
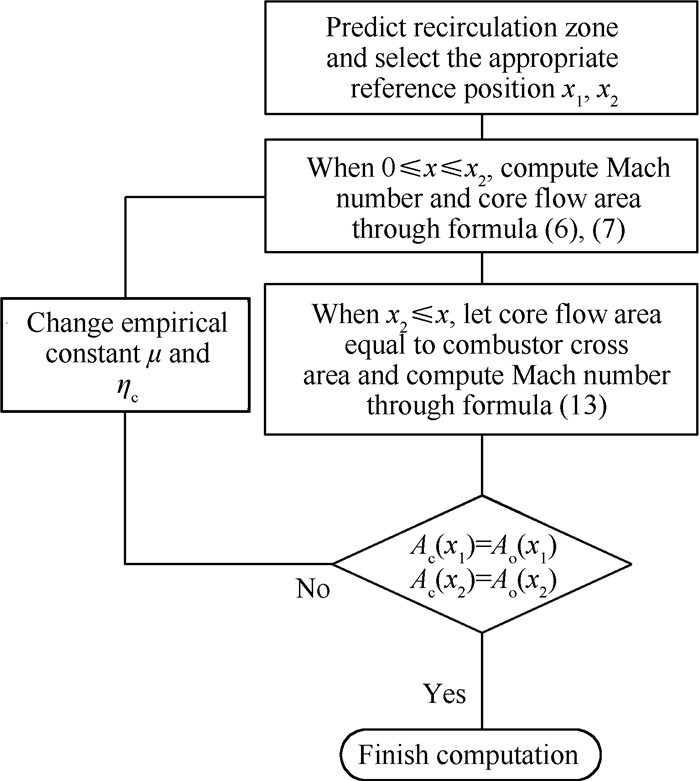
综上所述,超燃燃烧室芯流计算流程如图 3所示。
|
Fig. 3 Calculation process |
本次研究分别对气动斜坡[19]和凹腔[20]两种超燃燃烧室构型进行了验证,实验结果来自于北京航空航天大学直连式超燃冲压发动机试验台,仿真结果由CFD++进行计算,湍流模型为k-Ω (SST)模型,燃烧模型采用有限速率模型。通过对比发现,一维计算与仿真结果具有较好的一致性。
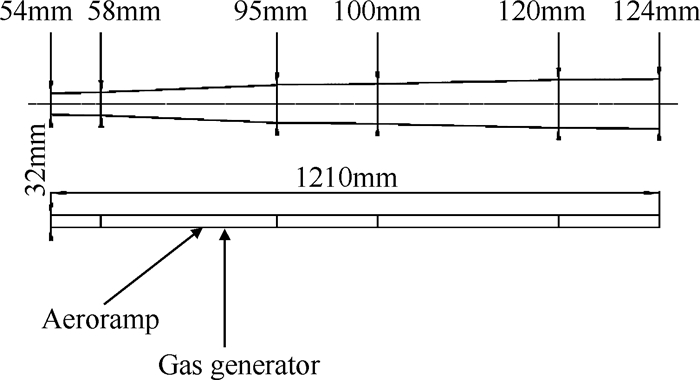
3.1 验证算例一:基于气动斜坡的超燃燃烧室基于气动斜坡的超燃燃烧室采用矩形截面设计,通过气动斜坡-燃气发生器结构促进火焰稳定,燃烧室入口马赫数为Ma=2,流量约为0.96kg/s,总压0.85MPa,总温1200K,燃料为乙烯,燃烧室结构如图 4所示,仿真选用1/2模型,并采用十组分十步化学反应机理进行计算。
|
Fig. 4 Combustor configuration with aeroramp |
图 5给出了当量比为0.3,0.37和0.5三种工况下实验和仿真的壁面静压分布,二者体现出较好的一致性,表明仿真结果能够较好地反映超燃燃烧室内部真实的流场结构,可以作为一维计算结果的验证算例。
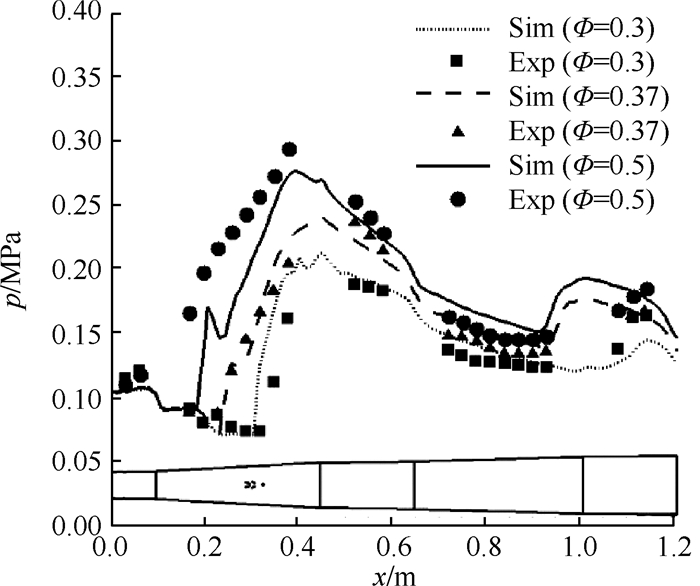
|
Fig. 5 Static pressure of the combustor with aeroramp |
图 6给出了三种工况下,x=0~0.6m区间内燃烧室芯流面积的计算结果,选取的参考截面为x1=0.55m,x2=0.6m。可以看出,流动过程的分离过程主要发生在x=0.2~0.45m区间内,且当量比越高,流动发生分离的位置越靠近上游,分离区内的芯流面积越小;在x≤0.2m段,芯流面积的大小存在波动,这是因为流动过程存在膨胀波,使壁面压力出现波动,进而影响到了芯流面积的计算结果。
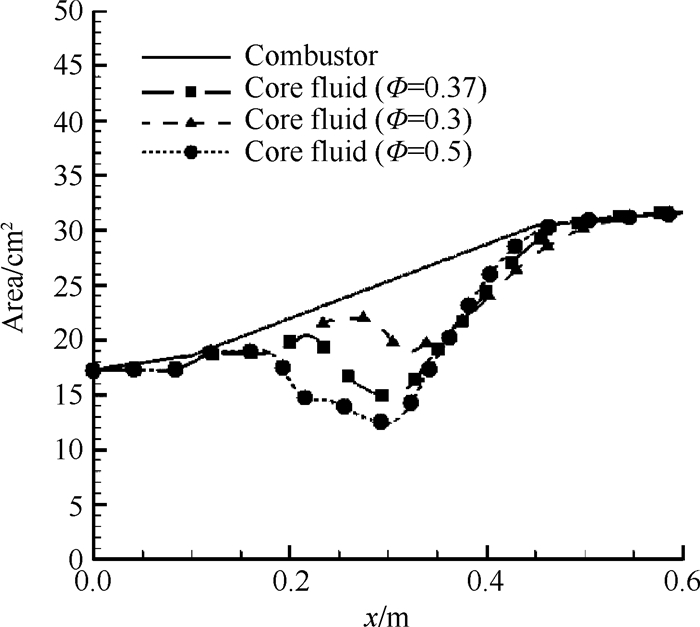
|
Fig. 6 Area of the aeroramp combustor core fluid |
图 7(a),(b),(c)给出了分离区内芯流面积和释热分布的一维计算结果和三维仿真结果,其中三维仿真的芯流面积是由燃烧室截面积减去回流区截面积获得的。整体而言,一维计算和三维仿真得到的释热分布具有较好的一致性,一维计算得到的芯流面积也能够较为准确地反应流动的分离再附过程;在数值上,一维计算得到的芯流面积略小于三维仿真结果,这是因为一维模型对燃烧室内的流动过程进行了简化,不能对附面层、流动不均匀等复杂的流动过程进行捕捉,而是将其影响反映到了芯流面积的计算结果中。
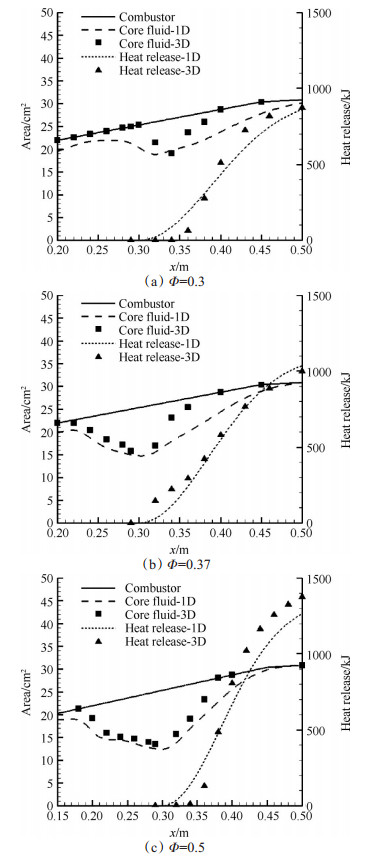
|
Fig. 7 Core fluid area and heat release of one dimension(1D) consequence and simulation(3D) consequence |
图 8给出了x方向速度u=0m/s等值面及x=0.3m,0.35m,0.4m,0.45m截面的密流(即密度与流向速度之积)分布云图。可以看出,回流区主要分布在x=0.3~0.4m段,在回流区下游,流密分布具有明显的不均匀性。
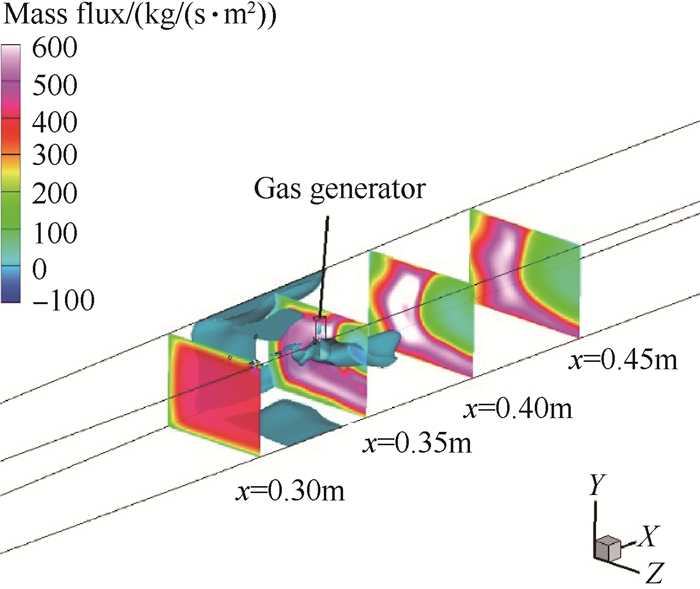
|
Fig. 8 U=0m/s isosurface and mass flux counter of x=0.3m, 0.35m, 0.4m, 0.45m |
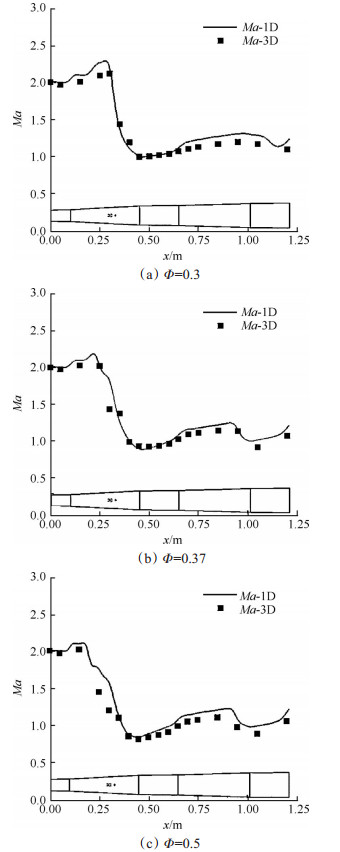
图 9(a),(b),(c)分别给出了Φ=0.3,0.37和0.5三种工况下,超燃燃烧室内马赫数分布的一维结果和三维结果。可以看出,两种工况下的一维计算结果均与三维计算结果具有较好的一致性。
|
Fig. 9 Mach number distribution of the combustor with aeroramp |
为进一步分析参考截面x1,x2的位置对释热分布的影响,研究中选取的多组参考截面进行了计算,结果如表 1所示。考虑x=0.65m处存在压缩波,而压缩波、膨胀波会对芯流面积的计算结果产生一定影响,因此参考截面均选取在x=0.65m上游位置。从表中可以看出,参考截面的位置对经验常数的计算结果影响较小,表征燃烧效率的经验常数ηc均在0.9附近。在三维仿真中,由于燃气发生器对乙烯燃烧具有较强的促进作用,因此获得了较高的燃烧效率——95.7%。通过对比可以发现,一维计算结果与三维仿真结果的误差在7%之内。因此可以认为在避免膨胀波、压缩波的前提下,参考截面位置对一维计算结果的影响相对不大。
|
|
Table 1 Influence of the reference surface on the empirical constant |
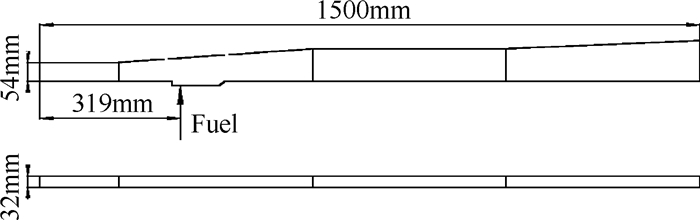
基于凹腔的超燃燃烧室构型采用矩形截面设计,燃烧室入口马赫数为Ma=2,流量约为1.5kg/s,总压2.0MPa,总温1900K,燃料为煤油,燃烧室结构如图 10所示,仿真选用1/2模型,并采用16组分23步化学反应机理进行计算。
|
Fig. 10 Combustor configuration with cavity |
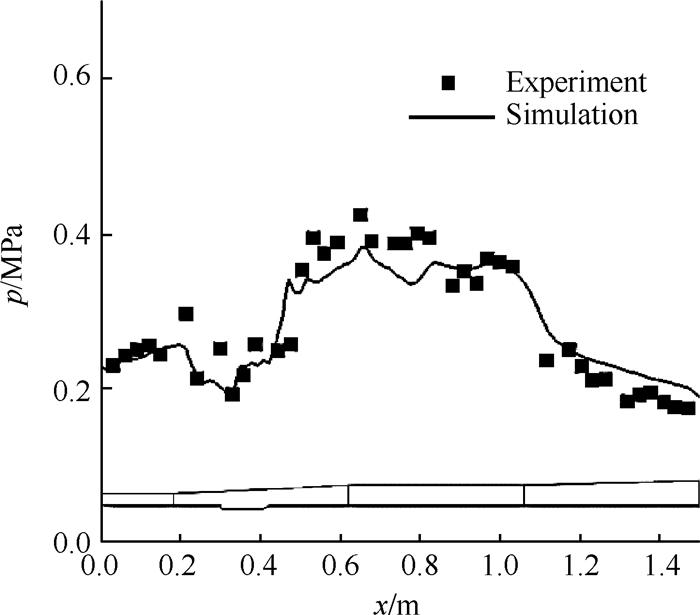
图 11给出了实验和仿真的壁面静压分布,二者体现出较好的一致性,表明仿真结果可以用于一维计算的验证算例。
|
Fig. 11 Static pressure of the combustor with cavity |
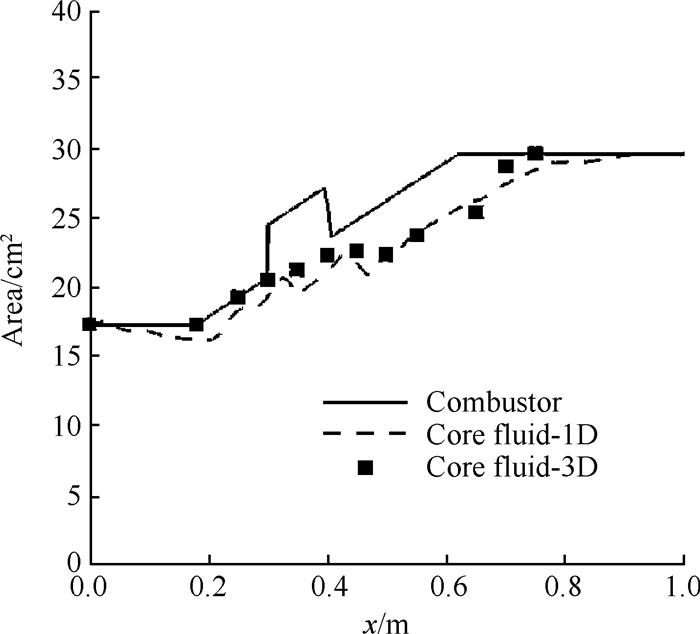
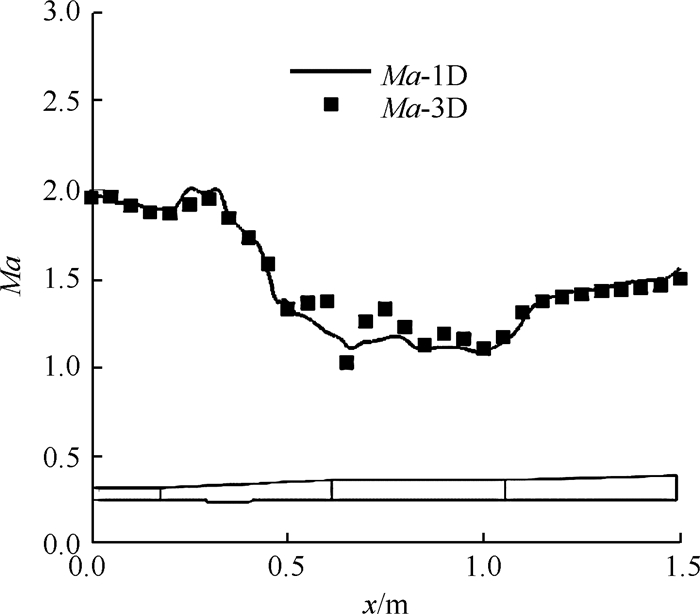
图 12和图 13给出了燃烧室内芯流面积和马赫数分布的一维计算与三维仿真的结果,选取x1=0.95m,x2=1.0m两截面作为参考截面。可以看出,虽然芯流面积的一维计算结果在x=0~0.3m区间内仍然受膨胀波、附面层的影响而出现波动,但整体而言,一维计算结果较为准确地捕捉到了燃烧室在x=0.3m~0.75m区间内流动分离再附的过程。与此同时,一维计算得到的马赫数分布也与仿真结果体现出较好的一致性,表明该一维方法可以用于以煤油为燃料、以凹腔为火焰稳定装置的超燃燃烧室芯流的计算。
|
Fig. 12 Core fluid area of one dimension(1D) consequence and simulation(3D) consequence(combustor with cavity) |
|
Fig. 13 Mach number of the combustor with cavity |
本文对双模态超燃燃烧室一维计算方法进行了研究,通过与两种燃烧室构型仿真结果的对比,可以得出以下结论:
(1) 通过对两个验证算例的分析,可以认为本文提出的一维分析模型能用于超燃燃烧室芯流面积的计算,对燃烧室芯流的分离再附过程和马赫数分布情况起到较好的预测作用。
(2) 通过选取参考截面获得超燃燃烧室释热分布情况的方法是可行的,并且通过该方法,可以使本文提出的一维分析方法适用于不同燃料、不同构型的超燃燃烧室芯流分析。
(3) 超燃燃烧室内的膨胀波、压缩波会对芯流面积的计算结果产生一定影响,因此参考截面应当在再附点后、膨胀波或压缩波出现前的位置选取。由验证算例一的结果表明,在避免膨胀波和压缩波的前提下,参考截面的位置对释热分布计算结果的影响不大,燃烧效率的波动在4%之内,与仿真结果的误差在7%之内。
后续的研究将针对如何降低膨胀波、压缩波对芯流面积计算结果的影响展开,从而进一步降低本文所述一维分析方法对参考截面选取位置的约束,使该一维分析方法具有更好的适用性。
| [1] |
陈强, 陈立红, 顾洪斌, 等. 释热分布对超燃冲压发动机性能的影响及优化[J]. 推进技术, 2009, 30(2): 135-138. (CHEN Qiang, CHEN Li-hong, GU Hong-bin, et al. Investigation of the Effect and Optimization of Heat Release Distributions in the Combustor on Scramjet Performance[J]. Journalof Propulsion Technology, 2009, 30(2): 135-138.)
(  0) 0) |
| [2] |
Birzer C, Doolan C J. Quasi-One-Dimensional Model of Hydrogen-Fueled Scramjet Combustors[J]. Journal of Propulsion Technology, 2009, 25(6): 1220-1225. DOI:10.2514/1.43716
(  0) 0) |
| [3] |
LSENS Radhakrishnan K. Multipurpose Kineties and Sensitivity Analysis Code for Homogeneous Gas-Phase Reactions[J]. AIAA Journal, 2003, 41(2): 848-855.
(  0) 0) |
| [4] |
王兰, 邢建文, 郑忠华, 等. 超燃冲压发动机内流性能的一维评估[J]. 推进技术, 2008, 29(6): 641-645. (WANG Lan, XING Jian-wen, ZHENG Zhong-hua, et al. One-Dimensional Evaluation of the Scramjet Flowpath Performance[J]. Journal of Propulsion Technology, 2008, 29(6): 641-645.)
(  0) 0) |
| [5] |
Torrez S M. Preliminary Design Methodology for Hypersonic Engine Flow Paths[C]. Bremen: 16 th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, 2009.
(  0) 0) |
| [6] |
李建平, 宋文艳, 肖隐利. 超燃冲压发动机/机体一体化优化设计[J]. 航空动力学报, 2011, 26(4): 874-879. (  0) 0) |
| [7] |
Tian L, Chen L H, Chen Q, et al. Quasi-One-Dimensional Multimodes Analysis for Dual-Mode Scramjet[J]. Journal of Propulsion and Power, 2014, 30(6): 1559-1567. DOI:10.2514/1.B35177
(  0) 0) |
| [8] |
刘敬华, 凌文辉, 刘兴洲, 等. 超音速燃烧室性能非定常准一维流数值模拟[J]. 推进技术, 1998, 19(1): 1-6. (LIU Jing-hua, LING Wen-hui, LIU Xing-zhou, et al. A Quasi One Dimensional Unsteady Numerical Analysis of Supersonic Combustor Performance[J]. Journal of Propulsion Technology, 1998, 19(1): 1-6.)
(  0) 0) |
| [9] |
William H Heiser, David T Pratt. Hypersonic Airbreathing Propulsion[M]. Washington DC: AIAA Press, 1994.
(  0) 0) |
| [10] |
张栋, 唐硕. 超燃冲压发动机燃烧室准一维建模与分析[J]. 弹道学报, 2015, 27(1): 85-91. (  0) 0) |
| [11] |
Billig F S, Dugger G L, Waltrup P J. Inlet-Combustor Interface Problems in Scramjet Engine[C]. France: Proceedings of the First International Symposium on Air-breathing Engines, 1972.
(  0) 0) |
| [12] |
俞刚, 李建国. 氢/空气超声速燃烧研究[J]. 流体力学实验与测量, 1999, 13(1): 1-12. (  0) 0) |
| [13] |
郭金雷, 谷良贤, 龚春林. 一种改进的冲压发动机一维流分析模型[J]. 推进技术, 2014, 35(5): 584-590. (GUO Jin-lei, GU Liang-xian, GONG Chun-lin. An Improved One-Dimensional Analysis Model for Ramjet[J]. Journal of Propulsion Technology, 2014, 35(5): 584-590.)
(  0) 0) |
| [14] |
张鹏, 俞刚. 超燃燃烧室一维流场分析模型的研究[J]. 流体力学实验与测量, 2003, 17(1): 88-92. (  0) 0) |
| [15] |
程柳维. 超声速燃烧室乙烯及其混合燃料点火及火焰特征研究[D]. 北京: 中国科学院力学研究所, 2017. http://www.irgrid.ac.cn/handle/1471x/1464604?mode=full&submit_simple=Show+full+item+record
(  0) 0) |
| [16] |
Mitani T, Hiraiwa T, Tarukawa, et al. Drag and TotalPressure Distributions in Scramjet Engines at Mach 8 Flight[J]. Journal of Propulsion and Power, 2002, 18(4): 953-960. DOI:10.2514/2.6022
(  0) 0) |
| [17] |
姜军, 初敏, 徐旭. 双模态超燃燃烧室性能准一维计算方法[J]. 推进技术, 2013, 34(6): 802-808. (JIANG Jun, CHU Min, XU Xu. A Quasi on Dimensional Method for Prediction of Dual Mode Scramjet Combustor Performance[J]. Journal of Propulsion Technology, 2013, 34(6): 802-808.)
(  0) 0) |
| [18] |
Micka D J, Torrez S M, Driscoll J F. Heat Release Distribution in a Dual-Mode Scramjet Combustor-Measurements and Modeling[C]. Bremen: 16 th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, 2009: 13-14.
(  0) 0) |
| [19] |
史新兴. 基于气动斜坡的超燃燃烧室数值模拟及实验研究[D]. 北京: 北京航空航天大学, 2010: 73-75.
(  0) 0) |
| [20] |
王辽, 韦宝禧, 章程亮, 等. 基于凹腔火焰稳定器的煤油超声速燃烧实验[J]. 北京航空航天大学学报, 2008, 34(8): 907-910. (  0) 0) |
 2018, Vol. 39
2018, Vol. 39


