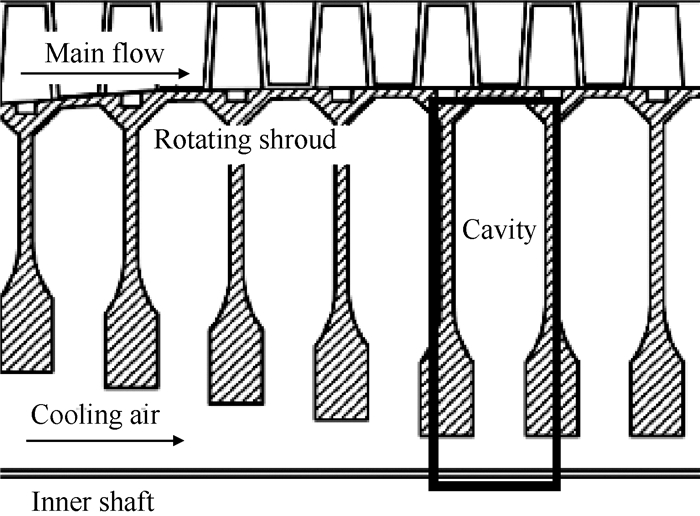
旋转盘腔结构是发动机空气系统中常见的结构,如图 1所示。盘腔内气体的流动换热特性直接影响发动机部件的冷却和封严,进而影响发动机的性能、寿命和可靠性[1]。
|
Fig. 1 Structure of rotating cavities in aero-engine |
对于旋转盘腔内的流动和换热问题,由于惯性力、哥氏力和离心浮升力的综合作用,流动结构复杂,影响因素较多,研究难度较大,早期是以实验为主,Farthing等[2, 3]、Bohn等[4]、周雷声等[5]、丁水汀等[6]对旋转盘腔进行了实验研究,主要探究了主流流量、转速以及盘面温度分布对盘腔内流动结构和换热特性的影响。
随着CFD技术的发展,数值模拟逐渐被应用到研究旋转盘腔的流动换热机理中,由于早期计算资源的缺乏,主要是进行稳态模拟。田淑青等[7~10]对无旋转轴和有旋转轴的轴向通流旋转盘腔进行了稳态数值模拟,分析了盘腔内流动结构、盘面换热和整体换热强度随雷诺数、旋转雷诺数、瑞利数等无量纲数的变化规律。分析了惯性力、离心浮升力和哥氏力对盘腔内流动的影响。发现盘腔内的流动可以划分成强迫对流区和类Rayleigh-Benard对流区,两个区域通过能量和质量交换相互影响。Dweik等[11]对两个大小不同、带旋转轴的轴向通流旋转盘腔模型进行了稳态模拟,发现盘腔内流动区域可以分为低半径处中心射流主导区和中高半径处离心浮升力主导的盘腔中半径区,不同区域的总体努塞尔数可以应用不同的经验关系式来预测,然而,要确定从强迫对流主导区到浮升力主导区的转变位置、要确定几何相关性,还需要进一步的CFD分析。Yi等[12]对轴向通流旋转盘腔进行了稳态数值模拟,发现不同的湍流模型和离散格式的选取对计算结果影响很大,要实现对旋转盘腔换热特性更精确的模拟,还需要进一步的研究。
由于盘腔内的流动是非定常的,稳态模拟的计算结果误差较大,因此近年来更多的学者采用了非稳态模拟。田淑青等[13]和谭勤学等[14, 15]根据Bohn等[4]的实验模型和实验条件,对带有旋转轴的轴向通流旋转盘腔模型进行了非稳态数值模拟,比较了数值计算结果与实验数据,发现误差在8%~30%,分析了体积力对旋转盘腔中流动的影响。Owen等[16]对轴向通流旋转盘腔的流动和换热进行了非稳态模拟,计算得到的温度云图和速度矢量图显示了腔内流动结构,将计算结果与实验值进行了比较。
为了进一步探究盘腔内流动和换热规律,本文根据文献[4]中的实验模型,对轴向通流旋转盘腔中的流动和换热情况进行了非稳态数值模拟,主要分析了旋转雷诺数对盘腔内流动结构和换热特性的影响。
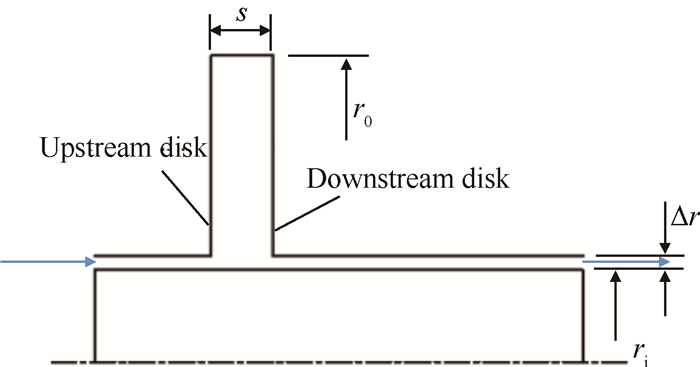
2 物理模型和计算方法本文计算模型为带有中心旋转轴的轴向通流旋转盘腔模型,取自Bohn等[4]的实验装置,如图 2所示,盘腔半径r0=0.4m,盘腔间隙比G=s/r0=0.2,旋转轴半径ri=0.12m,进气流道径向间隙Δr=18mm,入口段长度0.15m,出口段长度0.4m。
|
Fig. 2 Sketch of the CFD model |
图 3为计算用网格,采用O型网格,近壁面加密处理。经过网格独立性检验后,最终在盘腔轴向、径向、周向分别设置60,80,352个节点,网格总数374万,盘面第一层网格大小为0.04mm,网格膨胀率为1.1~1.3,在本文的计算工况中满足壁面y+都小于2。

|
Fig. 3 Grid of the CFD model |
计算域采用旋转坐标系,给定转速Ω(沿X轴正向)及参考压力138.477kPa。主流入口给定质量流量
|
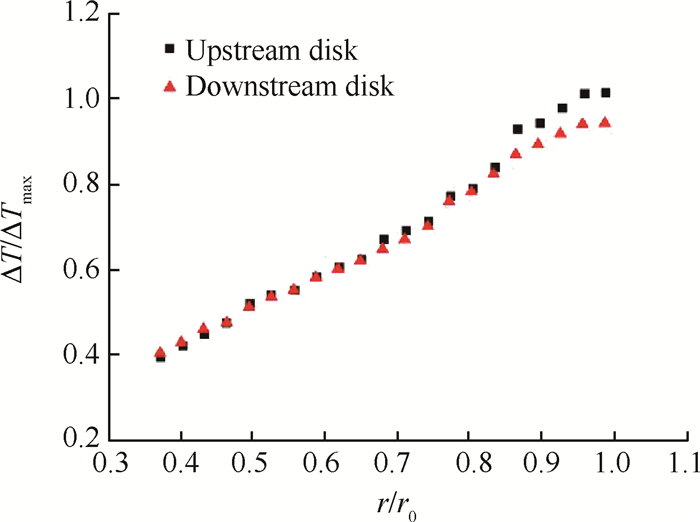
Fig. 4 Radial distributions of ΔT/ΔTmax on disks |
采用商业CFD软件ANSYS Fluent 15.0进行数值计算,对模型进行三维非稳态求解,湍流模型选用RNG k-ε模型,近壁面区域采用增强壁面处理Enhanced Wall Treatment,同时考虑粘性耗散的影响。压力速度耦合采用SIMPLE算法,压力项离散采用PRESTO格式,非稳态项采用二阶隐式,其余各项采用二阶迎风格式。计算时间步长在2~8ms,根据转速取不同值,能量方程残差值10-6,其余方程残差值10-4。在盘腔内设置两个监测点,在计算时监测出口质量流量以及监测点温度。
3 计算结果与讨论 3.1 数值算法验证本节以Bohn等[4]实验中的工况④作为验证算例,该工况的边界条件为:入口质量流量
| $ R{e_z} = 2\rho u{r_{\rm{i}}}/\mu $ | (1) |
| $R{e_\mathit{\Phi} } = \rho \mathit{\Omega }r_0^2/\mu $ | (2) |
式中ρ是气体密度,u是入口处主流轴向速度,μ是动力粘度,参考温度取入口处温度Tin。
本文中,因为每一个测点的温度、当地努塞尔数和旋流比都是周期性波动的,而这些值在任一半径位置的周向平均值都基本恒定,所以本文温度、当地努塞尔数和旋流比的计算值都是取最后一个时间步的的周向平均值。
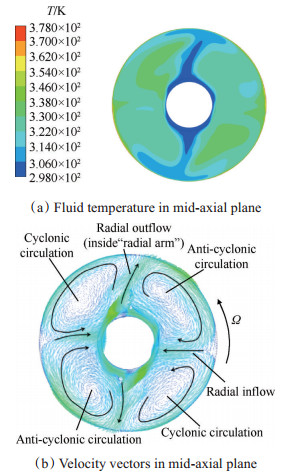
图 5为非稳态模拟得到的中轴面上的温度云图和速度矢量图,由图可知,轴向入流的冷气通过径向臂进入旋转盘腔,在盘罩附近分流,形成与盘腔转向相同的正旋区和与盘腔转向相反的反旋区,正、反旋区的气流在另一侧汇合,之后流出盘腔。在中轴面形成了清晰的两对涡结构,对应于径向臂两侧的正旋区和反旋区。
|
Fig. 5 Computed fluid temperature distribution and flow pattern in rotating cavity |
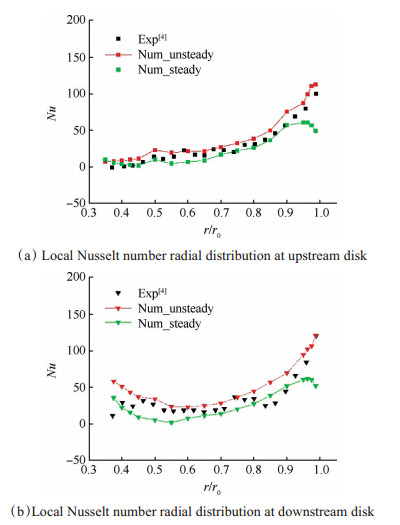
图 6为上、下游盘周向平均努塞尔数的径向分布,其中当地努塞尔数的定义式为
| $ Nu = qr/\lambda \left( {T - {T_{{\rm{in}}}}} \right) $ | (6) |
|
Fig. 6 Comparison of the computed Nu with the measurement [4] |
式中q是热流密度,r是半径,λ是空气的导热系数,T是当地温度。
为了比较非稳态模拟与稳态模拟的差异性,图中加入了稳态模拟的计算结果。从图中可以看出,在中、低半径区域,两种计算值的误差都较小,但在高半径区域,稳态模拟的计算值误差明显较大,表明本文所采用的非稳态计算方法能够对该问题获得较准确的结果,且与稳态模拟相比,总体误差较小。
上游盘Nu总体趋势是沿径向增大的,这是由于旋转使得高半径处相对速度增大引起的;下游盘壁面换热总体上是沿径向先下降再上升,这是由低半径区域的冲击强化换热引起的。在低半径区域有个别点Nu小于零,这是由于流经此处的气体已经经过高半径盘腔内壁面的加热作用,其温度高于该处壁面温度。下游盘低半径区域的Nu比上游盘高一些,这是由轴向进气对下游盘的冲击作用导致的。
3.2 旋转雷诺数对流动结构的影响分析保持入口质量流量不变,增大转速,即固定轴向雷诺数Rez=2×104,增大旋转雷诺数,观察流动结构的变化规律。
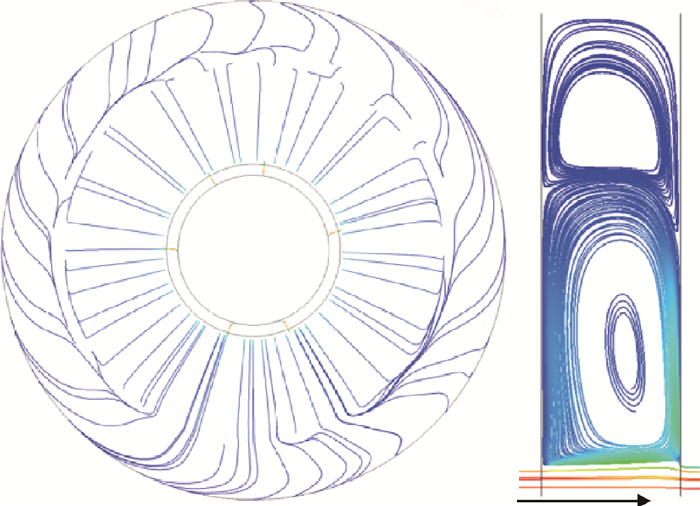
图 7为零转速下中轴面和r-z面的流动结构。由图可知,整个流动结构近似为中心对称的,在r-z面上形成了环形涡结构,将整个流动结构分为上下两个部分。中低半径处是轴向通流诱导的漩涡,高半径处是低半径漩涡所引发的二次流动。
|
Fig. 7 Streamlines on mid-axial plane and r-z plane for ReΦ=0 |
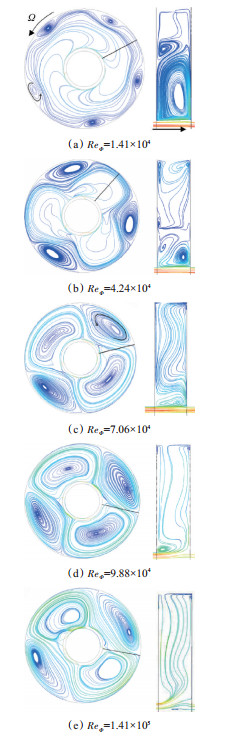
图 8为低转速下不同旋转雷诺数时中轴面和r-z面的流动结构演化图示,其中r-z面的选取位置在中轴面流线图中由黑线标出,即取在反旋区,该处为轴向通流进入盘腔引起的强迫对流旋涡最强的区域。
|
Fig. 8 Streamlines on mid-axial plane and r-z plane in the low rotational speed |
由图 8可知,在ReΦ=1.41×104时,低半径区域的流动结构仍然接近于中心对称,但在高半径区域的盘罩附近,产生了正旋涡,正旋涡随转速的增大而变大,并挤压低半径区域的强迫对流区,旋涡数目也发生了变化,在ReΦ=7.06×104时变成了两对涡。在旋转雷诺数从7.06×104增大到1.41×105的过程中,正旋涡有进一步增长变大的趋势。通过比较可以看到轴向通流引起的强迫对流涡随着旋转雷诺数的增大而减弱,是由高半径区域正旋涡的挤压导致的。在ReΦ=1.41×105时已经基本观察不到轴向通流引起的强迫对流涡,此时,在中轴面已经形成了由径向臂、正旋涡、反旋涡等结构组成的典型流动结构。
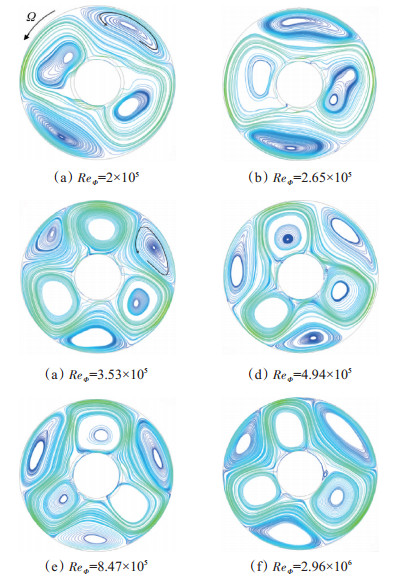
图 9为高转速下中轴面的流线图,高转速时r-z面不再产生轴向通流引起的强迫对流涡,在中轴面形成由径向臂、正旋涡、反旋涡等结构组成的典型流动结构。由图可知,当旋转雷诺数增大到2.65×105时,正旋涡被拉长(同时参考图 8)。进一步增大雷诺数到3.53×105时,旋涡对数由两对变为三对,这表明旋转雷诺数对中轴面的涡对数有影响。
|
Fig. 9 Streamlines on mid-axial plane in the high rotational speed |
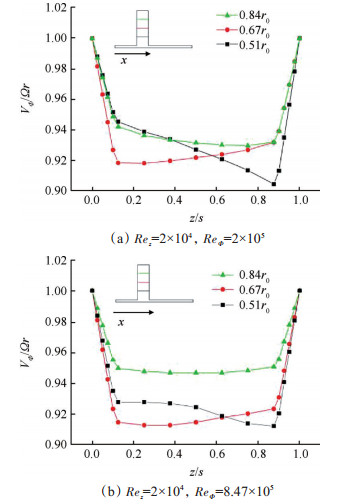
图 10为Rez=2×104,ReΦ不同时,不同径向位置处,周向平均旋流比VΦ/Ωr的轴向分布曲线。
|
Fig. 10 Axial variation of VΦ/Ωr at three radial positions at ReΦ=2×105 and ReΦ=8.47×105 |
ReΦ=2×105时,盘腔内流动核心的旋流比在0.9~0.94,在0.51r0处靠近下游盘的区域,曲线有明显的下降趋势,是因为气体在该区域进入盘腔,因此存在很大的正径向速度,从而使哥氏力的切向分量也很大且阻碍流体随盘旋转,所以曲线会有下降趋势。在两个高径向位置,径向速度较小,因此这两条曲线在下游盘附近没有下降趋势。在0.67r0处,在0.12 < z/s < 0.88区域,旋流比随z/s增大而增大,在0.84r0处,也就是正旋涡核心所处的位置,在0.12 < z/s < 0.88区域,旋流比随z/s增大基本不变。
ReΦ=8.47×105时,在0.51r0处,由于ReΦ较大,气流沿整个径向臂进入盘腔,因此与图 10(a)相比,0.51r0处的旋流比整体较低,且沿轴向的下降趋势不是很明显。在0.67r0处,旋流比曲线与ReΦ=2×105时差别不大。在0.84r0处,旋流比的轴向变化趋势与ReΦ=2×105时相似但数值较大,又因为0.84r0经过正旋涡旋转核心,所以说明该工况下正旋涡的相对转速较高。
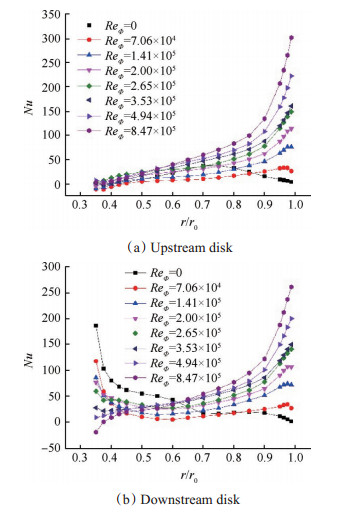
3.3 旋转雷诺数对换热特性的影响分析图 11为固定轴向雷诺数Rez=2×104,改变旋转雷诺数时,上、下游盘周向平均努塞尔数的径向分布。
|
Fig. 11 Radial distribution of local Nu on disks |
在图 11(a)中,ReΦ=0时,上游盘努塞尔数的分布曲线先上升后下降,在中低半径区域,换热强度沿径向增大,在高半径区域,换热强度沿径向减弱。结合图 7分析可知,在ReΦ=0时,高半径区域是低半径漩涡所引发的二次流漩涡,流动很弱,与低半径区域气体的质量热量交换较少,因此在稳定状态下,上游盘高半径区域换热较弱。ReΦ增大时,各个转速的曲线趋势相同,沿径向上升,在盘罩附近达到极大值。
在图 11(b)中,ReΦ=0时,由于气流的冲击作用,下游盘低半径区域的Nu较大。随着径向位置的升高,冲击作用的影响减弱,Nu开始减小,随后又沿径向增大,在盘罩附近达到极大值。旋转雷诺数升高时,低半径处冲击作用的影响越来越小,当ReΦ=4.94×105时,曲线趋势已经和上游盘很相似,冲击作用的影响已经变得很小。
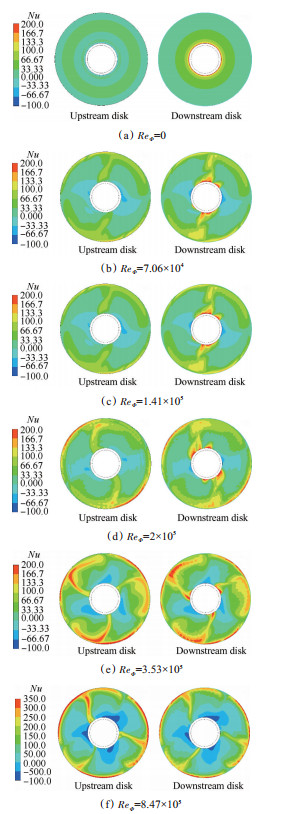
图 12为固定轴向雷诺数Rez=2×104,改变旋转雷诺数时,上、下游盘局部努塞尔数的分布云图。由图可知,ReΦ=0时下游盘整个低半径区域都受到气流冲击作用因而换热明显较强,在Nu云图中呈现红色。ReΦ=0~1.41×105 时,气体由于旋转作用进入盘腔,高半径处的正旋涡也开始压迫强迫对流区,使得上、下游盘Nu云图低半径处都出现蓝色区域,即气体径向出盘腔的区域,该区域的气体已经被盘加热过,温度高于低半径处的盘面温度,因此在该区域Nu < 0,且随着ReΦ的增大,该区域逐渐扩大,而下游盘低半径处受冲击的区域则越来越小,从而使下游盘低半径区域的周向平均努塞尔数降低,与图 11(b)对应。在ReΦ=2×105~8.47×105时,随着ReΦ的增大,正旋涡已经充满盘腔,轴向通流的强迫对流旋涡消失,而代之以沿径向臂的流动,对应于图中沿径向的努塞尔数较大的红色黄色区域。
|
Fig. 12 Distribution of Nu on disks at different ReΦ |
本文对轴向通流旋转盘腔模型进行了非稳态数值模拟,获得了盘腔内流动结构随ReΦ的演化特征,以及上、下游盘盘面换热强度随ReΦ的变化规律,在本文的计算参数范围内,可得出以下结论:
(1)在ReΦ=0时盘腔内流动结构中心对称,主要是由轴向通流引起的环形涡。随着ReΦ的增加,首先在盘罩附近形成了正旋涡并逐渐扩大,挤压低半径处的强迫对流区,中心对称的流动结构从高半径处开始被破坏,当正旋涡沿径向扩大到整个盘腔时,强迫对流涡消失,在盘腔中轴面形成由径向臂、正/反旋涡对等组成的流动结构,且中轴面涡对数随ReΦ的变化而变化。
(2)总体来看,上、下游盘的换热随着ReΦ的增大而增强。上游盘换热强度沿径向增加,低半径区域换热强度随ReΦ变化不大,高半径区域换热随ReΦ增大而增强较快。在下游盘低半径区域,换热随ReΦ的增大而减弱,高半径区域换热随ReΦ增大而增强;这是由低半径处冲击换热随ReΦ的增加而减弱引起的,当旋转雷诺数增大到4.94×105时,下游盘低半径区域受到的冲击作用减小到可以忽略。
| [1] |
张美华, 刘振侠, 胡剑平, 等. 旋转盘腔瞬态响应特性的研究[J]. 推进技术, 2014, 35(8): 1056-1062. (ZHANG Mei-hua, LIU Zhen-xia, HU Jian-ping, et al. Study of Transient Response Characteristics of Rotating Disc Cavity[J]. Journal of Propulsion Technology, 2014, 35(8): 1056-1062.)
(  0) 0) |
| [2] |
Farthing P R, Long C A, Owen J M, et al. Rotating Cavity with Axial Throughflow of Cooling Air-Flow Structure[J]. Journal of Turbomachinery, 1992, 114(1): 237-246. DOI:10.1115/1.2927991
(  0) 0) |
| [3] |
Farthing P R. Rotating Cavity with Axial Throughflow of Cooling Air-Heat Transfer[J]. Journal of Turbomachinery, 1992, 114(1): 229-236. DOI:10.1115/1.2927990
(  0) 0) |
| [4] |
Bohn D E, Deutsch G N, Simon B, et al. Flow Visualisation in a Rotating Cavity with Axial Throughflow[R]. ASME GT 2000-280.
(  0) 0) |
| [5] |
周雷声, 冯青, 武亚勇. 旋转涡轮盘腔中等转速下内部流场分布实验[J]. 推进技术, 2006, 27(4): 321-325. (ZHOU Lei-sheng, FENG Qing, WU Ya-yong. Experiment on the Velocity of the Flow Inside Rotating Disk Cavity under Mid Rotating Speed[J]. Journal of Propulsion Technology, 2006, 27(4): 321-325.)
(  0) 0) |
| [6] |
丁水汀, 潘文艳, 徐国强, 等. 同向旋转盘间非稳态传热特性的实验研究[J]. 热科学与技术, 2009, 8(2): 95-100. (  0) 0) |
| [7] |
田淑青, 陶智, 丁水汀, 等. 轴向通流旋转盘腔内流动不稳定性研究[J]. 北京航空航天大学学报, 2005, 31(4): 393-396. (  0) 0) |
| [8] |
田淑青, 陶智, 丁水汀, 等. 轴向通流旋转盘腔内类Rayleigh-Benard对流稳定性研究[J]. 热科学与技术, 2003, 2(3): 260-265. (  0) 0) |
| [9] |
田淑青, 陶智, 丁水汀, 等. 轴向通流旋转盘腔内换热的数值模拟[J]. 航空动力学报, 2005, 20(4): 656-661. (  0) 0) |
| [10] |
Tian S, Tao Z, Ding S, et al. Computation of Buoyancy-Induced Flow in a Heated Rotating Cavity with an Axial Throughflow of Cooling Air[J]. International Journal of Heat and Mass Transfer, 2008, 51(3): 960-968.
(  0) 0) |
| [11] |
Dweik Z, Briley R, Swafford T, et al. Computational Study of the Heat Transfer of the Buoyancy-Driven Rotating Cavity with Axial Throughflow of Cooling Air[R]. ASME GT 2009-59978.
(  0) 0) |
| [12] |
Yi W L, Zhang X H, Ji L C, et al. Coupled Fluid-Thermal-Solid Simulation of Axial Through-Flow Rotating Cavities[R]. ASME GT 2013-95053.
(  0) 0) |
| [13] |
Tian S, Zhu Y. Disk Heat Transfer Analysis in a Heated Rotating Cavity with an Axial Throughflow[R]. ASME GT 2012-69185.
(  0) 0) |
| [14] |
谭勤学, 任静, 蒋洪德. 轴向通流旋转盘腔中流动与传热数值研究[J]. 工程热物理学报, 2009, 30(7): 1129-1131. (  0) 0) |
| [15] |
Tan Q, Ren J, Jiang H. Prediction of 3D Unsteady Flow and Heat Transfer in Rotating Cavity by Discontinuous Galerkin Method and Transition Model[R]. ASME GT 2014-26584.
(  0) 0) |
| [16] |
Owen J M, Abrahamsson H, Lindblad K. Buoyancy-Induced Flow in Open Rotating Cavities[J]. Journal of Engineering for Gas Turbines & Power, 2007, 129(4): 1581-1589.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


