2. 大连理工大学 航空航天学院,辽宁 大连 116024
2. School of Aeronautics and Astronautics, Dalian University of Technology, Dalian 116024, China
随着当前航空工业的迅速发展,航空动力装置性能的要求也越来越高。压气机作为航空发动机三大核心部件之一,越发追求高压比、高效率,同时还要求其拥有足够的稳定性。采用高负荷扩压叶栅是实现压气机高压比、高效率的最直接方案,然而栅内二次流动的加剧和角区分离的恶化会造成严重的掺混损失,甚至诱发失速与喘振现象,极大地抑制了其性能的发展[1, 2]。现有的研究表明,采用高负荷扩压叶栅的同时辅之以附面层抽吸技术削弱附面层流动分离是提高压气机压比与效率的一条十分有效的途径[3]。
1997年,Kerrebrock等首次提出了吸附式压气机的概念,并对其热力学原理进行了一定的阐述[4]。随后,美国的NASA Gleen研究中心与MIT合作进行了一系列的吸附式压气机和风扇实验,结果发现通过特定位置吸除少量低能流体可以显著地降低损失并改善压气机性能[5~7],这些技术目前已部分应用于F414发动机改进型中[8]。Liesner等[9]和Gmelin等[10]以及Lemke等[11]通过实验与数值的方法研究了端壁抽吸效应,发现不同的端壁开槽位置对栅内二次流的控制效果有显著影响。国内在吸附式压气机研究方面起步较晚,且当前多以矩形叶栅模型和数值模拟为主。宋彦萍、陈浮等[12, 13]针对大转角扩压叶栅,深入探讨了吸气槽的抽吸位置、抽吸流量、几何尺寸、叶栅稠度及冲角裕度等对抽吸效果的影响。张华良等[14]在进行吸力面附面层抽吸研究中发现,以闭式分离为主要特征的叶栅流场其最佳抽吸位置在主分离区起始位置,而以开式分离为主要特征的叶栅流场最佳抽吸位置则在主分离区上游。郭爽等[15, 16]实验研究了端壁附面层抽吸对高负荷矩形扩压叶栅性能的影响,并探究了不同抽吸位置对叶栅损失的影响机制。
本文以亚声速高负荷扇形扩压叶栅为研究对象,进行附面层抽吸的研究。选择扇形扩压叶栅相较于矩形扩压叶栅更为接近实际,亦可获得各性能参数更为准确的径向分布规律。对扇形叶栅原型的总压损失特性进行分析发现,其下角区损失和分离程度远大于上角区。针对这一特性,在扇形叶栅下端壁不同位置开设流向槽进行抽吸,旨在获得不同抽吸位置对叶栅气动性能和栅内流场结构的影响规律;此外,探究下端壁单侧抽吸对上角区及叶栅整体性能的影响。
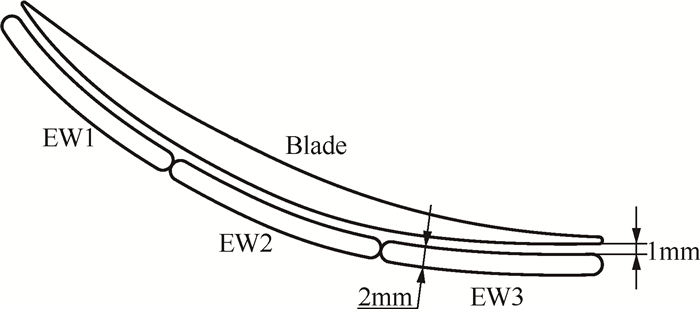
2 叶栅模型及数值模拟方法该扇形叶栅选用典型亚声速高负荷扩压叶型NACA65-K48,相关几何参数见表 1。下端壁开设流向抽吸槽方案如图 1所示,EW1,EW2,EW3三种方案槽的弧长均为叶片吸力面弧长的1/3,宽2mm。槽的近吸力面侧始终与吸力面垂直相距1mm,并于两端进行倒圆角处理。在初始设计方案中还包括尾缘后抽吸方案EW4,但其计算结果相对原型并无明显优化,本文不做讨论。在抽吸流量选择上,文末进行了原型进出口质量流量每0.25%递增的尝试,发现在抽吸流量超过1.00%后栅内会出现超声速,而在1.00%以内优化效果呈现先增后减的趋势,并在0.50%~0.75%保持相对稳定,故选择抽吸流量为原型叶栅质量流量的0.50%。
|
|
Table 1 Geometry parameters of cascade |
|
Fig. 1 Suction schemes |
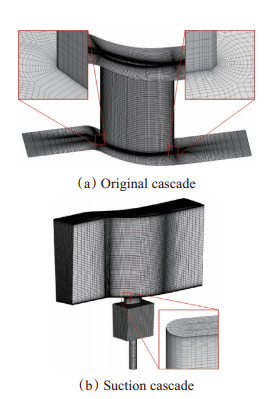
本次数值采用商业CFD软件ANSYS,原型三维网格用Turbo Grid绘制,选择H/J/C/L-Grid,入口雷诺数为878404,近壁面Y+值接近1,近壁面及前尾缘处加密以提高计算精度,如图 2(a)。抽吸槽网格以ICEM进行绘制,选用O网格,并在其进口处及两端适当加密以使网格尺寸在下端壁交界处相切合。为更加符合实际抽吸情况,在抽吸槽处出口下延一与扇形叶栅同心的环形真空腔体,再接抽吸管将气体抽出,如图 2(b)。真空腔体的存在起膨胀降压的作用,使抽吸槽抽吸过程更为顺畅。利用CFX来进行流体力学计算,选用SST湍流模型和Gamma-Theta转捩模型。计算域进口给定总温、总压及湍流强度,进口总压包含附面层文件,并微调进口总压以使各方案进口马赫数保持0.7不变。出口给定平均静压。叶表及各壁面均设为光滑绝热固壁,叶栅通道和真空腔体沿节距两侧设为扇形周期性交界面。
|
Fig. 2 Schematic of mesh |
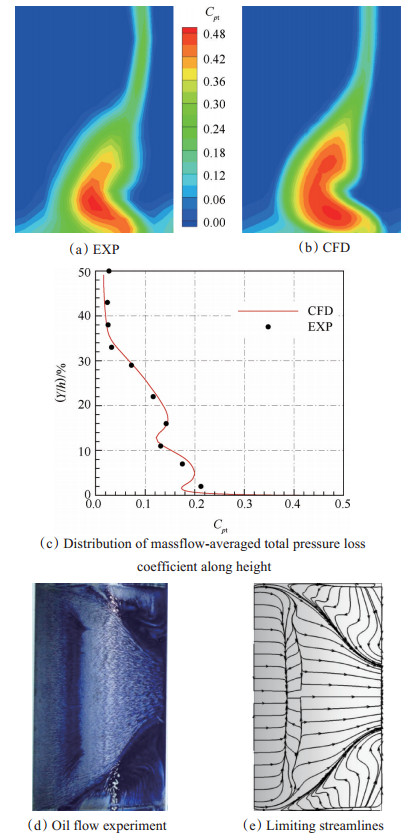
本次研究是对NACA65-K48这一高负荷叶型进行扇形叶栅的初步研究,由于暂时缺少该叶型的扇形叶栅实验数据,故只得以矩形叶栅替代进行校核,其在径向作用力考虑方面存在一定的客观局限性。下图即为在进口马赫数为0.7及冲角为0°时的实验结果(EXP)与数值结果(CFD)的对比。图 3(a)、(b)为距离尾缘0.7b距离的出口截面总压损失系数云图,图 3(c)为流量平均总压损失沿叶高分布,总压损失系数公式为
| $ {{C}_{p\text{t}}}=\left( {{p}_{\text{t}, \text{in}}}-{{p}_{\text{t}, \text{out}}} \right)/\left( {{p}_{\text{t}, \text{in}}}-{{p}_{\text{s}, \text{in}}} \right) $ | (1) |
|
Fig. 3 Numerical check |
式中
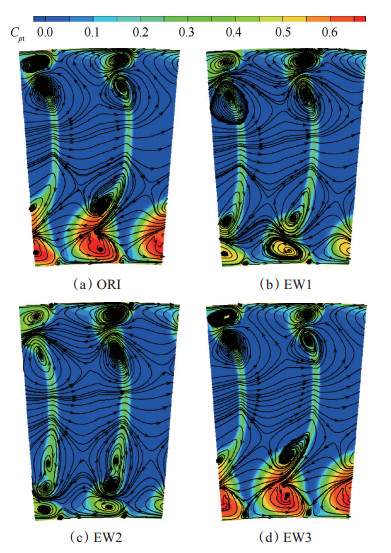
叶栅出口流场可以反映叶栅总体性能,并且直接影响下一级进气状况,是压气机稳定性的重要参考指标。图 4所示为出口截面总压损失系数云图及二次流线图,二次流定义参考文献[17]。原型叶栅由于吸力面角区大尺度分离,存在明显的角区高损失区域,且由于扇形叶栅内周向动能产生的离心力,使得下角区更易产生径向分离,故下角区损失远大于上角区损失。相对而言,型面损失则较小。角区损失区域内可以看到明显的通道涡、集中脱落涡、壁角涡结构,尤其通道涡涡核的位置基本对应损失极大值处,不难得出,通道涡等角区内复杂涡系是造成角区高损失的主要原因。这些旋涡由附面层分离和二次流动发展而来,积聚、掺混低能流体并促进附面层进一步分离,从而造成严重的角区损失。本文抽吸方案旨在改善下角区流场。
|
Fig. 4 Contours of total pressure loss coefficient and secondary flow in outlet |
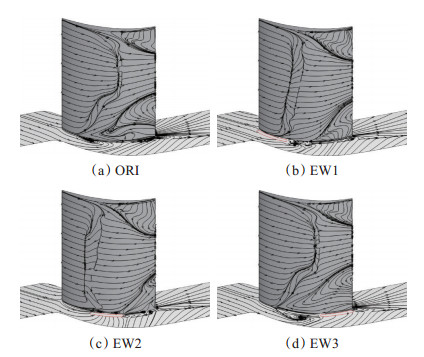
通过端壁流向槽附面层抽吸,吸除角区低能流体的同时削弱流向逆压梯度,从而抑制角区分离和涡系的形成,降低角区损失并增强栅内气体的通流能力。对比不同位置抽吸方案,可以发现EW1和EW2方案效果显著,下角区高损失区域尤其是径向尺寸明显减小,其通道涡和集中脱落涡的强度和影响范围也明显减弱,并向下端壁靠近。其中EW2方案损失削减最为明显,并且集中脱落涡受到抽吸的“牵扯”作用,在向下端壁发展的同时变得狭长并分化出了两个旋向相同的涡核,趋于耗散。EW3方案抽吸效果较差,其损失强度和涡系结构相较原型并未发生明显优化。结合极限流线(图 5)分析可知,EW1方案虽然吸除了部分来流附面层低能流体,但槽后新生附面层的分离并未得到有效抑制,故抽吸效果有限;EW2方案抽吸位置在角区分离起始位置下游附近,吸除低能流体的同时也吸除了端壁上的分离螺旋点,更有效地抑制和延迟了分离形成从而降低角区损失;EW3方案抽吸位置处发生分离的大部分低能流体已远离壁面,抽吸只能一定程度上吸除角区低能流体,而不能从根本上抑制角区分离。
|
Fig. 5 Limiting streamlines on suction surface |
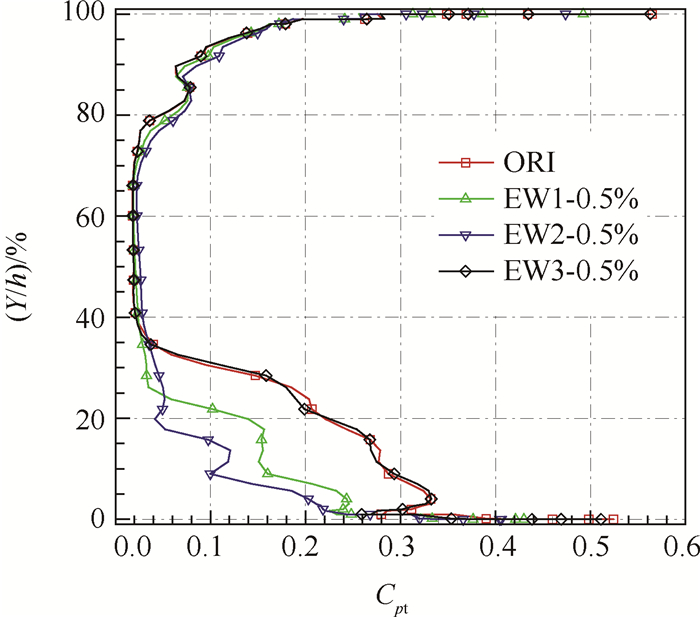
总压损失系数云图只能定性地给出损失分布,为进一步量化地比较总压损失的变化规律,给出流量平均总压损失系数沿叶高的分布(图 6)。从下端壁到35%叶高的下角区损失是原型叶栅尾迹损失的主要部分,近端壁处损失系数最大值达0.5左右。EW1和EW2方案其下角区损失系数大小和径向尺寸都显著减小,尤其是EW2方案,其下角区总压损失降低50%左右,径向尺寸降低至25%叶高附近,但因为栅后新生附面层的客观存在,使近端壁处损失系数最大值变化不大。EW3方案不能从根本上抑制角区分离,其抽吸效果不佳,相较于原型未能有明显优化。另一方面由于下端壁的抽吸作用,反使上角区分离有所加剧,故EW1和EW2方案的上角区损失和型面损失略微增加,但对整体总压损失的优化效果影响不大。EW1方案整体总压损失相对原型降低23.31%,EW2方案降低27.65%。
|
Fig. 6 Distribution of massflow-averaged total pressure loss coefficient along height |
叶栅损失大小和栅内壁面附面层的发展直接相关,而壁面极限流线则可以很好地反映附面层的流动状况,观察图 5原型叶栅的结果发现,附面层的分离和二次流动在上下吸力面角区均产生角区分离,由于逆压梯度的作用角区内存在严重的回流现象,并与中径主流区形成一条明显的分离线,下角区分离强度大于上角区。在吸力面型面中径处附近,由于叶表附面层的分离与再附产生了一狭长的分离泡,并在近端壁处趋于前缘。
进行附面层抽吸后流场明显改善(EW1,EW2,如图 5(b)、(c)),主要表现为下角区分离范围和回流强度明显减弱,分离结构越发趋向于开式分离;抽吸造成的低压使得吸力面泡式分离有所提前且上角区分离略微增强,但整体主流区域增大并趋于中径处,叶栅通流能力增强。其中EW2方案吸除了端壁分离螺旋点,有效地抑制和推迟了下角区的分离。EW3方案只在一定程度上削弱了角区回流,对栅后近端壁流场有一定改善,但效果有限。
4.3 型面载荷分析为探究附面层抽吸对叶栅扩压能力的影响,进行了叶片型面载荷分析,图 7为不同叶高处的型面静压系数的轴向分布。静压系数公式为
| $ {{C}_{p\text{s}}}=\left( {{p}_{\text{s}}}-{{p}_{\text{s}, \text{in}}} \right)/\left( {{p}_{\text{t}, \text{in}}}-{{p}_{\text{s}, \text{in}}} \right) $ | (2) |
|
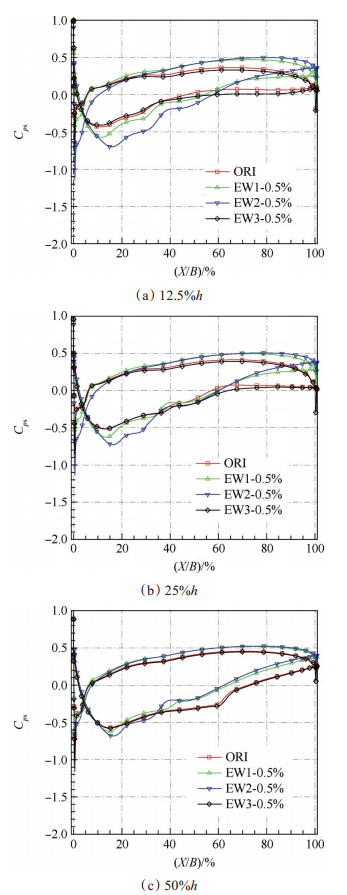
Fig. 7 Axial distribution of static pressure coefficient at different height |
式中
EW1、EW2方案下端壁附面层低能流体的抽吸有效抑制了角区分离,使得型面尤其是近端壁处负载能力提升(图 7(a)),具体表现为12.5%叶高处、5%到50%轴向弦长范围内吸力面静压系数的显著降低。但抽吸槽的存在加剧了槽前及周边端壁附面层的横向二次流动,对压力面近前缘处起到了卸压作用,从而在前缘到5%轴向弦长范围内产生了一定负增益。在靠近尾缘部分,由于前方抽吸槽的“牵扯”作用,使得流体趋于相对的低速高压状态,吸力面和压力面静压系数均有所增大,不过对该处负载能力影响不大。
随着叶高的增加,抽吸影响逐渐减弱,上述变化也逐渐变小,载荷分布亦趋于平滑过渡。在50%叶高处,吸力面分离泡位置所对应的一小段平直段由于抽吸作用明显前移,与图 5中叶表极限流线分析很好地吻合。对叶栅整体扩压能力进行对比,各抽吸方案静压比相对原型均有所增加,EW1方案增加6.37%,EW2方案增加8.69%。
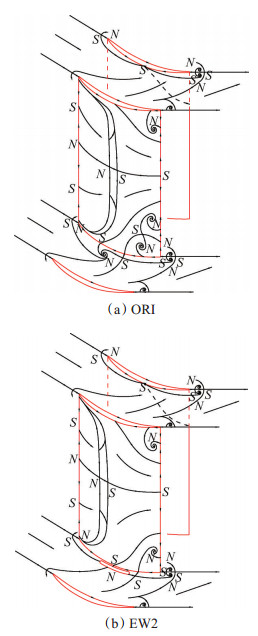
4.4 拓扑结构及旋涡模型附面层的分离和二次流动,是形成角区复杂涡系并造成高损失的主要原因,本节以原型和EW2方案为对象进行栅内摩擦力线拓扑结构和旋涡模型的建立。由于壁面一些鞍结点尺寸较小且位置不易观察,在图 8所示的拓扑结构中对局部结构的比例和位置进行了一定的调整,主要显示其结构特性,将其与壁面极限流线(图 5)结合分析,则可以更好地了解近壁面附面层的具体流动状态。由于压力面并无鞍结点,故图中不予显示。对比两图可看到,抽吸后下角区分离和回流明显改善,其内拓扑结构得到简化;上角区分离略微增强,吸力面泡式分离提前;抽吸槽吸除了下端壁分离螺旋点,使角区分离推迟,但其于栅内起到了类似于点汇的作用,可将其视为一分离结点。根据叶栅流场分析中壁面摩擦力线拓扑法则,对于无间隙的扇形静叶栅,其拓扑结构满足规律:每个节距内壁面摩擦力矢量场中总结点数比总鞍点数少两个。以N,S分别表示结点与鞍点,原型叶栅中N,S数为12,14,EW2方案N,S数为11,13,均满足公式
| $ \mathop{\sum }^{}N-\mathop{\sum }^{}S=-2 $ | (3) |
|
Fig. 8 Topological structure of friction lines on internal surface |
对旋涡结构进行分析时,借助旋涡判定Q准则来辅助进行旋涡的捕捉与定位,如图 9。Q定义为
| $ Q=\left( {{\Omega }_{ij}}{{\Omega }_{ij}}-{{S}_{ij}}{{S}_{ij}} \right)/2 $ | (4) |
|
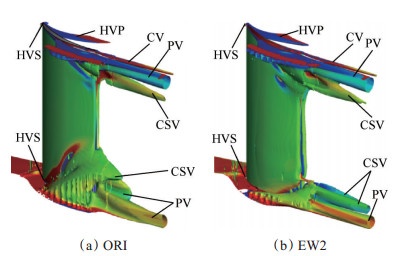
Fig. 9 Isosurface of Q |
式中
图 9中可明显观察到马蹄涡(HV)、通道涡(PV)、集中脱落涡(CSV)、壁角涡(CV)等旋涡结构。马蹄涡吸力面分支随流很快消失,而压力面分支在二次流作用下随流向吸力面发展,并在角区分离通道涡形成后汇入其中。叶栅出口则是典型的通道涡、集中脱落涡和壁角涡的组合结构。值得注意的是,在原型叶栅下角区通道涡和集中脱落涡之间多出一旋涡结构,通过对该处的轴向涡量输出发现其与通道涡正负相同。这是由于下角区的分离严重,通道涡受集中脱落涡的径向卷吸而衍生出的一旋涡结构,但该旋涡涡量较小且结构不稳定,很快随流消失,所以在距尾缘0.7b的出口截面二次流线(图 4(a))中未能捕捉到。抽吸之后,下角区分离大大减弱同时上角区略微增强,下角区通道涡的衍生涡消失,但集中脱落涡向下端壁发展同时趋于狭长,结合图 4(c)可知集中脱落涡分化出两个旋向相同的涡核。
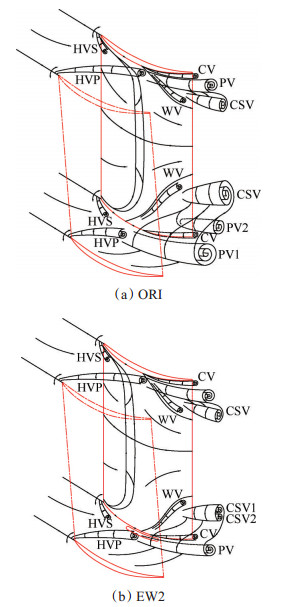
另外,图 9中也可以观察到在角区内、吸力面分离线对应位置还存在壁面涡(WV)结构,它和壁角涡一样都是通道涡形成后在近壁面衍生的产物,其涡量小,与通道涡旋向相反,并在靠近尾缘附近随流消失。最终建立旋涡模型如图 10所示。
|
Fig. 10 Vortex structure model |
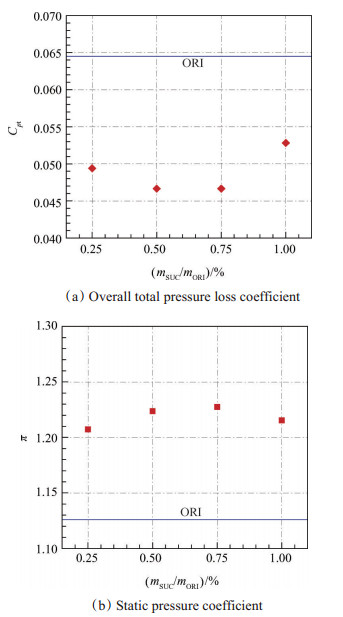
通过各抽吸槽方案的对比发现,在叶中部分(EW2)即角区分离起始位置下游附近开始进行抽吸效果最优。针对该方案,补充探究了抽吸流量对叶栅气动性能优化的影响,以叶栅整体总压损失系数和静压比来表征,抽吸流量分别为来流的0.25%,0.50%,0.75%,1.00%,结果如图 11所示。计算时发现当抽吸流量超过来流的1.00%时栅内会出现超声速并诱发激波,而在1.00%内叶栅性能优化效果呈现先增后减的趋势,并在0.50%~0.75%内保持相对的稳定。0.75%为最优抽吸流量,但相对于0.50%抽吸流量下叶栅性能已无明显提升。
|
Fig. 11 Effects of suction flow on aerodynamic performance |
本文通过对亚声速高负荷扇形扩压叶栅进行下端壁流向槽附面层抽吸的研究分析,得出以下结论:
(1)不同于矩形叶栅上下对称的损失分布,扇形叶栅由于径向力作用,其下角区分离程度和总压损失远大于上角区,可在叶栅下端壁单侧实施附面层抽吸,并通过较小的抽吸量获得明显的气动改善。
(2)下端壁附面层的抽吸可以有效抑制下角区分离和角区内回流,显著降低总压损失并提升近端壁附近的扩压能力,但上角区分离会略有增强。EW2方案0.50%抽吸流量时叶栅整体总压损失降低27.65%,静压比提升8.69%。
(3)对比不同位置抽吸方案,于角区分离起始位置下游附近开始抽吸的方案效果最佳,该方案吸除端壁分离螺旋点,有效抑制并推迟了角区分离;分离前抽吸可以吸除来自来流附面层低能流体,但对下游附面层的分离影响有限;分离后角区内的抽吸不能从根本上抑制角区分离,效果最差。
(4)下角区通道涡受集中脱落涡的径向卷吸作用于二者间衍生出一涡量较小且不稳定的旋涡结构;抽吸后(EW2),下角区涡系径向尺寸缩减,原型通道中衍生涡不再生成,但集中脱落涡趋于狭长并分化出两个旋向相同的涡核。
| [1] |
Hosny W, Tabako W. An Analysis of Losses and Secondary Flow in Turbine Cascade[R]. AD 71-736853.
(  0) 0) |
| [2] |
陆华伟, 阚晓旭, 钟兢军, 等. 正弯压气机静叶流道内流动结构分析[J]. 工程热物理学报, 2013, 34(10): 1828-1832. (  0) 0) |
| [3] |
Bollapragada S. Presentation at Engineering Design Review[R]. AD 2000-A385216.
(  0) 0) |
| [4] |
Kerrebrock J L, Reijnen D P, Ziminsky W S. Aspirated Compressors[R]. ASME 97-GT-525.
(  0) 0) |
| [5] |
Schuler B J, Kerrebrock J L, Merchant A A, et al. Design, Analysis, Fabrication and Test of an Aspirated Fan Stage[R]. ASME 2000-GT-618.
(  0) 0) |
| [6] |
Merchant A A, Drela M, Kerrebrock J L. Aerodynamic Design and Analysis of a High Pressure Ratio Aspirated Compressor Stage[R]. ASME 2000-GT-619.
(  0) 0) |
| [7] |
Ali Merchant, Kerrebrock Jack L, Adamczyk John J. Experimental Investigation of a High Pressure Ratio Aspirated Fan Stage[R]. ASME 2004-GT-53679.
(  0) 0) |
| [8] |
Bolln G W Jr, Field K J, Burnes R. F414 Engine Today and Growth Potential for 21st Century Fighter Mission Challenges[R]. ISABE 99-7113.
(  0) 0) |
| [9] |
Liesner K, Meyer R. Experimental Setup for Detailed Secondary Flow Investigation by Two-Dimensional Measurement of Total Pressure Loss Coefficients in Compressor Cascades[C]. Belgium: VKI XIX Biannual Symposium on Measurement Techniques in Turbomachinery, 2008.
(  0) 0) |
| [10] |
Gmelin C, Thiele F, Liesner K, et al. Investigations of Secondary Flow Suction in a High Speed Compressor Cascade[R]. ASME 2011 GT-46479.
(  0) 0) |
| [11] |
Lemke M, Gmelin C, Thiele F. Simulations of a Compressor Cascade with Steady Secondary Flow Suction[J]. Notes on Numerical Fluid Mechanics and Multidisciplinary Design, 2013, 121(1): 549-556.
(  0) 0) |
| [12] |
宋彦萍, 陈浮, 赵桂杰, 等. 附面层吸除对大转角压气机叶栅气动性能影响的数值模拟研究[J]. 航空动力学报, 2005, 20(4): 561-566. (  0) 0) |
| [13] |
陈浮, 宋彦萍, 赵桂杰, 等. 附面层吸除对压气机叶栅稠度特性影响[J]. 工程热物理学报, 2005, 26(2): 211-215. (  0) 0) |
| [14] |
张华良, 谭春青, 张新敬, 等. 采用附面层抽吸(BLS)控制流动分离的数值模拟[J]. 推进技术, 2009, 30(2): 192-196. (ZHANG Hua-liang, TAN Chun-qing, ZHANG Xin-jing, et al. Numerical Investigation on Application of Boundary Layer Suction to Control the Flow Separations[J]. Journal of Propulsion Technology, 2009, 30(2): 192-196.)
(  0) 0) |
| [15] |
郭爽, 陈浮, 陆华伟, 等. 端壁抽吸位置对大转角扩压叶栅流场及负荷的影响[J]. 推进技术, 2011, 32(3): 323-328. (GUO Shuang, CHEN Fu, LU Hua-wei, et al. Effects of Endwall Boundary Layer Suction Position on the Flow Field and Load in a High-Turning Compressor Cascade[J]. Journal of Propulsion Technology, 2011, 32(3): 323-328.)
(  0) 0) |
| [16] |
郭爽, 陆华伟, 宋彦萍, 等. 端壁附面层抽吸对大转角扩压叶栅旋涡影响的实验研究[J]. 推进技术, 2013, 34(11): 1466-1473. (GUO Shuang, LU Hua-wei, SONG Yan-ping, et al. Experimental Investigation on Effects of Endwall Boundary Layer Suction on Vortexes of High-Turning Compressor Cascades[J]. Journal of Propulsion Technology, 2013, 34(11): 1466-1473.)
(  0) 0) |
| [17] |
阚晓旭. 矩形扩压叶栅中应用叶尖小翼的性能研究[D]. 大连: 大连海事大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10151-1012345179.htm
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


