高超声速飞行器有着重要的军事意义以及潜在的经济价值,备受世界各国研究学者关注,随着研究的深入,传统的进气道设计如轴对称式进气道、二维压缩式进气道和三维侧压式进气道等已不能满足高超声速飞行器设计中的诸多需求,例如跨马赫数飞行、低马赫数下启动、进气道/燃烧室构型优化等[1]。三维内收缩式进气道以其较高的压缩效率和较低的总压损失成为未来高超声速技术发展的一个重要方向[2]。可以预见,高超声速进气道向三维内收缩方向发展将成为必然趋势,也必将引起高超声速飞行器总体方案的再一次变革。然而,由于压缩方式的差异,三维内收缩式进气道与二元进气道存在截然不同的流场结构、总体性能、进口形状和外形特征[3]。
国内外目前的三维内收缩进气道主要包括:Busemann进气道[4, 5],Jaw进气道[6],模块化乘波进气道[7]、REST进气道[8, 9]、Hycause[10]进气道等。
图 1为部分文献中涉及的进气道模型,分析这些进气道构型可以看出,三维内收缩式进气道均设计有V形溢流口。关于溢流口的研究,其中Tam等[11]和孙波等[12]分别对圆形流管、矩形流管流线跟踪进气道起动性能进行分析,结果表明:增加放气槽或者切除唇口,得到的唇口溢流面积增大,当来流马赫数较低或者进气道出口存在反压时,气流可以从唇口位置泄流,以利于进气道起动。潘瑾等[13]、金志光等[14]也开展了可调节唇口和定几何唇口对侧压式进气道起动性能影响的相关研究,结果表明:简单的唇口调节措施能在显著改善进气道各项总体性能参数的同时获得更高的流量系数。可见,相关研究主要集中于溢流口的气动性能,对于溢流口前缘的气动热研究相对较少。

|
Fig. 1 V-shaped leading edge of inward turning inlet |
有研究表明,在高超/超声速来流条件下,V形溢流口与平直溢流口相比,流场结构更加复杂,V形溢流口壁面附近存在严重的热载荷[15]。目前国内外主要针对飞行器头部以及其它形式进气道唇口热流进行了深入的研究[16~19],针对带有复杂流场的内收缩式进气道V形溢流口研究不多,比较相关的是肖丰收[15]、张志雨等[20]对带有圆角的V形结构研究得到了初步的流场结构,结论表明简单的增加倒圆半径并不一定能减小热载荷,相反可能带来复杂的干扰流场,同时也探究了其他参数如来流马赫数对热流的影响。
综上,本文针对高超声速三维内收缩式进气道的溢流口特征,对V形溢流口构型进行了抽象简化,通过CFD和实验相结合的方法,对简化V形溢流口热流进行分析。
2 研究对象及简化三维内收缩式进气道溢流口为空间三维曲线,流场结构特征强,分析难度大,对进气道V形溢流口进行简化,将有助于深入分析其流场结构。
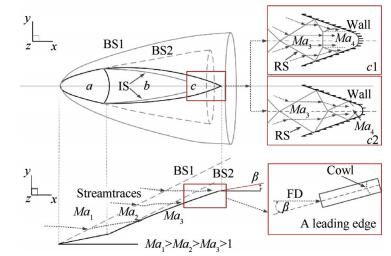
图 2给出的是一类典型的含预压缩前体的三维内收缩式进气道。根据流线追踪设计原理,在设计点条件下,无钝化的进气道溢流口即为内转激波起始位置,当来流参数偏离设计状态时(例如Ma较低,存在钝化等),进气道前体的激波不再附着于溢流口壁面,进气道流场将可能呈现出如图c1,c2所示的复杂流场。
|
Fig. 2 Schematic of inward turning inlet |
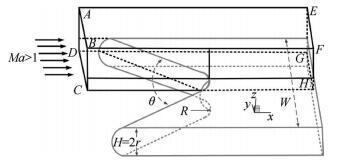
特别地,在图中c处,即为V形溢流口根部,流场结构异常复杂,存在着激波/激波相交反射,激波诱导三维分离等复杂流动现象。因此本文选取如图 2中c处区域作为研究对象,简化的V形构型如图 3所示。可以看出,其几何特征参数有四个:宽度W、钝化半径为r、前缘角θ以及倒圆半径R,其中r、W和R三个参数并不独立,尤其当经过头部激波压缩后的来流相同且内收缩式进气道入口一样时,影响溢流口根部流场结构的形状参数减为三个即:前缘角θ、钝化半径r、以及倒圆半径R。此时倒圆半径比R/r为可作为独立形状参数,因此后续主要对前缘角θ和倒圆半径比R/r对溢流口的热流影响进行研究。另外,为了简化起见,本文仅考虑了同一来流,且气流方向角为零,即图 2中β=0。
|
Fig. 3 Schematic of simplified V-shaped edge |
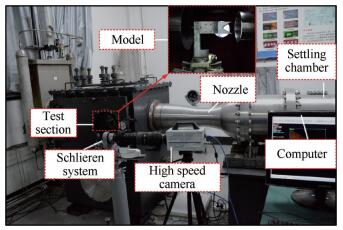
试验在国防科大LF-220自由射流风洞中进行,实验装置如图 4。该风洞喷管出口直径220mm,采用蓄热式电加热器加热高压空气,试验马赫数3~6,总压0.1~4MPa,总温300~700K。风洞配置有200mm纹影仪、高速相机、高频压力采集和5自由度攻角机构等测量测试设备。
|
Fig. 4 Diagram of experimental facility |
本文试验中,选用喷管的名义马赫数为4,实际校测马赫数为3.96,总压为0.3MPa。试验中利用高速相机捕捉纹影图像,采样频率为1000frame/s,单幅曝光时间为1μs。
3.2 计算方法本文数值计算采用有限体积法离散三维雷诺平均N-S方程,湍流模型采用二方程的SST K-ω模型,空间差分采用二阶迎风Roe格式,时间推进采用隐式时间积分法进行求解。
由于本文简化的V形溢流口具有两个方向对称性质(如图 3所示),因此为了进一步简化,提高计算效率,只计算了四分之一的模型,其余通过对称边界条件(DCHG,BCHF)给出(为进一步简化,假设实际过程中流场也是对称结构)。并且来流条件设为压力远场,马赫数为3.96,总压为0.3MPa,总温为907.6K,壁面为等温壁,温度为298K,出口给定压力出口条件。
4 网格无关性分析以下针对简化模型进行网格无关性分析,V形溢流口形状参数为θ=60°,R/r=2,r=5mm,本文选用了5套不同网格进行验证,具体网格参数如表 1中所示,其中涉及网格量和第一层网格距离壁面参数变化,其中壁面附近网格分布如图 5所示。
|
|
Table 1 Verification of grid dependency |
|
Fig. 5 Grid distribution on different direction |
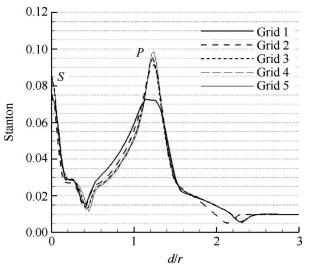
对V形溢流口提取xy对称面上沿壁面热流,横坐标为V形溢流口根部在对称面上沿壁面的距离以钝化半径无量纲后的位置参数,不同网格对热流影响如图 6,S点、P点分别为驻点(本文把V形溢流口根部作为驻点)、第二峰值点,分析可知,网格较为稀疏以及壁面大于1μm时,热流差别较大,尤其是P点,Grid 1和Grid 2误差达到27.8%,热流差别明显,当网格加密并且减小壁面距离后,热流差别很小,热流误差均小于2%,热流并没有收敛到某一个固定值,而是处于某一值附近振荡,但是误差已经很小,因此认为此时网格已经满足热流的计算要求,故本文选用Grid 3网格进行后续计算。
|
Fig. 6 Heat flux changes with different grids |
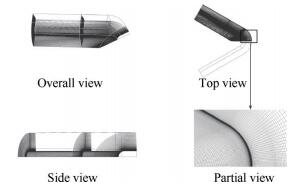
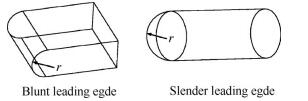
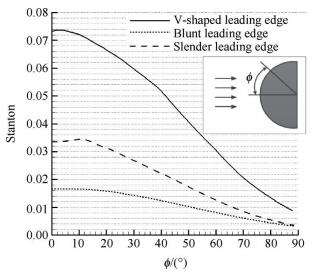
本文选用了钝头体、旋成体以及V形溢流口(具体见图 7),比较其在前缘钝化时的热流大小,其中保持所有构型钝化半径r均为5mm,并且V形溢流口形状参数为θ=30°,r=5mm,R/r=2,来流条件和3.2节中计算条件参数一致。提取壁面热流处沿钝化半径周向的热流,由于描述壁面气动加热最常使用的无量纲参数是Stanton,本文中均用无量纲量Stanton代表热流变化。并通过坐标变换将直角坐标变为极坐标形式,具体结果如图 8。
|
Fig. 7 Two types of blunt configurations |
|
Fig. 8 Heat flux changes with different shape |
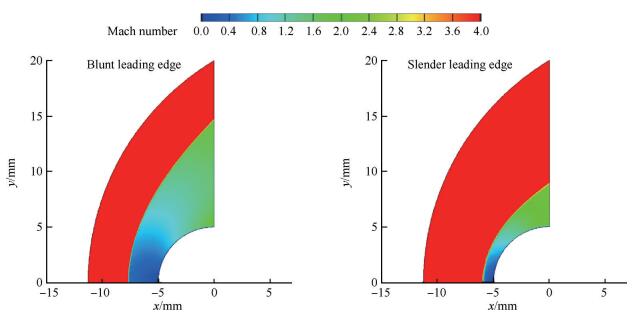
对比三类前缘钝化构型,可见不同构型热流差别很大,其中钝头体热流最小;对于旋成体而言,三维溢流明显,从而激波脱体距离更小(如图 9),热流也会更大;在非驻点区,沿着周向,钝头体和旋成体壁面热流最终趋于相同。对于V形溢流口,热流峰值约为二维钝头体的3~4倍,其产生高热流的机理和前面两个都不同,如图 9所示,前两种构型钝化前缘均只有一道弓形激波对气体作用,对于V形溢流口,存在激波/激波相交反射、激波/壁面干扰等复杂流场结构。
|
Fig. 9 Mach number contour of two types of blunt configurations |
值得注意的是,对于V形溢流口,峰值热流并没有出现在对称面中心线位置,但是中心线处热流和峰值热流差别不大,因此后续研究中可认为中心线上热流值为各点沿周向热流峰值,即中心线上热流能够代表V形钝化溢流口最大热流状态。
5.2 前缘角对V形溢流口的热流影响规律为了探究前缘角θ对V形溢流口热流的影响,本文选取了倒圆半径比R/r=2,前缘角θ分别为30°,45°,60°,75°的V形溢流口进行热流分析。
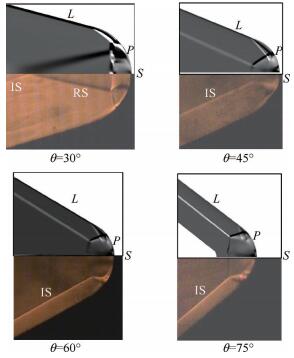
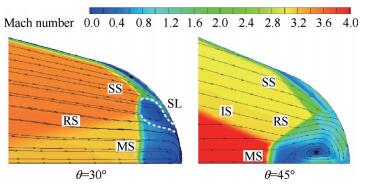
图 10给的是V形溢流口对称面上实验纹影和数值纹影结果对比图,其中IS代表入射激波,RS代表反射激波,SS代表分离激波。需要说明的是,本文关注的是V形溢流口根部复杂流场结构,因此为了能清晰捕捉到流场,实验纹影拍摄的是V形溢流口根部区域。从流场结构可以看出,改变前缘角θ大小,溢流口根部出现了两种结构(如图 11),这是因为前缘角θ很小时,V形溢流口根部距离上游激波入射点较远,溢流区较长,溢流口根部反压作用小,两道激波必然会先发生规则反射,引起的反射激波RS和根部区域作用,出现θ=30°的流场结构;前缘角θ较大时,V形溢流口根部距离上游激波入射点较近,溢流区相对较短,溢流口根部反压作用增强,两个入射激波规则反射并不能匹配下游反压条件,这时就会出现马赫反射,出现θ为45°,60°,75°的流场结构。值得注意的是,θ=45°,θ=60°和θ=75°在实验纹影中马赫反射形成的马赫杆并没有清晰地拍到,这是因为该马赫杆几乎和水平中心线垂直,试验中纹影仪刀口是水平放置,因此纹影图是密度在垂直方向的一阶导,对于该马赫杆结构,垂直方向密度变化不大,因此实验纹影清晰度较低,而对于数值纹影,分辨率相对较高,可以看到马赫杆。
|
Fig. 10 Schlieren images on different angle |
|
Fig. 11 Mach number contour of two types of flowfiled |
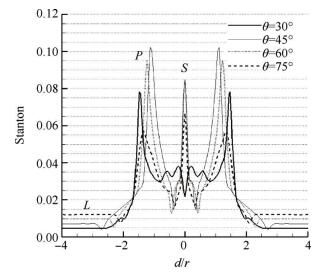
提取不同前缘角θ对称面上壁面热流如图 12所示,横坐标为V形溢流口根部在对称面上沿壁面的距离以钝化半径无量纲后的位置参数,可以看出热流变化规律也出现了对应的两种形式,这与流场结构是相对应的。
|
Fig. 12 Heat flux distributes on wall with different angle |
θ=30°时,驻点热流为极小值,沿着壁面向上游热流先增大后减小,观察流场可知,该前缘角θ下,是反射激波RS在根部产生的激波/激波干扰流场,并且气流汇聚于两道滑移线SL之间,汇聚效应比根部强,从而在滑移线尾部壁面附近出现热流峰值,而根部热流此时反而为极小值。θ > 30°后,均出现了两个热流峰值,第一极值点位于驻点处,是气流经过马赫杆压缩作用后的滞止点,第二峰值点和驻点热流峰值相当,甚至还比驻点热流高(θ=45°和θ=60°),究其原因是马赫反射中从三波点引出的滑移线将波后超声速区和亚声速区分开,亚声速区为马赫反射中马赫杆后方区域,超声速区为反射激波RS和分离激波SS相互作用的区域。超声速流道中反射激波RS和分离激波SS相互作用,最终使超声速射流滞止于壁面,引起此区域附近热流极大。经过根部复杂流场区域后,最终热流平稳(L点附近),趋于某一个固定值。
对以上算例分别提取驻点S、峰值点P以及平稳点L的热流如表 2所示,分析各个前缘角θ热流最大值可知,热流最大值和前缘角θ并不成单调变化,前缘角θ从30°增加到75°热流极大值出现先增加后减小的趋势,但是热流变化不明显,可见试图通过改变前缘角θ缓解热流,其改善的能力有限。在热流平稳L点处,热流和角度成正比,这是由于角度增大,气流溢流能力增强,根部反压对上游的作用减弱,从而入射激波角变小,对于该区域而言,斜激波压缩气流增强,则热流必然会增大,但是该区域相对于溢流口热流,其值很小,热防护应该重点考虑根部S点以及第二峰值P点。
|
|
Table 2 Heat flux with different angle |
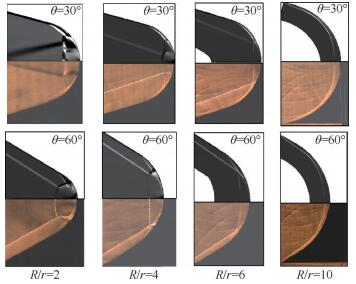
为了探究倒圆半径比R/r对V形溢流口根部的影响,本节重点对两个前缘角(θ=30°,θ=60°)进行分析,如图 13为前缘角θ=30°和θ=60°不同R/r下流场结构变化的数值纹影和实验纹影对比图,θ=30°时,从流场结构可知,不同R/r,出现了三类流场结构:R/r=2时,入射激波形成规则反射,引起的是反射激波在根部发生激波干扰;增大R/r后,入射激波形成的马赫反射,反射激波和分离激波发生作用,R/r=10后,入射激波合成一道曲线激波,分离激波消失。
|
Fig. 13 Schlieren images of CFD and experiment with different R/r |
θ=60°时只形成了两类流场,入射激波形成了马赫反射,并且滑移线两侧流场分别为超声速流场和亚声速流场,在超声速流道中,反射激波和分离激波相互作用将气流减速,导致流道的末端壁面热流极高。R/r增大后,气流溢流区变大,根部气流对上游作用减弱,同时马赫杆变长,根部亚声速区扩大,R/r=10后,流场和θ=30°类似,入射激波合成一道曲线激波,分离激波消失。
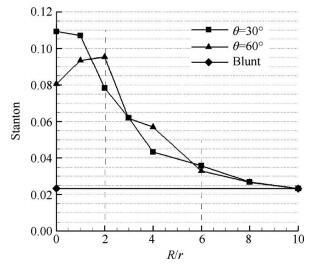
图 14为数值计算中各算例的峰值热流变化规律,其中Blunt算例为平直钝化前缘热流峰值,分析可知,由于存在复杂流场,V形溢流口热流比平直钝化前缘受到极高的热流,两种前缘角θ下,改变R/r均对V形溢流口的热流峰值有显著影响。当R/r < 2时,改变R/r并不一定有效减小热流,这与文献[15, 20]结论是一致的,因为此时存在超声速射流滞止于壁面,引起高的热流;但是如果继续增大R/r,可以看出峰值热流明显的减小,尤其2 < R/r < 6区间,热流显著减小,这是由于马赫杆变长,激波变弱,溢流区变大,壁面热流得到有效缓解。并且θ=30°中,最大热流和最小热流之比为4.7倍,θ=60°时为4.1倍,可见如果合理优化好V形溢流口的几何结构,可以减小高达75%~78%的热流,这对于内收缩式进气道是非常重要的。
|
Fig. 14 Heat flux changes with different R/r |
综上,对于进气道的设计,考虑气动性能时也要注意到可能带来的严重的气动热,即气动性能和热防护应同时关注。
6 结论本文结合数值计算和实验结果对简化V形溢流口前缘热流进行了分析,主要结论有:
(1)对比二维,三维钝化溢流口构型的气动热,钝化的V形溢流口热流比其它两类钝化构型的热流高,流场结构也更加复杂。
(2)改变倒圆半径比R/r出现了三类流场结构,分别为入射激波的规则反射、入射激波马赫反射以及入射激波合成曲线激波。
(3)改变前缘角θ,并不能显著降低热流,热流峰值仍然很高。不同倒圆半径范围影响峰值热流不同,当倒圆半径比R/r < 2时,增大倒圆半径并不一定能减小热流;当2 < R/r < 6时,改变倒圆半径热流变化很明显;之后增大倒圆半径比,热流变化不大。
(4)在进行进气道溢流口前缘设计中,尽可能避免前缘出现复杂的激波干扰流场,在满足气动性能的条件下,尽可能调整R/r > 6,从而降低前缘的热载荷。
| [1] |
王哲, 李旭昌. 高超声速三维内收缩式进气道研究进展[J]. 飞航导弹, 2014, 4: 79-87. (  0) 0) |
| [2] |
吴颖川, 贺元元, 贺伟, 等. 吸气式高超声速飞行器机体推进一体化技术研究进展[J]. 航空学报, 2015, 36(1): 245-260. (  0) 0) |
| [3] |
尤延铖, 梁德旺, 郭荣伟. 高超声速三维内压缩式进气道/乘波前体一体化设计研究评述[J]. 力学进展, 2009, 39(5): 513-525. DOI:10.6052/1000-0992-2009-5-J2008-094 (  0) 0) |
| [4] |
Billig F S. Design and Analysis of Streamline Traced Hypersonic Inlets[C]. Norfolk: 9th International Space Planes and Hypersonic Systems and Technologies Conference, 1999. http://arc.aiaa.org/doi/abs/10.2514/6.1999-4974
(  0) 0) |
| [5] |
Billig F S. Streamline Tracing: Technique for Designing Hypersonic Vehicles[J]. Journal of Propulsion and Power, 2000, 16(3): 465-471. DOI:10.2514/2.5591
(  0) 0) |
| [6] |
Malo-Molina F J, Gaitonde D V. Numerical Investigation of an Innovative Inward Turning Inlet[C]. Toronto: 17th AIAA Computational Fluid Dynamics Conference, 2005. http://arc.aiaa.org/doi/abs/10.2514/6.2005-4871
(  0) 0) |
| [7] |
尤延铖, 梁德旺. 基于内乘波概念的三维变截面高超声速进气道[J]. 中国科学, 2009, 39(8): 1483-1494. (  0) 0) |
| [8] |
Smart M K. Experimental Testing of a Hypersonic Inlet with Rectangular-to-Elliptical Shape Transition[J]. Journal of Propulsion and Power, 2001, 17(2): 276-283. DOI:10.2514/2.5774
(  0) 0) |
| [9] |
Smart K M, Trexler A C. Mach 4 Performance of Hypersonic Inlet with Rectangular-to-Elliptical Shape Transition[J]. Journal of Propulsion and Power, 2004, 20(4): 288-292.
(  0) 0) |
| [10] |
Walker H S. Hypersonic Collaborative Australia/United States Experiment (HYCAUSE)[R]. AIAA 2005-3254.
(  0) 0) |
| [11] |
Tam C J, Robert A B, Gary D S. Numerical Analysis of Streamline-Traced Hypersonic Inlets[R]. AIAA 2003-13.
(  0) 0) |
| [12] |
孙波, 张堃元. Busemann进气道起动问题初步研究[J]. 推进技术, 2006, 27(2): 128-131. (SUN Bo, ZHANG Kun-yuan. Preliminary Investigation on Busemann Inlet Starting Characteristics[J]. Journal of Propulsion Technology, 2006, 27(2): 128-131.)
(  0) 0) |
| [13] |
潘瑾, 张堃元. 可变内收缩比侧压式进气道自起动性能[J]. 推进技术, 2007, 28(3): 278-282. (PAN Jin, ZHANG Kun-yuan. Self-Starting Characteristics for Sidewall-Compression Inlet with Variable Internal Contraction Ratio[J]. Journal of Propulsion Technology, 2007, 28(3): 278-282.)
(  0) 0) |
| [14] |
金志光, 张堃元. 高超侧压式进气道简单唇口调节方案设计[J]. 推进技术, 2008, 29(1): 43-48. (JIN Zhi-guang, ZHANG Kun-yuan. Concept of a Varied Geometry Scramjet Inlet with Rotatable Cowl[J]. Journal of Propulsion Technology, 2008, 29(1): 43-48.)
(  0) 0) |
| [15] |
肖丰收. 若干典型高超声速激波干扰流动特性研究[D]. 合肥: 中国科学技术大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10358-1016319976.htm
(  0) 0) |
| [16] |
Duquesne N, Roquefort TAd. Numerical Investigation of a Three-Dimensional Turbulent Shock/Shock Interaction[R]. AIAA 98-0774.
(  0) 0) |
| [17] |
潘沙, 田正雨, 冯定华. 超燃冲压发动机唇口气动热计算研究与分析[J]. 航空动力学报, 2009, 24(9): 2096-2100. (  0) 0) |
| [18] |
Curran E T, Murthy S N B. Scramjet Propulsion[M]. New York: American Institute of Aeronautics and Astronautics Inc, 2000.
(  0) 0) |
| [19] |
贺旭照, 赵慧勇, 乐嘉陵. 吸气式高超声速飞行器气动力气动热的数值模拟方法及应用[J]. 计算物理, 2008, 25(5): 555-560. (  0) 0) |
| [20] |
张志雨, 肖丰收. 钝化V形前缘激波干扰特性研究[C]. 成都: 第十七届全国激波与激波管学术会议, 2016.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


