超声速进气道通过激波系的压缩使得来流减速增压达到发动机的使用要求,是冲压发动机的关键部件[1],国际上,对头部、旁侧、腹部等各形式的进气道布局进行了大量研究,总结了一定规律,美国AIAA系列丛书战术导弹设计[2]对不同布局的弹用进气道综合特性进行了详细比较,其中颌下进气道作为一种布局形式,具有迎面阻力小、攻角特性好等特点,在飞机、尤其是导弹布局中格外受到重视。美国最早在ASLAM导弹上对颌下进气道[3, 4]布局进行了研究,对进气道特性进行了综合论述。
王新月等[5]在一种颌下式进气道和前机身一体化设计技术中采用一种固定几何双斜板外压式进气道,获得了飞行马赫数Ma=1.4~1.8的进气道性能特性,研究表明所设计的颌下进气道工作稳定,进气效率高,采用激波系亚额定设计,使进气道稳定性增加,但由于进气道不可调以及亚额定设计,使得进气道阻力有所增加。
谢文忠等[6]分析了4种布局形式下超声速飞行器进气道的速度特性、迎角特性和侧滑角特性,对其中工作范围Ma=2.5~4.5,设计点Ma=4.0的颌下进气布局进气道进行了试验研究,结果表明颌下进气道具有良好的正迎角性能,但是负迎角性能较差,在0°~4°侧滑角,颌下进气道性能下降不大。
靖建朋等[7]对一种巡航马赫数4的颌下式三锥混压进气道进行了试验研究,得到了该进气道的气动特性,结果表明在Ma=3.5,攻角和偏航角为零时,随着出口反压的增加,进气道总压恢复系数先升高后降低,临界状态下进气道总压恢复系数最高;随着来流马赫数的增加,有攻角或偏航角的状态下,进气道的总压恢复系数呈线性下降趋势;进气道在由反压引起的不起动过程中具有再起动特性,再起动过程中无迟滞回路现象。
孟宇鹏等[8]对一种等熵压缩颌下进气道进行了研究,采用计算流体力学和风洞试验两种手段得到了进气道性能特性以及出口流场特性随攻角、侧滑角变化的规律。研究表明:相同设计马赫数下等熵压缩颌下进气道性能高于三锥压缩颌下进气道的性能;等熵压缩进气道在较小攻角下达到性能极值,随着攻角增大压缩效率和流量系数均会降低,随着侧滑角增大,性能降低;进气道出口流场不均匀度随着攻角的增大逐渐增大,流场畸变度不断增大。
李宏东等[9]研究了一种超声速颌下进气道的亚临界振荡特性,利用风洞试验,进行了来流马赫数Ma=2.5,3.5,4.0,不同攻角,不同节流状态的试验,获得了各状态下超声速颌下进气道的亚临界振荡的频率和压力幅值。
传统颌下进气道均为尖拱形式,采用部分角度的轴对称压缩外形和细长旋成体的结合方式,随着冲压发动机/进气道/飞行器高空高速飞行带来的一体化需求不断提高,国外对前体/进气道一体化的乘波布局设计技术[10~15]进行了大量研究,包含锥导乘波、吻切乘波、平面乘波以及内转式等多种形式。国内耿永兵等[16]对高马赫数等熵压缩乘波进气道设计方法进行了论述,向南军等[17]提出了基于弯曲压缩的压力可控基准流场设计方法,许少华等[18]、贺旭照等[19]也就锥导乘波和密切锥乘波设计方法进行了研究论述。
由于乘波压缩设计目前主要集中在高超声速进气道领域,进气道布局也以升力体、腹部及内转式为主,国内外采用颌下进气布局并且结合乘波设计的研究文献很少,随着冲压发动机性能需求的不断提高以及飞行器一体化程度不断加强,颌下进气布局和前体乘波设计相结合将具备进气道高性能和飞行器低阻力的综合优势,会成为一种典型的超声速飞行器布局形式之一,开展这方面的研究具有很大意义。
本文针对Ma=2.5~4.5工作的冲压动力装置,采用弯曲激波压缩基准流场和轴对称等熵压缩基准流场的锥导乘波设计方法,设计出超声速颌下乘波进气道方案,利用三维流场数值模拟获得了两种进气道基本计算性能,并选择了等熵压缩乘波设计的颌下进气道进行风洞吹风试验验证,得到了进气道的攻角特性和速度特性。设计结果表明颌下进气道具有头部乘波、流量系数大、总压恢复系数高的特点。
2 设计方法 2.1 轴对称弯曲激波基准流场设计基准流场的设计参考了南京航空航天大学张堃元教授提出的压力可控弯曲激波压缩设计方法。采用有旋特征线法计算激波后流场。本文在设计轴对称压缩面时,起始段设置一长度很短的圆锥,采用Taylor-Maccoll方程(方法略)求得该处流场参数,之后根据预先给定的壁面压力梯度分布,利用有旋特征线理论逐点求得物理型面。压力分布采用六阶的Bezier样条曲线,七个点控制样条曲线形状,前三个点控制起始端二阶导数,后三个点控制末端二阶导数,中间点调整样条曲线形状。设计需要的参数有来流马赫数、起始半锥角、壁面压力分布以及压缩面长度。
二维有旋特征线法左行、右行特征线方程为
| ${{\left. \frac{\text{d}y}{\text{d}x} \right|}_{\pm }}=\text{tan}\left( \theta \pm \alpha \right)$ | (1) |
式中θ, α分别为当地速度方向角和当地马赫角。
流线方程
| $\frac{{{\rm{d}}y}}{{{\rm{d}}x}} = {\rm{tan}}\theta $ | (2) |
沿流线假设总压不变,沿流线的相容方程
| ${\rm{dln}}{p^{\rm{*}}} = 0$ | (3) |
沿左右特征线相容方程
| $\begin{array}{*{20}{l}} {{{\left. {{\rm{d}}\left( {\nu \left( M \right) \mp \theta } \right)} \right|}_ \pm } - \frac{{{\rm{sin}}\left( {2\alpha } \right)}}{{2\gamma }}{\rm{dln}}{p^{\rm{*}}} - }\\ {\delta \frac{{{\rm{sin}}\alpha {\rm{sin}}\theta }}{{{\rm{sin}}\left( {\theta \pm \alpha } \right)}}{\rm{dln}}p = 0} \end{array}$ | (4) |
式中δ=1对应轴对称超声速流场;δ=0对应二维超声速流场。ν(M)为Prandtl Meyer函数,表达式为
| $ \begin{array}{*{20}{l}} {\nu \left( M \right) = \sqrt {\frac{{\gamma + 1}}{{\gamma - 1}}} {\rm{arctan}}\sqrt {\frac{{\gamma - 1}}{{\gamma + 1}}\left( {{M^2} - 1} \right)} - }\\ {\;\;\;\;\;\;\;\;\;\;{\rm{arctan}}\sqrt {{M^2} - 1} } \end{array} $ | (5) |
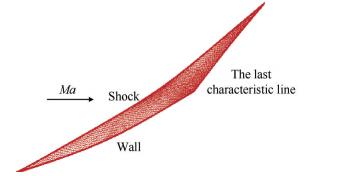
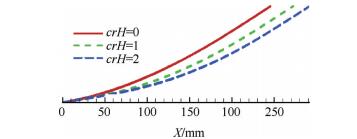
初始压缩角不易过小或过大,本文选取一个合适的初始压缩角为8°,设计前体的乘波马赫数为Ma=4.0,考虑到唇罩角和攻角范围,选取外压缩总转折角不超过30°,设计了不同的沿程压力分布弯曲激波压缩系统。图 1是轴对称弯曲激波压缩流场计算特征线网格,图 2是不同的曲面锥沿X向压力分布,图中的crH表示沿X向压力梯度。图 3为对应不同压力分布的沿X向曲面锥母线形状示意图,如图所示当crH越大,曲面锥沿程压力分布越接近于轴对称等熵压缩,当crH=0时,即压力梯度为常数,压缩形式为沿程线性压缩。研究发现,相同收缩比情况下,等压力梯度型面最短,越接近于等熵压缩,压缩面越长,总压恢复越高。
|
Fig. 1 Characteristics computing grids of axisymmetric curved shock field |

|
Fig. 2 Pressure distribution along X-direction of cone curve surface |
|
Fig. 3 Different configuration of the element of curved cone |
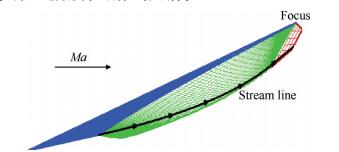
传统二元等熵压缩流场可以直接求解Prantdl-Meyer流动方程得到等熵压缩曲面,轴对称等熵压缩曲面需要采用无旋特征线法求解欧拉方程(方法略)。图 4是具有一定初始锥角的轴对称局部等熵压缩流场特征线网格,首先求解Taylor-Maccoll方程,获得初始锥形流场。以锥形流场出口边界为等熵压缩起始线,焦点(Focus)为旋转点,用无旋特征线法求解获得等熵压缩区,最后计算出无压缩区。
|
Fig. 4 Characteristics computing grids of axisymmetric isentropic compression field |
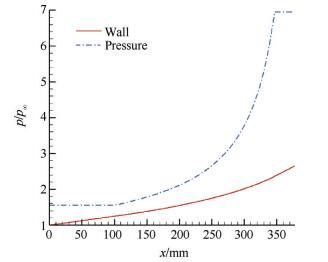
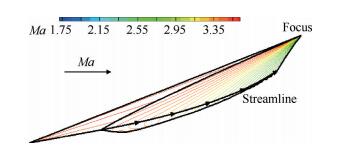
选取设计马赫数Ma=4.0,初始压缩角8°,总转折角28°,计算得到等熵压缩的X向压力分布见图 5。等熵压缩首先是在起始段通过锥形激波压缩,使得波后马赫数适当降低,进而通过微弱马赫波压缩到一定的压比实现总压恢复系数最大化。如图 6所示为等熵压缩流场马赫线图谱。
|
Fig. 5 Pressure distribution along-direction of isentropic compression surface |
|
Fig. 6 Ma contours of isentropic compression field |
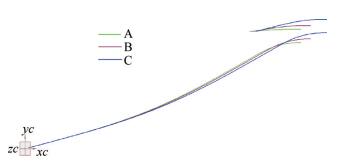
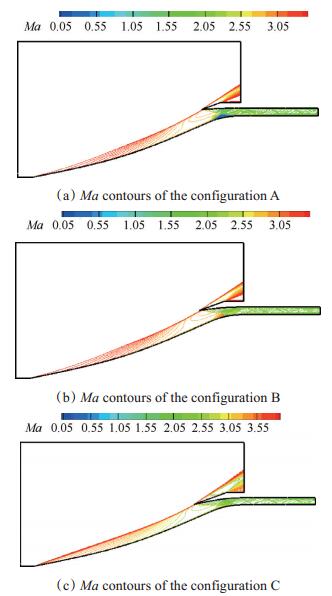
确定乘波设计点马赫数、进气道起始压缩半锥角、进气道外罩的捕获半径高度、进气道唇罩角以及总转折角等参数就可以设计进气道基准型面。通常采用混合压缩形式,需要确保进气道内压缩段为一定的收缩通道。喉道面积的设计需要根据自起动条件进口前马赫数正激波流量连续方程确定,并考虑到一定的设计裕度,以容纳较大的流量通过。图 7所示为经过优化设计得到的三种不同收缩比进气道基准型面,进气道A总收缩比为4.067,B为3.950,C为3.768,图 8所示为三种方案的等马赫线计算结果图谱。
|
Fig. 7 Basis configuration of three inlets |
|
Fig. 8 Ma contours of the three configurations at Ma=4.0, α=0° |
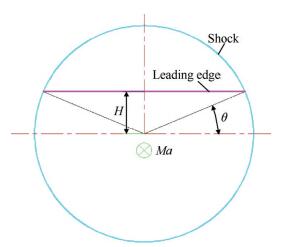
在弯曲激波压缩基准型面流场上采用流线追踪方法形成压缩面。进口前缘线距离轴对称旋转轴距离为H,展向张角为180°-θ。当H=0时,流线追踪获得的压缩面退化为轴对称弯曲激波压缩锥面,H越大,压缩面压缩量越小,θ越大,张角越小。本文颌下乘波进气道前缘采用了形状和结构最为简单的直线,两侧面直接采用一定夹角的流线截面,根据需要前缘线和两侧面也可以采用不同形式的曲线形状。本文乘波体进口截面如图 9所示。
|
Fig. 9 Inlet section of waverider field |
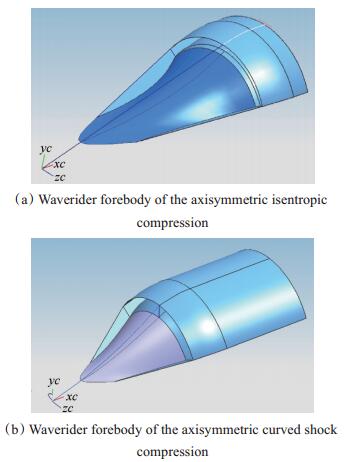
依据尺寸约束及捕获流量需求可以选择合适的展向角θ和前缘高度距离H,流线追踪生成进气道前体型面,等熵压缩的设计方法和弯曲激波压缩相同。采用轴对称等熵压缩基准流场和弯曲激波压缩基准流场经过优化选型分别得到了两种颌下进气道乘波前体型面,见图 10所示。由于基准压缩型线的不同,等熵压缩进气道的前体长度通常要长于弯曲激波压缩前体的长度。
|
Fig. 10 Two configurations forebody by waverider design |
对轴对称等熵压缩和弯曲激波压缩流线追踪生成的两种进气道开展流场数值计算,两种进气道的激波封口马赫数Ma=4.0,其中等熵压缩进气道总压缩角46°,进气道进口内收缩比1.15;弯曲激波压缩进气道总压缩角46°,进气道轴向尺寸显著缩短,进口前马赫数略高,内收缩比为1.48。
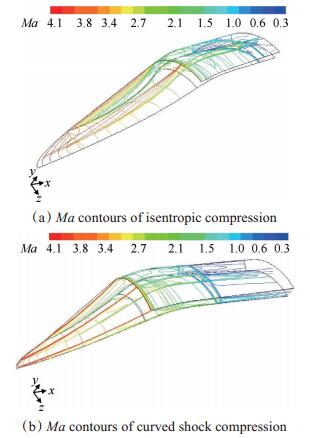
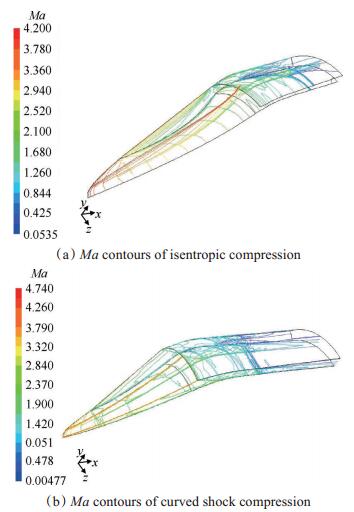
计算控制体网格划分及边界条件采用对称面半模形式,网格为六面体和五面体结构化网格,总数约400万,见图 11。数值计算应用商用计算流体力学软件,采用二阶精度迎风差分格式离散雷诺方程,耦合叠代算法,湍流模型为双方程标准k-ε湍流模型,采用标准壁面函数,收敛精度10-3。在超声速流动建立后,通过调整进气道出口反压模拟燃烧室压力,当结尾激波稳定于喉道部位时判定进气道进入临界工况,Ma=4.0,攻角0°和6°临界状态下两种进气道的计算流场分别见图 12和图 13,流场性能计算结果比较见表 1。计算结果表明:

|
Fig. 11 CFD meshes of inlet field |
|
Fig. 12 Ma contours on critical condition at Ma=4.0, α=0° |
|
Fig. 13 Ma contours on critical condition at Ma=4.0, α=6° |
|
|
Table 1 CFD performance of the two chin inlet |
(1)等熵压缩乘波进气道压缩效率高,唇口反射波强度低,没有引发附面层分离,进气道通道内波系结构保持较好。
(2)基于弯曲激波乘波设计的进气道激波面呈现内凹型,可以使得进口轴向尺寸显著缩短,通过设计压升规律,能有效降低入口前的马赫数,但弯曲激波带来的滑移层会使得总压损失增大。
(3)颌下进气道随着攻角增大,捕获流量系数增大,等熵压缩乘波前体长度长,因此攻角下流量系数也高于弯曲激波压缩方案的流量系数。
4 试验结果与讨论 4.1 试验设备和模型选取等熵压缩颌下乘波进气道前体,并匹配设计出带内通道的进气道完整气动型面(方法略)在国内FD06超声速风洞开展节流试验,以验证乘波进气道的设计性能。风洞试验段侧壁有观察窗,供纹影光学观察。风洞使用电子扫描阀进行测压,最大采样速度50kHz,量程为±0.2MPa,扫描精度±0.05%FS,压力校准精度可达±0.01%FS。本研究试验马赫数范围主要在Ma=2.5~4.0,攻角-6°~9°。
模型出口为直径D的圆形截面,设置皮托压力测量阵列,采用6等环面积“米”形分布,用来测量流场的当地总压。在测量截面壁面还设有8个静压测点,可以测量壁面静压。测量结果采用质量流量加权平均方法计算进气道出口的性能和流场。测量截面下游为电机驱动的节流堵锥,调节进气道下游出口压力,以模拟进气道超临界、临界到亚临界的不同工况。图 14所示为进气道模型试验照片。

|
Fig. 14 Waverider chin inlet experimental scheme and photo |
图 15为本研究中颌下乘波进气道在马赫数4.0,攻角6°时的前体进口部位纹影照片,可以清晰看到等熵压缩各道微弱压缩波汇交到进气道唇口的流动现象,照片下方给出了相对的中剖面流场数值计算图谱,圆圈表示纹影照片所处的位置。

|
Fig. 15 Experiment schlieren photo at Ma=4.0, α=6° |
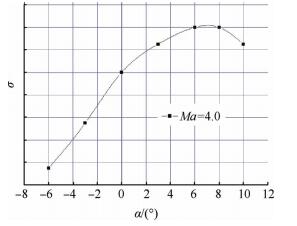
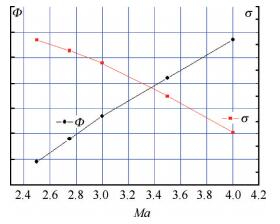
图 16为设计马赫数Ma=4.0进气道总压恢复系数随攻角变化关系。试验结果表明颌下乘波进气道在-6°~6°攻角总压恢复系数随攻角呈单调增大关系,最大总压恢复系数在攻角6°出现,并且在攻角6°~8°可以保持,随着攻角增大到10°,总压恢复系数下降。图 17所示为颌下乘波进气道流量系数随攻角变化趋势,结果表明在攻角-6°~8°,流量系数随攻角增大而增大,最大流量系数出现在攻角8°,而后随攻角增大到10°,流量系数快速下降。图 18为进气道性能随马赫数变化关系。试验结果表明随马赫数升高,进气道总压恢复系数降低,流量系数增大。
|
Fig. 16 Experiment total pressure recovery coefficient versus the angle of attack |

|
Fig. 17 Experiment mass flow ratio versus the angle of attack |
|
Fig. 18 Experiment performance versus the Ma |
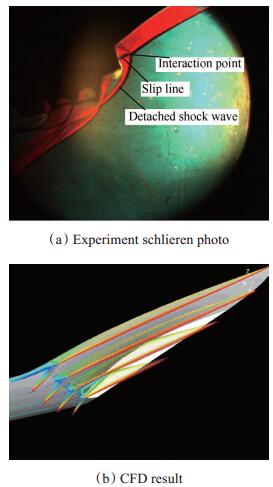
图 19给出了马赫数Ma=4.0,攻角10°进气道前体进口部位纹影照片。由于攻角的增大,图中前缘等熵压缩激波汇交点偏移至进气道唇口上游,并出现等熵压缩流场下游典型的涡面滑移线现象,进气道没有起动。这主要是由于攻角增大捕获流量增大,致使喉道壅塞造成了不起动现象。试验结果还发现不起动的流场结构十分稳定,没有出现喘振。图 19(b)中也给出了进气道头部三维流场数值计算结果,计算结果截取了头部不同的多个截面,流场结构表明进口流动稳定,波系结构和试验纹影比较一致。试验和计算结果表明10°攻角下,即使进气道不起动造成溢流,乘波设计仍具有一定的流动稳定性。
|
Fig. 19 Inlet unstart shock wave construction by experiment and CFD at Ma=4.0, α=10° |
基于特征线法和参数化设计,对轴对称弯曲激波压缩基准流场和等熵压缩基准流场求解,结合锥导乘波设计方法,可以设计出工作范围Ma=2.5~4.5的超声速颌下乘波进气道方案。通过流场数值计算和试验获得了进气道流场特性和试验结果,结果表明:
(1)颌下乘波进气方案能够在典型攻角飞行状态具有较高的流量系数和总压恢复系数。
(2)随着攻角增大,进气道压缩效率和流量系数提高,在Ma=4.0状态,该进气道总压恢复系数可以达到0.47,流量系数达到1.20。
(3)进气道在大攻角下由于捕获流量大幅增大出现了不起动现象,但流场结构和性能稳定。
(4)该进气道实现了和飞行器前体外形的高度融合设计,具有头部乘波、大捕获流量、高压缩特性。
| [1] |
刘兴洲. 飞航导弹动力装置[M]. 北京: 宇航出版社, 1992.
(  0) 0) |
| [2] |
Eugene L Fleeman. Tactical Missile Design[M]. Virginia: American Institute of Aeronautics and Astronautics, 2006.
(  0) 0) |
| [3] |
Frank F Webster, Bucy J A. ASALM-PTV Chin Inlet Technology Overview[R]. AIAA 79-1240.
(  0) 0) |
| [4] |
Frank F Webster. Evaluation of the ASALM-PTV Propulsion System Flight Data Correlation Results and Anylasis Techniques[R]. AIAA 81-1606.
(  0) 0) |
| [5] |
王新月, 廉小纯. 超声速颌下式进气道/前机身一体化方案设计[J]. 推进技术, 2002, 23(2): 142-145. (WANG Xin-yue, LIAN Xiao-chun. Supersonic Chin Inlet/Airframe Integration Design[J]. Journal of Propulsion Technology, 2002, 23(2): 142-145.)
(  0) 0) |
| [6] |
谢文忠, 郭荣伟. 4种布局形式下超声速飞行器进气道气动特性实验对比[J]. 南京航空航天大学学报, 2011, 43(1): 13-17. (  0) 0) |
| [7] |
靖建朋, 郭荣伟, 孙小平, 等. Ma4一级颌下式混压进气道试验[J]. 航空动力学报, 2012, 27(2): 387-394. (  0) 0) |
| [8] |
孟宇鹏, 朱守梅, 李宏东. 马赫数4.0颌下等熵混合压缩进气道技术研究[J]. 战术导弹技术, 2014(6): 69-74. (  0) 0) |
| [9] |
李宏东, 朱守梅, 朱璞, 等. 超声速颌下进气道亚临界振荡特性试验研究[J]. 推进技术, 2015, 36(11): 1601-1609. (LI Hong-dong, ZHU Shou-mei, ZHU Pu, et al. Experimental Investigation on Sub-Critical Oscillation Characteristics of Supersonic Chin Inlet[J]. Journal of Propulsion Technology, 2015, 36(11): 1601-1609.)
(  0) 0) |
| [10] |
Haney J W, Beaulieu W D. Wave Rider Inlet, Integration Issues[R]. AIAA 94-0383.
(  0) 0) |
| [11] |
LobbiaM, Suzuki K. Design and Analysis of Payload Op timized Waveriders[R]. AIAA 2001-1849.
(  0) 0) |
| [12] |
Ryan P Starkey, Falcon Rankins, Darryll Pines. Coupled Waverider/Trajectory Optimization for Hypersonic Cruise[R]. AIAA 2005-530.
(  0) 0) |
| [13] |
Kashif H J, Varnavas C S. Airframe-Propulsion Integration Methodology for Waverider-Derived Hypersonic Cruise Aircraft Design Concepts[R]. AIAA 2004-1201.
(  0) 0) |
| [14] |
Sannu M. Internal Axismmetric Conical Flow[J]. AIAA Joural, 1967, 5(7): 1043-1047.
(  0) 0) |
| [15] |
Adam Siebenhaar, Thomas J Bogar. Integration and Vehicle Performance Assessment of the Aerojet "TriJet" Combined-Cycle Engine[R]. AIAA 2009-7420.
(  0) 0) |
| [16] |
耿永兵, 刘宏, 丁海河, 等. 轴对称近似等熵压缩流场的乘波前体优化设计[J]. 推进技术, 2006, 27(5): 404-409. (GENG Yong-bing, LIU Hong, DING Hai-he, et al. Optimized Design of Waverider Forebody Derived from a Symmetric Near-Isentropic Compression Flow Fields[J]. Journal of Propulsion Technology, 2006, 27(5): 404-409.)
(  0) 0) |
| [17] |
南向军, 张堃元. 压缩面升压规律可控的高超进气道轴对称基准流场设计方法研究[C]. 昆明: 中国航空学会航空动力分会火箭发动机专业委员会2009年推进技术学术年会, 2009.
(  0) 0) |
| [18] |
许少华, 侯中喜, 葛爱学, 等. 锥导乘波构型设计、优化与分析[J]. 推进技术, 2008, 29(4): 448-453. (XU Shao-hua, HOU Zhong-xi, GE Ai-xue, et al. Design, Optimization and Analysis of Cone Derived Waverider[J]. Journal of Propulsion Technology, 2008, 29(4): 448-453.)
(  0) 0) |
| [19] |
贺旭照, 秦思, 周正, 等. 一种乘波前体进气道的一体化设计及性能分析[J]. 航空动力学报, 2013, 28(6): 1270-1276. (  0) 0) |
 2018, Vol. 39
2018, Vol. 39


