Nomenclature:
|
|
响应函数对于研究结构在流体中的振动和受力方面有着极为重要的作用,它将结构周围的湍流特性和由此产生的激振力联系在一起,这些结构不仅包括了水翼,桥梁,还有螺旋桨等。因此,结构在湍流中的非定常升力一直以来受到许多学者的关注和研究[1]。而响应函数则是联系水翼受到的冲击脉动和环境湍流的重要方程。Sears[2]基于薄翼,无限展长和单向波数的假设得到了著名的传递函数Sear函数。基于此理论,Liepmann[3]推导了在湍流脉动中无限长水翼的冲击响应公式,研究了湍流中水翼激振力的变化规律,在此过程中,他忽视了湍流展长方向的变化,认为水翼的冲击响应只是简单线性湍流脉动的结果。
随后,Ribner[4]研究了三维环境下的湍流问题,认为将简单的单方向的湍流波叠加以后可以得到三维湍流波模型,因此各向同性湍流下的激振力可以由各个方向的波数向量叠加起来得到。在此基础上,Liepmann[5],Franklin[6]将展长方向的湍流变量考虑在内,研究了三维有限长水翼在同向均匀的湍流中受力问题,认为可以使用Sear函数作为传递函数来研究有限长水翼问题,这种方法也被称为薄片理论,在该情况下,二维响应函数被一维Sear函数代替。然而薄片理论并不总是正确的,Etkin[7]发现在弦长尺寸与湍流尺度相比相似或更大的情况下,二维Sear函数不再适用,因此,此时薄片理论的误差不可忽略。Larose等[8, 9]也在随后的研究中证明了此观点。他们还发现湍流的扭曲,包括涡的伸展和旋转都能导致展长方向激振力相关性的增大。因此,为准确地描述三维水翼激振力的分布,运用三维理论并将展长方向的湍流变量考虑在内是很有必要的。
受到Ribner的研究启发,Graham[10]研究了三维湍流流域,在Sear函数的基础上,使用升力面法计算了包含两个方向波数(k1,k2)的无限长水翼激振力响应函数,该函数能够描述水翼受到的三维激振力。Filotas[11]则推导了斜流条件下水翼的二维响应函数,在较高频率或较低频率下,使用该响应函数带来的误差较小。随后,Filotas[12]将计算得到的响应函数与实验结果进行了比较,结果显示有较大偏差。而Jackson等[13]运用Graham推导的传递函数计算了矩形截面的无限长水翼的激振力并与风洞中相同模型的实验结果进行了比较,发现与实验值的吻合度较高。Franklin[6],Hakkinen等[14],Zhong等[15],Massaro等[16]和Li等[17]进行了截面不规则时水翼的非定常升力研究。
本文推导了有限长水翼的响应公式,研究了水翼展长、湍流尺度对基于薄片理论公式的影响,并进行了有限长水翼下洗速度和升力的相关性研究。
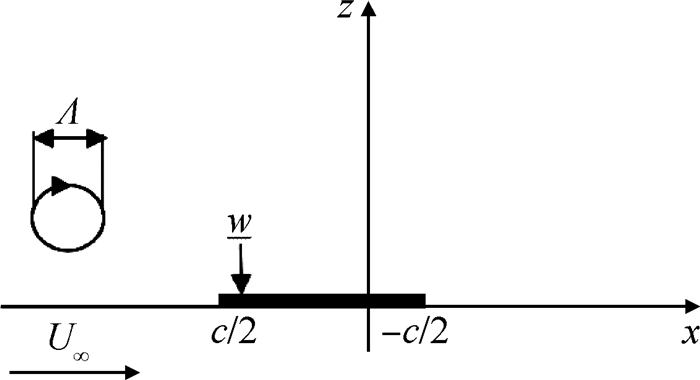
2 响应函数公式推导图 1给出了计算湍流中水翼非定常升力的数学模型。如图所示,来流速度为U∞;Λ为湍流尺度;w为下洗速度;x为流向方向;y为水翼展向方向;z为纵向方向;k1,k2,k3为x,y,z三个方向的波数;水翼弦长为C,展长为b。在推导响应函数公式时,一般将水翼假设为无厚度的薄翼,此时水翼受到的非定常升力L是由湍流场中速度脉动引起的。这里α(t)为下洗速度w引起的水翼攻角变化;h(τ,y)为升力L与攻角α(t)之间的传递函数;L为产生的非定常升力。此时沿水翼展向方向升力分布表示为
| ${\rm{d}}L = {\rm{d}}y\int_{ - \infty }^{ + \infty } h \left( {\tau, y} \right)\alpha \left( {t - \tau, y} \right){\rm{d}}\tau $ | (1) |
|
Fig. 1 Mathematical model |
由于湍流中的速度脉动是和统计有关的变量,所以使用均方值的概念更能准确地表达该物理量。整个水翼所受到的升力均方值为
| $\begin{array}{*{20}{l}} {\overline {{L^2}} = \int {\int_{ - b}^{ + \mathit{b}} {\int {\int_{ - \infty }^{ + \infty } h } } } \left( {{\tau _1}, {y_1}} \right)h\left( {{\tau _2}, {y_2}} \right) \cdot }\\ {\overline {\alpha \left( {t - {\tau _1}, {y_1}} \right)\alpha \left( {t - {\tau _2}, {y_2}} \right)} {\rm{d}}{y_1}{\rm{d}}{y_2}{\rm{d}}{\tau _1}{\rm{d}}{\tau _2}} \end{array}$ | (2) |
| $~~\overline{\alpha \left( t-{{\mathit{\tau }}_{1}}, {{y}_{1}} \right)\alpha \left( t-{{\mathit{\tau }}_{2}}, {{y}_{2}} \right)}=\mathit{\psi }\left( {{\tau }_{1}}-{{\mathit{\tau }}_{2}}, {{y}_{1}}-{{y}_{2}} \right) $ | (3) |
式中ψ(τ, Y)为攻角α(t)关于时间t和变量y的自相关函数。引入纵向方向速度w的自相关函数
| $\begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;{R_{ii}} = \overline {{u_i}\left( r \right){u_i}\left( {r + s} \right)} \\ \begin{array}{*{20}{l}} {{R_{ii}}\left( s \right) = \int {\int {\int_{ - \infty }^{ + \infty } {{\phi _{ii}}} } } \left( k \right) \cdot {{\rm{e}}^{{\rm{i}}\left( {k \cdot s} \right)}}{\rm{d}}{k_1}{\rm{d}}{k_2}{\rm{d}}{k_3} = }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\int_{ - \infty }^{ + \infty } {{\phi _{ii}}} \left( k \right) \cdot {{\rm{e}}^{{\rm{i}}\left( {k \cdot s} \right)}}{\rm{d}}V\left( k \right)} \end{array} \end{array} $ | (4) |
在薄翼假设中,由于水翼表面z方向坐标为零,所以(τ1-τ2)U∞=x1-x2且α=w/U∞,可知攻角的变化只与速度分量w有关(速度分量:u,v,w),于是得到
| $~\mathit{\psi }\left( {{\mathit{\tau }}_{1}}-{{\mathit{\tau }}_{2}}, {{y}_{1}}-{{y}_{2}} \right)={{R}_{\text{w}}}\left( {{x}_{1}}-{{x}_{2}}, {{y}_{1}}-{{y}_{2}}, 0 \right) $ | (5) |
将式(5)代入式(4)中得到
| $ \mathit{\psi }\left( {{\mathit{\tau }_{\rm{1}}} - {\mathit{\tau }_{\rm{2}}}\mathit{, }{\mathit{y}_{\rm{1}}} - {\mathit{y}_{\rm{2}}}} \right) = \int_{ - \infty }^{ + \infty } {{\phi _{\rm{w}}}\left( \mathit{\boldsymbol{k}} \right) \cdot {{\rm{e}}^{{\rm{i}}\left[{({x_1}-{x_2}){\mathit{k}_{\rm{1}}} + ({\mathit{y}_1} + {\mathit{y}_{\rm{2}}}){\mathit{k}_{\rm{2}}}} \right]}}} $ | (6) |
将上式代入式(2)得到
| $\overline {{L^2}} = \int_{ - \infty }^{ + \infty } {{\phi _{\rm{w}}}} \left( \mathit{\boldsymbol{k}} \right){\left| {\mathit{\Gamma }\left( {{k_1}, {k_2}} \right)} \right|^2}{\rm{d}}V\left( {\boldsymbol{k}} \right) $ | (7) |
式中
由于,
| $\begin{array}{l} {\phi _L}\left( {{k_1}} \right) = {\int {\int_{ - \infty }^{ + \infty } {\left| {\mathit{\Gamma }\left( {{k_1}, {k_2}} \right)} \right|} } ^2}{\phi _{\rm{w}}}\left( {{k_1}, {k_2}} \right){\rm{d}}{k_2}{\rm{d}}{k_3} = \\ \frac{1}{{8{{\rm{ \mathit{ π} }}^3}}}\int {\int {\int {\int {{{\int_\infty ^{ + \infty } {\left| {\mathit{\Gamma }\left( {{k_1}, {k_2}} \right)} \right|} }^2}} } } } {R_{\rm{w}}}\left( {{r_1}, {r_2}, {r_3}} \right)\cdot\\ {{\rm{e}}^{ - {\rm{i}}\left( {{k_1}{r_1} + {k_2}{r_2} + {k_3}{r_3}} \right)}}{\rm{d}}{k_2}{\rm{d}}{k_3}{\rm{d}}{r_1}{\rm{d}}{r_2}{\rm{d}}{r_3} \end{array} $ | (8) |
由于
| ${\phi _L}({k_1}) = \int_{ - \infty }^{ + \infty } \Gamma ({k_1},{k_2}){|^2}{\phi _w}({k_1},{k_2},0){\rm{d}}{k_2} $ | (9) |
从以上推导结果可以发现,不管w是否随z坐标改变,ϕL(k1)的大小与k3无关。这为以后推导带有攻角的水翼激振力宽频谱时提供了理论基础。现在需要求得|Γ(k1, k2)|,由Graham发现,水翼在湍流中的升力系数沿展向的分布如下
| ${C_L}\left( {y, t} \right) = 2{\rm{ \mathsf{ π} }}T\left( {{k_1}, {k_2}} \right)\frac{{w\left( {{k_1}, {k_2}, \omega } \right)}}{{{U_\infty }}}{{\rm{e}}^{{\rm{i}}\left( {{k_2}y - \omega t} \right)}}$ | (10) |
式中T(k1, k2)为传递函数,现将CL(y, t)沿展向方向进行积分,得到这个水翼的升力系数
| $\begin{array}{l} {C_L}\left( t \right) = \frac{1}{{2b}}\int_{ - b}^{ + b} {2{\rm{ \mathsf{ π} }}T} \left( {{k_1}, {k_2}} \right)\frac{{w\left( {{k_1}, {k_2}, \omega } \right)}}{{{U_\infty }}}{{\rm{e}}^{{\rm{i}}\left( {{k_2}y - \omega t} \right)}}{\rm{d}}y = \\ \;\;\;\;\;\;\;\;\;\;\;\;2{\rm{ \mathsf{ π} }}T\left( {{k_1}, {k_2}} \right)\frac{{{\rm{sin}}\left( {{k_2}b} \right)}}{{{k_2}b}}\frac{{w\left( {{k_1}, {k_2}, \omega } \right)}}{{{U_\infty }}}{{\rm{e}}^{ - {\rm{i}}\omega t}} \end{array} $ | (11) |
水翼升力还可以表述为三维传递函数Γ(k1, k2)与下洗速度eik1xw的乘积
| $L = \mathit{\Gamma }\left( {{k_1}, {k_2}} \right){{\rm{e}}^{{\rm{i}}{k_1}x}} \cdot w\left( {{k_1}, {k_2}, \omega } \right)$ | (12) |
结合式(12)和式(11)可得
| $\mathit{\Gamma }\left( {{k_1}, {k_2}} \right) = \left( {\frac{1}{2}\rho U_\infty ^2\left( {2bC} \right)} \right)\frac{{2{\rm{ \mathit{ π} }}}}{{{U_\infty }}}T\left( {{k_1}, {k_2}} \right)\frac{{{\rm{sin}}\left( {{k_2}b} \right)}}{{{k_2}b}}$ | (13) |
| $\begin{array}{*{20}{l}} {{\phi _{{C_{\rm{L}}}}}\left( \omega \right) = \frac{1}{{{U_\infty }}}\int_{ - \infty }^{ + \infty } {\frac{{4{\pi ^2}}}{{U_\infty ^2}}} \left| {T\left( {{k_1}, {k_2}} \right)} \right|^2 \cdot }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\left( {\frac{{{\rm{sin}}\left( {{k_2}b} \right)}}{{{k_2}b}}} \right)}^2}{\phi _{\rm{w}}}\left( {{k_1}, {k_2}} \right){\rm{d}}{k_2} = \frac{{4{\pi ^2}}}{{U_\infty ^3}}{\phi _{\rm{w}}}\left( {{k_1}} \right) \cdot }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\int_{ - \infty }^{ + \infty } {{{\left| {T\left( {{k_1}, {k_2}} \right)} \right|}^2}} \cdot {{\left( {\frac{{{\rm{sin}}\left( {{k_2}b} \right)}}{{{k_2}b}}} \right)}^2}{\mathit{\Phi }_{\rm{w}}}\left( {{k_1}, {k_2}} \right){\rm{d}}{k_2} = }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{4{\pi ^2}}}{{U_\infty ^2}}{\varphi _{\rm{w}}}\left( \omega \right)\int_{ - \infty }^{ + \infty } {{{\left| {T\left( {{k_1}, {k_2}} \right)} \right|}^2} \cdot } }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\left( {\frac{{{\rm{sin}}\left( {{k_2}b} \right)}}{{{k_2}b}}} \right)}^2}{\mathit{\Phi }_{\rm{w}}}\left( {{k_1}, {k_2}} \right){\rm{d}}{k_2}} \end{array} $ | (14) |
三维响应函数的表达式如下
| $\begin{array}{l} {A_{3D}}\left( \kappa \right) = \frac{{{U^2}}}{{4{{\rm{ \mathit{ π} }}^2}}}\frac{{{\phi _{{C_{\rm{L}}}}}\left( {{k_1}} \right)}}{{{\phi _{\rm{w}}}\left( {{k_1}} \right)}} = \\ {\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}\frac{{\mathop \smallint \nolimits_{ - \infty }^{ + \infty } {{\left| {T\left( {{k_1}, {k_2}} \right)} \right|}^2} \cdot {{\left( {\frac{{{\rm{sin}}\left( {{k_2}b} \right)}}{{{k_2}b}}} \right)}^2}{\phi _{\rm{w}}}\left( {{k_1}, {k_2}} \right){\rm{d}}{k_2}}}{{\mathop \smallint \nolimits_{ - \infty }^{ + \infty } {\phi _{\rm{w}}}\left( {{k_1}, {k_2}} \right){\rm{d}}{k_2}}} = \\ {\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}\mathop \smallint \nolimits_{ - \infty }^{ + \infty } {\left| {T\left( {{k_1}, {k_2}} \right)} \right|^2} \cdot {\left( {\frac{{{\rm{sin}}\left( {{k_2}b} \right)}}{{{k_2}b}}} \right)^2}{\mathit{\Phi }_{\rm{w}}}\left( {{k_1}, {k_2}} \right){\rm{d}}{k_2} \end{array} $ | (15) |
当采用薄片假设时,T(k1, k2)=Se(κ),κ为无因次频率。二维响应函数如式(16)所示
| ${\mathit{A}_{{\rm{2}}\mathit{D}}}\left( \kappa \right)\mathit{ = }{\int_{ - \infty }^{ + \infty } {\left| {Se\left( \kappa \right)} \right|} ^{\rm{2}}} \cdot {\left( {\frac{{\sin \left( {{k_2}b} \right)}}{{{k_2}b}}} \right)^{\rm{2}}}{\mathit{\Phi }_w}({k_1}, {k_2}){\rm{d}}{k_2} $ | (16) |
在以上公式中
采用Graham计算得到的传递函数为
| $\begin{array}{l} T\left( {{k_1}, {k_2}} \right) = \\ \left| {Se\left( {{k_1}C/2} \right)} \right|\frac{{1 + 3.2{{\left( {{k_1}C/2} \right)}^{1/2}}}}{{1 + 2.4{{\left( {{k_2}C/2} \right)}^2} + 3.2{{\left( {{k_1}C/2} \right)}^{1/2}}}} \end{array}$ | (17) |
在研究水翼升力的响应函数时,一般假定ϕw(k1, k2)是各向同性切均匀的湍流函数,Li等[17]指出
| ${\phi _{\rm{w}}}\left( {{k_1}, {k_2}} \right) = 4{a^4}\overline {{w^2}} \frac{{n\left( {n + 1} \right)\left( {k_1^2 + k_2^2} \right)}}{{{{\left[{1 + {a^2}\left( {k_1^2 + k_2^2} \right)} \right]}^{n + 2}}}}$ | (18) |
| ${\phi _{\rm{w}}}({k_1}) = \int_{ - \infty }^{ + \infty } {{\phi _{\rm{w}}}\left( {{\mathit{k}_{\rm{1}}}, {\mathit{k}_2}} \right){\rm{d}}{\mathit{k}_{\rm{2}}}} = 2\mathit{\Lambda }\overline {{\mathit{w}^{\rm{2}}}} \cdot \frac{{1 + 2\left( {n + 1} \right)k_1^2{a^2}}}{{{{\left[{1 + {a^2}\mathit{k}_1^2} \right]}^{n + 3/2}}}} $ | (19) |
式中n为流动系数,湍流尺度,
n=1/2时
| $\begin{array}{*{20}{l}} {{\phi _{\rm{w}}}\left( {{k_1}, {k_2}} \right) = 3{\mathit{\Lambda }^4}\overline {{w^2}} \frac{{k_1^2 + k_2^2}}{{{{\left[{1 + {\mathit{\Lambda }^2}\left( {k_1^2 + k_2^2} \right)} \right]}^{5/2}}}}}\\ {{\phi _{\rm{w}}}\left( {{k_1}} \right) = 2\mathit{\Lambda }\overline {{w^2}} \cdot \frac{{1 + 3k_1^2{\mathit{\Lambda }^2}}}{{{{\left( {1 + {\mathit{\Lambda }^2}k_1^2} \right)}^2}}}} \end{array}$ | (20) |
n=1/3时
| $\begin{array}{l} {\phi _{\rm{w}}}\left( {{k_1}, {k_2}} \right) = 1.76{\rm{ \mathit{ π} }}{a^4}\overline {{w^2}} \cdot \frac{{\left( {k_1^2 + k_2^2} \right)}}{{{{\left[{1 + {a^2}\left( {k_1^2 + k_2^2} \right)} \right]}^{7/3}}}}\\ {\phi _{\rm{w}}}\left( {{k_1}} \right) = \frac{{2\mathit{\Lambda }\overline {{w^2}} }}{3} \cdot \frac{{3 + 8k_1^2{a^2}}}{{{{\left( {1 + {a^2}k_1^2} \right)}^{11/6}}}} \end{array}$ | (21) |
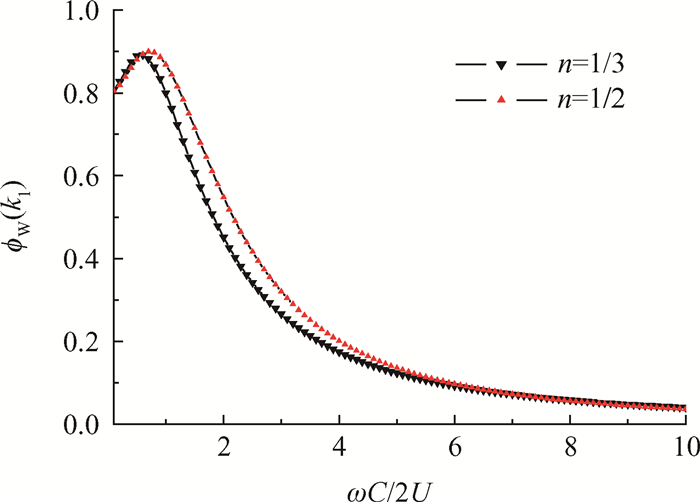
图 2给出了n=1/2和n=1/3时ϕw(k1)的大小。从图中可以看到,当
|
Fig. 2 Spectrum of the vertical velocity fluctuations |
图 3给出了n=1/2和1/3时的三维响应函数以及薄片假设下的二维响应函数计算结果,将计算得到的结果分别与实验结果,Fiotas计算结果以及Sear函数结果进行了比较,此时的计算参数为:Λ/C=0.4,b/C=0.28。从图中分析发现,薄片假设下的二维响应函数与三维响应函数和实验结果[20]相比都相差较大,这也证明了薄片理论的局限性。而n=1/2和1/3时三维响应函数的计算结果也不相同,从图中可以看到,两条曲线的区别主要存在于

|
Fig. 3 Admittance of a finite hydrofoil |
通过以上的计算发现了薄片理论的局限性,本节主要研究薄片理论在各种情况的误差程度,这里引入变量A3D/A2D表示该误差程度,表达式如式(22)所示,可以看到,该变量主要与水翼展长b以及湍流尺度Λ有关。下面主要研究不同水翼展长b和湍流尺度Λ下A3D/A2D的变化规律。
| $\frac{{{A_{3{\rm{D}}}}\left( \kappa \right)}}{{{A_{2{\rm{D}}}}\left( \kappa \right)}} = \frac{{{{\int_{ - \infty }^{ + \infty } {\left| {T\left( {{k_{\rm{1}}}, {k_2}} \right)} \right|} }^2} \cdot {{\left( {\frac{{\sin \left( {{k_2}b} \right)}}{{{k_2}b}}} \right)}^2}{\mathit{\Phi }_{\rm{w}}}\left( {{k_1}, {k_2}} \right){\rm{d}}{\mathit{k}_{\rm{2}}}}}{{{{\int_{ - \infty }^{ + \infty } {\left| {Se\left( \kappa \right)} \right|} }^2} \cdot {{\left( {\frac{{\sin \left( {{k_2}b} \right)}}{{{k_2}b}}} \right)}^2}{\mathit{\Phi }_{\rm{w}}}\left( {{k_1}, {k_2}} \right){\rm{d}}{\mathit{k}_{\rm{2}}}}} $ | (22) |
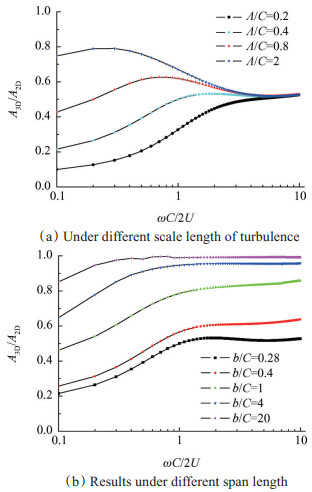
设定b/C=0.28,分别改变湍流尺度Λ的大小为Λ/C=0.2,Λ/C=0.4,Λ/C=0.8和Λ/C=2,计算得到的A3D/A2D如图 4(a)所示。设定Λ/C=0.4,改变水翼展长b的大小为b/C=0.28,b/C=0.4, b/C=1,b/C=4,b/C=20,计算得到的A3D/A2D如图 4(b)所示。
从图 4(a)分析发现:当无因次频率
从图 4(b)可以分析发现:与湍流尺度Λ的影响不同,在各个不同湍流尺度Λ下
从以上分析可以得出结论,虽然湍流尺度Λ和水翼展长b都能影响A3D/A2D的大小,但它们的影响规律却并不一样,在
当水翼展长b趋于零时,忽略展长的影响,研究任意截面响应函数的规律,此时ϕCL(k1, k2)的表达式为
| $\begin{array}{l} {\phi _{{C_{\rm{L}}}}}\left( {{k_1}, {k_2}} \right) = \mathop {{\rm{lim}}}\limits_{b \to 0} \frac{{4{{\rm{ \mathit{ π} }}^2}}}{{U_\infty ^2}}{\left| {T\left( {{k_1}, {k_2}} \right)} \right|^2} \cdot \\ {\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}{\left( {\frac{{{\rm{sin}}({\mathit{k}_{\rm{2}}}\mathit{b})}}{{{k_2}b}}} \right)^2}{\phi _{\rm{w}}}({\mathit{k}_1}, {\mathit{k}_{\rm{2}}}) = \\ {\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}\frac{{4{{\rm{ \mathit{ π} }}^{\rm{2}}}}}{{U_\infty ^1}}{\left| {T({\mathit{k}_1}, {\mathit{k}_{\rm{2}}})} \right|^2}{\phi _{\rm{w}}}({\mathit{k}_1}, {\mathit{k}_2}) \end{array} $ | (23) |
这里引入相关系数Coh(k1, ∆y),它表示着展向方向的相关性。
|
Fig. 4 Ratio of 3D and 2D aerodynamic admittance |
|
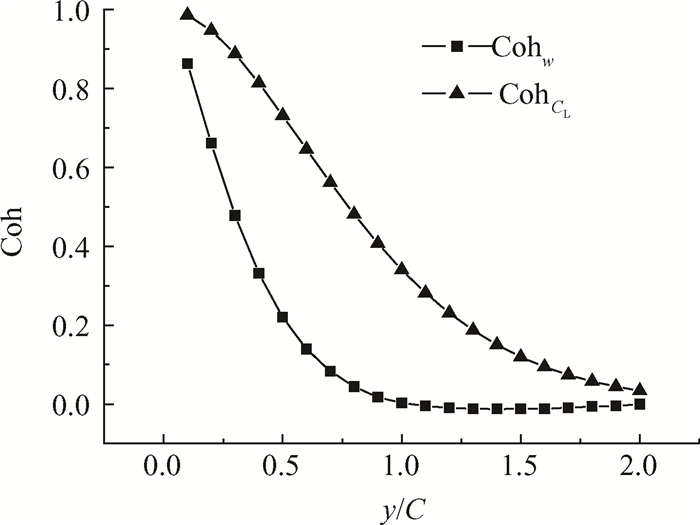
Fig. 5 Correlation coefficient distribution |
当采用薄片假设时,T(k1, k2)=T(k1, 0),有如下关系式
| $\begin{array}{l} {\rm{Co}}{{\rm{h}}_{{C_{\rm{L}}}}}\left( {{k_1}, {\rm{\Delta }}y} \right) = \\ \frac{{\frac{{4{{\rm{ \mathsf{ π} }}^2}}}{{U_\infty ^2}}{{\left| {T\left( {{k_1}, 0} \right)} \right|}^2}\mathop \smallint \nolimits_{ - \infty }^{ + \infty } {\phi _{\rm{w}}}\left( {{k_1}, {k_2}} \right){{\rm{e}}^{{\rm{i}}{k_2}{\rm{\Delta }}y}}{\rm{d}}{k_2}}}{{\frac{{4{{\rm{ \mathsf{ π} }}^2}}}{{U_\infty ^2}}{{\left| {T\left( {{k_1}, 0} \right)} \right|}^2}\mathop \smallint \nolimits_{ - \infty }^{ + \infty } {\phi _{\rm{w}}}\left( {{k_1}, {k_2}} \right){\rm{d}}{k_2}}} = {\rm{Co}}{{\rm{h}}_w}\left( {{k_1}, {\rm{\Delta }}y} \right) \end{array}$ | (24) |
从式(24)可以看出,薄片假设忽略了升力和速度分量w展向方向相关性的差异,这也是薄片假设在大多数情况下不适用的原因。
5 结论本文进行了有限长水翼响应函数公式的推导,研究了薄片理论的适用性和局限性和水翼升力系数和下洗速度的相关系数,得到了以下结论。
(1)当无因次频率较小(小于1时),湍流尺度越大,薄片理论的误差越小;当无因次频率较大时(大于5时),湍流尺度的大小不能影响薄片理论的误差。
(2)随着水翼展长b增大,薄片理论的误差减小,该参数对薄片理论的影响不受其他条件影响。
(3)升力系数的相关性比下洗速度更强,而薄片假设忽略了升力和下洗速度分量w展向方向相关性的差异,这是薄片假设在大多数情况下不适用的原因。
| [1] |
甘文彪, 周洲, 许晓平, 等. 基于改进SST模型的分离流动数值模拟[J]. 推进技术, 2013, 34(5): 595-602. (GAN Wen-biao, ZHOU Zhou, XU Xiao-ping, et al. Investigation on Improving the Capability of Predicting Separation in Modified SST Turbulence Model[J]. Journal of Propulsion Technology, 2013, 34(5): 595-602.)
(  0) 0) |
| [2] |
Sears William R. Some Aspects of Non-Stationary Airfoil Theory and its Practical Application[J]. Journal of the Aeronautical Sciences, 1941, 8: 104-108. DOI:10.2514/8.10655
(  0) 0) |
| [3] |
Liepmann H W. On the Application of Statistical Concepts to the Buffeting Problem[J]. Journal of the Aeronautical Sciences, 1952, 19(12).
(  0) 0) |
| [4] |
Ribner H S. Spectral Theory of Buffeting and Gust Response: Unification and Extension[J]. Journal of the Aeronautical Sciences, 1956, 23(12).
(  0) 0) |
| [5] |
Liepmann H W. Extension of the Statistical Approach to Buffeting and Gust Response of Wings of Finite Span[J]. Journal of the Aeronautical Sciences, 1955, 22(3): 197-200. DOI:10.2514/8.3305
(  0) 0) |
| [6] |
Franklin W D. The Dynamic Response of a Large Airplane to Continuous Random Atmospheric Disturbances[J]. Journal of the Aeronautical Sciences, 2015, 23(10): 917-930.
(  0) 0) |
| [7] |
Etkin B. Dynamics of Atmospheric Flight[J]. Dynamics of Atmospheric Flight, 1972(12): 547-548.
(  0) 0) |
| [8] |
Larose G L, Mann J. Gust Loading on Streamlined Bridge Decks[J]. Journal of Fluids & Structures, 1998, 12(5): 511-536.
(  0) 0) |
| [9] |
Larose G L. The Spatial Distribution of Unsteady Loading Due to Gusts on Bridge Decks[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2003, 91(12-15): 1431-1443.
(  0) 0) |
| [10] |
Graham J M R. Lifting Surface Theory for the Problem of an Arbitrarily Yawed Sinusoidal Gust Incident on a Thin Aerofoil in Incompressible Flow[J]. Aeronautical Quarterly, 2016, 21: 182-198.
(  0) 0) |
| [11] |
Filotas L T. Theory of Airfoil Response in a Gusty Atmosphere, Part Ⅰ: Aerodynamic Transfer Function[R]. UTIAS Report 139, 1969.
(  0) 0) |
| [12] |
Filotas L T. Theory of Airfoil Response in a Gusty Atmosphere, Part Ⅱ: Response to Discrete Gusts or Continuous Turbulence[R]. UTIAS Report 141, 1969.
(  0) 0) |
| [13] |
Jackson R, Graham J M R, Maull D J. The Lift on a Wing in a Turbulent Flow[J]. Aeronautical Quarterly, 2016, 24(1): 62-66.
(  0) 0) |
| [14] |
Hakkinen R J, Richardson A S J. Theoretical and Experimental Investigation of Random Gust Loads Part Ⅰ : Aerodynamic Transfer Function of a Simple Wing Configuration in Incompressible Flow[R]. NACA Tech. Rep, 1957-3878.
(  0) 0) |
| [15] |
Zhong Y, Li M, Wang K. The Lift on a Truss Girder in a Grid Generated Turbulence[C]. USA: International Colloquium on Bluff Body Aerodynamics and Applications, 2016.
(  0) 0) |
| [16] |
Massaro M, Graham J M R. The Effect of Three-dimensionality on the Aerodynamic Admittance of Thin Sections in Free Stream Turbulence[J]. Journal of Fluids & Structures, 2015, 57: 81-90.
(  0) 0) |
| [17] |
Li S, Li M, Liao H. The Lift on an Aerofoil in Grid-Generated Turbulence[J]. Journal of Fluid Mechanics, 2015, 771: 16-35. DOI:10.1017/jfm.2015.162
(  0) 0) |
| [18] |
Dryden H L, Schubauer G B, Mock W C J, et al. Measurements of Intensity and Scale of Wind-Tunnel Turbulence and Their Relation to the Critical Reynolds Number of Spheres[R]. NACA Tech. Rep. 5811937, 1937.
(  0) 0) |
| [19] |
Kármán V Theodore. Progress in the Statistical Theory of Turbulence[J]. Proceedings of the National Academy of Sciences, 1948, 34(11): 530. DOI:10.1073/pnas.34.11.530
(  0) 0) |
| [20] |
Lamson P. Measurements of Lift Fluctuations Due to Turbulence[R]. NACA TN 3880, 1957.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

