固体火箭发动机中推进剂药柱浇注成型后,由于壳体和推进剂材料热膨胀系数的差异,导致材料界面产生的后固化热应力以及固体发动机贮存期间所受重力载荷都会在很大程度上影响推进剂的力学性能和药柱结构完整性[1]。为了研究发动机药柱在长时间尺度、相对低温条件下的粘弹力学特性,分析发动机的结构完整性,考虑将长期受载的固体发动机药柱的粘弹特性等效为高温、短时间尺度的试验环境条件下HTPB推进剂的粘弹特性,因此研究HTPB推进剂非线性粘弹特性的时温等效具有重要意义。
国内外针对粘弹特性和时温等效规律进行了大量的研究,前者的研究热点主要集中在小应变条件下推进剂粘弹特性非线性本构和粘弹参数测定等方面[2~5];后者的研究热点主要集中在时温等效原理在各种非线性粘弹材料力学特性的研究应用。彭网大等[6]采用时间-温度折合变量的数据处理方法,得到了HTPB复合固体推进剂在不同参考温度下应力松弛模量特性变化曲线。胡全星等[7]依照最小二乘法原理,提出了由试验数据拟合出推进剂应力松弛模量主曲线及WLF方程中参数的方法,建立了统一的应力松弛模量主曲线拟合模型。张晓等[8]建立了推进剂单轴拉伸变形下的应变能函数和本构方程,并预测了不同应变率下的应力-应变曲线。王哲君等[9]通过推进剂单轴拉伸实验和扫描电镜实验,分析了低温高应变率条件下温度和应变率对推进剂力学参数的影响。赵培仲等[10]分别从WLF方程和自由体积理论出发,推导出了由于频率变化而引起温度变化的表达式,综合两者得出了关于时温等效的表达式。刘泉声等[11]基于不可逆过程的热力学内变量理论,建立了非线性应力-应变-温度方程,分析了岩石类材料的时温等效原理的一般理论表述,表明了岩石时温等效原理的客观存在。蒋佳荔等[12]运用时温等效原理研究了含水率为0.6%的木材试样的动态粘弹性质,结果表明时温等效与案例描述木材的动态刚度性质是适用的,但时温等效原理无法预测木材的松弛转变行为。然而,在针对HTPB推进剂这种高填充比的非线性粘弹材料,对其非线性粘弹特性的时温等效规律研究鲜有报道。
本文从数学角度推导出了HTPB推进剂非线性蠕变特性的时温等效理论表达式,给出了蠕变柔量主曲线拟合方法;通过不同温度、不同应力条件下的蠕变试验,得出参考温度20℃的蠕变柔量主曲线,验证了HTPB推进剂非线性粘弹特性时温等效的存在性;通过反复加载蠕变试验,分析了载荷变化对蠕变特性时温等效效应的影响。
2 时温等效理论表达式HTPB推进剂属于典型的非线性粘弹复合材料,在应变较大时会呈现明显的应力-应变非线性特征,这是由于HTPB推进剂高填充比和HTPB固化弹性体的自身结构所决定的[13]。因此在研究推进剂粘弹特性时必须考虑非线性因素,本文将使用Schapery单积分非线性本构方程来描述推进剂的非线性粘弹特性问题。
考虑温度随时间变化的Schapery单积分非线性蠕变型本构方程[14]为
| $ {\varepsilon = {h_0}{J_0}\sigma + {h_1}\int\limits_0^t {\rm{\Delta }}J\left( {\gamma - \gamma '} \right)\frac{{{\rm{d}}\left( {{h_2}\sigma } \right)}}{{{\rm{d}}t}}{\rm{d}}t + }\\ {{h_3}\int\limits_0 ^t {\rm{\Delta }}\varphi \left( {\gamma - \gamma '} \right)\frac{{{\rm{d}}\left( {{h_4}\phi } \right)}}{{{\rm{d}}t}}{\rm{d}}t} $ | (1) |
式中ε和σ分别为t时刻的应变和应力值;h0,h1,h2,h3,h4为应力函数,体现了应力-应变的非线性特征;φ(γ)为蠕变热函数;J0和ΔJ(t)是初始蠕变柔量和蠕变柔量转化量;ϕ为温度变化量;γ和γ′为折算时间,其定义式为
| $ {\gamma = \int\limits_0 ^t \frac{{{\rm{d}}t}}{{\rho \left[{\sigma \left( t \right), T} \right]}}}\\ {\gamma ' = \int\limits_0 ^{t'} \frac{{{\rm{d}}t'}}{{\rho \left[{\sigma \left( {t'} \right), T} \right]}}} $ | (2) |
式中ρ[σ(t), T]是与应力和温度相关的热力学函数,t'代表折算时间初始时刻。
考虑定应力蠕变过程时,除了零时刻,σ为常量,其余时间的应力变化率dσ/dt=0;同时当应力σ为常量时,应力函数h0,h1,h2,h3,h4成了常量;恒温状态下,温度变化量ϕ=0,dϕ/dt=0;折算时间初始时刻t'通常取零时刻;考虑到零时刻存在阶跃应力值,因此应力变化率dσ/dt在整个时间段的积分值等于零时刻施加的定应力值;最终得到式(2)的简化式为
| $\left\{ {\begin{array}{*{20}{l}} {\gamma = \int\limits_0 ^t \frac{{{\rm{d}}t}}{{\rho \left[{\sigma \left( t \right), T} \right]}} = \frac{1}{{\rho \left( {\sigma, T} \right)}}\int\limits_0 ^t {\rm{d}}t = \frac{t}{{{\rho _T}}}}\\ {\gamma ' = \int\limits_0 ^{t'} \frac{{{\rm{d}}t'}}{{\rho \left[{\sigma \left( t \right), T} \right]}} = \int\limits_0 ^0 \frac{{{\rm{d}}t'}}{{\rho \left( {\sigma, T} \right)}} = 0}\\ {\int\limits_0 ^t \frac{{{\rm{d}}\sigma }}{{{\rm{d}}t}}{\rm{d}}t = \sigma = {\rm{const}}} \end{array}} \right.$ | (3) |
将式(3)代入式(1),得到了蠕变柔量的表达式为
| $J\left( {t, T} \right) = \frac{\varepsilon }{\sigma } = {h_0}{J_0} + {h_1}{h_2}{\rm{\Delta }}J\left( {\frac{t}{{{\rho _T}}}, T} \right)$ | (4) |
在线性粘弹材料蠕变特性的时温等效研究中,有式(5)成立[15]
| $J\left( {t, {T_{{\rm{ref}}}}} \right) = J\left( {\frac{t}{{{a_T}}}, T} \right) + {b_T}$ | (5) |
式中aT,bT分别为水平移位因子和垂直修正因子;Tref,T分别为参考温度和试验温度。结合式(4)和式(5),可以得出HTPB推进剂的非线性蠕变特性的时温等效表达式为
| $\begin{array}{l} J\left( {t, {T_{{\rm{ref}}}}} \right) = {h_0}{J_0}\left( {{T_{{\rm{ref}}}}} \right) + {h_1}{h_2}{\rm{\Delta }}J\left( {\frac{t}{{{\rho _{{T_{{\rm{ref}}}}}}}}, {T_{{\rm{ref}}}}} \right) = \\ {h_0}\left[{{J_0}\left( T \right) + {b_T}} \right] + {h_1}{h_2}{\rm{\Delta }}J\left( {\frac{t}{{{\rho _{{T_{{\rm{ref}}}}}}{a_T}}}, T} \right) = \\ {h_0}{J_0}\left( T \right) + {h_1}{h_2}{\rm{\Delta }}J\left( {\frac{{{\rho _T}t}}{{{\rho _T}{\rho _{{T_{{\rm{ref}}}}}}{a_T}}}, T} \right) + {h_0}{b_T} = \\ J\left( {\frac{{{\rho _T}}}{{{\rho _{{T_{{\rm{ref}}}}}}{a_T}}}t, T} \right) + {h_0}{b_T} \end{array}$ | (6) |
令
| $J\left( {t, {T_{{\rm{ref}}}}} \right) = J\left( {\frac{t}{{{\alpha _T}}}, T} \right) + {\beta _T}$ | (7) |
从式(7)可以得知,参考温度条件下的定应力恒温蠕变行为可以用其他不同温度条件下的蠕变柔量-时间曲线叠合曲线来描述。
另一方面,
综上可以得知参考温度条件下蠕变柔量主曲线的拟合方法:首先试验获得HTPB推进剂标准哑铃型试件的ε-t曲线;根据ε-t曲线作出J(t, T)-t曲线,并对J(t, T)-t曲线进行垂直方向的βT修正;然后作出不同温度条件下的
下面将考虑不同温度和应力下的HTPB蠕变过程,通过以上蠕变柔量主曲线拟合方法作出不同应力水平的参考温度(20℃)的蠕变柔量主曲线,得到不同应力下的水平移位因子和垂直修正因子,同时分析不同应力下的蠕变柔量主曲线时温等效规律。
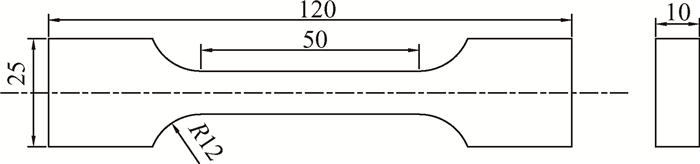
3 试验研究 3.1 试验准备本次试验采用的HTPB推进剂固含量为86%,高分子基体占比11.5%,添加剂占比2.5%;AP颗粒和铝粉含量分别为69%和17%;试验试件根据QJ924-85标准制作,其具体尺寸如图 1所示。
|
Fig. 1 Diagram of specimens sizes(mm) |
试验设备包括CMT6203台式微机控制电子万能试验机和恒温控制箱,如图 2所示,恒温控制箱的温度调节范围为-60~180℃,温度上下波动幅值小于1℃(稳定工作状态)。

|
Fig. 2 Equipment of creep experiment |
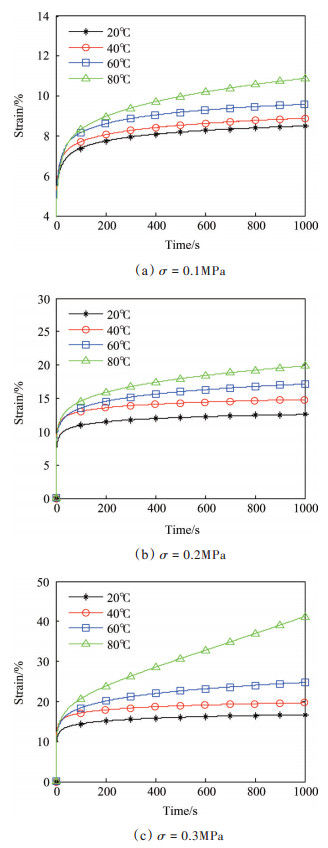
整个试验过程为定应力恒温状态的蠕变过程。定应力通过程序控制实现,加载力上下波动范围小于0.1N,温度波动范围小于1℃;试验过程的初始加载力大小分别为10N,20N,30N,对应的应力大小分别为0.1MPa,0.2MPa,0.3MPa,试验初始加载力的加载速率为50N/min,测试的温度组为20℃,40℃,60℃,80℃,蠕变试验测试结果如图 3所示。
|
Fig. 3 Strain-time curve of HTPB propellant creep experiment |
按蠕变速率波动临界值5%[16],将整个蠕变过程分两个阶段:
(1) 不稳定蠕变阶段(波动范围≤5%):蠕变速率不断降低,直至蠕变速率趋于平缓,达到最小蠕变速率,其持续时间相对整过蠕变过程较短。
(2) 稳定蠕变阶段(波动范围 > 5%):蠕变速率保持最小蠕变速率,蠕变的应变和时间近似呈线性关系,位移量随时间的增加均匀的增大。
对比同一应力、不同温度条件下的应变-时间曲线,随着温度升高,同一时刻的应变增大,体现了蠕变对温度的依赖性;观察试验温度80℃时的蠕变曲线,稳定蠕变阶段的最小蠕变速率相比同一应力条件的其他曲线有明显的增大,说明了此温度条件下的HTPB推进剂蠕变过程存在非线性粘弹特性。
3.3 垂直修正因子、水平移位因子及蠕变主曲线本文采用试验计算方法获取βT,先通过试验测得推进剂的弹性模量,然后通过式(8)计算求得垂直修正因子βT[17]
| ${\beta _T} = \frac{1}{{{E_{{\rm{ref}}}}}} - \frac{1}{E}$ | (8) |
式中Eref,E分别为推进剂试件在参考温度和试验温度条件下的初始弹性模量;初始弹性模量通过单向拉伸试验测得,试验方法参照QJ924-85标准;试验结果如图 4所示,βT值的计算结果如表 1所示。

|
Fig. 4 Uniaxial tensile curve of HTPB propellant at different temperatures |
|
|
Table 1 Revised value of βT under different temperature and stress |
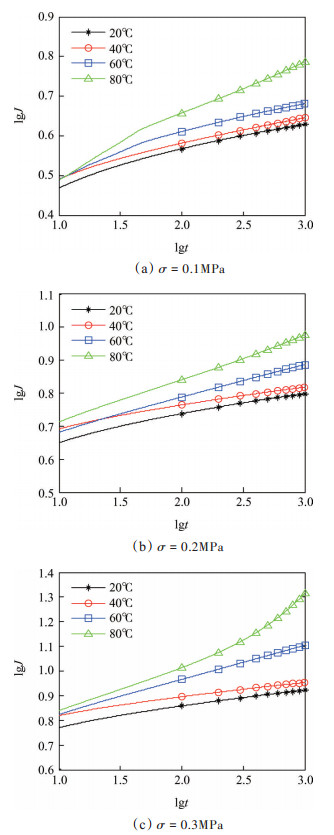
将ε-t曲线结合式(4)描绘出J(t, T)-t曲线并对曲线进行βT垂直修正,然后得到各温度下的lgJ(t, T)-lgt曲线,如图 5所示,其中蠕变柔量J的单位为MPa-1。
|
Fig. 5 Modified curves of creep compliance-time logarithmic |
从图 5可以看出:同一应力条件下,20℃,40℃和60℃的lgJ(t, T)-lgt曲线在稳定蠕变阶段有着良好的一致性;低温、低应力条件下的lgJ(t) -lgt曲线在稳定蠕变阶段有着良好的线性特征,但高温、高应力条件下曲线呈现一定的非线性趋势。
保持参考温度lgJ(t, T)-lgt曲线不动,其他温度条件下的lgJ(t, T)-lgt曲线沿着lgt轴方向水平移位,使得其余温度曲线与参考曲线有尽可能多的点重合和较好的连续性,最终得到不同应力条件下参考温度20℃的蠕变柔量拟合主曲线,如图 6所示,同时得到了水平移位因子lgαT的数值,如表 2所示。

|
Fig. 6 Creep compliance master curve under reference temperature 20℃ |
|
|
Table 2 Shift values lgαT under different conditions of temperature and stress |
从图 6中的各个应力条件下蠕变柔量主曲线可以看出:相邻温度水平条件下的蠕变柔量-时间对数曲线经过修正移位后能较好地重合;σ=0.3MPa条件下主曲线低温等效段有良好的一致性,但在高温等效段,其走向与低温等效段不一致,在时温等效试验时应尽量避开在此条件下的等效;0.1MPa,0.2MPa和0.3MPa应力条件下的蠕变柔量主曲线时间尺度从试验测试的103s分别延伸到了104.27s,104.17s和103.91s。
3.4 反复加载蠕变试验考虑到实际过程中,固体火箭发动机会经历次数相对较多的装配和载荷变化过程,本文又进行了反复加载蠕变试验,来研究时温等效在经历多次应力释放和重新加载后的蠕变过程中是否具有连续性。
试验使用试件和设备参数见3.1节,反复加载蠕变过程的初始加载力为20N,对应应力值为0.2MPa,试验过程保持恒温60℃,蠕变过程中每隔200s会经历一个程序控制的应力释放和快速重新加载过程,释放应力终点值为1kPa,应力加载速度为5MPa/s,加载应力终点值与初始应力相同;最终试验结果如图 7和图 8所示。

|
Fig. 7 Strain-stress curve of repeated creep experiment |

|
Fig. 8 Strain-time curve of repeated creep experiment |
从图 8的应变-时间曲线得出,通过程序控制保证应力释放前后的应力载荷条件不变的情况下,快速的应力释放和重新加载过程并不会影响整体的蠕变进程,即在对存在载荷变动的蠕变过程进行时温等效试验时,整个时温等效过程可以连续进行,不需要考虑载荷变动的影响。
4 结论通过本文研究,得到以下结论:
(1) 基于Schapery单积分非线性本构方程的时温等效数学表达式,从理论上表明了HTPB推进剂的时温等效效应;同应力、不同温度条件的蠕变柔量-时间对数曲线在稳定蠕变段良好的一致性进一步验证HTPB推进剂时温等效效应的存在性。
(2) 查看参考温度20℃条件下的不同应力的蠕变主曲线发现:通过时温等效效应得到的主曲线的时间尺度远远超过了试验测试时间尺度,三种应力条件下的主曲线的时间尺度分别从测试时间103s延伸到104.27s,104.17s,103.91s。
(3) 快速的应力释放和重新加载过程并不会影响整体的蠕变过程,可以将存在载荷变动的长期蠕变过程视为连续的蠕变过程,进行时温等效试验设计。
| [1] |
高凤莲. 某型固体火箭发动机药柱结构完整性研究[D]. 长沙: 国防科学技术大学, 2012.
(  0) 0) |
| [2] |
张建彬. 双基推进剂屈服准则及粘弹塑性本构模型研究[D]. 南京: 南京理工大学, 2013.
(  0) 0) |
| [3] |
常新龙, 赖建伟, 张晓军, 等. HTPB推进剂高应变率粘弹性本构模型研究[J]. 推进技术, 2014, 35(1): 123-127. (CHANG Xin-long, LAI Jian-wei, ZHANG Xiao-jun, et al. High Strain-Rate Viscoelastic Constitutive Model for HTPB Propellant[J]. Journal of Propulsion Technology, 2014, 35(1): 123-127.)
(  0) 0) |
| [4] |
高鸣. 固体推进剂体积松弛模量的数值解法[J]. 兵工学报, 1996, 17(3): 257-259. (  0) 0) |
| [5] |
黄小华, 冯夏庭. 复合固体推进剂拉伸蠕变柔量计算的新方法[J]. 固体力学学报, 2008, 29(1): 23-28. (  0) 0) |
| [6] |
彭网大, 杨风云, 廖庆惠, 等. HTPB复合固体推进剂粘弹特性研究-主松弛模量的时间、温度依赖性[J]. 推进技术, 1984, 5(2): 6-18. (PENG Wang-da, YANG Feng-yun, LIAO Qing-hui, et al. HTPB Composite Solid Propellant Viscoelastic Characteristics Research-Time and Temperature Dependence of Main Relaxation[J]. Journal of Propulsion Technology, 1984, 5(2): 6-18.)
(  0) 0) |
| [7] |
胡全星, 姜豫东. 推进剂松弛模量主曲线及W.L.F.方程参数的拟合处理[J]. 固体火箭技术, 2003, 26(2): 46-48. (  0) 0) |
| [8] |
张晓, 郑坚, 彭威, 等. HTPB复合固体推进剂粘弹性应变能及非线性本构模型[J]. 固体火箭技术, 2015, 38(6): 827-832. (  0) 0) |
| [9] |
王哲君, 强洪夫, 王广, 等. 低温高应变率条件下HTPB推进剂拉伸力学性能研究[J]. 推进技术, 2015, 36(9): 1426-1432. (WANG Zhe-jun, QIANG Hong- fu, WANG Guang, et al. Tensile Mechanical Properties of HTPB Propellant at Low Temperature and High Strain Rate[J]. Journal of Propulsion Technology, 2015, 36(9): 1426-1432.)
(  0) 0) |
| [10] |
赵培仲, 文庆珍, 朱金华. 时温等效方程的研究[J]. 橡胶工业, 2005, 27(3): 142-145. (  0) 0) |
| [11] |
刘泉声, 王崇革. 岩石时-温等效原理的理论与试验研究(Ⅰ):岩石时-温等效原理的热力学基础[J]. 岩石力学与工程学报, 2002, 21(2): 193-198. (  0) 0) |
| [12] |
蒋佳荔, 吕建雄. 杉木动态黏弹行为的时温等效性[J]. 林业科学, 2012, 48(2): 124-128. DOI:10.11707/j.1001-7488.20120218 (  0) 0) |
| [13] |
郝松林. 高填充复合推进剂的初始粘弹性泊松[J]. 固体火箭技术, 1996, 19(4): 46-50. (  0) 0) |
| [14] |
Schapery R A. On the Characterization of Nonlinear Viscoelastic Material[J]. Polymer & Engineering Science, 1969, 9(4): 295-310.
(  0) 0) |
| [15] |
LIU Quan-shen, ZHU Yuan-guang. Research for Time-Temperature Equivalence Effect of Rock (Ⅰ): Theory Research[J]. Rock and Soil Mechanics, 2011, 32(3): 641-646.
(  0) 0) |
| [16] |
Mukherjee A K, Bird J E. Experimental Correlation for High Temperature Creep[J]. Transaction of American Society for Metals, 1969, 62(5): 155-179.
(  0) 0) |
| [17] |
Willianms M L, Landel R F, Ferry J D, et al. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-Forming Liquids[J]. Journal of the American Chemical Society, 1955, 77(14): 3701-3707. DOI:10.1021/ja01619a008
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


