1 引言

航空发动机叶片是航空发动机关键零件之一，航空发动机特别是中小型航空发动机由于叶片的结构尺寸小、转速高，叶片所受的载荷特别复杂，其振动问题特别突出^{[1, 2]}。叶片除了承受稳态载荷产生的稳态应力之外，还承受着气动载荷引起的振动应力。在稳态应力和振动应力共同作用下，叶片容易发生疲劳破坏失效。因此，需要对高速旋转叶片进行振动测量，获取叶片的振动特性，为其是否能安全可靠运行提供依据，也可以为叶片的振动故障排除提供技术支持^[3]。

中小型航空发动机转速达到几万转/min，航空发动机叶片高速旋转，高速旋转叶片的振动测量难度不小。对于传统的叶片振动应力测量方法来说，需要解决应变片的粘贴位置有效性^[4]、粘贴可靠性以及信号有效传输性等问题。由于转子旋转的转速高，对应变片的成活率以及采集信号的信噪比提出了较大挑战。同时，由于测量通道限制以及受实际操作影响，传统的叶片振动应力测量方法一次只能测量某几个叶片的振动情况^{[5, 6]}。叶片振动应力测量，以采用滑环引电器进行信号传输为例，需要解决引电器与转子的同轴安装、引线在转子上的布置、测点位置的确定、应变片的粘贴等问题。

叶尖振幅测量作为一种新的非接触式叶片振动测量方法，基于欠采样的叶尖定时原理，经过复杂的数学运算来获取高速旋转叶片的振动参数^[7~11]。1967年，Hohenberg^[12]开发出了一种可用于叶片振幅监测的叶尖振幅测量系统，但是该系统只能粗略得到叶片的振动幅值，不能获得任何频率信息。20世纪70年代，Zablotskiy等^[13]开发出了一种名为ELURA的叶片振动监测系统。从此，基于不同方法的叶尖振幅测量系统得以提出，但是由于受到传感器尺寸、计算机处理速度和存储数据能力等限制，叶尖振幅测量系统直至近些年才真正应用在旋转机械上^[14]。

叶尖振幅测量能一次测量整圈叶片的振动情况，只需要在机匣上布置几支传感器就能进行测量，前期试验件的改装也比较少。但是它对传感器的布置有较高的要求，相应的数据后处理也更加复杂。同时，叶尖振幅测量还受到其它一些因素的影响，比如叶尖振幅测量用的叶尖探针容易受到油雾污染，从而影响采集信号的信噪比。转速波动也会对叶尖振幅的测量精度产生影响^[15]。叶尖探针安装在机匣上，机匣本身的振动也会影响到采集信号的好坏。航空发动机机匣上的管路以及附件比较多，会影响到叶尖探针的可安装数量及位置，进而影响到测量结果。此外，将叶尖振幅换算成振动应力结果，必须考虑在某阶共振模态下进行叶尖振幅和最大应力点应变的关系换算。而无论是仿真方法还是试验方法进行这种换算关系的确定难度都不小，精度难以把握，甚至这种换算关系的标定过程都无法实现。尽管叶尖振幅测量有它本身的一些缺陷，但是它作为一种新的叶片振动测量技术，正在工程上逐步应用起来，越来越受到了国内外学者和工程技术人员的关注^[16~20]。

本文以离心叶轮叶片为研究对象，分别采用振动应力测量方法与叶尖振幅测量方法对它们进行振动测量并进行相关对比分析。研究高速旋转叶片的振动特性，以振动应力测量结果为参考，验证了叶尖振幅测量在获取高速旋转叶片振动特性的可行性和有效性。

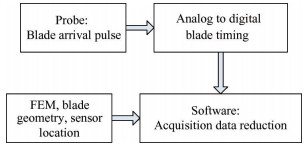
2 叶尖振幅测量方法

基于叶尖定时原理的叶尖振幅测量是一种非接触式的叶片振动测量方法，它的流程图如图 1所示。由叶尖探针观测到的叶尖到达时刻脉冲，经模数转换变成叶尖定时信号。同时软件结合有限元分析、叶片几何尺寸以及传感器位置等信息，对采集的数据进行解算，由此可获得叶片的振动参数。采集数据的解算是由周向傅里叶拟合（Circumferential Fourier Fit，CFF）算法来实现。

2.1 叶尖定时原理

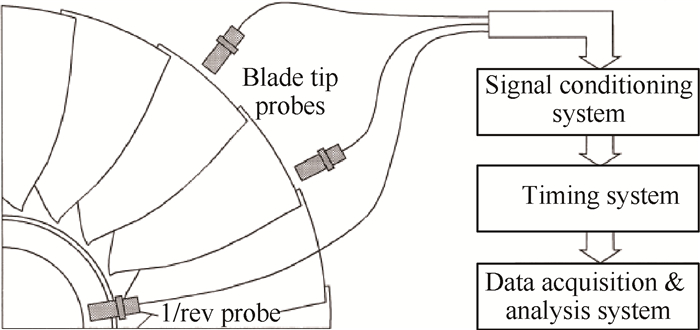
如图 2所示，周向安装在机匣上的叶尖探针（Blade tip probe）和转速探针（1/Rev probe）用于获取叶片经过叶尖探针的时间，即叶尖定时时间序列。采集的时间序列经信号调理系统和计时系统送入数据采集与分析系统，并经进一步分析处理可得到每个叶片的振动幅值、相位和频率^[21]。

假设转子包含$K$个叶片，在机匣上安装有$N$支叶尖探针，叶尖探针1与$n\left( {2 < n \le N} \right)$之间的相对安装角记为$α_n$，将叶尖探针1的安装角$α_1$设为0°。第$k$号叶片的位置记为$θ_k$，由于叶片在轮盘上均匀分布，若将第0号叶片位置定为$θ_0=0$，则第$k$号叶片的位置${\theta _k} = {\theta _0} + 2{\rm{ \mathit{ π} }}k/K$，$k \in \left( {0, 1, \cdots , K - 1} \right)$。

压气机试车时，叶片振动将会使得叶尖经过叶尖探针的时间提前或延后。在转子的第$i$转中，假设第$k$号叶片发生振动，其经过叶尖探针$n$的时间记为$t_{n, i}^k$。当叶片未发生振动时，该叶片经过叶尖探针$n$的理论时间记为$\bar t_{n, i}^{{\rm{}}k}$。当转子的转频${f_r}$为常数时，$\bar t_{n, i}^{{\rm{}}k}$可表示为

$ \bar t_{n, i}^{{\rm{}}k} = \frac{1}{{2{\rm{ \mathit{ π} }}{f_{\rm{r}}}}}\left( {{\alpha _n} + 2{\rm{ \mathit{ π} }}i - {\theta _k}} \right) $

(1)

由于叶片发生振动，在$t_{n, i}^k$时刻叶片有一角变形$X_{n, i}^k$，有

$ t_{n, i}^k = \frac{1}{{2{\rm{ \mathit{ π} }}{f_{\rm{r}}}}}\left( {{\alpha _n} + 2{\rm{ \mathit{ π} }}i - {\theta _k} - X_{n, i}^k} \right) $

(2)

将式（2）代入式（1），有

$ X_{n, i}^k = 2{\rm{ \mathit{ π} }}{f_{\rm{r}}}\left( {\bar t_{n, i}^{{\rm{}}k} - t_{n, i}^k} \right) = 2{\rm{ \mathit{ π} }}{f_{\rm{r}}}{\rm{\Delta }}t_{n, i}^k $

(3)

2.2 周向傅里叶拟合

叶尖定时信号属于欠采样信号，其采样不符合奈奎斯特采样定理。使用周向傅里叶拟合可以从叶尖定时信号中求解出叶片的振动参数。周向傅里叶拟合需要用到3支以上叶尖探针数据。假设叶片共振阶次$O$已知，在各转速下周向傅里叶拟合对叶尖定时信号进行正弦波最小均方拟合，即可获得叶片的振动特性。

在周向傅里叶拟合中，三参数最小均方拟合算法用于计算叶片的振动参数。由式（3）可获得在转子的第$i$转中第$k$号叶片经过叶尖探针$n$时的振动位移序列$X_{n, i}^k$，三参数最小均方拟合算法将$X_{n, i}^k$拟合成一个正弦波，拟合前提是已知正弦波的频率$f_0$^{[23, 24]}。将$X_{n, i}^k$拟合成正弦波$x_{n, i}^k$的表达式为

$ \begin{array}{*{20}{l}} {x_{n, i}^k = A{\rm{sin}}\left( {2{\rm{ \mathit{ π} }}{f_0}t_{n, i}^k + \phi } \right) + {C_0} = }\\ {\;\;\;\;\;\;\;\;{A_0}{\rm{sin}}\left( {2{\rm{ \mathit{ π} }}{f_0}t_{n, i}^k} \right) + {B_0}{\rm{cos}}\left( {2{\rm{ \mathit{ π} }}{f_0}t_{n, i}^k} \right) + {C_0}} \end{array} $

(4)

式中${f_0} = O \cdot f$为叶片振动频率，$O$为叶片共振阶次，${f_{\rm{r}}}$为转子的转频；$A$和$φ$分别为$t_{n, i}^k$时刻叶片的振动幅值和相位，其中${A_0} = A{\rm{cos}}\varphi $，${B_0} = A{\rm{sin}}\varphi $，$C_0$为直流分量。

假设$t_{n, i}^k$序列为$\left\{ {t_{1, i}^k, t_{2, i}^k, \cdots , t_{N, i}^k} \right\}$，对应的$X_{n, i}^k$序列为$\left\{ {X_{1, i}^k, X_{2, i}^k, \cdots , X_{N, i}^k} \right\}$。使用三参数最小均方拟合算法求解系数$A_0$，$B_0$和$C_0$，使得测量值$X_{n, i}^k$与拟合值$x_{n, i}^k$差值的平方和最小，即

$ {\left( {{A_0},{B_0},{C_0}} \right)^{\rm{T}}} = {\rm{argmin}}\left( {\mathop {\sum\limits_{n = 1}^N {{{\left[ {\begin{array}{*{20}{l}} {X_{n,i}^k - {A_0}{\rm{sin}}\left( {2{\rm{\pi }}{f_0}t_{n,i}^k} \right)}\\ { - {B_0}{\rm{cos}}\left( {2{\rm{\pi }}{f_0}t_{n,i}^k} \right) - {C_0}} \end{array}} \right]}^2}} }\limits^{} } \right) $

(5)

为了求解系数$A_0$，$B_0$和$C_0$，将式（4）写成矩阵形式

$ x_{n, i}^k = {\mathit{\boldsymbol{D}}_0}{\mathit{\boldsymbol{s}}_0} $

(6)

其中

$ \mathit{\boldsymbol{x}}_{n, i}^k = {\left( {x_{1, i}^k, x_{2, i}^k, \cdots , x_{N, i}^k} \right)^{\rm{T}}} $

(7)

$ {\mathit{\boldsymbol{D}}_0} = \left[ {\begin{array}{*{20}{c}} {{\rm{sin}}\left( {2{\rm{ \mathit{ π} }}{f_0}t_{1, i}^k} \right)}&{{\rm{cos}}\left( {2{\rm{ \mathit{ π} }}{f_0}t_{1, i}^k} \right)}&1\\ {{\rm{sin}}\left( {2{\rm{ \mathit{ π} }}{f_0}t_{2, i}^k} \right)}&{{\rm{cos}}\left( {2{\rm{ \mathit{ π} }}{f_0}t_{2, i}^k} \right)}&1\\ \vdots&\vdots&\vdots \\ {{\rm{sin}}\left( {2{\rm{ \mathit{ π} }}{f_0}t_{N, i}^k} \right)}&{{\rm{cos}}\left( {2{\rm{ \mathit{ π} }}{f_0}t_{N, i}^k} \right)}&1 \end{array}} \right] $

(8)

$ {\mathit{\boldsymbol{s}}_0} = {\left( {{A_0}, {B_0}, {C_0}} \right)^{\rm{T}}} $

(9)

由此，式（5）中的测量值和拟合值差值的平方和可表示为

$ {\left( {X_{n, i}^k - x_{n, i}^k} \right)^2} = {\left( {X_{n, i}^k - {\mathit{\boldsymbol{D}}_0}{\mathit{\boldsymbol{s}}_0}} \right)^{\rm{T}}}\left( {X_{n, i}^k - {\mathit{\boldsymbol{D}}_0}{\mathit{\boldsymbol{s}}_0}} \right) $

(10)

式（5）和式（9）可化为

$ {\left( {{A_0}, {B_0}, {C_0}} \right)^{\rm{T}}} = {\mathit{\boldsymbol{s}}_0} = {\left( {\mathit{\boldsymbol{D}}_0^{\rm{T}}{\mathit{\boldsymbol{D}}_0}} \right)^{ - 1}}\left( {\mathit{\boldsymbol{D}}_0^{\rm{T}}X_{n, i}^k} \right) $

(11)

由$A_0$和$B_0$可以得到叶片的振动幅值$A$和相位$φ$为

$ A = \sqrt {A_0^2 + B_0^2} $

(12)

$ \varphi = \left\{ {\begin{array}{*{20}{l}} {{\rm{arctan}}\left( {{B_0}/{A_0}} \right){\rm{}}\;\;\;\;\;{A_0} > 0}\\ {{\rm{arctan}}\left( {{B_0}/{A_0}} \right) + {\rm{ \mathit{ π} }}\;\;\;{A_0} < 0} \end{array}} \right. $

(13)

同时，得到拟合残差$r_{n, i}^k$及其均方根${\varepsilon _{{\rm{rms}}}}$为

$ r_{n, i}^k = X_{n, i}^k - {A_0}{\rm{sin}}\left( {2{\rm{ \mathit{ π} }}{f_0}t_{n, i}^k} \right) - {B_0}{\rm{cos}}\left( {2{\rm{ \mathit{ π} }}{f_0}t_{n, i}^k} \right) - {C_0} $

(14)

$ {\varepsilon _{{\rm{rms}}}} = \sqrt {\frac{1}{N}\sum\limits_{n = 1}^N {{{\left( {r_{n,i}^k} \right)}^2}} } $

(15)

事实上，转子转频${f_{\rm{r}}}$由试验测得，实际共振频率$f_0$事先未知，即叶片共振阶次$O$未知。由式（14）可知，叶片振动位移测量值和拟合值的理论拟合残差$r_{n, i}^k$为0，即所求的振动频率$f_0^{\rm{*}}$等于$f_0$，所求的共振阶次$O^*$等于$O$。但实际过程中，拟合残差$r_{n, i}^k$并不等于0，求解系数$A_0$，$B_0$和$C_0$的条件是拟合残差$r_{n, i}^k$的均方根${\varepsilon _{{\rm{rms}}}}$取最小值。由于式（11）中$A_0$，$B_0$和$C_0$的解与矩阵$D_0$直接相关。矩阵$D_0$中唯一的未知量为共振频率$f_0$，并且$f_0$的表达式中共振阶次$O$是一个正整数，且在一定的范围内取值。因此，可依次将该范围内的$O^*$值代入矩阵$D_0$，并计算相应的拟合残差$r_{n, i}^k$的均方根${\varepsilon _{{\rm{rms}}}}$。均方根取最小值${\rm{min}}{\varepsilon _{{\rm{rms}}}}$时对应的共振阶次$O^*$即为实际的共振阶次$O$，由此可进一步确定叶片共振频率$f_0$为

$ {f_0} = O\cdot{f_{\rm{r}}} $

(16)

3 高速旋转叶片振动测量 3.1 离心叶轮

离心叶轮的半截面图如图 3所示。为了解离心叶轮工作中叶片的振动情况和对叶片能否长期安全可靠工作进行评估，需对高速旋转叶片进行振动应力测量和叶尖振幅测量，并对两种测量结果进行对比，相互验证，以获得有效的高速旋转叶片振动测量技术和可靠的振动特性。

3.2 叶片振动应力测量

对离心叶轮叶片进行振动应力测量，基于有限元分析得到的叶身应力分布结果，试验中在叶片上选取2个位置粘贴应变片。由于受篇幅限制，以下只选取叶片1处位置（叶片进气边叶背平行前缘方向）的振动应力数据进行分析。在振动应力测量中，发动机试车上推至最大物理转速，在整个试验过程中，由应变测试系统连续采集应变片信号和转速信号。

3.3 叶片叶尖振幅测量

使用Hood公司的叶尖振幅测量系统进行叶尖振幅测量。该系统由激光叶尖探针、前置放大器、数据采集系统、信号分析软件等组成。在离心叶轮转子转轴上开一键槽，试验中使用磁电式转速探针测量转子转速。在离心叶轮外罩的中间截面和出口截面上各安装4支叶尖探针。中间截面4支叶尖探针和出口截面4支叶尖探针在离心叶轮外罩圆周截面上的安装角度见表 1，假设以离心叶轮外罩的正上方为0°。

Hood公司的叶尖振幅测量系统将每2支叶尖探针采集的叶尖定时信号，进行互相关分析得到一条随转速变化的振动位移曲线（即每个截面上4支传感器可得到6条振动位移曲线）。在整个慢扫描转速区间，从这些振动位移曲线中找出同时存在明显共振峰的转速区间作为周向傅里叶拟合分析的转速区间。同时系统软件会给出前30阶次的拟合度棒状图，系统软件将拟合度棒状条最高且数值接近于1的响应阶次初步认定为共振阶次（理论上共振阶次的拟合度为1）。之后在周向傅里叶拟合中，系统软件会综合一个截面的4支叶尖探针的叶尖定时信号，将它们拟合成一条幅频和相频曲线，并同时给出相应的拟合均方误差曲线。若叶片在之前初步确定的共振阶次确实发生了共振，则幅频曲线在相应的转速区间存在明显共振峰，对应的相频曲线的相位角变化180°，同时对应转速区间的拟合均方误差曲线的幅值接近于0。

4 结果分析

对比叶片振动应力测量和叶尖振幅测量结果，研究这两种方法识别叶片共振的能力，并对离心叶轮高速旋转叶片的振动特性进行研究。

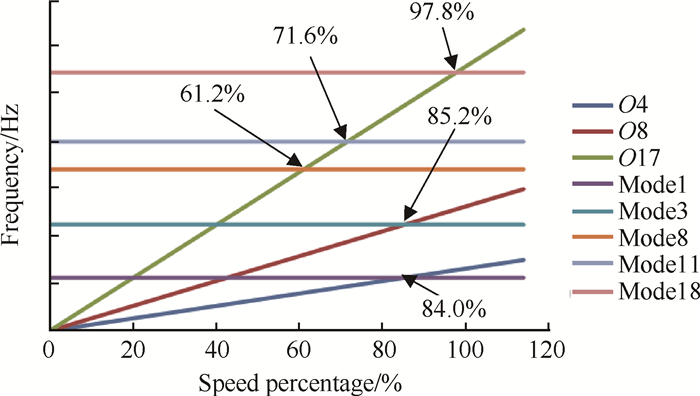
图 4为被测叶片的坎贝尔图。从图中可以看出，离心叶轮高速旋转叶片在整个转速范围内存在5个共振转速区（61.2%，71.6%，84.0%，85.2%，97.8%最大物理转速，图 4中横坐标的转速百分比定义为100%×转速/最大物理转速，下同），分别由转速的17倍频、4倍频及8倍频激励引起。其中17倍频激励引起的叶片共振较为明显，17倍频激励是由离心叶轮出口径向扩压器的叶片数引起。

表 2给出了叶片振动应力测量和叶尖振幅测量两种方法识别的叶片共振参数。由于受条件限制，叶尖振幅测量只给出了叶尖振动位移测量值，并没有给出叶身最大应力点处的振动应变值。叶片在不同共振阶次激励下，叶身最大应力点的位置不同，要将不同阶次下的叶尖振幅转换成叶身最大应力点处的振动应变，需要事先进行叶尖振幅与最大应力点处振动应变的关系标定，标定方法分为仿真方法与试验方法。仿真方法计算结果的准确性难以保证且不好验证，试验方法又受到激振频率过高导致振动台无法实施有效激振的限制。同时叶片振动应力测量中由于受到测量通道和实施难度的限制，不可能在所有可能的共振阶次的最大应力点处都粘贴应变片进行振动应力测量，只能在关注的几个共振阶次及共振模态的最大应力点附近布置有限的几个应变片进行振动应力测量。基于以上两方面的原因，本文将叶片振动应力测量结果与叶尖振幅测量结果进行对比，还只停留在叶片共振转速、发生共振的模态频率以及激励阶次上。而表 2同时给出的应变片粘贴点处的振动应变值及叶尖振幅值只能起到一个参考作用。

表 2表明叶片振动应力测量与叶尖振幅测量均能有效识别出高速旋转叶片的5阶共振模态。两种方法识别的共振转速差异（以振动应力测量为参考，下同）最大为0.56%，识别的共振频率差异（以振动应力测量为参考，下同）最大为1.78%。

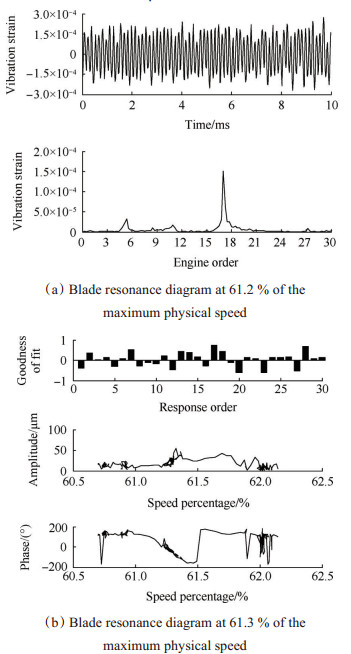
图 5为离心叶轮高速旋转叶片在转速17倍频激励下的8阶共振图。图 5（a）为振动应变测量结果，从图中可以看出叶片的共振转速为61.2%最大物理转速，共振阶次为转速的17倍频，叶片共振时振动应变为1.514×10^-4。图 5（b）为叶尖振幅测量结果，从图中可以发现叶片的共振阶次为17，叶片共振转速为61.3%最大物理转速，叶片共振时振动幅值为54.3μm。由叶片振动应力测量与叶尖振幅测量对比结果，可以发现二者识别的叶片共振阶次一致，识别的共振转速差异为0.16%，共振频率差异为0.39%。

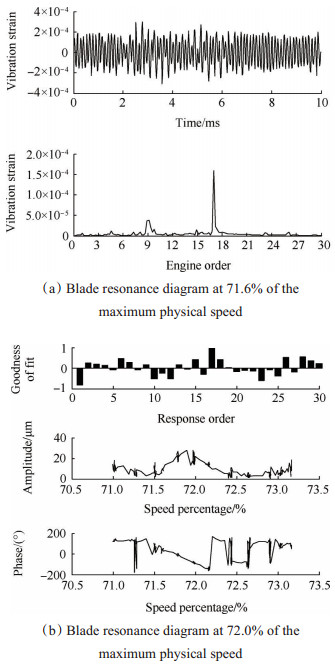
图 6为转速17倍频激励下离心叶轮高速旋转叶片的11阶共振图。由图 6（a）可知叶片的共振转速为71.6%最大物理转速，共振阶次为17阶，叶片共振时振动应变幅值为1.591×10^-4。由图 6（b）可以发现叶片的共振阶次为17，共振转速为72.0%最大物理转速，共振位移幅值为28μm。

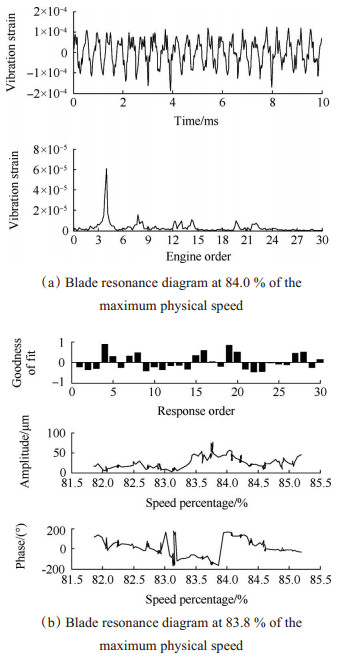
图 7为转速4倍频激励下离心叶轮高速旋转叶片的1阶共振图。图 7（a）中叶片的共振转速为84.0%最大物理转速，共振阶次为4，共振应变幅值为6.1×10^-5。图 7（b）中叶片的共振阶次同样为4，共振转速为83.8%最大物理转速，共振位移幅值为77μm。在共振转速处，相位有突变。

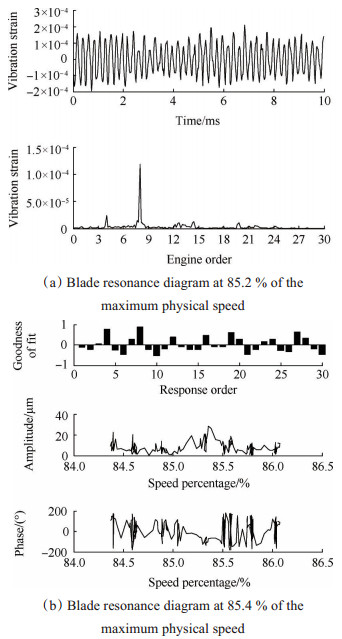
图 8为离心叶轮高速旋转叶片在转速8倍频激励下的3阶共振图。图 8（a）表明叶片的共振转速为85.2%最大物理转速，共振阶次为8，共振应变幅值为1.18×10^-4。图 8（b）同样显示叶片的共振阶次为8，共振位移幅值为28.3μm，共振转速为85.4%最大物理转速。

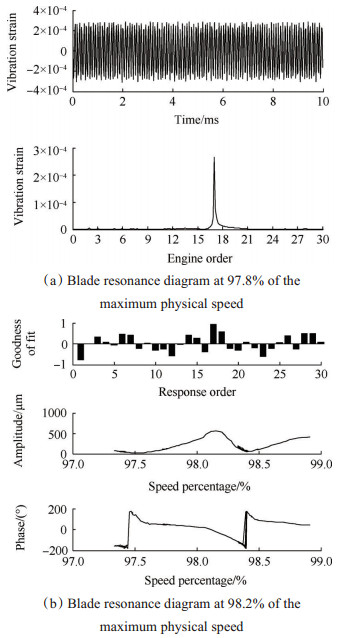
图 9为转速17倍频激励下的离心叶轮高速旋转叶片的18阶共振图。图 9（a）中叶片共振转速为97.8%最大物理转速，共振阶次为17，共振应变幅值为2.661×10^-4。图 9（b）中叶片的共振阶次为17，共振位移幅值为566.5μm，共振转速为98.2%最大物理转速。

需要说明的是，图 5~图 8中的叶尖振幅测量得到的幅频曲线和相频曲线毛刺较多，可能的原因是在这些转速下叶尖探针受到机匣较大振动、油雾污染等因素影响，叶尖定时信号受背景噪声的干扰较严重。同时由于叶尖振幅测量系统中设置的计时器触发脉冲计时的门槛值不能随着背景噪声大小自适应地调整，由此导致试验中部分叶尖定时脉冲丢失。但是总体而言，在高速旋转叶片共振转速处，其幅频曲线和相频曲线还是表现出较明显的共振特征。

5 结论

对离心叶轮高速旋转叶片进行振动测量，对比分析了振动应力测量与叶尖振幅测量两种方法的测量结果，得到的主要结论如下：

（1）离心叶轮叶片在整个转速范围内存在5个共振转速区，振动应力测量与叶尖振幅测量均能识别它们，且识别的使离心叶轮叶片发生共振的激励阶次相同。引起离心叶轮叶片发生共振的激励源有转速的4，8和17倍频，分别激起离心叶轮叶片的1，3，8，11和18阶共振。

（2）振动应力测量识别的离心叶轮叶片共振转速分别为61.2 %，71.6 %，84.0 %，85.2 %，97.8 %最大物理转速。叶尖振幅测量识别的离心叶轮叶片共振转速分别为61.3 %，72.0 %，83.8 %，85.4 %，98.2 %最大物理转速。二者识别的共振转速差异分别为0.16 %，0.56 %，0.24 %，0.23 %，0.41 %，识别的共振频率差异分别为0.39 %，0.56 %，1.78 %，0.07 %，0.40 %。由此说明振动应力测量与叶尖振幅测量均能有效识别高速旋转叶片的振动特性。

（3）叶尖振幅测量采集叶尖定时信号，并将它进行周向傅里叶拟合，可以准确获取叶片的共振阶次（频率）、振动幅值与相位。通过将叶尖振幅测量结果与振动应力测量结果进行对比，验证了叶尖振幅测量在高速旋转叶片振动测量中的有效性和可行性。