2. 先进航空发动机协同创新中心,北京 100191;
3. 航空发动机结构强度北京市重点实验室,北京 100191
2. Collaborative Innovation Center for Advanced Aero-Engine, Beijing 100191, China;
3. Beijing Key Laboratory of Structural Strength of Aero-Engine, Beijing 100191, China
GH4169合金是一种广泛应用于航空发动机核心部件的高温合金材料。激光冲击强化(Laser Shock Peening,LSP)利用强激光束产生的等离子冲击波冲击材料表面,使材料发生塑性变形,形成一定深度的残余应力层,从而有效提高材料的抗疲劳性能。因其效果好且适应性强,在材料表面强化中被广泛使用。美国的激光冲击强化技术的发展以残余压应力强化机制为指导,通过设计激光冲击参数,优化残余应力场来提高金属部件疲劳性能[1]。Chaswal[2]验证了LSP生成的残余应力对抑制IN718疲劳裂纹的萌生和扩展效果显著。Ganesh等[3]对SAE9260弹簧钢的LSP研究结果表明,强化后材料表面硬度提高了20%。Correa等[4]着重研究了脉冲序列前进方向等因素对材料应力分布和疲劳寿命的影响。此外,学者们对不同工艺参数下激光冲击强化的效果进行了研究[5~7],并取得了一定进展,但多为单一参数对残余应力场的影响,未考虑不同参数间的耦合作用。
影响LSP强化效果的工艺参数众多,强化过程不易控制且试验的重复性较差[8],因此通过数值模拟对LSP的关键工艺参数进行优化分析,对工程实际有重要意义。Vasu等[9]针对残余压应力松弛提出了二次LSP的方法(即对已经在服役的部件重新进行激光冲击),并优化了二次LSP的时间参数。王小平等[10]将强化类别分为三种:非相变硬化、相变硬化和熔凝,采用基于BP神经网络的优化方法对LSP处理后的表面强化类型进行了优化,目标参数仅为材料表面的强化类别编码。
LSP工艺有多个强化效果目标,它的工艺优化属于多目标优化问题,多目标优化设计的本质为求解问题的最优解集合(Pareto解集)。遗传算法(GA)是基于自然选择和遗传、变异的生物进化机制的优化算法,运行一次就能找到数个Pareto最优解,可高效求解多目标优化问题[11]。其中具有代表性的算法有:改进快速支配排序算法(NSGA-Ⅱ)[12, 13]、相邻培养式遗传算法(NCGA)和自适应变异遗传算法(AMGA)[14]。
为加快优化算法的寻优速度、降低时间消耗,采用代理模型的方法被广泛采用。Singh等[15, 16]针对LSP处理提出了一套优化算法和代理模型,并建立了板材冲击的参数化模型,但其优化目标仅有压应力单元的总体积,不够全面。Sibalija等[17]采用了基于退火模型的综合模拟优化方法,这种方法数据量小,不适用变量响应比较复杂的情况。黄恩德等[18]采用径向基神经网络模型(Radial Basis Function,RBF)构建目标参数与设计变量之间的近似模型,实现了排气蜗壳的优化设计。
本文基于建立的GH4169镍基高温合金平板数值模型,研究了LSP工艺参数对强化后的残余应力的影响规律。采用拟合精度较高的RBF模型和多种优化算法相结合的方法,完成了以残余应力为主要优化目标的LSP优化设计,得到了适用于GH4169高温合金材料的最佳LSP参数。
2 模型建立 2.1 激光冲击强化材料模型由于激光冲击的峰值压力极大,材料极易屈服发生塑性变形,因此需要选择适合动态冲击载荷下的材料本构模型。
本文采用常用的动态强化模型Johnson-Cook(J-C)模型[19],可有效描述材料在高应变率状态下的应力应变关系。J-C模型的表达式为
| $ {\sigma _{{\rm{eq}}}} = \left( {A + B\varepsilon _{{\rm{eq}}}^n} \right)\left[ {1 + C{\rm{ln}}\left( {\frac{\varepsilon }{{{\varepsilon _0}}}} \right)} \right]\left[ {1 - {T^{{\rm{*}}m}}} \right] $ | (1) |
式中
| $ {T^{\rm{*}}} = \frac{{T - {T_0}}}{{{T_{{\rm{melt}}}} - {T_0}}} $ | (2) |
LSP非热处理过程,暂不考虑温度因素。A,B,C,m和n的值需通过试验确定。GH4169的材料参数和J-C模型参数分别见表 1[20]和表 2[21]。
|
|
Table 1 Material parameters of GH4169 |
|
|
Table 2 J-C model parameters of GH4169 |
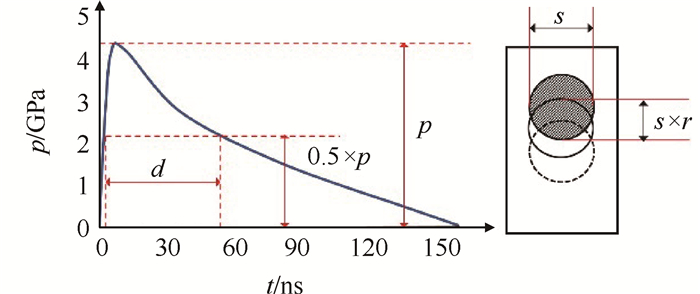
基于GH4169高温合金平板模型,选取脉冲宽度(Pulse width,d)、峰值压力(Peak pressure,p)、光斑尺寸(Spot size,s)和搭接率(Overlap rate,r)四项工艺参数,研究其对模型表面残余压应力(Surface residual stress,
|
Fig. 1 Laser pulse waveform |
LSP为高速动态处理过程,高质量的分网有利于提高计算结果准确性。文献[5]提出将冲击区域内单元特征长度与激光光斑尺寸的比值定义为网格密度并以此作为在不同激光光斑尺寸下有限元尺寸的评价。通过不同尺寸网格结果分析,得出当网格密度小于2.5%时分析结果趋于稳定。对于高应变率动态冲击过程的数值模拟,其计算要耗费较长时间。为节省运算时间,可考虑用GH4169高温合金平板件的二维模型(以下简称二维模型)代替三维模型[22],能有效提高运算效率。
考虑到模型的对称性,可只选1/4模型。单次冲击时二维模型由4mm×10mm的核心区域和厚度为0.2 mm的无限区域组成,网格划分如图 2所示。核心区域为四节点双线性减缩积分平面应变单元(CPE4R),用于得到受载后应力分布,无限区域为二维无限单元(CINPE4)。引入无限单元可以使动态分析中材料内部的应力快速稳定。模型核心区域划分为8个体积相等的区域,进行不同密度的网格划分,其中冲击区域最密,网格尺寸为83μm,其它区域逐渐稀疏。重复冲击时,GH4169高温合金平板模型加长,核心区域尺寸变为4mm×25mm,无限区域不变。

|
Fig. 2 Gridding of 2D plane structure |
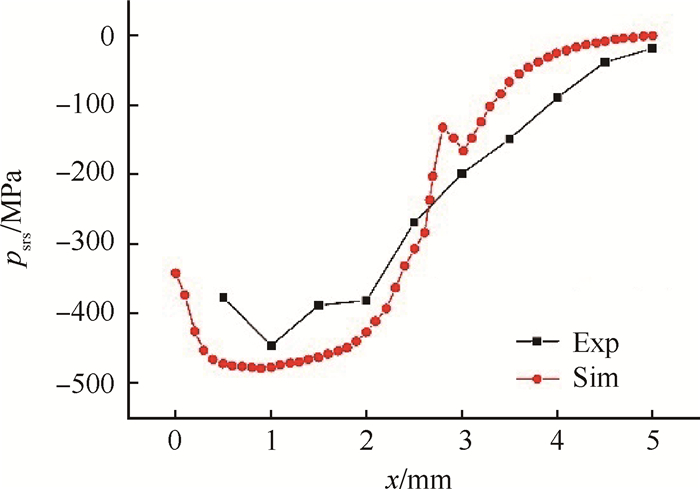
为了验证数值模拟结果的准确性,采取与文献[5]相同的参数设置并用相同的试验条件施加载荷,使用圆形光斑单次冲击,然后利用该文献中的试验结果进行对比。试验的应力结果通过X-350A型X射线应力测定仪进行测定得到。残余压应力沿材料表面方向的试验值及模拟值分布如图 3所示。由图可知,材料表面的最大残余压应力为-479MPa,而试验测得的表面最大残余压应力为-448MPa,二者相差为6.9%,应力的结果比较接近,数值模拟结果和试验结果具有比较好的一致性,说明已经建立的激光冲击强化的数值模拟方法能够在较大程度上模拟真实的情况。
|
Fig. 3 Surface residual stress of experimental value and simulation value |
以二维GH4169平板模型为研究对象,选取5 mm的光斑尺寸重复冲击材料表面,以残余应力作为考察目标。LSP的工艺参数范围如表 3所示[5]。
|
|
Table 3 Range of the LSP processing parameters |
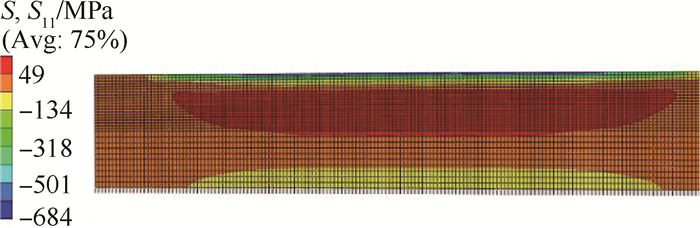
计算后的等效应力和x方向应力云图如图 4、图 5所示。可以看出,无限单元能有效实现材料内部应力的迅速稳定。材料表面最大残余压应力接近800MPa,应力层深度在0.57mm左右,沿深度方向,残余压应力逐渐减小,而后产生残余拉应力,总体呈波动形先增后减。对于重复冲击而言,表面的残余应力是在一定范围内波动的,表面特定区域内的平均残余应力相对最大残余应力更有代表性。

|
Fig. 4 Von Mises of 2D plane structure |
|
Fig. 5 Stress of 2D plane structure in x direction |
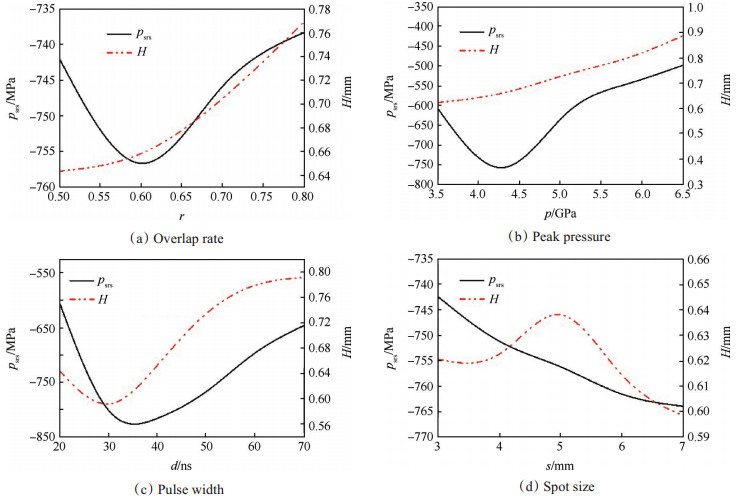
LSP工艺参数对表面残余压应力的影响规律如图 6所示。其他参数一定时,搭接率r直接决定光斑密度。由图 6(a)可知,当搭接率从0.5逐渐增大到0.8时,残余压应力先增后减,但变化范围在25MPa内,比较有限。搭接率对材料表面残余压应力影响不大;而残余压应力层深度变化明显,增加了27.2%,说明r主要影响残余压应力层的深度。
|
Fig. 6 Effects of processing parameters on surface residual stress distribution |
由图 6(b)可知,随着峰值压力p增大,残余压应力层深度呈线性增加趋势。p对残余压应力的影响十分显著,p从4.3 GPa增加到6.5GPa时,峰值压力降低了259MPa;当峰值压力的取值范围在4~4.5GPa时,残余压应力达到最大。这说明,在此区间内存在一个峰值压力值,此时可达到最佳的强化效果。
脉冲宽度d小于10ns时,材料表面未发生塑性变形,冲击波已消失,不具有实际意义。由图 6(c)可知,d从30ns增加到60ns时,残余压应力层深度显著加深。d小于40ns时,随d的增加,残余压应力明显增大,变化范围高达230MPa。当d较大时,残余压应力增加较缓。在工程应用中,可考虑采用相对较小的脉冲宽度以在保证强化效果的同时节约资源。
由图 6(d)可知,随光斑尺寸s增加,残余压应力反而下降,残余压应力层深度则先增后减,说明该范围存在光斑尺寸使残余应力层深度最深,但整体影响比较有限。分析认为,s增加时,光斑作用面积增大但相应的能量密度降低,材料表面单位面积受到的冲击波压力减小,从而产生使材料表层塑性变形量减小的影响,当压力减小的影响大于面积增加的影响时,残余压应力呈减小趋势。
4 冲击参数的多目标优化设计参数间的耦合性使单一参数的最优值往往不等于总体的最优值。因此需在已知规律的基础上,继续进行多参数优化研究。
4.1 设计变量选择的设计参数有搭接率r,光斑尺寸s,峰值压力p和脉冲宽度d,变量之间并不完全独立,其中p,d和s之间满足关系[23]
| $ p = 0.01\sqrt {\frac{\alpha }{{\alpha + 3}}} \sqrt Z \sqrt {{I_0}} $ | (3) |
式中
| $ {p^2}{s^2}d = 5.47E $ | (4) |
本文的优化目标中,
|
|
Table 4 Constraints of optimization design |
代理模型就是通过相对较少量的输入-响应的数据,来构造出一个能尽可能逼近真实物理结构的极限状态的模型。目的在于解决工程中可靠性评估或者优化中计算量过大的问题。
以r,s,p和d作为设计参数,
|
|
Table 5 R2 of responses |
三个优化目标中
三个优化目标分别为
| $ \left\{ {\begin{array}{*{20}{l}} {z = {\rm{min}}\left\{ {{f_1}\left( \mathit{\boldsymbol{x}} \right), {\rm{}}{f_2}\left( \mathit{\boldsymbol{x}} \right), {\rm{}}{f_3}\left( \mathit{\boldsymbol{x}} \right)} \right\}}\\ {{\rm{s}}.{\rm{t}}.{g_i}\left( \mathit{\boldsymbol{x}} \right) \le 0, i = 1, 2, 3, 4} \end{array}} \right. $ | (5) |
式中
设m和n是可行域中任意两个点,当满足如下条件时称m支配n:
(1)
(2)至少存在一个子目标,使m优于n。
除去所有支配点即得到Pareto最优解集合(也称Pareto前沿/非劣解),非劣解往往会形成一条边界线(面或超面)。
NSGA-Ⅱ是直接面向Pareto前沿的方法,首先对父代群体进行遗传操作,得到种群子群体,然后将两种群合并进行非劣排序和拥挤距离排序,形成新的种群,反复进行直到结束。拥挤距离指目标空间上某点与同一支配序上相邻两点之间的距离,拥挤距离的引入可保证Pareto最优解的多样性。
NCGA算法在进行交叉的时候,不是在具有完全不同的遗传因子信息的个体之间进行,而是在具有一定程度类似体的个体之间进行的,这种“相邻繁殖”使接近于Pareto前沿的解交叉繁殖的概率增大,容易在多峰性问题上得到好的结果。
AMGA算法在进化过程之外设立一个存档,用于保存进化过程中的非支配个体和相应的多目标函数值。外部存档的规模E和进化种群的规模P存在E < P的关系,最终的外部存档E即多目标优化的Pareto最优解集。
4.3 参数优化结果分析在优化过程取240个点,其中符合约束条件的点共192个,组成可行域,并获得Pareto最优解集(99个点)。可行域点的分布及Pareto最优解集如图 7所示。三种算法通过自身特定方式对Pareto最优解集进行选择运算,最终得到了各自算法多目标优化问题的最优解。
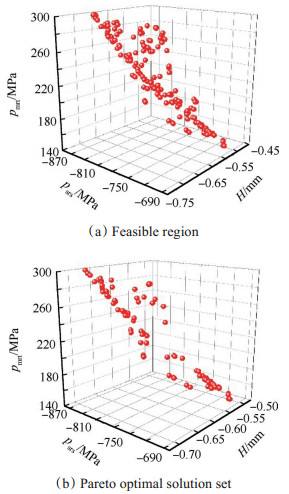
|
Fig. 7 Solutions of parameters optimization |
采用不同优化算法得到的优化结果如表 6所示。为了方便对比,以NSGA-Ⅱ算法所得优化目标值作为基准。采用NCGA算法所得的
|
|
Table 6 Result of multi-objective optimization |
将AMGA算法所得到的优化目标值与优化前的目标值进行对比如表 7所示。优化后的表面平均残余压应力明显提高,幅度达9.78%,且应力分布更加均匀,材料内部的最大残余拉应力降低了6.99%,残余压应力层深度略有降低。
|
|
Table 7 Comparison of optimization results |
通过本文研究,得到如下结论:
(1)峰值压力、搭接率和脉冲宽度增大时残余应力先增后减、光斑尺寸增大时残余应力则单调下降,四个工艺参数均为LSP处理的关键参数。
(2)优化之后,三种算法所得的残余压应力明显提高,残余拉应力明显降低,但残余压应力层深度无明显优化,整体优化效果较好。
(3)NCGA所得优化目标中残余压应力层深度较浅;NSGA-Ⅱ优化效果较均匀。采用AMGA所得的表面平均残余压应力绝对值比NCGA所得高59.4MPa,比NSGA-Ⅱ所得高22.9MPa。
(4)对于LSP的多目标优化,基于RBF代理模型的自适应变异遗传算法(AMGA)具有非常好的适用性,能够稳定快速的收敛到最优值,优化后最大残余拉应力降低了6.99%,表面平均残余压应力提高了9.78%。
| [1] |
李应红. 激光冲击强化理论与技术[M]. 北京: 科学出版社, 2013.
(  0) 0) |
| [2] |
Chaswal V. A Study of Laser Shock Peening on Fatigue Behavior of IN718 Superalloy: Simulations and Experiments[D]. Cincinnati: Cincinnati University, 2013. https://www.researchgate.net/publication/321757692_A_study_of_Laser_Shock_Peening_on_Fatigue_behavior_of_IN718Plus_Superalloy_Simulations_and_Experiments
(  0) 0) |
| [3] |
Ganesh P, Sundar R, Kumar H, et al. Studies on Fatigue Life Enhancement of Pre-Fatigued Spring Steel Specimens Using Laser Shock Peening[J]. Materials & Design, 2014, 54: 734-741.
(  0) 0) |
| [4] |
Correa C, Lara L R D, Díaz M, et al. Effect of Advancing Direction on Fatigue Life of 316L Stainless Steel Specimens Treated by Double-Sided Laser Shock Peening[J]. International Journal of Fatigue, 2015, 79: 1-9. DOI:10.1016/j.ijfatigue.2015.04.018
(  0) 0) |
| [5] |
桑毅. 激光冲击钛合金改善疲劳寿命的模拟与实验研究[D]. 江苏: 江苏大学, 2009.
(  0) 0) |
| [6] |
Warren A W, Guo Y B, Chen S C. Massive Parallel Laser Shock Peening:Simulation, Analysis, and Validation[J]. International Journal of Fatigue, 2008, 30(1): 188-197. DOI:10.1016/j.ijfatigue.2007.01.033
(  0) 0) |
| [7] |
Karbalaian H R, Yousefi-Koma A, Karimpour M, et al. Investigation on the Effect of Overlapping Laser Pulses in Laser Shock Peening with Finite Element Method[J]. Procedia Materials Science, 2015, 11: 454-458. DOI:10.1016/j.mspro.2015.11.045
(  0) 0) |
| [8] |
周建忠, 黄舒, 赵建飞, 等. 激光喷丸强化铝合金疲劳特性的数字化分析[J]. 中国激光, 2008, 35(11): 1735-1740. DOI:10.3321/j.issn:0258-7025.2008.11.013 (  0) 0) |
| [9] |
Vasu A, Gobal K, Grandhi R V. A Computational Methodology for Determining the Optimum Re-Peening Schedule to Increase the Fatigue Life of Laser Peened Aircraft Components[J]. International Journal of Fatigue, 2015, 70: 395-405. DOI:10.1016/j.ijfatigue.2014.07.008
(  0) 0) |
| [10] |
王小平, 王大承. 基于BP神经网络的20CrMo钢激光强化工艺参数优化控制[J]. 红外与激光工程, 2004, 33(3): 269-273. (  0) 0) |
| [11] |
Schaffer J D. Multiple Objective Optimization with Vector Evaluated Genetic Algorithms[C]. Hillsdale, NJ: International Conference on Genetic Algorithms, 1985: 93-100.
(  0) 0) |
| [12] |
Deb K, Pratap A, Agarwal S, et al. A Fast and Elitist Multiobjective Genetic Algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017
(  0) 0) |
| [13] |
丁伟, 刘波, 曹志鹏, 等. 基于多目标遗传算法的多级轴流压气机优化设计[J]. 推进技术, 2006, 27(3): 230-233. (DING Wei, LIU Bo, CAO Zhi-peng, et al. Optimization Design of Multistage Axial-Flow Compressor Using Multiobjective Genetic Algorithm[J]. Journal of Propulsion Technology, 2006, 27(3): 230-233.)
(  0) 0) |
| [14] |
Peng H, Tang S, Liu Q. AMGA2:Improving the Performance of the Archive-Based Micro-Genetic Algorithm for Multi-Objective Optimization[J]. Engineering Optimization, 2011, 43(4): 377-401. DOI:10.1080/0305215X.2010.491549
(  0) 0) |
| [15] |
Singh G, Grandhi R V, Stargel D S. Modified Particle Swarm Optimization for a Multimodal Mixed-Variable Laser Peening Process[J]. Structural & Multidisciplinary Optimization, 2010, 42(5): 769-782.
(  0) 0) |
| [16] |
Singh G, Grandhi R V. Mixed-Variable Optimization Strategy Employing Multifidelity Simulation and Surrogate Models[J]. AIAA Journal, 2010, 48(1): 215-223. DOI:10.2514/1.43469
(  0) 0) |
| [17] |
Sibalija T, Petronic S, Majstorovic V, et al. Modelling and Optimisation of Laser Shock Peening Using an Integrated Simulated Annealing-Based Method[J]. International Journal of Advanced Manufacturing Technology, 2014, 73(5-8): 1141-1158. DOI:10.1007/s00170-014-5917-1
(  0) 0) |
| [18] |
黄恩德, 楚武利. 非轴对称涡轮排气蜗壳优化设计[J]. 推进技术, 2016, 37(10): 1839-1846. (HUANG En-de, CHU Wu-li. Optimization Design of an Asymmetry Turbine Exhaust Hood[J]. Journal of Propulsion Technology, 2016, 37(10): 1839-1846.)
(  0) 0) |
| [19] |
Johnson G R, Cook W H. A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates and High Temperatures[C]. Hague: The 7th International Symposium on Ballistics, 1983.
(  0) 0) |
| [20] |
《中国航空材料手册》委员会. 中国航空材料手册[M]. 北京: 中国标准出版社, 2002.
(  0) 0) |
| [21] |
Arrazola P J, Kortabarria A, Madariaga A, et al. On the Machining Induced Residual Stresses in IN718 Nickel-Based Alloy:Experiments and Predictions with Finite Element Simulation[J]. Simulation Modelling Practice & Theory, 2014, 41(1): 87-103.
(  0) 0) |
| [22] |
吴先前, 黄晨光, 宋宏伟. 激光冲击强化诱导的残余应力影响因素分析[J]. 中国激光, 2010, 37(10): 2632-2637. (  0) 0) |
| [23] |
Fabbro R, Fournier J. Physical Study of Laser Produced Plasma in Confined Geometry[J]. Journal of Applied Physics, 1990, 68(2): 775-784. DOI:10.1063/1.346783
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


