超燃冲压发动机作为高超声速飞行器的核心部件,近年来受到各国的广泛关注。再生冷却作为其热管理的关键,将面临超临界态下的流动换热工况[1, 2]。
针对超临界碳氢燃料流动换热问题,学者集中注意力于其流动换热特性及影响因素[3~13]。Zhou等[3]对超临界压力下再生冷却通道内戊烷的换热特性进行了研究,得到了进口温度、壁温、质量流量、壁面热流密度、系统压力与中心流体温度间的关系。结果表明当流体温度接近拟临界温度时,换热恶化发生。壁面热流密度减小、进口质量流量增加和系统压力增加均使换热恶化的起始点和壁温峰值位置向后移动;Liu等[6]对正癸烷分别在管径为0.95mm和2mm的竖直管内不同进口压力、热流密度和流动方向下对流换热特性进行了实验研究。结果表明在高进口雷诺数下,浮升力和热加速效应均对管内换热没有显著的影响,然而当流动方向竖直向上且进口雷诺数较低时,浮升力严重弱化了换热强度;王彦红等[9]采用数值模拟的方式对超临界航空煤油的换热恶化机理进行了探究,发现在较高热流密度下热物性的剧烈变化使管内径向流场产生异变导致传热恶化的主要原因,而在低主流焓值区传热恶化由热加速作用导致,高主流焓值区主要由径向速度波动造成。
以上研究多基于竖直管或水平管展开,尤其在超临界碳氢燃料方面,鲜有在倾斜管内展开的研究,仅有少数学者对超临界水及二氧化碳在倾斜管内的流动换热进行研究。吴刚等[14]对倾角为22°的倾斜上升管内高温高压水的传热特性进行实验研究,发现由于浮升力引起的自然对流导致管道顶部壁温最高,底部壁温最低,并拟合得到倾斜管内的超临界水对流传热关联式。Taklifi等[15]对倾角为20°的倾斜管内超临界水的传热及压降特性进行实验研究,发现质量流量对二者的影响要大于热流密度,当质量流量与热流密度之比大于2.46kg/(kW·s)时,拟临界点附近出现换热强化现象。
而考虑到在飞行过程中,飞行器经常性地处于各种飞行姿态,其再生冷却系统内的碳氢燃料不可避免的需要面对倾斜流动工况,因此对倾斜管内超临界碳氢燃料的流动换热特性进行研究具有重要的实际意义。本文采用数值模拟的方式对倾斜圆管内超临界RP-3流动换热特性进行了探究,并分析了倾斜角度及质量流量对其影响规律,为超临界换热的应用提供借鉴。
2 数值计算方法本文利用ANASYS FLUENT 15.0对倾斜管内超临界碳氢燃料流动换热问题进行数值模拟研究,模拟过程中采用的几何模型、热物性模型、湍流模型及数值方法如下所示。
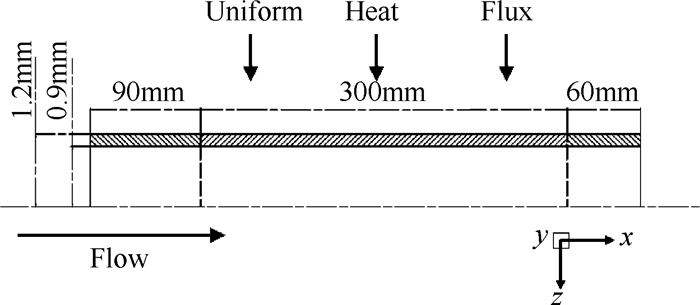
2.1 几何模型与网格划分本文选择细长圆管作为研究物理模型,见图 1。模型总长为450mm,内径为1.8mm,管壁厚为0.2mm。为了消除管道进出口影响,管道进口设置90mm长的流动稳定段,出口设置60mm长的绝热段,模型的倾斜角度分别为30°,45°和60°。
|
Fig. 1 Physics model |
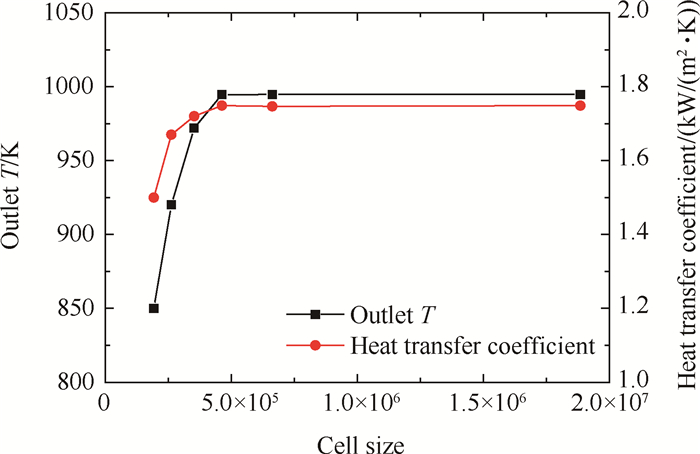
物理模型被划分为固体域和流体域。对流体壁面处网格进行加密,网格高度增长率为1.05,第一层网格高度为0.5μm,保证壁面第一层网格处y+ < 1以满足低雷诺数k-ε模型要求。网格无关解计算选择管道出口温度和对流换热系数作为考察指标,计算结果如图 2所示。当网格数超过462420后,考察指标基本保持不变,满足网格无关解条件。
|
Fig. 2 Grid independent solution |
本文研究超临界RP-3在管内的定常流动,因此无需考虑各控制方程内速度、压力、温度的非稳态项,各控制方程如下
连续方程
| $ \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial {x_i}}} = 0 $ | (1) |
式中
动量方程
| $ \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = \rho {g_i} - \frac{{\partial P}}{{\partial {x_i}}} + \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}} + \frac{\partial }{{\partial {x_j}}}\left( { - \rho \overline {{{u'}_i}{{u'}_j}} } \right) $ | (2) |
其中
| $ {\tau _{ij}} = \mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}} - \frac{2}{3}{\delta _{ij}}\frac{{\partial {u_k}}}{{\partial {x_k}}}} \right) $ | (3) |
式中
能量方程
| $ \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}H} \right) = \frac{\partial }{{\partial {x_i}}}\left( {\lambda \frac{{\partial T}}{{\partial {x_i}}} + \frac{{{\mu _{\rm{t}}}}}{{P{r_{\rm{t}}}}}\frac{{\partial H}}{{\partial {x_i}}}} \right) + {u_i}\frac{{\partial p}}{{\partial {x_i}}} + \dot Q + \phi $ | (4) |
式中湍流热流通量用Boussinesq假设来模化,
湍流模型选择LS低雷诺数
| $ {\mu _{\rm{t}}} = \rho {C_\mu }{f_\mu }\frac{{{k^2}}}{\varepsilon } $ | (5) |
式中
湍动能方程
| $ \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}k} \right) = \frac{\partial }{{\partial {x_i}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _{\rm{k}}}}}} \right)\frac{{\partial k}}{{\partial {x_i}}}} \right] + {P_{\rm{k}}} + {G_{\rm{k}}} - \rho \varepsilon - {S_{\rm{k}}} $ | (6) |
式中
湍流耗散率
| $ \begin{array}{*{20}{l}} {\frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}\varepsilon } \right) = \frac{\partial }{{\partial {x_i}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_i}}}} \right] + }\\ {{C_{\varepsilon 1}}{f_1}\frac{\varepsilon }{k}\left( {{P_{\rm{k}}} + {G_{\rm{k}}}} \right) - {C_{\varepsilon 2}}{f_2}\rho \frac{{{\varepsilon ^2}}}{k} + {S_\varepsilon }} \end{array} $ | (7) |
式中
RP-3作为一种烷烃类混合物,组成成分非常复杂,包括上百种烷烃、烯烃以及芳香烃等,通过完全模拟每种组分的物性从而获得RP-3混合物物性显然是不可行的。而单纯依靠实验直接对RP-3物性进行测量,工作量巨大且远远无法满足数值计算的物性数据库需求,由此提出了燃料的替代模型概念,即采用少数典型碳氢燃料组分组成混合物代替真实燃料进行实验研究。在前人研究基础上可知,由郑东等[17]提出的40%正癸烷,42%正十二烷,13%乙基环己烷,5%对二甲苯四组分替代模型在预测RP-3物性上表现最优。通过利用广义对应态法则获得该替代模型各温度下的热力学特性及输运特性,通过与北京航空航天大学超临界压力碳氢燃料多功能流动与换热实验台测得的RP-3热物性的对比,确定了该四组分替代模型的准确性[18]。故本文选择该替代模型并由此计算获得模拟所需物性库。
2.4 数值方法模型进出口边界条件分别设置为质量流量进口和压力出口,其余均设置为壁面,加热段外壁面给定恒定热流,进出口稳定段给定热流为0,相当于绝热壁,流固交界面设置为耦合壁面,以保证流体与管壁间的正常传热。控制方程的离散及求解方法选择基于压力的求解器,SIMPLE算法选作压力速度耦合方法,动量方程和能量方程的求解采用二阶迎风格式以保证精度,湍流方程的求解采用一阶迎风格式以保证稳定性,所有控制方程收敛条件为残差小于10-6。
3 计算结果与分析 3.1 计算方法验证为保证本文数值模拟方法的可行性,将数值模拟结果与实验数据进行对比。实验数据选自关于超临界RP-3流动换热实验研究的文献[19],实验工况选择系统压力5MPa,进口温度为373K,质量流量为3g/s,壁面热流密度分别为300kW/m2和400kW/m2,对比结果见图 3。可见在大部区域计算结果与实验结果基本吻合,但在x/d=20~60处,由于此时壁面附近流体接近拟临界区,物性变化剧烈,物性替代模型与湍流模型准确性下降,误差偏大。

|
Fig. 3 Comparison between calculation and experiment |
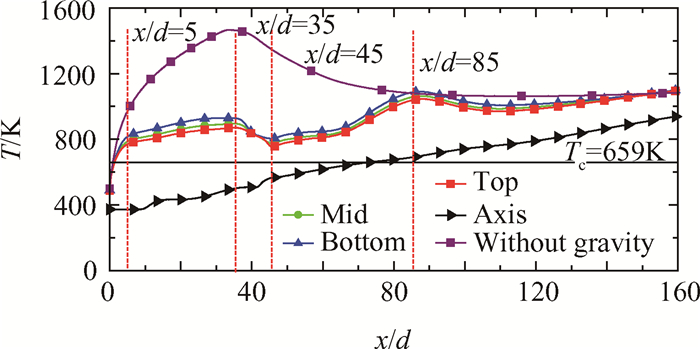
为了研究倾斜管内超临界RP-3的典型对流换热特性,选择倾角为45°,质量流量为0.3g/s,热流密度为300kW/m2,系统压力为3MPa,进口温度为373K作为基准工况,同时选择相同参数下无浮升力工况作为对照。图 4为管道沿程壁温及中心轴线温度分布,可见在考虑浮升力情况下,管壁温度最高达1050K,超过裂解反应发生温度。但由于本文重点研究物性的剧烈变化及浮升力对流动换热的影响,当管内流体处于拟临界点附近(500~800K)时,二者作用明显并导致换热规律发生变化,虽然峰值点壁面附近裂解效应显著,但该处远离拟临界点,物性变化平缓且浮升力作用效果较弱,不会对本文研究内容造成影响,故不予考虑。由图 4可知,考虑浮升力时,管壁温度将经历两次峰值,并随后出现幅度不等的回落;同一截面内,管壁温度呈现顶点最高,由上至下递减,底点最低的规律。无浮升力时,管壁温度仅出现一次峰值且截面内无温差。
|
Fig. 4 Distribution of wall temperature along the pipe |
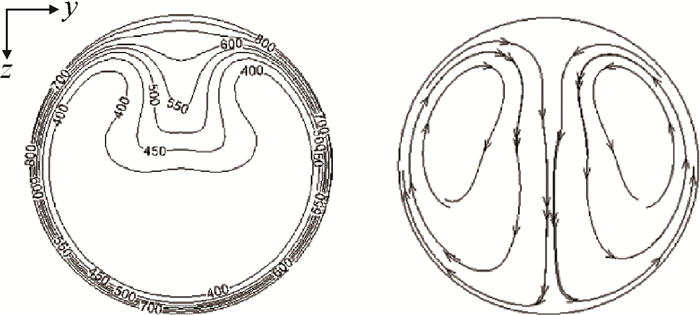
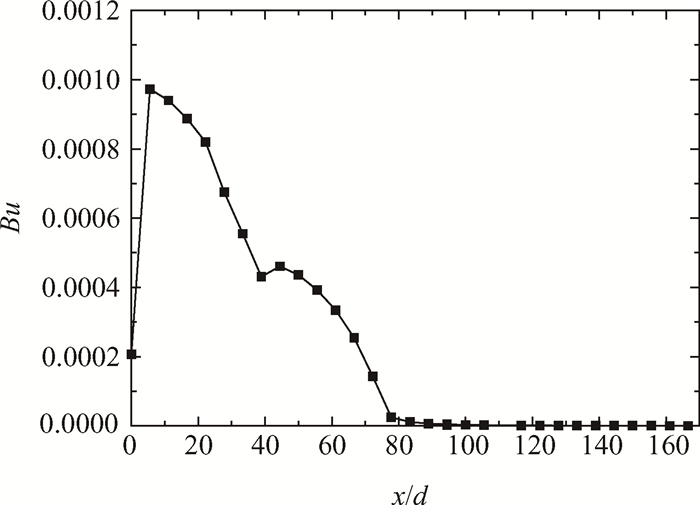
对于无浮升力情况目前已有大量研究,其峰值是由于管内流体跨临界时物性剧烈变化所致,由此可以判断45°倾斜管内两次峰值的特殊换热规律主要与浮升力作用有关。分析考虑浮升力的情况,由于起始段近壁面流体被迅速加热,x/d < 5时管壁温度急剧上升,而x/d > 5后,上升减缓。图 5给出了x/d=10截面内的流体温度与二次流分布,可以看出,近壁面处流体温度迅速上升进入超临界态,其密度约为100kg/m3,而内部流体仍处于亚临界态,其密度约为700kg/m3,内外流体间面临极大密度差。图 6为表征浮升力作用强弱的无量纲数Bu在管道沿程的分布情况,可以看出其在x/d=10时较大。因此,在浮升力的作用下,管道壁面附近的低密度流体由管道底点沿管壁运动至管道顶点,而管道内部流体运动至管道底点,在截面内形成一对关于x轴对称的涡。该截面涡具有两个作用效果,一是壁面附近的高温流体通过二次流被带至管道顶点,导致截面内顶点温度最高;二是管道中心低温流体被带向壁面,加强了管壁与内部流体间的对流换热,直接导致壁面温度上升趋势减缓。因此,由浮升力导致的截面二次流,对超临界RP-3管内的对流换热起到了强化作用。
|
Fig. 5 Distribution of fluid temperature and the secondary flow in x/d=10 |
|
Fig. 6 Distribution of Bu number along the pipe |
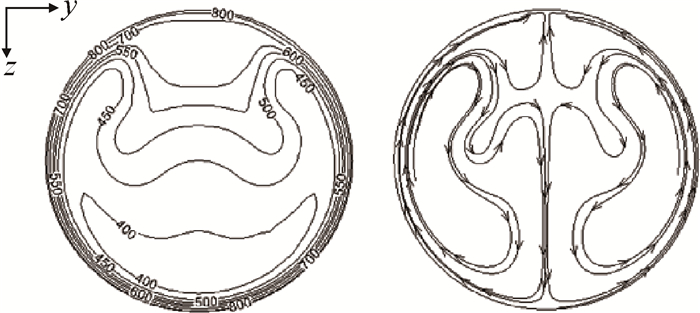
管壁温度在约x/d=35处达到第一次峰值,随后开始回落。由图 6可知,此时管道截面内浮升力作用效果虽然开始下降,但仍处于较高水平,由此引起的截面二次流大幅提高了管内对流换热水平。此外,二次流运动形式也发生了变化,图 7截取x/d=35处截面流体温度与二次流分布,相比x/d=10,截面上部高温流体由中心线向两边低温区运动后,受到较强浮升力的作用,形成第二组关于x轴对称的涡,管道中心冷流体由此分别运动至上下壁面,管壁温度下降。
|
Fig. 7 Distribution of fluid temperature and the secondary flow in x/d=35 |
当x/d > 45后,壁温再次上升。由于在前述过程中二次流强化管内对流,管道横截面内流体温度迅速均匀化,内外密度差减小,由图 6可见管内浮升力的作用强度继续下降,对对流换热的促进作用削弱。管道各截面湍动能分布如图 8,管内流体湍动能虽然开始增加,但仍处于较低水平。这是由于在截面内流体温度较为均匀,同时中心流体开始进入拟临界区,密度减小,热加速效应显现,二者共同作用导致管道壁面附近流体与内部流体间流向速度差较小,管内湍流强度处于较低水平,壁面热流难以传导至内部流体,壁面温度进入上升阶段。

|
Fig. 8 Distribution of turbulent kinetic energy along the pipe |
在x/d=85处,管道壁温达到第二次峰值,并随后开始下降。此时由图 6可知浮升力作用效果已基本消失;而随着管道中心流体温度超过拟临界温度,管内流体平均密度相较入口大幅减小,在热加速效应下,管内湍流开始发展,由图 8可见在x/d > 85后,湍动能急剧上升,其对于管壁与管内流体间的换热均起到促进作用,管壁温度下降。
伴随着壁温的下降,管内流体温度仍然持续上升,保持在拟临界温度之上,流体密度不再随温度剧烈变化,截面内密度差较小,由图 6可知浮升力对管内流动换热已经没有影响,倾斜管道的影响逐渐消失,管道的顶点、中点与底点温度基本相同,流动换热进入稳定状态。
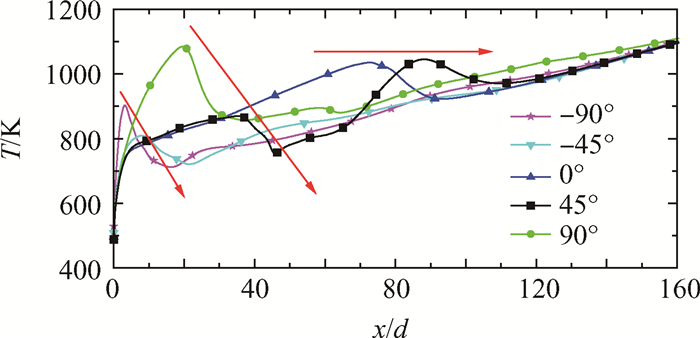
3.3 倾斜角度对超临界RP-3流动换热的影响图 9表示质量流量为0.3g/s,热流密度为300kW/m2,系统压力为3MPa时,不同倾角管道沿程顶点处壁温分布,水平与竖直管作为倾斜的极限情况予以考虑。由图可见,不同倾斜角度下管内流动换热表现出不同规律特性。
|
Fig. 9 Distribution of wall temperature along the pipe at different angles |
当倾角为90°时,进口处管壁温度飞升,出现典型换热恶化现象,这是由于近壁面处物性剧烈变化所致,对此已有大量研究,此时浮升力作用沿流向,仅对壁温峰值造成影响;当倾角减小为45°时,垂直流向的浮升力作用效果显现,由于二次流对换热的强化作用,进口处换热恶化消失,壁温平缓上升并随后经历两次峰值;当倾角减小为0°时,垂直流向的浮升力达到最大,壁温持续平缓上升,第一次峰值点大幅后移,同时由于管内流体始终保持较高温度均匀性,第二次峰值消失;当倾角继续减小时,流动方向转为向下,此时不论垂直流向或沿流向的浮升力作用均为强化对流换热,故可以看到-90°工况只在进口处出现远低于+90°工况的壁温峰值,-45°工况壁温峰值同样远低于+45°工况且位置前移,同时相比于-90°工况,由于垂直流向浮升力引起的二次流作用,其壁温峰值明显降低。而此后,二者温度均保持平缓上升,不再有壁温峰值出现。
对比上述各工况可以发现,由于垂直流向的浮升力影响,倾角越接近0°时,管道进口段二次流的作用越强,使得管壁温度能够保持平缓上升;而由于沿流向的浮升力影响,倾角为负时,壁温峰值将降低,且仅在入口段出现一次。
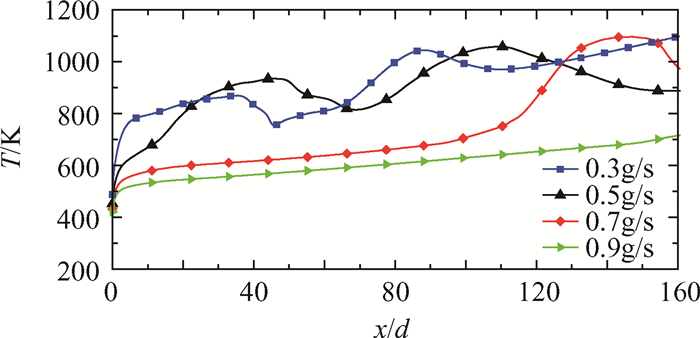
3.4 质量流量对超临界RP-3流动换热的影响质量流量对倾斜管内RP-3的对流换热有很大影响,图 10为管道倾斜角为45°,热流密度为300kW/m2,系统压力为3MPa时,不同质量流量下管道沿程壁温分布。由图可知,在较小质量流量下,由于上文所述二次流与湍流的共同作用,管壁温度会先后出现两次峰值;随着质量流量增大,管内湍流发展逐渐旺盛,管道进口段流体温度的均匀性得到改善,二次流的发生减弱,第一次峰值后移。
|
Fig. 10 Distribution of wall temperature along the pipe at different mass flux |
当质量流量达到0.7g/s时,二次流在入口段的作用已经几乎可以忽略,第一次峰值消失;第二次峰值出现的主要原因是壁面附近流体吸热后在热加速作用下轴向速度增大,截面内速度型转为平直,湍流减弱,管壁与内部流体间换热水平下降;而其后内部流体温度逐渐升高并越过拟临界温度,在热加速的作用下速度增大,截面内湍流再次发展,壁温开始下降。
随着质量流量增大,管壁热流密度保持不变,单位质量流体吸热减小,热加速作用被削弱,湍流的弱化再强化过程被延长,因此第二次峰值也随着质量流量的增大而向后移动。当质量流量达到0.9g/s时,壁温已近似线性上升。
4 结论(1)当质量流量为0.3g/s时,加热段进口近壁面处流体温度迅速升高,由于浮升力的作用,高温低密度流体向管道上壁面运动,产生截面内二次流,强化了内外流体间的对流换热,管壁温出现第一次回落;管内流体平均温度升高后,物性不均匀性得到改善,二次流作用效果减弱,湍流强度成为影响管壁温度的主要因素,热加速作用导致的湍流强化使管壁温出现第二次回落。
(2)不同倾角管内超临界RP-3的流动换热规律不同。倾角接近0°时,垂直流向的浮升力作用明显,管壁温度上升平缓;倾角为负时,沿流向的浮升力作用明显,壁温峰值降低,且仅存在于入口段。
(3)质量流量对倾斜管内超临界RP-3的流动换热影响明显。当质量流量为0.3g/s时,管内湍流较弱,由浮升力引起的二次流作用明显,管道壁温有两次峰值出现;而当质量流量为0.7g/s时,管内湍流旺盛,管道截面内流体均匀性得到改善,二次流难以发展,仅由于热加速的影响,出现一次壁温峰值。
(4)由浮升力引起的二次流和管内湍流发展是倾斜管内超临界碳氢燃料对流换热特性的两大决定因素,管道倾角及质量流量均会对该二者作用效果造成影响,关于系统压力、热流密度及管道截面形状等其他因素对其的影响规律,是后续探究的方向。
| [1] |
王增强. 航空发动机先进制造技术——高性能航空发动机制造技术及其发展趋势[J]. 航空制造技术, 2007, 520(1): 50-55. (  0) 0) |
| [2] |
汪小卫, 金平, 孙冰. 全流量补燃循环发动机推力室再生冷却技术研究[J]. 航空动力学报, 2008, 23(5): 909-915. (  0) 0) |
| [3] |
Zhou Weixing, Bao Wen, Qin Jiang, et al. Deterioration in Heat Transfer of Endothermal Hydrocarbon Fuel[J]. Journal of Thermal Science, 2011, 20(2): 173-180. DOI:10.1007/s11630-011-0454-9
(  0) 0) |
| [4] |
Koshizuka S, Takano N, Oka Y. Numerical Analysis of Deterioration Phenomena in Heat Transfer to Supercritical Water[J]. International Journal of Heat & Mass Transfer, 1995, 38(16): 3077-3084.
(  0) 0) |
| [5] |
CHEN Yu, WANG Yu, BAO Ze-wei, et al. Numerical Investigation of Flow Distribution and Heat Transfer of Hydrocarbon Fuel in Regenerative Cooling Panel[J]. Applied Thermal Engineering, 2016, 98(4): 628-635.
(  0) 0) |
| [6] |
Liu B, Zhu Y, Yan J J, et al. Experimental Investigation of Convection Heat Transfer of n-Decane at Supercritical Pressures in Small Vertical Tubes[J]. International Journal of Heat & Mass Transfer, 2015, 91(12): 734-746.
(  0) 0) |
| [7] |
Kim D K, Kim M H. Experimental Study of the Effects of Flow Acceleration and Buoyancy on Heat Transfer in a Supercritical Fluid Flow in a Circular Tube[J]. Nuclear Engineering and Design, 2010, 240(10): 3336-3349. DOI:10.1016/j.nucengdes.2010.07.002
(  0) 0) |
| [8] |
Shiralkar B S, Griffith P. Deterioration in Heat Transfer to Fluids at Supercritical Pressure and High Heat Fluxes[J]. Journal of Heat Transfer, 1968, 91(1): 67.
(  0) 0) |
| [9] |
王彦红, 李素芬, 东明. 垂直上升圆管内超临界航空煤油的传热恶化数值研究[J]. 推进技术, 2015, 36(1): 97-103. (WANG Yan-hong, LI Su-fen, Dong Ming. Numerical Study on Heat Transfer Deterioration of Supercritical Aviation Kerosene in Vertical Upward Circular Tubes[J]. Journal of Propulsion Technology, 2015, 36(1): 97-103.)
(  0) 0) |
| [10] |
何龙, 潘富敏, 林瑞森. 吸热型碳氢燃料催化裂解的研究述评[J]. 推进技术, 2001, 22(2): 97-100. (HE Long, PAN Fu-min, LIN Rui-sen. Review of Catalytic Cracking of Endothermic Hydrocarbon Fuel[J]. Journal of Propulsion Technology, 2001, 22(2): 97-100.)
(  0) 0) |
| [11] |
张强强, 汪旭清, 刘国柱, 等. 主动冷却通道内吸热型碳氢燃料热裂解结焦抑制机理[J]. 推进技术, 2013, 34(12): 1713-1718. (ZHANG Qiang-qiang, WANG Xu-qing, LIU Guo-zhu, et al. Inhibition Mechanism of Pyrolytic Cokes from Endothermic Hydrocarbon Fuels in Regenerative Cooling Channels[J]. Journal of Propulsion Technology, 2013, 34(12): 1713-1718.)
(  0) 0) |
| [12] |
张斌, 张春本, 邓宏武, 等. 超临界压力下碳氢燃料在竖直圆管内换热特性[J]. 航空动力学报, 2012, 27(3): 595-603. (  0) 0) |
| [13] |
严俊杰, 刘耘州, 闫帅, 等. 超临界压力下碳氢燃料在竖直圆管内对流换热实验研究[J]. 工程热物理学报, 2016, 37(11): 2385-2392. (  0) 0) |
| [14] |
吴刚, 毕勤成, 王汉, 等. 超临界压力水在倾斜上升管内传热的试验研究[J]. 西安交通大学学报, 2011, 45(5): 6-11. (  0) 0) |
| [15] |
Taklifi A, Hanafizadeh P, Behabadi M A A, et al. Experimental Investigation on Heat Transfer and Pressure Drop of Supercritical Water Flows in an Inclined Rifled Tube[J]. Journal of Supercritical Fluids, 2016, 107(1): 209-218.
(  0) 0) |
| [16] |
Tao Z, Cheng Z, Zhu J, et al. Effect of Turbulence Models on Predicting Convective Heat Transfer to Hydrocarbon Fuel at Supercritical Pressure[J]. Chinese Journal of Aeronautics, 2016, 29(5): 1247-1261. DOI:10.1016/j.cja.2016.08.007
(  0) 0) |
| [17] |
郑东, 于维铭, 钟北京. RP-3航空煤油替代燃料及其化学反应动力学模型[J]. 物理化学学报, 2015, 31(4): 636-642. DOI:10.3866/PKU.WHXB201501231 (  0) 0) |
| [18] |
程泽源, 朱剑琴, 金钊. 吸热型碳氢燃料RP-3替代模型研究[J]. 航空动力学报, 2016, 31(2): 391-398. (  0) 0) |
| [19] |
张春本. 超临界压力下碳氢燃料的流动与换热特性研究[D]. 北京: 北京航空航天大学, 2011.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


