2. 南京航空航天大学 无人机研究院,江苏 南京 210016
2. Research Institute of Unmanned Aircraft, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
在飞机飞行过程中,尤其是在起飞、着陆阶段,空气或者云层中的过冷水滴撞击到飞机与发动机迎风表面,会失去稳定而冻结在飞机表面。飞机部件结冰后,会减小飞机升力,增大阻力,降低发动机推力,严重时还可能导致机毁人亡[1~3]。飞机结冰主要分为霜冰、明冰、混合冰[4, 5],研究发现,明冰积冰时会形成典型的角状冰,对飞机和发动机的性能影响很大。研究飞机结冰对防、除冰以及保证飞行安全都具有重要的意义[6]。
飞机结冰研究一般通过工程估算、实验研究和数值模拟等方法。由于数值模拟代价低、周期短,近数十年来发展迅速,开发了一系列结冰软件。20世纪80、90年代开发的第一代结冰软件基于二维Messinger积冰模型[7],该模型仅求解积冰控制体的质量、能量守恒方程,而不考虑水膜的流动,认为控制体中未凝结的水全部进入下一个控制体,对水膜的处理过于简单。第一代结冰软件主要有美国NASA的LEWICE[8],英国的TRAJICE[9],法国的ONERA[10]等。这些软件主要研究二维翼型的结冰状况,但是飞机典型迎风面,如机翼根部,机翼自由端,发动机进口等部件的结冰具有明显的三维特征。第一代结冰软件对霜冰的模拟结果比较好,对明冰的模拟结果与试验有较大的误差,是因为来流温度较高时,迎风部件表面结明冰,其表面覆盖一层薄水膜,水膜的流动与传热对积冰相变有很大的影响。
20世纪90年代末,开始出现考虑表面水膜流动与传热的第二代结冰软件,最具代表性的是加拿大的FENSAP-ICE软件[11, 12],该软件建立了剪切力驱动水膜流动的结冰模型,但是水膜流动速度仅是剪切力的线性关系式,对水膜流动的模拟比较简单。易贤等[13]基于Messinger的二维积冰模型,提出了一种考虑液态水溢流效应的三维积冰计算模型,并针对该模型建立了表面单元内溢流水流动的分配方案。常士楠等[14]通过Fluent软件用户自定义函数功能编程求解三维机翼结冰过程,计算中将溢流方向沿机翼弦向和展向分解,以此改进Messinger结冰模型。申晓斌等[15]在Messinger结冰热力学模型的基础上,发展了一套三维的表面溢流水流动模型,用空气对表面的剪切力来确定溢流水的流动方向及流量分配,并对发动机进气道短舱前缘三维结冰进行了模拟。曹广州等[16~18]发展了国内首个三维积冰数学模型和计算方法,通过量纲分析的方法简化N-S方程,得到水膜流动和冰层生长的控制方程。水膜流动基于连续方程和动量方程,在空气剪切力的驱动下在冰层表面流动,水膜流动和积冰相变相耦合,克服了对水膜流动处理过于简单的缺点。
曹广州的三维积冰模型中假设水膜表面水分不蒸发,然而在真实自然条件下,由于水膜表面和外界空气中的水蒸气通常存在压差,水膜表面的部分水会产生蒸发,水蒸发会吸收潜热而带走一部分热量,从质量和能量传递两个方面影响结冰相变过程。
除了积冰模型外,积冰数值计算还包括:外部空气-水滴两相流计算、水滴撞击特性计算。近年来,随着计算流体力学的快速发展,很多研究者采用CFD的方法来获得两相流场和水收集系数[19~21]。
本文在曹广州三维积冰模型的基础上,建立考虑表面薄水膜蒸发的明冰积冰数学模型,发展考虑水膜蒸发的明冰积冰计算方法,据此开发明冰积冰计算程序,并选取NASA提供的结冰条件下的典型算例进行积冰模拟,并将计算结果与同条件下的NASA试验数据以及曹广州不考虑水膜蒸发的计算结果进行对比分析。
2 积冰模型和计算方法 2.1 基本假设建立明冰积冰模型时所作的基本假设:
(1)积冰过程中,空气、冰层、水膜都作常物性处理。
(2)本文的积冰模型基于积冰表面的贴体直角坐标系建立,并在微元控制体内离散,而且冰层表面的水膜厚度很小,量级在10-4m,故可忽略冰层表面的曲率,近似认为水膜在平面流动;水膜的流动速度也很小,量级在10-1m/s,水膜流动视为层流。
(3)积冰相变发生在冰-水交接面上,界面温度恒为结冰相变温度,忽略冰层的升华。
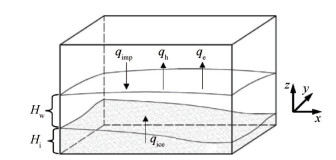
2.2 物理模型明冰积冰时冰层表面覆盖一层薄水膜,水膜外部是空气-过冷水滴两相流,水膜主要在空气剪切力的驱动下在冰层表面流动。因此积冰微元控制体可以分为三层:冰层、水膜、空气-过冷水滴两相流,如图 1所示,冰层厚度为Hi,水膜的厚度为Hw。水膜顶部有过冷水滴的撞击与水膜的蒸发,其中单位面积撞击量、蒸发量分别为为mimp,me,水膜底部单位面积积冰量为mice,min,mout分别为控制体中单位面积水膜的流入与流出率。

|
Fig. 1 Mass and momentum conservation in the control volume |
图 2给出了积冰控制体中能量传递过程,其中水膜顶部有对流换热,水膜蒸发吸收潜热,撞击水在控制体中被加热以及撞击水动能转变为热能,热流密度分别为qh,qe,qimp,水膜底部有水凝固释放潜热,热流密度为qice。
|
Fig. 2 Energy conservation in the control volume |
根据量纲分析法简化N-S方程,分别建立水膜流动传热和冰层生长的控制方程,再根据经验公式得到水膜蒸发量。
(1)水膜流动的连续方程
积冰表面水膜流动过程中,有过冷水滴的撞击加入,水结冰以及蒸发带走水分,将此三项处理为源项,得水膜流动连续方程为
| $ \begin{array}{*{20}{l}} {\frac{{\partial {H_{\rm{w}}}}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {\mathop \int_0^{{H_{\rm{w}}}}u\ {\rm{d}}z} \right) + \frac{\partial }{{\partial y}}\left( {\mathop \int_0^{{H_{\rm{w}}}}v\ {\rm{d}}z} \right) = }\\ {\frac{{{m_{{\rm{imp}}}}}}{{{\rho _{\rm{w}}}}} - \frac{{{m_{\rm{e}}}}}{{{\rho _{\rm{w}}}}} - \frac{{{\rho _{\rm{i}}}}}{{{\rho _{\rm{w}}}}}\frac{{\partial {H_{\rm{i}}}}}{{\partial t}}} \end{array} $ | (1) |
式中u,v分别为水膜在x,y方向的流动速度,ρw为水的密度。
(2)水膜流动的动量方程
水膜在剪切力的驱动下在冰层表面流动,量纲分析法简化得到水膜流动的动量方程为
| $ - \frac{1}{{{\rho _{\rm{w}}}}}\frac{{\partial p}}{{\partial x}} + {g_x} + \nu \frac{{{\partial ^2}u}}{{{\partial ^2}z}} = 0 $ | (2) |
| $ - \frac{1}{{{\rho _{\rm{w}}}}}\frac{{\partial p}}{{\partial y}} + {g_y} + \nu \frac{{{\partial ^2}v}}{{{\partial ^2}z}} = 0 $ | (3) |
| $ \frac{{\partial p}}{{\partial z}} = 0 $ | (4) |
边界条件
| $ {\left. u \right|_{z = 0}} = 0 $ | (5) |
| $ {\left. {\mu \frac{{\partial u}}{{\partial z}}} \right|_{z = {H_{\rm{w}}}}} = {\tau _{\rm{a}}} $ | (6) |
| $ {p_{z = {H_w}}} = {p_{\rm{a}}} $ | (7) |
式中μ是水的动力粘性系数,τa,pa分别为水膜表面的剪切力、空气压力。
(3)水膜流动的能量方程
飞机典型迎风面上的水膜厚度非常薄,量级在10-4m,流动速度也非常小,量级在10-1m/s,因此在积冰过程中,可以将水膜的传热过程视为稳态过程,量纲分析法简化N-S方程,得到水膜流动能量方程为
| $ \frac{\partial }{{\partial {x_{\rm{l}}}}}\left( {\frac{{\partial {T_{\rm{w}}}}}{{\partial {x_{\rm{l}}}}}} \right) = 0 $ | (8) |
式中Tw是水膜的温度。
水-冰界面恒为结冰相变温度,水-气界面有对流换热散热、撞击水滴动能的变化、对撞击水滴的加热以及水膜蒸发吸收的潜热,因此水膜在水-冰界面和水-气界面的传热边界条件分别为
| $ {\left. {{T_{\rm{w}}}} \right|_{z = 0}} = {T_{\rm{f}}} $ | (9) |
| $ \begin{array}{*{20}{l}} { - {\lambda _{\rm{w}}}{{\left. {\frac{{\partial T}}{{\partial z}}} \right|}_{z = {H_{\rm{w}}}}} = h\left[ {{{\left. {{T_{\rm{w}}}} \right|}_{z = {H_{\rm{w}}}}} - {T_{\rm{a}}}} \right] - \frac{1}{2}{m_{{\rm{imp}}}}U_\infty ^2 + }\\ {{m_{{\rm{imp}}}}{c_{{\rm{pw}}}}\left[ {{{\left. {{T_{\rm{w}}}} \right|}_{z = {H_{\rm{w}}}}} - {T_\infty }} \right] + {m_{\rm{e}}}{L_{\rm{e}}}} \end{array} $ | (10) |
式中Tf是结冰相变温度,h为对流换热系数,λw,cpw分别为水的导热系数和比定压热容,Ta,T∞分别为空气温度和来流温度,U∞为来流速度,me,Le分别为水膜的蒸发量、汽化潜热。
(4)冰层控制方程
与水膜同样的分析方法,得到冰层中的能量方程为
| $ \frac{\partial }{{\partial z}}\left( {\frac{{\partial {T_{\rm{i}}}}}{{\partial z}}} \right) = 0 $ | (11) |
边界条件为
| $ {\left. {{T_{\rm{i}}}} \right|_{z = 0}} = {T_{\rm{f}}} $ | (12) |
| $ {\lambda _{\rm{i}}}{\left. {\frac{{\partial {T_{\rm{i}}}}}{{\partial z}}} \right|_{z = - {H_{\rm{i}}}}} = 0 $ | (13) |
式中λi = 2.18W/(m∙K),为冰的导热系数。
冰层生长速度由Stefan条件决定,由于相变产生的潜热分别从水膜和冰层导出,可以得到冰层的生长速度方程为
| $ \frac{{\partial {H_{\rm{i}}}}}{{\partial t}} = \frac{1}{{{\rho _{\rm{i}}}{L_{\rm{f}}}}}\left( {{\lambda _{\rm{i}}}\frac{{\partial {T_{\rm{i}}}}}{{\partial z}} - {\lambda _{\rm{w}}}\frac{{\partial {T_{\rm{w}}}}}{{\partial z}}} \right) $ | (14) |
式中Lf=334400J/kg,为水的凝固潜热。
(5)水膜蒸发量
地球大气中包含空气和水蒸气,在温度一定的条件下,大气中所能容纳的水蒸气的含量也是一定的。空气中水蒸气含量达到最大值时称为饱和空气,饱和空气对应的水蒸气压力称为饱和水蒸气压,饱和水蒸气压与温度相关。
在结冰问题中,由于水膜表面的水蒸气分压力和来流的水蒸气的分压力存在压差,水膜表面的水分子会向周围空气传递,宏观上的表现就是水膜会发生蒸发,水膜质量变小。水蒸发量根据以下公式[4]计算
| $ {m_{\rm{e}}} = \frac{h}{{\rho {c_{{\rm{pw}}}}{R_{\rm{v}}}}} \times \left( {\frac{{{e_{\rm{s}}}}}{{{T_{\rm{s}}}}} - \frac{{{e_{\rm{l}}}}}{{{T_{\rm{l}}}}}} \right) $ | (15) |
| $ {e_{\rm{s}}} = \frac{{{{10}^{33.59051 + 0.0024804{T_{\rm{s}}} - \frac{{3142.31}}{{{T_{\rm{s}}}}}}}}}{{{T_{\rm{s}}}^{8.2}}} $ | (16) |
式中Ts,Tl分别为水膜温度和来流温度,es,el分别为水膜表面和来流的水蒸气饱和蒸汽压,ρ,cpw,Rv分别为水蒸气的密度、比定压热容、气体常数,Rv = 461.4J/(kg∙K)。
2.4 计算方法及步骤考虑水膜蒸发后,需要发展连续方程、能量方程以及水膜蒸发量的计算方法。水膜动量方程、冰层生长方程与文献[16]曹广州不考虑水膜蒸发的方程相同,求解方法也与文献[16]相同。
(1)水膜连续方程
考虑水膜蒸发后,水膜连续方程中增加源项水膜蒸发量me。由于水膜速度和水膜厚度相耦合,根据动量方程得到水膜沿厚度方向的速度平均值u,v,代入水膜连续方程可得
| $ \frac{{\partial {H_{\rm{w}}}}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {\bar u{\rm{d}}z} \right) + \frac{\partial }{{\partial y}}\left( {\bar v{\rm{d}}z} \right) = \frac{{{m_{{\rm{imp}}}}}}{{{\rho _{\rm{w}}}}} - \frac{{{m_{\rm{e}}}}}{{{\rho _{\rm{w}}}}} - \frac{{{\rho _{\rm{i}}}}}{{{\rho _{\rm{w}}}}}\frac{{\partial {H_{\rm{i}}}}}{{\partial t}} $ | (17) |
采用交错网格离散该方程,利用QUICK格式[22, 23]将水膜厚度插值到标量控制体边界。
(2)水膜能量方程
将边界条件(9)、(10)代入(8),求解水膜流动的能量方程,得到水膜中的温度分布为
| $ \begin{array}{*{20}{l}} {{T_{\rm{w}}} = {T_{\rm{f}}} + }\\ {\frac{{0.5{m_{{\rm{imp}}}}U_\infty ^2 - h\left( {{T_{\rm{f}}} - {T_{\rm{a}}}} \right) - {m_{{\rm{imp}}}}{c_{{\rm{pw}}}}\left( {{T_{\rm{f}}} - {T_\infty }} \right) - {m_{\rm{e}}}{L_{\rm{e}}}}}{{{\lambda _{\rm{w}}} + \left( {h + {m_{{\rm{imp}}}}{c_{{\rm{pw}}}}} \right){H_{\rm{w}}}}}z} \end{array} $ | (18) |
由式(18)知,水膜温度呈线性变化,而水膜很薄,沿水膜厚度温度变化小。
(3)水膜蒸发量
式(18)表明水膜温度沿厚度方向变化小,水膜底部温度恒为冰点温度Tf,故将水膜表面温度值近似为冰点温度Tf,可得水膜蒸发量为
| $ {m_{\rm{e}}} = \frac{h}{{\rho {c_{{\rm{pw}}}}{R_{\rm{v}}}}} \times \left( {\frac{{{e_{\rm{f}}}}}{{{T_{\rm{f}}}}} - \varphi \cdot \frac{{{e_\infty }}}{{{T_\infty }}}} \right) $ | (19) |
式中φ为相对湿度。
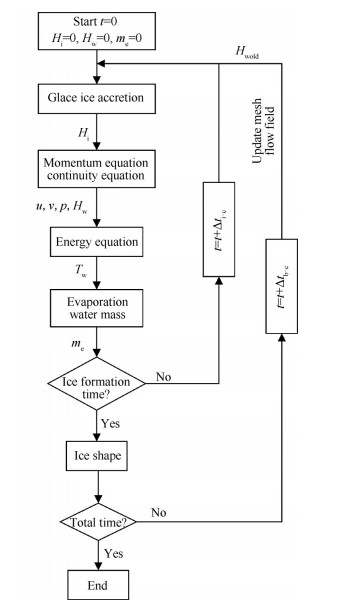
考虑水膜蒸发的积冰计算流程如图 3所示。其中Δti-c = 0.05s为积冰模拟时间步长,Δtb-c = 60s为冰形构建时间步长。计算步骤如下:
|
Fig. 3 Calculation progress of glaze icing simulation |
(1)积冰时间t=0时,水膜高度Hw,冰层高度Hi均为零,水膜蒸发量me也为零。
(2)在有水滴撞击或有水膜覆盖的区域利用式(14)求出明冰积冰时的冰层厚度Hi。
(3)求解水膜动量方程(2)~(4),得到水膜沿厚度方向的平均速度,代入水膜连续方程(1),求得水膜高度Hw,根据条件判断水膜厚度是否收敛,迭代直至收敛。
(4)求解水膜能量方程(8),得到水膜表面的温度Tw分布。
(5)根据式(19)计算水膜蒸发量。
(6)判断是否达到冰形构建时间,若没有,则积冰模拟时间步推进,继续下一时间步的求解,即重复(2)~(5);若达到,则构建冰形。
(7)判断是否达到积冰总时间,若没有,则冰形构建时间步推进,根据冰形更新翼型,重新划分网格,计算两相流场,重复步骤(2)~(6),此时水膜厚度为上一个时间步的水膜厚度Hwold,而冰层厚度依然为零;若达到,则计算结束。
3 算例验证及结果分析积冰数值计算分为三部分:空气-过冷水滴两相流计算、水滴撞击特性计算、水膜流动与积冰相变。两相流场计算为积冰计算提供空气剪切力τa,表面对流换热系数h,水滴撞击特性计算为积冰计算提供水收集系数β。这些参数直接影响水膜流动和积冰相变过程,因此为了直观对比是否考虑水膜蒸发对积冰计算结果的影响,首先确保两相流场及水收集系数的一致性。
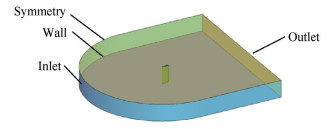
3.1 计算模型及边界条件选取NACA0012翼型作为研究对象,翼型弦长c=0.5334m,展向长度L=0.5m。计算模型如图 4所示,翼型上游取半径为10c的半圆柱域,下游取长10c,宽20c,高L的长方体域。计算域顶部的Symmetry面设置为对称面,底部的Wall设置为壁面,翼型设置为无滑移、粗糙壁面边界,壁面粗糙度由经验公式获得,壁面设置为与来流温度一致的等温壁面边界。计算域的进口Inlet面设置为速度进口边界,出口Outlet面设置为压力出口边界,计算模型与文献[16]一致。
|
Fig. 4 Computational model |
翼型关键结构参数及来流条件等见表 1。
|
|
Table 1 Key structural parameters and inflow conditions of airfoil |
选取翼型中部截面的空气剪切力、对流换热系数、水收集系数、结冰冰形与NASA试验结果以及LEWICE,文献[16]曹广州不考虑水膜蒸发的数值计算结果进行对比。
3.2 网格划分利用商业软件ICEM-CFD划分网格,由于数值计算时翼型采用壁面无滑移条件,壁面处水滴撞击速度为0,无法以此计算水收集系数,所以提取近壁面第一层网格的数据来代替壁面网格数据进行结冰计算,因此要求近壁面第一层网格长度非常小,壁面附近网格进行加密处理,本文第一层网格高度取为0.1mm。积冰过程中冰层是沿壁面外法线方向生长,要求网格与壁面的正交性要比较好,生成的机翼附近的计算网格如图 5所示。网格经过独立性验证,网格总量约为25万左右。

|
Fig. 5 Airfoil computational grid(part) |
利用商业软件ANSYS-CFX进行两相流场计算,采用欧拉-欧拉两相流法。空气相是连续相,采用κ-ε湍流模型结合Scalable壁面函数。由于粘性底层采用壁面函数法处理,所以划分网格时不需要在壁面区加密,只需要把第一个网格节点布置在对数律成立的区域内,即配置到湍流充分发展的区域,本文近壁面第一层网格y+ = 52 > 30,位于对数律成立的区域[24, 25];水滴相是离散相,采用Dispersed Phase Zero Equation湍流模型。传热模型为Thermal Energy,对流项离散格式采用High Resolution。
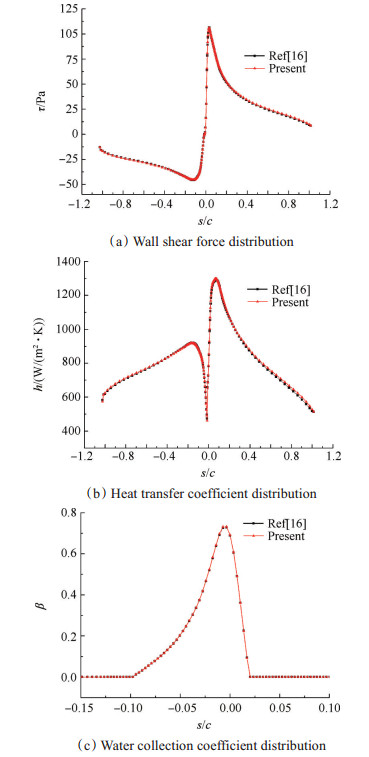
选取来流温度为267K的计算结果验证两相流场的一致性,本文与文献[16]的剪切力、对流换热系数、水收集系数对比如图 6所示,其他来流温度下计算结果也是类似。
|
Fig. 6 Parameters distribution of mid section |
图 6(a)是中部截面壁面处空气剪切力分布图,由图可知,升力面和压力面的剪切力都是先增大后减小(s/c > 0是升力面,s/c < 0是吸力面),最大值位于s/c=±0.05处,升力面剪切力的最大值大于压力面。剪切力分布与文献[16]的计算结果几乎重合。
图 6(b)是对流换热系数分布图,驻点处对流换热系数最小,在s/c=±0.05处达到极大值。升力面流速快,对流换热系数大于压力面。在水膜的流动传热中,对流换热系数不仅影响水膜表面的对流换热量,而且影响水膜表面水的蒸发量。对流换热系数与文献[16]分布也是一致的。
图 6(c)是水收集系数分布对比图,由于存在攻角,水收集系数分布不对称,翼型压力面水滴撞击极限位于s/c=-0.1,升力面位于s/c=0.02。水收集系数驻点处最大,为0.72。
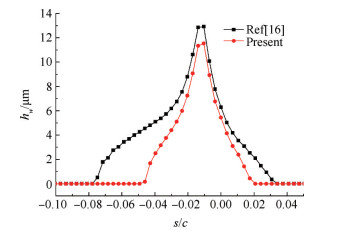
3.4 积冰计算结果及分析冰层表面水膜的分布以及传热传质会影响积冰冰形和积冰量。如图 7所示为本文和文献[16]水膜厚度(Hw)分布图。由图可知,水膜覆盖范围不对称,吸力面水膜覆盖范围小于压力面。本文计算结果与文献[16]的结果相比,水膜厚度变小,水膜分布范围也变小。这是由于考虑水膜蒸发后,水分的蒸发导致水膜厚度减小,并且由于水膜前锋处厚度较小,水分蒸发以及积冰相变导致水膜厚度变为零,水膜分布范围变小。
|
Fig. 7 Water film height |
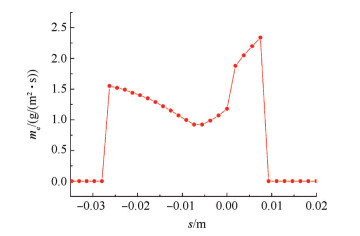
图 8是水蒸发量分布图,由图可知,驻点处蒸发量较小,驻点两侧蒸发量大,并且吸力面蒸发量大于压力面,水膜的平均蒸发量为1.5g/(m2·s)。式(15)表明水膜蒸发量与对流换热系数h呈线性关系,由图 6(c)知,驻点处对流换热系数小,驻点两侧对流换热系数大,因此,图 8所示水膜蒸发量分布合理。
|
Fig. 8 Amount of water evaporated |
由式(14)知,由于冰层底部取绝热边界,冰层温度始终为结冰相变温度Tf,水膜向冰层传递的热量为零,因而积冰量取决于水膜层向空气传递热量的大小。考虑冰层表面薄水膜蒸发后,水膜表面的传热主要有外部对流换热、水膜蒸发吸收的潜热以及对撞击水的加热量。
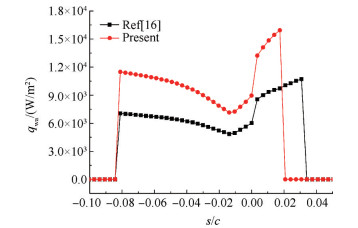
图 9给出了来流温度为265.3K时积冰计算的最后一个时间步中水膜向空气传递的热流密度(qwa)分布。由图可知,考虑水膜蒸发后,水膜向空气的传热量明显增大,驻点处传热量最小,升力面传热量比压力面大,没有水膜覆盖的部分,传热量突变为零。是由于考虑水膜蒸发后,水膜蒸发会吸收潜热,使得水膜传热量明显增大。水膜蒸发吸收的潜热Qe = me∙Le,与水膜蒸发量me呈线性关系,对比图 8可知,水膜传热量变化趋势与蒸发量相同。
|
Fig. 9 Amount of heat transferred by water film |
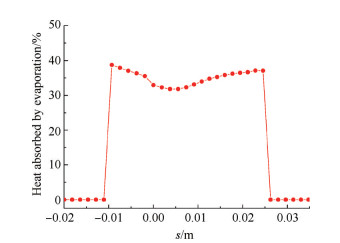
蒸发吸热所占百分比如图 10所示,由图可知,蒸发吸热占总传热量得百分比在35%左右,蒸发吸热量比较大,明冰积冰计算中考虑水膜的蒸发很有必要。
|
Fig. 10 Percentage of the heat absorption of evaporation |
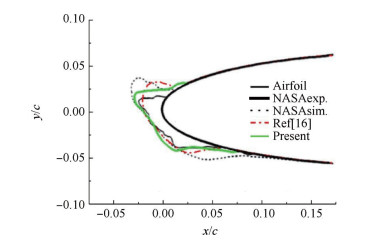
图 11给出了来流温度为265.3K时,本文结冰冰形与NASA试验、计算结果以及文献[16]曹广州不考虑水膜蒸发的计算结果对比,本文和文献[16]的冰形都是从翼型表面三维冰形结果中所提取出的中部截面处的二维冰形。
|
Fig. 11 Two-dimensional ice shape contrast at 265.3K |
如图 11所示,来流温度较高,为典型的明冰积冰状态。由于来流存在攻角,导致吸力面、压力面结冰范围不对称,升力面结冰范围小,压力面结冰范围大。结合图 9可知,升力面水膜向空气传递的热量大,积冰能力强,形成凸起的冰角,冰角形状与NASA试验结果吻合较好,而NASA计算结果以及文献[16]不考虑水膜蒸发的计算结果形成的冰角形状都与试验值有较大的偏离;压力面水膜向空气传递的热量相对较小,并且由图 7可知,压力面水膜覆盖范围大,因此虽然结冰量小,但是结冰范围大。压力面结冰量、结冰冰形的计算结果都与NASA试验结果拟合很好,而NASA数值计算结果结冰范围及结冰量都偏大。
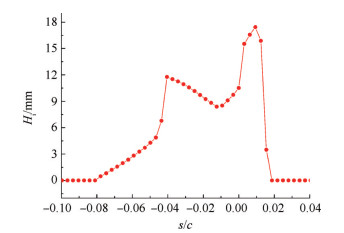
图 12给出了265.3K时的冰形厚度,结冰范围为s/c=-0.08到0.016,升力面结冰范围小,压力面结冰范围大。驻点冰层厚度较小,最大冰厚在s/c=0.009处,最大冰厚为1.8cm。
|
Fig. 12 Ice thickness at 265.3K |
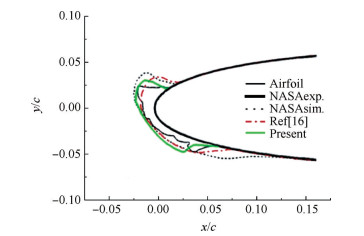
图 13给出了来流温度为267K的冰形对比。NASA数值计算结果的压力面、吸力面结冰极限都比试验结果大,曹广州数值计算结果压力面结冰极限与试验结果比较接近,但是吸力面结冰极限、冰角都偏大。本文考虑水膜蒸发后,由于水膜蒸发吸收热量,结冰能力增强,驻点附近结冰量增加。水膜前锋处水膜厚度小,水膜蒸发使得水膜覆盖范围减小,结冰范围也减小,结冰极限以及冰角都与NASA试验结果具有较好的一致性。
|
Fig. 13 Two-dimensional ice shape contrast at 267K |
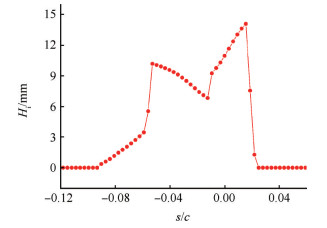
图 14给出了267K时的冰形厚度,结冰范围为s/c=-0.09到0.022。驻点冰层厚度较小,最大冰厚在s/c=0.016处,最大冰厚为1.5cm。
|
Fig. 14 Ice thickness at 267K |
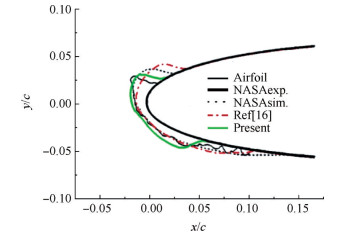
如图 15所示,268.7K时温度更高,冰角更加明显。本文考虑水膜蒸发后的积冰结果,对冰角的模拟显然优于NASA和曹广州不考虑水膜蒸发的计算结果。吸力面结冰极限也与NASA试验值接近,压力面结冰极限偏小,可能是由于蒸发使得水膜前锋处水分蒸发,水膜厚度变为零,结冰极限变小导致的。
|
Fig. 15 Two-dimensional ice shape contrast at 268.7K |
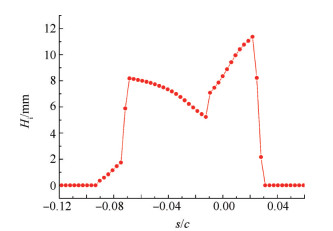
图 16给出了268.7K时的冰形厚度,结冰范围为s/c=-0.092到0.028。驻点冰层厚度较小,最大冰厚在s/c=0.022处,最大冰厚为1.2cm。
|
Fig. 16 Ice thickness at 268.7K |
通过分析可以得到如下结论
(1)本文积冰计算中,水膜的平均蒸发量为1.5g/(m2·s),蒸发吸收的热量占总传热的35%,积冰计算中考虑水膜的蒸发很有必要。
(2)水膜蒸发对积冰结果有重要的影响,考虑冰层表面薄水膜蒸发以后,明冰冰形、冰角形状与位置都与试验结果具有更好的一致性。
(3)水膜前锋处厚度比较薄,考虑水膜蒸发后,水膜蒸发使水膜厚度变为零,水膜覆盖范围变小,导致结冰极限也变小,本文明冰结冰极限与NASA试验结果更一致。
| [1] |
Lynch F T, Khodadoust A. Effects of Ice Accretions on Aircraft Aerodynamics[J]. Progress in Aerospace Science, 2001, 37(8): 669-767. DOI:10.1016/S0376-0421(01)00018-5
(  0) 0) |
| [2] |
Cole J A, Sand W R. Statistical Study of Aircraft Icing Accidents[R]. AIAA 91-0558. http://arc.aiaa.org/doi/abs/10.2514/6.1991-558
(  0) 0) |
| [3] |
Brumby R E. The Effect of Wing Ice Contamination on Essential Flight Characteristics[R]. AGARD-CP-496. 1991. http://www.dtic.mil/cgi-bin/GetTRDoc?AD=ADA246297
(  0) 0) |
| [4] |
胡娅萍. 航空发动机进口部件积冰的数值模拟研究[D]. 南京: 南京航空航天大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10287-2010079949.htm
(  0) 0) |
| [5] |
易贤. 飞机积冰的数值计算与积冰试验相似准则研究[D]. 绵阳: 中国空气动力学研究与发展中心, 2007. http://cdmd.cnki.com.cn/Article/CDMD-90113-2007189443.htm
(  0) 0) |
| [6] |
裘燮刚, 韩凤华. 飞机防冰系统[M]. 北京: 航空专业教材编审组, 1996.
(  0) 0) |
| [7] |
Messinger B L. Equilibrium Temperature of an Unheated Icing Surface as a Function of Airspeed[J]. Journal of Aeronautical Science, 1953, 20(1): 29-42. DOI:10.2514/8.2520
(  0) 0) |
| [8] |
Ruff G A, Berkowitz B M. User's Manual for the NASA Lewice Ice Accretion Prediction Code(LEWICE)[R]. NASA-CR-185129, 1990. https://www.researchgate.net/publication/24383493_Users_manual_for_the_NASA_Lewis_Ice_Accretion_Prediction_Code_LEWICE
(  0) 0) |
| [9] |
Wright W B, Gent R W, Guffond D. DRA/NASA/ONERA Collaboration on Icing Research Part Ⅱ-Prediction of Airfoil Ice Accretion[R]. NASA-CR-202349, 1997. http://trid.trb.org/view.aspx?id=471925
(  0) 0) |
| [10] |
Hedde T, Guffond D. Development of a Three-Dimensional Icing Code, Comparison with Experimental Shapes[R]. AIAA 92-0041. https://www.researchgate.net/publication/268462034_Development_of_a_three-dimensional_icing_code_-_Comparison_with_experimental_shapes
(  0) 0) |
| [11] |
Bourgault Y, Habashi W G, Beaugendre H. Development of a Shallow Water Icing Model in FENSAP-ICE[R]. AIAA 99-0246.
(  0) 0) |
| [12] |
Beaugendre H, Morency F, Habashi W G. ICE3D, FENSAP-ICE's 3D In-Flight Ice Acccretion Moduler[R]. AIAA 2002-0385.
(  0) 0) |
| [13] |
易贤, 桂业伟, 朱国林. 飞机三维结冰模型及其数值求解方法[J]. 航空学报, 2010, 31(11). (  0) 0) |
| [14] |
常士楠, 苏新明, 邱义芬. 三维机翼结冰模拟[J]. 航空学报, 2011, 32(2). (  0) 0) |
| [15] |
申晓斌, 林贵平, 卜雪琴, 等. 发动机进气道短舱前缘结冰三维模拟研究[J]. 航空学报, 2013, 34(3): 517-524. (  0) 0) |
| [16] |
曹广州. 迎风表面三维积冰的数学模型与计算方法研究[D]. 南京: 南京航空航天大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10287-1012016548.htm
(  0) 0) |
| [17] |
曹广州, 吉洪湖. 模拟飞机迎风面三维积冰的数学模型[J]. 航空动力学报, 2011, 26(9): 1953-1963. (  0) 0) |
| [18] |
曹广州, 吉洪湖, 斯仁. 迎风面三维积冰过程中水膜流动的计算方法[J]. 航空动力学报, 2015, 30(3): 0677-0685. (  0) 0) |
| [19] |
张丽芬, 刘振侠, 张斐, 等. 航空发动机旋转帽罩结冰表面换热系数研究[J]. 推进技术, 2017, 38(4). (ZHANG Li-fen, LIU Zhen-xia, ZHANG Fei, et al. Numerical Simulation of Heat Transfer Coefficient on Icing Surface of Rotating Cone in Aero-Engine[J]. Journal of Propulsion Technology, 2017, 38(4).)
(  0) 0) |
| [20] |
屈靖国, 吉洪湖, 胡娅萍, 等. 蛇形进气道影响下发动机进口部件[J]. 推进技术, 2016, 37(12). (QU Jing-guo, JI Hong-hu, HU Ya-ping, et al. Numerical Study on Water Droplets Impingement on Aero-Engine Entry Components with a Serpentine Inlet[J]. Journal of Propulsion Technology, 2016, 37(12).)
(  0) 0) |
| [21] |
卜雪琴, 林贵平. 基于CFD的水收集系数及防冰表面温度预测[J]. 北京航空航天大学学报, 2007, 33(10): 3810-3813. (  0) 0) |
| [22] |
王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2004.
(  0) 0) |
| [23] |
Versteeg H K, Malalasekera W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method[M]. New York: Wiley, 1995.
(  0) 0) |
| [24] |
Shin J, Bond T H. Results of an Icing Test on a NACA0012 Airfoil in the NASA Lewis Icing Research Tunnel[R]. AIAA 92-0647. http://arc.aiaa.org/doi/abs/10.2514/6.1992-647
(  0) 0) |
| [25] |
Shin J, Bond T H. Experimental and Computational Ice Shapes and Resulting Drag Increase for a NACA0012 Airfoil[R]. NASA-TM-105743, 1992. http://www.researchgate.net/publication/23580849_Experimental_and_computational_ice_shapes_and_resulting_drag_increase_for_a_NACA_0012_airfoil
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

