液体的射流雾化现象广泛存在于实际工程机械装置中,如内燃机、食品加工装置、喷涂装置等[1]。对于航空宇航推进系统来说,燃油的雾化特性与燃烧室内燃烧效率和污染物排放密切相关。研究高速射流雾化的物理过程,对于先进发动机燃烧室的设计和改进有重要指导意义。
静止或流动空气中的液体射流是复杂的时空多尺度两相流问题。液体射流进入空气后,受到气动力、表面张力、黏性力和惯性力的相互作用,射流场中出现小尺度的漩涡,导致射流表面失稳并产生微米尺度的液丝和液滴结构,此为液体射流首次破碎过程。在液相和气相之间的相互作用下,大尺度液滴继续破碎产生细小液滴,此为二次破碎过程。二次破碎产生的小液滴在发动机燃烧室内高温高压的环境中继续发生蒸发和掺混过程,最终点火并开始燃烧。首次破碎的动力学过程直接影响二次破碎过程,射流雾化最终产生的液滴数目、尺寸和空间分布特征,将直接影响发动机燃烧室的燃烧效率和低排放特征。
借助高速摄像技术或激光多普勒测速技术,可以对液体射流过程进行实验测量研究。Linne等[2]使用弹道成像的光学技术观测到了柴油射流首次雾化的复杂结构。Wang等[3]使用X射线成像技术对高压液体射流的时间演化过程进行了实验研究。Blaisot等[4]运用图像分析技术研究了液滴尺寸、形状和分布特征。由于射流速度越高,破碎历时越短,液滴尺寸越小,流场越复杂,对实验设备要求更高,难以实现精准测量。王雄辉等[5]采用了高速摄像仪对横向气流场中的液体圆形射流袋式破碎过程进行了实验研究。因此,在射流动力学的实验测量方面,现有研究对低速射流破碎现已有一定认识,而对于实际工程应用中的高速射流机理仍不明晰。
使用数值模拟方法分析射流破碎问题则主要存在两个方面的难点和挑战。
一是空间多尺度问题对网格分辨率要求高,计算量大。射流破碎形成的液丝或液滴往往处于几十微米甚至微米量级。为了准确捕捉这些动态变化的小尺度结构,通常推荐在每个液丝或液滴所在区域附近需要有5~10个网格点的解析度,由此使得射流破碎问题的模拟面临计算规模大、耗时长的挑战。
二是使用常规空间离散格式难以捕捉气液两相之间的锐利界面。常规的空间离散格式在求解大密度比的气液两相界面时存在较强的界面抹平现象,这对研究射流失稳和液滴破碎过程是十分不利的。
随着计算机计算能力的提高和并行求解技术的发展,第一个难点可以逐渐被克服,至少在现今的计算机条件下,采用数值模拟方法研究射流的首次破碎过程是可行的。而近几十年,国内外计算流体力学专家在体积追踪和锋面追踪等界面流模拟技术方面的努力和成果,使得第二个难点的解决也变为可能。
因此,采用界面流数值模拟方法对射流复杂过程进行计算研究已成为可能,广大科研工作者在这个领域开展了相关探索研究。Pan和Suga[6]采用Level Set方法对液体射流问题进行了数值模拟,研究了层流状态下的射流破碎情形。Menard等[7]将Level Set/VOF/GFM(Ghost Fluid Method)方法相结合,展示了三维射流进入静止空气的动力学过程。Gorokhovski和Herrmann[8]指出了DNS(Direct Numerical Simulation)方法用于研究射流现象的优势和挑战。Herrmann[9~11]使用改进的Level Set方法研究了横向射流和密度比等因素对射流长度和破碎特征的影响。Desjardins等[12, 13]提出了一类具有守恒特征的Level Set/GMF方法,模拟了不可压两相射流雾化问题。Fuster等[14]使用AMR(Adaptive Mesh Refinement)网格自适应技术模拟射流首次破碎过程,该技术能够降低网格量、节省计算资源。Shinjo和Umemura[1, 15~17]应用Level Set方法对射流雾化的内在机理进行了探索,研究了液丝及液滴产生过程、射流表面不稳定性的特征,以及射流头部的雾化特征,分析了气相湍流对雾化分布的影响。刘日超等[18]探究了射流柱的表面波和射流柱演变、断裂、破碎现象的关系。
可见,近些年,学者们针对射流雾化问题进行过大量数值研究,对破碎距离、雾化角和粒径分布等射流场结构的认识有了很大的进步。但是射流雾化过程十分复杂,现今对详细破碎机理的认识还不够全面和深入。为此,本文试图采用直接数值模拟技术,结合使用VOF界面流模拟方法和有界压缩格式,对速度为30m/s的射流进入静止空气的失稳和首次雾化过程进行有效的计算分析,以期获得对射流失稳机理和雾化破碎动力学更为细致的观察和认识。
本文引入了一种基于VOF算法追踪射流气液两相之间的锐利界面演化的直接数值模拟方法。为保证界面的尖锐性和有界性,引入了附加人工压缩项对流体界面运输方程进行修正,并将NVD(Normalized Variable Diagram)型高阶GDS(Gamma Differencing Scheme)有界压缩格式应用于方程的离散[19]。使用该数值方法,首先计算了速度为0.415m/s和1.04m/s的低速射流,对比Pan等[6]的数值模拟结果,分析了低速射流表面波的形式、射流破碎的不同模式和射流核心长度的影响因素等,验证了界面流模拟技术的准确性。
本文研究对象为速度为30m/s的高速液态燃料射流,关注其首次破碎的动力学机理。分析射流前锋与核心、雾化速度场与压力场的演化过程,阐述了射流液柱中扰动的产生和传播特性、液丝的形成与变化以及液滴的形成机制等。本文为实现高速射流的大规模模拟计算,将算例中的网格分区域进行加密,计算程序进行并行化处理,并行化代码在高性能计算设备天河二号上实现。
2 计算方法在求解两相流界面的演化问题时,若采用一般常规的空间离散方法,会产生非物理振荡和界面耗散问题,从而严重抹平介质界面。使用特殊的界面追踪模拟技术能够解决这一问题。该方法主要分为体积追踪(Volume Tracking)和锋面追踪(Front Tracking)两大类。VOF,Level Set和GFM是被广泛使用的体积追踪技术,其中VOF界面演化求解算法由Hirt和Nichols[20]最先提出。采用施主受主(Donor-Acceptor)形式的差分求解技术,通过引入流体体积比函数和运动界面输运方程,在每个时间步内求解动量方程和界面输运方程,从而获得网格单元内体积分数的变化,据此重构界面信息并获得界面附近网格单元的流通量[21]。
此处采用了本文作者在文中实现的一类基于非结构网格的格式压缩型VOF方法[22, 23]。该VOF方法采用人工压缩界面输运方程和GDS高分辨率格式[19],可以自动处理界面的拓扑演化,无需进行实时的界面重构,具有较高的计算效率。在文中应用这类VOF方法[22],本文作者对复杂的三维Rayleigh-Taylor不稳定性问题实现了并行模拟,系统研究了密度差和雷诺数对界面演化的影响,得到了上升气泡和下沉“尖钉”的时间发展规律。下文对该方法进行简要介绍,并用于对射流破碎过程进行直接数值模拟。
2.1 流体控制方程描述本文考虑的射流液体为不可压缩黏性流体,周围为不可压缩空气,考虑流体物性参数的空间变化、黏性应力,以及表面张力的作用,忽略能量输运过程。流体的流动满足三维质量守恒方程和动量守恒方程
| $ \left\{ {\begin{array}{*{20}{l}} {\nabla \cdot \mathit{\boldsymbol{v}} = 0}\\ {\frac{{\partial \rho \mathit{\boldsymbol{v}}}}{{\partial t}} + \nabla \cdot \left( {\rho \mathit{\boldsymbol{vv}}} \right) = - \nabla p + \mu {\rm{\Delta }}\mathit{\boldsymbol{v}} + \mathit{\boldsymbol{F}}} \end{array}} \right. $ | (1) |
式中
在VOF算法中,定义流体体积比函数
| $ C = \left\{ {\begin{array}{*{20}{c}} 0&{{\rm{gas}}}\\ {\left( {{\rm{}}0{\rm{}}, {\rm{}}1{\rm{}}} \right)}&{{\rm{interface}}}\\ 1&{{\rm{liquid}}} \end{array}} \right. $ | (2) |
控制体单元内的物性参数由流体体积函数决定,
| $ \rho = C{\rho _{\rm{l}}} + \left( {1 - C} \right){\rho _{\rm{g}}} $ | (3) |
| $ \mu = C{\mu _{\rm{l}}} + \left( {1 - C} \right){\mu _{\rm{g}}} $ | (4) |
式中ρl和ρg分别为液体和气体的密度,μl和μg分别为液体和气体的动力黏度系数。
此处考虑到两相流界面之间的表面张力作用,动量方程中引入表面张力项作为源项。射流中的气相和液相都属于牛顿流体,根据Brackbill等[24]提出的连续表面力模型CSF(The continuum surface force),表面张力项如下给定和计算
| $ \mathit{\boldsymbol{F}} = \sigma \frac{{\rho \kappa \nabla C}}{{\frac{1}{2}\left( {{\rho _{\rm{l}}} + {\rho _{\rm{g}}}} \right)}} $ | (5) |
式中σ为表面张力系数,κ为界面的曲率。
2.2 人工压缩界面输运方程气液两相流体界面的演化满足输运方程如下所示
| $ \frac{{\partial C}}{{\partial t}} + \left( {\mathit{\boldsymbol{v}} \cdot \nabla } \right)C = 0 $ | (6) |
式中,流体体积比函数C为台阶函数,其尖锐性和有界性等特征在离散过程中很难保留,使用常规的离散格式模拟界面间断会产生严重数值振荡或抹平效应。针对这一问题,文献[19]在流体界面输运方程中引入了一个自定义人工压缩项,构造出修正的界面输运方程如下
| $ \frac{{\partial C}}{{\partial t}} + \nabla \cdot \left( {\mathit{\boldsymbol{v}}C} \right) + \nabla \cdot \left[ {{\mathit{\boldsymbol{v}}_{\rm{r}}}C\left( {1 - C} \right)} \right] = 0 $ | (7) |
式中
| $ {\mathit{\boldsymbol{F}}_{\rm{r}}} = \mathit{\boldsymbol{S}} \cdot {\mathit{\boldsymbol{v}}_{\rm{r}}} = {\rm{max}}\left( {\left| {\mathit{\boldsymbol{n}}\left( {\mathit{\boldsymbol{S}} \cdot \mathit{\boldsymbol{v}}} \right)} \right|/{{\left| \mathit{\boldsymbol{S}} \right|}^2}} \right) $ | (8) |
其中
| $ \mathit{\boldsymbol{n}} = {\left( {\nabla C} \right)_{\rm{f}}}/\left| {{{\left( {\nabla C} \right)}_{\rm{f}}}} \right| $ | (9) |
考虑到界面间断问题对于算法格式的有界性要求,针对于非结构网格,文献[19]基于物理量梯度的归一化方法提出了NVD型高阶GDS有界格式,算法过程如下:
(1)由面
| $ {\tilde f_{\rm{C}}} = 1 - \frac{{{f_{\rm{D}}} - {f_{\rm{C}}}}}{{2{{\left( {\nabla f} \right)}_{\rm{C}}} \cdot d}} $ | (10) |
式中
(2)由
① 当
| $ {\tilde f_{\rm{f}}} = {\tilde f_{\rm{C}}} $ | (11) |
②
| $ {\tilde f_{\rm{f}}} = \frac{1}{2} + \frac{1}{2}{\tilde f_{\rm{C}}} $ | (12) |
③
| $ {\tilde f_{\rm{f}}} = - \frac{{\tilde f_{\rm{C}}^2}}{{2\beta }} + \left( {1 + \frac{1}{{2\beta }}} \right){\tilde f_{\rm{C}}} $ | (13) |
式中β为数值耗散程度相关参数,取值范围为0.1 ≤ β ≤ 0.5。
使用Jasak修正后的界面压缩输运方程,并将NVD型高阶GDS有界格式应用于方程的离散,由此构造出的VOF界面求解方法可高精度地模拟出射流破碎过程中气液两相之间锐利界面的演化。关于该VOF方法的具体实现可参考文献[22]。
3 算法验证本小节首先对层流状态下的低速射流破碎过程进行计算分析,以验证用第2小节介绍的界面流算法模拟射流问题的可行性。根据Reitz[25]的理论,不同入射速度下液体射流具有不同的破碎模式,主要分为四个阶段:
① 瑞利破碎模式(Rayleigh Breakup Regime)。
② 第一类风生破碎模式(The First Wind-induced Breakup)。
③ 第二类风生破碎模式(The Second Wind-induced Breakup)。
④ 雾化模式(Atomization Regime)。
不同射流模式的划分由三个重要的无量纲参数决定,分别为:表征惯性力与粘性力之比的Re数(Reynolds number)、表征惯性力与表面张力之比的We数(Weber number)、表征液体重力与表面张力之比的Bo数(Bond number),定义如下
| $ Re \equiv \frac{{{\rho _{\rm{l}}}{D_0}{U_0}}}{{{\mu _{\rm{l}}}}} $ | (14) |
| $ We \equiv \frac{{{\rho _{\rm{l}}}{D_0}U_0^2}}{\sigma } $ | (15) |
| $ Bo \equiv \frac{{gD_0^2{\rho _{\rm{l}}}}}{\sigma } $ | (16) |
式中D0为射流喷口圆孔的直径,U0为射流初始速度,σ为表面张力系数。
考察的两个低速射流验证算例取相同的Re数,区别在于算例二的We数和Bo数更高,流场的主要物性参数如表 1所示。将算例一和算例二的数值模拟结果与Pan等[6]的计算结果,从射流形态、表面波的发展、破碎模式和射流核心长度几个方面展开对比分析。
|
|
Table 1 Flow conditions of liquid and gas |
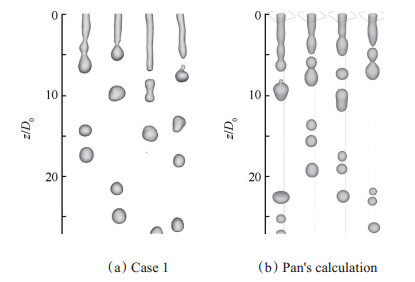
验证算例一和验证算例二之射流破碎过程的界面演化如图 1和图 2(共27个图像)所示,其中每个图像之间的时间间隔不固定。图中最上端为射流喷口位置,液体射流由圆形喷口进入静止空气,重力加速度方向竖直向下。
|
Fig. 1 Comparison of overall flow structure between case1 and Pan's calculation (Water jets into air at Re = 480, We = 3.1, Bo = 0.23. The images are arbitrarily taken snapshots) |
|
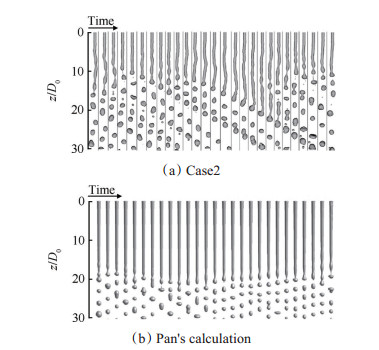
Fig. 2 Comparison of overall jet shape between case2 and Pan's calculation (Water jets into air at Re = 480, We = 7.45, Bo = 0.55. The time interval between two consecutive images Δt = 2ms) |
在重力、黏性力和表面张力的作用下,射流表面受到不稳定扰动,顶端膨胀形成液滴并脱落,已脱落的液滴在外力作用下呈现不规则形状。图 1和图 2都清晰呈现与Pan等[6]研究一致的射流破碎液滴夹止动力学现象,说明本文采用的VOF方法能够准确模拟出符合物理力学机制的射流结构。
射流表面的扰动有两种表现形式,分别为扩张波(Dilation wave)和正弦波(Sinuous wave)[6]。在较低的射流速度下,射流液柱在上述三种外力作用下,以中轴线为对称轴,间隔性出现直径增大和直径缩小的波动形态,称为扩张波。随着射流入射速度增大,液柱核心长度增加,液体与周围气体之间的气动力作用加强。加之射流本身结构不稳定,气动力对射流的微小扰动都会导致轴线波动。射流轴线的波动类似正弦曲线,被称为正弦波。
验证算例一,即图 1中射流过程的表面波主要表现为轴对称结构,即扩张波形式,射流破碎模式为瑞利破碎模式。
验证算例二中,本文的模拟结果图 2(a)中的液柱中轴线出现偏斜,譬如其中的13~20等图像中的液柱轴线的正弦波结构清晰可见,呈现有规则的不对称发展形态,说明气动力对射流破碎的影响逐渐显现,射流已进入不稳定状态,此时的射流破碎模式已从瑞利破碎模式,发展为风生破碎模式。而Pan等[6]的计算显示同一工况下的射流液柱仍主要表现为对称结构,尚未出现明显的波动失稳形态,参考图 2(b)。引起计算差异的因素可能与射流进口处的数值扰动导致的提前失稳有关,具体原因还在探究之中。
对比图 2与图 1中的射流液柱核心长度,能够验证Sallam等[26]关于射流形成机理的研究。射流入射速度越高,We数越大,射流核心的平均长度也越长。液体进入空气,射流前锋最先受到冲击,产生表面波并向液柱上游传递,射流核心在重力、黏性力和表面张力的作用下,长度先增加。当重力克服表面张力和黏性力的作用时,射流头部的液滴开始脱落。上游液柱直径在表面张力的作用下出现短暂收缩,而后在重力作用下继续增大,液柱失稳呈周期性变化。
4 物理模型描述与计算参数设置作为本文重点,此处将进一步研究高速燃油液体通过圆形喷口射流进入静止空气的射流破碎过程。发动机燃烧室雾化喷嘴喷射出的液柱受到的扰动主要来源于两方面,一部分来源于喷口干扰等不均匀的无规律的非物理扰动源,另一部分源于气液两相对流的相互作用。本文的研究对象为液体射流破碎过程受到的气动力作用,暂不考虑喷口扰动,强制均布的入射速度。考虑重力因素,设置重力方向与射流入射方向相同。流场具体参数见表 1。
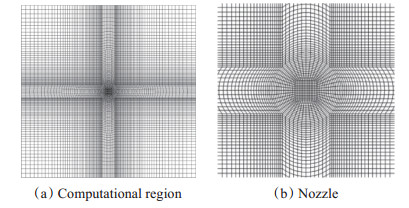
该高速液体射流算例的计算域设置为长方体,尺寸为10D × 10D × 21.7D。计算域尺寸取得足够大,一是为了保证射流破碎结构的完整性,二是能够避免计算域边界对射流主体的影响。由于采用的喷管入口直径小(0.1mm),射流速度高(30m/s),导致射流破碎产生的液丝和液滴尺寸小(几十微米量级)。若要捕捉到足够细致的流场结构信息,以确保对雾化破碎过程的高分辨率模拟,在射流核心区域需要至少达到微米量级的网格精度;而在远离射流主体的气相流场,对射流破碎过程的影响弱,可选用较粗的网格,以降低计算资源的浪费。图 3为分区加密网格示意。
|
Fig. 3 Cross-section mesh |
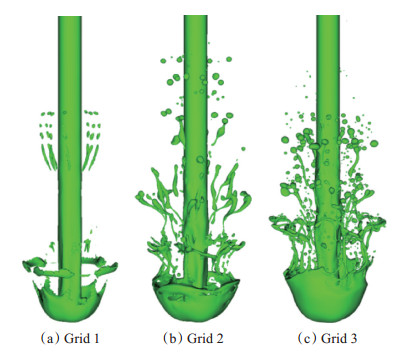
为了考察网格分辨率对流场结构细节模拟精度的影响,共设计三套不同规模的网格以供网格无关性实验。三套计算网格的规模和分辨率参见表 2,与之对应的射流整体结构模拟结果见图 4。
|
|
Table 3 Numerical setup |
|
Fig. 4 Comparisons of overall jet shape under three sets of grid |
粗网格Grid 1的模拟结果见图 4(a),可见最小分辨率为2.5μm的网格仅能大致模拟出射流主体及其头部的蘑菇状轮廓,边缘存在非物理的不光滑锯齿状结构,液丝结构也未能够准确刻画。图 4(b)能比较完整地展示射流失稳、蘑菇状头部及破碎产生液丝的过程,但是未能有效捕捉到液丝转变为液滴的演化过程,未能真实反映射流首次破碎的动力学过程。图 4(c)对应的是本次研究采用的规模最大的网格系统(约4亿网格),最小分辨率为0.5μm,图 4(c)能清晰展示射流失稳、液丝形成及破碎生成液滴的整个过程,有效反映了首次破碎机理。由此说明网格分辨率与数值模拟结果的解析精度密切相关,Grid3的网格足够精细到能够捕捉高速射流首次破碎的流场结构及其演化过程。
由于两个方面的原因,本文作者没有对更密的网格结果进行计算和讨论。其一,根据目前的对比计算分析,发现图 4所对应的第三套网格已经能对本文关注的射流柱失稳和首次破碎过程进行有效捕捉;其二,继续加密网格应该能对射流的二次破碎现象(即大液滴破碎成小液滴)加以考虑,但所需要的计算网格规模十分庞大,对海量数据的可视化处理技术要求也很高,研究团队目前可以利用的计算资源难以达到这个层次。本文目前的研究采用了约4亿个网格单元,如果在三维空间各个坐标方向加密一倍的话,将需要超过32亿的计算规模;考虑到计算稳定性要求,所需要的时间步长也将进一步缩小,从而极大增加计算时间。
下文继续基于图 4(c)中的计算结果对射流破碎过程展开流场结构和气动特性分析。
5 结果分析与讨论这一小节将分别从射流整体结构的演化过程、扰动的产生和传播、液丝的产生与变化以及液滴的形成机制,这四个方面对射流首次破碎机制展开深入的分析研究。
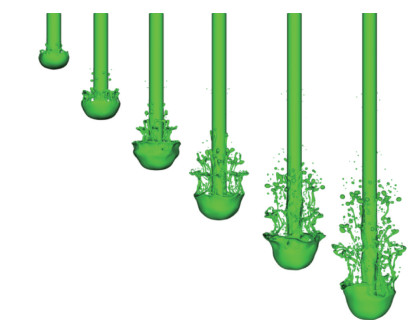
5.1 射流整体结构射流界面的演化过程见图 5,每张图片记录的时间间隔为15μs,从中可见射流整体结构。液体以30m/s速度喷射进入静止的空气,在冲击力作用下,头部边缘向外卷曲,形成蘑菇状结构。头部卷曲边缘的尖端最先变成薄片状。当其受到的气动力大于表面张力时,薄片结构发生破碎,产生环带状和条带状液丝,并向靠近喷口处的上游脱落。液丝结构不稳定,从其尖端会继续脱落液滴,液滴直径大小由液丝尺寸决定,与射流速度密切相关。此外,流场中还存在很多尺寸极小的卫星液滴,为二次破碎产生。液柱头部产生扰动并向上游液柱传递。此外,已脱落的自由液丝中的一部分会继续和液柱核心发生碰撞,发生融合或产生新的液丝,从而为液柱核心注入了新的扰动。因此液柱核心表面不稳定性逐渐增强,下游表面不再保持光滑,开始出现波动。整个射流过程中,蘑菇头体积有所增大,雾化程度不断提高,影响范围进一步扩大。
|
Fig. 5 Comparisons of overall flow structure at different times (The time interval between two consecutive images Δt = 15μs) |
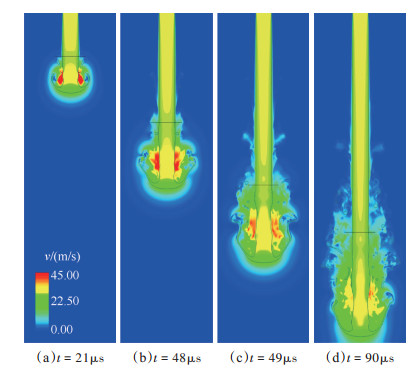
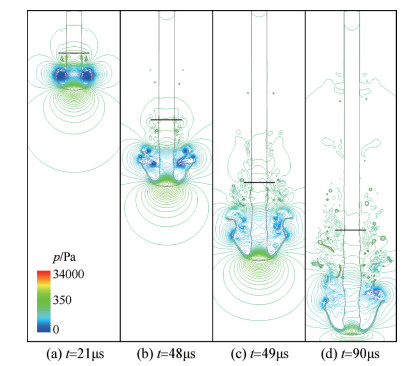
高速射流进入空气后,与周围的静止气体形成较大速度差,即剪切效应。气液两相之间的剪切效应使得空气由静止沿着射流方向开始加速,在粘性力和惯性力的作用下,气流速度不断增大,直至接近射流头部向外卷曲的边缘处受到阻挡。在射流头部边缘与液柱核心之间的蘑菇状结构内侧,气流速度加速到最大,如图 6所示。由于射流头部最先受到冲击,速度降低,形成液体低速高压区。而在头部边缘的后方,会形成一个或多个集中的气体高速低压区,如图 7。射流结构和流场的变化过程可分为如下两个阶段。
|
Fig. 6 Comparisons of velovity contours on longitudinal cross-section at different time |
|
Fig. 7 Comparisons of pressure isolines on symmetric plane at different times |
第一阶段流场呈对称结构,由t = 21μs,t = 48μs图像可见。此时,以流向不稳定性为主,卷曲的边缘呈轴对称,在后方产生强烈的轴对称涡,速度场和压力场也基本呈现轴对称状态。
第二阶段流场呈不对称结构,由t = 49μs,t = 90μs图像可见。随着射流不断向下游推移,轴对称结构会被新产生的非对称的流向涡破坏,从而增加整个流场的不稳定性。这整个过程也与液丝和液滴的形成密切相关。轴对称涡流结构被破坏,液柱头部与液核处产生的液丝和液滴越来越多,流场速度场和压力场高度紊乱。射流头部蘑菇状结构变大,其后的尾迹范围也增大。头部后方环流区域内部的气体高速低压区集中程度减小,范围变大,紊乱程度提高,并相对液柱向上游移动,速度场和压力场也基本呈现非轴对称状态。
5.2 扰动的产生和传播表面不稳定性的发展与液柱受到的扰动的产生和传播过程一致。受到扰动的液柱形态发生变化,产生表面波。图 6和图 7中的黑色横线为液柱表面受扰动部分和未受扰动部分的分界线。射流液柱可能受到的扰动主要有两个来源,分别为喷口处扰动和头部冲击扰动。本算例中,喷口处的边界条件不随时间变化,不产生喷口扰动。因而射流液柱受到的扰动只可能源于射流头部受到冲击后发生变形,从而与周围气体作用产生的非定常扰动,并从射流头部向喷口方向传播,由此造成受扰动部分和未受扰动部分的分界线位置并不固定。
扰动由下游射流头部向靠近喷口处的上游的传播可以通过气相和液相两个途径。气相主要为涡流和相对速度的作用:液柱头部卷曲的边缘后方会形成气体环流区,其中包括很多小的涡量,与液柱表面相互作用促进扰动的传播。观察扰动区域气相和液相的相对速度在不同位置有所不同。在液柱下游区域,附近气体速度比射流核心速度更快。在液柱上游区域,液相相对速度较快。相对速度的明显差异,使得液柱表面受到强烈的气动剪切力作用,图 6中可观察到表面波结构。但是表面波并不明显,波长较短,粘滞阻力很难在短时间内被克服,因此表面波不为主要的扰动传递方式。
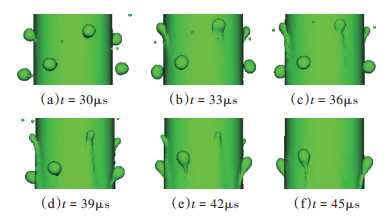
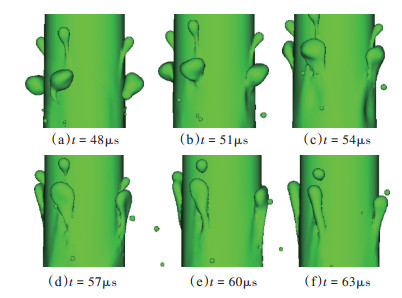
液相作用主要为液滴和液丝的再碰撞。再碰撞的过程将扰动传递给了上游,也促进了破碎的进程。再碰撞会产生两种结果。一是液滴碰撞的径向速度较高时,会融合到液柱内,如图 8所示。融合后的液柱表面仍较光滑。二是可能产生新的液丝,如图 9所示。此时,液滴碰撞的轴向速度较高而径向速度较低,碰撞后在液柱形成凸起如图 9(c)所示,在周围空气的摩擦力和压力作用下变扁平状,并向上游弯曲倾斜,如图 9(d),最终产生液丝可见于图 9(e),(f)。
|
Fig. 8 Droplet collision and fusion (liquid core) |
|
Fig. 9 New ligament formation from droplet collision (liquid core) |
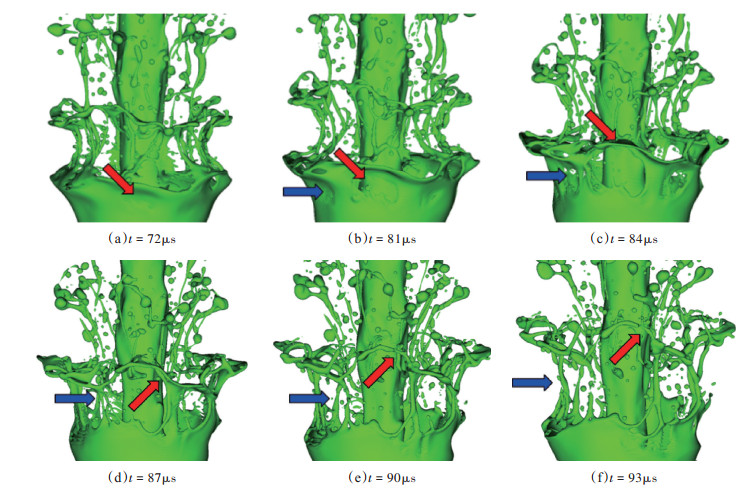
高速的液柱进入静止的气体之后,在前方阻力的挤压作用下,头部液体堆积并向外侧且向后侧转移。在与周围气体接触时,由于气液两相存在速度差,液柱表面受到剪切力。又由于表面张力的作用,表面发生变形扭曲。扭曲变形的液柱头部的边缘受剪切力最大而表面张力最小,会最先变薄,呈现薄片状结构。薄片结构不均匀,发生破碎,产生液丝。环带液丝的形成和破碎过程如图 10红色箭头所指,条带液丝如图 10中蓝色箭头所示。
|
Fig. 10 Ligament formation from tip edge |
首先分析红色箭头所指的环带液丝破碎过程。图 10(a)中红色箭头所指为射流头部边缘片状结构最薄处,由此发生破裂,产生孔洞。孔洞继续扩大,如图 10(b)。头部边缘以甜甜圈状环带液丝的形态脱落,如图 10(c),(d)。一方面环带液丝本身厚度不均匀,每处速度不完全相同,另一方面液丝周围气体扰动强烈,环带液丝的表面会产生非周期性表面波,进而从最不稳定的地方如图 10(e),(f)红色箭头处,发生破裂。
接下来讨论破碎过程条带状液丝的破碎过程。头部边缘其他较薄处如图 10(b)蓝色箭头处,与红色箭头所指位置均发生破裂,形成孔洞。随着头部继续以高速向下游运动液丝,将要脱落的边缘速度较低,与头部整体的相对运动方向向上游,则相邻的孔洞之间的液体会受到表面张力的轴向作用,出现轴向的条状液丝,整个过程如图 10(c),(f)蓝色箭头所示。该破碎方式与Sallam等[26]的实验观测结论一致。需要注意的是,与本文相比,文献[26]考虑的是高We和高Re情况,但其中展示的破碎规律与本文发现的结果定性上接近。至于其中是否存在数学分析上的相似性尚需进一步探讨。
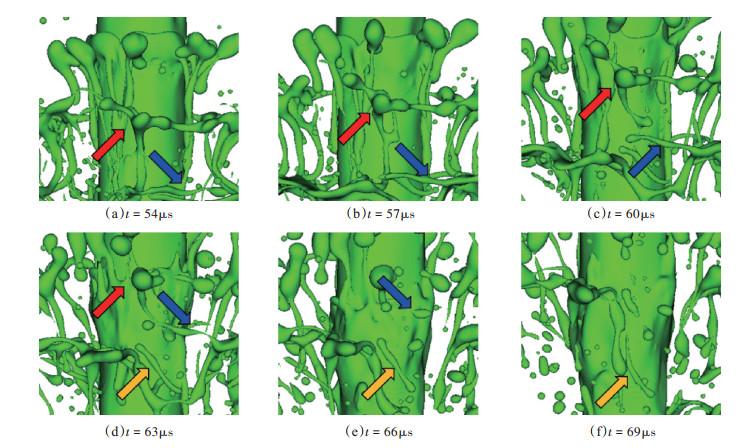
5.4 液丝的发展和液滴形成机制液滴一部分来源于气体与液柱表面的直接动力学作用,其形成机制与上文所述液丝形成机制相似。另一部分液滴来源于从液柱脱落的液丝。液丝结构不稳定,会发生进一步破碎,产生液滴。以图 11中蓝色箭头所指的液丝为例,产生液滴过程可分为液滴夹止动力学(Droplet pinch-off dynamics)的三个阶段。第一阶段如图 11(a),(b),液滴头部为高压区,在表面张力的作用下,泡状端部周围向内收缩,形成颈部结构,并向上游传播毛细波(Capillary waves)。第二阶段如图 11(c),在压力梯度和膨胀波(Rarefaction wave emanation)的作用下,液丝头部从上游吸收液体,体积逐渐增大,压力逐渐降低。颈部继续收缩,压力增大。液丝整体沿中心线拉伸。第三阶段如图 11(d),(e),当颈部收缩到足够细的程度,会被圆周向的表面张力夹断,液丝的泡状端部脱落成液滴。此外,图 11中红色箭头所指示的三岔液丝断裂过程与上述过程相似。液丝头部直径相对液滴平均直径较大,从颈部吸收更多液体,颈部直径缩小,端部体积继续增大,最终从颈部断裂产生液滴。
|
Fig. 11 Droplet formation from ligament and ligament development |
然而,图 11中黄色箭头所指的液丝与蓝色箭头所指液丝的最初形态相似,但是最终发展结果不同,此液丝并未如上所述从较细的颈部夹止产生液滴。该液丝沿轴向分布,最初与轴线有一定夹角,在气流作用下逐渐与轴线平行。这主要是由于液丝周围流场紊乱,气流相对液丝的速度向上,且数值较大,使液丝表面受到较大的向上游的气动力,并在气动力和表面张力的相互作用下伸长。液丝直径减小,长度增加,暂未产生液滴。这说明并非所有液丝的变化过程都会直接产生液滴。
6 结论本文采用直接数值模拟方法,研究了空气动力作用下射流的首次破碎机制。分析发现:
(1)射流进入静止的空气中,头部最先受到冲击和扰动,出现蘑菇状结构,进而发生破碎和雾化。
(2)头部产生的扰动通过气相和液相两个途径向上游传递,即气液速度差异所致的剪切力作用,以及脱落液丝和液柱核心的再碰撞,这些作用都为液柱核心注入了新的扰动,增加了液柱核心的不稳定性,加速破碎进程。
(3)破碎最初发生于头部边缘,在气动力作用下,边缘向外卷曲变为薄片状,当气动力大于表面张力时,薄片结构发生破碎,产生环带状液丝和条带状液丝。
(4)液丝结构不稳定,周围气流速度较低时,受到气动力影响较小,从尖端脱落液滴;周围气流速度较高时,液丝会在气动力作用下受拉伸变长,而非直接发生破碎。
以此为基础,下一步工作将在国家相关专项项目的支持下进行对应的实验研究,采用高速摄影、高速PIV和激光多普勒测速(PDA)技术对射流雾化过程的穿透深度、液滴尺寸分布等信息进行有效测量,并与相关计算开展对比验证。
| [1] |
Shinjo J, Umemura A. Simulation of Liquid Jet Primary Breakup: Dynamics of Ligament and Droplet Formation[J]. International Journal of Multiphase Flow, 2010(36): 513-532.
(  0) 0) |
| [2] |
Linne M A, Paciaroni M, Gord J R. Ballistic Imaging of the Liquid Core for a Steady Jet in Crossflow[J]. Applied Optics, 2005, 44(31): 6627-6634. DOI:10.1364/AO.44.006627
(  0) 0) |
| [3] |
Yujie Wang, Xin Liu, Kyoung-Su Im, et al. Ultrafast X-ray Study of Dense-Liquid-Jet Flow Dynamics Using Structure-Tracking Velocimetry[J]. Nature Physics, 2008(4): 305-309.
(  0) 0) |
| [4] |
Blaisot J B, Yon J. Droplet Size and Morphology Characterization for Dense Sprays by Image Processing: Application to the Diesel Spray[J]. Experiments in Fluids: Experimental Methods and Their Applications to Fluid Flow, 2005, 39(6): 977-994.
(  0) 0) |
| [5] |
王雄辉, 黄勇, 王方, 等. 横向气流中液体射流袋式破碎机理[J]. 推进技术, 2012, 33(2): 198-204. (WANG Xiong-hui, HUANG Yong, WANG Fang, et al. Bag Breakup of Round Liquid Jets in Crossflow[J]. Journal of Propulsion Technology, 2012, 33(2): 198-204.)
(  0) 0) |
| [6] |
Pan Y, Suga K. A Numerical Study on the Breakup Process of Laminar Liquid Jets into a Gas[J]. Physics of Fluids, 2006, 18.
(  0) 0) |
| [7] |
Menard T, Tanguy S, Berlemont A. Coupling Level Set/VOF/Ghost Fluid Methods: Validation and Application to 3D Simulation of the Primary Break-Up of a Liquid Jet[J]. International Journal of Multiphase Flow, 2007, 33(5): 510-524. DOI:10.1016/j.ijmultiphaseflow.2006.11.001
(  0) 0) |
| [8] |
Gorokhovski M, Herrmann M. Modeling Primary Atomization[J]. Annual Review of Fluid Mechanics, 2008, 40: 343-366. DOI:10.1146/annurev.fluid.40.111406.102200
(  0) 0) |
| [9] |
Herrmann M. A Balanced Force Refined Level Set Grid Method for Two-Phase Flows on Unstructured Flow Solver Grids[J]. Journal of Computational Physics, 2008, 227(4): 2674-2706. DOI:10.1016/j.jcp.2007.11.002
(  0) 0) |
| [10] |
Herrmann M. Detailed Numerical Simulations of the Primary Atomization of a Turbulent Liquid Jet in Crossflow[J]. Journal of Engineering for Gas Turbines and Power-Transactions of the ASME, 2010, 132(6): 1-10.
(  0) 0) |
| [11] |
Herrmann M, Arienti M, Soteriou M. The Impact of Density Ratio on the Primary Atomization of a Turbulent Liquid Jet in Crossflow[C]. Glasgow: Proceedings of the Asme Turbo Expo, 2010.
(  0) 0) |
| [12] |
Desjardins O, Pitsch H. Detailed Numerical Investigation of Turbulent Atomization of Liquid Jets[J]. Atomization and Sprays, 2010, 20(4): 311-336. DOI:10.1615/AtomizSpr.v20.i4
(  0) 0) |
| [13] |
Desjardins O, Moureau V, Pitsch H. An Accurate Conservative Level Set/Ghost Fluid Method for Simulating Turbulent Atomization[J]. Journal of Computational Physics, 2008, 227(18): 8395-8416. DOI:10.1016/j.jcp.2008.05.027
(  0) 0) |
| [14] |
Fuster D, Bague A, Boeck T, et al. Simulation of Primary Atomization with an Octree Adaptive Mesh Refinement and VOF Method[J]. International Journal of Multiphase Flow, 2009, 35(6): 550-565. DOI:10.1016/j.ijmultiphaseflow.2009.02.014
(  0) 0) |
| [15] |
Shinjo J, Umemura A. Surface Instability and Primary Atomization Characteristics of Straight Liquid Jet Sprays[J]. International Journal of Multiphase Flow, 2011, 37(10): 1294-1304. DOI:10.1016/j.ijmultiphaseflow.2011.08.002
(  0) 0) |
| [16] |
Shinjo J, Umemura A. Detailed Simulation of Primary Atomization Mechanisms in Diesel Jet Sprays (Isolated Identification of Liquid Jet Tip Effects)[J]. Proceedings of the Combustion Institute, 2011, 33(2): 2089-2097. DOI:10.1016/j.proci.2010.07.006
(  0) 0) |
| [17] |
Shinjo J, Xia J, Umemura A. Droplet/Ligament Modulation of Local Small-Scale Turbulence and Scalar Mixing in a Dense Fuel Spray[J]. Proceedings of the Combustion Institute, 2015, 35(2): 1595-1602. DOI:10.1016/j.proci.2014.06.088
(  0) 0) |
| [18] |
刘日超, 乐嘉陵, 杨顺华, 等. 直流喷射首次破碎的形变过程研究[J]. 推进技术, 2016, 37(7): 1334-1340. (LIU Ri-chao, LE Jia-ling, YANG Shun-hua, et al. Investigation of Deformation of Primary Breakup in Direct Injection[J]. Journal of Propulsion Technology, 2016, 37(7): 1334-1340.)
(  0) 0) |
| [19] |
Rusche Hen  0) 0) |
| [20] |
Hirt C W, Nichols B D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201-225. DOI:10.1016/0021-9991(81)90145-5
(  0) 0) |
| [21] |
邹建锋, 黄钰期, 应新亚, 等. VOF方法计算密度异重流[C]. 北京: 第十六届全国水动力学研讨会文集, 2002.
(  0) 0) |
| [22] |
邹建锋, 郑耀. 有界压缩VOF算法在界面流问题中的应用[J]. 浙江大学学报(工学版), 2008(2): 253-258. (  0) 0) |
| [23] |
傅燕妮. 气泡雾化过程的数值模拟研究[D]. 杭州: 浙江大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10335-1016073757.htm
(  0) 0) |
| [24] |
Brackbill J U, Kothe D B, Zemach C. A Continuum Method for Modeling Surface Tension[J]. Journal of Computational Physics, 1992, 100: 335-354. DOI:10.1016/0021-9991(92)90240-Y
(  0) 0) |
| [25] |
Reitz R D. Atomization and Other Breakup Regimes of a Liquid Jet[D]. Princeton, NJ: Princeton University, 1978. https://www.researchgate.net/publication/234466952_Atomization_and_other_breakup_regimes_of_a_liquid_jet
(  0) 0) |
| [26] |
Sallam K A, Dai Z, Faeth G M. Liquid Breakup at the Surface of Turbulent Round Liquid Jets in Still Gases[J]. International Journal of Multiphase Flow, 2002, 28(3): 427-449. DOI:10.1016/S0301-9322(01)00067-2
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


