近年来,吸气式高超声速推进技术中,超燃冲压发动机一直作为最佳的动力装置备受关注。这类发动机工作过程涉及众多学科问题,其中超声速下燃烧室内的湍流混合和高效燃烧一直是关注的重点之一。如何在更小的计算量下,尽量准确模拟湍流与燃烧相互作用,更是发动机设计者迫切希望解决的问题。
在涉及化学反应数值模拟中,无论雷诺平均数值模拟RANS(Reynolds-Averaged Navier-Stokes)或者大涡模拟LES(Large Eddy Simulation),平均(滤波)后的化学反应速率均因为强烈非线性而不能直接使用平均的温度和组分计算。为解决这个问题通常采用的燃烧模型有三类:火焰面类模型,PDF模型(Probability Density Function)和化学反应有限速率模型[1, 2]。火焰面模型从低速燃烧中发展而来,对于存在激波和火焰面相互作用等复杂超声速燃烧情况下的适用性还有待研究。PDF方法中要使用更准确的输运型PDF时,因为计算耗费过大,暂时还不能作为可行的工程手段。
化学反应有限速率模型近年来种类繁多,本文采用的是PaSR模型[1]和在此基础上引入的Ingenito提出的可压缩性修正方法[3]。在LES方面,Berglund等[4]采用单、双方程火焰面模型模拟了德国宇航研究中心(DLR)的氢燃料超燃冲压发动机燃烧室;之后使用PaSR模型计算了法国-日本联合实验室的ONERA燃烧室[5],同时考虑了单方程,双方程和七方程的氢燃料动力学机理,计算结果与实验吻合较好,并证明较为详细的动力学机理在复杂超声速湍流燃烧中是必要的。Baudoin等[2]对Volvo支板燃烧室模型进行模拟,对比了火焰面模型和四类化学反应有限速率模型,包括增厚火焰模型,EDC模型[6](Eddy Dissipation Concept),PaSR模型和设定概率密度函数模型PPDF[7]。四类模型尽管模型之间差别很大,但给出了相似的结果且与实验值吻合很好,比火焰面模型更优。Fureby等[8]在以前的基础上对PaSR模型进行了修正与完善,同样采用DLR燃烧室进行模拟验证,相比于双方程火焰面模型,PaSR模型更加准确,特别是针对燃烧区域的温度预测。
国内学者也对DLR燃烧室有过相关模拟研究,但使用PaSR模型的相对较少。范周琴等[9]在大涡模拟基础上使用火焰面模型计算了DLR燃烧室,对比分析二维与三维的结果,得到后者在捕捉流场细节和精确性方面明显优于前者。汪洪波等[10]在采用设定PDF方法计算该燃烧室时也获得了较好的结果,但因为LES网格尺度不足致使剪切层和大尺度涡边界区域亚格子速度脉动偏大。黄志伟等[11]则将PaSR模型引入OpenFOAM平台,采用与Baudoin一致的PaSR模型,对DLR燃烧室的计算结果与实验符合较好,其中双峰特性不明显,但峰值大小接近;作者还在文献[12]中论证了壁面粘性的影响,认为其主要影响在壁面附面层很窄的区域,关心核心流时采用无粘假设是合理的。
本文首先采用PaSR模型,对德国宇航研究中心(DLR)的氢燃料超燃冲压发动机的燃烧流动进行了数值模拟,深入分析了超声速燃烧室中湍流混合与燃烧相互作用的细节。再将Ingenito提出的可压缩性修正方法引入PaSR模型,提出了可压缩PaSR模型,考虑在化学反应有限速率模型中引入可压缩性对超声速燃烧的影响,对比分析了修正的影响和相关因素。
2 理论模型与数值方法 2.1 PaSR模型该模型与Magnussen提出的EDC模型[6]类似,均假设化学反应发生在小尺度湍流,也就是精细结构中(以上标*代表),其它称为周围流体区域(以上标0代表)。在详细化学反应计算中,精细结构区域被视为完全搅拌反应器(Well-stirred Reactors),也就是Perfectly Stirred Reactor(PSR),反应速率很高。周围区域的反应速率小到可以忽略。
从整体的观点来看,平均后的化学反应速率可视为
| $ {\overline {\dot \omega } _k} = \int\limits_\psi {P\left( \psi \right){{\dot \omega }_{\rm{F}}}\left( \psi \right){\rm{d}}\psi } $ | (1) |
式中P代表标量联合PDF,ψ = (T, Yk)T是样本组分矢量。PDF假定为双峰形状,可分解为一个精细结构分布和环绕分布
| $ P\left( \psi \right) = {\gamma ^{\rm{*}}}\delta \left( {\psi - {\psi ^{\rm{*}}}} \right) + \left( {1 - {\gamma ^{\rm{*}}}} \right)\delta \left( {\psi - {\psi ^0}} \right) $ | (2) |
由此平均化学反应速率为
| $ {\overline {\dot \omega } _k} = {\gamma ^{\rm{*}}}{\dot \omega _k}\left( {{\psi ^{\rm{*}}}} \right) + \left( {1 - {\gamma ^{\rm{*}}}} \right){\dot \omega _k}\left( {{\psi ^0}} \right) $ | (3) |
不考虑周围流体区域的化学反应进一步得到
| $ {\overline {\dot \omega } _k} = {\gamma ^{\rm{*}}}{\dot \omega _k}\left( {{\psi ^{\rm{*}}}} \right) $ | (4) |
式中γ*表示精细尺度结构的体积分数。EDC模型通过Kolmogorov尺度来表征,PaSR模型则混合使用了Kolmogorov尺度和化学反应解析尺度,认为
| $ {\gamma ^{\rm{*}}} = \frac{{{\tau _{{\rm{ch}}}}}}{{{\tau _{{\rm{ch}}}} + {\tau _{\rm{m}}}}} $ | (5) |
式中τm为湍流混合时间尺度,是Kolmogorov时间尺度τk和网格时间尺度τΔ的调和平均
Ingenito等在近十年的研究中逐步论证了可压缩性对超声速湍流燃烧的影响[3, 14, 15],并在此基础上提出了ISCM模型。其中对化学反应源项的影响主要包括分子碰撞频率和燃烧模式,并修正了湍动能方程,得到的化学反应源项计算式为
| $ \overline {\dot \omega } = {\gamma ^{\rm{*}}}\left( {1 + 2Ma_{\rm{S}}^2} \right)\dot \omega $ | (6) |
其中(1 + 2MaS2)是可压缩性对分子碰撞频率推导的修正关系,MaS是修正Ma数,依赖于湍流强度,一般为1%~10%。燃烧模型方面推导了超声速燃烧近似为定容燃烧,并认为化学反应发生在精细结构中,体积分数为网格体积的γ*。精细结构假定为管状理想搅拌器,η代表通过Kolmogorov假设计算的湍流特征长度,Δ为网格维度,因此γ* = (πη2Δ)/Δ3 = (πη2)/Δ2。
这样定义的体积分数与网格尺度关联密切,考虑到Ingenito是在LES条件下计算的,网格密度较小,而本文采用雷诺平均,因此精细结构体分数采用PaSR模型的算法,同时加入分子碰撞频率的修正关系,构成可压缩PaSR模型(C-PaSR)。
2.3 数值方法本文控制方程使用雷诺平均N-S方程组(RANS),湍流模型为两方程Menter-SST模型。无粘通量的求解使用Edwards低耗散通量分裂格式。为了保证解的有效性,计算应用了总变差衰减格式(TVD),三阶MUSCL插值,以及在三个方向(x,y和z方向)均使用了Van Leer通量限制器。决定层流能量输运能力的普朗特数为0.72,决定湍流能量传输的湍流普朗特数选取0.9,决定层流组分密度传输的层流施密特数为0.22,决定湍流组分密度传输的湍流施密特数选取0.9。化学反应机理使用NASA Langley的9组分18方程氢气-氧气反应动力学模型,其中来流组分包括氧气和氮气。
时间迭代格式为对角线近式分解(DAF),计算域均采用时间推进方法。选择当地时间步加速技术对求解过程进行加速,并采用自适应CFL数来确保计算稳定性。
3 计算构型与边界条件DLR氢燃料超燃冲压发动机简化模型模型如图 1所示[16],燃烧室入口高度为50mm,宽40mm,支板长32mm,高6mm,支板底部有15个均匀分布直径为1mm的小孔,用以氢气喷入。各小孔之间间距为3mm。坐标原点位于下壁面上楔形尖点上游35mm,即楔形尖点坐标为(25,35)。因为整个模型与流场具有很好的展向周期性,为了减小计算量,本文只采用一个喷孔,并将展向两个面设置为对称边界条件。最终生成318万结构化六面体网格,包括在喷孔、支板前缘、支板壁面和尾迹区加密以保证较好的网格分辨率。

|
Fig. 1 Schematic of the DLR supersonic combustion |
空气来流与氢气喷流条件见表 1,空气和氢气的湍流度分别为0.5%和5%。因为本算例雷诺数较高,求解上下壁面处的激波/边界层相互作用需要大量网格,因此采用Génin等[17]的结论,将上下壁面取为绝热滑移壁面,忽略边界层对中心流场的影响,节省计算资源。支板壁面采用绝热、无滑移边界条件,出口采用一阶外插边界条件。
|
|
Table 1 Inflow conditions |
图 2所示为实验纹影结果[16](上)和计算密度分布(下)。可以看到计算的燃烧室激波分布及剪切层形态与实验观测符合较好,说明流场计算结果可靠。

|
Fig. 2 Schlieren image of experimental result (top) density contour of simulation (bottom) |
因为采用PaSR模型和可压缩PaSR模型计算得到的流场特征参数分布云图差别不大,在整体分析流动特征时选择PaSR模型的结果做为代表。通过图 3过喷口中心的湍流特征参数分布云图可以看出,燃烧室点火发生在支板上下边缘来流空气与氢气形成反应剪切层,之后出现了混合控制的湍流扩散火焰,并稳定在尾迹区域。支板前缘形成的两道激波和后缘形成的两道膨胀波在燃烧室壁面反射形成复杂的波系结构。由于点火后支板尾部压力上升,剪切层不再汇聚而是扩展到稍宽于支板高度。超声速反应剪切层较为稳定,厚度较大,反射波系无法穿透中心射流,从而再次反射,在壁面和剪切层之间形成新的波系结构。剪切层也因此偏转,限制了尾迹区,最终形成尾迹区的流动与自由来流近似平行的状态,下游只出现一些细小的波系。因此整个燃烧区域可以大致分为三部分[4]:从支板底部到扩散火焰主导前的诱导区,此时反应发生在剪切层内;对流混合产生大尺度涡结构的过渡区,即OH等反应离子和最终产物浓度较高的区域;基本稳定的湍流燃烧区域。以上流场特征在马赫数云图表现最为明显,温度云图中也有所体现。

|
Fig. 3 Characteristics contours of PaSR model result in the centerplane |
一般以OH基团作为火焰面结构的表征,由图 3(d)可以看出支板后1~2个支板厚度的距离开始明显燃烧。结合喷口附近的流线图 4可以看到,此处为诱导区后的回流区。回流区结束后上下剪切层逐渐汇合,在中心形成一道混合层,剩余燃料继续反应,使得反应集中于流道中心附近,也在此集中了大量燃烧最终产物和反应中间产物。因此这类支板后超声速湍流燃烧的火焰结构类似于湍流抬举火焰。
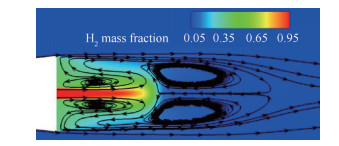
|
Fig. 4 Hydrogen field contour and streamlines in the injection and recirculation regions |
PaSR模型中精细结构体分数γ* = τch/(τch + τm)正是对化学反应源项的修正系数,通过湍流时间尺度和化学反应时间尺度代表当地的混合和燃烧的相对强弱,也是化学反应有限速率模型的主要修正。从图 5可以清晰地看到,除过渡区和稳定湍流燃烧区域,其它区域γ* =1,说明诱导区内混合不复杂,相较之下燃烧占主导地位。过渡区中间γ*较大,因为此处化学反应最为剧烈,符合未修正的快速化学反应假设。上下两侧γ*减小,出现混合与燃烧作用相当的区域,表明湍流混合的时间尺度与化学反应时间尺度相当。之后的稳定区中燃烧基本结束,湍流混合占据更加主导的作用,因此体积分数更小,修正更大。整个分布与湍流抬举火焰吻合,也与燃烧室下游实际流场情况结合很好,说明PaSR模型对于湍流燃烧相互作用的描述是合理的。

|
Fig. 5 Fine-structure volume fraction contour of PaSR model result |
图 6为三个截面的纵向温度分布,实验数据和RANS下火焰面模型的计算数据均源自文献[16]。计算采用的边界条件和初始状况与文献相同。其中X=78mm处的结果使用化学反应有限速率模型改进不大,同时没有预测出温度的双峰特性,有待使用LES进一步验证。X=125mm处结果较为满意,使用PaSR模型后温度峰值准确,但依然略高估了混合区域在横向的尺度。C-PaSR模型的结果偏移更多,结合后面X=233mm处情况来看应该是PaSR模型温度峰值预测依然偏高,这也是因为此处湍流燃烧相互作用依然较强。X=233mm处的温度分布在修正后非常理想[11]。考虑湍流燃烧相互作用后已将预估过高的温度峰值抑制,而C-PaSR模型则完美预测了此区域的温度分布。由此可见,化学反应有限速率模型对温度预测更加合理,可以在引入很小计算量的情况下带来可观的修正。

|
Fig. 6 Static temperature distributions |
图 7是燃烧流场中不同截面的轴向速度分布。其中左上为Y=25mm处,即通过喷孔中心轴线的轴向速度分布。计算结果在诱导区与实验存在较大偏差,对比图 2可知计算的回流区比实验的回流区小,逆向速度更高。采用两种PaSR模型的计算结果改进不大。
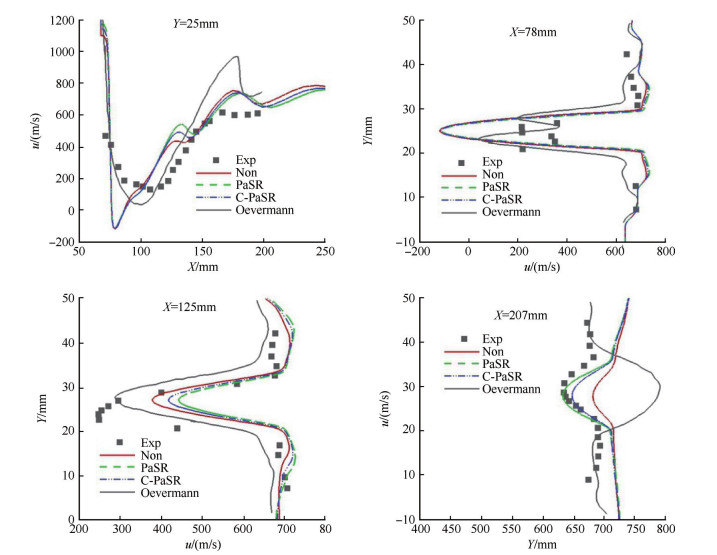
|
Fig. 7 Axis velocity distributions |
对比三个流向位置的速度分布可以看出,在X=78mm处和X=125mm处计算结果改进均不大。这两处近似为过渡区开始和结束的截面,即燃烧和湍流相互作用最为强烈的区域,虽然此处采用化学反应有限速率模型后对化学反应源项修正已经很大,但结果依然不理想,说明修正不足以预测出湍流燃烧相互作用较强区域内的双峰特性。考虑到Fureby等[8]在大涡模拟的条件下和Oevermann[16]使用火焰面模型均得到了X=78mm处的速度双峰特性,推测应该是在RANS条件下化学反应有限速率模型并不能得到混合较强区域的准确估计,此时没有火焰面模型结果理想,但在LES情况下对湍流燃烧相互作用的预测更加准确[8],这也是下一步的研究方向。X=125mm截面中实验结果速度不对称的原因未知,大量RANS和LES的结果均未表现出这一点[8, 11, 16]。X=207mm处,尾迹区与来流的速度差减小,PaSR模型的计算结果与实验值吻合很好,考虑了可压缩的C-PaSR模型则峰值偏差稍大。整体来看在燃烧不是很强烈的区域,化学反应有限速率模型可以获得较为理想的速度结果。
5 结论(1)整个燃烧区域可以大致分为三部分:从支板底部到抬举火焰主导前的诱导区,对流混合产生大尺度涡结构的过渡区,和基本稳定的湍流燃烧区域。诱导区内湍流混合不算强烈,化学反应占据主导地位;过渡区内部燃烧剧烈,两侧的剪切层湍流与燃烧的强度较为接近;湍流燃烧区中混合作用更加明显,相对燃烧过程更加重要,因此PaSR模型修正最大,结果也更加合理。
(2)PaSR模型中精细结构体积分数对化学反应源项的修正考虑了湍流特征时间尺度与化学反应时间尺度,修正分布与实际燃烧情况更加吻合,改善了湍流燃烧计算结果。
(3)考虑可压缩性的C-PaSR模型在燃烧区域对于温度和速度的预测均比PaSR模型计算结果略好,这在混合占主导的湍流燃烧区域体现更加明显,此时的修正结果也更接近实验值。
| [1] |
Sabelnikov V, Fureby C. Extended LES-PASR Model for Simulation of Turbulent Combustion[J]. Progress in Propulsion Physics, 2013(4): 539-568.
(  0) 0) |
| [2] |
Baudoin E, Yu R, Bai, et al. Comparison of LES Models Applied to a Bluff Body Stabilized Flame[R]. AIAA 2009-1178. http://arc.aiaa.org/doi/abs/10.2514/6.2009-1178
(  0) 0) |
| [3] |
Ingenito A, Bruno C. Physics and Regimes of Supersonic Combustion[J]. AIAA Journal, 2010, 48(3): 516-525.
(  0) 0) |
| [4] |
Berglund M, Fureby C. LES of Supersonic Combustion in a Scramjet Engine Model[J]. Proceedings of the Combustion Institute, 2007, 31: 2497-2504. DOI:10.1016/j.proci.2006.07.074
(  0) 0) |
| [5] |
Berglund M, Fedina E, Fureby C, et al. Finite Rate Chemistry Large-Eddy Simulation of Self-Ignition in a Supersonic Combustion Ramjet[J]. AIAA Journal, 2010, 48(3): 540-550. DOI:10.2514/1.43746
(  0) 0) |
| [6] |
Magnussen B F. The Eddy Dissipation Concept: a Bridge Between Science and Technology[C]. Lisbon: ECCOMAS Thematic Conference on Computational Combustion, 2005.
(  0) 0) |
| [7] |
Girimaji S S. Assumed PDF Model for Turbulent Mixing Validation and Extension to Multiple Scalar Mixing[J]. Combustion Science and Technology, 1991, 78: 177-196. DOI:10.1080/00102209108951748
(  0) 0) |
| [8] |
Fureby C, Fedina E, Tegner J. A Computational Study of Supersonic Combustion Behind a Wedge-Shaped Flameholder[J]. Shock Waves, 2014, 24: 41-50. DOI:10.1007/s00193-013-0459-2
(  0) 0) |
| [9] |
范周琴, 孙明波, 刘卫东. 支板喷射超声速燃烧流场三维大涡模拟[J]. 国防科技大学学报, 2011, 33(1): 1-6. (  0) 0) |
| [10] |
汪洪波, 孙明波, 范周琴, 等. 支板喷射超声速湍流燃烧的大涡模拟[J]. 推进技术, 2012, 33(4): 552-558. (WANG Hong-bo, SUN Ming-bo, FAN Zhou-qin, et al. Large Eddy Simulation of Supersonic Turbulent Combustion with a Strut Injector[J]. Journal of Propulsion Technology, 2012, 33(4): 552-558.)
(  0) 0) |
| [11] |
Huang Z W, He G Q, Wei X G. Large Eddy Simulation of Flame Structure and Combustion Mode in a Hydrogen Fueled Supersonic Combustor[J]. Hydrogen Energy, 2015, 40: 9815-9824. DOI:10.1016/j.ijhydene.2015.06.011
(  0) 0) |
| [12] |
黄志伟, 何国强, 秦飞, 等. 支板增强混合超声速燃烧的大涡模拟研究[J]. 固体火箭技术, 2015, 38(5): 664-670. (  0) 0) |
| [13] |
Moule Y, Sabelnikov V, Mura A. Highly Resolved Numerical Simulation of Combustion in Supersonic Hydrogen-Air Coflowing Jets[J]. Combustion and Flame, 2015, 161: 2647-2668.
(  0) 0) |
| [14] |
Ingenito A, Flora M G D, Bruno C. LES Modeling of Scramjet Combustion[R]. AIAA 2006-1383. http://arc.aiaa.org/doi/abs/10.2514/6.2006-1383
(  0) 0) |
| [15] |
Ingenito A, Flora M G D, Bruno C. A Novel Model of Turbulent Supersonic Combustion: Development and Validation[R]. AIAA 2006-4351. https://arc.aiaa.org/doi/abs/10.2514/6.2006-4351
(  0) 0) |
| [16] |
Oevermann M. Numerical Investigation of Turbulent Hydrogen Combustion in a SCRAMJET Using Flamelet Modeling[J]. Aerospace Science and Technology, 2000, 4(7): 463-480. DOI:10.1016/S1270-9638(00)01070-1
(  0) 0) |
| [17] |
Génin F, Menon S. Simulation of Turbulent Mixing Behind a Strut Injector in Supersonic Flow[J]. AIAA Journal, 2010, 48(3): 526-539. DOI:10.2514/1.43647
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

