对于涡扇发动机,内涵和外涵气流通过混合器部件进行掺混。随着混合距离的逐渐增加,内涵和外涵流体逐渐达到较好的掺混程度,即两股流体对应的混合效率沿流向逐渐提高。为了定量计算内外涵两股流体的混合效率,Frost教授1966年首先提出了经典热混合效率公式[1]。热混合效率的定义是:具有不同能量的、多股流体掺混过程中,混合流体温度分布的均匀程度。Frost教授在推导经典热混合效率公式时,假设混合过程满足一维轴向流动假设,同时在垂直于轴向的截面上,混合流体的静压保持不变。但在实际应用中发现:采用该经典热混合效率公式计算波瓣混合器下游流场混合效率时,热混合效率沿流向的变化规律不符合物理规律,甚至会出现负值[2]。由于波瓣混合器的皱褶型表面结构,在波瓣尾缘下游流场中诱导出相互逆转的大尺度流向涡序列,使得混合流场呈现典型的三维流动状态;与此同时,经典热混合效率公式自身分子分母存在的内在数学缺陷,使得经典热混合效率公式失效。
在经典热混合效率公式基础上,刘友宏教授和谢翌2011年引用概率论中的方差对横截面上混合流体实际温度分布与理想均匀分布的差异进行定量衡量,并推导出刘-谢热混合效率公式[2]。与Frost教授提出的经典热混合效率公式相比,刘-谢热混合效率公式显著拓宽了热混合效率公式的适用范围,使其能够直接应用于含有波瓣混合器的强迫掺混过程。基于刘-谢热混合效率公式,研究学者们针对涡扇发动机S型以及轴对称形式排气喷管中波瓣混合器几何结构修形,定量研究了不同修形方式对排气喷管气动热力性能的影响规律[3~5]。此外,通过刘-谢热混合效率公式,研究了波瓣混合器下游流场中强迫掺混过程对热混合效率发展趋势的影响规律[6~8],为涡扇发动机混合排气喷管中波瓣混合器结构的设计、优化提供了必要依据。
对于含有加力燃烧室的涡扇发动机,加力燃烧过程释放了大量的热量(内热源)、增加了混合燃气的质量流量(内质量源),从而使得刘-谢热混合效率公式中理想混合温度的计算方法失效,所以刘-谢热混合效率公式不能合理衡量加力燃烧过程中混合流体的热混合效率。为了将热混合效率公式的使用范围拓宽至加力燃烧状态,本文在刘-谢热混合效率公式基础上,改进刘-谢热混合效率公式中理想混合温度的计算方法、引入平均温差参数,提出了具有普适意义的新热混合效率公式——刘-杜热混合效率公式。对于本文提出的刘-杜热混合效率公式,不仅能够适用于含有内热源、内质量源的强迫掺混过程,同样适用于不含内热源、内质量源的强迫掺混过程。
2 刘-杜热混合效率公式的推导过程刘-谢热混合效率用参数ηLX表示,下标字母分别表示刘、谢,对应的计算公式[2]如式(1)所示。
| $ {\eta _{{\rm{LX}}}} = 1 - \frac{{\mathop \smallint \nolimits {{\left( {T - {T_{{\rm{mix}}, {\rm{inlet}}}}} \right)}^2}{\rm{d}}\dot m}}{{T{}_{{\rm{hot}}}^2\dot m{{\dot m}_{{\rm{hot}}}} + T_{{\rm{cold}}}^2{{\dot m}_{{\rm{cold}}}} - T_{{\rm{mix}}, {\rm{inlet}}}^2\left( {{{\dot m}_{{\rm{hot}}}} + {{\dot m}_{{\rm{cold}}}}} \right)}} $ | (1) |
式(1)中的Tmix, inlet为入口截面处内外涵流体理想混合后的温度,计算过程如式(2)所示。
| $ {T_{{\rm{mix}}, {\rm{inlet}}}} = \frac{{\int\limits_{{\rm{hot}}} {T{\rm{d}}\dot m} + \int\limits_{{\rm{cold}}} {T{\rm{d}}\dot m} }}{{{{\dot m}_{{\rm{hot}}}} + {{\dot m}_{{\rm{cold}}}}}} $ | (2) |
对于式(2)中的Tmix, inlet参数,基于内外涵入口截面上流体温度、质量流量计算得到,主要用于混合排气系统。采用式(1)计算刘-谢热混合效率时,对于不同混合距离的横截面,Tmix, inlet参数的数值始终保持不变。
对于加力燃烧室中的流动过程,特别是新型加力燃烧室,加力燃烧与内外涵流体混合过程同时发生,横截面上混合流体的理想混合温度,显然受到加力燃烧过程释放的大量热量(内热源)、增加的混合燃气质量流量(内质量源)的影响。因此,采用刘-谢热混合效率公式计算加力状态下加力燃烧室中的热混合效率,将存在物理意义和工程实际的明显缺陷,如本文图 9所示:在加力状态下横截面上温度方差显著升高,使得式(1)中第二项的计算结果大于1,从而导致刘-谢热混合效率值小于0。
|
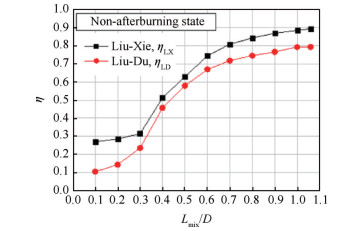
Fig. 1 Thermal mixing efficiency for the case with a lobe inward penetration angle of 10° under the non-afterburning state |
|
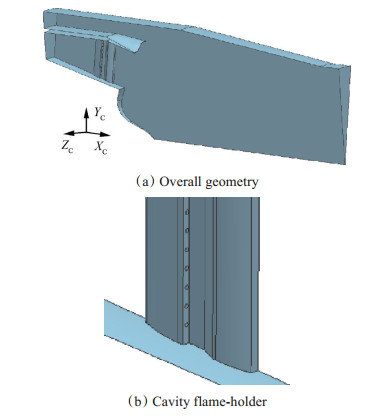
Fig. 2 Geometry of the investigated integrated afterburner |
|
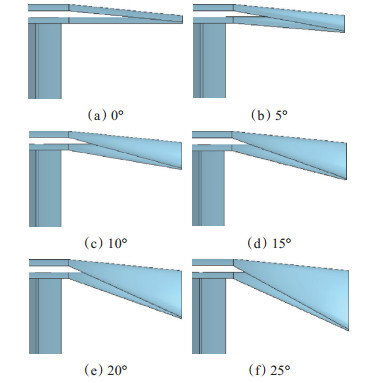
Fig. 3 Geometrical models with different lobe inward penetration angles |
|
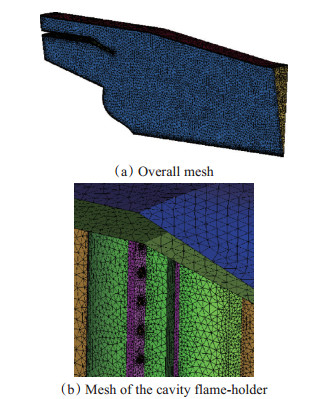
Fig. 4 Three dimensional mesh used in the simulation of flow field |
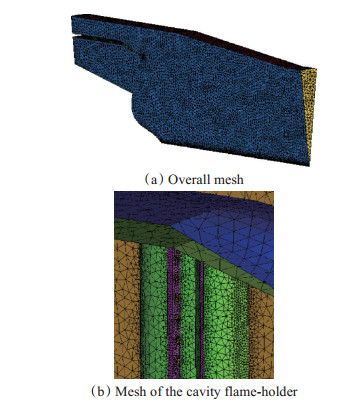
|
Fig. 5 Three dimensional mesh used in the simulation of radiation field |

|
Fig. 6 Geometrical model used in the validation investigation |
|
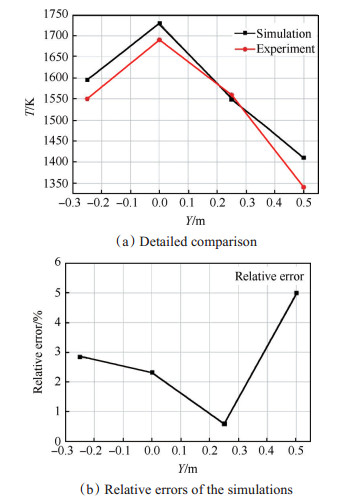
Fig. 7 Comparison between simulation and experimental results |

|
Fig. 8 Thermal mixing efficiency for the case with a lobe inward penetration angle of 10° under the afterburning state |
|
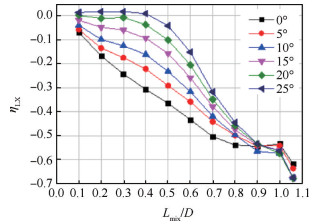
Fig. 9 Liu-Xie thermal mixing efficiency for the cases with different lobe inward penetration angles under the afterburning state |
针对刘-谢热混合效率公式应用于加力状态下混合过程的缺陷,本文计算理想混合温度时,基于能量守恒方程,得到每一个横截面上内外涵流体理想混合后的温度,用参数Tmix表示,相应的计算公式如式(3)所示。
| $ {T_{{\rm{mix}}}} = \frac{{\mathop \smallint \nolimits {C_p}T{\rm{d}}\dot m}}{{{C_{p, {\rm{mix}}}}{{\dot m}_{{\rm{mix}}}}}} $ | (3) |
在式(3)中,Cp为横截面上流体的定压比热容,Cp, mix为理想混合后混合流体对应的定压比热容,
在理想混合温度Tmix基础上,进一步定义横截面上的平均温差
| $ \overline {{\rm{\Delta }}T} = \frac{{\mathop \smallint \nolimits \left| {T - {T_{{\rm{mix}}}}} \right|{\rm{d}}\dot m}}{{{{\dot m}_{{\rm{mix}}}}}} $ | (4) |
基于理想混合温度Tmix以及平均温差
| $ {\eta _{{\rm{TM}}}} = 1 - \frac{{\overline {{\rm{\Delta }}T} }}{{{T_{{\rm{mix}}}}}} $ | (5) |
在式(5)中,Tmix以及
完全未混合状态下,在接触混合的起始截面上,内涵以及外涵流体分别均匀分布,此时可以得到
| $ \begin{array}{l} \mathop \smallint \nolimits {C_p}T{\rm{d}}\dot m = \int\limits_{{\rm{hot}}} {{C_p}T{\rm{d}}\dot m} + \int\limits_{{\rm{cold}}} {{C_p}T{\rm{d}}\dot m} = {C_{p, {\rm{hot}}}}{T_{{\rm{hot}}}}{{\dot m}_{{\rm{hot}}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{C_{p, {\rm{cold}}}}{T_{{\rm{cold}}}}{{\dot m}_{{\rm{cold}}}}\\ {T_{{\rm{mix}}}} = \frac{{\mathop \smallint \nolimits {C_p}T{\rm{d}}\dot m}}{{{C_{p, {\rm{mix}}}}{{\dot m}_{{\rm{mix}}}}}} = \frac{{{C_{p, {\rm{hot}}}}{T_{{\rm{hot}}}}{{\dot m}_{{\rm{hot}}}} + {C_{p, {\rm{cold}}}}{T_{{\rm{cold}}}}{{\dot m}_{{\rm{cold}}}}}}{{{C_{p, {\rm{mix}}}}\left( {{{\dot m}_{{\rm{hot}}}} + {{\dot m}_{{\rm{cold}}}}} \right)}}\\ \mathop \smallint \nolimits \left| {T - {T_{{\rm{mix}}}}} \right|{\rm{d}}\dot m = \left( {{T_{{\rm{hot}}}} - {T_{{\rm{mix}}}}} \right){{\dot m}_{{\rm{hot}}}} + \left( {{T_{{\rm{mix}}}} - {T_{{\rm{cold}}}}} \right){{\dot m}_{{\rm{cold}}}} \end{array} $ | (6) |
将式(6)带入到式(5)中,经过数学推导后,可以得到完全未混合状态下在接触混合起始截面上参数ηTM的值为
| $ {\eta _{{\rm{TM}}}} = 1 - \frac{{\left( {{T_{{\rm{hot}}}} - {T_{{\rm{mix}}}}} \right){{\dot m}_{{\rm{hot}}}} + \left( {{T_{{\rm{mix}}}} - {T_{{\rm{cold}}}}} \right){{\dot m}_{{\rm{cold}}}}}}{{\frac{{{C_{p, {\rm{hot}}}}{T_{{\rm{hot}}}}{{\dot m}_{{\rm{hot}}}} + {C_{p, {\rm{cold}}}}{T_{{\rm{cold}}}}{{\dot m}_{{\rm{cold}}}}}}{{{C_{p, {\rm{mix}}}}}}}} $ | (7) |
由式(7)可知,参数ηTM取值为0的前提条件为
| $ \begin{array}{*{20}{l}} {{C_{p, {\rm{mix}}}}\left( {{{\dot m}_{{\rm{hot}}}} + {{\dot m}_{{\rm{cold}}}}} \right)\left( {{T_{{\rm{hot}}}}{{\dot m}_{{\rm{hot}}}} - {T_{{\rm{cold}}}}{{\dot m}_{{\rm{cold}}}}} \right) = }\\ {2{{\dot m}_{{\rm{hot}}}}\left( {{C_{p, {\rm{hot}}}}{T_{{\rm{hot}}}}{{\dot m}_{{\rm{hot}}}} + {C_{p, {\rm{cold}}}}{T_{{\rm{cold}}}}{{\dot m}_{{\rm{cold}}}}} \right)} \end{array} $ | (8) |
在实际工作状态中接触混合起始截面上,内外涵流体对应的温度以及流量的数值并不一定能够满足式(8),因而导致在接触混合起始截面上参数ηTM大于0。这是不符合物理常识的,对于热混合效率参数,一般规定在接触混合起始截面上的热混合效率为0,完全混合时对应的热混合效率为1。因此,本文在热混合效率指标ηTM的基础上,参考文献[2]中的方差修正理念,提出了一种新型热混合效率计算公式,本文称之为刘-杜热混合效率公式,采用符号ηLD表示刘-杜热混合效率,下角标分别代表刘、杜。刘-杜热混合效率公式如式(9)所示。
| $ {\eta _{{\rm{LD}}}} = {\eta _{{\rm{TM}}}} - \frac{{{{(1 - {\eta _{{\rm{TM}}}})}^2}}}{{{{(1 - {\eta _0})}^2}}} \cdot {\eta _0} $ | (9) |
式中
| $ {\eta _{{\rm{TM}}}} = 1 - \frac{{\overline {{\rm{\Delta }}T} }}{{{T_{{\rm{mix}}}}}} $ | (10) |
| $ {\eta _0} = 1 - {\left. {\left( {\frac{{\overline {{\rm{\Delta }}T} }}{{{T_{{\rm{mix}}}}}}} \right)} \right|_{{L_{{\rm{mix}}}} = 0}} $ | (11) |
参数η0的含义是:在实际接触混合起始截面上,混合流体对应的ηTM数值。
3 理想状态下刘-杜热混合效率公式的定量验证本节针对上文提出的刘-杜热混合效率公式,通过公式推演,验证刘-杜热混合效率公式的取值范围为0至1。
通过对式(9)中的两项进行合并,可以得到
| $ {\eta _{{\rm{LD}}}} = \frac{{\left( {{\eta _{{\rm{TM}}}} - {\eta _0}} \right)\left( {1 - {\eta _{{\rm{TM}}}}{\eta _0}} \right)}}{{{{(1 - {\eta _0})}^2}}} $ | (12) |
因为η0以及ηTM满足不等式关系
| $ 0 \le {\eta _0} \le {\eta _{{\rm{TM}}}} \le 1 $ | (13) |
将式(13)中的不等式关系代入到式(12)中,可以得到ηLD ≥ 0。
为了证明刘-杜热混合效率ηLD的取值上限为1,即等价于证明式(14)中的不等式关系成立。
| $ \frac{{\left( {{\eta _{{\rm{TM}}}} - {\eta _0}} \right)\left( {1 - {\eta _{{\rm{TM}}}}{\eta _0}} \right)}}{{{{(1 - {\eta _0})}^2}}} - 1 \le 0 $ | (14) |
对于式(14)中的左侧部分,可以得到
| $ \begin{array}{*{20}{l}} {\frac{{\left( {{\eta _{{\rm{TM}}}} - {\eta _0}} \right)\left( {1 - {\eta _{{\rm{TM}}}}{\eta _0}} \right)}}{{{{(1 - {\eta _0})}^2}}} - 1 = }\\ {\frac{{\left( {{\eta _{{\rm{TM}}}} - 1} \right)\left[ {1 + {\eta _0}^2 - {\eta _0}\left( {{\eta _{{\rm{TM}}}} + 1} \right)} \right]}}{{{{(1 - {\eta _0})}^2}}}} \end{array} $ | (15) |
对于式(15)可以进一步得到
| $ 1 + {\eta _0}^2 - {\eta _0}\left( {{\eta _{{\rm{TM}}}} + 1} \right) \ge 1 + {\eta _0}^2 - 2{\eta _0} $ | (16) |
综合式(15)以及式(16),可得
| $ \frac{{\left( {{\eta _{{\rm{TM}}}} - {\eta _0}} \right)\left( {1 - {\eta _{{\rm{TM}}}}{\eta _0}} \right)}}{{{{(1 - {\eta _0})}^2}}} - 1 \le 0 $ | (17) |
即
| $ {\eta _{{\rm{LD}}}} \le 1 $ | (18) |
通过以上的公式推演过程,最终可以得到刘-杜热混合效率公式的取值范围为0至1,即
| $ 0 \le {\eta _{{\rm{LD}}}} \le 1 $ | (19) |
对于本文提出的刘-杜热混合效率公式,主要是为了解决刘-谢热混合效率公式在加力燃烧流场中的使用缺陷,同时刘-杜热混合效率公式也适用于非加力燃烧工况下热混合效率的计算研究。为此,针对同一非加力燃烧工况,将刘-杜热混合效率公式以及刘-谢热混合效率公式的计算结果,进行了对比分析验证。
基于波瓣内扩张角10°模型,通过本文开发的耦合计算程序,得到了非加力燃烧工况下的数值仿真结果。图 1为非加力燃烧工况下,刘-谢热混合效率公式以及刘-杜热混合效率公式对应的分布曲线。
在图 1中,Lmix的含义是:混合流场中横截面与波瓣尾缘截面沿流向的距离。根据图 1中的分布曲线可知:随着混合距离的增加,非加力状态下刘-谢热混合效率公式以及刘-杜热混合效率公式对应的数值均逐渐上升。在对比研究的整个混合范围内,刘-杜热混合效率公式对应的变化趋势与刘-谢热混合效率公式相同。
在波瓣混合器下游混合流场中,存在由波瓣皱褶型表面诱导出的大尺度流向涡阵列,对混合流体的混合过程起到主导作用。随着混合距离的增加,大尺度流向涡阵列的强度逐渐增强;经过一段混合距离之后,流向涡阵列逐渐耗散,其对应的强迫掺混能力逐渐降低。在流向涡阵列的影响下,混合流体对应的热混合效率增长速率呈现出先上升后下降的变化趋势。对于图 1中刘-杜热混合效率曲线,可见:随着混合距离的增加,Lmix/D=0.4截面上游区域热混合效率增长速率逐渐上升,Lmix/D=0.4截面下游区域热混合效率增长速率逐渐下降。在靠近一体化加力燃烧室出口附近区域,随着混合距离的增加,刘-杜热混合效率的增加已经非常微弱。
基于本节研究可见:对于本文提出的刘-杜热混合效率公式,在非加力状态下,其对应的热混合效率变化规律与刘-谢热混合效率公式是相容的;此外,可以采用刘-杜热混合效率公式,定量研究非加力状态下一体化加力燃烧室中的混合过程。
5 刘-杜热混合效率公式在一体化加力燃烧室中的应用 5.1 几何模型对加力燃烧室部件采用一体化设计思路,有助于降低加力燃烧室重量、提升加力燃烧室的稳定性[9~11]。一体化加力燃烧室包括内外涵入口、一体化支板火焰稳定器、混合器以及中心锥等部件。本文中研究的一体化加力燃烧室结构如图 2所示。
一体化加力燃烧室中波瓣混合器数目以及凹腔支板数目均为16,实际建立的几何模型包含半个凹腔支板结构,相应的扇形计算域圆周角度为11.25°。将一体化加力燃烧室的外涵入口外直径取定为D,其他关键无量纲几何尺寸如表 1所示。
|
|
Table 1 Fundamental dimensions of the integrated afterburner |
在凹腔支板表面开设一系列小孔,通过引用外涵冷气对凹腔表面进行冷却。凹腔支板火焰稳定器沿流向长度为110mm,凹腔表面冷气小孔数目为11,冷气小孔直径为4mm。基于一体化加力燃烧室模型建立了一组关于波瓣混合器内扩张角的几何模型,其对应的内扩张角分别为0°,5°,10°,15°,20°以及25°,如图 3所示。
5.2 空间离散网格在加力状态下,由喷油杆喷出的燃油在一体化加力燃烧室中逐渐燃烧,属于典型的三维两相湍流燃烧过程。采用OpenFOAM中的Simple Reacting Parcel Foam求解器对加力燃烧过程进行数值求解,同时采用本课题组开发的辐射换热求解器对一体化加力燃烧室中的辐射换热过程进行求解。辐射换热求解器与Simple Reacting Parcel Foam求解器耦合计算。与流场计算网格相比,辐射场计算网格较为稀疏[12]。因此,三维流场以及辐射场计算时,分别基于不同的三维非结构化网格。
对流场计算网格以及辐射场计算网格进行无关性研究后,得到网格数目合适的三维非结构化网格。对于三维流场计算网格,计算域主体网格为四面体网格、近壁区域设置边界层网格。三维流场计算网格数目约为40万,具体如图 4所示。
对于三维辐射场计算网格,其对应的网格数目约为20万,如图 5所示。
5.3 控制方程当考虑化学反应时,守恒形式的三维粘性流体N-S方程如式(20)所示。
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial y}} + \frac{{\partial \mathit{\boldsymbol{H}}}}{{\partial z}} = \frac{{\partial {\mathit{\boldsymbol{F}}_{\rm{v}}}}}{{\partial x}} + \frac{{\partial {\mathit{\boldsymbol{G}}_{\rm{v}}}}}{{\partial y}} + \frac{{\partial {\mathit{\boldsymbol{H}}_{\rm{v}}}}}{{\partial z}} + \mathit{\boldsymbol{S}} $ | (20) |
式中U是守恒型变量,F,G,H代表对流项,Fv,Gv,Hv代表粘性项,S代表化学反应源项。各个变量对应的具体表达式如式(21)所示。
| $ \begin{array}{l} \mathit{\boldsymbol{U}} = \left\{ {\begin{array}{*{20}{l}} {{\rho _i}}\\ {\rho u}\\ {\rho v}\\ {\rho w}\\ e \end{array}} \right\}\;\mathit{\boldsymbol{F}} = \left\{ {\begin{array}{*{20}{l}} {{\rho _i}u}\\ {\rho {u^2} + p}\\ {\rho uv}\\ {\rho wv}\\ {\left( {\rho e + p} \right)u} \end{array}} \right\}\;\mathit{\boldsymbol{G}} = \left\{ {\begin{array}{*{20}{l}} {{\rho _i}v}\\ {\rho uv}\\ {\rho {v^2} + p}\\ {\rho wv}\\ {\left( {\rho e + p} \right)v} \end{array}} \right\}\\ \mathit{\boldsymbol{H}} = \left\{ {\begin{array}{*{20}{l}} {\rho w}\\ {\rho uw}\\ {\rho vw}\\ {\rho {w^2} + p}\\ {\left( {\rho e + p} \right)w} \end{array}} \right\}\;{\mathit{\boldsymbol{F}}_{\rm{v}}} = \left\{ {\begin{array}{*{20}{l}} {\rho {D_i}\frac{{\partial {Y_i}}}{{\partial x}}}\\ {{\tau _{xx}}}\\ {{\tau _{yx}}}\\ {{\tau _{zx}}}\\ {u{\tau _{xx}} + v{\tau _{yx}} + w{\tau _{zx}} + {q_x}} \end{array}} \right\}\\ {\mathit{\boldsymbol{G}}_{\rm{v}}} = \left\{ {\begin{array}{*{20}{l}} {\rho {D_i}\frac{{\partial {Y_i}}}{{\partial y}}}\\ {{\tau _{xy}}}\\ {{\tau _{yy}}}\\ {{\tau _{zy}}}\\ {u{\tau _{xy}} + v{\tau _{yy}} + w{\tau _{zy}} + {q_y}} \end{array}} \right\}{\mathit{\boldsymbol{H}}_{\rm{v}}} = \left\{ {\begin{array}{*{20}{l}} {\rho {D_i}\frac{{\partial {Y_i}}}{{\partial z}}}\\ {{\tau _{xz}}}\\ {{\tau _{yz}}}\\ {{\tau _{zz}}}\\ {u{\tau _{xz}} + v{\tau _{yz}} + w{\tau _{zz}} + {q_z}} \end{array}} \right\} \end{array} $ | (21) |
在式(21)中,u,v,w分别对应于x,y,z方向的速度分量;ρ为气体密度,p为气体压力,e为气体比内能值;ρi代表各个组分的密度,Yi代表各个组分的质量分数值,w代表组分i对应的质量生成速率,τij的含义是剪切应力。
5.4 计算模型在Simple Reacting Parcel Foam求解器中,湍流模型选用经过验证的Realizable k-ε湍流模型[13],近壁面区域采用标准壁面函数。对于压力与速度的耦合算法,选用SIMPLE算法。两相流计算中,采用拉格朗日方法追踪喷雾颗粒的运动轨迹,同时考虑喷雾颗粒与气体连续相的相互耦合作用。对于计算过程中的燃烧模型,选用Open FOAM中的部分搅拌反应器(PaSR)模型,燃烧机理采用航空替代燃油C12H23单步化学反应机理。计算辐射换热时,考虑CO2,H2O以及碳黑粒子对辐射换热的影响,但是不考虑散射的影响。对于空间非均匀分布、非灰介质的辐射换热计算过程,采用全光谱关联k分布方法。为了数值计算的便捷性,事先已经基于HITEMP-2010分子光谱数据库创建了相应的k分布数据库。
5.5 边界条件内外涵入口均设定质量流量入口边界条件,给定相应的质量流量数值以及总温数值。内涵与外涵的质量流量比为4.08:1,相应的总温比为2.51:1。内涵入口介质为燃气、外涵入口介质为空气,各组分质量分数如表 2所示。
|
|
Table 2 Mass fractions of the gases in both the core and bypass flow entrance |
一体化加力燃烧室的出口设定为压力出口边界条件,对一体化加力燃烧室壁面、中心锥壁面、凹腔支板火焰稳定器壁面以及波瓣混合器壁面均设置绝热、光滑、无滑移固体壁面边界条件。加力燃烧时油气比为0.025,选用C12H23为航空替代燃油。对于当前计算域,总共设置了五个加力燃油喷射点,径向方向上喷油点彼此间隔均相等。加力燃油喷射角度与流动方向的夹角设定为60°,喷雾颗粒直径设定为50μm。计算辐射换热时,内外涵入口以及一体化加力燃烧室出口边界表面发射率为1.0,固体壁面边界表面发射率为0.95。考虑非灰碳黑颗粒对辐射换热的影响,碳黑颗粒体积分数设定为10-5。在求解辐射传输方程的有限体积方法中,离散立体角设置为(6,12)。
5.6 计算模型定量验证针对上文论述的计算模型,通过加力状态下凹腔支板火焰稳定器的实验测量结果[14],进行定量验证。几何模型中包含一个凹腔支板火焰稳定器部件,该部件位于二元加力燃烧试验段中,如图 6所示。
基于数值仿真结果,得到试验测量位置处(与入口截面沿流向距离为700mm)的温度值。试验测量值、数值仿真结果以及相对误差,如图 7所示。
根据图 7对比结果,数值计算结果与试验测量值之间最大温度偏差为70.4K,对应的相对误差为4.9%。基于对比验证结果可以得到:由三维两相湍流燃烧求解器Simple Reacting Parcel Foam与辐射换热求解器构成的耦合计算程序,可以用于加力燃烧室中三维两相湍流燃烧的数值仿真研究,具有较高的数值仿真精度。
5.7 结果与分析 5.7.1 加力状态下的热混合效率基于波瓣内扩张角10°模型,得到了加力状态下的数值仿真结果;进一步采用刘-谢热混合效率公式以及刘-杜热混合效率公式,计算得到混合流场中热混合效率沿流向的变化规律,如图 8所示。
基于图 8中刘-谢热混合效率的分布曲线可见:在研究的混合范围内,其对应的热混合效率值均为负值,并且呈现出逐渐下降的变化趋势;如此分布形式,明显违背了实际物理规律,从而说明刘-谢热混合效率公式无法适用于加力燃烧状态下热混合效率的定量研究。
对于刘-杜热混合效率,研究范围内取值位于0至1区间,并且呈现出逐渐上升的变化趋势。对于波瓣混合器下游流场,内外涵流体在大尺度流向涡以及剪切混合机理的共同影响下,逐渐混合均匀[15, 16]。在混合末尾段,大尺度流向涡强迫掺混内外涵流体的能力已经显著降低,使得混合流体热混合效率的增长速率逐渐降低。通过对图 8中刘-杜热混合效率分布曲线进行研究,可以发现:刘-杜热混合效率分布曲线能够很好地反映混合流体热混合效率沿流向的变化规律。基于刘-杜热混合效率公式,能够定量研究加力状态下一体化加力燃烧室中热混合效率的变化规律。
通过对非加力以及加力状态下波瓣内扩张角10°模型对应的刘-杜热混合效率(图 1以及图 8)进行对比研究,可以发现:在对比研究的所有横截面上,加力状态下的刘-杜热混合效率均低于非加力状态下的刘-杜热混合效率。其中,在一体化加力燃烧室出口截面上,与非加力状态相比,加力状态下的刘-杜热混合效率相对降低了6.4%。加力燃烧过程释放了显著的热量,明显提高了内涵核心流的温度水平,进而导致横截面上的温度不均匀程度上升,即对应于较低的刘-杜热混合效率数值。
5.7.2 不同波瓣内扩张角对应的热混合效率基于开发的耦合计算程序,得到加力状态下不同波瓣内扩张角模型对应的热混合效率分布曲线。图 9为刘-谢热混合效率公式对应的分布曲线。
由图 9可见,除了内扩张角25°模型,其他内扩张角模型在整个混合范围内对应的刘-谢热混合效率数值均小于0,与热混合效率的物理意义相悖。对于图 9中刘-谢热混合效率的分布曲线,再次证明刘-谢热混合效率公式不能适用于加力燃烧工况。
基于本文提出的刘-杜热混合效率公式,得到加力状态下不同波瓣内扩张角模型对应的热混合效率分布曲线,如图 10所示。

|
Fig. 10 Liu-Du Thermal mixing efficiency for the cases with different lobe inward penetration angles under the afterburning state |
对于本文研究的不同波瓣内扩张角模型,在整个混合范围内,随着混合距离的增大,混合流体对应的刘-杜热混合效率逐渐上升。在图 10中,对于Lmix/D=0.5截面上游区域,随着波瓣内扩张角的增加,混合流体对应的刘-杜热混合效率并没有呈现出逐渐上升的变化趋势;在Lmix/D=0.3以及0.4截面上,内扩张角25°模型对应的刘-杜热混合效率分别为0.097以及0.205,均分别低于其他所有模型。产生这种分布规律的原因是:随着波瓣内扩张角的增大,更多的外涵富氧气体与内涵气体进行混合,从而强化了一体化加力燃烧室中的加力燃烧过程;较强的加力燃烧过程释放出更多的热量,进一步加剧了横截面上的温度不均匀度;最终,抑制了较大内扩张角强化混合的能力,即对应于较低的刘-杜热混合效率。
在Lmix/D=0.5截面下游区域,随着波瓣内扩张角的增加,同一截面上混合流体对应的刘-杜热混合效率逐渐上升。与Lmix/D=0.5截面上游区域相比,下游区域中加力燃烧强度已经显著减弱,此时内扩张角对刘-杜热混合效率的影响起主导作用。在一体化加力燃烧室出口截面上,内扩张角25°模型对应的刘-杜热混合效率为0.779,相对于内扩张角0°模型增加了10.9%。
6 结论(1)本文提出的通用新型刘-杜热混合效率公式,能够考虑混合过程中内热源、内质量源的影响,可以用于非加力以及加力燃烧工况下热混合效率的计算研究。
(2)在非加力燃烧工况下,刘-杜热混合效率公式能够包容刘-谢热混合效率公式。
(3)在本文研究参数范围内,对于混合初始阶段,波瓣内扩张角增大时,强化了一体化加力燃烧室中的加力燃烧过程,导致混合流体对应的刘-杜热混合效率呈现出逐渐下降的变化趋势。
(4)在混合的后半段区域中,随着波瓣内扩张角的增加,同一截面上混合流体对应的刘-杜热混合效率逐渐上升。
(5)在一体化加力燃烧室出口截面上,波瓣内扩张角25°模型对应的刘-杜热混合效率为0.779,相对于波瓣内扩张角0°模型增加了10.9%。
| [1] |
Frost T H. Practical Bypass Mixing Systems for Fan Jet Aero Engines[J]. Aeronautical Quarterly, 1966, 17(2): 141-160. DOI:10.1017/S0001925900003760
(  0) 0) |
| [2] |
Xie Y, Liu Y H. A Modified Thermal Mixing Efficiency and Its Application to Lobed Mixer Nozzle for Aero-Engines[J]. Heat Transfer Research, 2011, 42(4): 317-335. DOI:10.1615/HeatTransRes.v42.i4
(  0) 0) |
| [3] |
Du L, Liu Y, Li T. Numerical Predictions of Scarfing on Performance of S-Shaped Nozzle with Asymmetric Lobe[J]. Journal of Propulsion and Power, 2014, 31(2): 604-618.
(  0) 0) |
| [4] |
刘友宏, 谢翌, 郭楠. 尾缘凹扇及综合修形对波瓣混合器性能影响[J]. 航空动力学报, 2010, 25(2): 243-250. (  0) 0) |
| [5] |
刘友宏, 张少鹏, 杨旭, 等. 波瓣尾缘切角对涡扇发动机混合排气系统气动热力性能影响[J]. 推进技术, 2013, 34(6): 734-740. (LIU You-hong, ZHANG Shao-peng, YANG Xu, et al. Effects of Cut Angles at Trailing Edge of Lobe on Aero-Thermodynamic Performance of Forced Mixing Exhaust System in Turbofan Engine[J]. Journal of Propulsion Technology, 2013, 34(6): 734-740.)
(  0) 0) |
| [6] |
杜力伟, 刘友宏, 邵万仁, 等. 波瓣数对波瓣S型混合二元喷管气动热力性能影响[J]. 航空动力学报, 2015, 30(4): 916-926. (  0) 0) |
| [7] |
刘友宏, 杜力伟, 李腾, 等. 非对称波瓣下外扩张角对S型喷管气动热力性能影响[J]. 推进技术, 2015, 36(5): 678-687. (LIU You-hong, DU Li-wei, LI Teng, et al. Effects of Downward-Outward Penetration Angle of an Asymmetric Lobed Mixer on Aero-Thermal Dynamical Performance of an S-Shaped Nozzle[J]. Journal of Propulsion Technology, 2015, 36(5): 678-687.)
(  0) 0) |
| [8] |
罗虎. 中心锥有无内突扩的波瓣引射器内流场数值模拟研究[J]. 应用数学和力学, 2014, 35(5): 554-564. DOI:10.3879/j.issn.1000-0887.2014.05.009 (  0) 0) |
| [9] |
李锋, 郭瑞卿, 李龙贤, 等. 整流支板和火焰稳定器的一体化设计加力燃烧室性能的数值模拟[J]. 航空发动机, 2012, 38(5): 6-9. (  0) 0) |
| [10] |
樊小倩. 支板凹腔一体化加力燃烧室设计与流场计算[D]. 北京: 北京航空航天大学, 2013.
(  0) 0) |
| [11] |
吴迪. 新型一体化加力燃烧室冷态流场试验研究[D]. 北京: 北京航空航天大学, 2008.
(  0) 0) |
| [12] |
Modest M F. Radiative Heat Transfer[M]. Salt Lake City: Academic Press, 2013.
(  0) 0) |
| [13] |
谢翌, 刘友宏. 瓣高宽比对波瓣强迫混合排气系统性能影响[J]. 航空动力学报, 2010, 25(12): 2787-2794. (  0) 0) |
| [14] |
王海龙. 新型火焰稳定器设计与研究[D]. 北京: 北京航空航天大学, 2011.
(  0) 0) |
| [15] |
Xie Y, Liu Y. Numerical Investigation of Mixing Length on Performance of Lobed Forced Mixer Nozzles[J]. Heat Transfer—Asian Research, 2011, 40(3): 205-216. DOI:10.1002/htj.v40.3
(  0) 0) |
| [16] |
Xie Y, Liu Y. Numerical Investigation of Lobe Spacing Ratio on Performance of Forced Mixer Nozzle[J]. Heat Transfer—Asian Research, 2011, 40(7): 593-607. DOI:10.1002/htj.v40.7
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


