高超声速进气道作为为超燃冲压发动机捕获和压缩空气的重要部件,其性能的好坏直接影响到发动机乃至整个推进系统能否正常工作。众所周知,进气道一般存在起动和不起动两种工作状态。然而,受各种因素的影响,进气道陷入不起动时,捕获流量急剧下降,造成溢流阻力与压差阻力大大增加,导致推进系统性能恶化,推力迅速下降,对飞行器造成灾难性的毁灭[1]。因此,进气道的稳定工作是实现推进系统高效运行、维持飞行器正常飞行的前提。基于此,进气道起动/不起动问题一直受到了广泛关注。Kantrowitz和Donaldson[2]基于近似无粘假设,提出了两个自起动收缩比极限,进气道内收缩比如果小于Kantrowitz极限时,可以不借助外界辅助即可实现自起动,而大于等熵极限时则不能起动。Wie等[3]通过试验手段研究了进气道总收缩比对不起动流场的影响,指出大收缩比进气道由于气流在喉道处阻塞引起“硬不起动”,而低内收缩比时由于在收缩段内存在大分离包引起“软不起动”。国内的梁德旺等[4]分析了面积收缩比、攻角、飞行高度等因素对高超声速进气道起动能力的影响,得出面积收缩比越大、雷诺数越低时进气道的起动马赫数越高。刘凯礼等[5]研究了飞行器发生俯仰振荡时对进气道不起动/再起动特性的影响。以上研究结果说明,进气道内收缩比和飞行器飞行状态的变化会影响进气道起动性能。此外,燃烧室压力的高低也会对进气道起动性能产生重要影响,目前对反压过高引起进气道不起动过程的研究已有不少。
文献[6]给出了当反压过高引起进气道不起动时,流场中激波瞬时运动速度在55~70m/s。Wagner等[7]则利用PIV技术和高速摄影对由反压引起的进气道不起动过程中流场结构的动态变化进行了研究,结果发现进气道在不起动时隔离段末端激波以大约26m/s的速度逆向传播,并存在频率为124Hz的剧烈振荡。Tan等[8]通过在隔离段出口安放堵块模拟反压,对进气道不起动振荡流态进行了试验研究。结果表明,随着阻塞比(即反压)的逐渐升高,流场的振荡经历了三个阶段:相对温和的“小喘”,无振荡,十分剧烈的“大喘”。Chang等[9]实验研究了不同阻塞比下不起动流场结构,发现存在两种新的流动形态,一种是无明显周期性的“大喘”和“小喘”混杂在一起的振荡形式;另一种是无振荡形式。Li等[10]在激波风洞中对某二元进气道在不同反压下流场的振荡特性进行了研究,发现随着阻塞比的增大,振荡频率也随之增大。
然而,高超声速飞行器在实际飞行过程中,需借助其它助推装置从低速逐渐加速,进气道在此期间经历了由不起动到起动的过程。对于此,已经获得一些研究结果:文献[11]采用非定常数值仿真的方法研究了轴对称进气道自起动过程,发现在起动过程中流场存在非定常振荡现象。刘雄等[12]侧重研究了某二维进气道在加速起动过程中唇口角构型对起动性能、起动过程的影响。Su等[13]则比较了不同加速度大小及不同加速路径下进气道的自起动性能,得出加速度越大,进气道越难起动,且等动压加速路径下自起动马赫数越高的结论。虽然,这些研究结果在一定程度上揭示了加速起动过程中的流动特性,但大都针对的是进气道处于亚临界或临界状态,并未考虑超临界时的情况。现如今,高超声速进气道工作在宽马赫数范围,在部分情况下会处于超临界工作状态[14, 15]。因此,本文主要针对大内收缩比进气道,研究分析其从不起动状态到最终超临界工作状态过程中的喘振特性以及作用机理,从而进一步加深对进气道加速起动过程中流场振荡现象的认识。
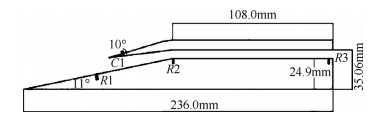
2 物理模型及数值仿真 2.1 物理模型本文所研究的对象是二元高超声速进气道,模型是参照文献[16]设计而成。图 1给出了该模型的示意图及主要尺寸。进气道外压缩段采用一级压缩,楔角为11°。进气道总收缩比为2.90,内收缩比为1.63。喉道高度10.16mm,唇罩长度63.5mm,隔离段长度为108mm。
|
Fig. 1 Schematic diagram of the inlet model |
采用商业计算流体力学软件Fluent14.0对整个流场进行数值模拟。控制方程采用二维可压缩Reynolds-averaged Navier-Stokes(RANS)方程。计算格式为Roe flux-difference splitting(Roe-FDS)格式,用二阶迎风格式对控制方程进行离散。湍流模型采用Shear-stress transport(SST)k-ω两方程模型,之所以选用该湍流模型是因为该模型对主流区高速流动和近壁面处低速流动的模拟具有很高的准确性[17]。气体模型采用理想气体模型,考虑到气体比热以及粘性随温度变化,分子粘性系数的变化采用Sutherland公式进行求解,比热随温度的变化采用五次多项式拟合。非稳态流动采用双时间步(Dual-time Stepping)隐式的时间离散方法求解。物理时间步长的初步选定参照文献[18]中的公式,初步选定其值为1μs。
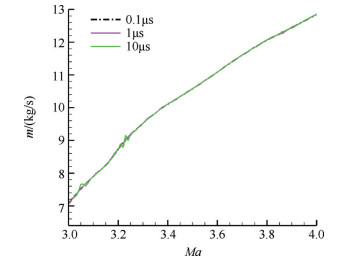
为了进一步验证时间精度的准确性,分别选取10μs,1μs,0.1μs三种不同时间步长进行非定常数值模拟。图 2给出了不同时间步长、加速过程中进口流量信号曲线(考虑计算时间成本,给出了Ma3~4的变化曲线)。从图中可以看出,时间步长的选取对数值计算结果存在一定的影响,1μs和0.1μs时间步长获得的曲线相重合,而10μs时间步长下流量曲线存在微小偏差。说明1μs时间步长满足计算要求。
|
Fig. 2 Compare the mass flow rate at inlet with different time steps |
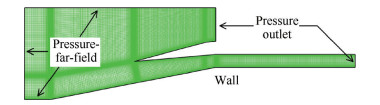
图 3给出了计算域和计算网格,网格在近壁面处以及唇罩附近进行了加密处理,以确保近壁面处网格的y+接近于1。壁面为无滑移绝热壁面。
|
Fig. 3 Computational domain and grids |
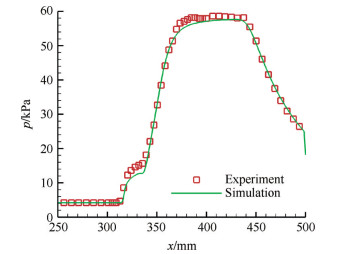
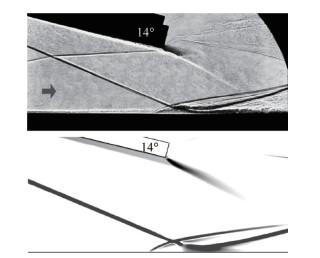
为了验证Fluent在高马赫数来流条件下计算能力,选取了Schülein[19]所进行的激波/边界层干扰实验。选择上板偏转角为14°,为保证近壁面处y+在1左右,平板第一层网格高度为0.01mm,总网格量在22万左右。数值模拟时采用来流马赫数Ma=5.0,总压和总温分别为2.12MPa和410K的来流条件。图 4给出了下平板表面数值计算与实验压力分布。对比压力分布规律,数值模拟和实验得到的压力分布吻合较好,对分离点位置预测也较为准确。图 5给出了实验纹影与计算结果对比图,从图中也可以看出计算结果与实验结果波系结构一致且吻合良好。说明Fluent在马赫数较高时的精度值是较为理想的。
|
Fig. 4 Computational and experimental results of static pressure along lower plate |
|
Fig. 5 Experimental and numerical schlieren images |
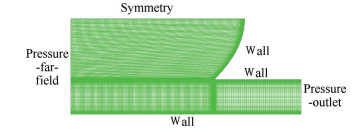
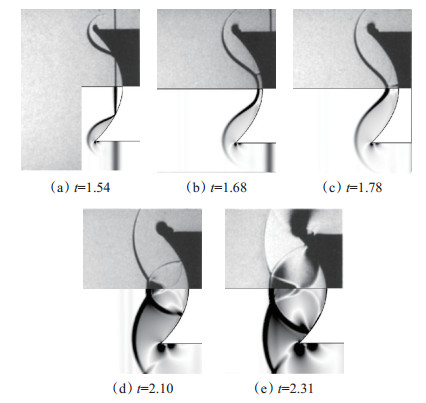
进气道加速起动过程是非定常的,存在剧烈的激波振荡,因此对计算工具非定常计算能力的校核很有必要。本文选用Izumi等[20]开展的运动激波聚焦反射试验,该实验中激波反射器的直径D=14mm,型面形状可表述为X = CY2。选取C=0.5的实验结果进行对比。图 6给出了激波反射器网格计算域和边界条件示意图,网格总量在12万左右。实验时来流运动激波马赫数Ma=1.5,其边界条件如表 1所示。图 7给出了运动激波聚焦反射过程中不同时刻的流场结构。其中图的上半部分为试验结果,下半部分为数值模拟结果,时间t采用γ1/2D/c1进行了无量纲化处理。这里γ是比热比,c1为运动激波前的声速。从图 7中可以看出数值模拟结果与试验结果吻合良好,说明本文所采用的数值计算方法能够模拟复杂非定常流场的变化过程。
|
Fig. 6 Computational domain and grids of parabolic reflector |
|
|
Table 1 Boundary condition of parabolic reflector |
|
Fig. 7 Comparison of experiment (upper picture) with computation (lower picture) |
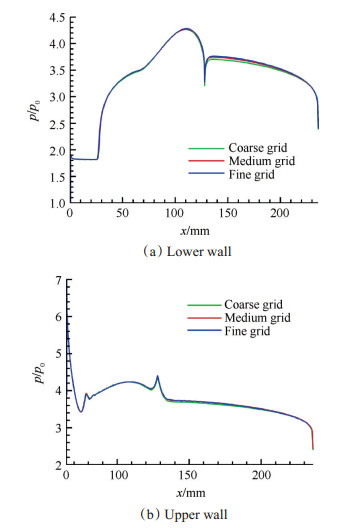
为了校验网格疏密程度对计算结果的影响。采用三种不同网格进行定常数值模拟,三种网格量大小见表 2。图 8给出了不同网格量下下壁面和上壁面的沿程压力分布。从图中可以看到尽管网格疏密程度不同,但结果十分接近。并且,中等网格和密网格下压力分布线几乎重合,考虑到计算量和时间成本,在接下来的研究中选取中等网格。
|
|
Table 2 Different grid densities |
|
Fig. 8 Surface pressure distributions of hypersonic inlet along |
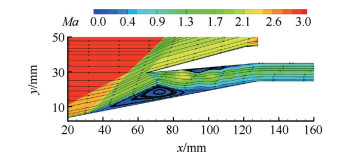
为了模拟进气道的加速起动过程,首先计算得到初始不起动流场。在本文中,造成进气道不起动的主要影响因素是来流马赫数较低。不起动初始流场的来流计算条件如表 3所示,隔离段出口压力为1倍来流静压。图 9给出了唇罩附近的马赫云图和流线图。可以明显看到进气道处于不起动状态,在压缩面上存在很大的分离区,并且唇罩内侧也存在局部分离,内压段存在明显激波串结构。此流场将作为加速计算的初始流场。
|
|
Table 3 Parameters of freestream |
|
Fig. 9 Mach number contours and streamlines near the inlet cowl |
尽管飞行器在飞行试验中经历的加速过程十分复杂[21, 22]。在本文中,选取了一个典型的加速过程,近似认为飞行马赫数随时间呈线性关系,具体可表达为
| $ Ma = M{\rm{a_0}} + kt $ | (1) |
式中Ma0为初始来流马赫数;k为加速度。这里设置初始值Ma0为3.0,k值取为1/s,在加速过程中来流压力和温度保持不变。
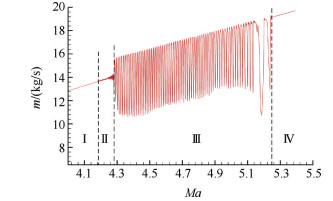
3 计算结果与讨论 3.1 不起动到起动过程的流动特性图 10给出了在加速过程中进气道内收缩进口流量的变化规律,其中横轴为来流马赫数,纵轴为进口流量,从图中可以看出在进气道进口流量与来流马赫数并不呈线性关系,在从进气道不起动到起动这个过程中流场存在振荡现象。结合实际流动特点,把整个过程分为四个阶段,如图中Ⅰ区域所示,在来流马赫数较低时,进口流量随时间增加逐渐上升,此时流场并没有发生振荡。直到来流马赫数增加到Ma=4.17时,如图中Ⅱ区域所示,进口流量开始出现小幅波动,流场开始出现振荡。随着时间的推移,流场振荡越来越剧烈,如Ⅲ区域所示,大幅度振荡从Ma=4.28持续到Ma=5.25。最终在Ma=5.25时进气道完全起动,如图中Ⅳ区域所示,此时振荡不复存在,进口流量随来流马赫数呈线性变化。
|
Fig. 10 Variation of the mass flow rate at inlet with freestream Mach number |
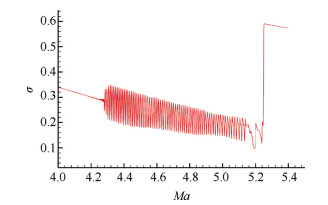
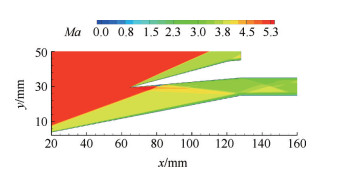
图 11给出了加速过程中总压恢复系数随来流马赫数的变化规律。不难看出,随着来流马赫数的增加,总压恢复系数逐渐降低,从Ma=4.17时开始出现波动,在Ma=4.28时出现大幅上下振荡,最终在Ma=5.25时阶跃上升,进气道起动。需要注意的是,进气道实现起动后处于超临界状态,前体激波入射在唇罩内侧,经反射后正好入射在肩部附近,流场结构如图 12所示。
|
Fig. 11 Variation of the total pressure recovery coefficient with freestream Mach number |
|
Fig. 12 Mach number contours at the started state |
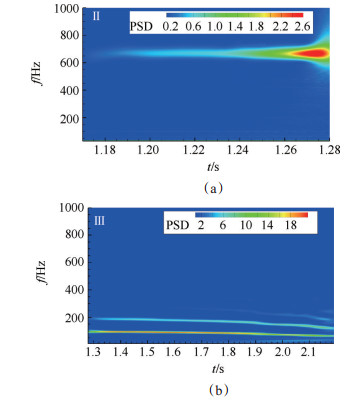
为了进一步得到加速起动过程中流场振荡频率随来流马赫数的变化关系,图 13给出了采用小波变换得到的第Ⅱ和Ⅲ阶段进口处流量信号的时频联合特征。在信号处理中采用了Morlet小波,以提高对频率的分辨能力。从图 13(a)中可见,在Ⅱ阶段,振荡能量在频率域内分布较为集中,其值在664Hz左右,且能量值逐渐增加,即流场振荡得越来越剧烈。而在Ⅲ阶段(图 13(b)),振荡能量主要集中在两个频带上,其中主频率在62~100Hz,二次谐振频率低于200Hz。并且,随着时间的推移(即来流马赫数的增加),主、次频率均逐渐降低。基于以上分析,对于大内收缩进气道的加速起动过程中的流场振荡,可概括为高频低幅振荡和低频高幅振荡两个阶段。
|
Fig. 13 Power-spectral-density contours of inlet during Ⅱ and Ⅲ oscillation periods |
图 14和图 15分别给出了低频振荡阶段(第Ⅲ阶段)唇罩侧C1点和下壁面典型位置R1,R2及R3点静压信号的功率谱密度云图。其中,各点位置如表 4所示。从图中可以看出,每个测点压力都存在振幅较大的基频振荡和振幅相对较小的二次谐振,这就说明进气道在加速起动过程中的喘振是全流道的喘振。比较图 14和图 15,不难发现唇罩侧C1测点处基频脉动能量值和二次谐振振荡幅值均远远大于下壁面上三个测点压力振荡幅值,这是因为分离激波入射点位置位于C1测点附近,从而导致该点压力振荡幅度最大。此外,对于下壁面三个测点,从图 15中可以看出位于喉道处R2测点压力振荡幅值最大,压缩面R1测点次之,隔离段出口R3测点压力振荡幅值最小。分析认为,喉道处的压力扰动经隔离段向下游传播时振荡能量不断衰减,因此隔离段末端处压力脉动能量显著低于喉道处。
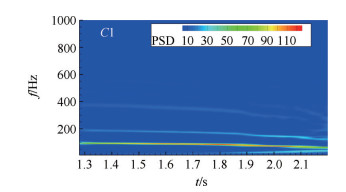
|
Fig. 14 Power-spectrum-density contours of pressure signal of C1 during Ⅲ oscillation period |
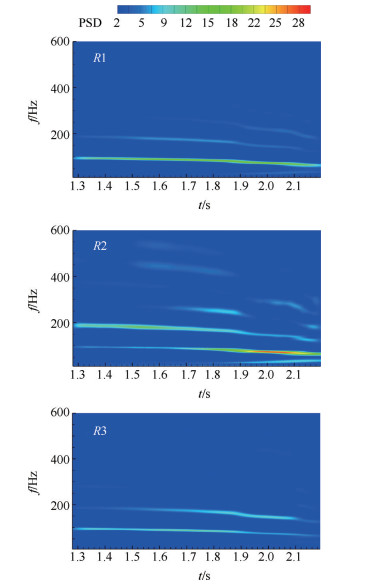
|
Fig. 15 Power-spectrum-density contours of pressure signal of R1, R2 and R3 during Ⅲ oscillation period |
|
|
Table 4 Distribution of pressure probes |
对于高频低幅振荡阶段(Ⅱ阶段)流场结构变化过程,此阶段压缩面分离激波距唇罩前缘一定距离处小幅摆动,这在文献[11]已有提及。而对于低频高幅振荡阶段(Ⅲ阶段),此时流场结构与上一阶段截然不同。为了说明此阶段流动结构演化过程,选取了时间t=1850.4ms至t=1862.8ms这一周期内的流场结构变化进行分析。图 16(a)~(j)给出了这个周期内流场的等马赫数云图。如图 16(a)所示,在t=1850.4ms时刻,可以看到在进气道压缩面以及内收缩段上表面存在较大的分离区,此时分离激波(准确的说是分离激波与前体激波相交后的激波)远离唇罩,在唇罩上方存在较大的超声速溢流,参照图 21,此时进气道进口捕获流量最小。随着压缩面分离点后移,分离区减小,分离激波也逐渐靠近唇口,正如图 16(b)所示,此时分离激波贴口,溢流消失,捕获流量达到最大值。在t=1855.6ms时,分离点进一步后移,不难发现,此时分离激波入射到唇罩内侧,由于入射位置过于靠近唇罩前缘,边界层发展不充分,因而造成边界层小尺度分离,分离区一直延伸到唇口前缘,其诱导形成一道唇罩斜激波,并与压缩面分离诱导激波相交。在t=1857.3ms时,随着激波入射位置的后移,唇罩内侧分离区进一步增大,收缩段上下表面分离区的增大造成超声速核心区减小,此时进口流量呈下降趋势。值得注意的是,从此刻开始,在收缩段内不断增大的逆压梯度作用下,压缩面分离区开始增大,分离点开始向上游移动。随着分离诱导激波的上移以及激波角的增大,在t=1858.3ms时,唇罩激波与分离激波相交产生的激波反射模式发生转变,由正常反射转变为马赫反射,从图 16(e)放大区域可以看出,从马赫杆的两个三波点发出两道滑流面。由于K-H不稳定性,滑流面造成下游流动一直处于不稳定状态,并且马赫杆很快向上游移动,形成一道正激波依附在唇罩前缘处,整个转变过程持续时间很短,仅经历了0.2ms,此时流场结构如图 16(f)所示。在t=1858.8ms时,此时唇罩依附激波不复存在,而是在唇罩前缘的前方形成一道唇罩脱体激波,此时来流经脱体激波的正激波部分后被减速为亚声速流。随着分离区和分离激波的波角的持续增大,分离激波与脱体激波交点逐渐靠近唇缘,亚声速溢流持续减小,直至消失,图 16(g)至图 16(i)反映了这一变化过程。在这之后,分离激波不断远离唇口,最终在t=1862.8ms时刻,如图 16(j),回到t=1850.4ms时刻的初始位置。
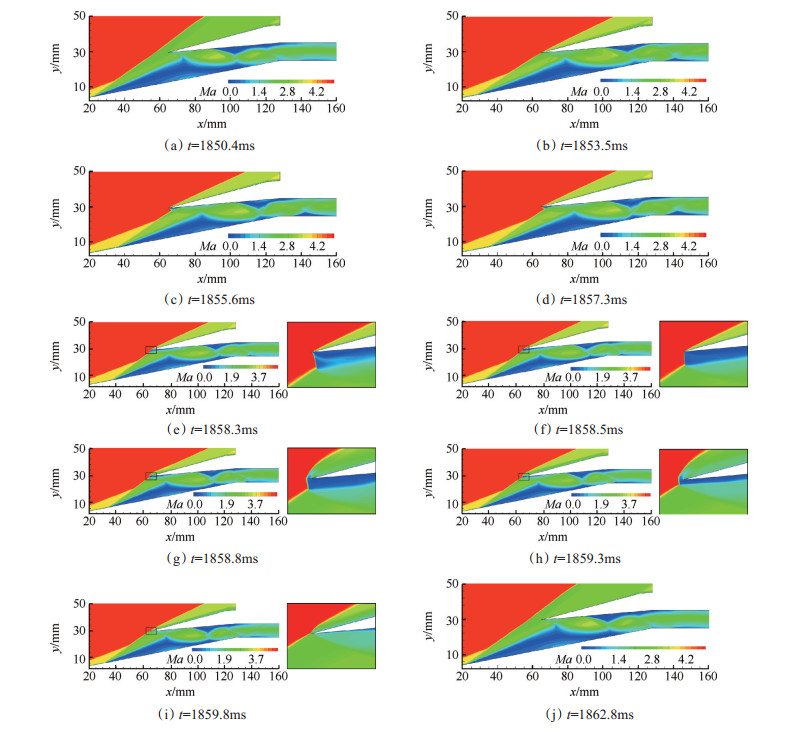
|
Fig. 16 Mach number contours at different times in one cycle |
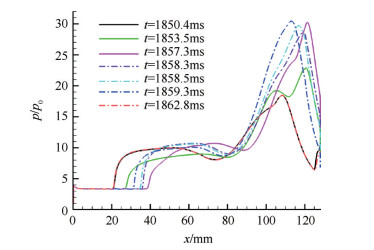
|
Fig. 17 Distributions of the pressure coefficients along the lower wall |
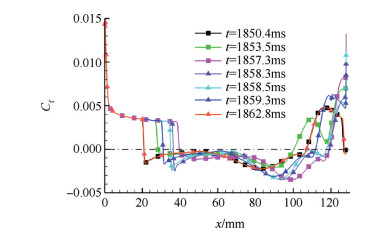
|
Fig. 18 Distributions of the skin-friction coefficients along the lower wall |
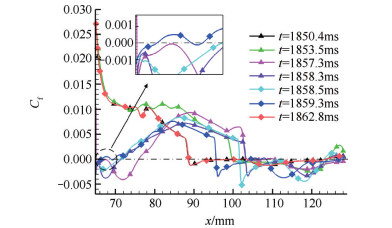
|
Fig. 19 Distributions of the skin-friction coefficients along the upper wall |
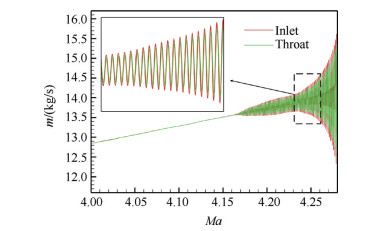
|
Fig. 20 Variation of the mass flow rate at inlet and throat with freestream Mach number |
|
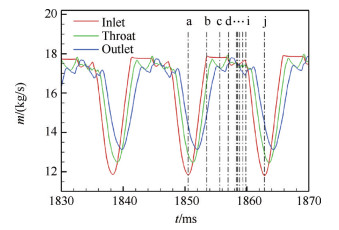
Fig. 21 Variation of the mass flow rate with the time |
图 17和图 18分别给出了一个振荡周期中几个典型时刻下壁面压力分布和摩擦阻力系数的分布情况。从图 17可以看出,由于振荡周期很短,来流条件认为是准定常的,因此在分离点之前每个时刻沿程压力分布曲线几乎重合。此外,不同时刻下壁面压力曲线的分布趋势也非常类似,壁面压力曲线经分离激波后都有突升,之后出现一个压力平台,略微下降后又急剧上升,最终在再附点附近达到最大值。在t=1850.4ms时,分离激波位于最上游位置,此时分离点处于x=20mm附近,随着时间的推移,可见分离点向下游移动,分离激波处在被“吞入”过程。直到t=1857.3ms时刻,分离激波运动到最下游位置,此时分离点位于x=40mm附近。在此之后,随着分离区增大,分离点沿压缩面前移,分离激波进入“吐出”阶段,图中的一系列虚线表明了这一逆向过程。直至t=1862.8ms,此时压力分布与初始时刻t=1850.4ms相重合。图 18中所给出的不同时刻下壁面摩擦阻力系数,摩擦阻力值小于零时表明壁面出现分离区,大于零时反之。从图中可以看出下壁面分离区的分离点和再附点随着时间的推移而不断变化,除了在t=1853.5ms时刻,在分离激波“吞入”过程中,分离点与再附点都向下游移动;在“吐出”阶段,则逆流向上移动。
图 19给出了唇罩内壁面不同时刻摩擦阻力系数分布,从图中可以看出唇罩侧分离区的变化情况。在t=1850.4ms和t=1853.5ms这两个时刻,唇罩前端没有出现分离。在t=1857.3ms时,唇罩前端壁面摩擦阻力系数由正值突降为负值,表明壁面出现了分离区,这与图 16(d)所观察到的流场结构是相一致的,下壁面强分离激波的入射造成当地附面层分离,再附点的位置位于x=76mm处。随着时间推移,分离激波入射位置向上游移动,从t=1858.3ms至t=1859.3ms时间段内,可以发现再附点的位置明显前移,分离区急剧减小,值得注意的是,在t=1859.3ms时刻,如图 19中放大区域所示,唇罩前端分离区转变为两个区域,对比图 16(h)中流场结构,分析原因可知:此时滑流面靠近唇罩内壁,与附面层相互作用,造成局部分离。直至t=1862.8ms时,分离区完全消失,此时摩擦阻力系数线与初始时刻完全重合。
3.3 流场振荡机理分析图 20给出了Ma=4至Ma=4.28的进口及喉道处质量流量变化曲线。从图中可以看出,在非振荡阶段两截面流量随马赫数的增加线性上升,且两者保持平衡,不存在流量差。在高频低幅振荡阶段,可以看到两者不断波动,幅度逐渐增大,并且振荡幅值和相位都存在差别,表明喉道处开始发生壅塞。
图 21给出了来流马赫数在Ma=4.85附近进气道进口、喉道以及出口质量流量随时间的变化。不难看出,虽然来流马赫数有所增加,但由于一个振荡周期的时间较短,可认为来流条件基本不变。由图可见,进、出口以及喉道处流量随时间都呈现出周期性变化,但三者之间又有不同,内压段进口流量相比于其它两者,其振荡幅值最大,而出口流量振荡幅度最小;三者随时间的变化并不同步,存在一定的相位差。对于进气道进口与喉道处流量严重不平衡,分析认为是对于大内收缩比进气道,内压段收缩较快,进口捕获流量在喉道处不能完全流过,发生壅塞,这也是导致流场振荡的主要因素。此外,不难发现,三个截面处流量在一个振荡周期内除了有大幅度的上升、下降外,其间还耦合着振荡幅度相对较小的二次谐振,这在前文功率谱密度云图中已有所显现。分析认为,二次谐振过程发生在分离诱导激波贴口至唇罩上方亚声速溢流消失阶段,即图 16中(b)~(i)阶段。
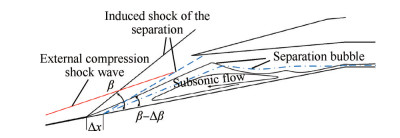
为了进一步说明喉道壅塞如何引起流场振荡,图 22给出了进口压缩面分离区和诱导激波主导的流场振荡机制示意图(唇罩侧波系结构做了省略处理)。一开始,分离诱导斜激波处在最上游位置,远离唇口,此时存在大量溢流,进入进气道内的空气流量较少,喉道处壅塞程度较低,于是,通道内形成低压波并前传,使得压缩面分离区减小并后移,分离诱导激波的倾角也随之减小,分离激波被吞入唇口。随着溢流量逐渐减小,捕获流量上升,壅塞加剧,内压段流量逐渐累积形成高压,内通道沿程逆压力梯度随之增加,势必导致压缩面分离区增大并前移,分离激波再次被推出唇口,此时唇罩前方的溢流量又再次增加,壅塞程度得到缓和。周而复始,从而形成振荡。
|
Fig. 22 Oscillation dominated by the ramp-side separation zone and separation induced shock |
采用二维非定常数值计算方法研究分析了大内收缩比二元进气道在加速起动过程中的流动特性,得出以下主要结论:
(1)在进气道由不起动到最终起动的动态过程中,流场依次经历了非振荡状态、高频低幅振荡状态、低频高幅振荡状态、非振荡起动状态。其中低频振荡所经历的时间远大于高频振荡,且高频振荡频率在664Hz左右;低频振荡频率主频从100Hz逐渐降低至62Hz,二次谐振频率集中在200Hz以下。
(2)造成流场高频低幅振荡的主要因素是气流在喉道处发生壅塞,喉道处严重的流动壅塞,使得进气道进入主频率为100Hz(并逐渐降低)的低频高幅喘振状态。气流在内压段内瞬时的积聚与排出导致收缩段内压力剧烈波动,进而形成以压缩面分离区和诱导激波为主导的流场振荡机制。
(3)由于进气道在起动后处于超临界状态,其在加速过程中伴随唇罩侧前端边界层分离,分离区的形成和消失使得收缩段内的流动更为复杂。此外,唇罩侧分离区的形成与消失造成的扰动是二次谐振产生的原因。
| [1] |
McClinton C, Hunt J, Ricketts R, et al. Airbreathing Hypersonic Technology Vision Vehicles and Development Dreams[R]. AIAA 99-4978. http://dl.acm.org/citation.cfm?id=887857
(  0) 0) |
| [2] |
Kantrowitz A, Donaldson C D. Preliminary Investigation of Supersonic Diffusers[J]. Technical Report Archive & Image Library, 1945, 72(2): 289-295.
(  0) 0) |
| [3] |
Wie D V, Kwok F, Walsh R. Starting Characteristics of Supersonic Inlets[R]. AIAA 96-2914. http://arc.aiaa.org/doi/abs/10.2514/6.1996-2914
(  0) 0) |
| [4] |
梁德旺, 袁化成, 张晓嘉. 影响高超声速进气道起动能力的因素分析[J]. 宇航学报, 2006, 27(4): 714-719. (  0) 0) |
| [5] |
刘凯礼, 张堃元. 俯仰振荡引起的二元高超声速进气道不起动/再起动特性[J]. 推进技术, 2010, 31(6): 676-680. (LIU Kai-li, ZHANG Kun-yuan. Unsteady Start /Unstart Characteristics of 2-D Hypersonic Inlet Caused by Oscillating Angle-of-Attack[J]. Journal of Propulsion Technology, 2010, 31(6): 676-680.)
(  0) 0) |
| [6] |
Rodi P E, Emami S, Trexler C A. Unsteady Pressure Behavior in a Ramjet/Scramjet Inlet[J]. Journal of Propulsion and Power, 1996, 12(3): 486-493. DOI:10.2514/3.24061
(  0) 0) |
| [7] |
Wagner J, Valdivia A, Yuceil K, et al. An Experimental Investigation of Supersonic Inlet Unstart[R]. AIAA 2007-4352. https://arc.aiaa.org/doi/abs/10.2514/6.2007-4352
(  0) 0) |
| [8] |
Tan H J, Sun S, Yin Z L. Oscillatory Flows of Rectangular Hypersonic Inlet Unstart Caused by Downstream Mass-Flow Choking[J]. Journal of Propulsion and Power, 2012, 25(1): 138-147.
(  0) 0) |
| [9] |
Chang J T, Wang L, Bao W, et al. Novel Oscillatory Patterns of Hypersonic Inlet Buzz[J]. Journal of Propulsion and Power, 2015, 28(6): 1214-1221.
(  0) 0) |
| [10] |
Li Z F, Gao W Z, Jiang H L, et al. Unsteady Behaviors of a Hypersonic Inlet Caused by Throttling in Shock Tunnel[J]. AIAA Journal, 2013, 51(10): 2485-2492. DOI:10.2514/1.J052384
(  0) 0) |
| [11] |
王卫星, 郭荣伟. 高超进气道自起动过程中流动非定常特性研究[J]. 航空学报, 2015, 36(10): 3263-3274. (  0) 0) |
| [12] |
刘雄, 王翼, 梁剑寒. 二维高超声速进气道加速启动过程数值研究[J]. 推进技术, 2015, 36(3): 328-335. (LIU Xiong, WANG Yi, LIANG Jian-han. Numerical Research on Accelerating Start Process of 2-Dimensional Hypersonic Inlet[J]. Journal of Propulsion Technology, 2015, 36(3): 328-335.)
(  0) 0) |
| [13] |
Su W Y, Hu Z, Tang P P, et al. Transient Analysis for Hypersonic Inlet Accelerative Restarting Process[J]. Journal of Spacecraft and Rockets, 2017, 54: 376-385. DOI:10.2514/1.A33601
(  0) 0) |
| [14] |
Shneider M N, Macheret S O. Modeling of Plasma Virtual Shape Control of Ram/Scramjet Inlet and Isolator[J]. Journal of Propulsion and Power, 2006, 22(2): 447-454. DOI:10.2514/1.16959
(  0) 0) |
| [15] |
Shneider M N, Macheret S O, Miles R B. Nonequilibrium Magnetohydrodynamic Control of Turbojet and Ram/Scramjet Inlets[R]. AIAA 2002-2251. https://arc.aiaa.org/doi/abs/10.2514/6.2002-2251
(  0) 0) |
| [16] |
Emami S, Trexler C A, Auslender A H, et al. Experimental Investigation of Inlet-Combustor Isolators for a Dual-Mode Scramjet at a Mach Number of 4[R]. NASA/TP 95-3502. http://www.researchgate.net/publication/2574325_Experimental_Investigation_of_Inlet-Combustor_Isolators_for_a_Dual-Mode_Scramjet_at_a_Mach_Number_of_4
(  0) 0) |
| [17] |
Menter F R, Kuntz M, Langtry R. Ten Years of Industrial Experience with the SST Turbulence Model[J]. Turbulence, Heat and Mass Transfer, 2003, 4(1): 625-632.
(  0) 0) |
| [18] |
赵昊, 谢旅荣, 郭荣伟, 等. 超声速进气道加速/减速过程起动/不起动现象研究[J]. 航空动力学报, 2015, 30(8): 1841-1852. (  0) 0) |
| [19] |
Schulein E. Skin Friction and Heat Flux Measurements in Shock/Boundary Layer Interaction Flows[J]. AIAA Journal, 2006, 44(8): 1732-1741. DOI:10.2514/1.15110
(  0) 0) |
| [20] |
Izumi K, Aso S, Nishida M. Experimental and Computational Studies Focusing Processes of Shock Waves Reflected from Parabolic Reflectors[J]. Shock Waves, 1994, 3(3): 213-222. DOI:10.1007/BF01414715
(  0) 0) |
| [21] |
Voland R, Auslender A, Smart M, et al. CIAM/NASA Mach 6. 5 Scramjet Flight and Ground Test[R]. AIAA 99-4848. http://dl.acm.org/citation.cfm?id=887858
(  0) 0) |
| [22] |
Li F, Choudhari M, Chang C L, et al. Transition Analysis for the HIFiRE-1 Flight Experiment[R]. AIAA 2011-3414. https://arc.aiaa.org/doi/abs/10.2514/6.2011-3414
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


