2. 航天器在轨故障诊断与维修重点实验室,陕西 西安 710043
2. Key Laboratory of Spacecraft In-Orbit Fault Diagnosis and Maintenance, Xi'an 710043, China
近地太阳同步轨道卫星在既定的轨道上运行时,其周期和轨道高度都是相对固定不变的,因此运行轨道通过的地面覆盖区域相应也是不变的。根据任务需求,为实现目标卫星周期性重访特定区域,需要通过轨道控制将目标卫星由平时轨道快速、精确机动至严格回归轨道,即在提升轨道高度的同时将严格回归轨道的某一条轨迹安排在特定的位置上,使得星下点弧段穿过特定区域。这实际上是目标卫星与严格回归轨道卫星交会的问题,即要在提升轨道高度的同时控制目标卫星与严格回归轨道卫星的相位差。严格回归轨道卫星为运行在严格回归轨道上且地面轨迹过特定区域的卫星,可根据目标轨迹网唯一确定轨道。相位差的控制是通过两颗卫星的角速度差来实现的,最终通过有效控制变轨时刻和两星的半长轴差来实现。
传统轨道机动方面的研究大多侧重于轨道拦截[1]、轨道交会[2]、轨控推力优化[3]、轨控姿态异常等技术[4],或缺乏考虑多约束条件的制约[5]。赵坚[6]使用解析方法对太阳同步(准)回归轨道卫星动力学特性进行了研究,分析了非球摄动、大气阻力摄动和太阳引力谐振等主要摄动因素的影响,并以此为依据对轨道保持方法进行了探讨,可以为轨道设计和轨道控制研究工作提供参考。Vtipil等[7]根据给定的重访周期和倾角,研究4阶重力势场下的回归轨道设计及其控制方法,并根据周期运动不断优化半长轴。王雪峰等[8]针对带推力约束的航天器三维空间机动轨道初始设计问题,提出了一种基于傅立叶级数展开的改进形状设计方法,可以为带有任务约束的航天器三维空间机动轨道的优化设计提供更优的初始参数及其解析解。杨盛庆等[9]通过分析太阳同步回归轨道的轨道根数和星下点经度/纬度的关系,推导了一组轨道根数的修正公式;基于高精度轨道动力学模型和升交点位置确定方法,构造了关于轨道半长轴和轨道倾角的迭代修正方法。针对偏心率矢量的动力学系统所具有的极限环特性,构造了平均法求其解析近似,从而实现冻结轨道特性对偏心率和近地点幅角的迭代修正,具有较高的回归精度。杨维廉[10]针对半长轴不断地衰变导致地面轨迹的东漂,以及太阳引力引起的倾角变化,给出了这些变化的解析模型以及轨道控制的策略。Sengupta等[11]针对回归轨道的设计和轨迹保持,构建轨道的对地覆盖于轨道要素的关系,给出了一种解析的方法,提供了较好的思路。何艳超等[12]为解决太阳同步回归轨道的标称设计问题,提出了一种基于高精度重力场的半解析优化方法,给出精确回归轨道优化设计的基准。曲宏松等[13]通过对轨道回归特性的分析,引入了设计太阳同步回归轨道Q值的方法,从理论上找到了太阳同步轨道设计中的关键,为复杂的轨道设计工作提供了一个可靠而易行的方法。Winkler等[14]以燃料最优为前提,利用光学相机和LIDAR技术进行相对导航,研究卫星自主轨控策略。Xu等[15]根据星下点覆盖率与轨道高度之间的关系,提出了一种回归轨道设计的解析算法,从升轨和降轨上保障成像质量。温生林等[16]针对低轨回归轨道卫星,建立了星下点轨迹漂移的数学模型,研究了星下点轨迹保持控制的问题,能有效地实现星下点轨迹保持的要求。Ormston等[17]从轨道特性、有效载荷限制、地面操作实施等方面对EarthCARE卫星的轨控策略进行分析,给出了半长轴和偏心率、倾角控制的最优方案,并得出并没有针对所有卫星的、统一的最优机动策略的结论。Nadoushan等[18]以重访周期、载荷侧摆能力、有效载荷幅宽作为约束条件,提出了一种基于数论的回归轨道设计方法,使用贝祖定理优化重访时间,计算简单,计算量小。Zhang等[19]对轨道控制方法的鲁棒性进行分析,研究了大气阻力和地球的非球形摄动,建立了一种脉冲控制策略,并对其误差极性了分析。He等[20]对定轨和轨道控制中存在的误差以及半长轴衰减速率进行分析,提出了一种基于平根的回归轨道维持策略,并通过数值模拟进行了验证。
严格回归轨道自动生成不仅仅涉及半长轴、相位差调整,还需要综合考虑轨控时间、燃料消耗、偏心率等约束条件,目前这方面的研究还很少。本文研究平面内的轨道机动,利用解析法和数值法的优势互补生成严格回归轨道根数,并优化带约束条件的多脉冲轨控策略,最后根据卫星运行轨迹边界环的保持要求,给出了严格回归轨道的控制窗口,实现了目标严格回归轨道自动生成与边界环保持。
2 严格回归轨道根数计算严格回归轨道是一种星下点轨迹周期性穿过特定区域,且具有严格重访周期的回归轨道,一般为日回归轨道。严格回归轨道根数(轨道半长轴a,偏心率e,轨道倾角i,升交点赤经Ω,近地点辐角ω和平近点角M)计算是轨道机动的前提。目标卫星在T0时刻轨道根数为a1,e1,i1,Ω1,ω1,M1,严格回归轨道卫星轨道根数为a2,e2,i2,Ω2,ω2和M2。为节省燃料、实现轨道快速机动,研究平面内的轨道转移,只对a2和M2进行调整,其余轨道根数不变。
2.1 严格回归轨道半长轴根据开普勒第三定律,轨道半长轴a决定节点周期TN。考虑到主要带谐项(J2)影响,太阳同步轨道卫星的节点周期为[21]
| $ {T_N} = 2{\rm{ \mathit{ π} }}{\left( {\frac{{{a^3}}}{\mu }} \right)^{\frac{1}{2}}}\left[{1-\frac{{3{J_2}R_{\rm{e}}^2}}{{2{a^2}}}\left( {3-\frac{5}{2}{\rm{si}}{{\rm{n}}^2}i} \right)} \right] $ | (1) |
式中n为轨道平均转速(含引力常数
| $ \begin{array}{*{20}{l}} {{T_\varphi } = {T_N}\{ 1 + \frac{{3{J_2}}}{{8{a^2}}}\left[{\left( {16-20{\rm{si}}{{\rm{n}}^2}i} \right)e\left( {{\rm{cos}}{f_{\rm{*}}}-{\rm{cos}}\omega } \right)} \right.-}\\ {\left. {\left( {12 - 15{\rm{si}}{{\rm{n}}^2}i} \right){e^2}\left( {{\rm{cos}}2{f_{\rm{*}}} - {\rm{cos}}2\omega } \right)} \right]} \end{array} $ | (2) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {{f_{\rm{*}}} + \omega = {u_{\rm{*}}} + \alpha }\\ {{\rm{sin}}{u_{\rm{*}}} = \frac{{{\rm{sin}}\varphi }}{{{\rm{sin}}i}}} \end{array}} \right. $ | (3) |
式中α为沿卫星运动方向从标准纬圈φ起量的角度,
| $ {T_\varphi } = \frac{{86400N}}{R} $ | (4) |
联合式(1)~(3)可建立起a,N,R的关系式,即通过解析法求解出严格回归轨道的初始半长轴,记为a。利用
| $ {\rm{\Delta }}\lambda = \frac{{360N}}{R} $ | (5) |
严格回归轨道一旦确定,Δλ应为固定值,而
(1) 设置轨道外推时间TF/d。
(2) 利用
(3) 提取出第j圈(
(4) 由步骤(3)计算出Q个卫星过降交点的经度,计算相邻两圈经度差的均值
通过上述过程建立
(a) 设置半长轴调整步长Δa,计算P个半长轴
(b) 由步骤(1)~(4)计算相应的降交点经度差
(c) 采用连分式插值法对
(1) 将进行半长轴修正后的轨道
(2) 从外推的星下点中获取纬度为φ的所有圈次的经度,从而可知第一圈降轨(假设为光学载荷卫星)通过纬度φ时的经度λ0,并粗略确定对应(λ, φ)的平近点角M
| $ \tilde M = {M_1}-\frac{{360}}{{{\rm{\Delta }}\lambda }}\left( {{\lambda _0}-\lambda } \right) $ | (6) |
(3) 设置
(4) 利用
(5) 利用连分式插值法对
通过上述步骤确定T0时刻严格回归轨道根数
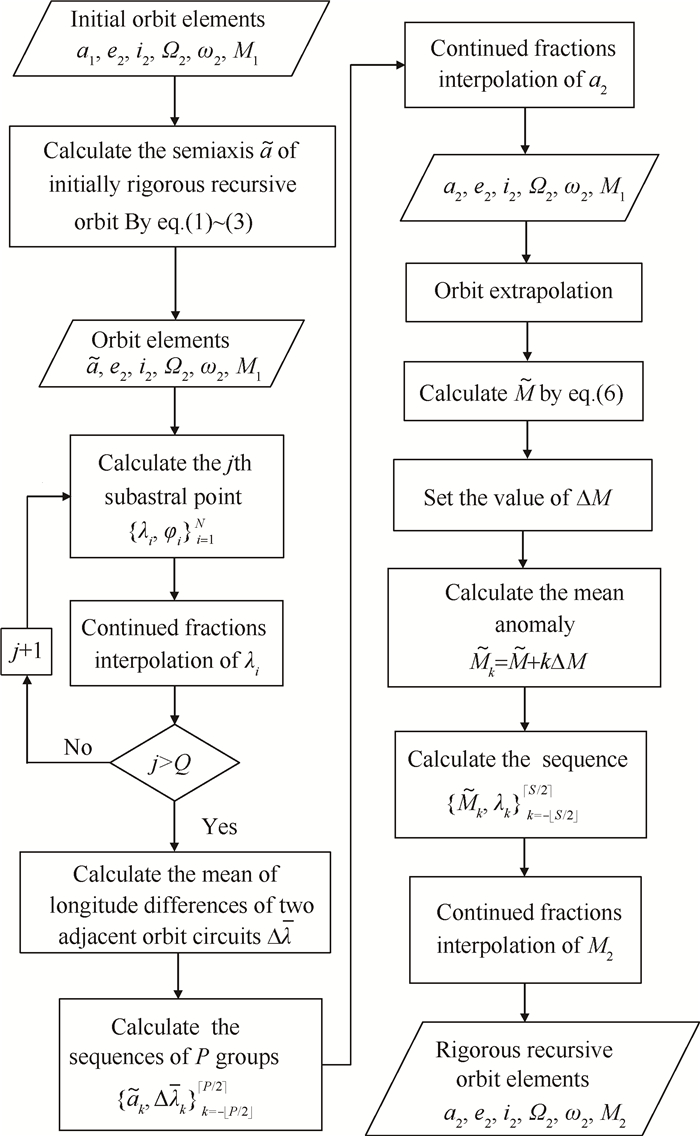
|
Fig. 1 Calculation flow of orbital elements |
(1) 控制误差。设轨道控制半长轴调整量为
(2) 偏心率。根据卫星偏心率的控制精度要求,应采用多脉冲进行轨道机动,且安排3~4次机动操作在远地点实施。若在机动过程中卫星轨道偏心率大于阈值
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{\Delta }}{e_x} = \frac{2}{V}{\rm{cos}}{u_0}{\rm{\Delta }}{V_{\rm{T}}}}\\ {{\rm{\Delta }}{e_y} = \frac{2}{V}{\rm{sin}}{u_0}{\rm{\Delta }}{V_{\rm{T}}}} \end{array}} \right. $ | (7) |
式中V是轨道速度,
(3) 轨控时间。采用程控变轨时,变轨后卫星应能以最短的时间进入国内测站可观测弧段,及时监控。为保证轨道控制和注入精度,要求控制前后至少有升轨、降轨各1圈的跟踪数据用于定轨,以便进行发动机推力标定和注入控后实测轨道根数。最后一次轨控为轨道修正,对速度进行微调,一般需要指定跟踪测站、跟踪弧段。
(4) 剩余燃料。相比平时轨道向严格回归轨道的正向转移,将严格回归轨道变为平时轨道是相反的逆向转移过程,此时轨控发动机需作反向的减速机动。两次轨道机动的燃料需求基本相同。若正向转移过程中燃料消耗量为
目标卫星半长轴比严格回归轨道卫星半长轴短,因此相对严格回归轨道卫星有一个正的角速度差,在抬高半长轴的同时将不断追赶严格回归轨道卫星,且随着半长轴逐渐接近严格回归轨道卫星,角速度差将越来越小。平时轨道向严格回归轨道转移过程就是要有效地利用这个角速度差,通过变轨时刻以及变轨量的合理安排,使得卫星在调整为回归轨道的同时与严格回归轨道卫星的相位差为零。
a1,a2分别表示目标卫星以及严格回归轨道卫星的轨道半长轴,平均角速度分别为n1,n2
| $ {n_j} = \sqrt {\frac{\mu }{{a_j^3}}} $ | (8) |
两星的角速度差为
| $ {\rm{\Delta }}n = {n_2} - {n_1} = - \frac{{3n}}{{2a}}{\rm{\Delta }}a $ | (9) |
经过时间t以后产生的相位差为
| $ {\rm{\Delta }}u = {\rm{\Delta }}nt = - \frac{{3{\rm{\Delta }}a}}{{2a}}nt $ | (10) |
式中
轨道转移必须进行若干次半长轴调整,若每次调整后剩余调整量为
| $ {\rm{\Delta }}{u_i} = \frac{{3n}}{{2a}}\left( {{\rm{\Delta }}{a_{ri}}{t_i} + \frac{1}{2}\dot at_i^2} \right) $ | (11) |
式中
| $ {\rm{\Delta }}{a_i} = {\rm{\Delta }}{a_{r\left( {i - 1} \right)}} - {\rm{\Delta }}{a_{ri}} + \dot a{t_i} $ | (12) |
轨控过程中,相对相位总的变化量为
| $ {\rm{\Delta }}{u_a} = \sum\limits_{i = 1} ^N {\rm{\Delta }}{u_i} $ | (13) |
轨道调整完成的时间为
| $ {t_a} = \sum\limits_{i = 1} ^N {t_i} $ | (14) |
若第1次轨控开始前的等待时间为t0,则总的相位变化为
| $ {\rm{\Delta }}{u_{pw}} = {\rm{\Delta }}u{t_0} + {\rm{\Delta }}{u_a} $ | (15) |
总的变轨时间为
| $ {t_{pw}} = {t_0} + {t_a} $ | (16) |
半长轴调整过程中相对相位的变化量为
当变轨指令发出以后,如果严格回归轨道卫星与目标卫星的角距
| $ {t_w} = \frac{{{\rm{\Delta }}{u_0} - {\rm{\Delta }}{u_1}}}{{{\rm{\Delta }}{u_D}}} $ | (17) |
当
最后一次机动,机动开始的时刻应选择在卫星到达标称位置加上Δuw。Δuw值根据严格回归轨道允许的漂移范围ΔL决定。同时目标半长轴也应作适当的调整,使得调整结束后,轨迹转而向西漂移,直接进入轨迹保持阶段。
4 严格回归轨道控制窗口为了使卫星的地面轨迹实现回归,即经过一个回归周期以后地面轨迹回到同一地方,要求严格回归轨道卫星运行周期(相应地要求半长轴)严格保持不变。但由于大气阻力的影响将使得半长轴不断降低,实现轨迹完全回归是不可能的。地面轨迹保持的任务是将地面轨迹控制在以标称位置为中心的一定宽度的回归区内,其关键是准确地计算出半长轴偏置量Δa。
令某一时刻卫星的半长轴a(比如上述T0时刻严格回归轨道半长轴a2)相对机动轨道半长轴a0的偏差为
| $ \dot a = - {C_{\rm{D}}}\frac{S}{M}\bar \rho n{a^2} $ | (18) |
式中CD为大气阻力系数;S为阻力有效面积;M为卫星质量;ρ为沿轨道的平均大气密度,与太阳活动、地磁指数等因素有关系;n为卫星平均运动角速度。
t天后区域(λ, φ)处轨迹的漂移量ΔLt为
| $ {\rm{\Delta }}{L_t} = - \frac{{3{\rm{ \mathit{ π} }}{R_e}}}{{{a_0}}}\left( {{\rm{\Delta }}at + \frac{1}{2}\dot a{t^2}} \right){\rm{cos}}\varphi {\rm{}} $ | (19) |
根据边界环保持要求,轨迹的漂移量应满足
考虑到误差因素,为避免半长轴超调而导致轨迹偏离所需的范围,在调整时应保守一些,即偏置量取得小一些,轨控时间间隔短一些。实际的偏置量可取
| $ {\rm{\Delta }}a' = \left( {\sqrt {1 - \xi } - \eta } \right){\rm{\Delta }}a $ | (20) |
式中ξ为半长轴变化率的相对误差,且
| $ \left( {\sqrt {1 - \xi } - 2\eta } \right){\rm{\Delta }}a \le {\rm{\Delta ''}} \le \sqrt {1 - \xi } {\rm{\Delta }}a $ | (21) |
为有效地进行轨迹调整,必须使得
目标卫星在UTC时刻2016年2月3日04:00:00.0000的六个轨道根数如表 1所示;严格回归(日回归)轨道参数N=1d,R=15;重访区域中心λ=109°,φ=34°;重返区域轨迹的漂移量ΔL=5km。经计算,严格回归轨道根数如表 1所示。图 2(a)为标称严格回归轨道卫星的轨迹漂移量,2016年2月17日16:05:50将飘出东边界;图 2(b)为修正轨道,即标称严格回归轨道半长轴6938460.584m加上边界环保持半长轴控制量110.778m,这样目标卫星直接进入轨迹保持阶段,开始西漂,且一个月内未超出边界环。表 2为严格回归轨道卫星过特定重访区域的时间及星下点经纬度坐标,回归周期约为24h,符合严格回归轨道回归周期要求。
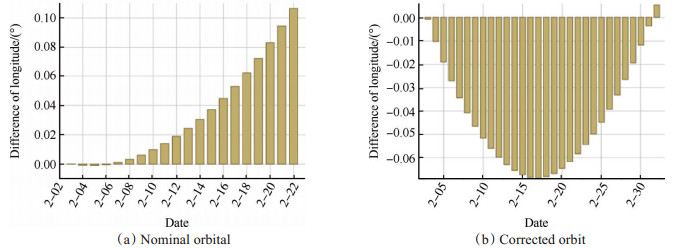
|
Fig. 2 Ground-track drift |
|
|
Table 1 Orbital elements of the initial orbit and the rigorous recursive orbit |
|
|
Table 2 Subastral points of the rigorous recursive orbit |
根据轨控约束条件,制定了多脉冲轨控策略,如表 3所示。其中,卫星质量为3t,燃料携带量为420kg,轨道偏心率要求小于0.0025,轨道控制的最大误差为10%。轨控发动机最长连续工作时间为1000s,经计算一次轨控最多可将半长轴抬高27km。为便于状态监视,在国内可见弧段实施多脉冲轨控,如表 3所示,最大单次半长轴控制量约21km,满足轨控发动机点火时长要求。整个控制过程在5d内完成,燃料消耗59.9kg,燃料剩余量满足日回归轨道转平时轨道以及轨迹网保持要求。
|
|
Table 3 Orbit control strategy of multiple pulses |
通过本文的研究,得到以下结论:
(1) 综合利用数值法和解析法,可以快速计算出高精度严格回归轨道半长轴和平近点角,重访周期误差约10s(严格回归周期为24h),满足精度要求;后续可以采用更加优秀的算法代替连分式插值进一步提高计算精度。
(2) 5个批次轨控均在国内可见弧度实施,单次轨控半长轴最大增量小于21km,满足发动机连续工作时长要求;第5次轨控对前4次轨控半长轴和相位变化进行最终修正。需要注意的是,因外界扰动,轨控过程中轨道倾角、升交点赤经、近地点辐角也会发生微小变化,为提高控制精度,后续还需深入研究轨控过程中卫星姿态扰动、催化床温度、燃料消耗导致卫星质心变化等因素造成的影响。
此外,由于轨控发动机连续工作时长的限制,多批次轨控实施制约多、周期长、风险大,极大制约着卫星的快速轨道机动能力;因此,具有更高性能的轨控发动机是优化轨控策略的重要前提。
| [1] |
Leeghim H. Spacecraft Intercept Using Minimum Control Energy and Wait Time[J]. Celestial Mechanics & Dynamical Astronomy, 2013, 115(1): 1-19.
(  0) 0) |
| [2] |
李晨光, 肖业伦. 多脉冲C-W交会的优化方法[J]. 宇航学报, 2006, 27(2): 172-176. (  0) 0) |
| [3] |
刘旭辉, 方蜀州, 王玉林, 等. 基于微型固体推力器阵列的轨道控制点火算法[J]. 推进技术, 2011, 32(3): 301-306. (LIU Xu-hui, FANG Shu-zhou, WANG Yu-lin, et al. Ignition Algorithm of Solid Propellant Micro-thruster Array for Orbit Control[J]. Journal of Propulsion Technology, 2011, 32(3): 301-306.)
(  0) 0) |
| [4] |
陆正亮, 张翔, 于永军, 等. 使用固体火箭发动机的快速机动卫星质量矩控制研究[J]. 推进技术, 2017, 38(5): 1165-1172. (LU Zheng-liang, ZHANG Xiang, YU Yong-jun, et al. Study on Satellite Mass Moment Control for Fast Orbit Maneuver Using Solid Rocket Motor[J]. Journal of Propulsion Technology, 2017, 38(5): 1165-1172.)
(  0) 0) |
| [5] |
李四平, 刘锦阳, 国凤林, 等. 轨道机动的时间-能量综合最优控制[J]. 宇航学报, 2010, 31(1): 137-142. (  0) 0) |
| [6] |
赵坚. 太阳同步(准)回归轨道卫星的轨道保持方法研究[J]. 中国空间科学技术, 2004, 24(4): 60-64. (  0) 0) |
| [7] |
Vtipil S D, Newman B. Determining an Earth Observation Repeat-Ground-Track Orbit for an Optimization Methodology[J]. Journal of Spacecraft and Rockets, 2012, 49(1).
(  0) 0) |
| [8] |
王雪峰, 方群, 孙冲. 一种航天器空间机动轨道的改进形状设计方法[J]. 宇航学报, 2015, 36(11): 1242-1247. DOI:10.3873/j.issn.1000-1328.2015.11.004 (  0) 0) |
| [9] |
杨盛庆, 杜耀珂, 陈筠力. 基于迭代修正方法的严格回归轨道设计[J]. 宇航学报, 2016, 37(4): 420-426. (  0) 0) |
| [10] |
杨维廉. 太阳同步回归轨道的长期演变与控制[J]. 航天器工程, 2008, 17(2): 26-30. (  0) 0) |
| [11] |
Sengupta P, Vadali S R, Alfriend K T. Satellite Orbit Design and Maintenance for Terrestrial Coverage[J]. Journal of Spacecraft and Rockets, 2010, 47(1).
(  0) 0) |
| [12] |
何艳超, 徐明, 张润宁, 等. 高精度重力场下回归轨道半解析优化设计[J]. 宇航学报, 2016, 37(5): 526-534. (  0) 0) |
| [13] |
曲宏松, 张叶, 金光. 基于Q值选取的太阳同步回归轨道设计算法[J]. 宇航学报, 2008, 16(9): 1688-1694. (  0) 0) |
| [14] |
Winkler T, Kaplinger B, Wie B. Optical Navigation and Fuel-Efficient Orbit Control Around an Irregular-Shaped Asteroid[C]. Boston: AIAA Guidance, Navigation, and Control (GNC) Conference, 2013.
(  0) 0) |
| [15] |
Xu M, Huang L. An Analytic Algorithm for Global Coverage of the Revisiting Orbit and Its Application to the CFOSAT Satellite[J]. Astrophysics and Space Science, 2014, 352(2): 497-502. DOI:10.1007/s10509-014-1939-2
(  0) 0) |
| [16] |
温生林, 闫野, 张华. 低轨回归轨道卫星轨迹漂移特性分析与控制[J]. 系统工程与电子技术, 2015, 37(3): 613-619. (  0) 0) |
| [17] |
Ormston T, Mardle N, Kuijper D. Orbit Control Manoeuvre Strategy for EarthCARE[C]. Pasadena: SpaceOps 2014 Conference, 2014.
(  0) 0) |
| [18] |
Nadoushan M J, Assadian N. Repeat Ground Track Orbit Design with Desired Revisit Time and Optimal Tilt[J]. Aerospace Science and Technology, 2015, 40: 200-208. DOI:10.1016/j.ast.2014.11.007
(  0) 0) |
| [19] |
Zhang J, Yang K, Qi R, et al. Robustness Analysis Method for Orbit Control[J]. Acta Astronautica, 2017, 137: 15-24. DOI:10.1016/j.actaastro.2017.03.034
(  0) 0) |
| [20] |
He Y, Xu M, Jia X, et al. High-Precision Repeat-Groundtrack Orbit Design and Maintenance for Earth Observation Missions[J]. Celestial Mechanics and Dynamical Astronomy, 2017, 128(2-3): 275-294. DOI:10.1007/s10569-017-9753-0
(  0) 0) |
| [21] |
章仁为. 卫星轨道姿态动力学与控制[M]. 北京: 北京航空航天大学出版社, 1998.
(  0) 0) |
| [22] |
刘林. 航天器轨道理论[M]. 北京: 国防工业出版社, 2000.
(  0) 0) |
| [23] |
李声峰, 陈栋栋. 连分式逼近与多项式逼近的计算效果比较研究[J]. 蚌埠学院学报, 2015, 4(4): 29-31. (  0) 0) |
| [24] |
刘锐, 陈雄, 周长省, 等. 非正交界面下的插值耦合传热方法[J]. 推进技术, 2016, 37(1): 90-97. (LIU Rui, CHEN Xiong, ZHOU Chang-sheng, et al. Development of Interpolation Method for Conjugate Heat Transfer in Non-Orthogonal Interfaces[J]. Journal of Propulsion Technology, 2016, 37(1): 90-97.)
(  0) 0) |
| [25] |
毛晓芳, 汪凤山, 杨晓红, 等. 小推力双组元姿控发动机性能研究[J]. 推进技术, 2012, 33(6): 987-990. (MAO Xiao-fang, WANG Feng-shan, YANG Xiao-hong, et al. Investigation on Performance of Small-Thrust Bi-Propellant Thruster for Attitude Control[J]. Journal of Propulsion Technology, 2012, 33(6): 987-990.)
(  0) 0) |
| [26] |
杨嘉犀. 航天器轨道动力学与控制(上册)[M]. 北京: 中国宇航出版社, 1995.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


