2. 中国科学院大学,北京 100190;
3. 中国航空发动机研究院,北京 101304;
4. 中国燃气涡轮研究院,四川 成都 610500
2. University of the Chinese Academy of Sciences, Beijing 100190, China;
3. Aero Engine Academy of China, Beijing 101304, China;
4. China Gas Turbine Establishment, Chengdu 610500, China
转子叶片是压气机和涡轮中完成功能转换的重要零件,在发动机工作时承受着复杂的多物理场载荷,如惯性离心力、气动力、热负荷、机械负荷等,随着航空发动机研制技术水平的发展,转子叶片因离心力、热负荷等稳态载荷作用引起的结构故障大幅度降低,而因气流激励带来的振动问题以及高循环疲劳失效问题较为突出,成为设计人员尤为关注的关键问题之一[1, 2]。航空发动机出现的很多重大事故都与叶片振动引起的高周疲劳失效(High Cycle Fatigue,简称HCF)有关[2, 3],例如:美国海军统计表明每型航空发动机研制及试车周期中平均发生2.5个HCF问题[4],美国F100系列发动机在研制过程中因高涡叶片断裂导致试验台毁坏,我国也有发动机高涡叶片断裂导致飞机停飞、新研发动机因涡轮叶片断裂致使研制周期和费用严重增加的问题发生。因此,叶片的HCF问题对航空发动机的安全性、操作性能和及时出勤率等构成严重威胁,并导致巨额的研制费用和维修费用。
为了解决叶片高周疲劳问题,美国实施了国家级HCF研究试验计划、英国建立了斯贝MK202发动机应力标准,其中一个关键工作是开展动应力测量。叶片动应力测量技术国外在20世纪80年代中期就已积累了丰富的经验,后续在先进的测量手段方面开展了大量研究[5],于90年代将遥测技术引入发动机试验中,在部分发动机上进行了系统集成,目前已实现了遥测系统的微型化、部件化,并成功用于发动机动应力测量[6, 7],动应力已与温度、压力等列为常规的测量内容。国内动应力测量技术发展相对较晚,天津大学开展了涡轮机叶片叶端定时测量技术研究,设计了一套基于非接触激光光纤传感器的光学叶端定时测量系统[8];武汉理工大学开展了基于光纤光栅传感器的旋转叶片振动测试技术研究,提出了一套基于光纤光栅传感器的叶片测量振动应变测量系统,并利用该方法在试验器上完成了单个静止叶片的振动应力测试,结果表明,第一阶固有频率实验测量值和仿真分析值误差在10%以内,第三阶固有频率实验测量值和仿真分析值误差在3%以内[9];上海交通大学开展了基于光学传感器的非接触式间断测量技术研究,并在部件试验器上开展了某机组高中压汽缸内转子的第18级叶片振动频率的测量,结果表明测量值与计算值误差为3.14%[10]。但在航空发动机工程研制领域,直到现在整机动应力测量还没有在型号研制中成为常规测试内容,只是当叶片出现断裂时,才不得不开展。为了寻找引发发动机压气机叶片裂纹的因素,吴岳庚等利用引电器方式在整机上实现了对发动机压气机转子叶片动应力的测量,捕捉到了相对应力比较大的发动机转速区域[11~13];为了寻找引发某发动机低压涡轮叶片裂纹的因素,曹昆华等利用引电器测量方式,成功测量到了发动机低涡叶片动频频谱图,获取了动应力最大区域的共振频率[14];李仙丽等提出了一种基于遥测技术的高温动应力测量系统方案,并利用该方法对某发动机高压涡轮叶片进行了动应力测量,发现发动机转速24频谱激励激起的涡轮叶片三阶模态的动应变幅值最大约为8×10-4[15]。刘美茹等采用非接触旋转叶片振动测量系统测量模拟转子叶片振动特性,试验结果表明,叶片出现裂纹后,叶片动频显著下降[16]。
综上,近年来国内在发动机动应力测量方面取得了很大进展,能够有效测量中大推力涡扇发动机叶片共振频率及其动应变幅值(应变片可直接敷设在裂纹发生处),但应用于小尺寸发动机时,由于其尺寸小、结构紧凑、运行转速更高等特殊性,须在几个方面进一步开展研究工作:一是在小尺寸叶片上、最大应力处无法敷设应变片时,应变片的敷设区域如何选择;二是如何将适于粘贴应变片位置的应变值准确地转化为最大应力处的应力值;三是高温、高转速环境下,如何保证测量系统的工作稳定性。针对上述问题,考虑应变片+引电器方式具有成本低、测量精度高等优点,本文设计了一套基于引电器的航空发动机高压涡轮叶片动应力测量系统,利用数值计算和试验相结合的方式,以某小尺寸涡喷发动机为研究对象,开展了引电器冷却技术、应变片敷设技术、动应力测量技术等研究工作。本文研究工作可为小尺寸高转速发动机涡轮叶片的动应力测量工作提供测试技术、分析方法和数据参考。
2 叶片危险模态计算分析目前国内鲜有针对工作转速40kr/min、温度900℃以上、尺寸30mm以下高压涡轮叶片振动应力测试的公开报导。本文以某小推力涡喷发动机为应用对象开展整机动应力测量,以对测试中的关键技术问题进行详细阐述。为确保在台架试车中,可以准确测试高压涡轮叶片的最大振动应力及其对应的工作转速,首先采用有限元法对叶盘振动特性进行计算分析,初步确定可能存在的共振模态,以便在试验中有所预判。
2.1 研究对象研究对象为某小推力涡喷发动机,最高转速为40kr/min,对应涡轮前燃气温度为950℃;慢车转速为65%最高转速,对应涡轮前燃气温度为480℃,高压涡轮为整体叶盘,涡轮叶片为24片。
2.2 计算模型、网格划分及边界条件根据高压涡轮叶盘循环对称的结构特点,建立一个扇区的实体模型,并选用10节点四面体SOLID187单元划分网格,共建立155538个单元,231234个节点,如图 1所示。计算中,对图中面A节点施加轴向和周向位移约束。

|
Fig. 1 Finite element model of the high pressure turbine blade |
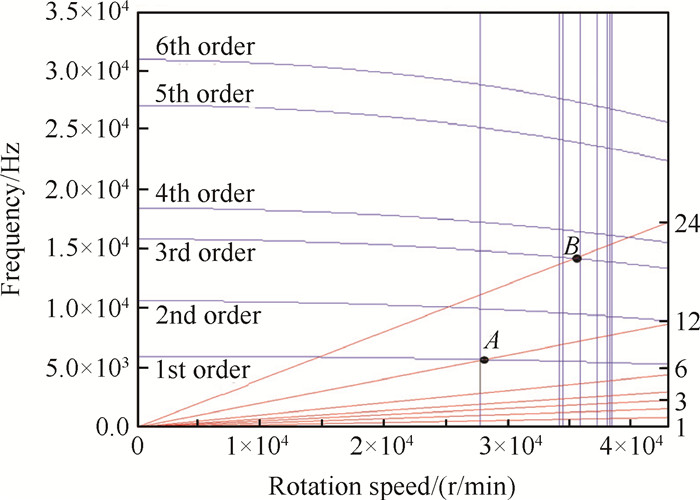
分别在不同转速,考虑离心负荷带来的预应力效应,并带入对应工况温度时的材料机械性能参数,求解叶片的动频曲线,并进一步绘制Campbell图求解叶片的共振频率,如图 2所示。图中蓝色横线表示叶片动频随发动机转速变化的情况,由于材料的弹性模量随工作温度(转速)的升高而降低,因此叶片的动频曲线随转速升高呈下降趋势。图中通过坐标原点的红色射线代表与转速成倍数关系的激励,可表示为N×Ω/60(N为构造系数,如静子叶片数或上游支板、支柱数目;Ω为转速,单位r/min)。图中动频曲线与激励射线的交点即为发动机实际工作时,叶片可能出现的共振点。
|
Fig. 2 Campbell diagram of the turbine blade |
由图 2可见,在主要停留转速,涡轮叶片有两阶模态可能被激起:一是在发动机转速为28.138kr/min时,转速12倍频的尾流激励(燃烧室12个燃油喷嘴)可能激起叶片的第1阶模态,如图中共振点A所示;二是在发动机转速为35.413kr/min时,转速24倍频的尾流激励(24片高压涡轮导向叶片)可能激起叶片的第3阶模态,如图中共振点B所示。
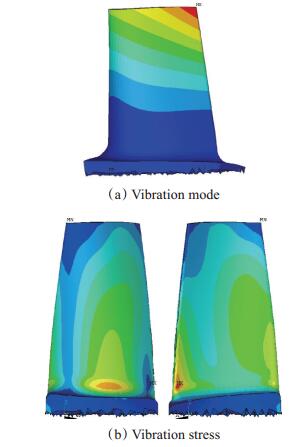
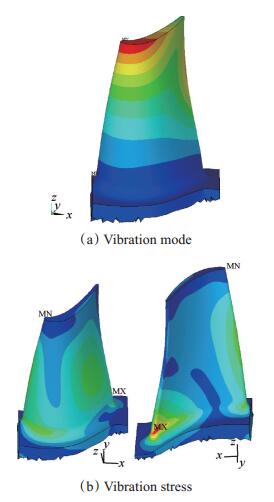
2.3.2 叶片振型及模态应力分布分析进一步提取两个共振点对应的叶片振型及模态应力分布,如图 3和图 4所示。可见,涡轮叶片以第1阶和第3阶模态振动时,最大相对振动应力均出现在涡轮叶片排气边尾缘叶根附近。
|
Fig. 3 The first order vibration mode and vibration stress distribution |
|
Fig. 4 The third order vibration mode and vibration stress distribution |
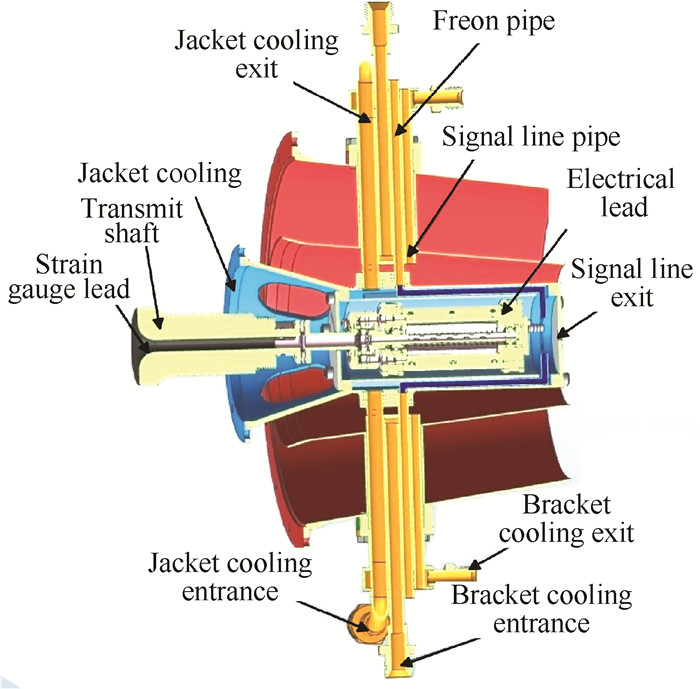
本文利用引电器法对涡轮叶片动应力进行测试,应力测试系统由高温应变计、应变计引线、高速刷环引电器、连接线路(采用1/4桥路)和动态测试系统等组成。测试硬件在选择时重点关注频响范围、允许使用温度、精度及量程,最终选用的试验设备及技术指标如表 1所示,在发动机中的安装形式如图 5所示。
|
|
Table 1 Composition of the measurement system |
|
Fig. 5 Measurement system installed in the engine |
在动应力测试中,可依据公式(1)将贴片应变转换得到叶片振动应力
| $ {\sigma _{\max }} = m \times \sigma = m \times \left( {E \times \xi \times \eta } \right) $ | (1) |
式中σmax为叶片的最大应力值;m为应力转换系数,其定义为叶片以某阶模态共振时,叶身最大振动应力与贴片处振动应力的比值,σ为贴片处振动应力值,其计算方法为材料弹性模量E与贴片处测量应变值ξ以及系数η的乘积,系数η由桥路接法、桥压、应变片灵敏度系数等因素决定。
3.3 应变片敷设位置确定由图 3,图 4可见,最理想的应变片敷设位置是在叶片排气边尾缘根部,从而可以直接捕捉到叶片的最大振动应力值。但由于试验对象为小推力涡喷发动机涡轮叶片,叶片展向长度为30mm左右,由于叶根圆角的存在,在实际操作中不可能在叶根位置牢固的敷设应变片。且由图 3(b),图 4(b)可见,最大应力区域的应力梯度极大,而应变片测试结果实际上是其粘贴面积内的应变总值,因此大应力梯度必然带来较大的测试误差[17];依据以下三个原则进行了高温涡轮叶片的应变片敷设位置选取:(1)具备足够面积的平整粘贴空间;(2)应力梯度小;(3)所关心阶次的模态应力值相对较大。对于所关注的第1阶模态,应变片可敷设在图 6(a)位置;对于所关注的第3阶模态,应变片可敷设在图 6(b)位置。
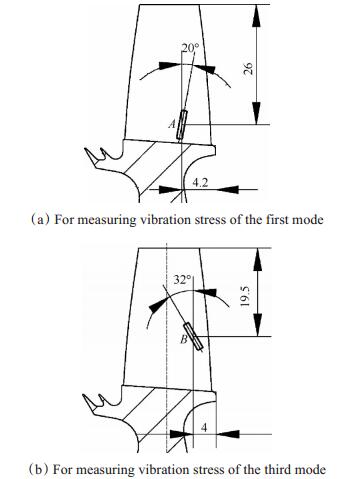
|
Fig. 6 Locations of the strain gauges |
由图 3(a)和图 4(a)所示计算结果,可确定第1阶与第3阶模态振动的应力转换系数m分别为2.78和3.13。
3.4 恶劣环境下应变片可靠性敷设技术高压涡轮转子叶片属于发动机的高温部件,在试验过程中,应变片及引线不仅工作环境温度高,还要承受高速、高压的气流冲击作用,此外,应变片及引线随叶片高速旋转,会承受较大的惯性载荷。因此,应变片或导线的脱落乃至损坏一直是限制涡轮叶片振动应力测试的一大难题。试验涡轮叶片表面比较光滑,为了实现紧固黏贴,必须首先对叶片表面进行磨砂,增加粗糙度;然后利用陶瓷(ROHIDE)喷涂,以实现应变片牢固敷设在叶片表面,并用融化的陶瓷棒封闭应变片的基底,以起到隔温作用。
4 试验结果及讨论 4.1 叶片振动应力测量试验 4.1.1 试验过程为了确定试验发动机高压涡轮叶片的共振转速,选取了两片叶片分别敷设应变片a和应变片b,将发动机转速由慢车状态缓慢推至最大转速状态,测试得到叶身关键位置A,B的动态应变幅值随转速变化如图 7所示。
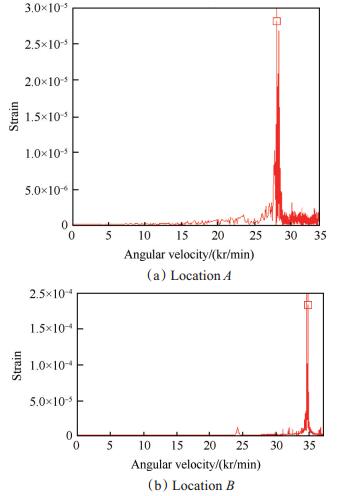
|
Fig. 7 Dynamic strain amplitude-rotational speed relationships |
图中应变片a出现时域峰值对应的转速为27.960kr/min,最大应变幅值为2.9×10-5,结合共振图分析结果可知,其对应Campbell图中的共振点A,由12倍频转速激励激起,激振力频率为5.410kHz。应变片b出现时域峰值对应的转速为34.920kr/min,最大应变幅值为2.17×10-4,其对应Campbell图中的共振点B,由24倍频转速激励激起,激振力频率为13.920kHz。与试验结果相比,计算获得的共振转速值相对误差很小。
根据测试获取的A点和B点振动应力值,利用公式(1)计算得到叶片的最大振动应力值,见表 2。可见,由12倍频激振力激起的叶片1阶振动应力最大值仅为15.0MPa,符合相关设计规范;而由24倍频激振力激起的叶片3阶振动应力最大值为112.7MPa,会对涡轮叶片带来一定的高周疲劳损伤积累。
|
|
Table 2 Dynamic stress measurement at location A and B |
动应力测量能够准确获取发动机的共振转速与最大应力对应的应变片应变值,但是由之得出的应力值可信度一直是一个难题,文献[11~16]也只是给出了共振转速及对应的应变片应变值,没有给出准确的动应力值。为了验证测试结果准确性,针对共振转速,开展了高周疲劳试验。
4.2.1 试验载荷确定分析试验发动机涡轮叶片为24片,在实际工程中,由于制造、装配等误差因素,同级各叶片的自振频率具有一定程度的差异,因而叶片共振转速不是一个点,而是一个转速范围。此共振转速区域的确定方式为:理论共振转速值±叶片最大频差所对应的转速范围,叶片最大频差可依据非旋转态时模态试验的测试结果获得。
由模态测频结果,叶片一阶振动频差为65Hz,对应转速范围为65Hz×60/12=325r/min;二阶振动频差为65Hz,对应转速范围为162.5r/min。因此,在进行高循环疲劳试验时,需要考虑的转速范围为27960±325r/min和34920±162.5r/min,应在此转速范围内加密转速台阶,可按照发动机控制精度能够实现的最小转速台阶(160r/min)进行试验。根据我国现行航空发动机研制国军标中对不同材料构件高疲劳循环次数的要求,该发动机涡轮叶片使用的镍基高温合金应满足大于1×107的高循环循环寿命,可确定如表 3所示的考核转速及累积运转时间。
|
|
Table 3 Accumulative running time of the high cycle fatigue test for different speeds |
按图 8所示的载荷谱开展试车,当试验时间累积至1.25h后(完成了第1阶振动考核的50%运转时间),用孔探仪观测叶片,未发现叶片有裂纹;继续开展第3阶振动考核,当试验时间达到1.6h时,用孔探仪观察涡轮叶片,发现7片高压涡轮叶片出现裂纹,均位于涡轮叶片排气边尾缘叶根附近,与图 5(b)给出的振动应力幅值区吻合,其中一个叶片的裂纹长度达2.3mm,验证了24倍频激振力激起叶片3阶共振的危害性,也说明了测试的动应力值的可信性。
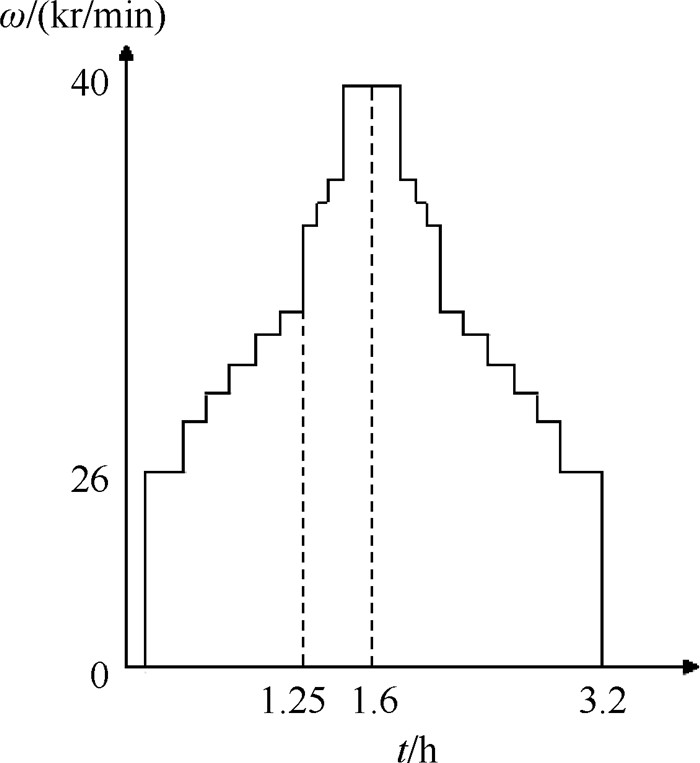
|
Fig. 8 Load spectrum used in the high cycle fatigue test |
(1)提出了基于引电器的小推力发动机高温涡轮叶片动应力测量方案,建立了相应的测试系统,可有效解决小尺寸发动机涡轮叶片振动应力的测试难题,能够实现40kr/min转速、950℃环境温度范围内旋转件振动应力测试,该测量方案和测试系统可为其它小型发动机叶片动应力测试提供一定的参考。
(2)利用提出的振动应力测量技术,测试得到了小型发动机转速在34.92kr/min时高压涡轮叶片振动应力,阐述的测试方案和技术细节可为相关研究提供重要技术参考。
(3)通过高周疲劳试验验证,利用本文提出的应变-应力转换方法获取的动应力值具有较高的可信度和可操作性。
| [1] |
Srinivasan A V. Vibrations of Bladed-Disk Assemblies-A Selected Survey[J]. ASME Joural of Vibration, Acousties, Stress, and Reliability in Design, 1984, 106: 165-168. DOI:10.1115/1.3269162
(  0) 0) |
| [2] |
Srinivasan A V. Flutter and Resonant Vibration Characteristics of Engine Blade[J]. ASME Joumal of Engineering for Gas Turbines and Power, 1997, 119: 742-775. DOI:10.1115/1.2817053
(  0) 0) |
| [3] |
Thomson D. US HCF Program Overview[C]. New Orleans: 10th National Turbine Engine High Cyclic Fatigue Conference, 2005.
(  0) 0) |
| [4] |
Cifone A. Keynote Address[C]. New Orleans: 10th National Turbine Engine High Cyclic Fatigue Conference, 2005.
(  0) 0) |
| [5] |
黄春峰, 候敏杰, 石小江. 航空发动机振动测量技术方法研究[J]. 测控技术, 2009, 28(增刊): 21-26. (  0) 0) |
| [6] |
DeAnna R G, Wireless Telemetry for Gas-Turbine Engine[R]. NASA/TM-2000-209815, 2000.
(  0) 0) |
| [7] |
Long S A, Edney S L, Reiger P A, et al. Telemetry System Integrated in a Small Gas Turbine Engine[J]. Journal of Engineering for Gas Turbines & Power, 2012, 134(4): 1-5.
(  0) 0) |
| [8] |
王宇华, 段发阶, 叶声华, 等. 涡轮叶片振动的非接触测量[J]. 宇航计测技术, 2002, 22(2): 20-24. (  0) 0) |
| [9] |
孙亮志. 基于光纤光栅传感的旋转叶片振动测试与分析[D]. 武汉: 武汉理工大学, 2013. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2363796
(  0) 0) |
| [10] |
滕丽娜, 佟德纯, 陈兆能. 汽轮机叶片动频的非接触间断测量法[J]. 振动测试与诊断, 2000, 20(4): 279-282. (  0) 0) |
| [11] |
吴岳庚, 龚寅生, 张松林. 某压气机叶片动频测量的试验研究[J]. 燃气涡轮试验与研究, 1999, 12(4): 58-62. (  0) 0) |
| [12] |
彭建, 刘兵. 压气机转子叶片动频动应力测试技术和应用研究[J]. 燃气涡轮试验与研究, 2003, 16(1): 10-13. (  0) 0) |
| [13] |
卢艳辉, 梅庆, 雷沫枝, 等. 高转速压气机转子叶片的动应力测试与动力学设计评估[J]. 推进技术, 2014, 35(10): 1398-1403. (LU Yan-hui, MEI Qing, LEI Mo-zhi, et al. Vibration Stress Test and Dynamical Evaluation for High Rotational Speed Compressor Blades Through Numerical and Experimental Method[J]. Journal of Propulsion Technology, 2014, 35(10): 1398-1403.)
(  0) 0) |
| [14] |
曹昆华, 黄家经. 某型发动机低压涡轮转子叶片动测技术及应用研究[J]. 燃气涡轮试验与研究, 2008, 21(1): 22-25. (  0) 0) |
| [15] |
李仙丽, 罗乘川, 安奕忱, 等. 基于遥测技术的发动机涡轮转子叶片动应力测量[J]. 燃气涡轮试验与研究, 2014(6): 53-56. (  0) 0) |
| [16] |
刘美茹, 朱靖, 滕光蓉, 等. 非接触旋转叶片振动测量系统在转子叶片裂纹故障试验中的应用[J]. 燃气涡轮试验与研究, 2015(4): 45-52. (  0) 0) |
| [17] |
蔡宁泊, 侯乃先, 张成成. 航空发动机振动应力测量的贴片可靠性及优化分析[J]. 推进技术, 2016, 37(10): 1964-1969. (CAI Ning-bo, HOU Nai-xian, ZHANG Cheng-cheng. Reliability and Optimization Analysis of Strain-Gauge[J]. Journal of Propulsion Technology, 2016, 37(10): 1964-1969.)
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


