2. 中国空气动力研究与发展中心 超高速空气动力学研究所 高超声速冲压发动机技术重点实验室,四川 绵阳 621000
2. Science and Technology on Scramjet Laboratory, Hypervelocity Aerodynamics Institute CARDC, Mianyang 621000, China
高超声速一体化试验模型开展风洞试验的主要目的是为了获得不同姿态下的气动力载荷,尤其是推力/阻力、升力和俯仰力矩,激波风洞和脉冲燃烧风洞是开展高超声速一体化飞行器技术研究的主要地面设备[1, 2],这两类风洞的试验时间从几百微秒至几百毫秒不等[2~4],启动时激发的测力系统振动至试验结束仍无法停止,试验过程中测力天平输出结果均为动态信号。而当前用于数据处理的天平公式为静态校准所得,未考虑动态特性对结果的影响,导致测力结果存在误差。
针对脉冲风洞瞬态测力问题,国外针对激波风洞开展了大量研究,主要可分为加速度计天平测力[5~11]和应力波天平测力[12~14]。Tanno等[5~7]发展了一种加速度计短时风洞模型测力方法,试验和仿真结果对比证明毫秒量级的激波风洞能够准确获得模型推力。Singh等[8, 9]和Naumann等[10]获得了激波风洞中自由模型的加速度,并采用卷积积分的方法得到了试验模型的气动力。Laurence等[11, 12]采用高速相机采集了试验模型在激波风洞中自由飞行的轨迹,然后采用高精度算法对结果进行修正,最终计算求得较为准确的推力/阻力,但该方法对于俯仰力矩的测量仍然较为困难。Robinson等[13, 14]设计了三分量应力波天平,并在激波风洞中开展了测力试验,试验结果与理论预测吻合较好。Marineau等[15]采用惯性补偿方法对缩尺Apllo返回舱模型进行了测力试验,并进行了惯性力补偿,结果与CFD仿真结果一致,但测试模型尺度仅为6英寸,尺寸较小。
近几年,国内发展了多座长试验时间脉冲型高超声速风洞,比如中国空气动力研究与发展中心(简称CARDC)Φ2.4m脉冲燃烧风洞运行时间可达300ms[1, 2, 16],中科院力学所JF12高超声速激波风洞试验时间也超过100ms[17, 18],短时测力技术得到了充分发展和应用。刘洪山等[19]总结了应力波天平在国内激波风洞上的应用,王锋等[20]将载荷辨识技术应用于Φ2.4m脉冲燃烧风洞模型测力,根据天平输出信号和测力系统载荷传递函数之间的关系,进行了输入载荷辨识。文献[17]中根据JF12的特点设计了相应的杆式和盒式应变天平,并在试验中获得了准确的气动力载荷。
综合国内外脉冲型高超声速风洞瞬态测力的研究现状发现,应力波天平和加速度计天平应用广泛,但难以应用到尺度大、质量重的模型。而国内所建设的脉冲风洞试验时间较长,模型尺度大、质量重,多采用应变式天平[21],但由于试验过程中的动态特性,应变式测力天平只能够通过均值来衡量试验模型的气动力,要进一步提高天平的测力精度以及缩短天平稳定时间,必须对天平动态输出结果进行惯性补偿。
2 测力天平动力学建模本文研究对象为三分量测力天平,其结构如图 1所示,由(a)~(e)组成,分别为浮动框、固定框、支撑梁、轴向测量元件、法向和俯仰力矩测量元件。其总体尺寸为:长460mm,宽160mm,高90mm。试验过程中,浮动框与模型支撑框架相连,固定框与风洞基座相连,试验过程中风洞来流作用在试验模型,使天平检测梁产生变形,应变计输出相应的应变值,进而根据校准公式得到试验模型的气动力载荷。
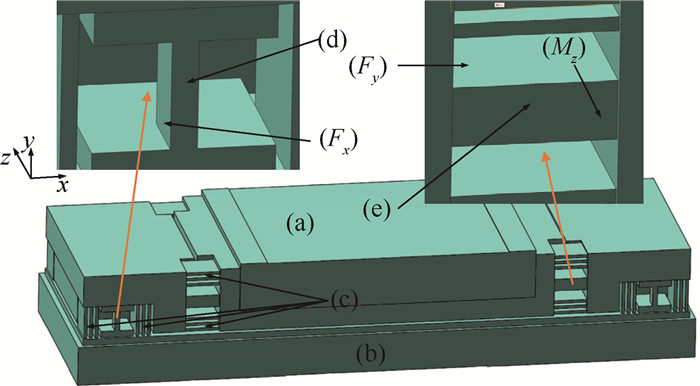
|
Fig. 1 3-component force balance |
测力天平简化结果如图 2(a)所示,盒式测力天平的支撑结构和测量结构均为梁,相对浮动框和固定框其质量很小,可以忽略,建模过程中将其简化为具有三分量刚度的弹簧。试验过程中,固定框视为静止,浮动框与模型一起振动,引起弹性测量元件产生应变,检测试验过程中的气动力载荷。
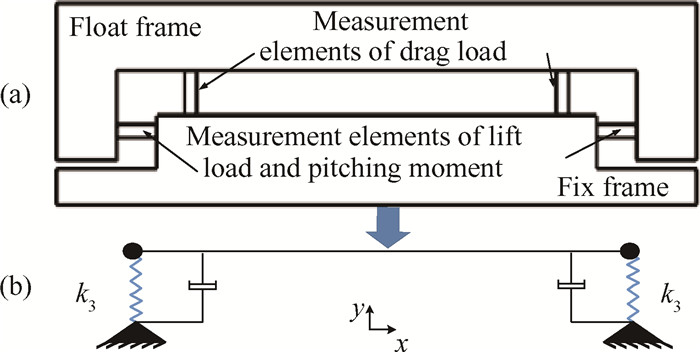
|
Fig. 2 Simplified model of the force balance |
测力天平可进一步简化为图 2(b)所示的结构,测量元件为具有x,y和Mz三分量刚度的弹簧,由于天平结构的对称性,弹力k1x,k1y,k1Mz分别等于k2x,k2y,k2Mz,固定框简化为地面,浮动框简化为两端弹簧支撑的杆。
根据图 2(b)建立天平动力学方程
| $ \mathit{\boldsymbol{M\ddot q + C\dot q + Kq = F}} $ | (1) |
式中M,C,K分别为天平的质量矩阵、阻尼矩阵和刚度矩阵,q为天平位移矩阵,F为其受到的外部载荷。
式(1)表明,要获得试验过程中的动态载荷,不仅需要考虑测力天平输出的弹性载荷,还需要考虑浮动框的惯性载荷。由于试验过程中天平浮动框以整体振动为主,可以通过多点组合的方式获得天平振动时的加速度,各方向振动的质量,可以通过建模软件进行计算获得,从而获得模型的惯性输出载荷。弹性输出载荷,即为天平输出结果,两者在时域范围内进行叠加,即可实现惯性力补偿。
3 仿真分析 3.1 测力天平虚拟标定为了对测力天平进行瞬态分析,首先需获得天平弹性输出与所受载荷的对应关系,因而需对其进行静态虚拟标定。
测力天平应变计的位置根据使用时测量元件应变量来确定,为了增加输出电压,应变计一般位于测量元件根部,并减小敏感栅长度,且尽量保持纵轴线和测量元件主应变方向一致,以得到最大的信号输出和最小的信号间干扰。该天平应变计位置如图 3所示,其中11~18检测y向应变,输出轴向力(推力/阻力)Fx,21~28,61~68检测x向应变,通过改变惠斯顿电路组桥方式,输出法向力(升力)Fy和俯仰力矩Mz,以上电路均为全桥电路(其中第一个数字1,2,6分别代表Fx,Fy和Mz分量,第二个数字1~8分别为测点编号,括号内的编号表示位于天平的对侧相应位置)。

|
Fig. 3 Strain-gauge and accelerator detection points of the 3-component force balance |
天平静态校准公式为
| $ \mathit{\boldsymbol{F = U}} \cdot \mathit{\boldsymbol{X}} $ | (2) |
式中
| $ \mathit{\boldsymbol{X = }}{\mathit{\boldsymbol{U}}^{ - 1}} \cdot \mathit{\boldsymbol{F}} $ | (3) |
由式(3)知,对测力天平进行标定,需对其施加3个正交载荷,分别得到相应的应变值,而后确定测力天平的系数矩阵。
对测力天平进行虚拟标定,其有限元模型如图 4所示,采用六面体单元,以利于准确获得测点坐标及应变值,支撑梁和检测梁均加以细化,浮动框和固定框等应变较小位置网格较为粗糙,该模型共11.14万节点,1.7万网格。载荷施加位置为天平上表面,固定位置为天平下表面。

|
Fig. 4 Finite element model of the 3-component force balance |
天平Fx(推力/阻力)、Fy(升力)、Mz(俯仰力矩)设计载荷分别为1kN,5kN,1kN·m,标定即施加以上载荷。
通过有限元分析获得应变矩阵为
| $ \mathit{\boldsymbol{U = }}\left( {\begin{array}{*{20}{c}} {477.235}&{ - 0.0003}&{ - 1.6861}\\ { - 0.02065}&{511.695}&{ - 0.015}\\ {13.707}&{ - 0.02}&{486.585} \end{array}} \right) $ | (4) |
进而计算得到天平的系数矩阵为
| $ \mathit{\boldsymbol{X = }}\left( {\begin{array}{*{20}{c}} {2.095195}&{7.56 \times {{10}^{ - 6}}}&{7.26 \times {{10}^{ - 3}}}\\ {8.28 \times {{10}^{ - 5}}}&{9.771446}&{6.05 \times {{10}^{ - 5}}}\\ { - 5.90 \times {{10}^{ - 2}}}&{4.01 \times {{10}^{ - 4}}}&{2.054935} \end{array}} \right) $ | (5) |
从系数矩阵X中可以看出,对角线主系数外,x13(轴向力输入对俯仰力矩输出的干扰系数)和x61(俯仰力矩输入对轴向力输出的干扰系数)相对其他4项很大,说明该天平弹性输出结果中,轴向力和俯仰力矩间的耦合较为严重,且由x13 < x61可知,俯仰力矩对轴向输出的干扰大于轴向力对俯仰力矩输出的干扰,其余4项值很小,说明轴向力、俯仰力矩和法向力之间的干扰很小。在静态加载条件下,可以通过天平的系数矩阵的干扰项对其进行消除,天平信号处理时亦是通过对有效试验时间内的动态输出结果取均值(转化为静态信号),进而求解气动力载荷。但对于试验所测动态载荷的处理,则需要对其进行惯性载荷补偿。
3.2 天平模态及载荷分析 3.2.1 试验过程中载荷变化图 5为5m量级标模试验中总压和轴向振动信号。从图中可以看出,风洞启动过程总压上升,达到一定幅值后,以该幅值为基准值进行小幅震荡,持续约500ms,该时间段内模型受到振荡载荷作用。天平所受推力、阻力和俯仰力矩分别如图所示,从图中可以看出,Fx,Fy和Mz均存在大幅振荡,黑色细线为各分量载荷滤波后结果,各分量近似为阶跃载荷。综合分析试验过程中试验段总压和各分量载荷变化规律,确定对测力天平振动特性研究时,可对其施加阶跃载荷和正弦载荷,分析测力天平的动态输出规律。
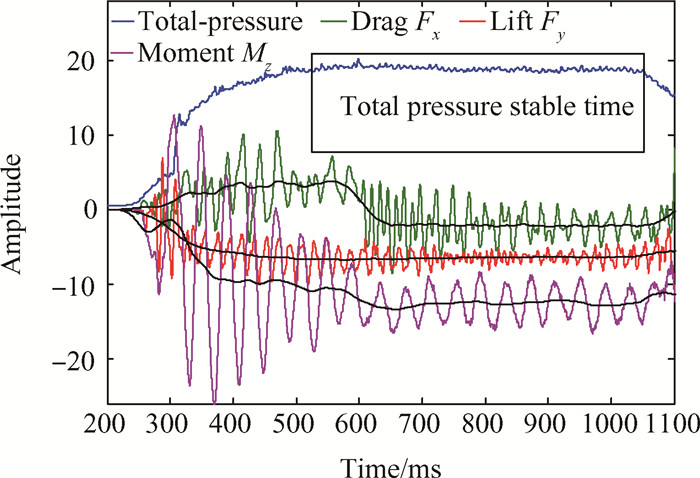
|
Fig. 5 Signal of the fore balance and the total pressure of the test section |
为确定正弦载荷频率,必须得到测力天平轴向、法向和俯仰方向振动的固有频率,因此对其进行模态分析。分析时边界条件与标定时一致,结果表明,测力天平的x向(轴向)振动为一阶振动,y向(法向)振动为二阶振动,俯仰振动为五阶振动。振动频率及振型如表 1和图 6所示。测力系统的刚度主要取决于天平刚度,加入模型后,系统质量大幅增加,固有频率远低于天平固有频率,因此,分析时只考虑低于天平固有频率的正弦载荷,各分量频率分别为200Hz,300Hz和700Hz,约为天平固有频率的1/2。
|
|
Table 1 The first six modes parameter of the force balance |
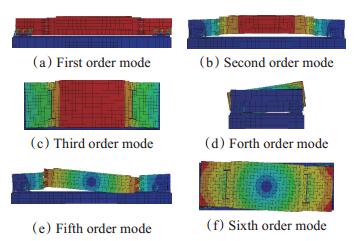
|
Fig. 6 The first six modes of force balance |
研究过程中阻尼输出载荷可以忽略,但是阻尼不仅影响结构共振时的稳定状态,而且影响结构振动稳定所需时间,因此瞬态分析时必须设置阻尼系数。学术界对阻尼的研究不断加深,提出了多种阻尼理论[22, 23],Rayleigh阻尼理论以其在有限元方法中的优势,得到了广泛应用,其表达为
| $ \mathit{\boldsymbol{C = }}\alpha \mathit{\boldsymbol{M + }}\beta \mathit{\boldsymbol{K}} $ | (6) |
文献[24]和有限元软件均通过式(7)求解Rayleigh阻尼系数。
| $ \left[ \begin{array}{l} \alpha \\ \beta \end{array} \right] = \frac{2{{\omega _1}{\omega _2}}}{{\omega _2^2 - \omega _1^2}}\left[ {\begin{array}{*{20}{c}} {{\omega _2}}&{ - {\omega _1}}\\ { - \frac{1}{{{\omega _2}}}}&{\frac{1}{{{\omega _1}}}} \end{array}} \right]\left[ \begin{array}{l} {\xi _1}\\ \xi_2 \end{array} \right] $ | (7) |
式中ω1,ω2为关注振动的频率范围,ω1,ω2分别为起始和截止频率,应将关心的振动频率包含在内,两者均为角频率,单位为rad/s,计算时应将f乘以2π。ξ1,ξ2分别为ω1,ω2频率对应的粘性阻尼系数,对于一般机械系统,取值范围为0.03~0.05,此处取ξ1=ξ2=0.04。根据不同分析状态确定关注频率,获得相应的阻尼系数如表 2所示。
|
|
Table 2 Parameter of Rayleigh damping |
本文采用惯性补偿方法。精确求解天平惯性载荷非常困难,但从测力天平振型中可以看出,轴向振动时,天平浮动框和前后连接件整体振动,法向振动和俯仰振动为浮动框振动,因此对应的振动质量mx为天平浮动框和前后连接件的质量,my为天平浮动框的质量,Jz为浮动框绕旋转中心的转动惯量。计算获得质量矩阵如下
| $ \mathit{\boldsymbol{M = }}\left( {\begin{array}{*{20}{c}} {{m_x}}&{}&{}\\ {}&{{m_y}}&{}\\ {}&{}&{{J_z}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {26.71}&{}&{}\\ {}&{17.82}&{}\\ {}&{}&{0.134} \end{array}} \right) $ | (8) |
组合图 3中A1~A6点的加速度作为天平浮动框的加速度,算法如下
| $ \mathit{\boldsymbol{A = }}\left( \begin{array}{l} {a_x}\\ {a_y}\\ {a_{Mz}} \end{array} \right) = \left( {\begin{array}{*{20}{c}} {\frac{1}{6}}&{\frac{1}{6}}&{\frac{1}{6}}&{\frac{1}{6}}&{\frac{1}{6}}&{\frac{1}{6}}\\ {\frac{1}{6}}&{\frac{1}{6}}&{\frac{1}{6}}&{\frac{1}{6}}&{\frac{1}{6}}&{\frac{1}{6}}\\ {\frac{1}{4}}&{\frac{1}{4}}&{ - \frac{1}{4}}&{ - \frac{1}{4}}&0&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {A{1_x}}&{A{1_y}}&{A{1_y}}\\ {A{2_x}}&{A{2_y}}&{A{2_y}}\\ {A{3_x}}&{A{3_y}}&{A{3_y}}\\ {A{4_x}}&{A{4_y}}&{A{4_y}}\\ {A{5_x}}&{A{5_y}}&{A{5_y}}\\ {A{6_x}}&{A{6_y}}&{A{6_y}} \end{array}} \right) $ | (9) |
根据牛顿第二定律,惯性力计算结果为
| $ {\mathit{\boldsymbol{F}}_{\rm{I}}} = \mathit{\boldsymbol{M}} \cdot \mathit{\boldsymbol{A = }}\left( {\begin{array}{*{20}{c}} {{m_x}}&{}&{}\\ {}&{{m_y}}&{}\\ {}&{}&{{J_z}} \end{array}} \right)\left( \begin{array}{l} {a_x}\\ {a_y}\\ {a_{Mz}} \end{array} \right) $ | (10) |
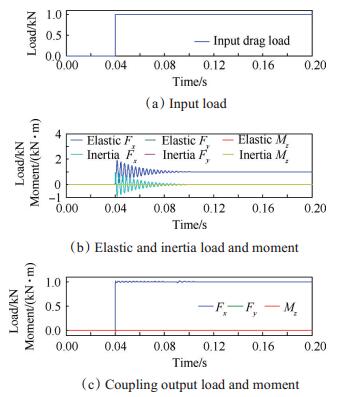
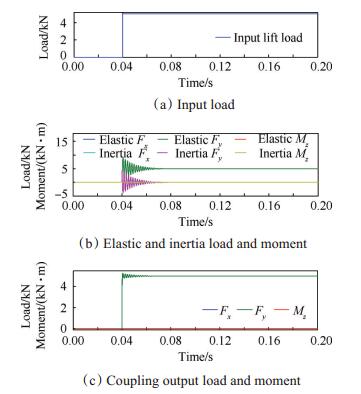
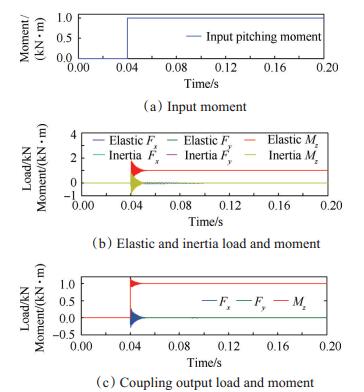
图 7,图 8,图 9分别为轴向力、法向力和俯仰力矩作用时天平的动态响应结果。图 7(a),图 8(a),图 9(a)为输入载荷,0~40ms为初始阶段,载荷值为0,40~40.1ms为加载阶段,Fx,Fy和Mz幅值分别增加到1kN,5kN和1kN·m,40.1~200ms为稳定阶段,阻尼参数如表 2所示。
|
Fig. 7 Analysis result of the force balance under the actions of the axial step load |
|
Fig. 8 Analysis result of the force balance under the actions of the normal step load |
|
Fig. 9 Analysis result of the force balance under the actions of the pitching moment |
图 7(b),8(b),9(b)分别为单分量加载时天平弹性输出(通过式(2)求得)和惯性输出(通过式(10)求得),从图中可以看出,加载后,两者均以恒定周期振动,在阻尼作用下,超调量不断减小直至0,但该过程持续时间较长。
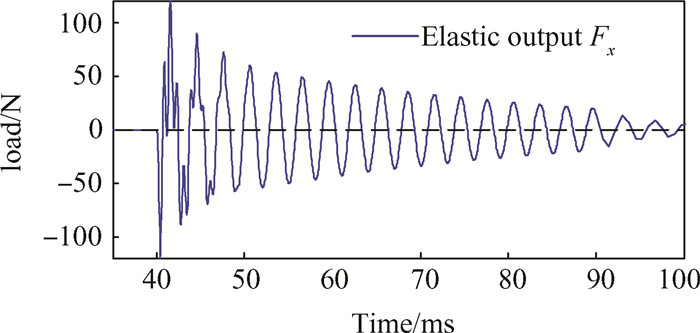
图 7(c),8(c),9(c)分别为单分量加载时弹性力和惯性力的叠加结果。从图中可以看出,惯性补偿后,载荷波动的超调量大幅下降,平衡所需时间也大幅减小。图 7(c),8(c)结果显示,当轴向力和法向力作用时,其余分量输出结果接近于0,说明单独施加轴向力和法向力,对其余分量的干扰很小。图 9(c)显示,施加俯仰力矩时,法向输出接近于0,轴向输出不为0,35~100ms结果如图 10所示,从周期特性分析,前段干扰波形振动频率为1315.79Hz,主振动频率为333.33Hz,分别对应天平五阶和一阶固有频率,这说明天平轴向输出结果开始为以上二阶振动的耦合,主振动几个周期后,小波消失,从时间上看,此时浮动框绕z轴旋转振动已停止,浮动框及前后连接部位按照相同规律振动,轴向弹性输出按照一阶振动规律逐渐衰减。
|
Fig. 10 Axial elastic load output of the force balance under the action of the pitching moment |
图 11为三分量阶跃加载时天平的动态响应结果。图 11(a)为输入载荷,其值为以上单分量载荷的综合。图 11(b)显示了Fx,Fy和Mz的弹性力输出结果,从图中可以看出,各分量均以输入载荷为均值进行周期振动,超调量逐渐降低。载荷施加后,瞬时结果偏离均值较大,幅值分别达到989N,4146.1N和797.1N·m。图 11(c)为Fx,Fy和Mz的惯性力输出结果。图 11(d)为惯性补偿后各分量输出结果,从图中可以看出,惯性补偿后三分量载荷超调量大幅度减小,分别为162.6N,574.4N和38N·m。对比发现惯性补偿后载荷趋于平衡,而且平衡所需时间大幅缩短,这为短时风洞测力获得稳定输出提供了保障。
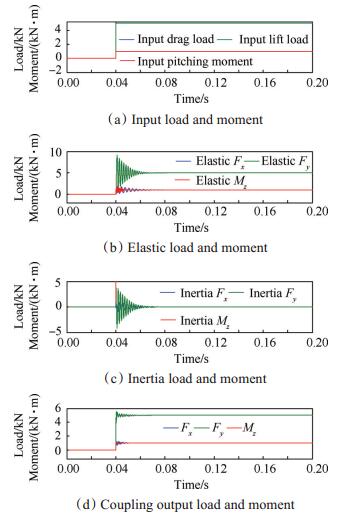
|
Fig. 11 Analysis result of the force balance under the action of the 3-component step load |
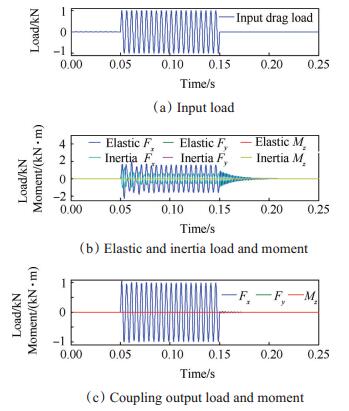
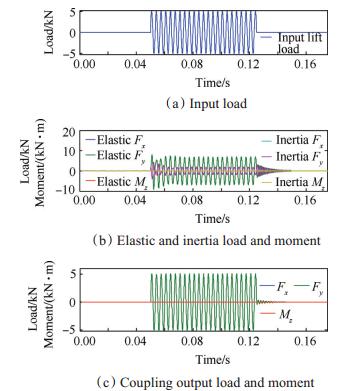
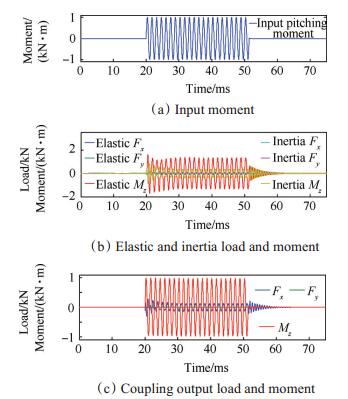
对测力天平进行单分量正弦加载,瞬态分析结果如图 12~14所示。其中,图 12(a),13(a),14(a)分别为Fx,Fy和Mz的输入载荷曲线,频率分别为200Hz,300Hz和700Hz,振幅分别为1kN,5kN和1kN·m。各分量载荷加载时间如表 3所示,阻尼参数如表 2所示。
|
Fig. 12 Analysis result of the force balance under the actions of the axial sine load |
|
Fig. 13 Analysis result of the force balance under the actions of the normal sine load |
|
Fig. 14 Analysis result of the force balance under the actions of the pitching sine moment |
|
|
Table 3 Loaded period of each component |
图 12(b),13(b),14(b)分别为单分量加载时弹性力和惯性力输出结果,从图中可以看出,载荷施加后,天平振动按照输入载荷和天平自由振动叠加的规律进行,而后为强迫振动。轴向和法向单独加载时,其余分量的弹性输出均接近于0;俯仰力矩作用时,法向力输出接近于0,但由于干扰作用,轴向力输出为正弦振动信号,结果不为0。
图 12(c),13(c),14(c)分别为惯性补偿后的输出载荷结果。图 12(c),13(c)显示,轴向和法向单独加载时,加载分量上输入输出一致,其余分量输出接近于0。俯仰力矩加载时,力矩输入输出一致,法向输出结果为0,轴向力输出结果不为0,但振动频率与加载频率一致,说明该振动为强迫振动。
3.3.6 三分量正弦载荷作用时的振动规律图 15为三分量正弦加载时,测力天平的动态响应。图 15(a)为施加载荷,其中0~20ms为初始阶段,输入载荷为0,20~70ms为加载阶段,轴向、法向和俯仰力矩载荷频率分别为200Hz,300Hz和700Hz,幅值分别为1kN,5kN和1kN·m,70~100ms为结束阶段,载荷值为0。图 15(b)为弹性力输出结果,三分量幅值分别达到2210.2N,9316N和1730.2N·m。加载后,三条曲线在一定时间内,均偏离正弦曲线,而后转化为强迫振动。图 15(c)为惯性力输出结果,图 15(d)为惯性补偿后输出结果。从图中可以看出,轴向力输入输出瞬时值存在偏差,频率特性及幅值特性基本一致。法向力输入输出周期相同,幅值存在一定偏差。俯仰力矩输入输出基本一致。以上结果表明,惯性补偿后虽未实现输入输出完全一致,但相对补偿前得到了极大的改善,幅值分别为1024.1N,5375.7N和1070.8N·m,幅值误差率均低于10%。
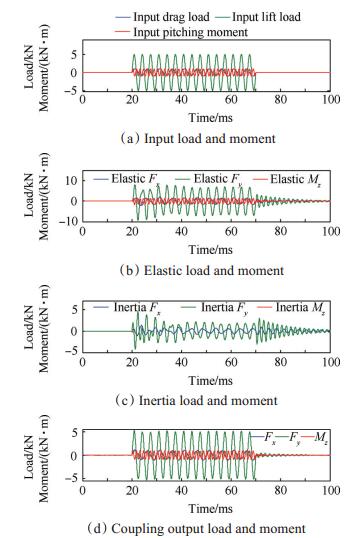
|
Fig. 15 Analysis result of the force balance under the actions of the 3-component sine load |
图 16,17分别为测力系统(包括支架、天平和试验模型三部分)在三分量阶跃载荷和正弦载荷加载时的输出变化规律。对比图 11和图 16,图 15和图 17结果可以发现,惯性补偿后,测力系统的输出结果与输入结果更一致,这是因为试验模型安装后,浮动框刚度得到了很大的提高,使得模型振动过程中弹性变形降低,测点的加速度更能体现模型振动,从而更加有利于惯性补偿方法的实现。
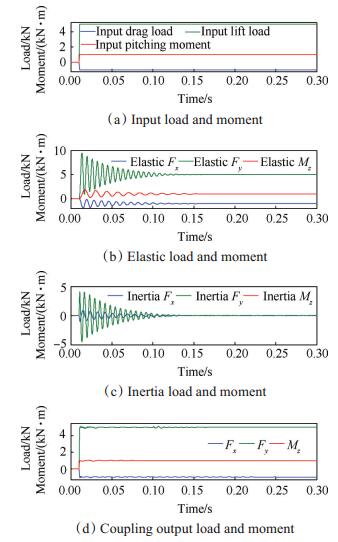
|
Fig. 16 Analysis result of the force-measurement system under the actions of the 3-component step load |
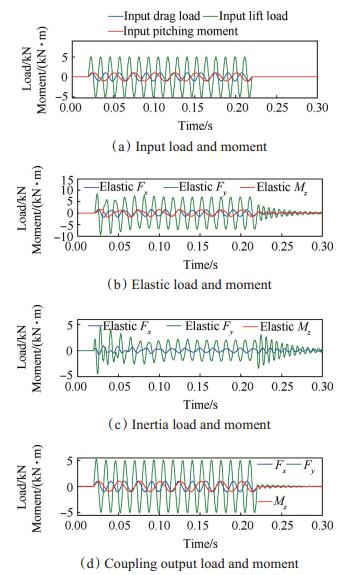
|
Fig. 17 Analysis result of the force-measurement system under the actions of the 3-component sine load |
上述仿真结果表明,轴向、法向单独加载时,惯性补偿后加载分量上输入输出保持一致,其余分量输出趋近于0。俯仰力矩加载时,法向载荷输出趋近于0,俯仰力矩输入输出一致,对轴向载荷的干扰较大。分析造成该现象的原因,从静态分析结果可知,俯仰力矩加载时,轴向力应变存在一定输出,记为a,使得天平俯仰力矩阶跃加载时,轴向力应变以a为均值进行振动,然而浮动框以Mz的固有频率自由振动,且该振幅远大为于a,这必然引起轴向力振动在一段时间内按照轴向和俯仰两者的耦合规律进行振动,直至浮动框俯仰振动停止,轴向振动开始以相应的固有频率为周期进行振动。求解惯性力的加速度测点位于浮动框,此时浮动框和前后连接部位非刚体振动,导致惯性力在耦合振动阶段与轴向力振动存在差异,轴向力完全补偿变得非常复杂。该现象同样解释了正弦俯仰力矩加载时轴向力输出为正弦结果。
三分量阶跃载荷加载时,法向力和俯仰力矩输入输出保持一致,轴向力输出受到干扰,加载完成一段时间内载荷输入输出偏差较大,但很快趋于稳定。三分量正弦加载时,补偿后输入输出具有相同的频率特性,说明各分量输出均以强迫振动为主,但因为分量间的干扰作用,导致轴向和法向输入输出之间存在一定偏差,惯性补偿的引入对瞬时结果输出起到了很大的改善作用。
4 结论本文对三分量测力天平进行了动力学建模、虚拟校准、模态分析和瞬态分析,获得了相应的动态响应规律,得到以下结论:
(1)天平系数矩阵表明轴向力和俯仰力矩之间耦合较强,法向力和轴向力、俯仰力矩之间的耦合较弱。
(2)单分量加载分析结果表明,惯性补偿后加载分量上载荷输入输出保持一致,且轴向和法向加载对其他分量干扰很小,俯仰力矩加载对轴向力输出干扰较为明显。
(3)三分量加载分析结果表明,惯性补偿后法向和俯仰方向输入输出保持一致,轴向输出受俯仰力矩干扰,但频率特性相同,幅值略有偏差。
(4)分析结果显示,惯性补偿后,瞬时输出结果接近输入值,阶跃加载时各分量的超调量分别为162.6N,574.4N和38N·m,正弦加载时各分量的超调量分别为24.1N,375.7N和70.8N·m,较大补偿前大幅度减小。而且振动稳定时间大幅缩短,这对短时风洞测力获得稳定输出具有重要意义。
| [1] |
乐嘉陵, 刘伟雄, 贺伟, 等. 脉冲燃烧风洞及其在火箭和超燃发动机研究中的应用[J]. 实验流体力学, 2005, 19(1): 1-10. (  0) 0) |
| [2] |
刘伟雄, 谭宇, 毛雄兵, 等. 一种新运行方式脉冲燃烧风洞研制及初步应用[J]. 试验流体力学, 2007, 21(4): 59-64. (  0) 0) |
| [3] |
Bertin J J, Cummings R M. Fifty Years of Hypersonic Where We're Been, Where We're Going[J]. Aerospace Sciences, 2003, 39: 511-536. DOI:10.1016/S0376-0421(03)00079-4
(  0) 0) |
| [4] |
姜宗林, 余鸿儒. 高超声速激波风洞研究进展[J]. 力学进展, 2009, 39(6): 765-775. (  0) 0) |
| [5] |
Tanno H, Kodera M, Komuro T, et al. Aerodynamic Force Measurement on a Large-Scale Model in a Short Duration Test Facility[J]. Review of Scientific Instruments, 2005, 76(3).
(  0) 0) |
| [6] |
Tanno H, Komuro T, Takahashi M, et al. Unsteady Force Measurement Technique in Shock Tubes[J]. Review of Scientific Instruments, 2004, 75(2): 532-536. DOI:10.1063/1.1641156
(  0) 0) |
| [7] |
Tanno H, Komuro T, Sato K, et al. Free-Flight Measurement Technique in the Free-Piston High-Enthalpy Shock Tunnel[J]. Review of Scientific Instruments, 2014, 85(4).
(  0) 0) |
| [8] |
Singh P, Menezes V, Irimpan K J, et al. Impulse Force Balance for Ultrashort Duration Hypersonic Test Facilities[J]. Shock and Vibration, 2015(8).
(  0) 0) |
| [9] |
Singh P, Trivedi S, Menezes V, et al. Dynamic Calibration and Validation of an Accelerometer Force Balance for Hypersonic Lifting Models[J]. The Scientific World Journal, 2014(6).
(  0) 0) |
| [10] |
Naumann K W, Ende H, Mathieu G, et al. Millisecond Aerodynamic Force Measurement with Side-Jet Model in the ISL Shock Tunnel[J]. AIAA Journal, 1993, 31(6): 1068-1074. DOI:10.2514/3.11730
(  0) 0) |
| [11] |
Laurence S J, Karl S. An Improved Visualization-Based Force-Measurement Technique for Short-Duration Hypersonic Facilities[J]. Experiments in Fluids, 2010, 48(6): 949-965. DOI:10.1007/s00348-009-0780-9
(  0) 0) |
| [12] |
Laurence S J, Hornung H G. Image-Based Force Measurement in Hypersonic Facilities[J]. Experiments in Fluids, 2009, 46(2): 343-353. DOI:10.1007/s00348-008-0565-6
(  0) 0) |
| [13] |
Robinson M J, Mee D J, Tsai C Y, et al. Three-Component Force Measurements on a Large Scramjet in a Shock Tunnel[J]. Journal of Spacecraft and Rockets, 2004, 41(3): 416-425. DOI:10.2514/1.10699
(  0) 0) |
| [14] |
Robinson M, Hannemann K. Short Duration Force Measurements in Impulse Facilities[C]. San Francisco: 25th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, 2006.
(  0) 0) |
| [15] |
Marineau E C. Force Measurements in Hypervelocity Flows with an Acceleration Compensated Piezoelectric Balance[J]. Journal of Spacecraft and Rockets, 2011, 48(4): 697-700. DOI:10.2514/1.A32047
(  0) 0) |
| [16] |
乐嘉陵. 吸气式高超声速技术研究进展[J]. 推进技术, 2010, 31(6): 641-649. (LE Jia-ling. Progress in Air-breathing Hypersonic Technology[J]. Journal of Propulsion Technology, 2010, 31(6): 641-649.)
(  0) 0) |
| [17] |
Wang Y, Liu Y, Luo C, et al. Force Measurement Using Strain-gauge Balance in a Shock Tunnel with Long Test Duration[J]. Review of Scientific Instruments, 2016, 87(5).
(  0) 0) |
| [18] |
姜宗林, 李进平, 赵伟, 等. 长试验时间爆轰驱动激波风洞技术研究[J]. 力学学报, 2012, 44(5): 824-831. DOI:10.6052/0459-1879-12-160 (  0) 0) |
| [19] |
刘洪山, 徐翔, 姜华. 应力波天平在国内激波风洞上的应用[J]. 实验流体力学, 2006, 20(1): 36-39. (  0) 0) |
| [20] |
王锋, 贺伟, 毛鹏飞, 等. 脉冲风洞测力系统建模与载荷辨识方法研究[J]. 振动与冲击, 2015, 34(1): 94-103. (  0) 0) |
| [21] |
王泽江, 唐小伟, 宋文萍, 等. 圆截面超燃冲压发动机冷态内流测力试验[J]. 推进技术, 2016, 37(4): 617-623. (WANG Ze-jiang, TANG Xiao-wei, SONG Wen-ping, et al. Zero-Fuel Internal Flow Force Test for Circular Cross Section Scramjet Engine[J]. Journal of Propulsion Technology, 2016, 37(4): 617-623.)
(  0) 0) |
| [22] |
Gounaris G D, Anifantis N K. Structural Damping Determination by Finite Element Approach[J]. Computers and Structures, 1999, 73(1): 445-452.
(  0) 0) |
| [23] |
Spears R E, Jensen S R. Approach for Selection of Rayleigh Damping Parameters Used for Time History Analysis[J]. Journal of Pressure Vessel Technology, 2009, 134(6): 67-75.
(  0) 0) |
| [24] |
Pan D, Chen G, Wang Z. Suboptimal Rayleigh Damping Coefficients in Seismic Analysis of Viscously Damped Structures[J]. Earthquake Engineering and Engineering Vibration, 2014, 13(4): 653-670.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


