2. 先进航空发动机协同创新中心,北京 100191
2. Collaborative Innovation Center of Advanced Aero-Engine, Beijing 100191, China
形状记忆合金(Shape Memory Alloy,SMA)因具有独特的形状记忆效应和优秀的超弹性阻尼效应,在振动控制方面的研究与应用发展十分迅速。在航空航天[1, 2]领域,SMA的应用已从机身[3]、机翼[4]等部位扩展至发动机结构[5, 6],如尾喷口、进气口[7]、涡轮叶片[8]、机匣[9]等部位。但是目前应用SMA进行结构的振动控制研究,大多数主要采用形状记忆效应的驱动力控制方式和大变形的超弹性阻尼方式[10],很少采用SMA弹性模量的温变特性进行变刚度控制的方法。
一方面,在航空发动机中由于大多数结构能够承受的载荷和变形具有严格限制[11],因此上述两种方式的应用都具有一定的局限性,而利用SMA温变过程中弹性模量的大幅度改变和形状记忆效应受限引起的恢复力调整结构刚度特性从而实现振动主动/半主动控制也是发展方向之一[12],Wang等[13]和Williams等[14]利用SMA随温度改变弹性模量发生变化的特性开展了变刚度动力吸振器的研究,实现了对主体结构宽频段振动能量的有效吸收。
另一方面,为了对SMA受力过程中的超弹性变形和形状记忆效应进行准确描述,研究人员一直试图找到合理的本构模型。经过多年的发展,本构模型逐渐从一维发展至多维,并从简单的热力学模型发展到可以考虑相变过程和形状记忆效应的复杂模型。本构模型的发展使描述SMA的力学特性更加准确和详细,但目前大量研究主要集中在微观层面[15, 16]与细观层面[17~20],如SMA应力应变的演化机理、载荷温度作用下的相变产生和发展等问题一直是材料科学领域的研究热点。宏观层面上虽然也进行了相关的理论与试验研究,但依然停留在静力学领域[21, 22]。由于SMA弹性模量受环境因素的影响规律十分复杂,仅从应力应变关系入手,不但难以准确描述材料的动力学参数特征,更会因为其规律的复杂性造成本构模型参数众多,给计算分析带来困难。因此,目前存在的本构模型都难以准确地应用于结构的动力学分析,需要提出一种新的宏观本构模型来描述SMA在振动环境下的力学特性,并且具有较高的计算精度和效率,以满足实际工程应用需要。
基于上述应用需求,为了对实际复杂结构和工程应用环境进行模拟,实现对SMA材料的仿真计算功能和变刚度振动控制特性研究,本文在文献[23]试验研究的基础上,基于粘弹性材料本构关系建立了SMA宏观本构模型,并借助非线性有限元分析软件ABAQUS提供的二次开发接口—用户材料子程序(User-defined Material Mechanical Behavior,UMAT)编写材料本构程序。通过对准静态拉伸试验和动态试验的仿真计算,验证本构程序的正确性。针对不同激励引起的结构振动响应,采用变刚度控制方法进行了仿真计算,掌握了变刚度控制的机理和控制参数影响规律。
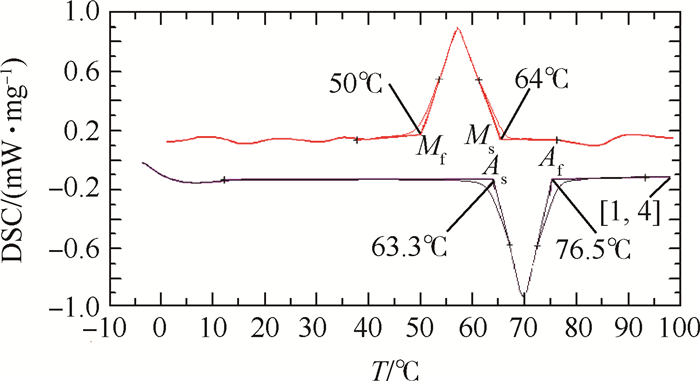
2 SMA本构模型及UMAT子程序本文采用的SMA材料为由中科院沈阳金属所提供的Ti50Ni41Cu9,与传统的TiNi-SMA相比,Cu元素的加入能降低合金的相变热滞,得到更快的热响应速度。采用示差扫描量热法(Differential Scanning Calorimetry,DSC)对上述成分SMA材料进行相变温度测试,结果如图 1所示[23],图中Ms,Mf,As,Af分别表示马氏体相变开始、结束及奥氏体开始、结束温度点。
|
Fig. 1 DSC curves of Ti50Ni41Cu9-SMA |
UMAT子程序的核心是输出材料的Jacobian矩阵,用于表示每一个增量步中应力和应变的更新,而要建立Jacobian矩阵就需要通过材料的本构模型推导三维∂Δσ/∂Δε的表达式。根据静力学和动力学材料参数测试结果,SMA材料在小变形情况下与粘弹性材料性能类似,因此从唯象理论的角度可以采用粘弹性本构模型进行等效[24, 25]。首先建立其三维应力应变本构方程,将三维应力张量和应变张量分解为球形张量和偏斜张量
| $ \left[ {\begin{array}{*{20}{c}} {{\sigma _{11}}}&{{\sigma _{12}}}&{{\sigma _{13}}}\\ {{\sigma _{21}}}&{{\sigma _{22}}}&{{\sigma _{23}}}\\ {{\sigma _{31}}}&{{\sigma _{32}}}&{{\sigma _{33}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \sigma &0&0\\ 0&\sigma &0\\ 0&0&\sigma \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\sigma _{11}} - \sigma }&{{\sigma _{12}}}&{{\sigma _{13}}}\\ {{\sigma _{21}}}&{{\sigma _{22}} - \sigma }&{{\sigma _{23}}}\\ {{\sigma _{31}}}&{{\sigma _{32}}}&{{\sigma _{33}} - \sigma } \end{array}} \right] $ | (1) |
| $ \left[ {\begin{array}{*{20}{c}} {{\varepsilon _{11}}}&{{\varepsilon _{12}}}&{{\varepsilon _{13}}}\\ {{\varepsilon _{21}}}&{{\varepsilon _{22}}}&{{\varepsilon _{23}}}\\ {{\varepsilon _{31}}}&{{\varepsilon _{32}}}&{{\varepsilon _{33}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{e_{\rm{p}}}}&0&0\\ 0&{{e_{\rm{p}}}}&0\\ 0&0&{{e_{\rm{p}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\varepsilon _{11}} - {e_{\rm{p}}}}&{{\varepsilon _{12}}}&{{\varepsilon _{13}}}\\ {{\varepsilon _{21}}}&{{\varepsilon _{22}} - {e_{\rm{p}}}}&{{\varepsilon _{23}}}\\ {{\varepsilon _{31}}}&{{\varepsilon _{32}}}&{{\varepsilon _{33}} - {e_{\rm{p}}}} \end{array}} \right] $ | (2) |
式中σ为平均正应力,ep为平均正应变,其表达式分别为
| $ \begin{array}{*{20}{l}} {\sigma = \frac{1}{3}\left( {{\sigma _{11}} + {\sigma _{22}} + {\sigma _{33}}} \right) = \frac{1}{3}{\sigma _{kk}}, }\\ {{e_{\rm{p}}} = \frac{1}{3}\left( {{\varepsilon _{11}} + {\varepsilon _{22}} + {\varepsilon _{33}}} \right) = \frac{1}{3}{\varepsilon _{kk}}} \end{array} $ | (3) |
对于各向同性弹性介质,应力球形张量与应变球形张量成正比,应力偏斜张量与应变偏斜张量成正比,其关系可以表示为
| $ \left[ {\begin{array}{*{20}{c}} \sigma &0&0\\ 0&\sigma &0\\ 0&0&\sigma \end{array}} \right] = 3K\left[ {\begin{array}{*{20}{c}} {{e_{\rm{p}}}}&0&0\\ 0&{{e_{\rm{p}}}}&0\\ 0&0&{{e_{\rm{p}}}} \end{array}} \right] $ | (4) |
| $ \left[ {\begin{array}{*{20}{c}} {{\sigma _{11}} - \sigma }&{{\sigma _{12}}}&{{\sigma _{13}}}\\ {{\sigma _{21}}}&{{\sigma _{22}} - \sigma }&{{\sigma _{23}}}\\ {{\sigma _{31}}}&{{\sigma _{32}}}&{{\sigma _{33}} - \sigma } \end{array}} \right] = 2G\left[ {\begin{array}{*{20}{c}} {{\varepsilon _{11}} - {e_{\rm{p}}}}&{{\varepsilon _{12}}}&{{\varepsilon _{13}}}\\ {{\varepsilon _{21}}}&{{\varepsilon _{22}} - {e_{\rm{p}}}}&{{\varepsilon _{23}}}\\ {{\varepsilon _{31}}}&{{\varepsilon _{32}}}&{{\varepsilon _{33}} - {e_{\rm{p}}}} \end{array}} \right] $ | (5) |
式中K为体积模量,G为剪切模量,表示为
| $ K = \lambda + \frac{{2G}}{3}, \;\;G = \frac{E}{{2\left( {1 + \upsilon } \right)}} $ | (6) |
式中λ为拉梅系数,E为弹性模量,υ为材料泊松比,表示为
| $ \lambda = \frac{{2\upsilon G}}{{1 - 2\upsilon }} $ | (7) |
用sij表示应力偏量,eij表示应变偏量,式(1)、式(2)可表示为
| $ {s_{ij}} = {\sigma _{ij}} - \frac{1}{3}{\sigma _{kk}}{\delta _{ij}}, \;\;{e_{ij}} = {\varepsilon _{ij}} - \frac{1}{3}{\varepsilon _{kk}}{\delta _{ij}} $ | (8) |
式中δij为Kronecker符号,满足
| $ {\delta _{ij}} = \left\{ {\begin{array}{*{20}{l}} {1\;\;\;\;\;{\rm{}}\;\;\left( {i = j} \right)}\\ {0\;\;\;\;\;{\rm{}}\left( {i \ne j} \right)} \end{array}} \right. $ | (9) |
采用粘弹性材料的Kelvin-Voigt模型[26]进行计算,三维本构方程可以表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{s_{ij}} = 2G{e_{ij}} + 2C{{\dot e}_{ij}}}\\ {\sigma = 3K{e_{\rm{p}}}} \end{array}} \right. $ | (10) |
式中C为粘性阻尼系数,对于每个单元可以表示为
| $ {C_{\rm{e}}} = 2\zeta {L^2}\sqrt {\rho E} $ | (11) |
式中ζ为阻尼比,根据试验确定,L为单元特征长度,ρ为材料密度。
将式(8)带入式(10),计算得到三维应力应变分量关系为
| $ \begin{array}{l} {\sigma _{11}} = 2G\left( {{\varepsilon _{11}} - {e_{\rm{p}}}} \right) + 2C\left( {{{\dot \varepsilon }_{11}} - {{\dot e}_{\rm{p}}}} \right) + 3K{e_{\rm{p}}}\\ {\sigma _{22}} = 2G\left( {{\varepsilon _{22}} - {e_{\rm{p}}}} \right) + 2C\left( {{{\dot \varepsilon }_{22}} - {{\dot e}_{\rm{p}}}} \right) + 3K{e_{\rm{p}}}\\ {\sigma _{33}} = 2G\left( {{\varepsilon _{33}} - {e_{\rm{p}}}} \right) + 2C\left( {{{\dot \varepsilon }_{33}} - {{\dot e}_{\rm{p}}}} \right) + 3K{e_{\rm{p}}}\\ {\sigma _{12}} = {\sigma _{21}} = 2G{\varepsilon _{12}} + 2C{{\dot \varepsilon }_{12}}\\ {\sigma _{13}} = {\sigma _{31}} = 2G{\varepsilon _{13}} + 2C{{\dot \varepsilon }_{13}}\\ {\sigma _{32}} = {\sigma _{23}} = 2G{\varepsilon _{32}} + 2C{{\dot \varepsilon }_{32}} \end{array} $ | (12) |
引入中心差分算子
| $ {{\dot f}_{t + \frac{{{\rm{\Delta }}t}}{2}}} = \frac{{{\rm{\Delta }}f}}{{{\rm{\Delta }}t}}, {\rm{}}{f_{t + \frac{{{\rm{\Delta }}t}}{2}}} = {f_t} + \frac{{{\rm{\Delta }}f}}{2} $ | (13) |
则式(12)可写为
| $ \begin{array}{l} {\sigma _{11t}} + \frac{{{\rm{\Delta }}{\sigma _{11}}}}{2} = \\ 2\left( {{G_t} + \frac{{{\rm{\Delta }}G}}{2}} \right)\left[ {\left( {{\varepsilon _{11t}} + \frac{{{\rm{\Delta }}{\varepsilon _{11}}}}{2}} \right) - \left( {{e_{{\rm{pt}}}} + \frac{{{\rm{\Delta }}{e_{\rm{p}}}}}{2}} \right)} \right] + \\ 2\left( {{C_t} + \frac{{{\rm{\Delta }}C}}{2}} \right)\left( {\frac{{{\rm{\Delta }}{\varepsilon _{11}}}}{{{\rm{\Delta }}t}} - \frac{{{\rm{\Delta }}{e_{\rm{p}}}}}{{{\rm{\Delta }}t}}} \right) + 3\left( {{K_t} + \frac{{{\rm{\Delta }}K}}{2}} \right)\left( {{e_{{\rm{pt}}}} + \frac{{{\rm{\Delta }}{e_{\rm{p}}}}}{2}} \right)\\ {\sigma _{22t}} + \frac{{{\rm{\Delta }}{\sigma _{22}}}}{2} = \\ 2\left( {{G_t} + \frac{{{\rm{\Delta }}G}}{2}} \right)\left[ {\left( {{\varepsilon _{22t}} + \frac{{{\rm{\Delta }}{\varepsilon _{22}}}}{2}} \right) - \left( {{e_{{\rm{pt}}}} + \frac{{{\rm{\Delta }}{e_{\rm{p}}}}}{2}} \right)} \right] + \\ 2\left( {{C_t} + \frac{{{\rm{\Delta }}C}}{2}} \right)\left( {\frac{{{\rm{\Delta }}{\varepsilon _{22}}}}{{{\rm{\Delta }}t}} - \frac{{{\rm{\Delta }}{e_{\rm{p}}}}}{{{\rm{\Delta }}t}}} \right) + 3\left( {{K_t} + \frac{{{\rm{\Delta }}K}}{2}} \right)\left( {{e_{{\rm{pt}}}} + \frac{{{\rm{\Delta }}{e_{\rm{p}}}}}{2}} \right)\\ {\sigma _{33t}} + \frac{{{\rm{\Delta }}{\sigma _{33}}}}{2} = \\ 2\left( {{G_t} + \frac{{{\rm{\Delta }}G}}{2}} \right)\left[ {\left( {{\varepsilon _{33t}} + \frac{{{\rm{\Delta }}{\varepsilon _{33}}}}{2}} \right) - \left( {{e_{{\rm{pt}}}} + \frac{{{\rm{\Delta }}{e_{\rm{p}}}}}{2}} \right)} \right] + \\ 2\left( {{C_t} + \frac{{{\rm{\Delta }}C}}{2}} \right)\left( {\frac{{{\rm{\Delta }}{\varepsilon _{33}}}}{{{\rm{\Delta }}t}} - \frac{{{\rm{\Delta }}{e_{\rm{p}}}}}{{{\rm{\Delta }}t}}} \right) + 3\left( {{K_t} + \frac{{{\rm{\Delta }}K}}{2}} \right)\left( {{e_{{\rm{pt}}}} + \frac{{{\rm{\Delta }}{e_{\rm{p}}}}}{2}} \right)\\ {\sigma _{12}} + \frac{{{\rm{\Delta }}{\sigma _{12}}}}{2} = \\ 2\left( {{G_t} + \frac{{{\rm{\Delta }}G}}{2}} \right)\left( {{\varepsilon _{12t}} + \frac{{{\rm{\Delta }}{\varepsilon _{12}}}}{2}} \right) + 2\left( {{C_t} + \frac{{{\rm{\Delta }}C}}{2}} \right)\frac{{{\rm{\Delta }}{\varepsilon _{12}}}}{{{\rm{\Delta }}t}}\\ 2\left( {{G_t} + \frac{{{\rm{\Delta }}G}}{2}} \right)\left( {{\varepsilon _{12t}} + \frac{{{\rm{\Delta }}{\varepsilon _{12}}}}{2}} \right) + 2\left( {{C_t} + \frac{{{\rm{\Delta }}C}}{2}} \right)\frac{{{\rm{\Delta }}{\varepsilon _{12}}}}{{{\rm{\Delta }}t}}\\ 2\left( {{G_t} + \frac{{{\rm{\Delta }}G}}{2}} \right)\left( {{\varepsilon _{13t}} + \frac{{{\rm{\Delta }}{\varepsilon _{13}}}}{2}} \right) + 2\left( {{C_t} + \frac{{{\rm{\Delta }}C}}{2}} \right)\frac{{{\rm{\Delta }}{\varepsilon _{13}}}}{{{\rm{\Delta }}t}}\\ {\sigma _{32}} + \frac{{{\rm{\Delta }}{\sigma _{32}}}}{2} = \\ 2\left( {{G_t} + \frac{{{\rm{\Delta }}G}}{2}} \right)\left( {{\varepsilon _{32t}} + \frac{{{\rm{\Delta }}{\varepsilon _{32}}}}{2}} \right) + 2\left( {{C_t} + \frac{{{\rm{\Delta }}C}}{2}} \right)\frac{{{\rm{\Delta }}{\varepsilon _{32}}}}{{{\rm{\Delta }}t}} \end{array} $ | (14) |
雅可比矩阵J(i, j)表示第j个应变分量的改变量引起的第i个应力分量的变化,即计算各方向应力增量对应变增量的变化率。由于SMA为各向同性材料,且振动过程中弹性模量主要由主应变ε11引起变化,因此在每个积分点的Jacobian矩阵中不对弹性模量进行微分计算,而以每个积分时间点初始应变增量计算当前步的弹性模量数值,完成当前积分时间点计算后,下一积分时间点开始时对弹性模量进行更新,从而更新下一积分时间点的Jacobian矩阵。
根据式(14),将每个方程分别对不同方向应变增量求偏导数,Jacobian矩阵元素可以表示
| $ \begin{array}{*{20}{l}} {\frac{{\partial {\rm{\Delta }}{\sigma _{ii}}}}{{\partial {\rm{\Delta }}{\varepsilon _{ii}}}} = 3\left( {{K_t} + \frac{{{\rm{\Delta }}K}}{2}} \right)}\\ {\frac{{\partial {\rm{\Delta }}{\sigma _{ii}}}}{{\partial {\rm{\Delta }}{\varepsilon _{jj}}}} = 3\left( {{K_t} + \frac{{{\rm{\Delta }}K}}{2}} \right) - 2\left( {{G_t} + \frac{{{\rm{\Delta }}G}}{2}} \right) - \frac{4}{{{\rm{\Delta }}t}}\left( {{C_t} + \frac{{{\rm{\Delta }}C}}{2}} \right)}\\ {\frac{{\partial {\rm{\Delta }}{\sigma _{ij}}}}{{\partial {\rm{\Delta }}{\varepsilon _{ij}}}} = 2\left( {{G_t} + \frac{{{\rm{\Delta }}G}}{2}} \right) + \frac{4}{{{\rm{\Delta }}t}}\left( {{C_t} + \frac{{{\rm{\Delta }}C}}{2}} \right)\;\;\;\;\left( {i \ne j} \right)} \end{array} $ | (15) |
式中Kt,ΔK,Gt,ΔG,Ct,ΔC都只取决于ε11和Δε11的变化。至此,基于粘弹性固体Kelvin-Voigt模型,完成增量形式的三维本构模型的Jacobian矩阵已经建立。
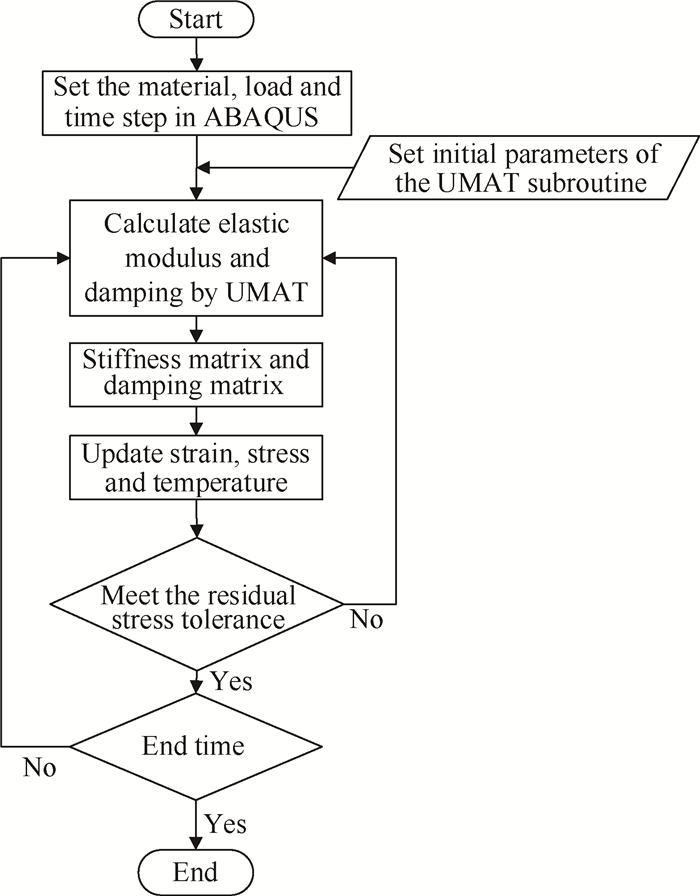
通过在主程序中每个载荷步对UMAT子程序的调用,实现SMA材料本构模型在有限元程序中的计算。主程序调用UMAT的求解过程如图 2所示,主要过程为:
|
Fig. 2 Calculation process of the main program |
(1)在主程序中建立有限元模型,并设置响应的求解模块,建立边界条件、载荷及载荷步设置。
(2)在每一个载荷增量步开始时,主程序调用UMAT子程序,子程序读入应变增量、时间步长、载荷增量、当前载荷步的初始应力、应变等变量,子程序根据用户定义的本构模型求解应力增量,并更新应力和其它变量,然后根据Jacobian矩阵建立整体刚度矩阵和阻尼矩阵传输给主程序。
(3)主程序根据当前载荷步求解位移增量并进行平衡校核,满足指定容差后完成子步并进行下一步求解过程,直至结束。
SMA变刚度控制主要依赖环境温度的改变,因此UMAT子程序中除需要输入基本的材料参数,如泊松比、密度等参数外,还需要提供初始温度、变温方向、变温速率、转换时间等温度加载控制参数。此外,UMAT在计算SMA弹性模量和等效粘性阻尼系数的过程中,还需要输入与弹性模量变化相关的主应变方向和单元特征尺寸参数,设置UMAT子程序控制参数见表 1。
|
|
Table 1 Control parameters of the UMAT material subroutine |
为了验证所编写的UMAT子程序的正确性,根据SMA准静态力学性能试验和SMA动态试验过程,建立对应的有限元模型并进行仿真验证。
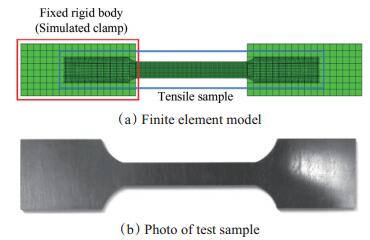
3.1 准静态力学试验仿真准静态力学试验采取拉伸试验的方式以测量材料的弹性模量,对应的试验件和有限元模型如图 3所示。计算模型由两部分组成:两端的刚体夹具和中段的拉伸试验件,标距长度与试验件一致。
|
Fig. 3 Finite element model and sample for tensile test |
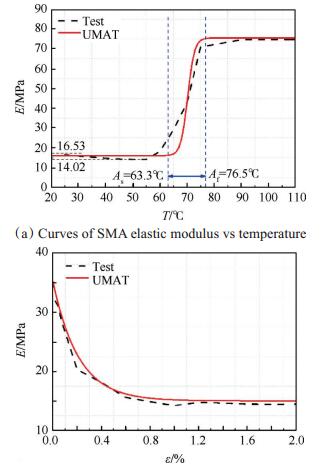
采用ABAQUS并结合UMAT子程序模拟拉伸试验过程,针对温度变化和应变幅值变化计算模型的应力应变曲线,并根据曲线计算材料的弹性模量,仿真计算结果与实测结果[23]对比如图 4所示。
|
Fig. 4 Quasi-static mechanical test results |
分析图 4可知,仿真计算中由于数据点更为精细,因此相变温度区间与DSC测试结果吻合较好;由于计算模型中忽略了马氏体状态下温度升高所造成的弹性模量下降过程,因此马氏体状态弹性模量始终保持恒定,但从数据对比来看,实测值下降过程并不明显,考虑到实际使用中这一过程非常短暂,因此可以适当忽略这一变化过程。达到奥氏体后,弹性模量保持不变,并与实测值吻合度较高;马氏体弹性模量随应变增大呈指数趋势降低,变化趋势和数据与实测吻合度较好,可以准确地描述SMA的弹性模量随应变的变化过程。
3.2 动态力学试验仿真由于SMA弹性模量的复杂变化特性,带有SMA材料的振动系统实质为变参数非线性系统,在恒温小变形状态下,非线性系统主共振频率与派生线性系统固有频率接近,因此采用扫频的方式测试结构的主共振频率。动态试验中所采用的SMA板尺寸为110mm×40mm×2mm,采用短边悬臂支承。试验装置系统和有限元模型如图 5所示,模型单元数5250,节点数27302。激励点为板悬臂端,激励方式为集中力激励。

|
Fig. 5 Test system and model of SMA plate |
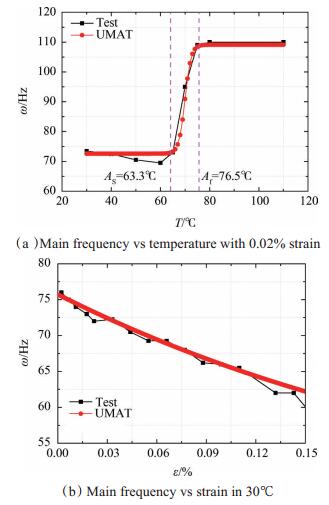
动态主共振频率仿真计算中,材料弹性模量不但随温度发生变化,还随应变的增大而明显降低。因此,频率特性计算过程较为复杂,只能采用瞬态动力学方法,除需要加载UMAT材料子程序外,还需要激振力频率循环程序和激振力幅值搜索程序共同完成计算。主共振频率随温度和应变变化的计算结果如图 6所示。
|
Fig. 6 Variation curves of main frequency of SMA plate |
根据图 6分析,类似静态拉伸过程,由于本构模型中忽略了马氏体状态小幅值的弹性模量变化过程,因此马氏体频率计算结果主要取决于本构模型中马氏体初始弹性模量的取值,相变过程中和相变结束后计算结果与实测值误差较小;而由于UMAT子程序能够考虑弹性模量随应变变化的过程,因此计算结果与实测值吻合较好。因此,从整体数值上分析,采用UMAT计算的精度较高。
动态频率特性对比进一步证实了UMAT材料子程序的准确性,由于其能够较好地模拟SMA材料的宏观弹性模量变化规律,因此计算精度较高,并且能够对更加复杂的模型进行计算分析,具有很好的工程应用价值。
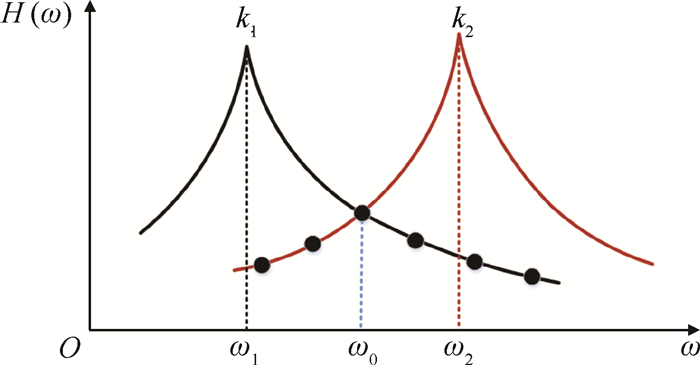
4 SMA变刚度振动控制仿真 4.1 变刚度振动控制原理利用SMA进行振动主动控制,其原理就是通过改变SMA的弹性模量,改变结构的主共振频率,主动避开激振频率,实现整个控制频率范围内“无峰值”响应。图 7所示为典型的可变刚度系统幅频响应曲线。为了尽可能降低考察频率范围内系统的振动响应水平,理想的情况是:当激振频率ω < ω0时,系统刚度为k2;激振频率ω>ω0时,系统刚度为k1;激振频率ω=ω0时,k1,k2均可。在这种情况下,系统稳态幅频曲线按照如图 7所示的带“●”号的曲线变化,此时,系统成为“无峰值”响应系统,其自身振幅和外传力都得到了最佳控制。
|
Fig. 7 Sketch of amplitude-frequency response curves of variable stiffness system |
然而,实际情况下刚度的变化与载荷的变化通常难以同步,变刚度时不可避免地存在着弹性恢复力的不连续,系统原有平衡被破坏,导致系统在ω=ω0时的实际响应幅值一般大于图 7中ω0时的响应值,并且有可能由于刚度的突变造成响应的瞬时放大,系统出现失稳。制定合理的控制策略并增大系统的阻尼,有助于变刚度瞬态响应的迅速衰减和整体响应水平的降低,下面对控制参数变化对稳态过程和瞬态过程的响应进行仿真研究。
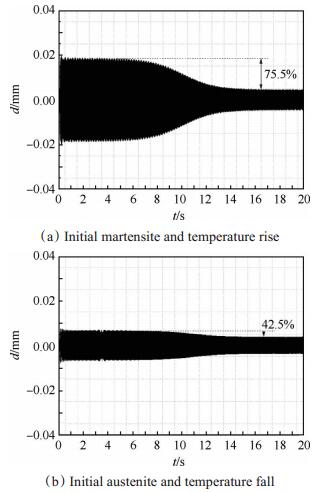
4.2 稳态振动响应变刚度控制鉴于振动控制原理的一致性,利用3.2中的SMA有限元模型,保持约束条件不变,对其主共振频率响应进行控制仿真,由图 6可知,马氏体状态(30℃)结构主振动频率为73Hz,奥氏体状态(100℃)结构主共振频率为107Hz。当结构在0.1N幅值的定频激励作用下发生稳态振动时,进行温控变刚度操作,慢变控制过程稳态振动响应变化如图 8所示,位移响应的测点为板悬臂端。
|
Fig. 8 Vibration control of variable stiffness by temperature control |
分析图 8可知,系统振动响应稳定后对其进行变温操作,弹性模量随之发生改变,系统的主共振频率逐渐偏离激振频率,当温度变化比较缓慢时,控制过程中响应变化平稳,没有出现显著的非线性特征;控制完成后,升温变刚度振动控制响应降低了75.5%,降温变刚度振动控制响应降低了42.5%,振动都得到了有效的控制。
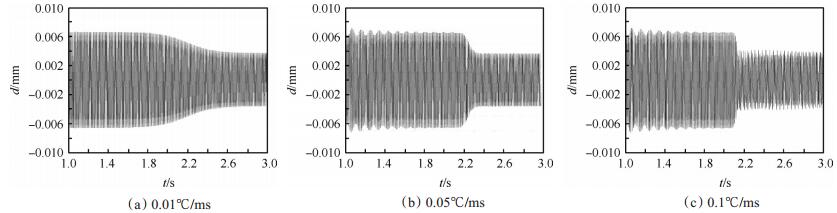
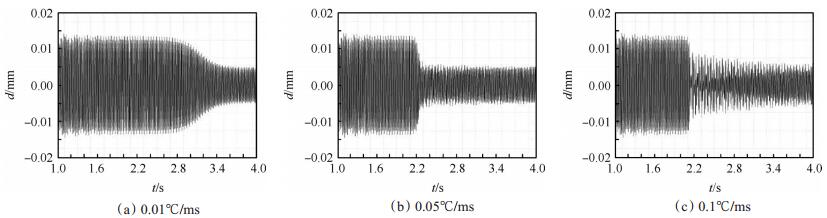
可变参数非线性振动系统中参数变化速率会导致系统非线性程度加大,严重时会造成系统振动响应的瞬时放大和失稳,此外,振动控制应用中,总是尽量提高控制速度以尽快降低响应,因此有必要考察温度加载速率的影响。鉴于控制机理的一致性,只针对降温变刚度操作进行分析。在主共振频率点(107Hz)和非主共振频率点(120Hz)对模型进行激振,分别采用0.01℃/ms,0.05℃/ms,0.1℃/ms的变温速率,激励幅值一致,计算结构变刚度控制过程振动响应的变化,结果如图 9,图 10所示。
|
Fig. 9 Influence of stiffness change velocity in non-main vibration frequency(120Hz) |
|
Fig. 10 Influence of stiffness change velocity in main vibration frequency(107Hz) |
根据曲线对比分析,无论激振频率靠近或远离主共振频率点,当系统发生稳态振动时,降温变刚度控制都能够有效降低振动响应。由于激励频率靠近共振点时初始响应较大,因此控制效果更为明显;对于非主共振频率激励引起的强迫振动,随着变温速率的逐渐加快,振动响应在SMA相变开始后均平稳下降,当速率达到0.1℃/ms时,振动响应出现波动,但在很短的时间内即达到稳定。不同速率的减振效果相同,说明响应的最终变化程度与控制速率无关,只取决于系统刚度的变化程度;在主共振频率激励下,相同激振力幅值引起的响应显著提高,当变温速率低于0.05℃/ms时,随着SMA在温度控制下发生马氏体相变,系统的振动幅值平缓降低,然而当温度变化速率达到0.1℃/ms时,虽然经过衰减,响应最终达到相同水平,但控制过程所需时间增加。
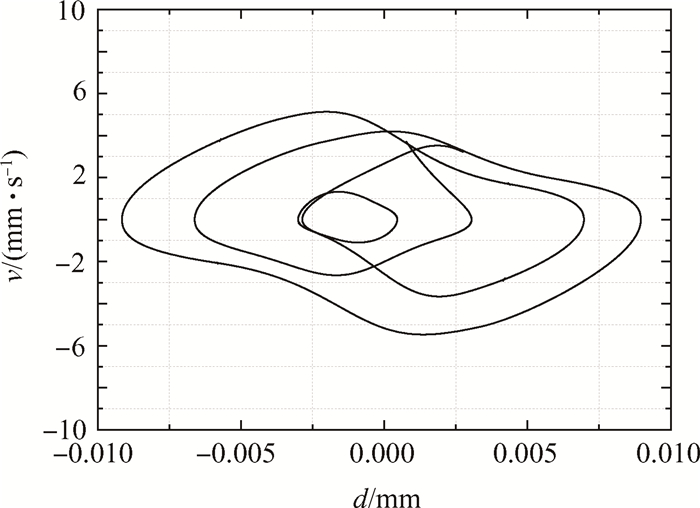
重点分析0.1℃/ms速率控制下响应变化过程的频率成分。如图 11所示,大速率变刚度控制时,控制开始前和完成后时域响应均处于稳定状态,频域成分只存在激振力主频,其他倍频和分频成分不可见。而在控制过程中,主频附近对称分布一些峰值较小的频带且相平面图 12表明,控制过程中瞬时系统出现类似混沌的运动轨迹。虽然控制过程中的响应变化较为复杂,但最终响应总会趋于稳定,控制效果依然只取决于变刚度程度。

|
Fig. 11 Frequency response with the control rate of 0.1℃/ms |
|
Fig. 12 Phase plane of displacement response during control |
某些情况下激励频率是变化的,系统必须要跨越主共振频率点,例如发动机在启动和停车过程中有时需要通过低阶临界转速。虽然可以采用加速或增大阻尼等方式尽量降低最大响应峰值,但由于实际情况下通过速率不可能无限制增大,对于一些阻尼欠佳的结构,瞬时过大的峰值响应有可能无法通过主共振频带,甚至造成结构损伤,因此有必要针对瞬态激励引起的振动响应进行振动控制仿真研究。
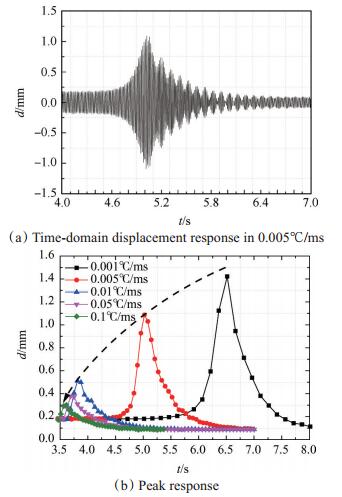
由于系统激励并不会长时间停留在主共振频率附近,可以采用对向变刚度控制方法对瞬态响应进行振动控制,即当激振频率升高时,通过降温操作降低系统的主共振频率,或反向操作,不但可以进一步使通过速率加快,更大程度地降低峰值响应,并且由于系统主共振频率逐渐远离激振频率,也可以避免振动能量积累造成响应放大。采用相同模型,分析结构以不同变刚度速率通过共振点的响应控制情况,在固定激振频率(90Hz)下,采用不同的变温速率进行计算。变刚度跨越共振频率的时域响应和不同变温速率下峰值响应对比如图 13所示。
|
Fig. 13 Time-domain response of transient vibration during control process |
根据图 13分析,变刚度控制下系统完成主共振频率点的跨越,出现响应峰值后,主共振频率逐渐远离激振频率,瞬态响应出现波动,并在阻尼的作用下缓慢衰减,下降过程平缓,没有再次出现更大的峰值点;采用不同的变刚度速率通过相同激振频率时,变温速率越快,峰值响应越小,并且降低程度逐渐加大。变温范围相同时,通过共振点后,响应衰减达到相同水平,证明减振效果只与变刚度程度相关,与控制速率无关。
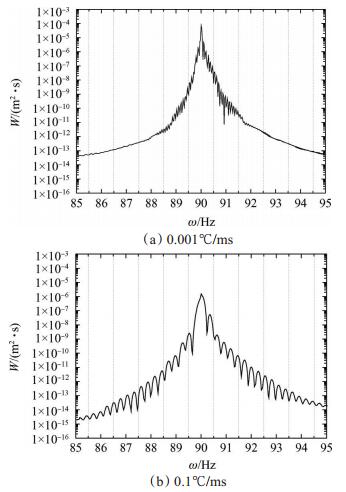
由于计算步长能够完整描述振动波形,因此快速变温时峰值响应的下降在一定程度上取决于振动的非线性特征。如图 14所示,变刚度速率较快时,主频周围会产生明显的自发频带。自发频带对主频振动能量具有一定的分散作用,可以降低系统的最大峰值响应,这与文献[23]试验研究结果能很好吻合,进一步验证了仿真研究的正确性。
|
Fig. 14 Power spectrum of displacement response in different control rate |
根据上述仿真结果可知,在变刚度结构振动控制应用中,针对不同的激励源,通过采取合适的控制策略,可以有效地消减振动能量,实现结构振动的主动/半主动控制。此外,相比于其他控制方式,SMA变刚度控制是无损可循环过程,因而具有较好的工程应用价值。
5 结论本文采用试验结合理论的方法,分析了SMA可变参数系统的动力学特征,为变刚度结构的振动控制设计提供了一种理论分析方法,并得到了以下结论:
(1)与现有的经典SMA微细观静力学本构关系不同,本文基于宏观弹性模量力学关系式建立的本构模型,能够准确描述振动过程中SMA应变和温度增量对弹性模量的影响,从宏观层面较好地反映材料动力学性能的变化特征,是一种适用于动力学分析的材料本构关系,通过对静力学和动力学材料性能试验的仿真计算对比,验证了本构模型的正确性,解决了SMA在动力学领域缺少成熟数值计算方法的难题。
(2)变刚度控制可以有效降低定频激励引起的稳态共振响应,在一定范围内,温度改变速率越大,控制过程历时越短,但当速率达到一定程度时,响应会出现剧烈地跳动,虽然最终在阻尼作用下依然能够达到相同的振动控制水平,但控制过程需要的时间却相对增长。
(3)采用对向变刚度控制可以有效降低变频激励下的瞬态振动响应,提高变温速率使系统产生明显的自发频带,有助于分散主频的振动能量,可以有效降低主频处峰值响应。
由于文中所采用本构模型不是直接对应力应变关系进行描述,因此当应变达到一定程度时,无法反映出孪晶马氏体和变形马氏体之间的晶格变化,也无法描述由应力诱导的马氏体相变超弹性过程,因而,本文所建立的材料本构模型以及有限元计算方法只适用于小变形振动情况,对于大幅值的振动,必须在本构方程和有限元计算方法中考虑大变形产生的非线性特征。
| [1] |
Bil C, Massey K, Abdullah E J. Wing Morphing Control with Shape Memory Alloy Actuators[J]. Journal of Intelligent Material Systems and Structures, 2013, 24(7): 879-898. DOI:10.1177/1045389X12471866
(  0) 0) |
| [2] |
Hartl D J, Lagoudas D C. Aerospace Applications of Shape Memory Alloys[J]. Journal of Aerospace Engineering, 2007, 221(4): 535-552.
(  0) 0) |
| [3] |
Mohammad T, Jeng-jong R, Chuh M. Thermal Post-buckling and Aero Elastic Behavior of Shape Memory Alloy Reinforced Plates[J]. Smart Materials and Structures, 2002, 11(2): 297-307. DOI:10.1088/0964-1726/11/2/313
(  0) 0) |
| [4] |
Kudva J N. Overview of the DARPA Smart Wing Project[J]. Journal of Intelligent Material Systems and Structures, 2004, 15(4): 261-267. DOI:10.1177/1045389X04042796
(  0) 0) |
| [5] |
Hartl D J, Lagoudas D C, Calkins F T, et al. Use of a Ni60Ti Shape Memory Alloy for Active Jet Engine Chevron Application: I. Thermomechanical Characterization[J]. Smart Materials and Structures, 2010, 19(1): 15-20.
(  0) 0) |
| [6] |
任德新, 张大义, 何易峰, 等. 带颗粒型金属橡胶夹层阻尼结构的振动响应研究[J]. 推进技术, 2015, 36(1): 124-129. (REN De-xin, ZHANG Da-yi, HE Yi-feng, et al. Vibration Response Investigation on Structures with Particle Metal Rubber Damper Fillings[J]. Journal of Propulsion Technology, 2015, 36(1): 124-129.)
(  0) 0) |
| [7] |
Dunne J P, Hopkins M A, Baumann E W, et al. Overview of the Sampson Smart Inlet[M]. Los Angeles: SPIE Digital Library, 1999, 380-390.
(  0) 0) |
| [8] |
Caldwell N, Gutmark E, Ruggeri R. Heat Transfer Model for Blade Twist Actuator System[J]. Journal of Thermophysics and Heat Transfer, 2007, 21(2): 352-360. DOI:10.2514/1.23120
(  0) 0) |
| [9] |
Hong J, Yan W. Experimental Investigation on the Vibration Tuning of a Shell with a Shape Memory Alloy Ring[J]. Smart Materials & Structures, 2015, 24(10).
(  0) 0) |
| [10] |
王永军. 含形状记忆合金复合结构振动特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1809459
(  0) 0) |
| [11] |
于平超, 马艳红, 张大义, 等. 具有局部非线性刚度的复杂转子系统动力学模型及振动特性分析[J]. 推进技术, 2016, 37(12): 2343-2351. (YU Ping-chao, MA Yan-hong, ZHANG DA-yi, et al. Dynamic Model and Vibration Characteristic Analysis on Complex Rotor System with Local Nonlinear Stiffness[J]. Journal of Propulsion Technology, 2016, 37(12): 2343-2351.)
(  0) 0) |
| [12] |
Leary M, Schiavone F, Subic A. Lagging for Control of Shape Memory Alloy Actuator Response Time[J]. Material and Design, 2010, 31(4): 2124-2128. DOI:10.1016/j.matdes.2009.10.010
(  0) 0) |
| [13] |
Wang L X, Melnik V N R. Nonlinear Dynamics of Shape Memory Alloy Oscillators in Tuning Structural Vibration Frequencies[J]. Mechatronics, 2012, 22(12): 1085-1096.
(  0) 0) |
| [14] |
Williams A K, Chiu T C G, Bernhard J R. Nonlinear Control of a Shape Memory Alloy Adaptive Tuned Vibration Absorber[J]. Journal of Sound and Vibration, 2005, 288(12): 1131-1155.
(  0) 0) |
| [15] |
Abeyaratne R, Knowles J K. On the Driving Traction Acting on a Surface of Strain Discontinuity in a Continuum[J]. Journal of the Mechanics and Physics of Solids, 1990, 38(3): 345-360. DOI:10.1016/0022-5096(90)90003-M
(  0) 0) |
| [16] |
Ball J M, James R D. Fine Phase Mixtures as Minimizers of Energy[J]. Archive for Rational Mechanics and Analysis, 1987, 100(1): 13-52. DOI:10.1007/BF00281246
(  0) 0) |
| [17] |
Gao X J, Huang M S, Brinson L C. A Multivariant Micromechanical Model for SMAs Part Ⅰ: Crystallographic Issues for Single Crystal Model[J]. International Journal of Plasticity, 2000, 16(10-11): 1345-1369. DOI:10.1016/S0749-6419(00)00013-9
(  0) 0) |
| [18] |
Huang M S, Gao X J, Brinson L C. A Multivariant Micromechanical Model for SMAs Part Ⅱ: Polycrystal Model[J]. International Journal of Plasticity, 2000, 16(10-11): 1371-1390. DOI:10.1016/S0749-6419(00)00014-0
(  0) 0) |
| [19] |
Bertacchini O W, Lagoudas D C, Patoor E. Thermomechanical Transformation Fatigue of TiNiCu SMA Actuators under a Corrosive Environment, Part Ⅰ: Experimental Results[J]. International Journal of Fatigue, 2009, 31(10): 1571-1578. DOI:10.1016/j.ijfatigue.2009.04.012
(  0) 0) |
| [20] |
Hartl D J, Solomou A, Lagoudas D C, et al. Phenomenological Modeling of Induced Transformation Anisotropy in Shape Memory Alloy Actuators[C]. San Diego: 2012 SPIE Smart Structures/NDE Conference, 2012, 8342(M).
(  0) 0) |
| [21] |
Auriccchio F, Petrini L. Improvements and Algorithmical Considerations on a Recent Three-Dimensional Model Describing Stress-Induced Solid Phase Transformations[J]. International Journal for Numerical Methods in Engineering, 2002, 55(11): 1255-1284. DOI:10.1002/(ISSN)1097-0207
(  0) 0) |
| [22] |
Peng X, Pi W, Fan J. A Micro Structure-Based Constitutive Model for the Pseudoelastic Behavior of NiTiSMAs[J]. International Journal of Plasticity, 2008, 24(6): 966-990. DOI:10.1016/j.ijplas.2007.08.003
(  0) 0) |
| [23] |
杨鑫, 洪杰, 马艳红, 等. SMA智能梁结构振动控制试验研究[J]. 航空学报, 2015, 36(7): 2251-2259. (  0) 0) |
| [24] |
郭大智, 任瑞波. 层状粘弹性体系力学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2001.
(  0) 0) |
| [25] |
胡梦佳, 李书, 王远达. 主动约束层阻尼板结构动力学建模[J]. 振动、测试与诊断, 2013, 33(s1): 198-201. (  0) 0) |
| [26] |
周云. 粘弹性阻尼减震结构设计[M]. 武汉: 武汉理工大学出版社, 2006.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

