2. 先进航空发动机协同创新中心,北京 100083
2. Collaborative Innovation Center for Advanced Aero-Engine, Beijing 100083, China
转子叶片作为航空发动机的关键结构件,其性能直接影响着整机的工作效率和可靠性。叶片工作过程中的激励频率范围较宽,同时承受着较大的气动载荷、机械载荷和热载荷,容易发生强迫振动或共振。过大的振动应力使得转子叶片产生高循环疲劳损伤,大幅降低叶片的使用寿命,最终发生断裂[1]。为了尽可能地降低共振时的振动应力,避免叶片断裂故障的发生,多种阻尼减振技术被广泛运用于转子叶片的设计中。IHPTET报告给出了粘弹性阻尼、气体薄膜阻尼、颗粒阻尼和干摩擦阻尼[2],其中干摩擦阻尼因其使用方便、减振效果显著,具有较好的热稳定性,是转子叶片减振设计的主要阻尼形式。
缘板阻尼器是采用一小块金属放置在叶片间缘板以下的空腔内,通常为楔形、半圆柱形或者平板形。当接触面相对位移达到某个临界值,阻尼器与缘板开始发生相对滑动,将振动能量转换成热能,来抑制叶盘结构的振动。缘板阻尼器是典型的B-B型阻尼结构,与相邻的叶片之间至少有两个接触面,不会显著影响转子叶片整体的模态和刚度。根据接触面的摩擦系数、接触刚度等参数的大小,通过调节阻尼器的质量,来控制阻尼器的减振效果。1980年,Griffin基于宏滑动模型对缘板阻尼器开展了早期的研究,发现在激振力恒定时存在最佳正压力[3];Cigeroglu等[4]基于微滑动模型和高阶谐波平衡法对楔形缘板阻尼器进行了有限元分析;Panning等[5]通过实验分析了楔形阻尼器和半圆柱形阻尼器对叶片振动的影响;Petrov等[6]对楔形阻尼器和非对称“开裂形”阻尼器模型进行了详细的理论推导;Chen等[7]建立了带缘板阻尼结构的叶片等效质量模型,利用迭代求解的思想列出了叶片非线性响应的计算流程,其结果与郝燕平等[8]的实验测量值具有较好的一致性。
目前,大多数文献主要研究摩擦模型的构建和改进,提出多种摩擦阻尼系统的非线性响应求解方法。具有代表性的有:Zmitrowicz[9]较早采用有限元模型分析了带凸肩结构的涡轮叶片的响应分析;Berthillier等[10]利用模态综合法对带阻尼结构叶片进行了动力响应分析;Zucca等[11]采用谐波平衡法对摩擦接触结构进行了非线性动力学分析;Ma等[12]求解了带有叶冠结构的转子叶片的非线性响应;单颖春[13]利用时频转换法分别求解了带缘板阻尼器与带凸肩的叶片的响应。尽管非线性响应求解方法被不断地改进,但是激振力总是被简化为恒定的集中力或均匀分布力,这与实际的激振力分布相差较大,并且开展非线性分析耗时较长,不便于工程设计。
本文从振动应力与阻尼比的角度,在无需计算非线性响应的条件下,提出了一种有效的缘板阻尼器设计方法。通过对转子叶片进行模态分析,提取模态应力最大值及接触位置处的模态位移值,给定不同的振动应力幅值,计算了不同接触条件下阻尼比变化规律。
2 单自由度模型缘板阻尼器位于叶片根部的缘板处,对叶片的固有振动特性影响较小,可用集总参数的单自由度模型代替复杂的叶片-阻尼器模型。在对转子叶片进行有限元计算时,将其离散为多个自由度的振动模型,假设叶片受到的外部激振力为f(t),其动力学振动方程[14]为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{M\ddot y}} + \mathit{\boldsymbol{C}}\dot y + \mathit{\boldsymbol{Ky}} = \mathit{\boldsymbol{f}}\left( t \right)}\\ {\mathit{\boldsymbol{y}} = {{\left[ {{y_1}\;\;\;{y_2}\;\; \cdots \;\;{y_n}} \right]}^{\rm{T}}}}\\ {\mathit{\boldsymbol{f}}\left( t \right) = {{\left[ {{f_1}\left( t \right)\;\;\;\;{f_2}\left( t \right)\;\; \ldots \;\;{f_n}\left( t \right)} \right]}^{\rm{T}}}} \end{array}} \right. $ | (1) |
式中y为位移向量,M为质量矩阵,C为阻尼矩阵,K为刚度矩阵。
假设{ϕ}i为叶片的各阶模态向量,位移向量y可以写成
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{y}} = \sum\limits_{i = 1}^n {{\left\{ \phi \right\}}_i}{\eta _i}\left( t \right)}\\ {{{\left\{ \mathit{\boldsymbol{\phi}} \right\}}_i} = {{\left[ {\begin{array}{*{20}{c}} {{\phi _{i1}}}&{{\phi _{i2}}}& \cdots &{{\phi _{{\rm{in}}}}} \end{array}} \right]}^{\rm{T}}}} \end{array}} \right. $ | (2) |
由于一阶弯曲振动是实际叶片的主要振动模态,本文主要研究缘板阻尼器对叶片一阶振动特性的影响,忽略其他阶模态的耦合效应。将式(2)代入式(1),方程两边同时乘以第一阶模态向量的转置向量ϕ1T,根据质量矩阵与刚度矩阵的正交性,可以得到
| $ \begin{array}{*{20}{l}} {{{\left\{ \mathit{\boldsymbol{\phi}} \right\}}_1}^{\rm{T}}\mathit{\boldsymbol{M}}{{\left\{ \phi \right\}}_1}{{\ddot \eta }_1}\left( t \right) + {{\left\{ \mathit{\boldsymbol{\phi}} \right\}}_1}^{\rm{T}}C{{\left\{ \phi \right\}}_1}{{\dot \eta }_1}\left( t \right) + }\\ {\;\;\;\;\;\;{{\left\{ \mathit{\boldsymbol{\phi}} \right\}}_1}^{\rm{T}}\mathit{\boldsymbol{K}}{{\left\{ \phi \right\}}_1}{\eta _1}\left( t \right) = {{\left\{ \mathit{\boldsymbol{\phi}} \right\}}_1}^{\rm{T}}f\left( t \right)} \end{array} $ | (3) |
将系统等效到缘板阻尼器与叶片的接触位置处的单自由度系统,如图 1所示,假设叶片在接触点处的一阶模态位移为ϕ1d,即位移向量{ϕ}1的第d个分量。
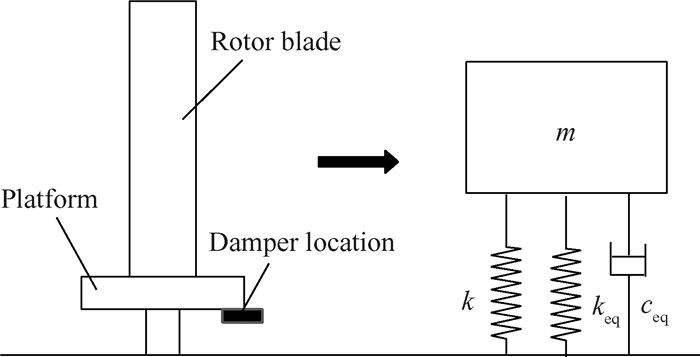
|
Fig. 1 Equivalent single degree of freedom model of rotor blade with an underplatform damper |
| $ {\left\{ \mathit{\boldsymbol{\phi}} \right\}_1} = {\left[ {\begin{array}{*{20}{c}} {{\phi _{11}}}&{{\phi _{12}}}&{\begin{array}{*{20}{c}} \cdots &{{\phi _{1d}}}& \cdots \end{array}}&{{\phi _{1n}}} \end{array}} \right]^{\rm{T}}} $ | (4) |
根据归一化理论,对带有缘板阻尼器的叶片模型的一阶模态参数进行等效处理,转换到接触点处以集总质量m和集总刚度k表示的单自由度模型,忽略结构本身的阻尼,振动微分方程可写为
| $ {\phi _{1d}}m{\phi _{1d}}{{\ddot \eta }_1}\left( t \right) + {\phi _{1d}}k{\phi _{1d}}{\eta _1}\left( t \right) = {\phi _{1d}}{f_d}\left( t \right) $ | (5) |
对比式(3)和式(5),得到
| $ \left\{ {\begin{array}{*{20}{l}} {{{\left\{ \mathit{\boldsymbol{\phi}} \right\}}_1}^{\rm{T}}\mathit{\boldsymbol{M}}{{\left\{ \phi \right\}}_1} = {\phi _{1d}}m{\phi _{1d}}}\\ {{{\left\{ \mathit{\boldsymbol{\phi}} \right\}}_1}^{\rm{T}}\mathit{\boldsymbol{K}}{{\left\{ \phi \right\}}_1} = {\phi _{1d}}k{\phi _{1d}}} \end{array}} \right. $ | (6) |
根据模态质量与模态刚度的关系{ϕ}1TK{ϕ}1={ϕ}1TM{ϕ}1ω12,可得到集总参数的表达式
| $ \left\{ {\begin{array}{*{20}{l}} {m = \frac{{{{\left\{ \mathit{\boldsymbol{\phi}} \right\}}_1}^{\rm{T}}\mathit{\boldsymbol{M}}{{\left\{ \phi \right\}}_1}}}{{{\phi _{1d}}^2}}}\\ {k = \frac{{{{\left\{ \mathit{\boldsymbol{\phi}} \right\}}_1}^{\rm{T}}\mathit{\boldsymbol{M}}{{\left\{ \phi \right\}}_1}}}{{{\phi _{1d}}^2}}{\omega _1}^2} \end{array}} \right. $ | (7) |
利用通用有限元程序进行模态分析,归一化的方式有两种:振型归一化和质量归一化。振型归一化是将模态位移向量除以最大模态位移值,而质量归一化是将模态位移向量除以模态质量的平方根,从而使得归一化后的模态质量等于1,本文采取质量归一化的有限元分析结果。为了计算叶片在接触点处的集总参数,根据刚度的定义,要求接触点的模态位移为单位位移。但是无论采用振型归一化还是质量归一化,都无法满足该前提条件,因此需要对有限元分析结果进行适当的处理。
假设对接触点等效的归一化模态位移为
| $ \left\{ {\begin{array}{*{20}{l}} {m = \frac{{{{\left\{ { \mathit{\boldsymbol{\bar\phi}} } \right\}}_1}^{\rm{T}}\mathit{\boldsymbol{M}}{{\left\{ {\bar \phi } \right\}}_1}}}{{{{\bar \phi }_{1d}}^2}} = \frac{1}{{{{\bar \phi }_{1d}}^2}}}\\ {k = \frac{{{{\left\{ { \mathit{\boldsymbol{\bar\phi}} } \right\}}_1}^{\rm{T}}\mathit{\boldsymbol{M}}{{\left\{ {\bar \phi } \right\}}_1}}}{{{{\bar \phi }_{1d}}^2}}{\omega _1}^2 = \frac{{{\omega _1}^2}}{{{{\bar \phi }_{1d}}^2}}} \end{array}} \right. $ | (8) |
由振动方程可知,振动应力与振动位移的微分有关,对于给定的模态振型,振动应力与振动位移的比值为定值。对于给定的实际振动应力σv,实际振动位移xv可表示为
| $ {x_{\rm{v}}} = \frac{{{x_{{\rm{ref}}}}}}{{{\sigma _{{\rm{ref}}}}}}{\sigma _{\rm{v}}} $ | (9) |
式中xref为模态相对位移,σref为模态应力。
3.1 干摩擦模型干摩擦模型描述了接触面上非线摩擦力与相对位移的数学关系,为了考虑接触结构的局部弹性变形,Griffin[3]提出了滞后弹簧模型,即将弹簧单元与库伦阻尼对串联起来。根据接触面宏滑动之前是否消耗振动能量,干摩擦模型可分为宏滑动模型(Macro-slip Model)和部分滑动模型,而按照不同的接触结构,部分滑动模型可分为Mindlin球接触模型(Sphere Model)和局部微滑动模型(Micro-slip Model)。Mindlin详细分析了球体与弹性半空间体的接触,并给出了非线性摩擦力与相对位移的理论表达式[15],这里主要阐述宏滑动模型和局部微滑动模型。
假设系统受到的激励力是简谐变化的,接触点的相对位移x可表示为
| $ x = A{\rm{cos}}\left( {\omega t + \varphi } \right) = A{\rm{cos}}\theta $ | (10) |
式中A为振动幅值,ω为振动角频率,φ为振动初始相位。对于不考虑微滑动现象的宏滑动模型,在接触面滑动之前,接触的两个物体仅发生弹性变形,其非线性摩擦力为
| $ {f_n} = \left\{ {\begin{array}{*{20}{l}} {\mu N + {k_d}\left( {x - A} \right)}&{\left( {0 \le \theta \le \beta } \right)}\\ { - \mu N}&{\left( {\beta \le \theta \le {\rm{ \mathsf{ π} }}} \right)}\\ { - \mu N + {k_d}\left( {x + A} \right)}&{\left( {{\rm{ \mathsf{ π} }} \le \theta \le \beta + {\rm{ \mathsf{ π} }}} \right)}\\ {\mu N}&{\left( {\beta + {\rm{ \mathsf{ π} }} \le \theta \le 2{\rm{ \mathsf{ π} }}} \right)} \end{array}} \right. $ | (11) |
式中β=arccos(1-2A0/A), A0=μN/kd,μ为摩擦系数,N为接触面正压力,kd为接触面上切向接触刚度。
宏滑动模型不适用于考虑微滑动效应的情况,有必要进一步分析局部微滑动模型的非线性摩擦力。由于微滑动现象会改变接触面的接触刚度,为了衡量其变化程度,引入刚度比例因子λ,定义为
| $ \lambda = {k_{d0}}/{k_{{\rm{gross}}}} $ | (12) |
式中kd0为单调加载时接触面的初始切向接触刚度,kgross为振动位移从零到最大值的变化过程的接触刚度平均值。
类比文献[15],单调加载时,切向载荷Q与接触面切向位移x之间的关系可表示为
| $ x = L\left( Q \right) = \lambda {A_0}\left[ {1 - {{\left( {1 - \frac{Q}{{\mu N}}} \right)}^{\frac{1}{\lambda }}}} \right] $ | (13) |
式中Q为切向位移幅值所对应的切向载荷的大小,迟滞曲线如图 2所示。
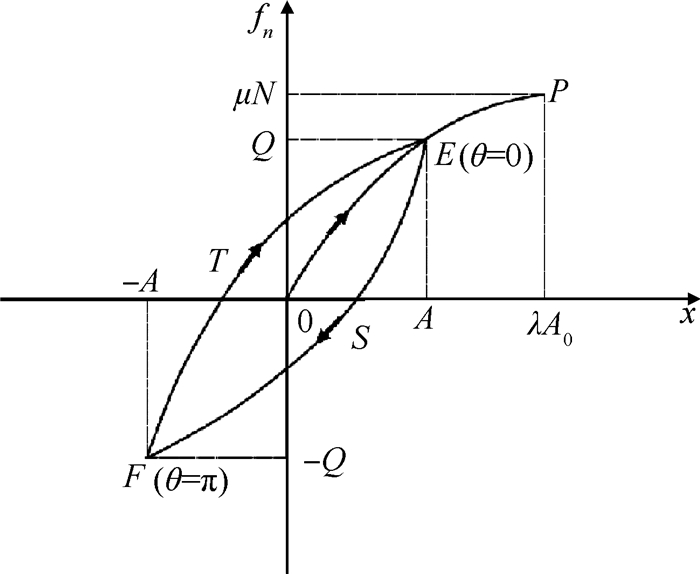
|
Fig. 2 Hysteresis curve of a micro-slip model |
对于卸载(0 ≤ θ ≤ π)过程ESF,有
| $ {f_n} = \mu N\left[ {1 - {{\left( {1 - \frac{A}{{\lambda {A_0}}}} \right)}^\lambda }} \right] - 2\mu N\left[ {1 - {{\left( {1 - \frac{{A - x}}{{2\lambda {A_0}}}} \right)}^\lambda }} \right] $ | (14) |
对于加载(π≤θ≤2π)过程FTE,有
| $ {f_n} = - \mu N\left[ {1 - {{\left( {1 - \frac{A}{{\lambda {A_0}}}} \right)}^\lambda }} \right] + 2\mu N\left[ {1 - {{\left( {1 - \frac{{A + x}}{{2\lambda {A_0}}}} \right)}^\lambda }} \right] $ | (15) |
干摩擦减振的机理是接触的两个物体产生相对滑动,在接触面上将机械能转换为热能而耗散系统的振动能量,从而降低最大振幅和减小振动应力。从摩擦耗能的角度看,能量法考虑的是在一个振动循环过程中,摩擦耗能相对总动能的变化。
摩擦耗能即为摩擦力在一个周期内所做的功,在已知非线性摩擦力随相对切向位移变化的迟滞曲线的情况下,可以通过求解迟滞曲线的面积间接获取摩擦耗能,根据非线性摩擦力的表达公式,摩擦耗能Wf可表示为
| $ {W_{\rm{f}}} = \mathop \oint \nolimits {f_n}{\rm{d}}x = \int_{\rm{ \mathsf{ π} }}^{2{\rm{ \mathsf{ π} }}} {f_n}{\rm{d}}\theta - \int_0^{\rm{ \mathsf{ π} }} {f_n}{\rm{d}}\theta $ | (16) |
下面进一步分析阻尼比与摩擦耗能之间的关系,令ωd为振动角频率,阻尼比为ζ,其与固有频率ωn的关系为:
| $ \frac{{{W_{\rm{f}}}}}{{{W_{{\rm{max}}}}}} = 4{\rm{ \mathsf{ π} }}\frac{c}{{2m{\omega _d}}} \approx 4{\rm{ \mathsf{ π} }}\zeta $ | (17) |
因此,在已求得阻尼耗能与最大动能时,阻尼比可近似表示为
| $ \zeta = \frac{1}{{4{\rm{ \mathsf{ π} }}}}\frac{{{W_{\rm{f}}}}}{{{W_{{\rm{max}}}}}} $ | (18) |
当系统呈现稳态的周期性振动时,作用在结构上的激励均是周期性变化的,包括接触面上的非线性摩擦力。因此,为了便于求解非线性响应,可以将非线性摩擦力表达为振动位移x(t)和振动速度
| $ {f_n}\left( t \right) = {k_{{\rm{eq}}}}x\left( t \right) + {c_{{\rm{eq}}}}\dot x\left( t \right) + f_{n{\rm{c}}}^0 $ | (19) |
式中keq和ceq分别是附加的等效刚度与等效阻尼,fnc0为与位移无关的量。
利用谐波平衡法(HBM),分别将振动位移x(t)和非线性摩擦力fn(t)进行傅里叶展开。由于缘板阻尼器正常工作时受到的正压力很大,采用一次谐波平衡法就具有足够高的精度[4],由傅里叶级数公式,可得到附加的等效刚度与等效阻尼表达式
| $ \left\{ {\begin{array}{*{20}{l}} {{k_{{\rm{eq}}}} = \frac{1}{{{\rm{ \mathsf{ π} }}A}}\int_0^{2{\rm{ \mathsf{ π} }}} {f_n}\left( \theta \right){\rm{cos}}\theta {\rm{d}}\theta }\\ {{c_{{\rm{eq}}}} = - \frac{1}{{{\rm{ \mathsf{ π} }}{\omega _1}A}}\int_0^{2{\rm{ \mathsf{ π} }}} {f_n}\left( \theta \right){\rm{sin}}\theta {\rm{d}}\theta } \end{array}} \right. $ | (20) |
对于一般的带有接触结构的振动系统,可将振动系统在接触位置处等效为x0方向的单自由度系统,假设单自由度系统的集总质量为m,结构阻尼为c,集总刚度为k。原离散的多自由度系统振动方程可进一步简化为
| $ m{{\ddot x}_0}\left( t \right) + \left( {c + {c_{{\rm{eq}}}}} \right){{\dot x}_0}\left( t \right) + \left( {k + {k_{{\rm{eq}}}}} \right){x_0}\left( t \right) = {f_{\rm{e}}}\left( t \right) - f_{n{\rm{c}}}^0 $ | (21) |
由于在实际工程分析中,系统的结构阻尼相比干摩擦阻尼较小,一般在减振分析中可以忽略,即c = 0。根据振动系统阻尼比的定义,阻尼比可表示为
| $ \zeta = \frac{{{c_{{\rm{eq}}}}}}{{2\sqrt {m\left( {k + {k_{{\rm{eq}}}}} \right)} }} $ | (22) |
缘板阻尼器减振设计的具体分析过程,如图 3所示。
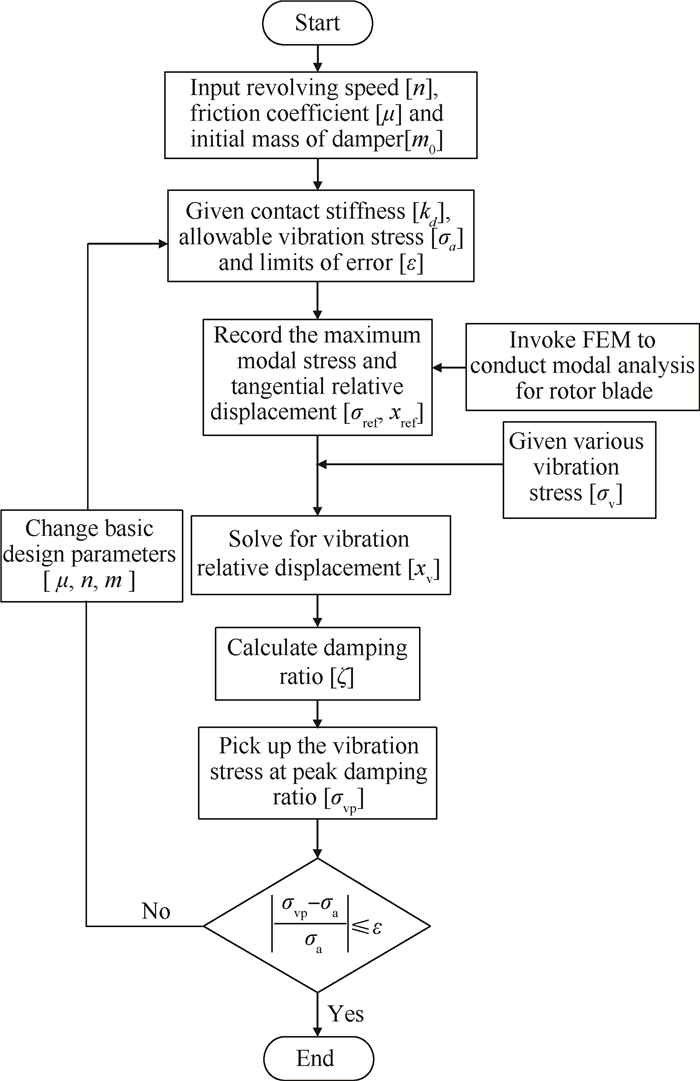
|
Fig. 3 Algorithmic framework flowchart |
为了验证所提出方法的有效性,采用半圆形缘板阻尼器结构,建立带有缘板阻尼器的叶片有限元模型,如图 4所示。由于缘板阻尼器位于叶片根部的缘板处,对叶片固有特性的影响可以忽略,只需对不带阻尼器的叶片振型进行减振分析,这也是基于单自由度模型的前提。
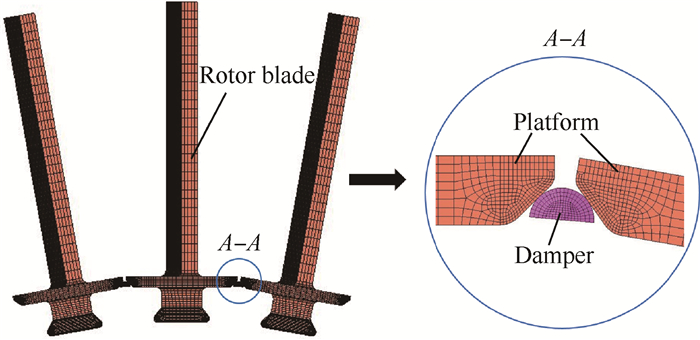
|
Fig. 4 Finite element model of blade with an underplatform damper |
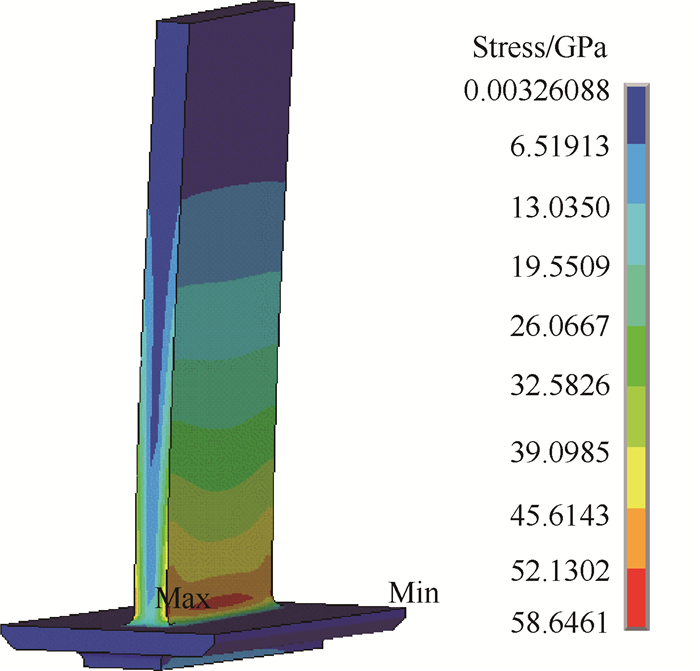
约束叶片榫头两个侧面的法向自由度以及部分端面节点的轴向自由度,分别施加100%转速、84%转速和68%转速,对叶片进行模态分析。由于缘板阻尼器的减振对象为转子叶片,忽略榫头约束处的应力集中,当施加100%转速时,叶片(隐藏榫头部分)的一阶弯曲振型如图 5所示,可知最大振动应力出现在叶片前缘的根部。
|
Fig. 5 Von Mises stress distribution of the 1st mode for a rotor blade model |
在实际工作中,缘板阻尼器同时与相邻的两个叶片接触,所提供的总阻尼比等于左右两个接触面的阻尼比之和。提取叶片缘板与阻尼器接触面节点的切向模态位移进行平均,分别得到阻尼器左右接触面的归一化位移ϕ1d_L和ϕ1d_R,将单个叶片模型转化为以集总质量m与集总刚度k表达的单自由度模型。
在给定工况下,阻尼比的大小依赖于接触面相对位移的大小。根据缘板阻尼器动力学分析[17],将阻尼器与左右缘板的接触简化为两个接触点,在接触面的局部坐标系下,提取左接触点相对右接触点的位移值,进而得到接触面的切向相对位移xref_L和xref_R。
考虑到工程中多用应力作为评价标准,因而通过模态分析得到最大模态Von Mises应力σref与接触面的切向相对位移xref关系,进而得到阻尼比与振动应力的关系。叶片一阶弯曲振动时,所需的各参数见表 1。
|
|
Table 1 Parameters for damping analysis of a rotor blade under different rotating speeds |
无论是带阻尼结构叶片响应的求解,还是阻尼器设计程序的输入,都需要预先确定接触面的特征参数准确值,包括接触面摩擦系数μ,接触刚度kd和刚度比例因子λ。接触刚度和刚度比例因子随着接触面正压力的变化而改变,而不同转速决定了阻尼器的离心力不同,进而影响接触面的正压力。文献[18]给出了详细的接触刚度分析,不同转速条件下接触面的接触刚度和刚度比例因子见表 2。
|
|
Table 2 Contact parameters for different rotating speeds |
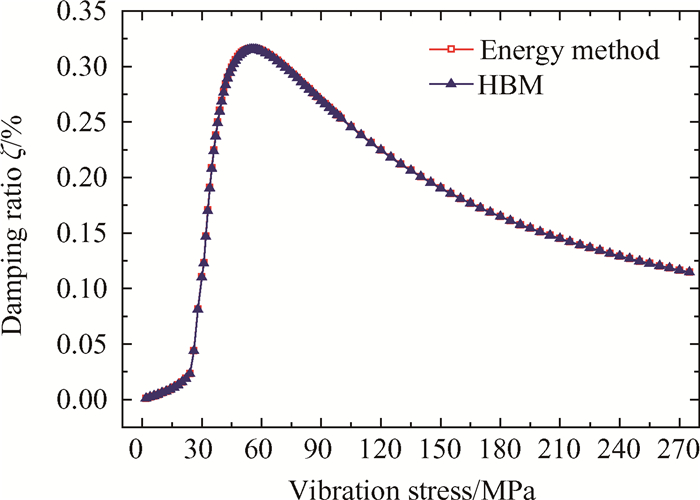
给定阻尼器初始质量为m0=8.16g,初始摩擦系数为μ= 0.3,根据减振分析理论,考虑微滑动效应,分别利用能量法(Energy method)和谐波平衡法(HBM)求解不同振动应力条件下的阻尼比。在最大转速下,这两种方法得到的阻尼比曲线如图 6所示,可知在给定的振动应力范围内,两者相差很小,验证了该减振分析方法的有效性和准确性。
|
Fig. 6 Comparison between energy method and HBM |
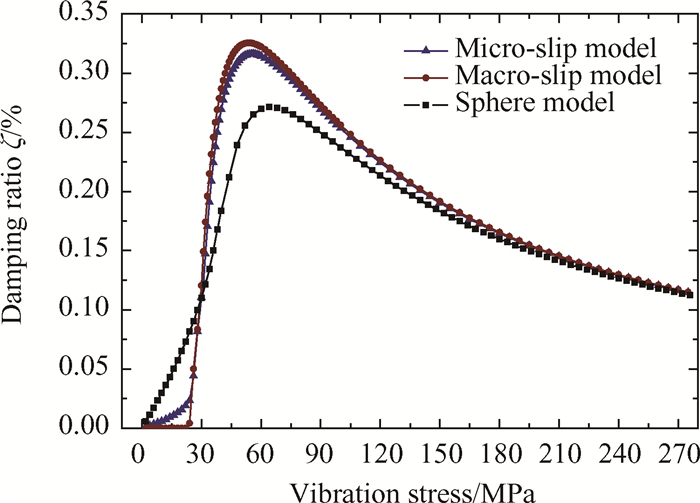
滑动摩擦模型的选择直接关系到接触面非线性摩擦力的求解,进而影响阻尼比。不同模型体现在刚度比例因子的取值,宏滑动模型(Macro-slip model)和Mindlin球接触模型(Sphere model)的刚度比例因子分别为λmac=1和λs=1.5,而微滑动模型(Micro-slip model)取决于阻尼器的具体形状。当施加最大转速时,基于不同滑动模型得到的阻尼比曲线如图 7所示。由图可知,宏滑动模型与微滑动模型对应的阻尼比曲线较为接近,而基于Mindlin球接触模型得到的阻尼比曲线偏差较大。若采用Mindlin球接触模型近似求解圆柱形阻尼器的接触,峰值阻尼比偏低,导致结果误差较大;若不考虑微滑动效应,采用宏滑动模型进行减振分析,存在能够提供阻尼的临界振动应力门槛值,峰值阻尼比略微偏高,但几乎不影响阻尼比的分布。
|
Fig. 7 Characteristic curves of damping ratio for different dry friction models |
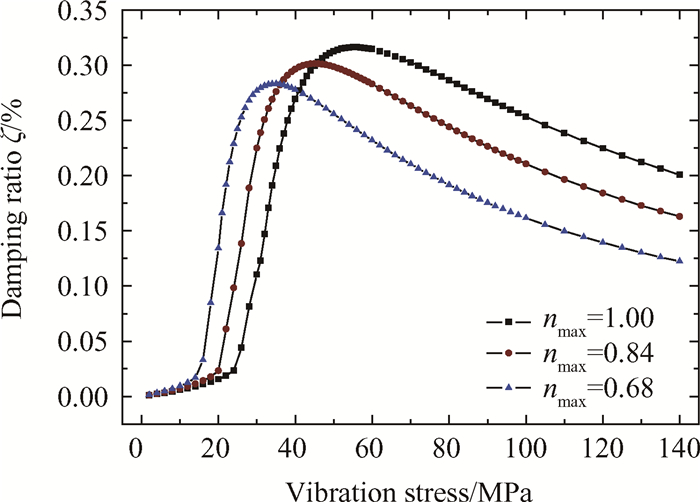
施加不同的转速,不仅使得接触面的正压力不同,而且影响叶片的固有特性参数,进而影响接触参数和阻尼比。本文分别取了n/nmax=1,0.84,0.68三种转速状态,考虑微滑动的阻尼比特性曲线如图 8所示。随着转速的增加,峰值阻尼比略有提升,而且峰值阻尼比对应的振动应力明显增大,从而影响许用振动应力幅值对应的阻尼比。
|
Fig. 8 Characteristic curves of damping ratio for different rotating speeds |
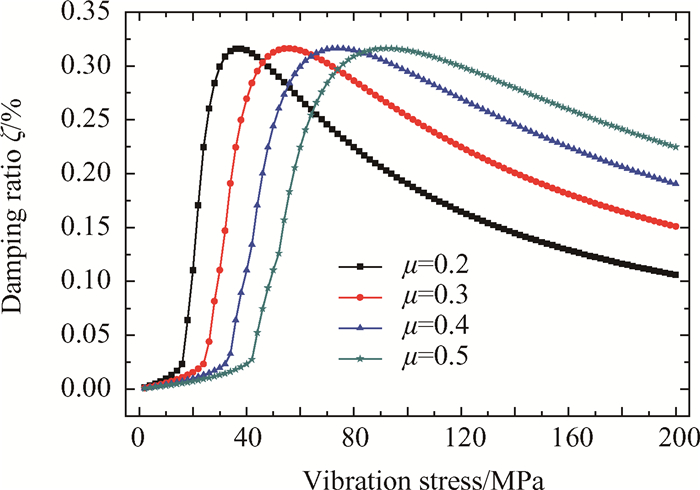
综合以上分析,基于微滑动模型,对100%转速利用谐波平衡法分析进一步开展阻尼比的参数敏感性分析,包括摩擦系数、接触刚度和阻尼器质量。摩擦系数取决于接触面的光滑程度,随着阻尼器工作时间的延长,接触面会变得逐渐光滑,使得摩擦系数发生一定的变化。分别取四种典型的摩擦系数(μ = 0.2, 0.3, 0.4, 0.5),相应的阻尼比特性曲线如图 9所示。摩擦系数的变化不会影响峰值阻尼比的大小,仅仅改变峰值阻尼比对应的振动应力,也就是只改变阻尼比特性曲线的峰值位置,并不改变其形状。
|
Fig. 9 Characteristic curves of damping ratio for different friction coefficients |
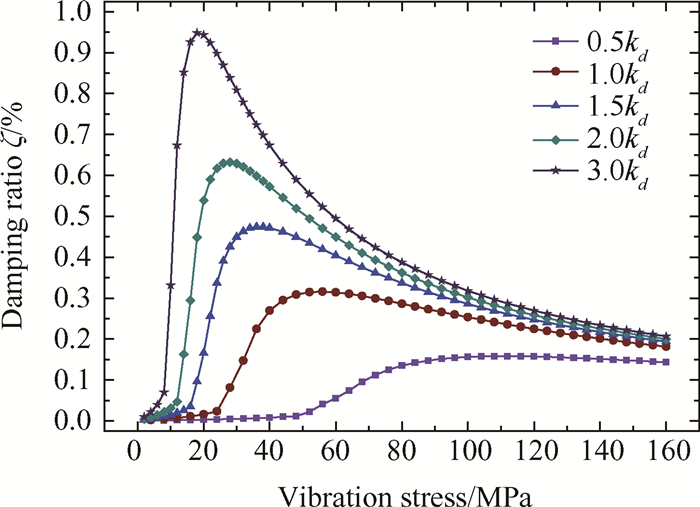
接触参数的准确与否直接关系到接触状态的转换,进而影响求解结果的准确程度。为了分析接触刚度的变化对减振效果的影响,取n/nmax=1.00转速对应的参数为基值kd,分别采用不同的接触刚度(0.5kd, 1.0kd, 1.5kd, 2.0kd, 3.0kd)计算阻尼比曲线,如图 10所示。由图可知,接触刚度的变化显著影响峰值阻尼比的大小,接触刚度越大,阻尼器所能提供的阻尼比越大,但峰值阻尼比对应的振动应力相应减小。
|
Fig. 10 Characteristic curves of damping ratio for different contact stiffness |
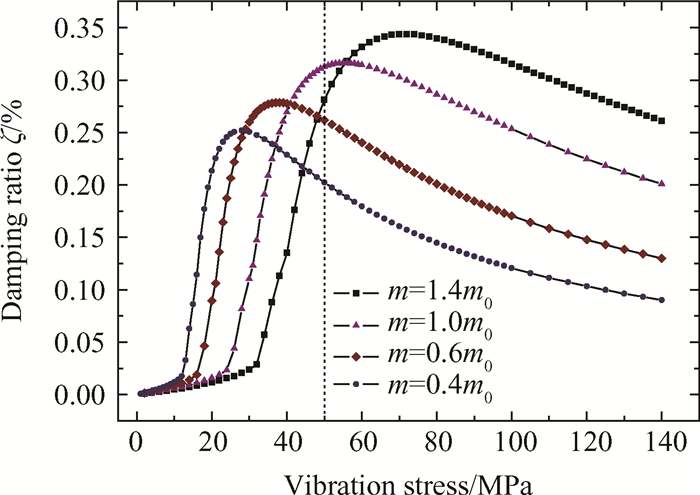
阻尼器质量作为阻尼器设计的关键参数,直接影响其减振效果。当阻尼器分别取不同的质量(0.4m0, 0.6m0, 1.0m0, 1.4m0)时,阻尼比特性曲线如图 11所示。由图可知,随着阻尼器质量的增大,峰值阻尼比及其对应的振动应力均增大。
|
Fig. 11 Characteristic curves of damping ratio for dampers with different mass |
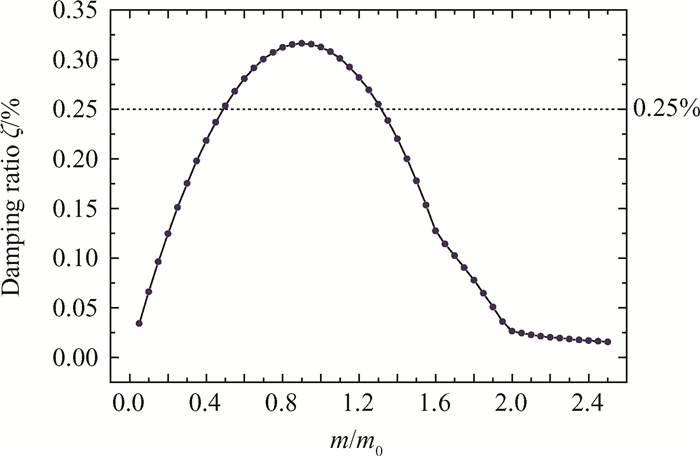
当给定许用振动应力幅值为σa=50MPa时,提取所对应的阻尼比,可得到该振动应力水平下,阻尼比随阻尼器质量的变化曲线,如图 12所示。由图可知,随着阻尼器质量的增大,阻尼比先增大后减小,当阻尼器质量为0.9m0时,该振动应力水平下缘板阻尼器所提供的阻尼比最大。若减振目标为阻尼器提供至少0.25%的阻尼比,由图 12可知,阻尼器质量需在0.5m0 < m < 1.3m0范围内。
|
Fig. 12 Damping ratio distribution for different damper mass (σa = 50MPa) |
通过以上分析可知,在不同转速条件下,改变接触面摩擦系数、接触刚度、阻尼器质量等参数能显著改善缘板阻尼器的减振效果。对于给定的许用振动应力幅值和目标阻尼比,可计算得到相应的设计参数的取值范围。与求解叶片的非线性响应的方法相比,本文提出的方法大大减小了计算成本,且从许用振动应力出发,为带有缘板阻尼器的转子叶片参数化设计提供了理论依据。
5 结论基于归一化理论,将实际带有缘板阻尼器的转子叶片简化为集总参数表示的单自由度模型,详细推导并计算了阻尼比与振动应力的关系,提出了一种无需计算复杂耗时的非线性响应的缘板阻尼器减振设计方法。主要结论如下:
(1)对带有半圆形缘板阻尼器的转子叶片进行了示例分析,Von Mises振动应力最大点均出现在叶片前缘根部,同时叶背根部应力也较大;通过对比能量法和谐波平衡法的计算结果,验证了所提出方法的准确性,并分析了转速、接触参数、阻尼器质量等设计参数对减振特性的影响。
(2)缘板阻尼器在工作转速范围内能够提供的临界阻尼比有限,且随着振动应力的变化而变化。对于文中示例,在100%转速下,摩擦系数取μ = 0.3时,考虑接触面的微滑动效应,若给定叶片许用振动应力幅值为σa=50MPa,最佳缘板阻尼器质量为7.34g,其峰值阻尼比为0.33%左右。
后续将开展关于所提出的减振设计方法的实验验证研究,进一步验证该方法的准确性和有效性,并探索将其用于叶冠和凸肩等其他形式的减振结构。
| [1] |
王延荣, 田爱梅. 叶/盘结构振动分析中几个问题的探讨[J]. 推进技术, 2002, 23(3): 233-236. (WANG Yan-rong, TIAN Ai-mei. Discussion on Several Problems in Vibration Analysis of Bladed-Disk Assemblies[J]. Journal of Propulsion Technology, 2002, 23(3): 233-236.)
(  0) 0) |
| [2] |
陈璐璐, 张大义, 文敏, 等. 带凸肩风扇叶片振动特性及设计方法研究[J]. 推进技术, 2015, 36(9): 1389-1394. (CHEN Lu-lu, ZHANG Da-yi, WEN Min, et al. Dynamical Effects of Shrouds on Fan Blade Vibration and Its Corresponding Design Method[J]. Journal of Propulsion Technology, 2015, 36(9): 1389-1394.)
(  0) 0) |
| [3] |
Griffin J H. Friction Damping of Resonant Stresses in Gas Turbine Engineering Airfoils[J]. Journal of Engineering for Power, 1980, 102(2): 329-333. DOI:10.1115/1.3230256
(  0) 0) |
| [4] |
Cigeroglu E, An N, Menq C H. A Microslip Friction Model with Normal Load Variation Induced by Normal Motion[J]. Nonlinear Dynamics, 2007, 50(3): 609-626. DOI:10.1007/s11071-006-9171-4
(  0) 0) |
| [5] |
Panning L, Sextro W, Popp K. Optimization of Interblade Friction Damper Design [C]. Munich: ASME Turbo Expo 2000: Power for Land, Sea, and Air, 2000.
(  0) 0) |
| [6] |
Petrov E P, Ewins D J. Advanced Modeling of Underplatform Friction Dampers for Analysis of Bladed Disk Vibration[J]. Journal of Turbomachinery, 2006, 129(1): 143-150.
(  0) 0) |
| [7] |
CHEN Yu-di, WANG Yan-rong. A Method for the Resonant Response Evaluation of Blades System with Underplatform Dampers[C]. Guiyang: 6th International Symposium on Instrumentation & Control Technology Sensors Automatic Measurement Control & Computer Simulation, 2014.
(  0) 0) |
| [8] |
郝燕平, 单颖春, 朱梓根. 缘板摩擦阻尼器的减振实验研究[J]. 航空动力学报, 2001, 16(1): 55-58. (  0) 0) |
| [9] |
Zmitrowicz A. A Vibration Analysis of a Turbine Blade System Damped by Dry Friction Forces[J]. International Journal of Mechanical Sciences, 1981, 23(12): 741-761. DOI:10.1016/0020-7403(81)90012-6
(  0) 0) |
| [10] |
Berthillier M, Dupont C, Mondal R, et al. Blades Forced Response Analysis with Friction Dampers[J]. Journal of Vibration & Acoustics, 1998, 120(2): 468-474.
(  0) 0) |
| [11] |
Zucca S, Firrone C M. Nonlinear Dynamics of Mechanical Systems with Friction Contacts: Coupled Static and Dynamic Multi-Harmonic Balance Method and Multiple Solutions[J]. Journal of Sound & Vibration, 2014, 333(3): 916-926.
(  0) 0) |
| [12] |
MA Hui, YIN Fan-lin, WU Zhi-yuan, et al. Nonlinear Vibration Response Analysis of a Rotor-Blade System with Blade-Tip Rubbing[J]. Nonlinear Dynamics, 2016, 84(3): 1225-1258. DOI:10.1007/s11071-015-2564-5
(  0) 0) |
| [13] |
单颖春. 叶轮机械叶片干摩擦减振研究[D]. 北京: 北京航空航天大学, 2002. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y479867
(  0) 0) |
| [14] |
倪振华. 振动力学[M]. 西安: 西安交通大学出版社, 1989.
(  0) 0) |
| [15] |
Koh K H, Griffin J H, Filippi S, et al. Characterization of Turbine Blade Friction Dampers[J]. Journal of Engineering for Gas Turbines & Power, 2005, 127(4): 237-245.
(  0) 0) |
| [16] |
Rao S S(著). 李欣业, 张明路(译). 机械振动[M]. 北京: 清华大学出版社, 2009.
(  0) 0) |
| [17] |
Sanliturk K Y, Ewins D J, Stanbridge A B. Underplatform Dampers for Turbine Blades: Theoretical Modeling, Analysis, and Comparison with Experimental Data[C]. Indiana: ASME 1999 International Gas Turbine and Aeroengine Congress and Exhibition, 1999. http://www.researchgate.net/publication/266732223_Underplatform_dampers_for_turbine_blades_Theoretical_modeling_analysis_and_comparison_with_experimental_data
(  0) 0) |
| [18] |
Allara M. A Model for the Characterization of Friction Contacts in Turbine Blades[J]. Journal of Sound & Vibration, 2009, 320(320): 527-544.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

