2. 航空发动机数值仿真研究中心,北京 100083;
3. 先进航空发动机协同创新中心,北京 100083
2. Aeroengine Numerical Simulation Research Center, Beijing 100083, China;
3. Collaborative Innovation Center for Advanced Aero-Engine, Beijing 100083, China
航空发动机转子叶片减振设计中常采用缘板阻尼器、叶冠和凸肩等结构,工作时依靠这些阻尼结构与叶片接触面之间的干摩擦耗能提供阻尼。在干摩擦阻尼器设计或计算中,首先要对摩擦面进行建模。由于摩擦机理的复杂性,两个接触体之间的摩擦往往与材料属性、温度、表面粗糙度等多种因素有关。工程中常用的摩擦模型有经典库伦摩擦模型[1]、线性迟滞弹簧模型[2, 3]以及Iwan模型[4]等。在摩擦模型建模及计算中,接触刚度通常是首先需要确定的参数,然而接触刚度一般较难确定,通常依赖经验给定一个较为合理的数值[5]。接触刚度选取不合理易导致计算结果失真或难以收敛。国内外学者围绕接触刚度进行了大量研究,发展了相关数值仿真和实验方法,但目前尚未形成普适算法。
利用有限元法计算接触刚度是一种较为简单有效的方法,文献[6]对比了三种估算接触刚度的方法,结果表明有限元法的计算精度最高。史亚杰等[7]利用通用有限元软件计算干摩擦阻尼器的切向接触刚度,考查了接触面正压力、摩擦系数、阻尼器材料属性和阻尼器接触面半径等对切向接触刚度的影响。有限元法的缺点一方面是计算结果具有局限性,接触刚度的值通常只适用于某一个具体的计算模型;另一方面利用有限元法计算的切向接触刚度与实际值相比通常偏高[8]。文献[9]通过实验手段研究了干摩擦阻尼器的切向接触刚度,首次揭示了切向接触刚度与激振力幅值之间的关系。Schwingshackl等[10]对摩擦系数和切向接触刚度进行了实验研究,结果表明切向接触刚度与接触体的温度、材料属性以及接触面压力相关,切向刚度的量级始终在107N/m以内,在缺乏实验数据时切向刚度可选取3 × 107N/m。
微滑动摩擦模型能够刻画接触面处于粘滞状态时接触面发生局部滑动的现象。在微滑动摩擦建模中,Iwan模型得到了广泛应用和推广[11~14]。根据“弹簧+摩擦副”(Jenkins Element)组合方式的不同,Iwan模型大致可以分为“并联-串联”和“串联-串联”两种形式。大多数的微滑动摩擦模型均属于Iwan模型的推广,包括Menq等[15]提出的用“剪切层”的概念描述摩擦面。另一方面,文献[16]从接触力学角度出发研究接触面之间的微滑动,推导了接触面相对滑动位移与切向力之间的关系式,基于Masing假设[17],得到了摩擦力迟滞环的表达式。与Iwan模型相比,文献[16]中的结果具有更加明确的物理意义。
本文基于文献[16]的研究,以带圆角平板的接触模型为研究对象推导干摩擦阻尼器的切向接触刚度的理论表达式,包括初始切向接触刚度和微滑动阶段平均切向接触刚度;在文献[18]发展的微滑动摩擦模型的基础上,推导模型中经验系数的解析表达式,基于Masing假设建立工程中可用的微滑动摩擦迟滞环数学模型。
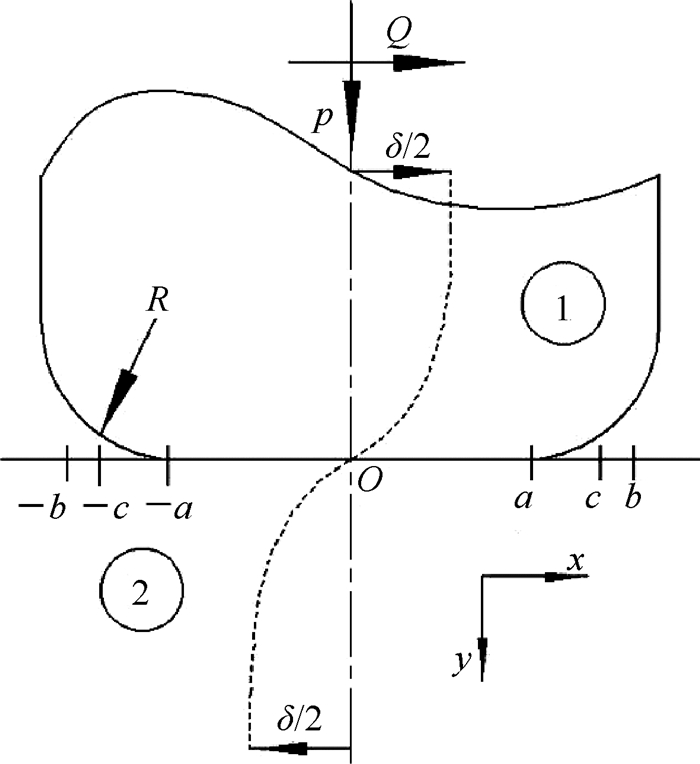
2 干摩擦接触区力学模型当干摩擦阻尼器长度方向尺寸远大于接触区宽度时,其接触区可以简化为带圆角的平板与无限大半平面的二维接触模型,如图 1所示。图中p和Q分别为阻尼器单位长度的正压力和切向力,a,b以及c分别对应阻尼器平直段、接触区以及粘滞区宽度的一半,R为圆角半径,δ为两接触体中心线远点之间的切向相对位移。
|
Fig. 1 Flat rounded contact model |
由文献[16]可知,仅考虑接触体材料相同的情况,两接触体远点之间的切向相对位移与切向力之间满足
| $\delta = \frac{2}{{{\rm{ \mathsf{ π} }}{E^{\rm{*}}}}}\left[ { - \int_{ - b}^b q\left( r \right){\rm{ln}}\left| {\frac{r}{b}} \right|{\rm{d}}r + Q\left( {{\rm{ln}}\left| {\frac{L}{b}} \right| + \frac{v}{{1 - v}}} \right)} \right]$ | (1) |
式中E*=E/[2(1-v2)],E和v分别为接触体的弹性模量与泊松比,,q(r)为接触面上的摩擦力分布,L为阻尼器长度。为分析简便需要,对式(1)进行无量纲化处理,记
| $\varphi = \frac{r}{b}, \bar q\left( \varphi \right) = \frac{{bq\left( \varphi \right)}}{{\mu p}}, \bar Q = \frac{Q}{{\mu p}}, \bar \delta = \frac{{{\rm{ \mathsf{ π} }}{E^{\rm{*}}}\delta }}{{2\mu p}}$ | (2) |
式中μ为摩擦系数,故式(1)可以改写为
| $\bar \delta = - \int_{ - 1}^1 \bar q\left( \varphi \right){\rm{ln}}\left| \varphi \right|{\rm{d}}\varphi + \bar Q\left( {{\rm{ln}}\left| {\frac{L}{b}} \right| + \frac{v}{{1 - v}}} \right)$ | (3) |
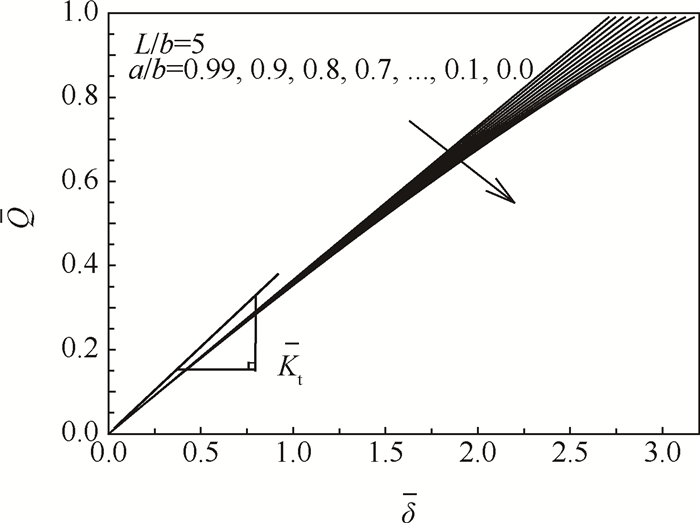
式(3)为摩擦力初始加载曲线的无量纲表达式,结果如图 2所示,当给定参数a/b和L/b时,初始加载曲线唯一确定。
|
Fig. 2 Normalized initial loading curves |
文献中通常将摩擦力加载或卸载曲线初始时刻的斜率即初始切向接触刚度定义为切向接触刚度。本文中出现的Kt均代表初始切向接触刚度,即
| ${K_{\rm{t}}} = {\left. {\frac{{{\rm{d}}Q}}{{{\rm{d}}\delta }}} \right|_{\delta = 0}}$ | (4) |
由于式(3)中的切向力分布q(φ)与切向力Q相关,难以直接对方程两边求导以得到初始切向接触刚度。尽管如此,从图 2中可以看出,当给定参数L/b时,参数a/b的变化主要改变加载曲线后半段的走势,而几乎不改变初始切向接触刚度的数值大小,于是可以利用a/b=0时,即圆柱与平板接触时的特例来计算初始切向接触刚度。这里可首先定义无量纲初始切向接触刚度
| ${{\bar K}_{\rm{t}}} = {\left. {\frac{{{\rm{d}}\bar Q}}{{{\rm{d}}\bar \delta }}} \right|_{\bar \delta = 0}}$ | (5) |
实际切向接触刚度与无量纲切向接触刚度之间的关系为
| ${K_{\rm{t}}} = \frac{{{\rm{ \mathsf{ π} }}{E^{\rm{*}}}}}{2}{{\bar K}_{\rm{t}}}$ | (6) |
根据接触力学基本理论,圆柱与平板接触时的压力以及切向力分布分别为
| $p\left( x \right) = \frac{{2p}}{{{\rm{ \mathsf{ π} }}{b^2}}}\sqrt {{b^2} - {x^2}} $ | (7) |
| $ q\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {\mu p\left( x \right) - \frac{{2\mu p}}{{{\rm{ \mathsf{ π} }}{b^2}}}\sqrt {{c^2} - {x^2}} \;\;\;\;\;\;\;\;\left| x \right| < c}\\ {\mu p\left( x \right)\begin{array}{*{20}{c}} {}&{}&{}&{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;c \le \left| x \right| \le b} \end{array}} \end{array}} \right. $ | (8) |
将式(8)的无量纲式代入式(3)中,并对方程左右两边同时求导,可得
| $ {{\bar K}_{\rm{t}}} = \frac{1}{{{\rm{ln}}2 + {\rm{ln}}\left| {\frac{L}{b}} \right| + \frac{v}{{1 - v}}}} $ | (9) |
由式(6),实际初始切向接触刚度
| $ {K_{\rm{t}}} = \frac{{{\rm{ \mathsf{ π} }}{E^{\rm{*}}}}}{{2\left( {{\rm{ln}}2 + {\rm{ln}}\left| {\frac{L}{b}} \right| + \frac{v}{{1 - v}}} \right)}} $ | (10) |
由上式可知,初始切向接触刚度的值仅与接触体材料属性以及参数L/b有关。当a/b,即圆柱与平板接触时
| $ b = \sqrt {\frac{{4pR}}{{{\rm{ \mathsf{ π} }}{E^{\rm{*}}}}}} $ | (11) |
可得
| $ {K_{\rm{t}}} = \frac{{{\rm{ \mathsf{ π} }}{E^{\rm{*}}}}}{{{\rm{ln}}\left( {\frac{{{\rm{ \mathsf{ π} }}{E^{\rm{*}}}{L^2}}}{{pR}}} \right) + \frac{{2v}}{{1 - v}}}} $ | (12) |
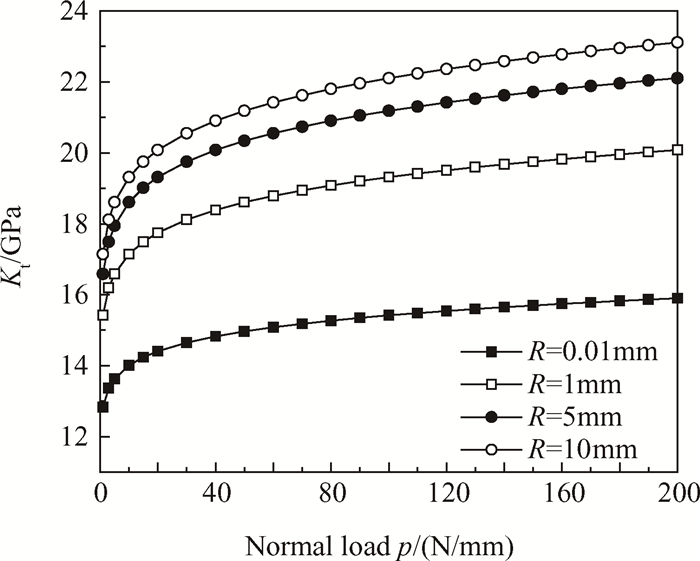
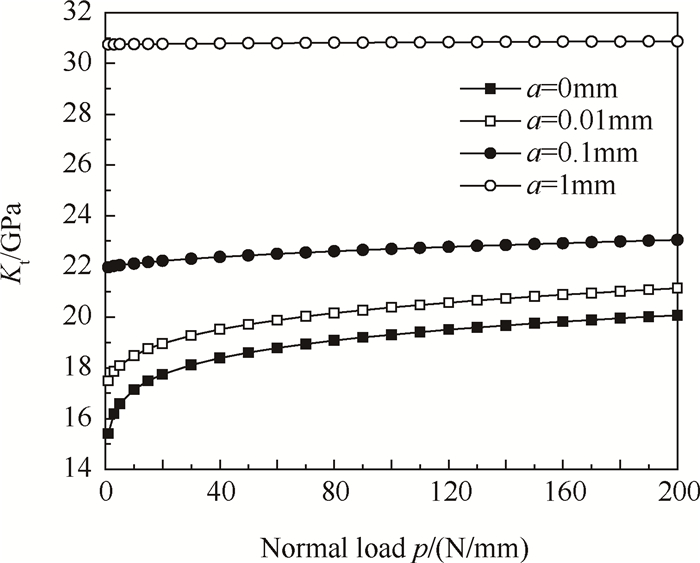
式(10)和式(12)即通常文献中所定义的切向接触刚度的解析表达式。由于p为单位长度的法向压力,因此本文给出的切向接触刚度实为单位长度的切向接触刚度,将式(10)和式(12)等式右边项乘以阻尼器长度L得到的切向接触刚度量纲即为N/mm。需要说明的是式(10)适用于带圆角平板的接触模型,式(12)则仅针对的是圆柱与平板接触的模型。给定接触区部分参数见表 1,对于圆柱与平板接触,切向接触刚度如图 3所示,随着接触面正压力和接触半径的增大而逐渐增大,当正压力增大到一定程度时,切向接触刚度增大趋势放缓。对于更一般的带圆角平板的接触情况,应用式(10)求切向接触刚度,结果如图 4所示。可以看出,当接触区平直段尺寸较小时,切向接触刚度随正压力的变化与图 3中的结果类似,随着平直段尺寸增大,切向接触刚度几乎不随正压力发生变化,这是由于此时正压力对接触区宽度的影响不大。
|
|
Table 1 Properties of contact bodies |
|
Fig. 3 Tangential contact stiffness of cylinder and plate contact model |
|
Fig. 4 Tangential contact stiffness of flat rounded contact model (R=1mm) |
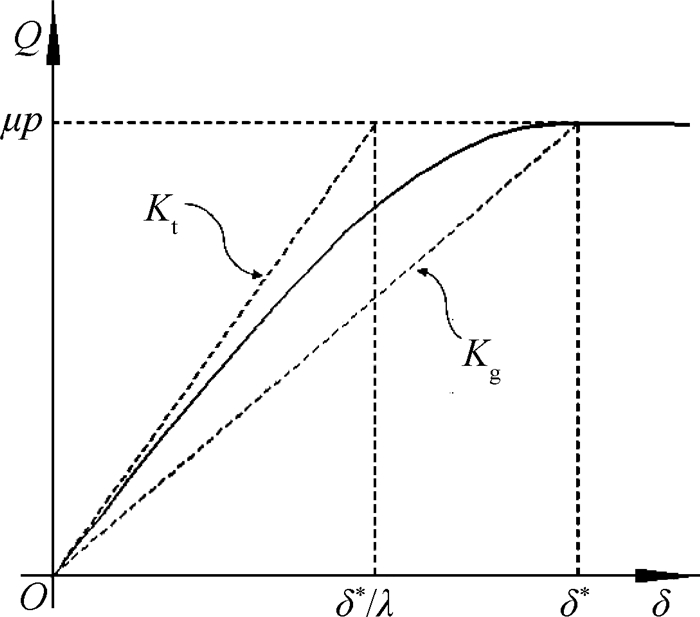
若定义在整个微滑动阶段的平均切向接触刚度为
| $ {K_{\rm{g}}} = \frac{{\mu p}}{{{\delta ^{\rm{*}}}}} $ | (13) |
式中δ*为接触面即将发生整体滑动时的切向相对位移,如图 5所示。由式(3),容易得到平均切向接触刚度的无量纲表达式为
|
Fig. 5 Tangential contact stiffness during microslip |
| $ {{\bar K}_{\rm{g}}} = \frac{1}{{ - \mathop \smallint \nolimits_{ - 1}^1 \bar p\left( \varphi \right){\rm{ln}}\left| \varphi \right|{\rm{d}}\varphi + {\rm{ln}}\left| {\frac{L}{b}} \right| + \frac{v}{{1 - v}}}} $ | (14) |
式中p(φ)为接触面压力分布,且p(φ)=bp(φ)/p。将式(7)的无量纲式代入式(14)可得圆柱与平板接触时的无量纲平均切向刚度
| $ {{\bar K}_{\rm{g}}} = \frac{1}{{\frac{1}{2} + {\rm{ln}}2 + {\rm{ln}}\left| {\frac{L}{b}} \right| + \frac{v}{{1 - v}}}} $ | (15) |
同式(6),有
| $ {K_{\rm{g}}} = \frac{{{\rm{ \mathsf{ π} }}{E^{\rm{*}}}}}{2}{{\bar K}_{\rm{g}}} $ | (16) |
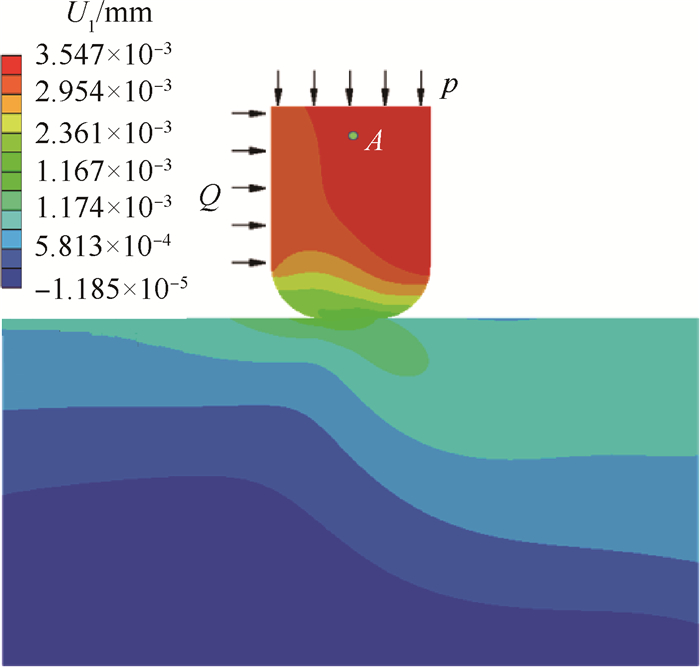
文献[8]研究的缘板阻尼器与叶片的接触区可视为圆柱面与平板接触模型,其有限元模型计算得到的切向接触刚度与实验值相比偏高约25%,并认为造成误差的原因为有限元模型未考虑接触区表面粗糙度。文献[19]在研究微动磨损时采用了和本文相同带圆角平板接触模型,出于对比考虑,本文建立与之相同的有限元模型,即对于带圆角的平板接触模型,平直段半宽度a=1.525mm,圆角半径R=3.05mm;圆柱与平板接触时(a=0),接触圆弧面半径R=10mm,材料均为Ti6Al4V。利用通用有限元软件ABAQUS建立二维平面应变接触模型,进行准静态分析,如图 6所示,接触区单元尺寸约为10μm,A点的x方向位移即为式(1)中的δ。图示为正压力p=180N/mm并作用切向力Q时带圆角平板接触模型的x方向位移云图。
|
Fig. 6 Distribution of displacement in x direction of flat rounded contact model |
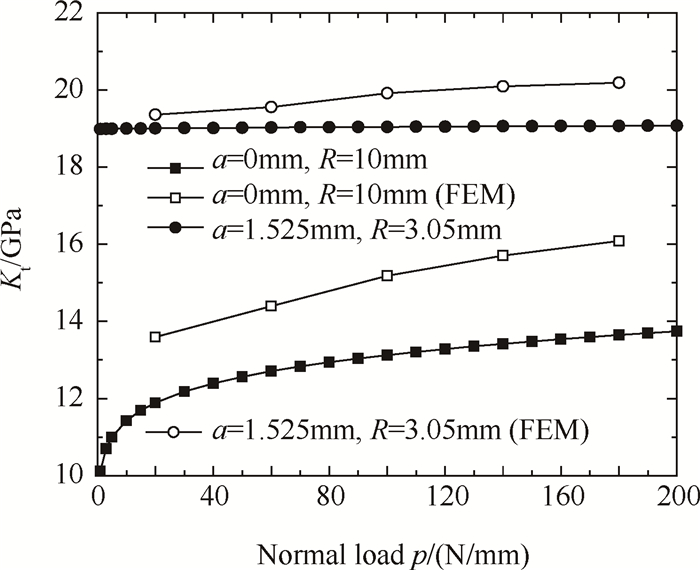
采用有限元法得到的切向接触刚度与式(10)和式(12)计算得到的理论解的对比如图 7所示。对于圆柱与平板接触的情况,图示有限元结果与理论解相比偏高约17.9%,与文献[8]相比,相对误差减小约7.1%,一定程度上验证了利用式(10)和式(12)计算切向接触刚度的可靠度;对于带圆角的平板接触模型,有限元解与理论解较为接近,图示最大相对误差不超过5.9%。
|
Fig. 7 Comparison of results between FEM and analytical method |
与线性迟滞弹簧模型等宏滑动模型不同,微滑动摩擦模型能够描述接触面发生局部相对滑动的现象,具体表现为初始加载阶段摩擦力随着切向相对位移的增大而发生软化。与式(1)相比,文献[18]给出了一种更为简单的微滑动初始加载曲线的通用表达式,其摩擦力初始加载曲线为
| $ \delta \left( Q \right) = \lambda A\left[ {1 - {{\left( {1 - \frac{Q}{{\mu p}}} \right)}^{1/\lambda }}} \right] $ | (17) |
式中A=μp/Kt,λ为实验系数,λA即为图 5所示δ*。
观察式(17)不难发现,系数λ与切向接触刚度有关,具体为
| $ \lambda = \frac{{{K_{\rm{t}}}}}{{{K_{\rm{g}}}}} = \frac{{{{\bar K}_{\rm{t}}}}}{{{{\bar K}_{\rm{g}}}}} $ | (18) |
将式(9)和式(14)代入上式可得
| $ \lambda = \frac{{ - \mathop \smallint \nolimits_{ - 1}^1 \bar p\left( \varphi \right){\rm{ln}}\left| \varphi \right|{\rm{d}}\varphi + {\rm{ln}}\left| {\frac{L}{b}} \right| + \frac{v}{{1 - v}}}}{{{\rm{ln}}2 + {\rm{ln}}\left| {\frac{L}{b}} \right| + \frac{v}{{1 - v}}}} $ | (19) |
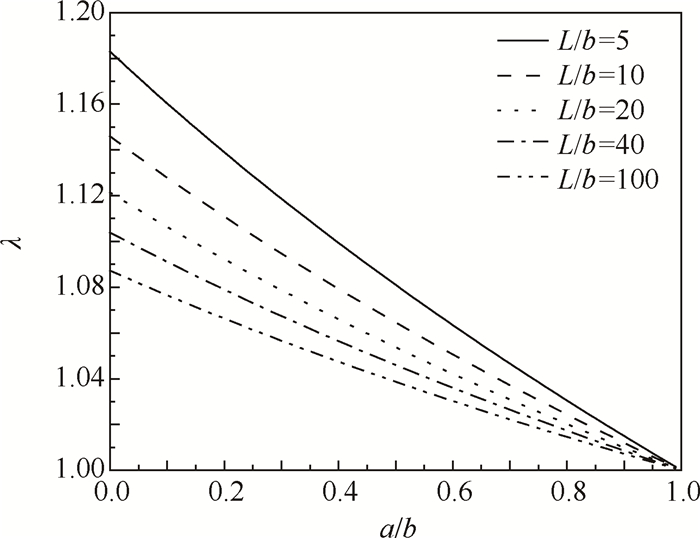
由图 8可以看出,随着阻尼器平直段尺寸和轴向长度的增大,λ的值逐渐减小;对于本文研究的带圆角平板的接触模型,考虑到L >> b,λ的值通常在1.00 ~1.15并始终大于1;当λ = 1时,式(17)退化为线性迟滞弹簧摩擦模型。文献[20]以椭球型弹性体表征接触体粗糙表面,研究摩擦面的微滑动现象,当摩擦方向与椭球长轴垂直时,由迟滞环计算得到λ ≈ 1.03;当摩擦方向与椭球长轴平行时,λ ≈ 1.24,即λ的值约在1.03~1.24,与本文给出的区间大致吻合。
|
Fig. 8 λas a function of a/b and L/b |
当接触面处于微滑动阶段时,根据Masing假设,摩擦力迟滞环可由初始加载曲线获得。具体地,卸载曲线表达式为
| $ {\delta _{\rm{u}}} = - {\delta _0} + 2\lambda A\left[ {1 - {{\left( {1 - \frac{{{Q_0} + Q}}{{2\mu p}}} \right)}^{1/\lambda }}} \right] $ | (20) |
重加载曲线
| $ {\delta _{\rm{r}}} = {\delta _0} - 2\lambda A\left[ {1 - {{\left( {1 - \frac{{{Q_0} - Q}}{{2\mu p}}} \right)}^{1/\lambda }}} \right] $ | (21) |
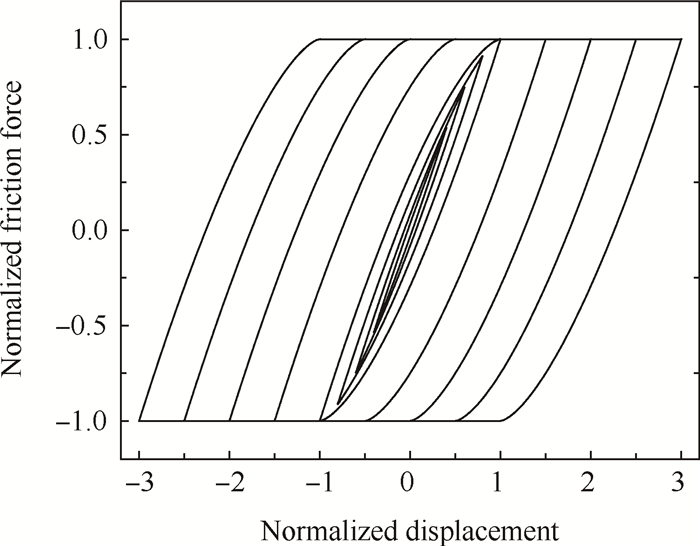
式中δ0和Q0分别为振幅和摩擦力幅值。给定微滑动状态下的振幅,由式(20)和式(21)可得到完整的摩擦力迟滞环。当接触面发生宏滑动时,若认为摩擦力始终保持滑动摩擦力不变,得到的典型摩擦力迟滞环如图 9所示,可以看出,当阻尼器振幅尚未达到宏滑动临界振幅时,摩擦力迟滞环的面积不等于零,此时接触面通过局部的滑动摩擦耗能。
|
Fig. 9 Typical friction hysteresis loops |
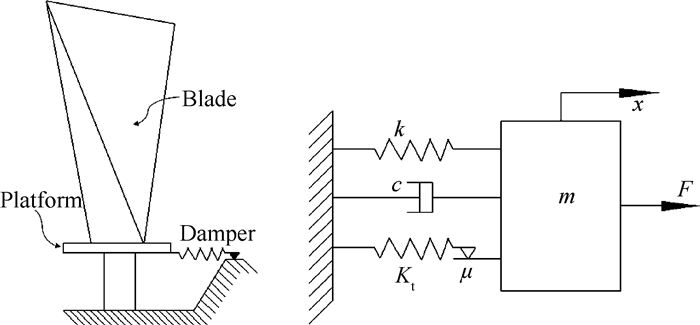
对于工程中常用的B-G型(叶片-基础型)缘板阻尼器分析模型,当考虑叶片的一阶弯曲振动时,可将其模化为单自由度质量-弹簧系统[21, 22],如图 10所示。由文献[23],典型转子叶片单自由度系统的等效参数质量m=20kg,等效弯曲刚度k=1.8×107N/mm。以半圆柱型缘板阻尼器为例,阻尼器与叶片的材料属性见表 1。阻尼器半径R = 2.5mm,长度方向尺寸L = 20mm,单位长度的法向压力p = 20N mm,摩擦系数μ = 0.4。
|
Fig. 10 B-G underplatform damper and its mass spring model |
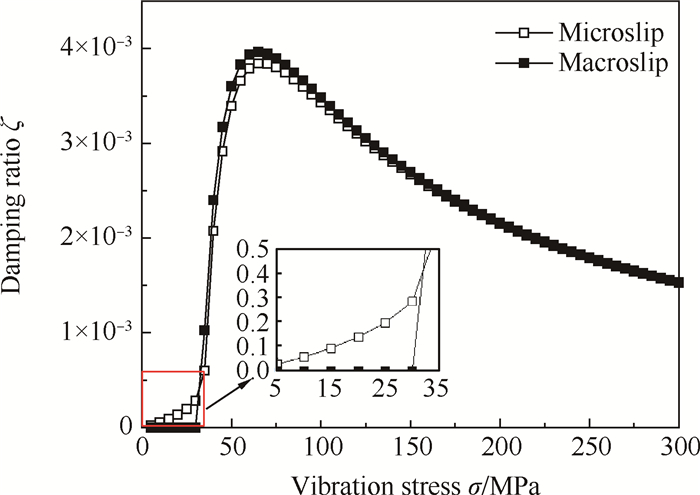
利用式(12)和式(16)可得初始切向接触刚度Kt≈22.4GPa,平均切向接触刚度Kg≈21.1GPa,系数λ≈1.06。设计中常用干摩擦阻尼器所能提供的阻尼比随转子叶片最大振动应力的变化曲线衡量阻尼器的抑振效果。当系统振动频率一定时,叶片最大振动应力与振幅之比为定值。本例得到的微滑动阶段阻尼比特征曲线如图 11所示,可以看出当接触面未发生整体滑动时,与宏滑动模型相比,考虑微滑动的干摩擦阻尼器仍能提供较为可观的阻尼比。
|
Fig. 11 Damping ratio of B-G underplatform damper |
通过本文研究,得出以下结论:
(1)初始切向接触刚度的值仅与接触体的材料属性、阻尼器轴向长度与接触区半宽度的比值L/b有关,平均切向接触刚度还与接触面的压力分布有关。
(2)利用有限元法计算得到的切向接触刚度值与理论解之间的计算误差与文献中有限元解的误差相比减小约7.1%。
(3)所发展的微滑动摩擦模型可以用来计算缘板阻尼器微滑动时提供的阻尼比,且实验系数λ的值随着L/b和a/b的增大而逐渐减小,对于本文研究的带圆角的平板接触模型,λ的值一般在1.00~1.15。
| [1] |
王海飞, 陈果. 考虑多叶片-机匣多点变形转静碰摩模型的机匣响应特征与验证[J]. 推进技术, 2016, 37(1): 128-145. (WANG Hai-fei, CHEN Guo. Casing Response Characteristics and Its Verification Considering Multiple Blades-Casing Multiple Point Deformation Roter-Stator Rubbing Mode[J]. Journal of Propulsion Technology, 2016, 37(1): 128-145.)
(  0) 0) |
| [2] |
Griffin J. Friction Damping of Resonant Stresses in Gas Turbine Engine Airfoils[J]. Journal of Engineering for Gas Turbines and Power, 1980, 102(2): 329-330.
(  0) 0) |
| [3] |
Wang J H, Chen W K. Investigation of the Vibration of a Blade with Friction Damper by HBM[J]. Journal of Engineering for Gas Turbines & Power, 1993, 115(2): 660-664.
(  0) 0) |
| [4] |
Iwan W D. A Distributed-Element Model for Hysteresis and Its Steady-State Dynamic Response[J]. Journal of Applied Mechanics, 1966, 33(4).
(  0) 0) |
| [5] |
陈璐璐, 张大义, 文敏, 等. 带凸肩风扇叶片振动特性及设计方法研究[J]. 推进技术, 2015, 36(9): 1389-1394. (CHEN Lu-lu, ZHANG Da-yi, WEN Min, et al. Dynamical Effects of Shrouds on Fan Blade Vibration and Its Corresponding Design Method[J]. Journal of Propulsion Technology, 2015, 36(9): 1389-1394.)
(  0) 0) |
| [6] |
Siewert C, Panning L, Schmidt-Fellner A, et al. The Estimation of the Contact Stiffness for Directly and Indirectly Coupled Turbine Blading[C]. Reno: ASME Turbo Expo 2006: Power for Land, Sea, and Air, 2006: 841-853. http://www.researchgate.net/publication/267499905_The_Estimation_of_the_Contact_Stiffness_for_Directly_and_Indirectly_Coupled_Turbine_Blading
(  0) 0) |
| [7] |
史亚杰, 朱梓根. 阻尼器切向接触刚度的有限元分析及应用[J]. 航空动力学报, 2009, 24(6): 1292-1298. (  0) 0) |
| [8] |
Szwedowicz J, Kissel M, Ravindra B, et al. Estimation of Contact Stiffness and Its Role in the Design of a Friction Damper[C]. Reno: ASME Turbo Expo 2001: Power for Land, Sea, and Air. 2001. http://www.researchgate.net/publication/267483467_Estimation_of_Contact_Stiffness_and_its_Role_in_the_Design_of_a_Friction_Damper
(  0) 0) |
| [9] |
郝燕平, 朱梓根. 叶片摩擦阻尼器切向刚度研究[J]. 航空动力学报, 2002, 17(4): 426-431. (  0) 0) |
| [10] |
Schwingshackl C W, Petrov E P, Ewins D J. Measured and Estimated Friction Interface Parameters in a Nonlinear Dynamic Analysis[J]. Mechanical Systems & Signal Processing, 2012, 28(2): 574-584.
(  0) 0) |
| [11] |
李一堃, 郝志明, 章定国. 基于六参数非均匀密度函数的伊万模型研究[J]. 力学学报, 2015, 47(3): 513-520. (  0) 0) |
| [12] |
Rajaei M, Ahmadian H. Development of Generalized Iwan Model to Simulate Frictional Contacts with Variable Normal Loads[J]. Applied Mathematical Modelling, 2014, 38(15-16): 4006-4018. DOI:10.1016/j.apm.2014.01.008
(  0) 0) |
| [13] |
Cigeroglu E, Lu W, Menq C H. One-Dimensional Dynamic Microslip Friction Model[J]. Journal of Sound & Vibration, 2006, 292(3): 881-898.
(  0) 0) |
| [14] |
Cigeroglu E, An N, Menq C H. A Microslip Friction Model with Normal Load Variation Induced by Normal Motion[J]. Nonlinear Dynamics, 2007, 50(3): 609-626. DOI:10.1007/s11071-006-9171-4
(  0) 0) |
| [15] |
Menq C H, Bielak J, Griffin J H. The Influence of Microslip on Vibratory Response, Part Ⅰ: A New Microslip Model[J]. Journal of Sound & Vibration, 1986, 107(2): 279-293.
(  0) 0) |
| [16] |
Allara M. A Model for the Characterization of Friction Contacts in Turbine Blades[J]. Journal of Sound & Vibration, 2009, 320(3): 527-544.
(  0) 0) |
| [17] |
Segalman D J, Starr M J. Inversion of Masing Models Via Continuous Iwan Systems[J]. International Journal of Non-Linear Mechanics, 2008, 43(1): 74-80. DOI:10.1016/j.ijnonlinmec.2007.10.005
(  0) 0) |
| [18] |
Marquina F J, Coro A, Guti Rrez A, et al. Friction Damping Modeling in High Stress Contact Areas Using Microslip Friction Model[C]. Reno: ASME Turbo Expo 2008: Power for Land, Sea, and Air. 2008: 309-318.
(  0) 0) |
| [19] |
Mcveigh P A, Harish G, Farris T N, et al. Modeling Interfacial Conditions in Nominally Flat Contacts for Application to Fretting Fatigue of Turbine Engine Components[J]. International Journal of Fatigue, 1999, 21(99): 157-165.
(  0) 0) |
| [20] |
Olofsson U, Hagman L. A Model for Micro-Slip between Flat Surfaces Based on Deformation of Ellipsoidal Elastic Bodies[J]. Tribology International, 1997, 30(8): 599-603. DOI:10.1016/S0301-679X(97)00028-5
(  0) 0) |
| [21] |
Wang J H, Chen W K. Investigation of the Vibration of a Blade with Friction Damper by HBM[J]. Journal of Engineering for Gas Turbines & Power, 1992, 115(2): 660-664.
(  0) 0) |
| [22] |
Chen Yu-Di, Wang Yan-Rong. A Method for the Resonant Response Evaluation of Blades System with Underplatform Dampers [C]. China: International Conference Vibroengineering, 2014.
(  0) 0) |
| [23] |
陈毓迪. 带冠叶片阻尼模型与振动特性分析[D]. 北京: 北京航空航天大学, 2014.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


