2. 哈尔滨工业大学 基础与交叉科学研究院,黑龙江 哈尔滨 150001
2. Academy of Fundamental and Interdisciplinary Sciences, Harbin Institute of Technology, Harbin 150001, China
近年来,随着航空航天技术的迅速发展,发动机推力与飞行器速度迅速提升[1]。高温燃烧及气动加热所带来的热防护问题已经成为备受关注的研究焦点之一[2, 3]。以涡轮发动机为例,下一代发动机的设计指标已经达到2400K的水平[4, 5]。在冷却需求节节攀升的情况下,飞行器核心部件需求更高效的冷却技术来进行热防护。
发汗冷却相比对流冷却、冲击冷却及膜冷却等常规主动冷却方式,冷却效率更高[6],具有更好的覆盖性及可控性[7],是先进主动热防护系统的备选技术之一[8]。目前发汗冷却的研究有许多分支,大体可分为如下几个方面:
在冷却剂方面,Zhao等[9]开展了液态水为冷却剂的发汗冷却实验研究;李青等[10]对氢气在多孔陶瓷内的发汗冷却过程进行了研究;Huang等[11]使用航空煤油作为冷却介质,在马赫数2.8的条件下通过实验研究了激波对发汗冷却的影响规律。
在结构方面,Jiang等[12]对支板发汗冷却进行了实验研究,冷却剂可以有效地保护支板不被烧蚀;Arai等[13]对多孔陶瓷涂层进行了发汗冷却实验研究,结果表明其拥有优异的渗透性;石小祥等[14]提出一种用于发汗冷却的六边形冷却孔排布结构,结果表明该种结构能有效提高平均冷却效率;谭晓茗等[15]使用红外热成像技术研究了发汗孔板出流孔复合角对冷却效率的影响。
在理论方面,Jiang等[16]对多孔介质局部非热平衡模型进行了分析研究;Lindner等[17]则使用局部非热平衡模型对发汗冷却中的相变过程进行了研究;Aybar等[18]对带多孔壁面的圆管内的壁面加质流动进行了数学建模;Lachaud等[19]提出了一种全新的多孔介质局部热平衡模型。
总体上看,有发汗冷却的研究关注点主要集中在液态及气态冷却剂,支板等发汗冷却结构,多孔介质换热模型。本文研究侧重于冷却剂流动及加质壁面边界层流动,以氮气作为冷却介质,使用金属烧结多孔介质进行发汗冷却实验,结合数值模拟研究注入率对多孔介质壁面温度及冷却效率的影响规律,通过实验和模拟结合的方式对发汗冷却过程中边界层的变化规律进行了研究。
2 实验装置及测量方法 2.1 实验装置及材料实验装置如图 1所示,由金属基底和氟化钙风道两部分组成。金属基底使用致密不锈钢材料制成,并在基底平板中央设置有长60mm,宽10mm,深5mm的槽道,用于将多孔介质实验材料固定于基底平板上。实验段风道与上游风道采用方形法兰连接以确保气密性。
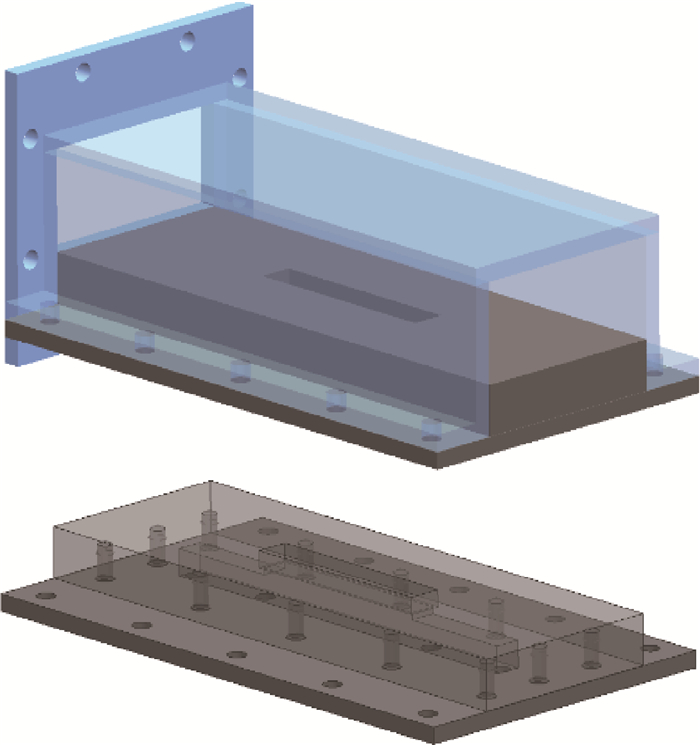
|
Fig. 1 Configuration of experimental device |
金属基底又分为上半平板和下半平板两个部分,并使用螺栓对上下两部分进行连接并实现密封。上半平板内部设置有冷却剂腔室,下半平板设置有冷却剂注入口和测温测压口。冷却剂由下半平板的注入口进入上半平板的冷却剂腔室,最后由压差的驱动下渗透多孔介质达到热端表面。
实验采用金属颗粒烧结多孔材料,其整体形态如图 2所示。金属颗粒成分06Cr17Ni12Mo2,其微观形态如图 3所示。决定该多孔材料性能的核心参数如下:平均粒径15μm,孔隙率0.25,比表面积3×105/m。

|
Fig. 2 Experimental sample of metal sintered porous materials |

|
Fig. 3 SEM photo of metal sintered porous materials |
多孔材料单吹法测试显示体积流量随压力梯度的变化呈线性关系,如图 4所示,方差为0.994,线性程度高,材料具有良好且稳定的渗透性能。
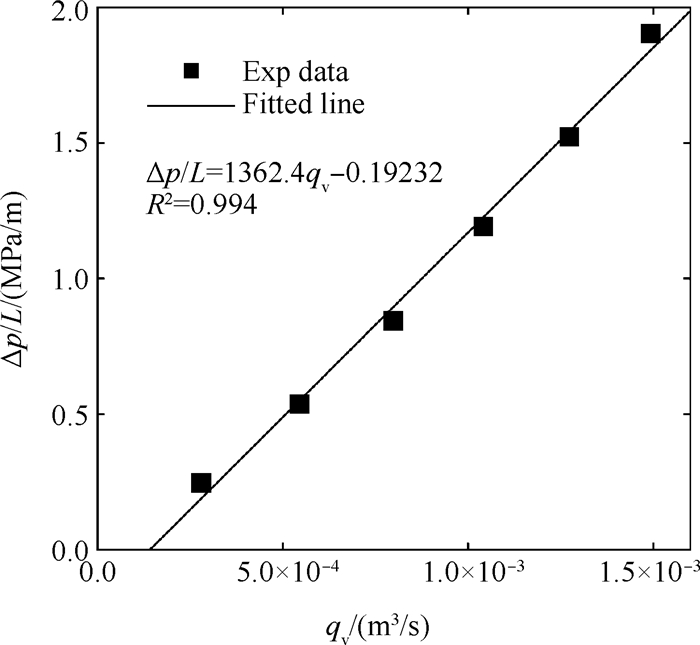
|
Fig. 4 Relationship between pressure gradient and volume flow |
实验系统如图 5所示,电加热功率3kW,主流雷诺数1.35×105,来流总温373K,该条件下可进行长时间加热试验,可确保采集到的实验数据处于热平衡状态下。加热空气经过蜂窝状稳流器后形成流量均匀的来流,充分发展的来流进入实验段透明矩形风洞并对实验件表面进行加热。
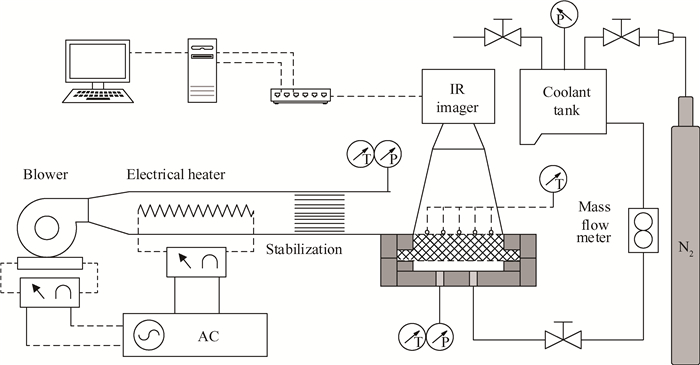
|
Fig. 5 Sketch of experimental system |
主流温度、冷却剂温度、发汗表面校核点温度采用K型热电偶进行测量,并采用冰瓶校正。多孔介质发汗表面温度采用FLIR SC660型红外热像仪进行测量,并通过热电偶测量数据进行校正。冷却剂压力采用Micro Sensor MPM489型绝压变送器进行测量。冷却剂流量采用Sevenstar D07型质量流率计进行控制。主流速度采用国标JJG518-98 L型皮托管进行测量。采用NI cRIO-9073高速采集系统进行数据采集。
冷却剂由高压氮气瓶进行供给,经由减压阀降压至0.3MPa后进入稳压箱中。从稳压箱中流出的氮气经由质量流量控制器后进入冷却剂腔室,并通过多孔介质注入到主流当中。
2.3 实验数据处理本文研究中,使用注入率来衡量冷却剂的使用量,注入率定义为
| $F = \frac{{{\rho _{\rm{c}}}{u_{\rm{c}}}}}{{{\rho _\infty }{u_\infty }}}$ | (1) |
式中ρc为冷却剂密度,uc为冷却剂速度,ρ∞为主流密度,u∞为主流速度。冷却剂在多孔介质内流动的平均速度为达西速度。主流及冷却剂密度由测量得到的温度与压力通过NIST数据库得出。
对于发汗表面,平均冷却效率定义为式(2),无量纲冷却效率范围为0~1,数值越大则冷却效果越好。
| $\eta = \frac{{{t_\infty } - {t_{\rm{w}}}}}{{{t_\infty } - {t_{\rm{c}}}}}$ | (2) |
式中tw为多孔材料上壁面平均温度,t∞为主流温度,tc为冷却剂温度。
对于局部位置,局部冷却效率定义为
| $\eta = \frac{{{t_{{\rm{iw}}}} - {t_{{\rm{cw}}}}}}{{{t_\infty } - {t_{\rm{c}}}}}$ | (3) |
式中tiw和tcw分别为局部位置没有冷却剂注入时的表面温度与冷却剂注入后的表面温度。当局部位置扩大为整个发汗表面,局部冷却效率与平均冷却效率等效。
3 实验结果与分析本文研究了不同注入率条件下发汗冷却的效果。图 6给出了在注入率分别为5.42%,10.75%,16.24%,21.81%,27.64%及33.50%时红外热像仪所记录的多孔介质热端表面温度分布。
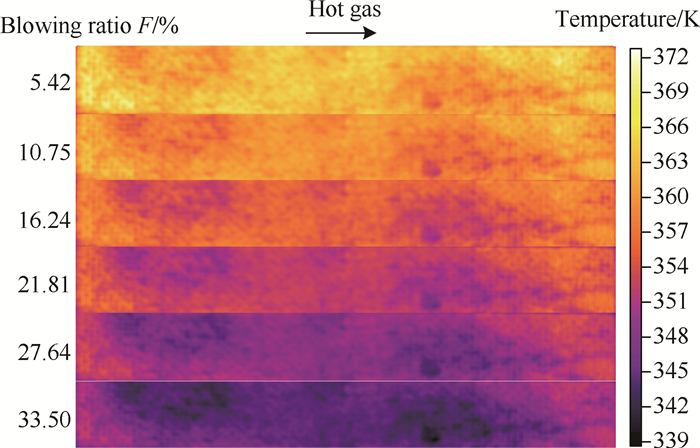
|
Fig. 6 Temperature distributions of the porous surface |
图像显示,氮气的注入率直接影响了表面温度分布,随着氮气注入率的增大,表面温度呈下降趋势。无氮气注入时,表面的平均温度趋近于主流温度。当氮气注入率逐步增加,热端表面平均温度分别为364.4K,360.9K,356.6K,353.0K,349.1K和345.9K。温度降低的幅度与注入率呈线性变化趋势。在冷却剂压力保持均匀稳定的条件下,图 6中表面温度分布存在一定的不均匀性,这是由于材料表面颗粒分布因有限的加工工艺而存在不均匀性,但冷却效率的分析结果显示整体规律没有受到影响。
图 7给出了平均冷却效率随注入率的变化趋势,并同时给出了最高温度、最低温度及平均温度。冷却效率均随着注入率的增大呈线性上升的规律。当注入率为33.5%时,平均冷却效率可达到45%。随着注入率的增大,冷却效率的增幅逐渐减小。
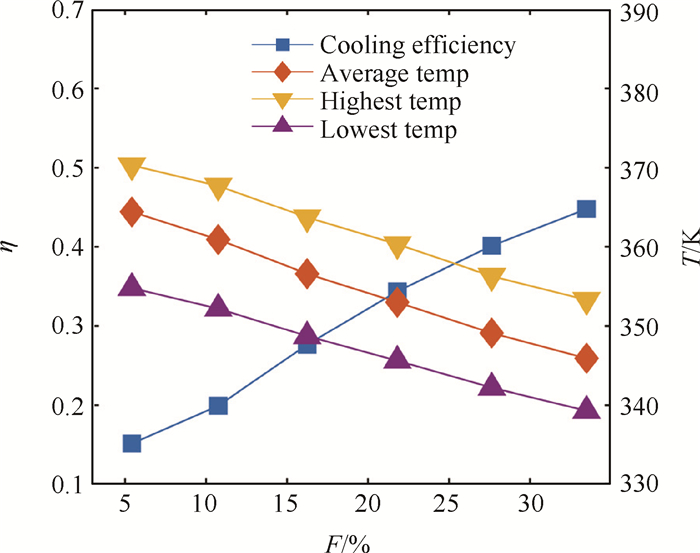
|
Fig. 7 Average cooling efficiencies and temperatures |
从温度的角度来看,发汗表面的最高温度、最低温度及平均温度的趋势是一致的。发汗表面大部分区域的温度都趋近于表面平均温度。在低注入率和高注入率下,最高温度和最低温度的温差都在10K左右。虽然由于多孔介质加工工艺导致壁面温度存在一定的不均匀性,但无论最高温度还是最低温度的变化规律均符合壁面温度的平均规律。
沿来流方向,发汗表面的冷却效率也有一定变化。图 8展示了不同注入率下的局部冷却效率随位置的变化规律。
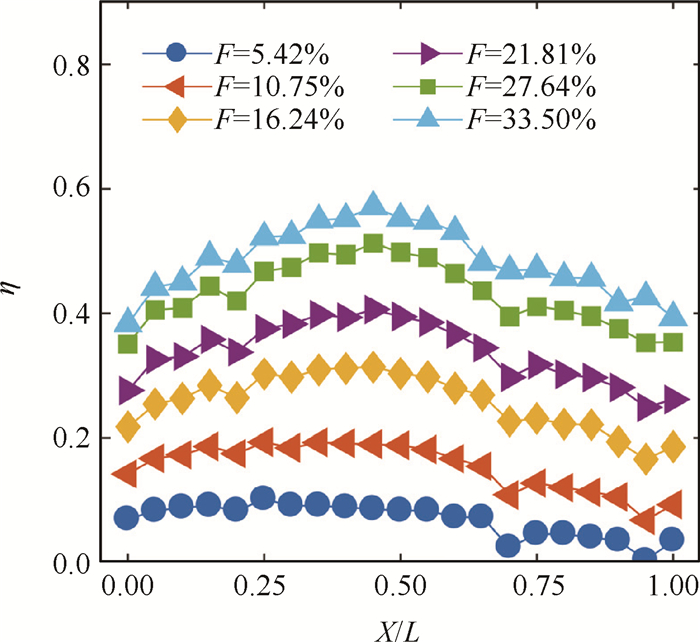
|
Fig. 8 Local cooling efficiencies |
多孔介质上游(X/L < 0.5)表面的冷却效率沿程增加,这是多孔介质表面的加质流动产生的效果。随着冷却剂的注入,多孔介质表面的边界层沿着来流方向不断增厚,温度边界层也在增厚,壁面热流强度下降,冷却效率不断上升。
多孔介质上游(X/L > 0.5)表面的冷却效率出现回落,并且区域平稳。在这段区域内,边界层厚度在区域稳定的情况下不再对冷却效率产生剧烈影响,未冷却的金属基底对多孔介质固体部分热传导的影响开始凸显出来,使得冷却效率较上游部分出现下降。
4 模拟结果与分析本文所采用二维计算区域如图 9所示,由主流通道,多孔介质区域与冷却腔三部分组成。计算区域采用结构化网格划分。在多孔介质与主流交界面、主流壁面附近进行局部加密以满足边界层计算的要求。网格数量12万,验证满足网格无关性要求。主流入口及出口均延伸一定距离,以避免入口和出口效应对模拟结果的影响。
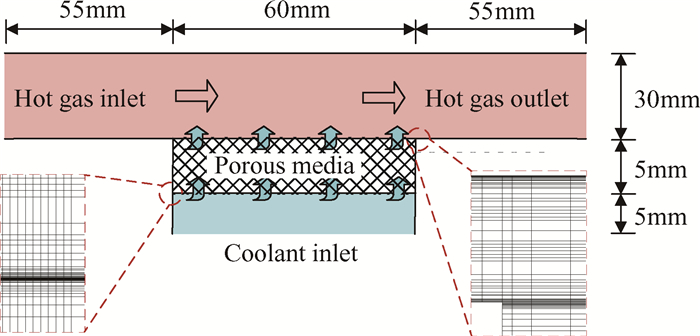
|
Fig. 9 Physical model for simulation |
本文采用局部非热平衡模型和局部热平衡模型对多孔介质内的换热进行模拟。
局部热平衡模型如式(4)所示,为单温度方程。当使用此模型时,多孔介质内金属骨架的温度和内部流体的温度被考虑为同一个温度,忽略了金属骨架和流体之间的换热。
| $\begin{array}{*{20}{l}} {\frac{\partial }{{\partial t}}\left( {\varepsilon {\rho _{\rm{f}}}{E_{\rm{f}}} + \left( {1 - \varepsilon } \right){\rho _{\rm{s}}}{E_{\rm{s}}}} \right) + \nabla \cdot \left( {\nabla \left( {{\rho _{\rm{f}}}{E_{\rm{f}}} + p} \right)} \right) = }\\ {\;\;\;\;s_{\rm{f}}^h + \left[ {{k_{{\rm{eff}}}}\nabla T - \left( {\sum\limits_i {{h_i}{J_i}} } \right) + \left( {\overline {\bar \tau } \cdot v} \right)} \right]} \end{array}$ | (4) |
局部非热平衡模型如式(5)所示,为双温度方程。当使用此模型时,多孔介质内金属骨架的温度和内部流体的温度被分别考虑,此时还需要补充多孔介质内部的换热关联式,本文采用Xu等[20]提出的换热关联式进行计算,如式(6)所示。
| $\left\{ {\begin{array}{*{20}{l}} {\frac{\partial }{{\partial t}}\varepsilon \left( {{\rho _{\rm{f}}}{E_{\rm{f}}}} \right) + \nabla \cdot \left( {v\left( {{\rho _{\rm{f}}}{E_{\rm{f}}} + p} \right)} \right) = }\\ {\nabla \cdot \left( {\varepsilon {k_{\rm{f}}}\nabla {T_{\rm{f}}} - \left( {\sum\limits_i {{h_i}{J_i}} } \right) + \left( {\overline {\bar \tau } \cdot v} \right)} \right) + }\\ {S_{\rm{f}}^h + {h_{{\rm{fs}}}}{A_{{\rm{fs}}}}\left( {{T_{\rm{f}}} - {T_{\rm{s}}}} \right)}\\ {\frac{\partial }{{\partial t}}\left( {\left( {1 - \varepsilon } \right){\rho _{\rm{s}}}{E_{\rm{s}}}} \right) = }\\ {\nabla \cdot \left( {\left( {1 - \varepsilon } \right){k_{\rm{s}}}\nabla {T_{\rm{s}}}} \right) + S_{\rm{s}}^h + {h_{{\rm{fs}}}}{A_{{\rm{fs}}}}\left( {{T_{\rm{s}}} - {T_{\rm{f}}}} \right)} \end{array}} \right.$ | (5) |
| $N{u_{{\rm{sf}}}} = \left( {0.933{\varepsilon ^2} - 0.245\varepsilon + 0.0165} \right)R{e_{\rm{d}}}^{0.8}P{r^{\frac{1}{3}}}$ | (6) |
实验数据与两种模型的模拟结果对比如图 10所示。在本文研究的注入率范围内,由局部非热平衡模型得出的冷却效率可以和实验数据达到较好的吻合。而局部热平衡模型没有考虑多孔介质内金属骨架和流体之间的换热,远远低估了发汗冷却的冷却效率。
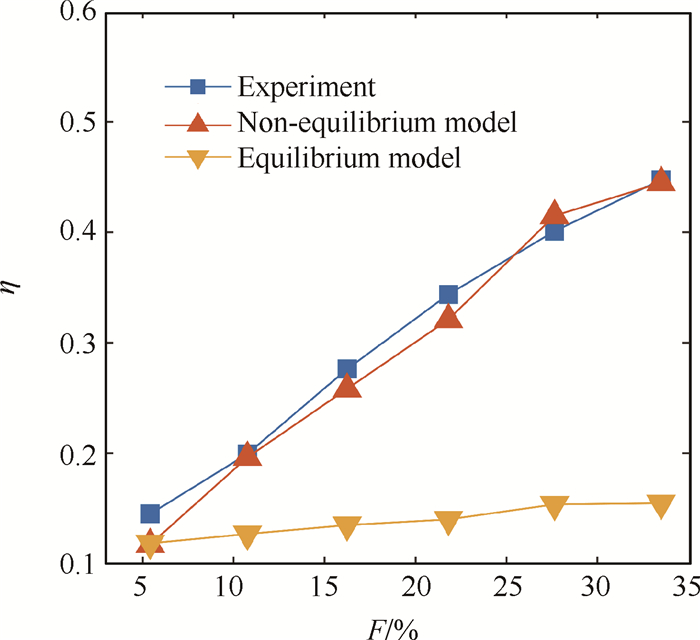
|
Fig. 10 Comparison of cooling efficiencies between experimental results and numerical calculations |
图 11给出了使用局部非热平衡模型的条件下,注入率分别为5.42%,16.24%及33.49%时的温度分布。由图可见随着冷却剂注入率的增大,多孔介质内部的温度显著下降。在注入率为33.49%时,可以看到多孔介质形成了明显的低温膜层。冷却剂膜层随注入率的增加而增厚,这是加质壁面流动中边界层增厚的现象。图像显示冷却剂膜层对下游非多孔介质区域的壁面也可以起到一定的冷却效果。
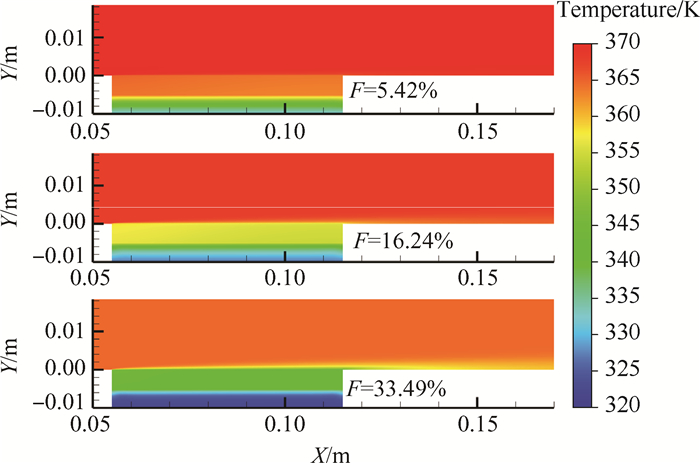
|
Fig. 11 Temperature distributions in the simulations |
在图 11的温度场显示,同一注入率下多孔壁面边界层沿来流方向增厚,不同注入率下注入率越高边界层越厚。图 12和图 13从边界层内的速度分布分别讨论了同一注入率和不同注入率下的规律。
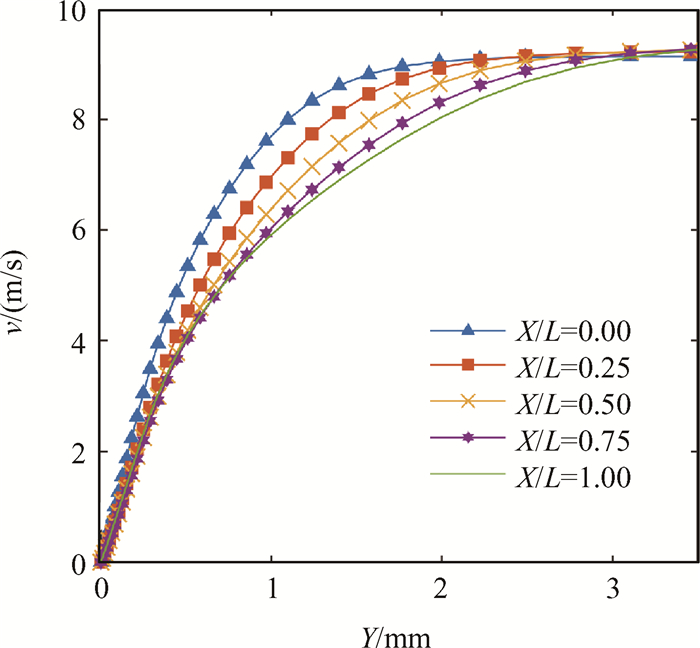
|
Fig. 12 Velocity distributions under the blowing ratio 33.49% |
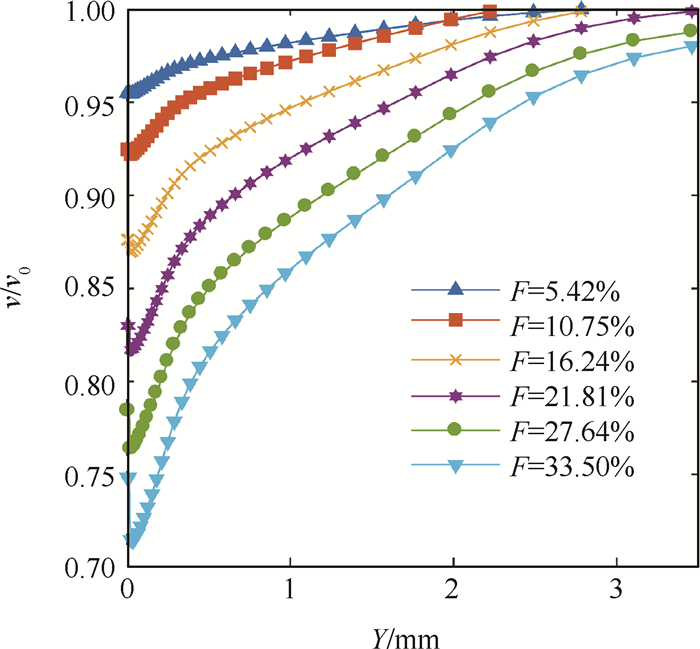
|
Fig. 13 Velocity distributions at the position X/L=1 |
当注入率为33.49%时,多孔壁面在X/L=0,0.25,0.5,0.75,1五个位置的边界层内的速度分布如图 12所示。X/L=0代表多孔壁面最靠近上游的位置,X/L=1代表多孔壁面最靠近下游的位置。图 12显示在X/L=0位置,边界层厚度约为1.5mm,而在X/L=1的位置边界层厚度超过了3mm。在下游位置,多孔壁面边界层有了明显的增厚,这对提升冷却效率起到了积极的作用。
当考察不同注入率下边界层的变化时,本文采用了速度比的方式来进行考量。没有冷却剂注入时边界层内流体的速度为v0,当存在冷却剂注入时为v,定义速度比为v/v0,速度比越小则边界层增厚的效果越明显。
仅关注X/L=1的位置,不同注入率下多孔壁面边界层内的速度比如图 13所示。随着注入率的增加,速度比在粘性底层出现显著的下降,最低接近0.7,边界层由于冷却剂的注入被推厚的效果显著。不同注入率之间速度比的变化间距较为稳定,这和图 10中冷却效率变化呈现线性规律是一致的。
5 结论本文在雷诺数1.35×105和总温373K的来流条件下,对金属烧结多孔介质平板发汗冷却进行实验和模拟研究,得出如下结论:
(1)以氮气为冷却剂的发汗冷却可以提供良好的冷却效果,当注入率为33.5%时平均冷却效率接近0.45。
(2)多孔壁面平均冷却效率随注入率的增大而提升,冷却效率与注入率之间呈线性变化趋势。
(3)局部非热平衡模型在考虑多孔介质金属骨架和流体之间的换热的前提下,能准确还原发汗冷却过程。
(4)同一注入率下多孔壁面边界层沿来流方向增厚,不同注入率下注入率越高边界层越厚。边界层增厚对提升冷却效率起到了积极的作用。
本研究在低焓来流条件下进行,将在后续的研究中开展高焓来流条件下的发汗冷却实验。
| [1] |
Fry R S. A Century of Ramjet Propulsion Technology Evolution[J]. Journal of Propulsion and Power, 2014, 20(1): 27-58.
(  0) 0) |
| [2] |
Bouchez M, Dufour E, Cheuret F, et al. Multi-Level Coupled Simulations of Cooled Structures in the ATLLAS European Program[C]. Bremen: 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, 2009.
(  0) 0) |
| [3] |
Osipov V, Hafiychuk H, Devine E, et al. Risk Assessment and Scaling for the SLS LOx ET[R]. NASA/TP-2012-216485.
(  0) 0) |
| [4] |
Mohammed I, Talib A R A, Sultan M T H, et al. Temperature and Heat Flux Measurement Techniques for Aeroengine Fire Test: A Review[J]. Series: Materials Science and Engineering, 2016, 152(1): 012036.
(  0) 0) |
| [5] |
Young J B, Wilcock R C. Modeling the Air-Cooled Gas Turbine, Part 1: General Thermodynamics[J]. Journal of Turbomachinery, 2002, 124(2): 207-213. DOI:10.1115/1.1415037
(  0) 0) |
| [6] |
Song K D, Sang S H, Scotti S J. Transpiration Cooling Experiment for Scramjet Engine Combustion Chamber by High Heat Fluxes[J]. Journal of Propulsion and Power, 2006, 22(1): 96-102. DOI:10.2514/1.11300
(  0) 0) |
| [7] |
Reimer T, Kuhn M, Gülhan A, et al. Transpiration Cooling Tests of Porous CMC in Hypersonic Flow[C]. San Francisco: 17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, 2011. http://arc.aiaa.org/doi/abs/10.2514/6.2011-2251
(  0) 0) |
| [8] |
Schwanekamp T, Meyer F, Reimer T, et al. System Studies on Active Thermal Protection of a Hypersonic Suborbital Passenger Transport Vehicle[C]. Atlanta: 19th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, 2014.
(  0) 0) |
| [9] |
Zhao L, Wang J, Ma J, et al. An Experimental Investigation on Transpiration Cooling under Supersonic Condition Using a Nose Cone Model[J]. International Journal of Thermal Sciences, 2014, 84(4): 207-213.
(  0) 0) |
| [10] |
李青, 孙纪国. 多孔陶瓷氢气发汗冷却特性研究[J]. 推进技术, 2014, 35(10): 1387-1391. (LI Qing, SUN Ji-guo. Experimental Investigation of Transpiration Cooling Through Porous Ceramics Using Hydrogen[J]. Journal of Propulsion Technology, 2014, 35(10): 1387-1391.)
(  0) 0) |
| [11] |
Huang Z, Zhu Y H, Xiong Y B, et al. Investigation of Transpiration Cooling for Sintered Metal Porous Struts in Supersonic Flow[J]. Applied Thermal Engineering, 2014, 70(1): 240-249. DOI:10.1016/j.applthermaleng.2014.02.076
(  0) 0) |
| [12] |
Jiang P X, Huang G, Zhu Y, et al. Experimental Investigation of Combined Transpiration and Film Cooling for Sintered Metal Porous Struts[J]. International Journal of Heat and Mass Transfer, 2017, 108: 232-243. DOI:10.1016/j.ijheatmasstransfer.2016.12.014
(  0) 0) |
| [13] |
Arai M, Suidzu T. Porous Ceramic Coating for Transpiration Cooling of Gas Turbine Blade[J]. Journal of Thermal Spray Technology, 2013, 22(5): 690-698. DOI:10.1007/s11666-013-9883-1
(  0) 0) |
| [14] |
石小祥, 胡好生, 杨卫华, 等. 弯曲壁面冲击加发散冷却结构的冷却效果实验研究[J]. 推进技术, 2017, 38(3): 630-636. (SHI Xiao-xiang, HU Hao-sheng, YANG Wei-hua, et al. Experimental Investigation on Cooling Performance of Impingement/Effusion Cooling Structures on Concave Wall[J]. Journal of Propulsion Technology, 2017, 38(3): 630-636.)
(  0) 0) |
| [15] |
谭晓茗, 赵乃芬, 房人麟, 等. 出流孔复合角对发散孔板冷却效率的影响研究[J]. 推进技术, 2016, 37(6): 1092-1097. (TAN Xiao-ming, ZHAO Nai-fen, FANG Ren-lin, et al. Research on Cooling Characteristics of Effusion Wall with Compound Angle[J]. Journal of Propulsion Technology, 2016, 37(6): 1092-1097.)
(  0) 0) |
| [16] |
Jiang P X, Ren Z P. Numerical Investigation of Forced Convection Heat Transfer in Porous Media Using a Thermal Non-Equilibrium Model[J]. International Journal of Heat and Fluid Flow, 2001, 22(1): 102-110. DOI:10.1016/S0142-727X(00)00066-7
(  0) 0) |
| [17] |
Lindner F, Nuske P, Weishaupt K, et al. Transpiration Cooling with Local Thermal Nonequilibrium: Model Comparison in Multiphase Flow in Porous Media[J]. Journal of Porous Media, 2016, 19(2): 131-153. DOI:10.1615/JPorMedia.v19.i2
(  0) 0) |
| [18] |
Aybar H S, Faridani M M. Mathematical Modeling of Transpiration Cooling in Cylindrical Domain[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2015, 229(7): 1310-1324. DOI:10.1177/0954410014550049
(  0) 0) |
| [19] |
Lachaud J, Scoggins J B, Magin T E, et al. A Generic Local Thermal Equilibrium Model for Porous Reactive Materials Submitted to High Temperatures[J]. International Journal of Heat and Mass Transfer, 2017, 180: 1406-1417.
(  0) 0) |
| [20] |
Xu R N, Huang Y L, Jiang P X, et al. Internal Heat Transfer Coefficients in Microporous Media with Rarefaction Effects[J]. Science China Technological Sciences, 2012, 55(10): 2869-2876. DOI:10.1007/s11431-012-4994-3
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


