随着作战飞机飞行速度、高度的不断提高,机动性的不断增加,隐身性要求的不断提高,航空发动机无一例外必须在畸变进气条件下工作,进口气流的不均匀会降低压气机稳定性,飞行安全受到极大影响。因此,分析畸变进气下压气机动态失稳过程特征和机制,进而为压气机稳定性控制方法提供依据,对提高发动机稳定工作裕度,增强飞行安全具有重要意义。
旋转失速是压气机进入不稳定工作状态的一个重要因素,在对其机理的研究和探索中发现了模态波型和突尖型两种主要的失速先兆类型。Moore和Greitzer [1, 2]从压缩系统稳定性角度出发,建立了描述旋转失速和喘振动态过程及其特性的二维非定常不可压缩非线性模型,Moore-Greitzer模型导致了模态波型失速先兆的发现,其成果为压缩系统稳定性研究发展奠定了重要的理论基础。而突尖型失速先兆则最早由Day [3]在试验中发现。对突尖型失速先兆目前认可度较高的理论包括叶尖泄漏流“前缘溢流”和“尾缘倒流”的突尖型失速先兆判定准则[4, 5],以及叶片前缘分离造成的“龙卷风涡”流动结构引起的低压区在叶顶附近传播的突尖产生机制[6, 7]等。
畸变进气下压气机稳定性分析方面,研究人员发展了平行压气机模型[8]、激盘模型[9]以及三维彻体力模型[10~12]等多种模型,这些模型在预测进气畸变对压气机性能和稳定边界的影响、畸变传递特性等方面有一定的优势,但对更为根本的畸变进气诱发流动失稳的物理机制往往力不从心。Lin等[13, 14]在Moore-Greitzer模型基础上进行扩展,将畸变网与压缩系统看作一个整体,首次对总压畸变条件下失稳的触发机制进行了理论分析,模型结果很好地符合了实验中失速先兆长尺度扰动向短尺度扰动的转化的现象。Salunkhe等[15]利用小波变换研究一单级轴流风扇的失速先兆触发机制,发现在均匀进气和反向旋转畸变进气下由短尺度扰动触发,在静态和同向旋转畸变进气下由长尺度扰动触发。蒋华兵等[16]探讨了插板总压畸变对单级低速轴流压气机失速形式、失速强度、失速频率的影响,失速扰动经历形成、发展、衰减甚至消失的过程。张明明等[17]通过全周CFD数值模拟再现了畸变进气下压气机旋转失速现象,发现旋转失速临近时一阶模态幅值灵敏度显著增大,该特征可作为系统失速预警先兆。可见,畸变进气影响下压气机动态失速特征和失稳触发机制比均匀进气更加复杂,还需进行广泛深入的研究探讨。
由于畸变进气下动态失速信号具有非线性、非稳态的复杂特性,对数据处理方法提出了较高的要求。小波变换是一种时频分析方法,在非平稳数据分析中具有较大的优势,已被众多研究者用于压气机动态失速特性的分析[6, 14, 15, 18~22],但受制于小波系数谱能量发散问题,其能量分布范围较宽且边界较模糊,难以精确地得到动态失速过程中各种扰动的时频特征,因此有必要进行更先进的数据分析方法的应用探索。
本文进行了均匀进气和周向畸变条件下压气机动态失速过程实验。采用常规的时域观察、频域快速傅里叶变换(Fast Fourier Transform,FFT),以及同步压缩小波变换[23](Synchrosqueezed wavelet transforms,SWT)、基于SWT变换的空间模态分析和小波相干性等三种较新的时频域分析方法,对动态失速特性进行分析。通过文献[13]压气机集总系统模型对比实验结果,分析了周向畸变进气下压气机动态失速特征的产生机制。
2 实验装置及测量方法 2.1 大尺寸低转速压气机试验台实验在中国空气动力研究与发展中心高速所大尺寸低转速压气机试验台上完成,图 1为试验台结构示意图。试验台主要由变频电机、增速箱、测扭器和1.5级压气机组成。试验台压气机设计参数见表 1。实验中压气机物理转速为1440r/min,该实验转速下压气机最大压比约1.04。
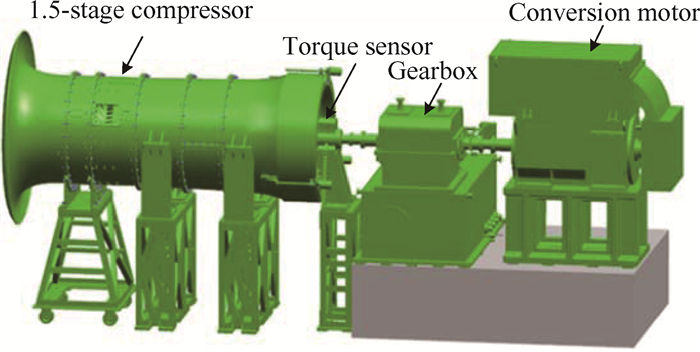
|
Fig. 1 Experiment rig structure diagram |
|
|
Table 1 Design parameters of tested compressor |
周向畸变进气实验采用了180°周向总压畸变网,其主要由支撑网架和细网组成。支撑网架通过整流罩前端的连接座安装于试验台进气钟口前端。畸变进气条件下进行了两种畸变网位置实验,位置1阻塞区位于钟口下半部,位置2阻塞区位于钟口右半部。
2.3 测试系统压气机主要设置有5个测量截面,如图 2所示。0~4各截面外壁面周向均布4个静压测点,1截面周向均布8支五点梳状总压探针,4截面周向均布4支五点梳状总压探针。压气机扭矩和转速由Torquemeters公司ET2700型测扭器获取。动态失速过程的压力信号通过2截面外壁面周向11个XCQ-062型Kulite高频动态压力传感器获得。传感器周向布局如图 3所示,S1~S11相邻传感器间隔30°,S11和S1之间为光学视窗位置故未设传感器。通过试验台增速箱输出轴上的键相槽和磁电式传感器获取每转一个脉冲的锁相信号。动态压力信号和锁相信号通过DEWETRON数据采集系统同步采集,采样频率为20kHz。
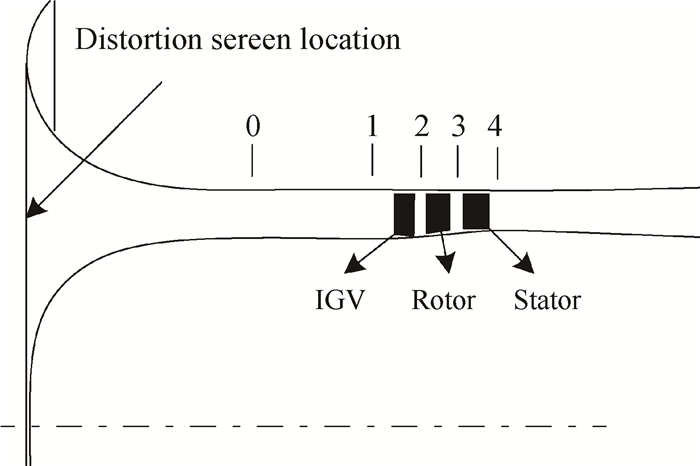
|
Fig. 2 Compressor measurement section |
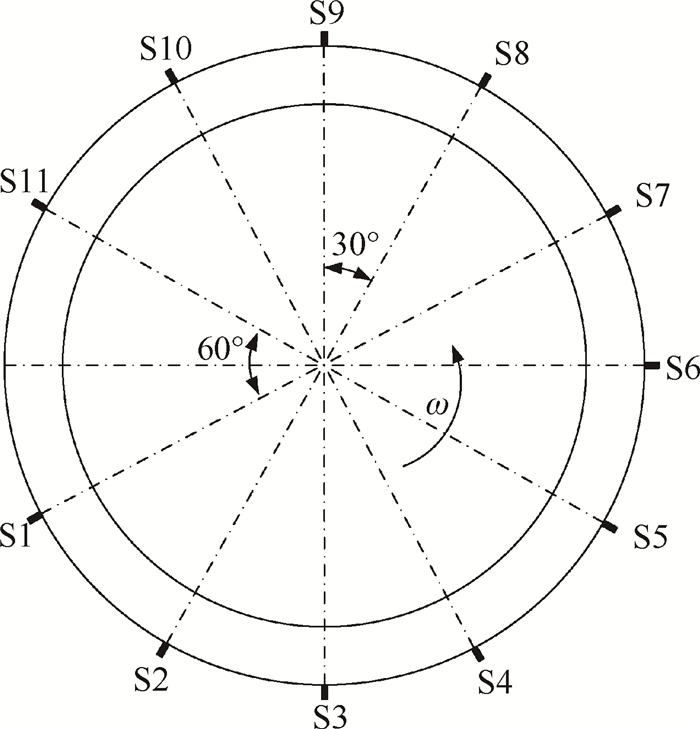
|
Fig. 3 Circular arrangement of dynamic pressure sensors |
通过提取锁相信号峰值,将原始信号由时间序列转换为转子转数序列,在保证足够的分析频率下,为降低数据量,以16倍叶片通过频率(Blade Pass Frequency,BPF),即592frot(转子转动频率)对信号进行了阶比重采样。
对预处理后的动态压力信号首先采用时域观察和频域FFT变换分析,而后采用SWT变换、基于SWT的空间模态分析和小波相干性等三种较新的时频域方法进行分析。下面给出本文时频域分析方法的介绍。
3.1 SWT变换SWT变换是近年来新出现的一种时频分析方法,由Daubechies [23]提出。它是在小波时频变换的基础上,根据信号各组成分量的时频特征,压缩重组时频曲线,达到提高时间和频率分辨率的目的。SWT变换主要包括以下几个步骤:
(1)连续小波变换。SWT变换首先对信号x(t)进行连续小波变换,得到小波系数Wx(a, b),计算公式为
| $ {W_x}\left( {a, b} \right) = \int_{ - \infty }^\infty {x\left( t \right){a^{ - 1/2}}{\psi ^{\rm{*}}}\left( {\frac{{t - b}}{a}} \right){\rm{d}}t} $ | (1) |
式中a为尺度,b 为平移因子,ψ为小波母函数,“*”表示共轭。
本文选取的小波母函数为Morlet小波,具有相对良好的时间聚集性、较高的频率分辨率并包含相位信息,在动态失速信号分析中应用较为广泛[19]。Morlet小波是一种单频复正弦调制高斯波,其时域和频域的表达式分别为
时域:
| $ \psi \left( t \right) = {\pi ^{ - 1/4}}{{\rm{e}}^{{\rm{i}}{\omega _0}t}}{{\rm{e}}^{ - {t^2}/2}}, {\omega _0} \ge 5 $ | (2) |
频域:
| $ \hat \psi \left( \omega \right) = {\pi ^{ - 1/4}}\sqrt 2 {{\rm{e}}^{ - \frac{1}{2}{{\left( {\omega - {\omega _0}} \right)}^2}}} $ | (3) |
选取小波中心频率ω0 = 6。
(2)计算瞬时频率。瞬时频率ωx(a, b)可通过下式计算
| $ {\omega _x}\left( {a, b} \right) = - {\rm{i}}{\left[{{W_x}\left( {a, b} \right)} \right]^{ - 1}}\frac{\partial }{{\partial b}}{W_x}\left( {a, b} \right) $ | (4) |
由时间-尺度平面(b, a)转化到时间-频率平面[b, ωx(a, b)]。
(3)同步压缩变换。将任一中心频率ωl附近区间
| $ {T_x}\left( {{\omega _l}, b} \right) = {\left( {{\rm{\Delta }}\omega } \right)^{ - 1}}\sum\limits_{{a_k}:\left| {\omega \left( {{a_k}, b} \right) - {\omega _l}} \right| \le \Delta \omega 2} {{W_x}\left( {{a_k}, b} \right){a_k}^{ - 3/2}{{\left( {{\rm{\Delta }}a} \right)}_k}} $ | (5) |
式中ωl-ωl-1=Δω,ak-ak-1=(Δa)k。
SWT变换是一种正反无损变换[23],通过反变换可重构信号x(t)。SWT的反变换为
| $\begin{array}{*{20}{l}} {x\left( t \right) = {\rm{Re}}\left[{C_\psi ^{-1}\left( {\int_0^{ + \infty } {{W_x}\left( {a, b} \right){a^{-\frac{3}{2}}}{\rm{d}}a} } \right)} \right]{\rm{}} \approx }\\ \ \ \ \ \ {{\rm{Re}}\left[{C_\psi ^{-1}\sum\limits_k {{W_x}\left( {a, b} \right)a_k^{-\frac{3}{2}}{{\left( {{\rm{\Delta }}a} \right)}_k}} } \right] = }\\ \ \ \ \ \ \ \ \ \ \ {{\rm{Re}}\left[{C_\psi ^{-1}\sum\limits_l {{T_x}\left( {{\omega _l}, b} \right)\left( {{\rm{\Delta }}\omega } \right)} } \right]} \end{array} $ | (6) |
式中
空间模态分析也称为空间离散傅里叶分析,由Longley [24]首先提出。该方法对多个信号经过适当滤波后,通过空间离散傅里叶变换,提取出各阶模态的幅值,从而用几个低阶模态的能量来判断其先兆。但通常失速先兆空间模态能量较弱,对滤波截止频率十分敏感,且该方法无法同时分辨出不同波动频率下的空间模态信息。
本文将SWT时频变换结果与空间模态分析结合,发展了基于SWT变换的空间模态分析。利用SWT可重构性质,对周向各位置传感器信号SWT变换系数的实部,进行离散傅里叶变换。该方法无需滤波,且可分辨出不同频率下的空间模态变化情况。空间k阶模态表达式为
| $ {A_k}\left( {{\omega _l}, t} \right) = \frac{1}{N}\sum\limits_{n = 1}^N {{\rm{Re}}\left[{T\left( {{\theta _n}, {\omega _l}, t} \right)} \right]{{\rm{e}}^{{\rm{i}}k{\theta _n}}}} $ | (7) |
式中N为动态压力传感器数量,θn为传感器周向弧度位置,T为传感器信号SWT变换系数。
3.3 小波相干性小波性相干性在压气机动态失速研究中还较少见,Zhang等[19]利用该方法跟踪旋转扰动的发展情况,但只分析了信号的相关性,对扰动相位差的变化未进行分析。本文利用小波相干性方法分析周向不同位置动态压力信号在时频域上的相关性和相位差变化情况。
若给定两个时间序列x(t)和y(t),其交叉小波变换的定义为
| $ {W_{xy}}\left( {a, b} \right) = {W_x}\left( {a, b} \right){W_y}^{\rm{*}}\left( {a, b} \right) $ | (8) |
式中Wx(a, b)和Wy(a, b)分别是x(t)和y(t)的小波变换。对应的交叉小波功率谱为|Wxy(a, b)|。交叉小波功率谱表示两个时间序列在每个时间和频率上的局部协方差。
小波相干将两个时间序列的功率谱归一化。被用来度量时频空间中x(t)和y(t)的局部相关程度。两个时间序列小波相干Rxy(a, b)定义如下
| $ {R_{xy}}\left( {a, b} \right) = \frac{{\left| {S\left( {{W_{xy}}\left( {a, b} \right)} \right)} \right|}}{{\sqrt {S\left( {{{\left| {{W_x}\left( {a, b} \right)} \right|}^2}} \right)S\left( {{{\left| {{W_y}\left( {a, b} \right)} \right|}^2}} \right)} }} $ | (9) |
式中S表示时域和频域的平滑谱运算[25]。
小波相干分析的是两个时间序列在不同频率点上的相关程度,但是没有提供相位信息。小波相位差给出了此相位信息
| $ {\varphi _{x, y}}\left( {a, b} \right) = {\rm{ta}}{{\rm{n}}^{ - 1}}\left( {\frac{{{\rm{Im}}\left( {S\left( {{W_{xy}}\left( {a, b} \right)} \right)} \right)}}{{{\rm{Re}}\left( {S\left( {{W_{xy}}\left( {a, b} \right)} \right)} \right)}}} \right) $ | (10) |
图 4(a)~(c)分别为压气机均匀进气、畸变网位置1和位置2畸变进气下的时域信号和频域FFT幅频谱。时域信号截取实验旋转失速起始前后各40转动态压力信号,分别对失速起始前40转和后40转的信号进行了FFT分析。

|
Fig. 4 Dynamic stall signals analysis in time and frequency domains |
图 4(a)均匀进气条件下,由时域图可见突尖型扰动引发了压气机旋转失速,突尖扰动形成初始阶段传播速度较快,沿着转子转动方向传播,扰动范围迅速增大,传播速度减慢,通过时域分析不难得到周向形成的失速团个数为1,最终稳定失速团的旋转速度约30%转子转速。FFT幅频图中,旋转失速前1frot,2frot,4frot和37frot即BPF及其倍频清晰可见,BPF的幅值要远高于其他频率幅值;在10 frot和2BPF频率之间,存在较低幅值的宽带扰动,其特征与压气机旋转不稳定性[26]相似,通常认为是由转子叶顶流场的非定常波动引起的;压气机均匀进气下没有出现低频模态波失速先兆。旋转失速发生后0.3frot即失速团旋转频率及其倍频出现,转子转动频率被淹没,此时BPF幅值相对失速前有所降低。
图 4(b)为畸变网位置1实验。由时域图可见失速前一些传感器信号在BPF规则波动的基础上出现了不规则的“毛刺”,对比畸变网位置观察发现这种不规则扰动首先出现在畸变网尾缘附近,在转出畸变区后不规则扰动受到抑制,扰动尺度减小,若该扰动在转入畸变区前不能被抑制消失,便触发压气机进入旋转失速状态。通过旋转失速前FFT分析可知“毛刺”主要由宽带非定常扰动引起,在畸变网尾缘S6附近宽带非定常扰动最强。另外一个有趣的现象是frot频率波动也出现幅值大小的变化,但其最大值在S9位置,即非畸变区的中心位置,S9后frot频率幅值迅速减小,在S11后已经消失,原因可能是转子叶轮在周向畸变作用下,轴向受力不一致,发生一定的倾斜,使非畸变区中心位置由于转子结构不对称性引起的转子转动频率扰动加强导致。不同于均匀进气,周向畸变进气下旋转失速前出现约0.225frot的低频扰动。发生旋转失速后失速团旋转频率约0.3frot,与均匀进气条件相同。
为排除压气机结构不对称性等偶然因素对上述实验结果的影响,将畸变网逆时针旋转90°,使其处于位置2。实验结果,如图 4(c)所示,通过观察该位置实验结果,宽带非定常扰动、frot扰动最强的位置相对位置1实验都相应滞后了约90°,证实这些实验现象与畸变网位置具有相关性。同时也出现了0.225frot的低频扰动。这些现象复现了位置1实验结果,排除了实验偶然因素影响。下面仅以畸变网位置2实验结果进行相关时频域分析。
4.2 SWT变换分析图 5为畸变网位置2畸变进气下,SWT变换图。图中可以同时清晰得到BPF、失速团扰动、frot扰动和旋转失速前出现的低频扰动等信息在时频域内的演变情况。旋转失速前frot和BPF频率之间的宽带非定常扰动在畸变网前缘的S3位置最弱,而后宽带非定常扰动逐渐增强,在畸变网尾缘S9处扰动变得最为复杂无序,在转出畸变区后的S11处,扰动尺度发生收缩,演化出周期性非常明显的强弱间隔变化,变化周期约4.4倍转子周期,与低频扰动的频率周期相一致。到S1位置宽带非定常扰动尺度进一步收缩,个别扰动已经消失,到S3位置除靠近失速点的短尺度扰动还存在外,其他短尺度扰动都已被抑制消失。虽然这种扰动尺度转化现象在Lin等[14]和Salunkhe等[15]的实验中已经利用小波变换得出,Lin等将该现象称为“Long-to-short”扰动尺度转化现象。但本文实验及使用的分析方法对不同周向位置扰动尺度的变化及扰动周期性分化等现象刻画得更加清晰,可更准确得到现象的本质特征。失速起始后0.3frot左右的失速团转动频率及其二倍频出现,在高频区域由于失速团区域流动遭到破坏,引起非定常脉动增强,故出现扰动强弱间隔变化,并对BPF频率造成破坏。由较强扰动的范围在一个扰动周期中所占的比例,可看出失速团所占周向范围的大小。
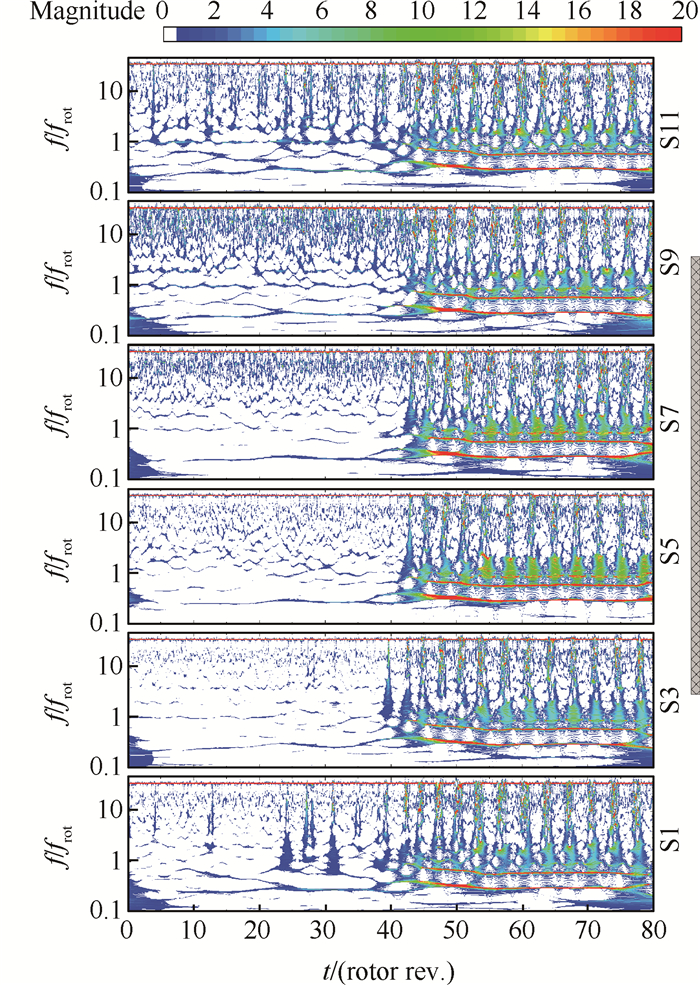
|
Fig. 5 SWT of signals for distortion screen position 2 |
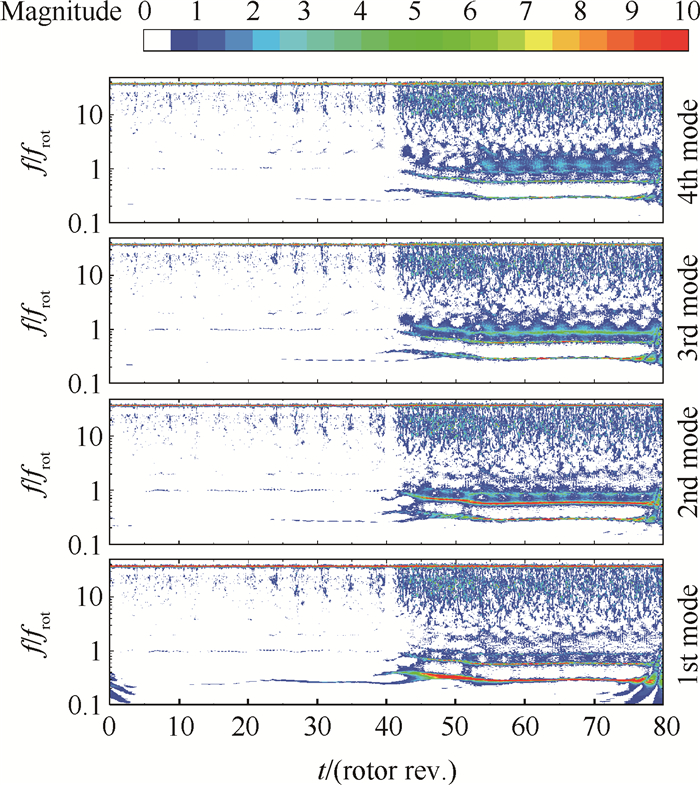
SWT变换得到了信号的时频特性,但若判断扰动特别是低频扰动空间分布特性还需进行空间模态分析。图 6为畸变网位置2畸变进气下,周向11个动态压力传感器信号基于SWT变换的前四阶空间模态幅值分布图。旋转失速前低频扰动波的一阶空间模态最明显,说明该扰动周向只存在1个扰动波。对0.3frot的失速团旋转频率同样也是一阶空间模态幅值最强,所以周向失速团的个数为1个,与时域分析一致。由于失速团波动幅度较大,还存在明显的高阶倍频,所以二阶空间模态中失速团2倍频幅值增大,三阶空间模态中失速团3倍频幅值增大。对于图中frot和BPF之间较高频率范围内的扰动多为非定常的随机脉动,在各低阶模态中均有呈现,且没有明显的强度差别。
|
Fig. 6 Former four spatial modes based on SWT for distortion screen position 2 |
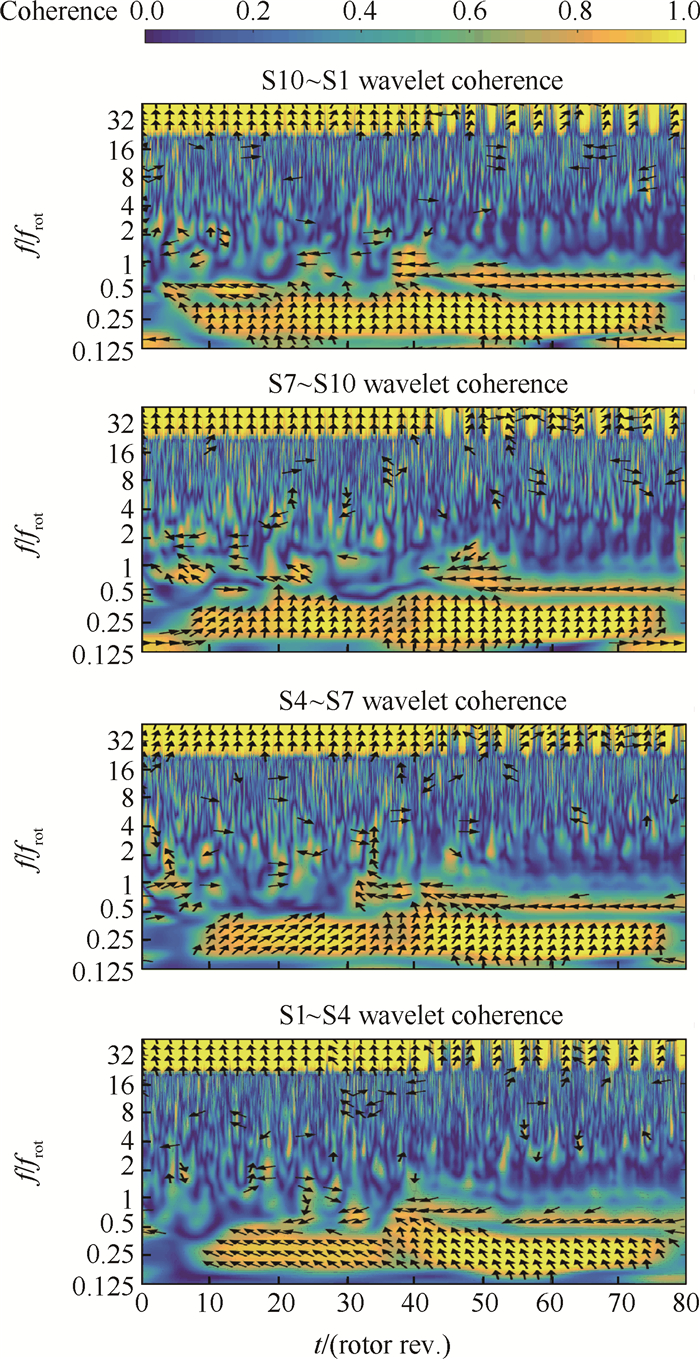
图 7为畸变网位置2,周向90°间隔的S1,S4,S7和S10信号之间小波相干性分析结果。图中箭头方向表示两个信号的相位差,方向水平向右表示相位差为0°,逆时针相位差增大。由图不难分析出,相关性较高的区域代表的频率有BPF、旋转失速前的一阶模态扰动以及失速团转动频率等。其中BPF频率信号相位差在旋转失速前均为90°,这是因为转子叶片数为37个,转子在转动中会形成37阶的空间模态,而周向均匀布置的4个测点数,与37互质,则每个测点信号会处于正弦波的4个不同相位,所以信号之间相位差均为90°。而一阶空间模态扰动各信号之间相位差却并非均匀分布的90°,各信号相位差不一致说明,周向畸变进气下旋转失速前形成的一阶模态扰动周向传播速度并不均匀,与通常均匀进气下匀速传播的模态波先兆特征有所不同。由图分析可知,该一阶模态扰动由S1~S4,即由非畸变区刚进入畸变网前缘时,信号之间相位差最大,表示此段区域内该扰动波速度最小,而畸变区内S4和S7之间相位差最小,表示此段区域扰动波速度最快,而在刚转出畸变网尾缘的S7~S10和进入非畸变区后的S10~ S1,信号相位差均约为90°,表示这段区域扰动波速度减慢到正常的传播速度。由于实验周向畸变强度较弱,周向畸变对波动较强的失速团传播速度并未产生较大的影响,基本沿周向匀速传播。
|
Fig. 7 Wavelet coherence for distortion screen position 2 |
为更深入理解周向畸变进气下压气机动态失速特性本质,通过物理模型对比实验结果对动态失速过程机制进行分析。
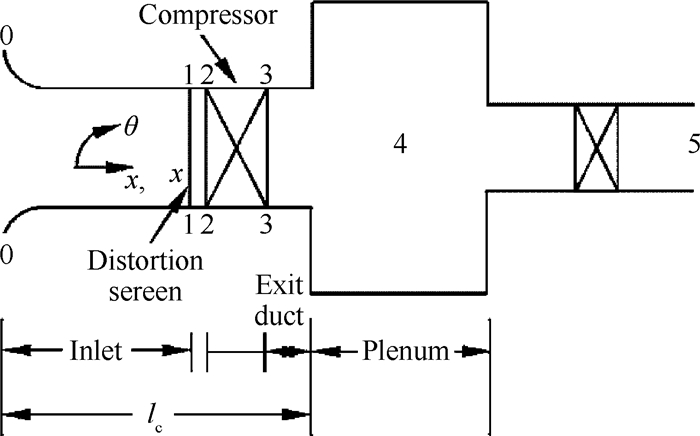
5.1 集总系统模型建立参考文献[13, 14],建立试验台压气机稳态周向畸变条件下的集总系统模型,模型示意图见图 8。
|
Fig. 8 Lumped system model with inlet distortion[13] |
从进气管道到集气箱的总静压升为
| $ \psi = {\psi _{\rm{c}}}\left( \phi \right) - l_{\rm{c}}^{\rm{*}}\frac{{\partial \phi }}{{\partial {t^{\rm{*}}}}} - \lambda _{\rm{r}}^{\rm{*}}\frac{{\partial \phi }}{{\partial \theta }} - {K_{\rm{L}}}\left( \theta \right){\phi ^2} $ | (11) |
式中ψc(ϕ)为压气机轴对称特性,ϕ为流量系数,KL(θ)为周向分布的总压损失系数,且
| $ \begin{array}{*{20}{l}} {\psi = \frac{{{p_4} - {p_{{\rm{T}}0}}}}{{\rho u_{\rm{m}}^2}}, {\rm{}}{\psi _{\rm{c}}}\left( \phi \right) = \frac{{{p_{\rm{c}}}\left( \phi \right)}}{{\rho u_{\rm{m}}^2}}, {\rm{}}\phi = \frac{{{u_x}}}{{{u_{\rm{m}}}}}, {t^{\rm{*}}} = \frac{t}{{R/{u_{\rm{m}}}}}, {\rm{}}}\\ {l_{\rm{c}}^{\rm{*}} = \frac{{{l_{\rm{I}}} + {\lambda _{{\rm{IGV}}}} + {\lambda _{\rm{r}}} + {\lambda _{\rm{s}}} + {l_{\rm{E}}}}}{R}, {\rm{}}\lambda _{\rm{r}}^{\rm{*}} = \frac{{{\lambda _{\rm{r}}}}}{R}} \end{array} $ |
式中ρ为气体密度,um为转子平均半径处线速度,ux为轴向进气速度,R为平均半径,lI为进气管道长度,lE为出口管道长度,λIGV,λr,λs分别表示导流叶片、转子和静子轴向有效长度。叶片轴向有效长度由下式表示
| $ \lambda = {b_x}\frac{K}{{{\rm{co}}{{\rm{s}}^2}\alpha }} $ | (12) |
式中bx为叶片轴向弦长,K为考虑叶排间隙及非定常粘性影响的系数[1],α为叶片有效安装角。
集气箱和节流阀模型为
| $ 4l_{\rm{c}}^{\rm{*}}{B^2}\frac{{{\rm{d}}\psi }}{{d{t^{\rm{*}}}}} = \mathit{\Phi } - \sqrt {\gamma \psi } $ | (13) |
式中B为Greitzer-B参数[1],γ为节流阀系数。Φ为瞬时周向平均流量系数
表 2为实验压气机集总系统模型无量纲参数的取值。
|
|
Table 2 Values of dimensionless parameters |
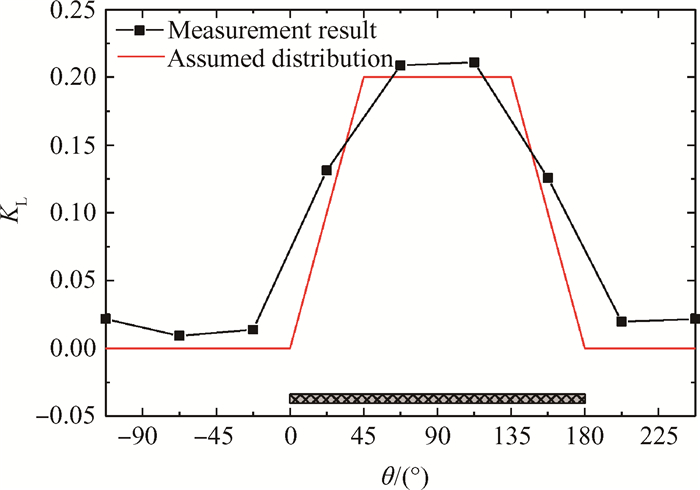
由于实验中畸变网安装在进气钟口前端,与模型中畸变网的位置并不一致,本文以压气机在节流过程中,由1截面测量得到的径向平均总压损失和平均进气动压关系的线性拟合曲线的斜率为参考作为压气机进口总压损失系数。图 9为实验测得的和模型假设的压气机进口周向总压损失系数曲线。
|
Fig. 9 Distribution of total pressure loss coefficient at compressor inlet |
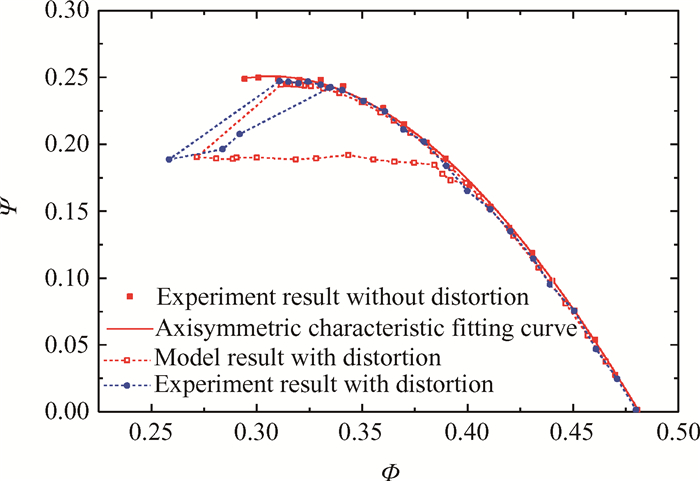
压气机的轴对称特性ψc(ϕ),通过均匀进气下压气机总静压升特性实验数据拟合曲线给出,如图 10中的实线。式(14)为实验数据得到的五次拟合曲线公式
| $ \begin{array}{*{20}{l}} {{\psi _{\rm{c}}}\left( \phi \right) = - 693.43{\phi ^5} + 1336.41{\phi ^4} - 994.03{\phi ^3} + }\\ \ \ \ \ \ \ \ {339.66{\phi ^2} - 51.22\phi + 2.99} \end{array} $ | (14) |
|
Fig. 10 Experiment and model results of compressor characteristics |
应用谱方法求解方程(11)和(13),得到畸变进气下模拟的压气机特性,如图 10所示。可见,由于实验总压畸变强度较小,实验和模型得到的总压畸变对压气机总静压升影响均较小,但近失稳点流量系数比均匀进气条件均有所增大。模型对压气机稳定状态特性模拟较好,对旋转失速滞后环特性未能准确模拟,但这不影响利用该模型的对压气机动态失速过程中参数演化情况进行定性分析。
图 11为模型在不同节流阀系数γ下,流量系数周向分布的变化情况。可见在γ = 3时,流量系数周向分布基本与畸变网总压损失系数分布相对应,但随着γ减小,系统非线性作用增强,低流量系数区逐渐向转子转动方向偏移。在近失稳点γ = 0.41,流量系数最低点偏移到了畸变网尾缘附近,而流量系数最高点在畸变网前缘附近,这与实验中宽带非定常扰动的强弱变化位置相对应。通常在近失速点,流量系数越低则进气攻角越大,流动越不稳定,更容易引起非定常扰动。
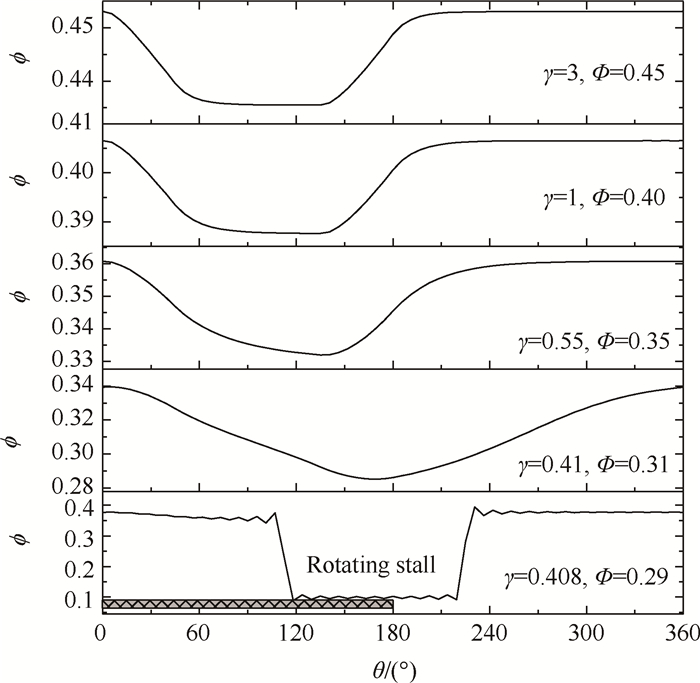
|
Fig. 11 Flow coefficient variation at different throttle coefficient |
图 12为压气机动态失速过程中,由模型得到的流量系数ϕ在时间和周向空间上的演化图谱。可见,在旋转失速发生前,周向各位置ϕ在时间方向上都出现了周期性波动,这与周向畸变实验旋转失速前出现的0.225frot一阶模态扰动是对应的。图中最低流量系数区出现在畸变网尾缘附近,在转出畸变区后低流量系数区的时间尺度逐渐缩小,出现周期性间隔变化,最终旋转失速前形成的倒数第二个最低流量系数区演化形成的短尺度流量系数区穿过畸变区,并在尾缘附近引发了旋转失速。模型中低流量系数尺度的变化与实验中SWT变换得到的非定常扰动尺度的转化情况相吻合,进一步说明动态失速过程中系统低流量系数区的演变是造成非定常扰动尺度变化的原因。
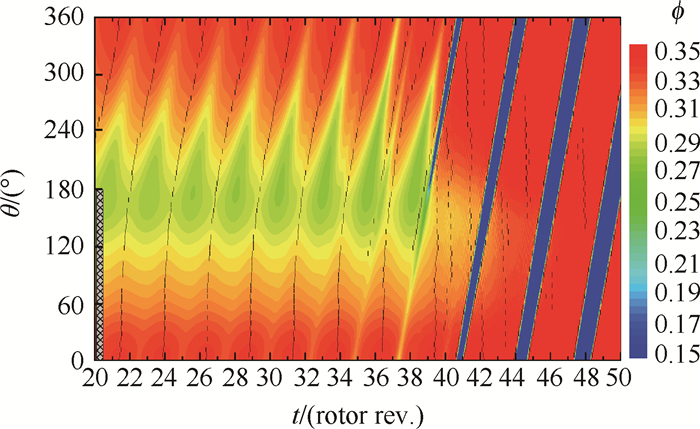
|
Fig. 12 Simulated flow coefficient contours |
图 12中的黑色线段表示周向各位置ϕ在时间轴上波动的峰值点,可见在旋转失速前,畸变区周向不同位置之间相位差变化很小,在进入非畸变区后,相位变化增大,该结果与实验中应用小波相干性分析得到的周向不同位置信号之间一阶模态扰动相位差变化情况一致,说明实验中一阶模态扰动周向传播速度不均匀现象是畸变进气下压气机系统作用的结果。
6 结论通过本文研究,得到以下结论:
(1)通过时域、频域和时频域等方法分析得到,在周向畸变进气下,实验压气机旋转失速前出现0.225frot一阶模态扰动,该扰动波沿周向传播的速度不均匀,畸变区内速度较快,转出畸变区时速度减慢。宽带非定常扰动在畸变区尾缘附近最强,在畸变区前缘附近最弱,并存在尺度转化现象。转子转动频率扰动周向也出现强度变化,最大值出现在非畸变区中心附近的测点。
(2)由周向畸变条件下集总系统模型和实验结果分析可得,旋转失速前非定常扰动周向强度和尺度变化主要受流量系数变化的影响,而一阶模态扰动周向传播速度不均匀现象是畸变进气下压气机系统特性作用的结果。实验和模型结果符合较好,说明本文采用的数据分析方法合理有效,同时也说明模型合理地复现了畸变进气下系统的动态失速特性。
(3)本文研究结果对畸变进气下压气机失速预警和稳定性控制研究具有一定的指导意义,比如利用信号相关性变化作为失速预警时,检测信号可选在非定常扰动最强的畸变区尾缘位置。而利用空间模态作为失速预警时则可根据扰动相位变化合理调整传感器周向分布,以便更有效地对空间模态辨识。在稳定性控制方面可对低流量系数区出现的位置加强流动控制,以增强稳定性控制效果。
| [1] |
Moore F K, Greitzer E M. A Theory of Post-Stall Transients in Axial Compressor Systems, Part Ⅰ : Development of Equations[J]. Journal of Engineering for Gas Turbines and Power, 1986, 108(1): 68-76. DOI:10.1115/1.3239887
(  0) 0) |
| [2] |
Greitzer E M, Moore F K. A Theory of Post-Stall Transients in Axial Compressor Systems, Part Ⅱ: Application[J]. Journal of Engineering for Gas Turbines and Power, 1986, 108(2): 231-239. DOI:10.1115/1.3239893
(  0) 0) |
| [3] |
Day I J. Stall Inception in Axial Flow Compressor[J]. Journal of Turbomachinery, 1993, 115(1): 1-9. DOI:10.1115/1.2929209
(  0) 0) |
| [4] |
Hoying D A, Tan C S, Vo H D, et al. Role of Blade Passage Flow Structures in Axial Compressor Rotating Stall Inception[J]. Journal of Turbomachinery, 1999, 121(4): 735-744. DOI:10.1115/1.2836727
(  0) 0) |
| [5] |
Vo H D, Tan C S, Greitzer E M. Criteria for Spike Initiated Rotating Stall[J]. Journal of Turbomachinery, 2005, 130(1): 155-165.
(  0) 0) |
| [6] |
Inoue M, Kuroumaru M, Tanino T, et al. Comparative Studies on Short and Long Length-Scale Stall Cell Propagating in an Axial Compressor Rotor[J]. Journal of Turbomachinery, 2001, 123(3): 24-30.
(  0) 0) |
| [7] |
Pullan G, Young A M, Day I J, et al. Origins and Structure of Spike-Type Rotating Stall[J]. Journal of Turbomachinery, 2015, 137(5).
(  0) 0) |
| [8] |
Mazzawy R S. Multiple Segment Parallel Compressor Model for Circumferential Flow Distortion[J]. Journal of Engineering for Power, 1977, 99(2): 288-296. DOI:10.1115/1.3446288
(  0) 0) |
| [9] |
Hawthorne W R, Mitchell N A, Mccune J E, et al. Nonaxisymmetric Flow through Annular Actuator Disks: Inlet Distortion Problem[J]. Journal of Engineering for Power, 1978, 100(4): 604-617. DOI:10.1115/1.3446409
(  0) 0) |
| [10] |
Hale A, Davis M, Kneile K R. Turbine Engine Analysis Compressor Code: TEACC Part Ⅰ : Technical Approach and Steady Results[C]. Reno: Proceedings of the AIAA 32nd Aerospace Sciences Meeting, 1994: 10-13.
(  0) 0) |
| [11] |
Gong Y, Tan C S, Rordon G S, et al. A Computational Model for Short Wavelength Stall Inception and Development in Multistage Compressors[J]. Journal of Turbomachinery, 1999, 121(4): 726-734. DOI:10.1115/1.2836726
(  0) 0) |
| [12] |
尹超, 胡骏, 严伟, 等. 多级轴流压气机进气畸变模型研究[J]. 推进技术, 2016, 37(12): 2278-2287. (YIN Chao, HU Jun, YAN Wei, et al. Investigation of Multistage Axial Compressor Distortion Analysis Model[J]. Journal of Propulsion Technology, 2016, 37(12): 2278-2287.)
(  0) 0) |
| [13] |
Lin F, Chen J. Theoretical Study of Inlet-Distortion-Induced Instability of Axial Compression Systems[J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2006, 220(4): 327-342. DOI:10.1243/09576509A07704
(  0) 0) |
| [14] |
Lin F, Li M, Chen J. Long-to-Short Length-Scale Transition: A Stall Inception Phenomenon in an Axial Compressor with Inlet Distortion[J]. Journal of Turbomachinery, 2006, 128(1): 130-140. DOI:10.1115/1.2098808
(  0) 0) |
| [15] |
Salunkhe P B, Pradeep A M. Stall Inception Mechanism in an Axial Flow Fan under Clean and Distorted Inflows[J]. Journal of Fluids Engineering, 2010, 132(12): 121102. DOI:10.1115/1.4002921
(  0) 0) |
| [16] |
蒋华兵, 陆亚钧, 袁巍, 等. 进气畸变对低速轴流压气机失速特性的影响[J]. 航空动力学报, 2008, 23(2): 355-360. (  0) 0) |
| [17] |
张明明, 李可仰, 董万静. 周期扰动下低压压气机旋转失速先兆辩识[J]. 推进技术, 2016, 37(5): 871-878. (ZHANG Ming-ming, LI Ke-yang, DONG Wanjing. Identification on Rotating Stall Precursor of a LowPressure Compressor via Periodic Perturbations[J]. Journal of Propulsion Technology, 2016, 37(5): 871-878.)
(  0) 0) |
| [18] |
Liao S, Chen J. Time-Frequency Analysis of Compressor Rotating Stall by Means of Wavelet Transform[R]. ASME 96-GT-57.
(  0) 0) |
| [19] |
Zhang H, Yu X, Liu B, et al. Using Wavelets to Study Spike-Type Compressor Rotating Stall Inception[J]. Aerospace Science and Technology, 2016, 58: 467-479. DOI:10.1016/j.ast.2016.09.006
(  0) 0) |
| [20] |
向宏辉, 侯敏杰, 杨荣菲, 等. 基于希尔伯特-黄与小波变换的压气机失速信号分析方法[J]. 燃气涡轮试验与研究, 2015, 28(5): 1-5. (  0) 0) |
| [21] |
鞠鹏飞, 宁方飞. 跨声压气机近失速流动特征的数值模拟研究[J]. 推进技术, 2016, 37(6): 1055-1064. (JU Peng-fei, NING Fang-fei. Numerical Study of Near-Stall Flow Feature on Transonic Compressor[J]. Journal of Propulsion Technology, 2016, 37(6): 1055-1064.)
(  0) 0) |
| [22] |
贺象, 银越千, 黄生勤, 等. 低速轴流压气机旋转失速演化机制研究[J]. 航空发动机, 2016, 42(5): 81-86. (  0) 0) |
| [23] |
Daubechies I, Lu J, Wu H T. Synchrosqueezed Wavelet Transforms: An Empirical Mode Decomposition-Like Tool[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 243-261. DOI:10.1016/j.acha.2010.08.002
(  0) 0) |
| [24] |
Longley J P. Inlet Distortion and Compressor Instabilities[D]. Cambridge: Cambridge University, 1988.
(  0) 0) |
| [25] |
Grinsted A, Moore J C, Jevrejeva S. Application of the Cross Wavelet Transform and Wavelet Coherence to Geophysical Time Series[J]. Nonlinear Processes in Geophysics, 2004, 11(5/6): 561-566. DOI:10.5194/npg-11-561-2004
(  0) 0) |
| [26] |
Wu Y, Wu J, Zhang G, et al. Experimental and Numerical Investigation of Flow Characteristics near Casing in an Axial Flow Compressor Rotor at Stable and Stall Inception Conditions[J]. Journal of Fluids Engineering, 2014, 136(11).
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


