随着航空技术和人们生活需求的不断提高,对航空器的噪声指标也在不断提高,相比于西方航空界,我国对航空器噪声的重视程度还远远不够。但是,随着C919的成功首飞,我国必将参与到世界商用大飞机的竞争中,此时,研究适航标准中占重要地位的航空噪声就尤为必要[1]。航空发动机是飞机各部件中的最主要噪声源,涡扇发动机是商用飞机的主要噪声源。而对于涡扇发动机,噪声主要包括以下两类:风扇/压气机噪声和喷流噪声。随着气动声学技术的日益发展和涡扇发动机涵道比的逐步提升,喷流噪声已经得到较大抑制,风扇/压气机噪声的比重日益突出[2~4]。
对于工作在亚声速下的风扇/压气机,其主要噪声是由非定常叶片气动力引起的。这种由非定常气动力引起的噪声主要产生于转子叶片与静子叶片之间的相互干涉。针对这种噪声,最著名的莫过于Ty⁃ ler和Sofrin于1962年发表的对叶轮机噪声的研究结果[5],研究表明,这种非定常气动力噪声的某些模态所对应的方位相速度大大超过叶片转子的机械转速。在多数情况下,这些模态的方位相速度可以超过声速,从而成为可以在管道中向远场传播的模态。这些传播模态主要取决于转子叶片数目和静子叶片数目、转子旋转速度以及气流的绝对速度等因素。Holste和Neise [6]将这一理论拓展到两排转子干涉的情况,Zhang等[7]更进一步的拓展到两排转子与多排静子干涉的情况。近年来,针对风扇/压气机离散噪声的研究[8, 9]主要根据Tyler-Sofrin转静干涉理论及其拓展理论,风扇/压气机转子静子相互干涉所引发的叶片非定常气动力已成为一个无法忽视的叶轮机械噪声源。
为了研究和降低风扇/压气机噪声,在实际测试中有效的噪声测量技术是必不可少的。对于风扇/压气机噪声的研究来讲,测量频谱只能初步分析噪声源的情况。但是如果想要准确判断噪声的发生机理并且用于进行有效的降噪设计,就必须进行模态测量实验[10, 11]。
对于叶轮机械管道的周向声模态的测量,无论从模态分解技术还是测量方法都已经比较成熟。传统的模态分解方法是对周向阵列上传声器所测的噪声信号进行空间傅里叶分解,获得各频率下描述周向模态及其模态幅值的二维模态谱[12, 13]。Pieter Si⁃ jtsma和Jörgen Zillmann在2007年发表的文章中介绍了四种模态分解技术:传统的方均根(RMS)模态分解技术、对角线移除(DR)模态分解方法、与参考信号互相关(CC)模态分解技术和主成分分析(PC)模态分解技术[14]。研究者们对比分析过这四种模态分解技术,在对管道内声模态进行分解时,RMS方法和PC方法受背景噪声的影响较大,DR方法严重影响第二占优模态的幅值,CC模态分解技术可以降低随机噪声对模态幅值分解结果的影响,是四种模态分解技术中的最优方法[2, 14]。这些模态分解方法满足著名的Shannon-Nyquist采样定理,他们的研究表明,如果想要分解出一个m阶周向模态,阵列上传声器的数量最少为2m[15]。为满足这一定理,在航空发动机噪声测量过程中所使用的传声器数量过于庞大。针对这一问题,研究者们提出了两种解决方法:(1)改进原有的模态测量装置[16, 17];(2)基于模态分解方法提出新的处理技术[18, 19]。两种方法均能用较少的传声器测量高阶周向声模态。
本文的工作围绕北京航空航天大学单级低速轴流压气机TA36展开,利用20路沿管道齐平安装的传声器组成的周向传声器阵列测量压气机不同转速下的噪声信号。处理数据得到前传噪声的频谱特性及周向模态特性,并将实验测得的结果与转静干涉噪声理论结果进行对比。进一步分析了实验结果与理论结果的不同之处。
2 实验设备实验在TA36单级低速轴流压气机上进行,压气机的主要性能参数见表 1。实验使用G.R.A.S.46BP压力场传声器,属于1/4 inch传声器,有效测量频率范围10Hz~70kHz,测量的最大声压级为169dB,传声器灵敏度为1.5mV/Pa。数据采集系统为NI公司的PXI平台,可同步采集48路传感器信号。
|
|
Table 1 Parameters of TA36 |
实验台结构简图如图 1所示,实验中主要由20只传声器组成的周向传声器阵列进行测量。传声器阵列距离压气机转子前缘139cm。根据模态分解采用的算法要求,在转子前缘上游19cm处设置了一只参考传声器。在静子尾缘下游30cm处有4个承力支板。图 2给出了从管道入口方向看去传声器阵列中各传声器的位置及编号。
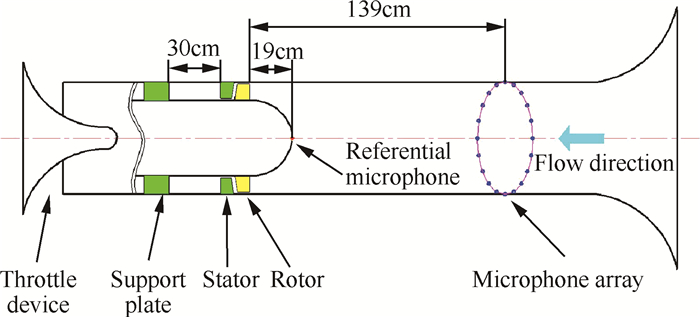
|
Fig. 1 Microphone array location on experimental setup |
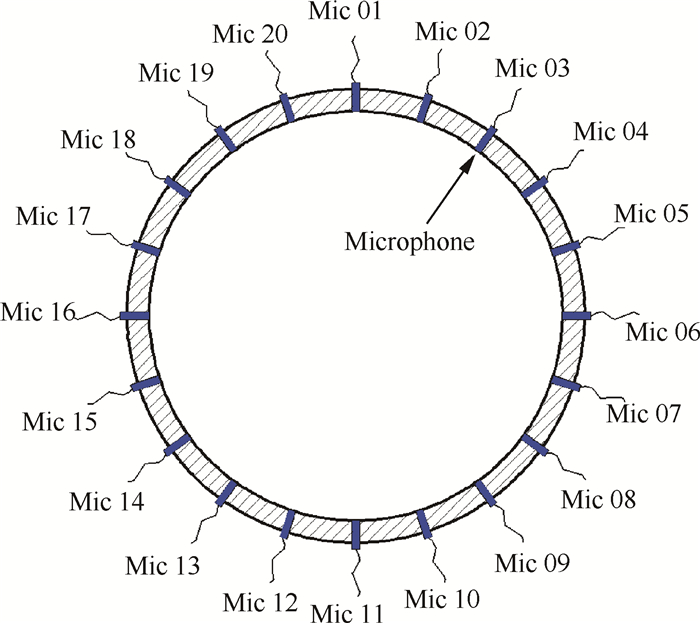
|
Fig. 2 Schematic of microphone array location and microphone serial number |
根据Tyler和Sofrin提出的转静干涉噪声经典理论,压气机转静干涉形成的旋转压力模态可以通过以下方式描述:令转子叶片数为B,静子叶片数为V,则转静干涉形成旋转压力模态的n次谐波的周向模态阶数为
| $ m = nB + kV $ | (1) |
式中k是-∞~+∞之间的任意整数,其意义是静子叶片产生的畸变的空间谐波。
根据管道声学理论[1],每个旋转压力模态在管道中都对应一个截止频率。管道中声波波数的关系式为
| $ {k^2} = k_{xmn}^2 + k_{rmn}^2 $ | (2) |
式中k为波数,kxmn为轴向波数,krmn为径向波数。只有轴向波数为实数,声波方能沿轴向远场传播。此时的波数应满足
| $ k = \left( {\frac{\omega }{{{c_0}}}} \right) > {k_{rmn}} $ | (3) |
或
| $ \omega > {c_0}{k_{rmn}} = {\omega _{mn, {\rm{cut}} - {\rm{off}}}} $ | (4) |
式中ωmn, cut-off为截止角频率。此频率的意义表明,对于特定模态的声波,其实际频率只有高于这一频率才能向远场传播。对于给定的模态(m,n),其截止频率为
| $ f_{mn}^c = j'\left( {m, n} \right)\frac{{{c_0}}}{{2{\rm{ \mathsf{ π} }}R}} $ | (5) |
式中j′ (m, n) = krmnR为该模态对应的特征数。
无流动状态下该实验台管道前10阶周向模态的截止频率,如表 2所示。本实验台为低速压气机,最高流动马赫数仅为0.05,对于截止频率的影响相对较小[20],所以表 2中的截止频率可以近似看作后续实际实验中的截止频率。
|
|
Table 2 Cut-off frequency of circumferential modes in test duct |
叶轮机械的主导离散风扇噪声主要是由风扇转子与静子之间相互干涉产生的。风扇产生的噪声在管道内传播时伴随着不同的旋转螺旋路径,这种空间模式被叫做旋转模态。在连续性、均匀流和无粘假设条件下,风扇所产生的旋转模态噪声可以用线性欧拉方程表示[2]
| $ \left\{ {\begin{array}{*{20}{l}} {\left( {\frac{\partial }{{\partial t}} + {v_0} \cdot \nabla } \right)\rho ' + {\rho _0}\nabla \cdot v' = 0}\\ {{\rho _0}\left( {\frac{\partial }{{\partial t}} + {v_0} \cdot \nabla } \right)v' + \nabla \rho ' = 0} \end{array}} \right. $ | (6) |
对于刚壁无限长圆管道,线性欧拉方程有如下解
| $ p'(x, r, \theta, t) = \sum\limits_{m = - \infty }^\infty {{A_m}{J_m}({k_r}r){{\rm{e}}^{{\rm{i}}\left( {\omega t - {k_x}x - m\theta } \right)}}} $ | (7) |
式中m为周向模态数,Jm为第一类贝塞尔函数的第m阶值。在刚壁边界条件下,在r=R(内壁半径)处满足d[Jm(rkr)]/dr=0。第n阶轴向波数kr可以求解,n为整数从1开始,Am为第m阶周向模态的幅值。假设背景流动为均匀流v0=(Mjc0, 0, 0),c0为声速。
模态分解方法的目的就是求解式(7)中Am的值。本文只研究周向声模态分解,式(7)可以简化为
| $ {{p'}_\omega }\left( \theta \right) = \sum\limits_{m = - \infty }^\infty {{A_{m\omega }}{{\rm{e}}^{{\rm{-i}}\mathit{m}\theta }}} $ | (8) |
一种典型的模态分解方法中,Am的值可以由下式求解
| $ {A_{m\omega }} = \frac{1}{N}\sum\limits_{K = 1}^N {{P_K}\left( \omega \right)} {{\rm{e}}^{{\rm{i}}\mathit{m}{\theta _K}}} $ | (9) |
在本文所述的工作中,利用一种与参考信号相关(CC)模态分解技术,即借鉴Pieter Sijtsma和Jörgen Zillmann在2007年发表的论文[14]中提供的互谱分析算法,编写了一个新的模态幅值计算程序。该算法中Am的值可以由以下公式求解
| $ {A_{m\omega }} = \frac{1}{N}\sum\limits_{K = 1}^N {\frac{{{P_K}P_0^{\rm{*}}{{\rm{e}}^{{\rm{i}}m{\theta _K}}}}}{{{{\left( {{P_0}P_0^{\rm{*}}} \right)}^{1/2}}}}} $ | (10) |
式中*表示复数的共轭。这个算法所涉及到的各复数压力幅值,均由传声器测得的原始时域信号经快速傅立叶变换得到。可以看出,此种算法需要阵列中传声器的信号和参考点信号(靠近转子叶片)进行交叉谱分析,这种方法可以减小干扰信号对模态分解结果的影响,其可靠性与准确性均经过了实验的检验[2, 14]。
在本实验的实际操作中,由于传声器阵列由20个传声器组成,因而其只能准确分辨m=-9~10内的20个声模态,其余模态的声信号将混叠于上述20个模态中。
4 实验结果分析本文在1500~2700r/min转速下对该压气机的前传噪声特性进行了测量。实验中,传声器的采样频率为32768Hz,采样时长6s,快速傅里叶变换采用的点数为65536个,平均次数为100次,频谱分辨率为0.5Hz。本节主要分析该压气机实验台的噪声频谱特性和管道周向声模态分解结果。
4.1 频谱特性 4.1.1 理论频谱特性表 3为根据Tyler和Sofrin的转静干涉理论计算出的周向声模态阶数,m=-15~19。表 3最后一列为根据谐波数和截止频率计算出的截止转速。当实际压气机转速高于截止转速时,此截止转速对应的声模态从截止声模态转变为可传声模态。从表 3可以看出,根据Tyler和Sofrin提出的转静干涉理论,在实验台设计转速范围内,实验台在1倍叶片通过频率(1BPF)和2倍叶片通过频率(2BPF)下不存在可以向远场传播的周向声模态。在本实验测试范围内,3~ 6倍叶片通过频率下均存在可以向远场传播的周向声模态。
|
|
Table 3 In-duct circumferential mode analysis |
从图 3可以看出,离散噪声是该压气机的主要声源,都明显高于附近的宽频噪声,这与压气机噪声特性的认知是相符的。但实验台的噪声信号测量结果显示,在1500~2700r/min转速的频谱图上,1BPF和2BPF上探测到了明显的信号峰值。尤其值得关注的是在2700r/min转速时,2BPF处的信号峰值已经超过了其余各阶BPF的信号峰值,如图 3(e)所示,这与表 3中转静干涉噪声理论预测结果是相违背的。从图 3中还可以发现,在3~6倍BPF处出现了信号峰值,这与转静干涉噪声理论预测结果是相符合的。
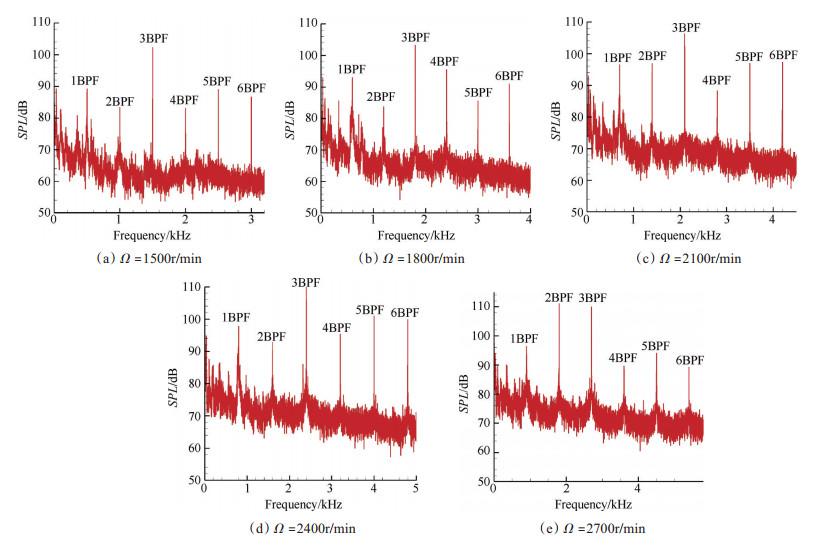
|
Fig. 3 Sound pressure spectra of Mic01 at different rotating speed |
通过观察实验频谱数据可以发现,这种未被预测到的噪声频率明显与BPF相关,所以可以排除是由于管道外环境的影响。从图 1可以看出,传声器阵列距离转子前缘139cm(约2.3倍内径),阵列所处位置已属于远场[5],可以排除是由于检测到了衰减声信号。
针对1BPF和2BPF处检测到明显峰值的情况,提出三种可能的原因:(1)静子出口处的旋流与下游的支板(包含四个圆柱支架)发生干涉,发出包含可传播模态的噪声信号;(2)转静干涉产生的声模态被截止时,其声信号仍会向前传播一小段距离,传播必然穿过包含着复杂流动的动叶流场,声模态很可能发生散射,散射后的模态的截止频率低于该噪声的频率,从而可以向远场传播;(3)进气畸变与转子干涉产生噪声。压气机在地面工作时,会吸入强烈的湍流气团。转子叶片与进气湍流气团的干涉会产生很强的单音噪声。
4.2 模态分解结果为了进一步分析上述异常现象产生的原因,仅仅依靠频谱分析是远远不够的,还需要对压气机噪声的模态特性进行分析。下面根据频谱分析结果,将分别对高阶谐波频率(3BPF~6BPF)和低阶谐波频率(1BPF~2BPF)下的声模态进行分析。
4.2.1 高阶谐波频率下模态分析结果图 4为不同转速高阶BPF对应的模态幅值分布图。模态分解结果显示,当理论存在可传声模态时,实际测得的主导模态和表 3依据转静干涉噪声理论预测的主导模态完全一致。如图 4(a)所示,3BPF模态谱上的实际主导模态为m=6,表 3中理论预测的主导模态为m=6,故3BPF处的理论结果和实际结果相符。从图 4(b)可以看出,4BPF的模态谱上的实际主导模态为m=- 1,理论预测的主导模态为m=- 1,故4BPF处的理论结果和实际结果相符。图 4(c)表明5BPF的模态谱上的实际主导模态为m=-1,理论预测的主导模态为m=-8和m=19(混叠于m=-1),故5BPF处的理论结果和实际结果相符。如图 4(d)所示,6BPF的模态谱上的实际主导模态为m=-8,理论预测的主导模态为m=12(混叠于m=-8)和m=-15(混叠于m=5),故6BPF处的理论结果和实际结果相符。
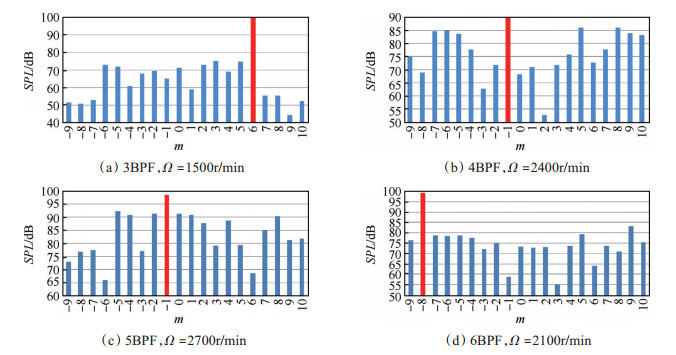
|
Fig. 4 Mode amplitude of noise at higher order BPF |
经过分析图 5可以发现,1BPF处存在不同于转静干涉理论的模态产生机制。在实际模态分解结果中还可以发现,不同转速对应1BPF下的实际主导模态是不同的,而且主导模态分布在以0模态对称的范围内。如图 5(a)所示,主导模态为m=-2,-1,0,1,2,包含该1倍叶片通过频率下所有的可传声模态,主导模态近乎是等幅值分布。随着转速的增加,主导模态的范围越来越大。
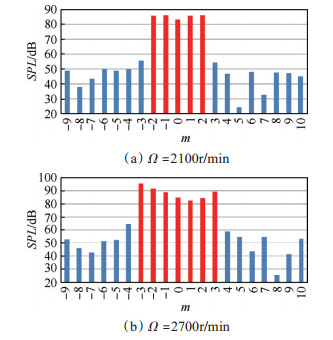
|
Fig. 5 Mode amplitude of noise at 1BPF |
从上述模态分布的现象可以排除第一种可能性。因为假设静子出口旋流与支板相互干涉发出包含可传播模态的噪声信号,此种情况亦可使用式(1)来预测,只是B变为压气机静子数,V变为支板数。那么根据计算结果,1BPF处的预测主导模态包括m=-1和3,不会是一个范围内的模态,更不会随转速升高而改变,所以,第一种假设不成立。
上述模态分布的现象同样否定了第二种可能性。转静干涉噪声主要由位于转子后的静子叶片发出,当转静干涉产生的声模态被截止时,其声信号仍会向前传播一小段距离,传播必然穿过包含着复杂流动的动叶流场,声模态很可能发生散射,从绝对值较高的模态转变为较低的模态。但是,此类散射会向固定的几个模态进行,也不会呈现出图 5的模态分布。
当压气机在地面实验时,空气从压气机进口的四周被吸入(压气机捕获面积远大于进气道进口面积)时,会同时吸入强烈的湍流气团[21]。大气中的湍流团在被吸入压气机后,会被轴向拉长,研究人员曾测量过地面静止实验时吸入发动机的湍流气团尺度,发现其轴向尺度一般是横向尺度的100~200倍[1],不再具备均匀各项同性的特点。由于湍流团的轴向尺度非常大,压气机的叶片通过频率往往会大于湍流团通过叶片的频率,旋转的叶片就会在湍流涡衰减之前周期性的去切割湍流团,此时湍流团就类似于转静干涉噪声中的静子,转子叶片与湍流团发生干涉产生噪声,辐射的噪声能量恰好集中在各阶BPF上。用p表示畸变引起的空间谐波数,则式(1)变为
| $ m = sB + p $ | (11) |
由于湍流团的周向非均匀性,类似于静子叶片数的不确定性,p可以取-∞~+∞之间的任意整数,因此与转子干涉产生的旋转模态包含各个模态,由于管道的截止效应,绝对值较高的模态被截止,就会产生如图 5所示的模态分布。当转速为2100r/min时,1BPF=700Hz,根据表 2,1BPF恰好在2模态截止频率(576Hz)和3模态的截止频率(766Hz)之间。根据之前的分析,进气畸变与转子干涉产生的噪声包含各个模态,但是3模态及以上模态将被截止,不能向远场传播,所以最终模态分解结果应该是-2~+2模态占主导,如图 5(a)所示。
当飞机在空中飞行时,吸入的湍流气团要小于地面实验的情况,而且由于空气是直接冲入进气道的(即发动机捕获面积与进气道面积相当),这时吸入的湍流气团不会被轴向拉长,湍流气团的横向尺度非常大[1],湍流气团与转子的干涉单音并不突出(叶片在周向遇到的是相似的气流团)。
分析图 6可以发现,2BPF处同样存在不同于转静干涉理论的模态产生机制。在实际模态分解结果中还可以发现,不同转速对应2BPF下的实际主导模态是不同的,而且主导模态分布在以0模态对称的范围内。如图 6(a)所示,主导模态为-4~4模态,包含该2倍叶片通过频率下所有的可传声模态,主导模态近乎是等幅值分布。随着转速的增加,主导模态的范围越来越大。模态分解结果都与进气畸变转子干涉产生噪声的模态分布完全吻合。
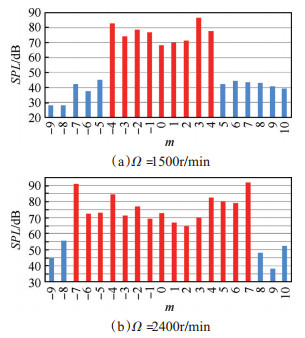
|
Fig. 6 Mode amplitude of noise at 2BPF |
为了验证3BPF处是否满足进气畸变与转子干涉产生噪声这一现象。在原有实验的基础上进行了补充实验,测试了1000~1400r/min转速下噪声的周向模态特性。3BPF对应的截止转速为1353r/min,即当实际转速低于这一转速时,6模态的噪声将被截止,不能向远场传播,如表 3所示。此时,3BPF处的情况将与1BPF和2BPF处相同,即根据转静干涉理论不存在可传声模态。
图 7为不同转速下3BPF对应的模态幅值。模态分解结果可以看出,当转速为1380r/min时,6模态是主导模态,符合转静干涉理论。当转速降至1350r/min时,此时3BPF(1350Hz)略低于6模态对应的截止频率1369Hz(如表 2所示),可以发现6模态对应幅值已不占优,此时主导模态为-5~5模态。这一现象充分证明了表 2和表 3中的截止频率和截止转速是正确的。当转速降为1050r/min时,此时3BPF(1050Hz)处的模态分解情况显示主导模态为-4~4模态,±5模态被截止(表 2中显示±4对应截止频率是970Hz,±5对应截止频率是1171Hz)。这些模态分解结果都与进气畸变与转子干涉产生噪声的模态分布完全吻合。
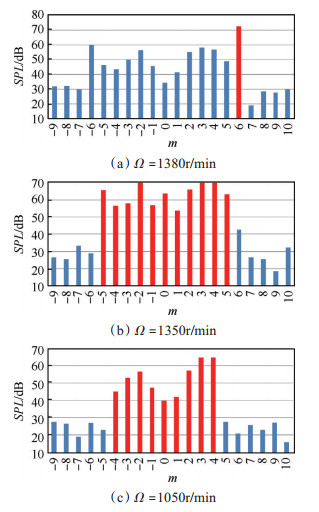
|
Fig. 7 Mode amplitude of noise at 3BPF |
从图 7还可以看出,当理论存在可传声模态时,由畸变转子干涉产生的噪声是相对较小的,转静干涉噪声占主导地位。当根据转静干涉噪声理论计算出的所有可传声模态截止之后,畸变转子干涉产生的噪声才占主导地位。
5 结论通过本文研究,得到以下结论:
(1)对各转速下根据Tyler-Sofrin转静干涉噪声理论预测存在可传播模态的各阶BPF的模态分解显示,实际测得的主导模态和依据转静干涉噪声理论预测的主导模态完全相同。
(2)在各转速下理论预测不可能出现可传播模态的1BPF,2BPF频率上实测到了明显的信号峰值。模态分解结果显示,1BPF和2BPF处存在可传声模态,可传声模态分布在关于0模态对称的范围内,随转速提高而扩大。经分析这是由于进气畸变与转子相互干涉产生了噪声。当转静干涉噪声对应的声模态全部被截止后,畸变转子干涉产生的噪声往往会占主导地位。
(3)针对风扇/压气机的噪声特性及控制方法研究中,特别是对此类低速轴流风扇/压气机,仅依据转静干涉噪声理论对其进行模态分析是不完备的,可能会错误地分析其噪声特性,还会使声衬等降噪技术的效果大打折扣。无论在地面还是在高空,进气畸变始终是存在的,只是程度大小不同,进气畸变与转子相互干涉产生的噪声在理论研究和工程实际方面都是不容忽视的。
| [1] |
乔渭阳. 航空发动机气动声学[M]. 北京: 北京航空航天大学出版社, 2010.
(  0) 0) |
| [2] |
王良锋, 乔渭阳, 纪良, 等. 轴流风扇/压气机管道周向声模态的测量[J]. 航空动力学报, 2014, 29(4): 917-926. (  0) 0) |
| [3] |
王良锋, 乔渭阳, 纪良, 等. 风扇进口噪声预测模型的改进[J]. 推进技术, 2015, 36(2): 226-231. (WANG Liang-feng, QIAO Wei-yang, JI Liang, et al. An Improved Prediction Model for Fan Inlet Noise[J]. Journal of Propulsion Technology, 2015, 36(2): 226-231.)
(  0) 0) |
| [4] |
纪良, 乔渭阳, 王良锋, 等. 普通室内机翼尾缘噪声降噪的实验研究[J]. 推进技术, 2015, 36(5): 703-712. (JI Liang, QIAO Wei-yang, WANG Liangfeng, et al. Experimental Investigation of Airfoil Trailing- Edge Noise Reduction in a Normal Indoor Test Bed[J]. Journal of Propulsion Technology, 2015, 36(5): 703-712.)
(  0) 0) |
| [5] |
Tyler J M, Sofrin T G. Axial Flow Compressor Noise Studies[J]. Transactions of the Society of Automotive Engineers, 1962, 70: 309-332.
(  0) 0) |
| [6] |
Holste F, Neise W. Noise Source Identification in a Propfan Modal by Means of Acoustical Near Field Measurements[J]. Journal of Sound and Vibration, 1997, 203(4): 641-665. DOI:10.1006/jsvi.1996.0890
(  0) 0) |
| [7] |
Enghardt L, Zhang Y, Neise W. Experimental Verification of a Radial Mode Analysis Technique Using WallFlush Mounted Sensors[C]. Berlin: 137th Meeting of the Acoustical Society of America, 1999.
(  0) 0) |
| [8] |
Enghardt L, Tapken U, Kornow O, et al. Acoustic Mode Decomposition of Compressor Noise under Consideration of Radial Flow Profiles[R]. AIAA 2005-2833.
(  0) 0) |
| [9] |
Faustmann C, Zerobin S, Spataro R, et al. On the Acoustics of a Turning Mid Turbine Frame with Embedded Design in a Two-Stage Test Turbine[J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power & Energy, 2015, 229(5): 529-538.
(  0) 0) |
| [10] |
Arnold F, Tapken U, Bauers R, et al. Turbomachinery Exhaust Noise Radiation Experments, Part 2: In-Duct and Far-Field Mode Analysis[R]. AIAA 2008-2858.
(  0) 0) |
| [11] |
Huang X. Real-Time Location of Coherent Sound Sources by the Observer-Based Array Algorithm[J]. Measurement Science & Technology, 2011, 22(6): 065501.
(  0) 0) |
| [12] |
Castres F O, Joseph P F. Experimental Investigation of an Inversion Technique for the Determination of Broadband Duct Mode Amplitudes by Use of Near-Field Sensor Arrays[J]. Journal of the Acoustical Society of America, 2007, 122(2): 848-859. DOI:10.1121/1.2747166
(  0) 0) |
| [13] |
Suzuki T, Day B J. Comparative Study on Mode-Identification Algorithms Using a Phased-Array System in a Rectangular Duct[J]. Journal of Sound & Vibration, 2015, 347(7): 27-45.
(  0) 0) |
| [14] |
Sijtsma P, Zillmann J. In-Duct and Far-Field Mode Detection Techniques[R]. AIAA 2007-3439.
(  0) 0) |
| [15] |
Blacodon D. Spinning Mode Analysis of the Acoustic Field Generated by a Turboshaft Engine[J]. Journal of Aircraft, 2015, 29(6): 1073-1079.
(  0) 0) |
| [16] |
Daniel L Sutliff. Turbofan Duct Mode Measurements Using a Continuously Rotating Microphone Rake[J]. International Journal of Aeroacoustics, 2007, 6(2): 147-170. DOI:10.1260/147547207781041859
(  0) 0) |
| [17] |
Sutliff D L. Rotating Rake Turbofan Duct Mode Measurement System[J]. Journal of the Acoustical Society of America, 2005, 118(3): 1864-1864.
(  0) 0) |
| [18] |
Huang X. Compressive Sensing and Reconstruction in Measurements with an Aerospace Application[J]. AIAA Journal, 2013, 51(4): 1011-1016. DOI:10.2514/1.J052227
(  0) 0) |
| [19] |
Yu W, Huang X. Compressive Sensing Based Spinning Mode Detections by In-Duct Microphone Arrays[J]. Measurement Science & Technology, 2016, 27(5): 055901.
(  0) 0) |
| [20] |
Zhou D, Wang X, Chen J, et al. Sound Generation by Non - Synchronously Oscillating Rotor Blades in Turbomachinery[J]. Journal of Sound & Vibration, 2015, 355: 150-171.
(  0) 0) |
| [21] |
Peake N, Parry A B. Modern Challenges Facing Turbomachinery Aeroacoustics[J]. Annual Review of Fluid Mechanics, 2011, 44(1): 227-248.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


