吸气式高超声速飞行器进气道内存在多次激波反射,激波/激波干扰和激波/边界层干扰等现象使得流动变得非常复杂,气动加热问题严重[1]。飞行器长时间在严酷气动环境作用下可能会产生大的结构变形,而变形会对进气道性能带来一定影响[2, 3]。尤其是对于吸气式临近空间飞行器,为了弥补发动机能力的不足,需要在提高升阻比的同时,尽可能地减轻结构重量,所以在结构设计时多采用轻质材料和大型薄壁结构;这种结构设计在高马赫数、长时间飞行条件下气动力/热/结构多物理场间的耦合效应特别突出[4]。因此,针对临近空间长时间巡航飞行的吸气式动力高超声速飞行器,研究多场耦合效应对进气道性能的影响规律是十分有意义的。
气动力/热/结构多场耦合问题是一个交叉融合了空气动力学、传热学和固体力学的非线性耦合问题[5],即使各相关物理场均使用简化方法,耦合计算对计算资源的消耗仍然是巨大的。早期气动力/热/结构耦合分析均以Roger的三个基本假设[6]为基础,对耦合流程进行简化,发展了多种含简化模型的气动力/热/结构多场耦合分析方法,此时的研究对象也多限于平板、机翼等简单外形[7~9]。近些年来,随着计算机水平的不断发展,使用CFD-CTSD全数值方法研究气动力/热/结构多场耦合问题成为主要发展趋势,在该类方法中,气动力和气动热为同一物理场,均由CFD方法同时求解获得。在耦合方法研究方面,Lohner等首次提出了紧耦合和松耦合的概念,并基于其定义的松耦合算法提出了一套适用于气动力/热/结构多场耦合的松耦合计算策略[10];Tran等基于流-固耦合串行交错耦合推进的方法发展了流场、温度场、应力应变场、动网格场的多场耦合计算理论,并开展了翼型与二维平板的多场耦合计算研究[11]。Haupt等则在德国宇航中心DLR主导的IMENS项目的需求之下,采用松耦合方法建立了一套适用于多场耦合分析的数值模拟平台,并针对襟翼缝隙、通用喷管和机头罩开展了算例分析,以验证平台的有效性[12]。
国内在气动力/热/结构多场耦合分析方法方面也开展了大量研究。张兵等[13]采用共享内存技术的方式开发了适用于通用CFD软件和有限元软件的多场耦合计算平台,并针对典型高超声速机翼进行了气动弹性效应分析。李昱霖[14]对近年来国内外针对气动力/热/结构多场耦合开展的研究进行了归纳总结,从物理含义出发对各子学科间的相互耦合关系和建模进行了整理,给出了计算方法和求解思路。中国空气动力研究与发展中心刘磊等[15]首次提出了可供气动力/热/结构多场耦合试验参考的相似准则,并分析了热气动弹性变形对机翼内部温度场的影响。西北工业大学叶坤等[16]基于模态的方法对不同厚度的二维进气道薄壁结构进行了气动弹性分析,指出在进气道的气动设计和结构设计中应考虑气动弹性对性能的影响。大连理工大学刘健等[17]发展了一种适用于多层复杂热防护结构的气-固耦合快速热分析方法,并通过了钝锥、圆柱等算例的考核。总的来说,国内尽管在飞行器气动力/热/结构多场耦合效应方面已进行了大量研究,但针对进气道前体由于多场耦合效应带来的热气动弹性变形影响研究开展还相对比较少。
本文以吸气式高超声速进气道为研究对象,采用中国空气动力研究与发展中心自主开发的热环境/热响应耦合计算分析平台FL-CAPTER[18]对进气道前体的气动力/热/结构多场耦合效应进行了数值模拟研究,分析了长时间巡航状态下进气道前体多场耦合效应,获得了进气道前体压缩面和唇口由于多场耦合效应带来的变形量,研究了热气动弹性变形对进气道入口参数的影响,得到了规律性的认识。
2 数值计算方法本文多场耦合分析采用团队自主研发的具有自主知识产权的热环境/热响应耦合计算分析平台FL-CAPTER。该软件涵盖数值气动热模拟、结构传热模拟、结构应力/应变模拟等功能模块,可开展单独模块的计算或不同物理场间的耦合计算,软件经过大量考核验证,在多个型号中得到了广泛应用[18~20]。
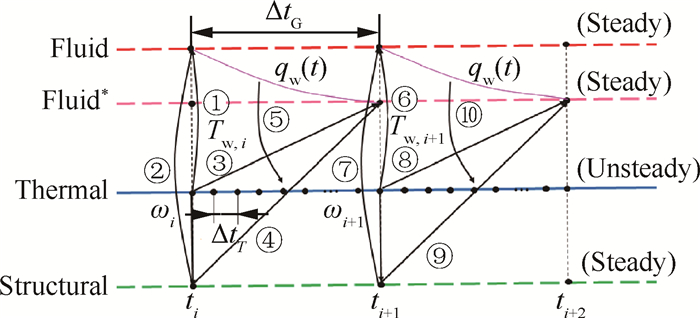
2.1 多场耦合策略考虑到工程实际应用中的效率问题,不同物理场间的耦合方法采用时间修正的松耦合方法,具体如图 1所示。
|
Fig. 1 Fluid-thermal-structural coupling method |
流场计算通过准定常求解三维Navier-Stokes方程获得,温度场通过数值求解三维热传导方程获得,应力应变场通过数值求解弹性力学微分方程组获得。其中,ti是第i阶段的起始时刻,ti+1为第i阶段的终止时刻,ΔtG=ti+1-ti为考虑变形的间隔时间,可随i值变化而变化。在每一阶段,均同时计算ti和ti+1时刻的流场;当温度场以ΔtT的时间步长向前推进时,对应时间曲线上的环境边界通过两端流场解插值获取。结构应力应变分析视为准稳态,针对每一阶段的结束时刻ti+1开展基于该时刻压力和温度分布的应力应变场求解并据此更新计算外形。同时,计算过程中充分考虑交界面上的数据传递,流场计算时均假定存在ti时刻的壁温分布。在将环境热流传递至壁温边界条件时,引入对应温度条件下的热壁修正公式以加快收敛速度,此时热壁修正公式表示为
| $ {q_{{T_{i + N \cdot {\rm{\Delta }}i}}}} = {q_{{T_i}}} \cdot \frac{{\left( {{h_{{\rm{re}}}} - {h_{{T_{i + N \cdot {\rm{\Delta }}i}}}}} \right)}}{{\left( {{h_{{\rm{re}}}} - {h_{{T_i}}}} \right)}} $ | (1) |
式中Ti为ti时刻的温度分布,Ti+N·Δi为从ti时刻推进N时间迭代步时的结构温度分布,q为热流,h为焓值。
2.2 各物理场计算方法流场计算基于结构网格,采用有限体积方法数值求解三维Navier-Stokes控制方程组。在空间离散方面,单元重构采用带有Van-Albada限制器的MUSCL(Monotonic Upstream-Centered scheme for Conservation Laws)方法,无粘通量计算采用Hanel修正的van Leer通量向量分裂方法,粘性通量计算采用传统的二阶中心格式,时间推进方面采用LU-SGS隐式迭代方法,湍流模型采用基于两方程的SST湍流模型。同时,计算时需要考虑壁面温度变化的影响,以结构传热获得的壁面温度作为壁面边界条件。
温度场求解基于非结构网格单元,采用有限体积方法,通过求解热传导控制方程得到。单元边界面上的温度梯度由高斯定理得到,时间方向采用二阶Runge-Kutta方法进行离散。外形有气流流过的面采用对流加热边界,其它部分为绝热边界。在材料交界面处,根据热流在界面处的唯一性和连续性,得到交界面处的等效导热系数,从而得到交界面处的热流。
应力/应变场分析控制方程为不考虑内热源与体载荷的热弹性力学控制方程,采用有限元方法对弹性力学控制方程组进行求解。对于物体受热产生的应力问题,物体由于热膨胀一般主要产生线应变,而剪切应变为零。这种由于热变形产生的应变可以看出初应变,对于普通问题,稳态热应力计算在温度场分析后进行。
2.3 网格变形技术飞行器由于多场耦合效应产生局部变形,需采用网格变形技术使计算网格在保留当前网格拓扑结构不变的前提下,准确反映出物面边界的形状变化,更新计算外形。
目前,常见的网格变形技术有:代数插值法、弹簧法、弹性体法、Delaunay图法和径向基函数法(RBF)等[21, 22]。以上方法均有各自的特点和适用范围。对气动力/热/结构多场耦合问题,一般不会出现极大变形的极端情况。所以本文采用RBF网格变形技术。
RBF网格变形技术的基本原理是运用径向基函数对物面边界网格点的位移进行插值或拟合,并利用构造出的径向基函数序列将物面的位移效应光滑的分散到整个网格区域节点上。基于径向基函数的基本原理,网格位移可表示为
| $f\left( \mathit{\boldsymbol{r}} \right) = \sum\limits_{i = 1}^N {{w_i}\varphi \left( {\left\| {\mathit{\boldsymbol{r}} - {\mathit{\boldsymbol{r}}_i}} \right\|} \right)} $ | (2) |
式中,对本文研究对象,r为空间任意一点的位置,f(r)为该点的网格位移,ri为第i个物面插值结点的位置,φ为所选用的某种径向基函数,‖r-ri‖为该空间点至第i个物面插值结点的距离,wi为与第i个插值结点对应的权重系数,N为选用的径向基函数的总数目。
网格变形的结果依赖于径向基函数的选取,本文研究采用Wendland’s C2径向基函数,其表达式为
| $ \varphi \left( \zeta \right) = {\left( {1 - \zeta } \right)^4}\left( {4\zeta + 1} \right) $ | (3) |
为验证本文提出的流场/传热耦合方法的有效性,采用经典的高超声速二维圆管开展了算例验证[23, 24]。计算模型可近似为一无限长圆管,其外半径为38.1mm,内半径为25.4mm。圆管材料为不锈钢,计算的来流马赫数为6.47,来流压力为648.1Pa,来流温度为241.5K,结构初始温度为294.4K,计算假设为层流状态。
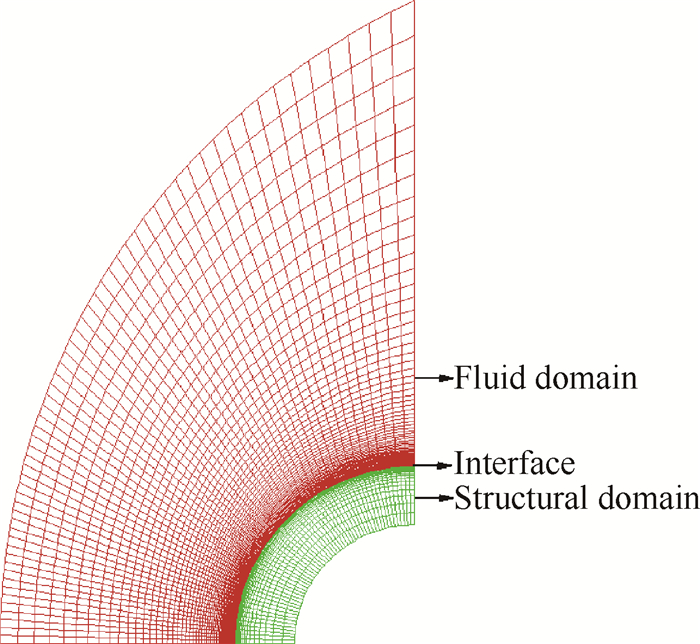
计算网格如图 2所示,流体域和固体域均采用结构网格。对1/4圆管,流场网格数为100×61,物面附近第一层网格雷诺数约为8,固体区域网格数为60×30。
|
Fig. 2 Grids of the tube |
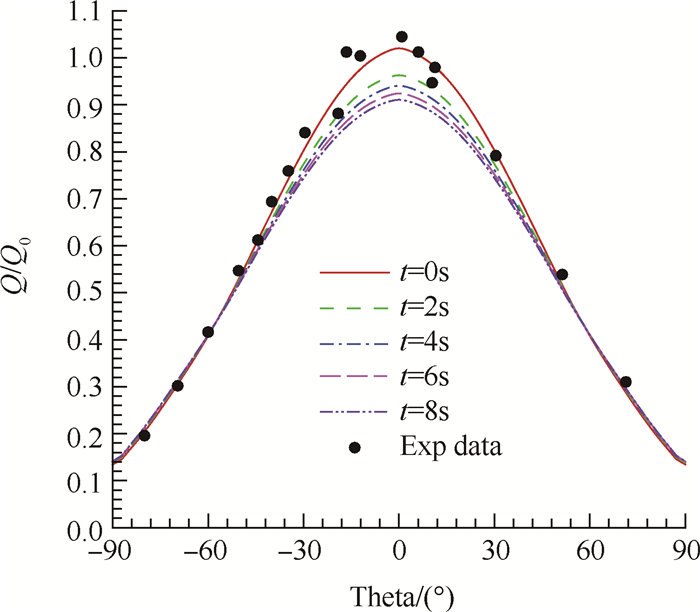
图 3给出了计算得到的圆管表面热流与试验结果的对比曲线,图中纵坐标热流以初始时刻驻点热流进行无量纲化,横坐标为圆管周向角度,驻点位置对应0°。可以看出,计算得到的圆管表面热流与试验吻合较好,随着圆管加热时间的不断增加,圆管温度越来越高,边界层内的温度梯度越来越小,物面热流密度不断下降。
|
Fig. 3 Comparison of the heat flux between computation and experiment |
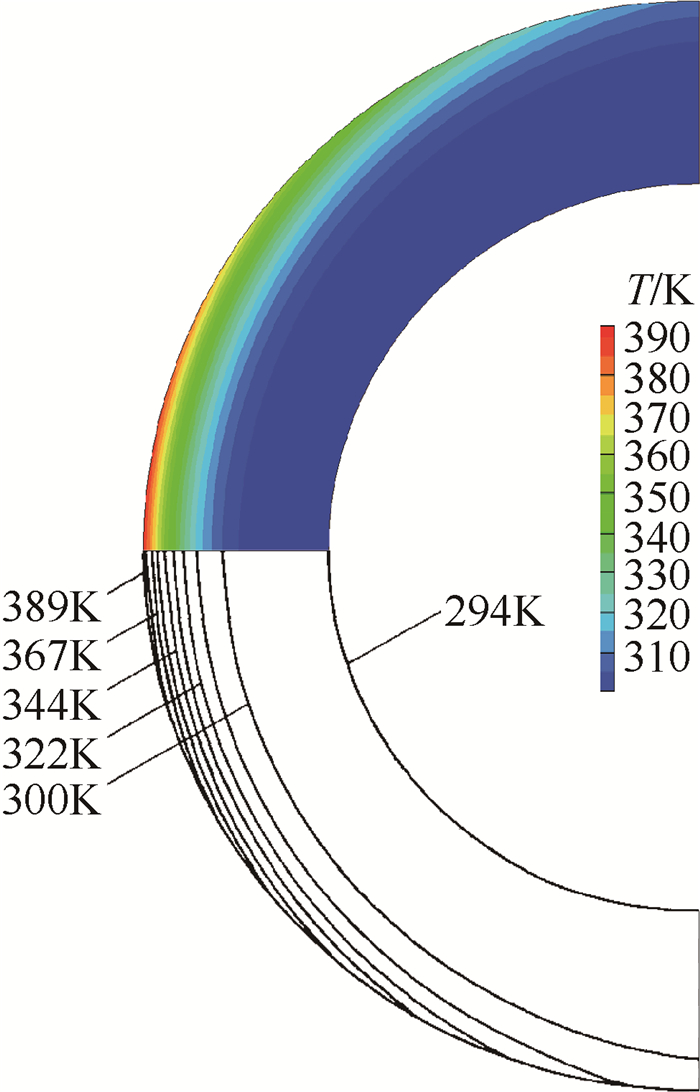
图 4给出了2s时刻本文计算的结构内部温度分布与Wieting团队[24]数值模拟的温度分布对比图。可以看到,本文与文献的计算结果无论是定性还是定量讲都是一致的,计算的最大温度均位于圆管前缘驻点区域,量值约为389K,验证了本文流场/传热耦合计算方法的可靠性。
|
Fig. 4 Comparison of the temperature distribution between computation and reference at t=2s |
结构变形特征作为高超声速飞行器在气动力/热/结构多场耦合作用下的宏观表现,其预测的准确性至关重要。为此,自主设计了用于多场耦合计算方法验证的两级压缩楔外形,并在中国空气动力研究与发展中心Φ0.6m高温高超声速风洞中开展了初步验证性试验。
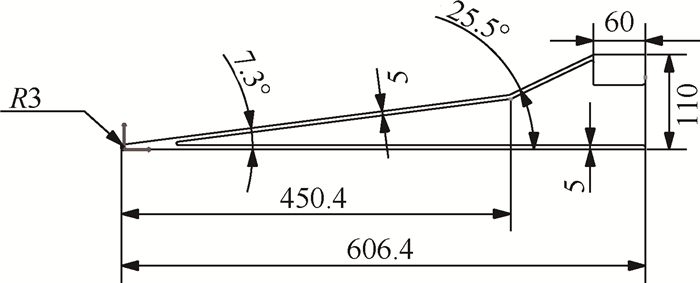
风洞试验模型详细尺寸如图 5所示,模型材质为不锈钢,模型厚度为5mm,风洞试验马赫数为5.5,来流攻角为10°,来流静压3506.6Pa,来流静温208K,风洞试验时间10s。考虑到加装测压、测热传感器可能对模型的刚度和强度带来一定影响,暂未开展压力和热流等数据的测量,通过前景照明成像技术获得了模型宏观变形量。
|
Fig. 5 Size of the experimental model (mm) |
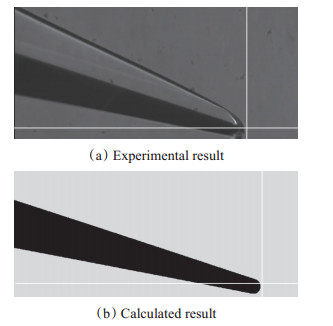
图 6给出了采用前景照明成像技术获得的7s时刻模型宏观变形量对比,图中标线位置为模型安装的起始位置,起始时刻模型背风面最低点和最前端与标线重合。可以看出,模型结构在气动力和气动热共同作用下产生了连续的变形,7s时刻模型发生了较大的宏观可见变形量,多场耦合计算得到的模型宏观变形量与风洞试验采用光学方法测量得到的变形量具有较好的一致性。
|
Fig. 6 Comparison of the calculated displacement with the experimental data at t=7s |
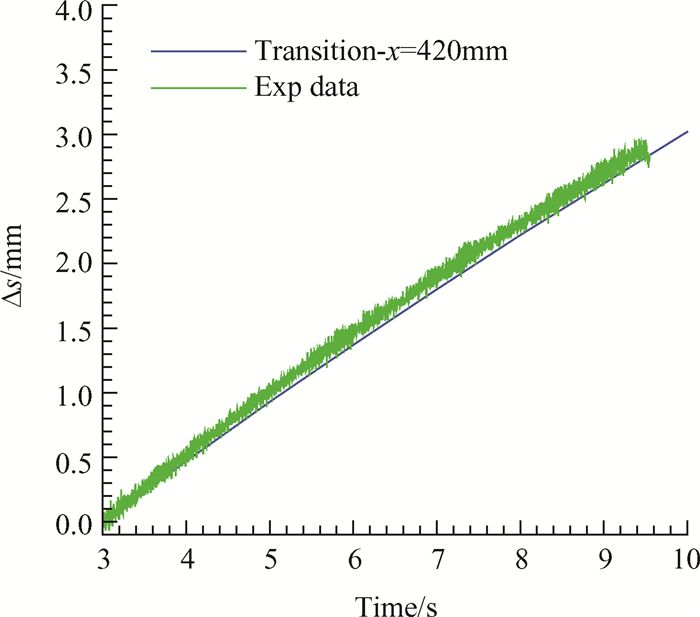
为了量化多场耦合效应对模型宏观变形量的影响,结合高速摄影和图像处理技术,得到了模型在不同时刻下的宏观变形量。考虑到风洞试验初期,流场建立过程中模型存在轻微的振动,会对辨识出来的模型变形量产生一定影响,这里暂不做分析。在3s以后,风洞流场气流趋于稳定,此时的实验数据在软件考核方面具有重要的参考价值。图 7给出了流场稳定后数值预测得到的模型最大变形量相对3s时刻的变形量差值与试验数据的对比曲线,流场模拟时考虑了转捩影响,转捩位置根据γ-Reθ的关联转捩模型[25]预测获得,对应的转捩位置在压缩拐角附近,即x=420mm处。可以看出,数值预测得到的变形量增量与风洞试验结果吻合较好,模型整体变形量与变形趋势基本保持一致,初步验证了本文多场耦合分析方法的有效性。
|
Fig. 7 Comparison of the maximum displacement history between computation and experiment |
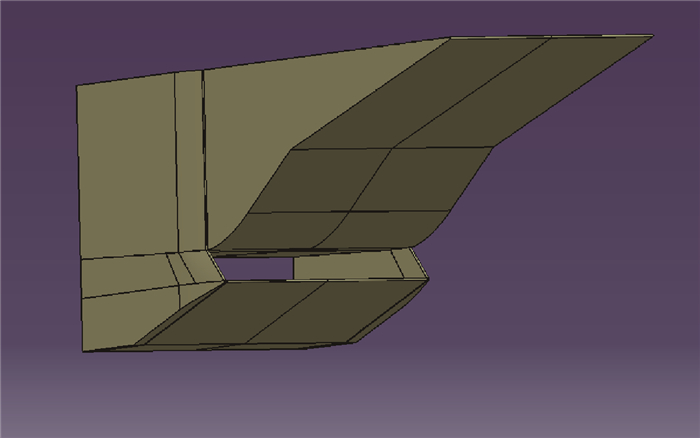
本文针对带侧板的二元高超声速进气道外形,开展多场耦合效应分析研究。该进气道构型基于德宇航GK-01进气道外形[26],设计马赫数7.0,模型总长度为585mm,两级压缩面相对水平方向夹角分别为9°和20.5°,唇口平直,肩部采用等熵膨胀曲面过渡到喉道,两侧侧板采用后掠设计,后掠角度为60°,进气道捕获面积为100mm×100mm,前缘半径为0.5mm,具体外形如图 8所示。
|
Fig. 8 Configuration of the analyzed inlet model |
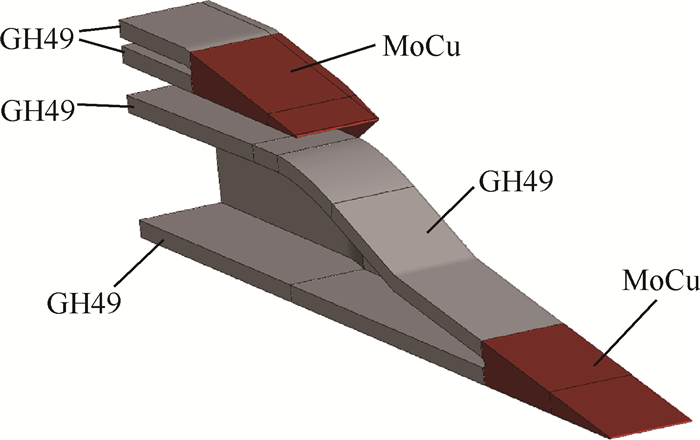
带侧板的二元高超声速进气道模型结构防热方案如图 9所示,为钼渗铜和高温合金GH49组合的材料配置方案。其中,钼渗铜区域和侧板区域为实心结构,其它GH49区域为薄壁结构,薄壁结构的厚度取为10mm,侧板厚度取为5mm。相关防热材料的物性参数见文献[27]。
|
Fig. 9 Material properties of the inlet model |
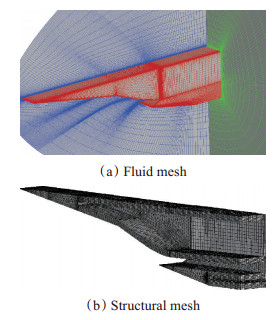
流场和结构场计算网格如图 10所示。流场计算采用多块对接结构网格,半模网格总量约为320万,边界层内网格第一层间距取1μm,对应网格雷诺数约为7,网格第一层间距满足y+<1。结构场计算采用三棱柱和六面体混合的网格单元,网格总量约为4.8万,其中三棱柱单元1.6万,六面体单元3.2万。温度场和应力应变场计算采取相同网格节点不同边界条件的方式实现。
|
Fig. 10 Meshes of the inlet model |
针对本文研究的进气道构型和材料配置方案,采用FL-CAPTER软件,进行了多场耦合效应数值模拟分析。具体计算条件为:巡航马赫数7.0,攻角0°,飞行高度23.5km,气动加热时间共计60s。
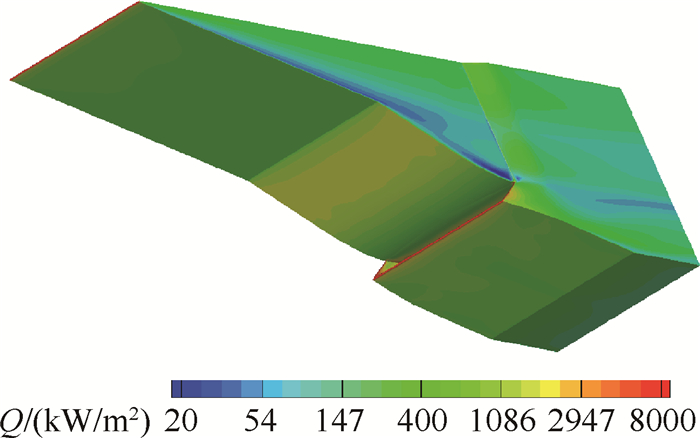
图 11给出了数值模拟得到的进气道表面热流分布云图。可以看出,高热流区域主要集中在压缩面前缘、进气道唇口以及喉道内存在复杂激波/激波、激波/边界层干扰的区域;进气道侧板前缘由于存在一定的后掠角,使得其峰值热流低于进气道唇口位置。进气道唇口前缘虽然半径与压缩面前缘相同,但由于激波干扰作用,其热流明显高于压缩面前缘。
|
Fig. 11 Heat flux of the inlet surface |
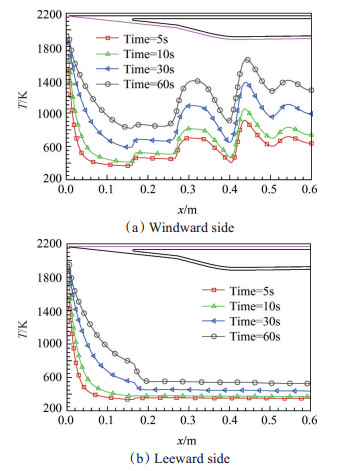
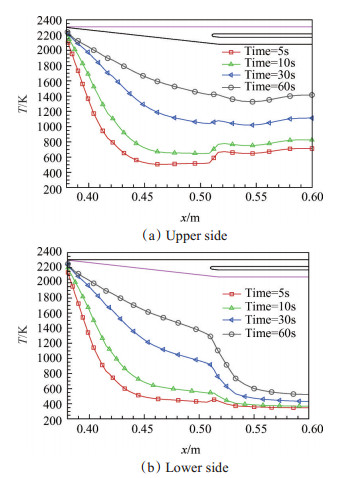
图 12和图 13分别给出了进气道压缩面和进气道唇口附近不同时刻的温升情况对比。可以看出,高温度区域与高热流区域相对应,结构最大温度出现在压缩面前缘和唇口前缘位置,且温升速度很快,其中,唇口前缘由于存在激波/激波干扰现象,热流较压缩面前缘更高,温升也更快。二级压缩面区域和喉道内存在激波/边界层干扰现象的区域也会形成温度局部峰值区域,但其温升速率较前缘位置更低。此外,随着传热时间的推进,模型表面温度逐渐升高,内外壁面温差逐渐减小,但背风区的温度值一直处于较低水平。
|
Fig. 12 Comparison of temperature distribution at different times in the compression ramp zone |
|
Fig. 13 Comparison of temperature distribution at different times in the cowl zone |
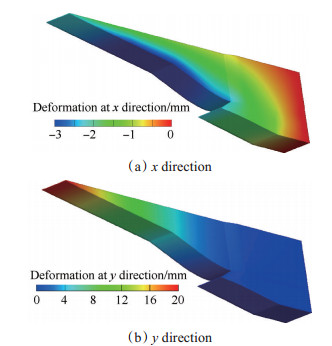
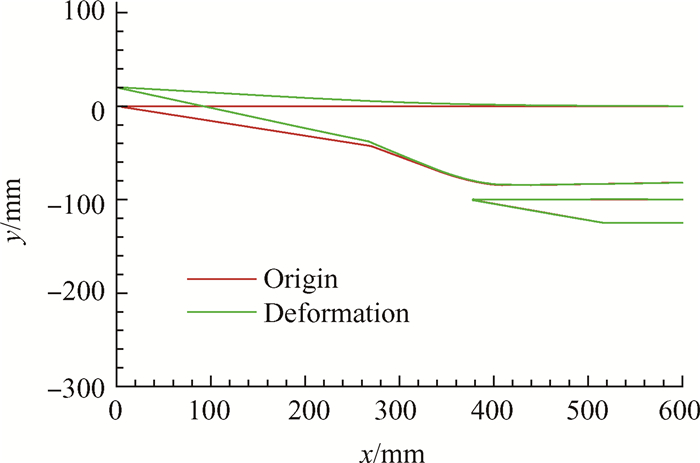
结构温度的变化不仅会引起材料特性发生变化,不均匀的温度分布还会引起热应力,进而改变结构刚度。图 14给出了进气道模型表面的位移量云图,图 15给出了模型变形前后外轮廓的对比。可以看出,变形主要发生在y方向,即模型的俯仰方向,其它方向的位移很小;模型的最大位移发生在进气道前体压缩面最前端,上翘约20mm,进气道唇口处由于侧板的连接,起到了一定的加固、约束的作用,唇口变形量相对较小。轴向位移最大位置产生在二级压缩面附近,方向指向模型后方,最大变形量约为3mm。
|
Fig. 14 Displacement contour of the inlet model |
|
Fig. 15 Outer contour of the inlet model before and after deformation |
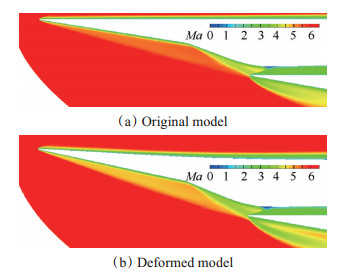
进气道前体压缩面变形会对进气道性能产生一定影响。图 16给出了由于多场耦合效应带来的变形对进气道中心剖面马赫数分布云图的影响对比。可以看出,由多场耦合效应引起的结构变形使得进气道偏离设计状态,激波入射点位置不再位于唇口附近,激波边界层干扰效应增强,喉道附近的分离区域有所增大。
|
Fig. 16 Effects of the deformation on the Mach number contour of the inlet model |
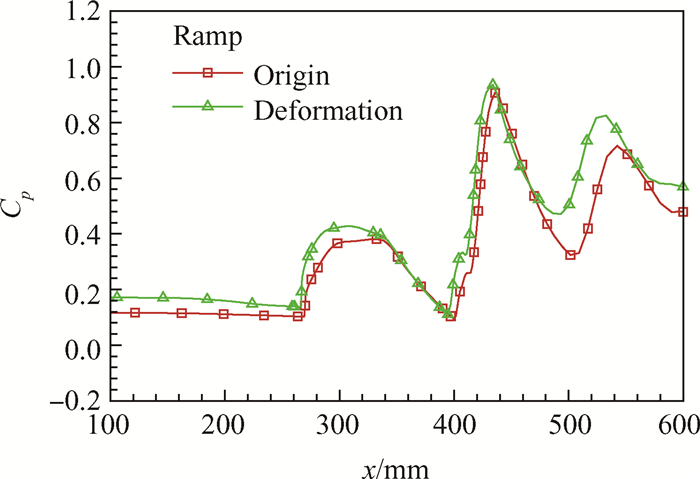
图 17给出了变形前后进气道压缩面的压力分布对比。可以看出,进气道前体压缩面发生上翘后,进气道的捕获面积增大,压缩面上当地攻角变大,导致压力分布有所增高,考虑结构变形后进气道内的静压较无变形情况更高。表 1给出了多场耦合带来的热变形对进气道入口参数的影响对比。可以看出,多场耦合效应带来的变形使得进气道内的质量流量有所增大,相比无变形状态,变形后质量流量增加约4.2%,喉道截面的平均马赫数降低,压力逐渐升高,总压恢复系数逐渐降低。
|
Fig. 17 Pressure distribution of the inlet's compression ramp before and after deformation |
|
|
Table 1 Effects of the coupling induced deformation on inlet parameters of the hypersonic intake |
本文针对吸气式高超声速进气道,采用FL-CAPTER软件研究了多场耦合效应对进气道入口参数的影响,得到以下结论:
(1)本文针对两级压缩楔外形计算获得的模型变形量与风洞试验吻合较好,说明建立的多场耦合分析方法可用于飞行器气动力/热/结构多场耦合效应分析。
(2)对吸气式高超声速进气道,喉道附近存在复杂的激波/边界层干扰现象,气动加热严重,结构温度快速升高;背风区域气动加热作用小,温升较慢,不均匀的温度分布引起热应力,使得模型刚度发生变化,产生了一定的变形量。
(3)在本文的计算条件下,多场耦合效应使得进气道前体压缩面发生向上的位移,最大位移量约为20mm,考虑变形影响后,进气道偏离设计状态,激波边界层干扰效应增强,喉道附近的分离区域有所增大,进气道入口的质量流量增加约4.2%,喉道平均马赫数降低,静压升高,总压恢复系数降低。
本研究基于马赫7条件下的巡航飞行状态开展。在该马赫数下,来流总温较高,分析时间内所设计的防热结构方案已趋于材料温度极限,但开展的多场耦合效应对进气道入口参数的影响规律仍具有一定的参考意义。在进行进气道结构设计时,应重视多场耦合变形带来的影响,尽量选用刚度较大的材料或通过增加加强筋等结构加固措施抵抗变形。
| [1] |
Kazmar R R. Airbreathing Hypersonic Propulsion at Pratt & Whitney-Overview[R]. AIAA 2005-3256.
(  0) 0) |
| [2] |
Heather K, Francisco P, Juan J A. Sensitivity of the Performance of a 3-Dimensional Hypersonic Inlet to Shape Defomations[R]. AIAA 2014-3228.
(  0) 0) |
| [3] |
杨顺凯, 张堃元, 王磊. 高超声速进气道弹性压缩面自适应无源控制概念研究[J]. 推进技术, 2015, 36(11): 1633-1639. (YANG Shun-kai, ZHANG Kun-yuan, WANG Lei. Research on Self-Adaptive and Passivity-Based Control Concept of Hypersonic Adjustable inlet with Elastic Compression Surface[J]. Journal of Propulsion Technology, 2015, 36(11): 1633-1639.)
(  0) 0) |
| [4] |
Witeof Z D, Neergaard L J, Vanderwyst A S. Dynamic Fluid-Thermal-Structural Interaction Effects in Preliminary Design of High Speed Vehicles[R]. AIAA 2016-1321.
(  0) 0) |
| [5] |
McNamara J J, Friedmann P P. Aeroelastic and Aerothermoelastic Analysis in Hypersonic Flow: Past, Present, and Future[J]. AIAA Journal, 2011, 19(6): 1089-1122.
(  0) 0) |
| [6] |
Roger M. Aerothermoelasticity[J]. Aerospace Engineering, 1958, 17(10): 34-43.
(  0) 0) |
| [7] |
Culler A J, Mcnamara J J. Impact of Fluid-Thermal-Structural Coupling on Response Prediction of Hypersonic Skin Panels[J]. AIAA Journal, 2011, 49(11): 2393-2406. DOI:10.2514/1.J050617
(  0) 0) |
| [8] |
Ericsson L E, Almroth B O, Bailie J A. Hypersonic Aerothermoelastic Characteristics of a Finned Missile[J]. Journal of Spacecraft, 1979, 16(3): 187-192. DOI:10.2514/3.57641
(  0) 0) |
| [9] |
Gee D J, Sipcic S R. Coupled Thermal Model for Nonlinear Panel Flutter[J]. AIAA Journal, 1999, 37(5): 642-650. DOI:10.2514/2.765
(  0) 0) |
| [10] |
Lohner R, Yang C, Cebral J. Fluid-Structure-Thermal Interaction Using a Loose Coupling Algorithm and Adaptive Unstructured Grids[R]. AIAA 98-2419.
(  0) 0) |
| [11] |
Tran H, Farhat C. An Integrated Platform for the Simulation of Fluid-Structure-Thermal Interaction Problems[R]. AIAA 2002-1307.
(  0) 0) |
| [12] |
Haupt M C, Niesner R, Unger R, et al. Computational Aero-Structural Coupling for Hypersonic Applications[R]. AIAA 2006-3252.
(  0) 0) |
| [13] |
张兵, 韩景龙. 多场耦合计算平台与高超声速热防护结构传热问题研究[J]. 航空学报, 2011, 32(3): 400-409. (  0) 0) |
| [14] |
李昱霖. 气动热结构多学科分析及高效优化策略研究[D]. 北京: 北京理工大学, 2014. http://cdmd.cnki.com.cn/article/cdmd-10007-1014086709.htm
(  0) 0) |
| [15] |
刘磊. 高超声速飞行器热气动弹性特性及相似准则研究[D]. 绵阳: 中国空气动力研究与发展中心, 2014. http://cdmd.cnki.com.cn/Article/CDMD-90113-1015551898.htm
(  0) 0) |
| [16] |
叶坤, 叶正寅, 屈展. 高超声速进气道气动弹性的影响研究[J]. 推进技术, 2016, 37(12): 2270-2277. (YE Kun, YE Zheng-yin, QU Zhan. Effects of Aeroelasticity on Performance of Hypersonic Inlet[J]. Journal of Propulsion Technology, 2016, 37(12): 2270-2277.)
(  0) 0) |
| [17] |
刘健, 原志超, 杨凯, 等. 高超声速飞行器多层复杂热防护结构气-固耦合快速热分析方法[J]. 推进技术, 2016, 37(2): 227-234. (LIU Jian, YUAN Zhi-chao, YANG Kai, et al. Fast Algorithm of Coupled Flow-Thermal for Multi-Layered Complex TPS of Hypersonic Aircraft[J]. Journal of Propulsion Technology, 2016, 37(2): 227-234.)
(  0) 0) |
| [18] |
桂业伟, 刘磊, 耿湘人, 等. 气动力/热与结构多场耦合计算策略与方法研究[J]. 工程热物理学报, 2015, 36(5): 1047-1051. (  0) 0) |
| [19] |
桂业伟, 刘磊, 杜雁霞. 热防护系统耦合分析方法与应用[J]. 现代防御技术, 2014, 42(4): 9-14. (  0) 0) |
| [20] |
刘磊, 桂业伟, 耿湘人, 等. 热气动弹性变形对飞行器结构温度的影响研究[J]. 空气动力学报, 2015, 33(1): 31-35. (  0) 0) |
| [21] |
张伟伟, 高传强, 叶正寅. 气动弹性计算中网格变形方法研究进展[J]. 航空学报, 2014, 35(2): 303-319. (  0) 0) |
| [22] |
Rendall T C S, Allen C B. Efficient Mesh Motion Using Radial Basis Functions with Data Reduction Algorithms[J]. Journal of Computational Physics, 2009, 229(7): 6231-6249.
(  0) 0) |
| [23] |
Dettmer W, Peri D. A Computational Framework for Fluid-Rigid Body Interaction: Finite Element Formulation and Applications[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195: 1633-1666. DOI:10.1016/j.cma.2005.05.033
(  0) 0) |
| [24] |
Wieting A R. Experimental Study of Shock Wave Interference Heating on a Cylindrical Leading Edge[R]. NASA TM-100484, 1987.
(  0) 0) |
| [25] |
Langtry R. A Correlation-Based Transition Model Using Local Variables for Unstructured Parallelized CFD Codes[D]. Stuttgrart: Stuttgrart University, 2006.
(  0) 0) |
| [26] |
Hohn O, Gulhan A. Experimental Investigation on the Influence of Yaw Angle on the Inlet Performance at Mach 7[R]. AIAA 2010-938.
(  0) 0) |
| [27] |
《中国航空材料手册》编委会. 中国航空材料手册(第2卷). 变形高温合金铸造高温合金(第2版)[M]. 北京: 中国标准出版社, 2002.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


