液体火箭发动机尾焰具有高温、高速、大流量的特点[1],其具有强烈的红外辐射特性,对红外预警、追踪及发动机热防护等具有重要指导意义。液体火箭尾焰射流为富燃燃气,未完全燃烧的高温燃气在进入环境大气后与空气中氧气掺混发生复燃反应,进而改变尾焰流场特性。尾焰的红外辐射特性主要取决于尾焰温度及主要辐射组分浓度,因此复燃反应会对尾焰红外辐射特性产生一定影响[2]。由于复燃反应的计算涉及到复杂的化学反应机理,导致仿真计算难度和工作量大大增加,因此深入研究复燃反应对尾焰红外辐射特性的影响对实际应用有重要意义。
国内外针对火箭发动机尾焰辐射特性的研究以仿真计算为主,目前,关于发动机尾焰红外辐射特性的研究已取得许多成果。王伟臣等[3]采用流场与辐射传输耦合计算的方法研究了火箭发动机羽流近场的红外辐射特性。郑才浪等[4]采用有限体积法研究了固液火箭发动机尾焰的红外辐射特性;申文涛等[5]对不同飞行状态下的固液火箭尾焰红外辐射特性进行了研究;丰松江等[6]研究了燃烧室内燃烧模型对尾焰辐射特性的影响;Lenoe D M等[7]研究了尾焰成分在高空发生复燃反应对同温层的影响;姜毅等[8]研究了复燃对固体火箭尾焰流场的影响;刘尊洋等[9]研究了固体粒子对固体火箭复燃尾焰红外辐射特性的影响;蔡红华等[10]研究了复燃对液氧煤油发动机尾焰冲击特性的影响。上述成果从不同角度研究了火箭发动机尾焰红外辐射特性,为尾焰辐射特性研究奠定了基础。
目前,关于固体火箭尾焰复燃流场的研究较为成熟,而针对液体火箭尾焰复燃流场的研究还不完善,仍需进一步研究。本文则关于复燃反应对液体火箭尾焰红外辐射特性的影响以及相关影响因素进行了深入研究。
本文研究了复燃反应对液体火箭发动机尾焰流场特性的影响,探究了尾焰复燃对红外辐射特性的影响,并进一步讨论了飞行条件改变对复燃尾焰红外辐射特性产生的影响,较为全面地分析了液体火箭尾焰复燃对流场及红外辐射特性的影响。
2 物理模型和计算方法 2.1 控制方程控制方程采用二维N-S方程来描述,其质量、动量和能量方程的基本形式[11]为
| $ \frac{{\partial \left( {\rho \phi } \right)}}{{\partial t}} + {\rm{div}}\left( {\rho U\phi } \right) = {\rm{div}}\left( {{\mathit{\Gamma} _\phi }{\rm{grad}}\phi } \right) + {S_\phi } $ | (1) |
式中ϕ为通用变量,代表u, v, T等变量;ρ为流体密度;U为速度矢量,Γϕ为对应于ϕ的扩散系数,Sϕ为相应的源项。
2.2 流场模型采用FLUENT软件计算复燃尾焰流场,求解基于密度的隐式求解器,耦合求解连续方程、能量方程和组分输运方程。喷管壁面采用标准壁面函数处理;湍流模型采用Standard k-ε双方程模型[12]。
2.3 有限速率化学反应模型尾焰复燃反应主要发生在近场燃气与空气混合区域,该区域为超声速区域,故选择有限速率化学反应模型[13]。化学反应源项根据Arrhenius公式计算,其中第r个反应的化学方程式为
| $ \sum\limits_{i=1}^{N}{{{{{v}'}}_{i,r}}{{M}_{i}}}\underset{{{k}_{\text{b},r}}}{\overset{{{k}_{\text{f},r}}}{\mathop{\rightleftarrows }}}\,\sum\limits_{i=1}^{N}{{{{{v}''}}_{i,r}}{{M}_{i}}} $ | (2) |
式中N为系统化学物质总数目,ν’i, r,ν”i, r分别为反应物和生成物的化学计量数,Mi为组分的化学式,kf, r,kb, r分别为正向和逆向的化学反应速率常数。
根据Arrhenius公式,正向反应速率为
| $ {k_{{\text{f}}, r}} = {A_r}{T^{{\beta _r}}}\exp \left( {-{E_r}/RT} \right) $ | (3) |
式中Ar为指前因子,βr为温度指数,Er为反应活化能,单位为kJ/mol,R为通用气体常量,单位为J/(mol·K)。
化学反应引起组分i净生成率Ri, r为
| $ {R_{i, r}} = \mathit{\Gamma} \left( {{{v''}_{i, r}}- {{v'}_{i, r}}} \right)\left( {{k_{{\text{f}}, r}}\prod\limits_{j = 1}^N {{{\left[{{C_{j, r}}} \right]}^{{{\eta '}_{j, r}}}}} - {k_{{\text{b}}, r}}\prod\limits_{j = 1}^N {{{\left[{{C_{j, r}}} \right]}^{{{\eta ''}_{j, r}}}}} } \right) $ | (4) |
式中Γ为第三体因素,[Cj, r]为反应物组分摩尔浓度,η’j, r、η”j, r为正(逆)向反应速率。
能量方程中化学反应源项Sh表达式为
| $ {S_h} =-\sum\limits_i {\frac{{h_i^0}}{{{M_{w, i}}}}{R_i}} $ | (5) |
式中hi0为气体组分i的标准生成焓。
2.4 气体辐射参量本文采用化学反应模型包括12种组分,对于液体火箭发动机,燃烧产物中主要辐射组分为CO2和H2O,因此本文基于HITRAN 2008及HITEMP 2010数据库[14],采用逐线积分法计算各气体组分的光谱吸收系数。混合气体的光谱吸收系数[15]为各气体组分光谱吸收系数的代数和,根据如下经验公式计算
| $ {\kappa _\alpha } = \frac{{273C \cdot p}}{{1 \times {{10}^5}T}}{\kappa _{{\text{STP}}}} $ | (6) |
式中C为气体组分的摩尔百分数;p为气体实际压强(Pa);T为气体实际温度(K);κSTP为标准温度水平的光谱吸收系数(cm-1)。
2.5 反向蒙特卡洛法反向蒙特卡洛法(BMC)是终点开始,逆向追踪光束路径,从而确定沿路径发射的辐射能进入探测器的数量,其主要依据为辐射传递中的交易原理[16]。BMC法在处理小面元或者小立体角接收到能量辐射量问题时非常有效,利用发射、反射和吸收等传递过程的概率模型,统计到达被测目标的各个体元和面元的热射线数量。
如图 1所示,从面元0沿着θ角方向在立体角dΩ内发射的能量被其他面元i和体元j沿着θk角方向在微元立体角dΩk吸收的能量可以表示为
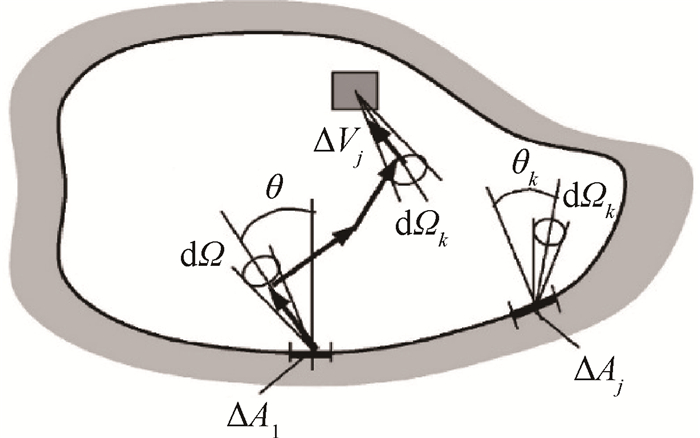
|
Fig. 1 Radiation transfer sketch of BMC method |
| $ {Q_{0 \to i}} = \Delta {A_0}{\varepsilon _0}\cos \theta d\mathit{\Omega} {I_{\text{b}}}\left( {{T_0}} \right)R{D_{0, ik}} $ | (7) |
| $ {Q_{0 \to j}} = \Delta {A_0}{\varepsilon _0}\cos \theta {\text{d}}\mathit{\Omega} {I_{\text{b}}}\left( {{T_0}} \right)R{D_{0, jk}} $ | (8) |
式中ε0是微元面的发射率,ΔA0是面元0的面积,Ib(T0)是对应温度下的黑体辐射强度,RD0, jk使辐射传递因子,即由面元0在立体角dΩ内发射的能量被其他面元i或体元j以微元立体角dΩk吸收的能量比例因子,其中考虑直接辐射部分以及各种可能的反射等过程。
同理,面元i或者体元j沿着θk角方向在微元立体角dΩk发射出来的能量被面元0沿着θ角方向在微元立体角dΩ吸收的能量可以表示为
| $ {Q_{i \to 0}} = \Delta {A_i}{\varepsilon _i}\cos {\theta _k}{\text{d}}{\mathit{\Omega} _k}{I_{\text{b}}}\left( {{T_i}} \right)R{D_{i, k0}} $ | (9) |
| $ {Q_{j \to 0}} = {\kappa _j}{\text{d}}{\mathit{\Omega} _k}\Delta {V_j}{I_{\text{b}}}\left( {{T_j}} \right)R{D_{j, k0}} $ | (10) |
式中κj为体元j的吸收系数,ΔAi是面元i的面积,ΔVj是体元j的体积,辐射传递因子RDj, k0或者RDi, k0是指从面元i或者体元j发射出来的能量沿着θ角方向在立体角dΩ内进入面元0的能量的比例因子。
若T0=Ti或T0=Tj,则面元ΔA0与面元ΔAi或体元ΔAj之间无净热交换,即Q0→i=Qi→0或Q0→j=Qj→0。
若T0=Ti或T0=Tj,Ib(T0)=Ib(Ti)或Ib(T0)=Ib(Tj),则可计算得到以下关系,即
| $ \Delta {A_0}{\varepsilon _0}\cos \theta {\text{d}}\mathit{\Omega} R{D_{0, jk}} = \Delta {A_i}{\varepsilon _i}\cos {\theta _k}{\text{d}}{\mathit{\Omega} _k}R{D_{j, k0}} $ | (11) |
| $ \Delta {A_0}{\varepsilon _0}\cos \theta {\text{d}}\mathit{\Omega} R{D_{0, jk}} = {\kappa _j}{\text{d}}{\mathit{\Omega} _k}\Delta {V_j}R{D_{j, k0}} $ | (12) |
计算出辐射传递因子之后,可以通过上式计算得到面元0在立体角dΩ内所吸收的辐射热量。对于正向蒙特卡洛法模拟,在一个封闭系统内面元ΔA0沿着θ角方向在立体角dΩ内所获得的辐射能量如式(13)所示
| $ \begin{gathered} {Q_0} = \sum\limits_i {\sum\limits_k {\Delta {A_i}\cos {\theta _k}{\text{d}}{\mathit{\Omega} _k}R{D_{i, k0}} \cdot {\varepsilon _i}{I_{\text{b}}}\left( {{T_i}} \right)} } + \hfill \\ \;\;\;\;\;\;\;\sum\limits_j {\sum\limits_k {\Delta V{\text{d}}{\mathit{\Omega} _k}R{D_{j, k0}} \cdot {\kappa _j}{I_{\text{b}}}\left( {{T_j}} \right)} } \hfill \\ \end{gathered} $ | (13) |
BMC法可得到辐射能量如下式所示
| $ \begin{gathered} {Q_0} = \sum\limits_i {\sum\limits_k {R{D_{0, ik}}{I_b}\left( {{T_i}} \right) \cdot \Delta {A_0}{\varepsilon _0}\cos \theta {\text{d}}\mathit{\Omega} + } } \hfill \\ \;\;\;\;\;\;\;\sum\limits_j {\sum\limits_k {R{D_{0, jk}}{I_b}\left( {{T_j}} \right) \cdot \Delta {A_0}{\varepsilon _0}\cos \theta {\text{d}}\mathit{\Omega} } } \hfill \\ \end{gathered} $ | (14) |
为计算辐射能量,正向蒙特卡洛法需要跟踪所有面元i和体元j发射的能量束,而反向蒙特卡洛方法只需要跟踪面元0发射的能量束即可,效率远高于正向蒙特卡洛法。
2.6 仿真模型液体火箭发动机尾焰结构具有对称性,因此计算区域选取发动机喷管及尾焰流场为一体的二维轴对称模型,以此简化计算。本文尾焰流场计算区域如图 2所示。
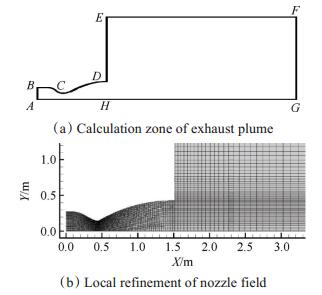
|
Fig. 2 Sketch of calculation zone |
图 2(a)中喷管喉部半径为145.93mm,喷管扩张比为8.6。HG为尾焰外流场计算域轴向尺寸,FG为径向尺寸,本文中HG为50m,FG为20m。计算域采用结构网格划分,网格总数约15万。如图 2(b)所示,喷管内及尾焰近场流场特性变化比较剧烈,故对其进行局部加密,以提高计算精度。由于尾焰远场流场特性变化较小,采用较为稀疏的网格以减小计算量,提高计算效率。通过多次仿真计算并与试验结果对比表明,本文采用的网格划分方案具有较好的无关性。
如图 2(a)所示,AB为喷管入口,本文采用压力入口边界条件,压强为6.898MPa,温度为3339.62K。BCD为喷管壁面,采用标准壁面函数;ED和EF为环境远场,给定环境压强61700Pa,温度为262.2K,自由来流马赫数为0.6;FG为压力出口条件,设定为环境远场参数;AHG为计算域对称轴,对称轴上径向变量梯度为0。
本文采用UDMH/NTO(偏二甲肼、四氧化二氮)作为发动机推进剂,混合比为2.206。喷管入口各气体组分含量由燃烧室热力计算得到,在计算中忽略小比例组分,仅考虑H2O,CO2,CO,H2,O2,N2,NO,N,NO2,H,O,OH这12种主要组分,自由来流中仅考虑O2和N2,各组分含量如表 1所示。根据文献[17]中反应模型,本文采用其中12种组分18步反应模型模拟复燃反应,其详细反应机理如表 2所示,化学反应速率来源于NIST Chemical Kinetic Database,表中M为第三体,不参与化学反应。
|
|
Table 1 Species mole fraction in nozzle and free flow |
|
|
Table 2 Finite rate chemistry reaction[17] |
为研究复燃反应对液体火箭发动机尾焰红外辐射特性的影响,利用反向蒙特卡洛法针对圆柱体计算区域内的尾焰计算红外辐射特性,圆柱区域轴向、径向和周向划分节点数分别为400,400和101。选取辐射计算波段为1.5~5.5μm,分辨率为15cm-1。
3 计算结果与讨论 3.1 仿真校验为验证本文计算模型的正确性,采用本文建立的模型,根据文献[18]中仿真边界条件,计算了火箭发动机尾焰流场及光谱红外辐射特性,并与文献中实验及仿真数据进行对比,如图 3所示。
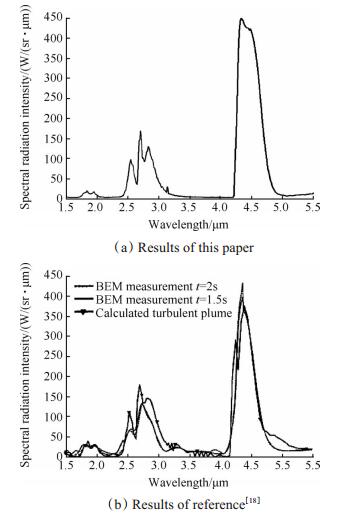
|
Fig. 3 Spectral radiation of exhaust plume |
对比图 3(a)和(b)可以发现,在1.5~5.5μm的辐射计算波段内,本文结果与文献[18]结果均在2.5~3.0μm以及4.2~4.7μm波段内出现较强的光谱辐射强度,其余波段内强度较低,具有强烈的选择性。光谱辐射强度随波长变化整体规律基本相同,仅在峰值处存在部分差异,在主要辐射波段内,本文结果与文献结果中光谱辐射强度最大差值比例在12.4%以内。由于本文与文献中反应模型选取有一定差异,并且复燃尾焰红外辐射特性的计算涉及到详细的化学反应机理、混合气体吸收系数以及红外辐射传输方程求解等复杂的计算过程,以上误差在允许范围内,因此可认为本文所建立的计算模型是可靠的。
3.2 复燃对尾焰流场特性的影响基于本文建立的计算模型,计算了飞行高度为4km的液体火箭发动机复燃尾焰流场,计算得到温度分布云图如图 4所示,图 4中上半部分为复燃反应流,下半部分为冻结流。提取y=0.3m处轴向温度数据及发动机出口不同位置处径向温度数据,得到温度分曲线,如图 5所示。
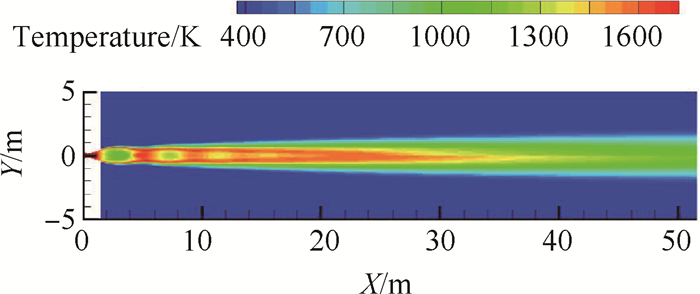
|
Fig. 4 Temperature contour of exhaust plume |
|
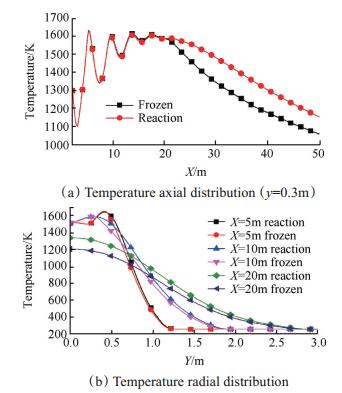
Fig. 5 Temperature distribution of exhaust plume |
从图 4中可以看出,复燃反应增加了尾焰流场中的高温区域。图 5(a)中,在x < 20m范围内,尾焰轴线温度变化基本相同。当x>20m时,反应流轴向温度高于冻结流,且温度相对增幅在一定范围内呈增大趋势。图 5(b)中,反应流高温区径向范围较冻结流小幅增加,且尾焰边界区域内复燃反应所导致的温度变化更为明显。
发动机出口尾焰主流为超声速状态,高速逸出的高温燃气与环境氧气掺混程度较低,因此x < 20m时复燃反应速率较低,对温度分布无太大影响。随轴向、径向距离增加,在环境大气的作用下,尾焰边界区域及发动机出口较远处燃气气流速度相对降低,导致相应区域内燃气与氧气掺混程度增加,当混合比及温度达到一定条件时复燃反应速率较高,进而大幅影响尾焰温度分布。在本文选取的计算域内,y=0.3m处轴向温度最大相对增幅可达15.4%,径向温度最大相对增幅可达16.3%。综上所述,复燃反应对尾焰的温度场影响较大,为准确计算尾焰流场温度分布特性,不能忽略复燃反应所产生的影响。
本文提取CO2和H2O组分的轴向分布数据(y=0.3m),得到摩尔浓度曲线,如图 6所示。
|
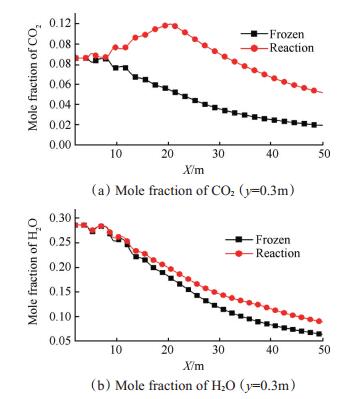
Fig. 6 Mole fraction of species axial distribution |
从图 6中可以发现,在尾焰流场中后部区域内复燃反应流的CO2和H2O的摩尔浓度高于冻结流,且在一定范围内浓度相对增幅呈增大趋势。在y=0.3m轴向方向上,反应流H2O浓度平均相对增幅可达47.5%,CO2浓度平均相对增幅可达53.4%
复燃反应是尾焰中可燃性高温燃气与大气中氧气相互掺混而发生的二次燃烧,因此可燃性组分含量因复燃反应发生而降低,而对应的燃烧产物组分含量会随之增大。与尾焰温度分布规律近似,尾焰前端复燃反应速率较低,复燃反应对组分浓度影响相对较小;随轴向、径向距离变化,复燃反应速率随掺混程度发生变化,对组分浓度影响程度不同。综上所述,复燃反应对尾焰组分分布影响较大,在准确研究尾焰组分分布情况时需要考虑复燃反应所带来的影响。
3.3 复燃对尾焰红外辐射特性的影响采用本文模型计算了液体火箭发动机复燃尾焰流场表面光谱辐射特性,将反应流与冻结流辐射数据对比,如图 7所示。
|
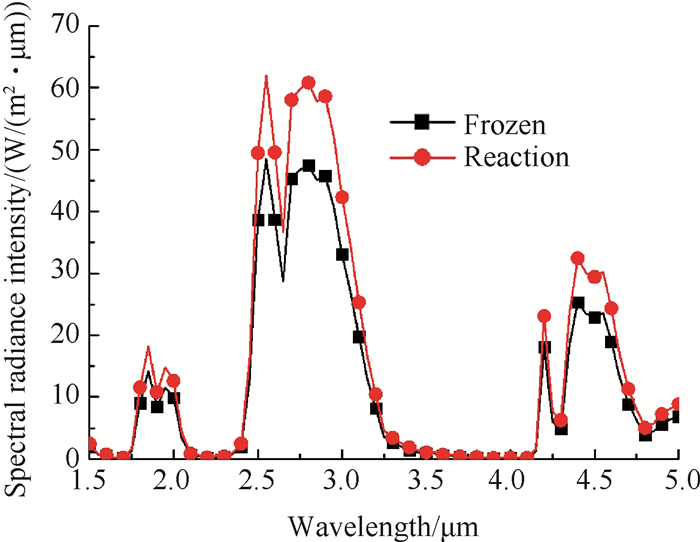
Fig. 7 Comparison of spectral radiation of plume |
从图 7中可以发现,尾焰红外光谱辐射具有很强的光谱选择性,其中2.5~3.0μm和4.2~4.7μm为主要辐射波段。光谱辐射波段仅由辐射气体种类决定,与辐射气体组分含量无关,复燃反应对主要辐射波段范围影响很小。本文选取的计算波段内,反应流红外光谱辐射强度均高于冻结流,这是由于复燃反应导致H2O和CO2两种主要辐射气体组分浓度增大及尾焰流场温度增大所致。在主要辐射波段2.5~3.0μm和4.2~4.7μm内反应流辐射强度最大增幅分别可达28.9%及31.5%。可以认为,复燃反应可以导致主要辐射波段内尾焰表面光谱辐射强度大幅增加,因此在准确计算液体火箭发动机尾焰红外辐射特性时,需要考虑复燃反应所带来的影响。
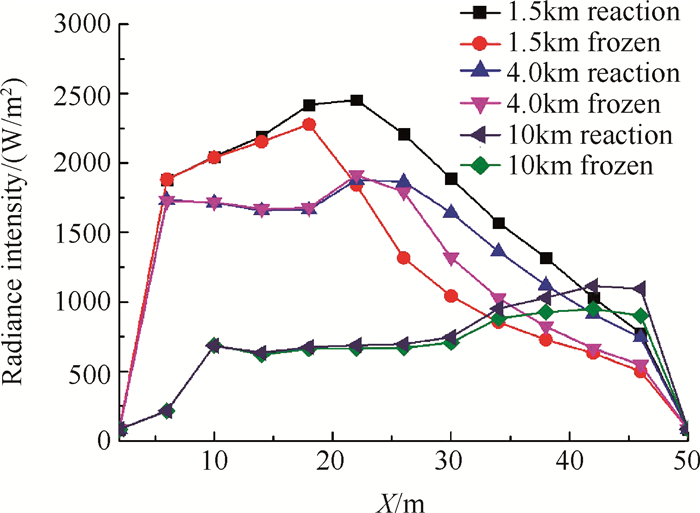
3.4 飞行条件对复燃尾焰辐射特性的影响图 8为不同飞行高度(1.5,4,10km)下反应流与冻结流尾焰辐射强度轴向分布对比。从图 8中可以发现,随飞行高度增加,尾焰轴向辐射强度及复燃反应所引起的红外辐射强度增幅均呈降低趋势,飞行高度为10km时辐射强度最大增幅仅10.7%。环境压强随飞行高度增加显著降低,液体火箭发动机尾焰膨胀更加充分,其与增大的飞行速度的共同作用下,尾焰与环境热量交换速率增大,导致尾焰整体温度降低。在实际飞行过程中,环境大气中氧气含量随飞行高度增加而降低,飞行速度随之增大,二者共同作用下导致高温燃气与氧气掺混程度降低,抑制复燃反应速率,进而导致其引起的红外辐射强度增幅随高度增加而逐渐降低。
|
Fig. 8 Radiation distribution at different heights |
本文建立了一个适用于液体火箭发动机复燃尾焰流场及红外辐射特性的计算模型,据此研究了复燃反应对液体火箭发动机尾焰红外辐射特性的影响,得到以下结论:
(1) 复燃反应对尾焰流场特性影响较大,可显著增加尾焰燃气空气混合区域的温度,其中轴向温度最大相对增幅可达15.4%,径向最大可达16.3%。复燃反应可增加CO2和H2O等燃烧产物浓度,CO2和H2O轴向浓度相对增幅分别可达47.5%和53.4%。
(2) 复燃反应对尾焰光谱辐射强度影响较大,可显著增强主要辐射波段内的尾焰光谱辐射强度,其中在2.5~3.0μm和4.2~4.7μm波段内复燃导致最大辐射强度增幅分别可达28.9%和31.5%。
(3) 飞行高度改变会对复燃尾焰辐射特性产生影响,随飞行高度增加尾焰轴向整体辐射强度及复燃所引起的辐射强度增量均呈降低趋势。
(4) 根据本文模型计算得到复燃反应会对液体火箭发动机尾焰流场及红外辐射特性产生较大影响的结论,因此在准确计算液体火箭发动机尾焰流场红外辐射特性时,不能忽略复燃反应所带来的影响。
| [1] |
吴睿, 聂万胜, 蔡红华, 等. 偏二甲肼/四氧化二氮火箭发动机尾焰流场特性三维仿真研究[J]. 导弹与航天运载技术, 2016(5): 74-79. (  0) 0) |
| [2] |
Wang W C, Wei Z J, Zhang Q, et al. Influence of Afterburning on Infrared Signature of Rocket Motor Exhaust Plume[J]. Journal of Aerospace Power, 2010, 25(11): 2612-2618.
(  0) 0) |
| [3] |
王伟臣, 李世鹏, 张峤, 等. 火箭发动机羽流红外特性计算方法研究[J]. 推进技术, 2010, 31(4): 423-427. (WANG Wei-chen, LI Shi-peng, ZHANG Qiao, et al. Research on the Calculation Method of Infrared Signature of Rocket Motor Exhaust Plume[J]. Journal of Propulsion Technology, 2010, 31(4): 423-427.)
(  0) 0) |
| [4] |
郑才浪, 朱定强, 乔要宾. 固液混合火箭发动机尾焰的红外特性研究[J]. 红外, 2013, 34(10): 20-24. DOI:10.3969/j.issn.1672-8785.2013.10.005 (  0) 0) |
| [5] |
申文涛, 董超, 朱定强, 等. 固液混合火箭发动机喷焰红外辐射特性分析[J]. 航空动力学报, 2012, 27(8): 1874-1880. (  0) 0) |
| [6] |
丰松江, 聂万胜, 解庆纷, 等. 燃烧室内燃烧模型对尾焰流场及其辐射的影响[J]. 火箭推进, 2006, 32(2): 6-10. (  0) 0) |
| [7] |
Leone D M. Active Chlorine and Nitric Oxide Formation from Chemical Rocket Plume Afterburning[J]. AIAA Journal, 2000, 96.
(  0) 0) |
| [8] |
姜毅, 傅德彬. 固体火箭发动机尾喷焰复燃流场计算[J]. 宇航学报, 2008, 29(2): 615-620. (  0) 0) |
| [9] |
刘尊洋, 邵立, 汪亚夫, 等. 复燃对固体火箭尾焰红外辐射特性的影响[J]. 光学学报, 2013, 33(6): 32-39. (  0) 0) |
| [10] |
蔡红华, 聂万胜, 丰松江. 复燃对液氧煤油发动机尾焰冲击特性影响[J]. 推进技术, 2016, 37(10): 1922-1927. (CAI Hong-hua, NIE Wan-sheng, FENG Song-jiang. The Effect of Afterburning on the Impact Characteristics of LOX/Kerosene Rocket Engine Plume[J]. Journal of Propulsion Technology, 2016, 37(10): 1922-1927.)
(  0) 0) |
| [11] |
陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 2003.
(  0) 0) |
| [12] |
王振国. 液体火箭发动机燃烧过程建模与数值仿真[M]. 北京: 国防工业出版社, 2012.
(  0) 0) |
| [13] |
赵坚行. 燃烧的数值模拟[M]. 北京: 科学出版社, 2002.
(  0) 0) |
| [14] |
Zhang H, Modest M F. Evaluation of the Planck-Mean Absorption Coefficients from HITRAN and HITEMP Databases[J]. Journal of Quantitative Spectroscopy & Radiative Transfer, 2002, 73(6): 649-653.
(  0) 0) |
| [15] |
董士奎, 余其铮, 谈和平, 等. 燃烧产物二氧化碳高温辐射的窄谱带模型参数[J]. 航空动力学报, 2001, 16(4): 355-359. (  0) 0) |
| [16] |
Liu L H. Backward Monte Carlo Method Based on Radiation Distribution Factor[J]. Journal of Thermophysics & Heat Transfer, 2012, 18(1): 151-153.
(  0) 0) |
| [17] |
Zavelevich F S, Molchanov A M, Ushakov N N. Computation of Gas and Multiphase Supersonic Jets with Nonequilibrium Processes[J]. Journal of Thermophysics & Heat Transfer, 2015, 29(3): 587-593.
(  0) 0) |
| [18] |
Devir A, Lessin A, Cohen Y, et al. Comparison of Calculated and Measured Radiation from a Rocket Motor Plume[C]. Reno: Aerospace Sciences Meeting and Exhibit, 2013.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


