对于工程系统或产品而言,各种参数不可避免地都具有不同程度的不确定性,由于不确定性的存在,导致了工程系统或产品的功能或特性响应具有一定的波动性。因此只有充分考虑各种不确定性的设计或优化结果才更加符合工程实际情况。为了减小各参数的不确定性对功能或特性响应的影响程度,稳健性设计的思想被引入工程设计领域[1, 2]。
稳健性设计是通过选择合适的设计参数水平来减小各参数不确定对目标响应影响程度,其设计思想最早是以Taguchi方法为代表的试验设计方法[3, 4],通过试验设计的方法计算每次试验的信噪比,然后从中选择最优的水平组合。由于Taguchi方法一般只适用于单目标、少变量的离散参数优化问题,对复杂的工程优化问题具有一定的局限性。考虑到复杂工程稳健性优化问题多参数、高非线性等特点,众多学者提出了基于响应面的稳健性优化方法,通过建立参数与响应之间的近似函数关系模型,然后利用建立的近似函数构造稳健性优化模型进行优化计算[5~8]。由于基于响应面方法的稳健性优化在每次优化迭代过程中都需要进行数千次蒙特卡洛模拟(Monte Carlo Simulation,MCS)统计得出目标响应的均值和标准差,对于复杂模型其计算量较大。
为了进一步提高优化求解效率,Vining[9]和Lin[10]等提出了一种基于双响应面(Dual response surface method,DRSM)的稳健性优化方法,其核心思想是首先利用试验设计方法建立若干参数组合,针对每次试验利用MCS进行抽样统计得出每组参数相对应的均值及标准差,然后利用多项式响应面建立参数与目标响应均值以及标准差之间的近似函数。由于多项式响应面对于高度非线性函数拟合精度问题近年来众多学者也提出了基于Kriging、支持向量机、神经网络的双响应面稳健性优化方法[11, 12]。双响应面方法可直接求解目标响应的均值以及标准差,因此与直接基于响应面稳健性优化方法相比在每次优化迭代无需进行数千次抽样来计算目标响应的均值和标准差,大大减少了优化迭代时间。
无论是直接基于响应面优化过程还是双响应面模型的建立,其计算的核心都是通过抽样统计的方法获取目标响应的均值以及标准差,这个过程是利用MCS进行大量抽样来统计响应的均值和标准差,而统计结果的准确的准确性与抽样的次数相关,这就意味着如果需要获取高精度统计结果必须进行数万次抽样,而这也导致了计算效率的降低。
为了克服不确定性计算效率较低的问题,一些近似方法得到发展,其中一阶二次矩方法是不确定性分析应用较为广泛的方法之一。一次二阶矩(First order second moment,FOSM)方法是一种基于泰勒展开的不确定分析方法,由于其具有较高的计算效率因此在工程不确定性分析中具有广泛的应用[13~15]。均值一次二阶矩(Mean value first order second moment,MVFOSM)方法是通过对随机参数在其均值点进行泰勒展开来近似函数响应的均值和标准差,与传统基于抽样统计方法不同的是,均值一次二阶矩方法的使用将不确定分析转换为确定性分析问题,也就是说无需抽样统计可以直接得出目标响应的概率参数。Lee[16]应用FOSM和改进一次二阶矩(Advanced first order second moment,AFOSM)两种方法近似目标响应的均值以及标准差进行稳健性优化,通过对两种方法的对比结果显示FOSM方法计算较为方便,而AFOSM方法则具有较好的稳定性。对大多实际工程问题而言,参数与目标响应之间的函数关系式无法利用显式函数进行表达,进而无法直接对参数进行偏导数求解,因此无法直接利用FOSM方法进行求解。为了解决隐式函数偏导数求解问题,Huang[17]和Maskey[18]将有限差分法引入到FOSM中求解函数的偏导数,为基于隐式函数一次二阶矩方法的求解提供了方法。
本文针对工程稳健性优化计算效率以及精度问题提出一种基于MVFOSM模型稳健性优化方法。利用MVFOSM来计算目标响应均值以及标准差,并结合概率分位数区间模型构造稳健性优化模型。与传统的基于抽样统计方法不同的是,提出的方法不需要进行抽样统计就可构造稳健性优化模型,也就是说提出的方法可以将不确定优化问题转换为确定性优化问题。
2 数学模型 2.1 均值一次二阶距方法一次二阶矩方法是一种有效的估计函数的均值以及标准差的近似方法,其核心是对函数在随机参数期望点进行泰勒展开。假设随机变量X=[x1, x2, ..., xn],其函数U=f(X),将函数在随机变量均值点μx=[μx1, μx2, ..., μxn]展开并对进行线性化转换则有[17]
| $ U \approx {\left. {f\left( {{\mu _{{x_1}}}, {\mu _{{x_2}}}, \cdots, {\mu _{{x_n}}}} \right) + \sum\limits_{i = 1}^n {\left( {{x_i}-{\mu _{{x_i}}}} \right)} \frac{{\partial f}}{{\partial {x_i}}}} \right|_{{\mu _x}}} $ | (1) |
根据式(1),目标函数U的均值可以表示为
| $ {\mu _Y} = E\left( U \right) = f\left( {{\mu _{{x_1}}}, {\mu _{{x_2}}}, \cdots, {\mathit{\boldsymbol{\mu }} _{{x_n}}}} \right) $ | (2) |
目标函数U的方差可以由输入变量的方差以及协方差获得,具体表达式如式(3)所示
| $ \begin{array}{l} {\mathop{\rm var}} \left( U \right) = E\left[{{{\left( {\sum\limits_{i = 1}^n {\left( {{x_i}-{\mu _{{x_i}}}} \right)} {{\left. {\frac{{\partial f}}{{\partial {x_i}}}} \right|}_{{\mathit{\boldsymbol{\mu }}_x}}}} \right)}^2}} \right] = \sum\limits_{i = 1}^n {{{\left( {{{\left. {\frac{{\partial f}}{{\partial {x_i}}}} \right|}_{{\mathit{\boldsymbol{\mu }}_x}}}} \right)}^2}} .\\ {\mathop{\rm var}} \left( {{x_i}} \right) + 2\sum\limits_{i = 1}^n {\sum\limits_{j \ne i}^n {\left( {{{\left. {\frac{{\partial f}}{{\partial {x_i}}}} \right|}_{{\mathit{\boldsymbol{\mu }}_x}}}} \right)} } \left( {{{\left. {\frac{{\partial f}}{{\partial {x_i}}}} \right|}_{{\mathit{\boldsymbol{\mu }}_x}}}} \right){\mathop{\rm cov}} \left( {{x_i}, {x_j}} \right) \end{array} $ | (3) |
式(3)中cov(xi, xj)为变量xi与xj的协方差,可由式(4)获得
| $ {\mathop{\rm cov}} \left( {{x_i}, {x_j}} \right) = E\left[{\left( {{x_i}-{\mu _{{x_i}}}} \right)\left( {{x_j}-{\mu _{{x_j}}}} \right)} \right] $ | (4) |
如果式(4)中随机变量之间相互独立,则协方差为零,目标函数的标准差可简化为
| $ {\sigma _U} = \sqrt {\sum\limits_{i = 1}^n {{{\left( {{{\left. {\frac{{\partial f}}{{\partial {x_i}}}} \right|}_{{\mathit{\boldsymbol{\mu }}_x}}}} \right)}^2}\sigma _{{x_i}}^2} } $ | (5) |
由式(2)和式(5)可得函数U的概率密度函数(Probability density function,PDF)和累积概率密度函数(Cumulative distribution function,CDF)如式(6)和式(7)所示
| $ {f_U}\left( y \right) = {\left\{ {\frac{1}{{2\pi \sigma _U^2}}} \right\}^{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.} \!\lower0.7ex\hbox{$2$}}}}{\rm{e}}\left[{\frac{{-{{\left( {y-{\mu _U}} \right)}^2}}}{{2\sigma _U^2}}} \right] $ | (6) |
| $ {F_U}\left( y \right) = {\left\{ {\frac{1}{{2\pi \sigma _U^2}}} \right\}^{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.} \!\lower0.7ex\hbox{$2$}}}}\int_{- \infty }^y {{\rm{e}}\left[{\frac{{-{{\left( {y-{\mu _U}} \right)}^2}}}{{2\sigma _U^2}}} \right]{\rm{d}}y} = \mathit{\Phi} \left( {\frac{{y -{\mu _U}}}{{{\sigma _U}}}} \right) $ | (7) |
对于参数与响应之间为隐式函数关系的情况,由于无法直接求解函数偏导数,可选择有限差分法进行求解[17, 18],具体计算过程如式(8)所示
| $ {\left. {\frac{{\partial f}}{{\partial {x_i}}}} \right|_{{\mathit{\boldsymbol{\mu }}_x}}} = \frac{{{f^\Delta }-{f^\mu }}}{{\Delta {x_i}}}, i = 1, 2, \cdots, n $ | (8) |
式(8)中fΔ=f(μx1, μx2, ..., μxi+Δxi, ..., μxn),fμ=f(μx1, μx2, ..., μxi, ..., μxn),Δxi为差分区间,有三种选择,具体可参看文献[18]。
2.2 稳健性优化模型对稳健性优化问题而言,通常是以目标响应的均值以及标准差作为优化对象,利用二者之间各种线性或非线性组合构造稳健性优化模型,进而进行优化迭代求解。而对于工程实际而言,虽然大多目标响应随机抽样后呈现出正态或其他分部特性,但由于各种不确定参数有界性的影响,导致目标响应不确定性区间也是有界的,并不是随着分布特性一直延伸。对于工程数据不确定性而言,通常使用[μ-kσ, μ+kσ](k=1, 2, ...6)区间来描述不确定性,其中μ和σ分别为其统计均值及标准差,k越大说明不确定数据落入其中概率越大,而工程数据通常取k=3。因此本文算例均以[μ-3σ, μ+3σ]区间作为稳健性优化目标,区间越小则目标响应的波动越小,也就意味着稳健性程度越好。
假设Z~N(0, 1)标准正态分布,若zα满足
| $ P\left\{ {Z < {z^\alpha }} \right\} = \alpha, 0 < \alpha < 1 $ | (9) |
则称zα为正态分布上α分为点。根据标准正态分布定义,区间[μ-3σ, μ + 3σ]可以转换为[z0.0013, z0.9987]。根据式(7)和式(9)可得
| $ {F_U}\left( {{z^{0.0013}}} \right) = P\left\{ {Y \le {z^{0.0013}}} \right\} = \mathit{\Phi} \left( {\frac{{{z^{0.0013}}-{\mu _U}}}{{{\sigma _U}}}} \right) = 0.0013 $ | (10) |
| $ {F_U}\left( {{z^{0.9987}}} \right) = P\left\{ {Y \le {z^{0.9987}}} \right\} = \Phi \left( {\frac{{{z^{0.9987}}-{\mu _U}}}{{{\sigma _U}}}} \right) = 0.9987 $ | (11) |
由式(10)和式(11)可得
| $ {z^{0.0013}} = {\mu _U} + {\mathit{\Phi} ^{-1}}\left( {0.0013} \right){\sigma _U} $ | (12) |
| $ {z^{0.9987}} = {\mu _U} + {\mathit{\Phi} ^{-1}}\left( {0.9987} \right){\sigma _U} $ | (13) |
式中Φ-1()为概率累积函数逆运算。令z0.00130.9987=z0.9987-z0.0013,则稳健性优化模型为
| $ \begin{array}{l} {\rm{Find}}\;\;\;\;\mathit{\boldsymbol{x}}{\rm{ = }}\left[{{x_1}, {x_2}, \cdots, {x_{n1}}} \right]\\ {\rm{Min}}\;\;\;\;\;Z\left( \mathit{\boldsymbol{x}} \right) = z_{0.0013}^{0.9987}\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\;{\mathit{\boldsymbol{x}}_{\rm{L}}} < \mathit{\boldsymbol{x}} < {\mathit{\boldsymbol{x}}_{\rm{V}}} \end{array} $ | (14) |
式(14)中,Z(x)为优化目标函数,x为设计参数向量,xL和xV分别为设计参数下限和上限。
3 算例 3.1 悬臂梁端面位移稳健性优化本文选取文献[17]中悬臂梁模型如图 1所示,悬臂梁在均布载荷作用下其右端面具有一定的垂直位移,稳健性优化目标就是通过选择合适的设计参数水平使得各输入参数不确定情况下臂梁端面垂直位移变化范围越小越好。

|
Fig. 1 Cantilever beam model |
端面位移Y与参数之间函数关系如式(15)所示
| $ Y = \frac{{Q{L^4}}}{{8EI}} $ | (15) |
式中Q为均匀分布载荷如图 1所示,L是悬臂梁长度,E为材料弹性模量,I为截面惯性矩。其中Q,L为设计参数,E,I为随机参数,具体数值如表 1所示。表 1中Q,L的均值区间表示其设计点的取值范围。表 1中参数均服从正态分布。
|
|
Table 1 Variables mean and standard deviation of cantilever beam |
根据式(15),选取设计参数优化区间中点进行不确定性分析,本文以MCS 105次后统计结果为参考,验证提出方法求解精度,抽样后悬臂梁右端垂直位移Y的概率密度直方图如图 2所示。
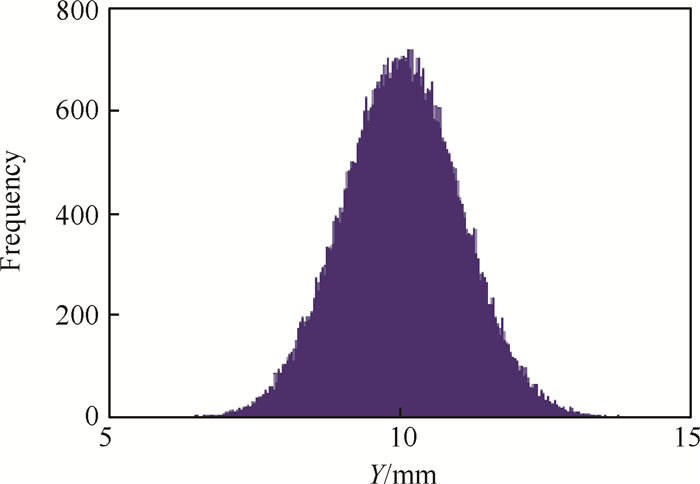
|
Fig. 2 Probability density histogram of Y |
将式(15)利用MVFOSM方法进行求解,求解后的PDF与CDF分别如图 3(a)和图 3(b)所示。图中可以看出基于MVFOSM方法求解的结果与MCS抽样得出的结果基本保持一致。
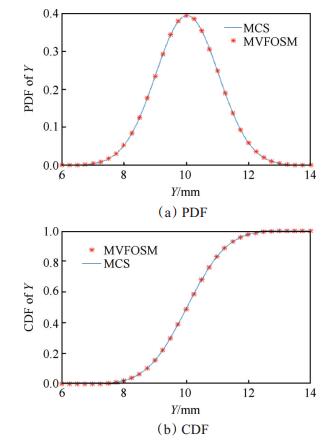
|
Fig. 3 PDF and CDF of vertical displacement Y |
为了从计算精度和效率两方面来对比MVFOSM与MCS两种方法分析结果,表 2列举了两种方法计算得出的7个概率分位数点的计算结果以及耗费时间。
|
|
Table 2 Quantiles calculation results of Y |
从表 2中的计算结果可以看出,两种方法计算结果的相对误差为万分之二左右,基于MVFOSM方法计算精度与MCS的结果相当。而基于MVFOSM方法与MCS计算时间分别为0.011s和1.041s,相差了近100倍,这是因为基于MVFOSM方法计算的概率分位数值不需要进行抽样统计,因此计算时间与基于抽样统计的方法相比将会大幅减少。
根据式(14)建立稳健性优化模型如式(16)所示
| $ \begin{array}{l} {\rm{Find}}\;\;\;\;{\mathit{\boldsymbol{x}}^*}{\rm{ = }}\left[{Q, L} \right]\\ {\rm{Min}}\;\;\;\;\;W\left( {{\mathit{\boldsymbol{x}}^*}} \right) = Y_{0.0013}^{0.9987}\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\;\mathit{\boldsymbol{x}}_{\rm{L}}^* < {\mathit{\boldsymbol{x}}^*} < \mathit{\boldsymbol{x}}_{\rm{V}}^* \end{array} $ | (16) |
式(16)中,x为设计参数向量,Y0.00130.9987为悬臂梁垂直位移的[Y0.0013, Y0.9987]概率分位数区间,xL*和xV*分别为设计参数优化区间下限和上限如表 1所示。
为了验证基于MVFOSM方法稳健性优化结果的精度和计算效率,基于MCS与DRSM方法优化结果将于本文提出方法结果进行对比,其中响应面模型选择二次多项式响应面。图 4为三种方法优化迭代过程。表 3为三种方法优化结果以及计算时间。
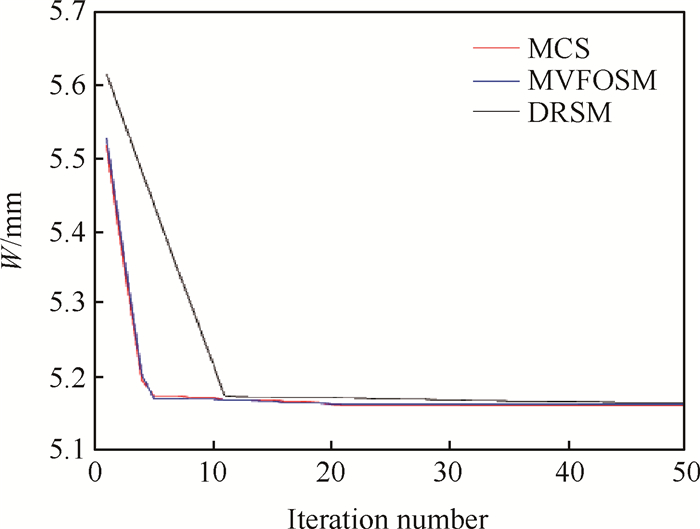
|
Fig. 4 Robust optimization iteration process of W |
|
|
Table 3 Robust optimization result of cantilever beam vertical displacement |
从表 3中可以看出,MVFOSM方法与MCS方法优化结果较为接近,而双响应面计算精度最低,这是因为双响应面方法在建立响应面模型时模型误差所导致。从计算时间来看MVFOSM与双响应面方法计算时间较为接近,这是因为基于这两种方法在每次优化迭代时无需进行大量抽样统计。虽然基于双响应面模型优化计算效率与基于MVFOSM方法相近,然而建立双响应面模型时每个试验水平都需要进行数万次抽样,获取相对应的均值以及标准差,因此建立双响应面过程也需要耗费大量时间。
3.2 涡轮转子径向变形稳健性优化选择某发动机涡轮转子为研究对象,其示意图如图 5所示,其径向变形δ(mm)在参数不确定性影响下具有一定波动,因此需要选择合适设计参数组合使涡轮转子径向变形对参数变化敏感性降低。图 5中x1为涡轮盘盘心厚度,θ为轮盘中部两侧面夹角角度。
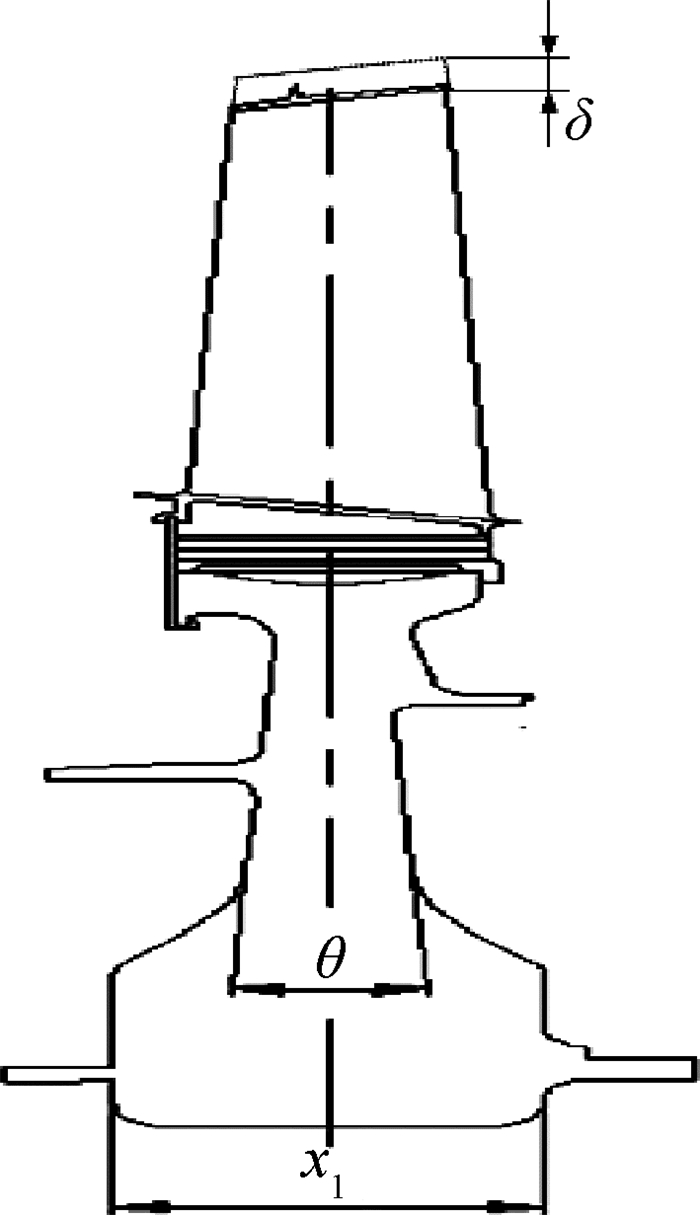
|
Fig. 5 Structure of turbine rotor |
本例选取涡轮盘盘心温度T1,涡轮叶片叶尖温度T2,转速ω为载荷随机变量,涡轮盘以及叶片弹性模量Ed和Eb作为材料随机参数,盘心厚度x1,轮盘中部两侧夹角θ为设计参数。选取各参数取值如表 4所示,各参数均服从正态分布。其中设计参数区间与算例1相同为设计点的优化范围。
|
|
Table 4 Variables mean and standrad deviation of turbine rotor |
由于涡轮转子输入参数与径向变形之间无直接显式函数关系表达式,因此需要借助响应面模型来进行拟合,考虑到参数与径向变形之间函数关系非线性程度较高,本例选取Kriging模型[19, 20]来拟合参数与变形之间函数关系式。对建立好的近似模型进行预测精度验证,结果如图 6所示,预测值的均方根误差为5.7432×10-4。
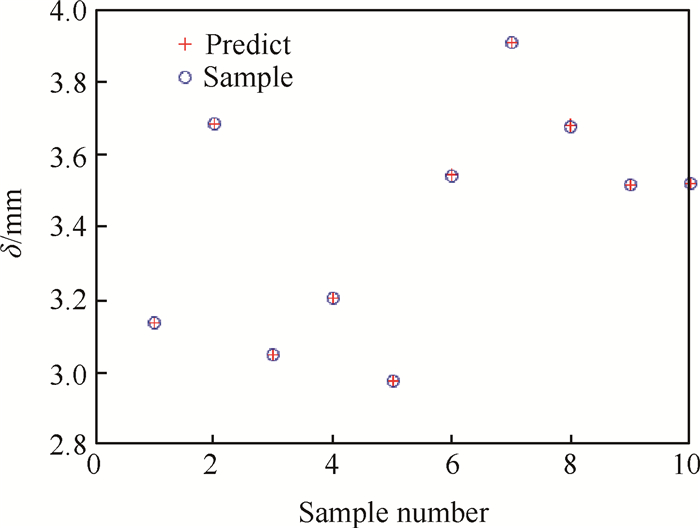
|
Fig. 6 Result of Kriging model predict |
对建立好的Kriging模型在设计参数优化区间中点利用MCS进行105次抽样,抽样后的径向变形概率直方图如图 7所示。
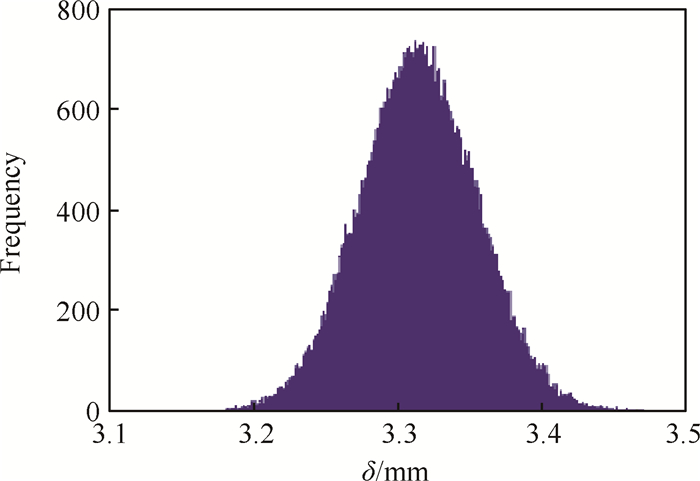
|
Fig. 7 Probability density histogram of δ |
将Kriging模型利用MVFOSM方法进行求解,考虑到近似模型为隐式方程,因此采用式(8)进行偏微分求解,其中Δxi=μxi/1000,求解后的PDF与CDF分别如图 8(a)和8(b)所示。
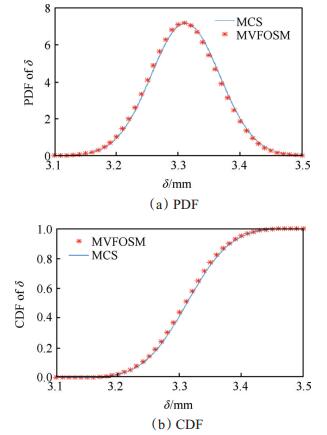
|
Fig. 8 PDF and CDF of radial deformation δ |
与算例1相同,分别对涡轮转子径向变形7个概率分位数点进行求解,结果如表 5所示。
|
|
Table 5 Quantiles calculation results of δ |
从表 5中的计算结果可以看出,两种方法计算结果较为相近,但相对误差与算例1相比较高,这是因为利用有限差分法计算偏导数的误差所导致。而基于MVFOSM与MCS计算时间分别为0.019s和4.645s。
根据式(14)建立稳健性优化模型如式(17)所示
| $ \begin{array}{l} {\rm{Find}}\;\;\;\;{\mathit{\boldsymbol{x}}^\Delta }{\rm{ = }}\left[{{x_1}, \theta } \right]\\ {\rm{Min}}\;\;\;\;\;{W_1}\left( {{\mathit{\boldsymbol{x}}^\Delta }} \right) = \delta _{0.0013}^{0.9987}\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\;\mathit{\boldsymbol{x}}_{\rm{L}}^\Delta < {\mathit{\boldsymbol{x}}^\Delta } < \mathit{\boldsymbol{x}}_{\rm{V}}^\Delta \end{array} $ | (17) |
式(17)中,xΔ为设计参数向量,δ0.00130.9987为涡轮转子径向变形的[δ0.0013, δ0.9987]概率分位数区间,xLΔ和xVΔ分别为设计参数优化区间下限和上限如表 4所示。
与算例1相同,提出的方法与基于MCS和DRSM方法优化结果进行对比。优化迭代过程如图 9所示。优化后的结果如表 6所示。
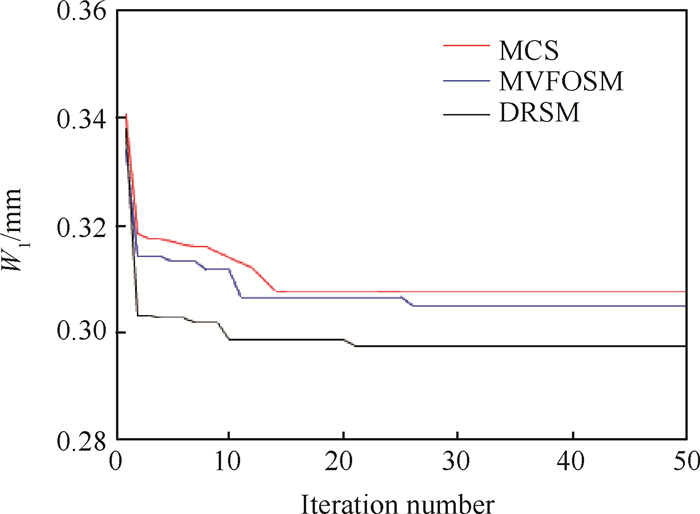
|
Fig. 9 Robust optimization iteration process of W1 |
|
|
Table 6 Robust optimization results of turbine rotor radial deformation |
从表 6中的结果可以看出,基于MVFOSM方法结果与MCS结果最为接近,DRSM方法精度最低。而双响应面方法与MVFOSM优化迭代时间相差不大。优化结果显示,提出的基于MVFOSM稳健性优化方法在保证一定计算精度情况下,可以极大提高计算效率。
4 结论本文针对工程稳健性优化,提出一种基于MVFOSM稳健性优化方法。通过对两个工程稳健性优化算例的计算结果分析,得到如下结论:
(1) 利用MVFOSM方法可直接计算功能函数的均值以及标准差,而无需进行大量的抽样统计,因此提出的方法可将不确定性优化转化为确定性优化,计算效率将得到提高。
(2) 通过与传统基于MCS和DRSM方法相比,两个算例的优化结果均显示提出的方法与MCS方法计算结果相对误差为0.1%左右,DRSM方法计算精度最低。而计算时间与DRSM相当,仅为MCS的1%左右。因此提出的稳健性优化方法更加适用于复杂工程结构稳健性优化设计。
| [1] |
Doltsinis I, Kang Z. Robust Design of Structures Using Optimization Methods[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(23): 2221-2237.
(  0) 0) |
| [2] |
Parkinson A. Robust Mechanical Design Using Engineering Models[J]. Transactions of the ASME Journal of Mechanical Design, 1995(117): 48-54.
(  0) 0) |
| [3] |
Gijo E V, Scaria J. Product Design by Application of Taguchi's Robust Engineering Using Computer Simulation[J]. International Journal of Computer Integrated Manufacturing, 2012, 25(9): 761-773. DOI:10.1080/0951192X.2012.665186
(  0) 0) |
| [4] |
Sun G, Fang J, Tian X, et al. Discrete Robust Optimization Algorithm Based on Taguchi Method for Structural Crashworthiness Design[J]. Expert Systems with Applications, 2015, 42(9): 4482-4492. DOI:10.1016/j.eswa.2014.12.054
(  0) 0) |
| [5] |
Elsayed K, Lacor C. Robust Parameter Design Optimization Using Kriging, RBF and RBFNN with Gradient-Based and Evolutionary Optimization Techniques[J]. Applied Mathematics & Computation, 2014, 236(4): 325-344.
(  0) 0) |
| [6] |
高伟钊, 莫旭辉, 付锐, 等. 基于Kriging的泡沫填充锥形薄壁结构耐撞性6σ稳健性优化设计[J]. 固体力学学报, 2012, 33(4): 370-378. (  0) 0) |
| [7] |
崔杰, 张维刚, 常伟波, 等. 基于双响应面模型的碰撞安全性稳健性优化设计[J]. 机械工程学报, 2011, 47(24): 97-103. (  0) 0) |
| [8] |
吴小锋, 刘春节, 干为民, 等. 面向外啮合齿轮泵困油问题的健壮性设计[J]. 航空动力学报, 2015, 30(11): 2721-2729. (  0) 0) |
| [9] |
Vining G, Myers R. Combining Taguchi and Response Surface Philosophies-a Dual Response Approach[J]. Journal of Quality Technology, 1990, 22(1): 38-45. DOI:10.1080/00224065.1990.11979204
(  0) 0) |
| [10] |
Lin D K J, Tu W. Dual Response Surface Optimization[J]. Journal of Quality Technology, 1995, 27(1): 34-39. DOI:10.1080/00224065.1995.11979556
(  0) 0) |
| [11] |
Zhou X J, Ma Y Z, Tu Y L, et al. Ensemble of Surrogates for Dual Response Surface Modeling in Robust Parameter Design[J]. Quality and Reliability Engineering International, 2013, 29(2): 173-197. DOI:10.1002/qre.1298
(  0) 0) |
| [12] |
Arungpadang T R, Kim Y J. Robust Parameter Design Based on Back Propagation Neural Network[J]. Korean Management Science Review, 2012, 29(3): 81-89. DOI:10.7737/KMSR.2012.29.3.081
(  0) 0) |
| [13] |
Wang S J, Kuochin H. The Application of the First-Order Second-Moment Method to Analyze Poroelastic Problems in Heterogeneous Porous Media[J]. Journal of Hydrology, 2009, 369(1): 209-221.
(  0) 0) |
| [14] |
Wan C, Xu Z, Dong Z Y, et al. Probabilistic Load Flow Computation Using First-Order Second-Moment Method[C]. San Diego: IEEE Power and Energy Society General Meeting, 2012.
(  0) 0) |
| [15] |
Raviprakash A, Prabu B, Alagumurthi N. Mean Value First Order Second Moment Analysis of Buckling of Axially Loaded Thin Plates with Random Geometrical Imperfections[J]. International Journal of Engineering, Science and Technology, 2010, 2(4): 150-162.
(  0) 0) |
| [16] |
Lee T W. A Study for Robustness of Objective Function and Constraints in Robust Design Optimization[J]. Journal of Mechanical Science and Technology, 2006, 20(10): 1662-1669. DOI:10.1007/BF02916270
(  0) 0) |
| [17] |
Huang B, Du X. Probabilistic Uncertainty Analysis by Mean-Value First Order Saddlepoint Approximation[J]. Reliability Engineering & System Safety, 2008, 93(2): 325-336.
(  0) 0) |
| [18] |
Maskey S, Guinot V. Improved First Order Second Moment Method for Uncertainty Estimation in Flood Forecasting[J]. Hydrological Sciences Journal, 2003, 48(2): 183-196. DOI:10.1623/hysj.48.2.183.44692
(  0) 0) |
| [19] |
赵勇, 李本威, 朱飞翔, 等. 基于QPSO算法的压气机特性代理模型优化[J]. 推进技术, 2014, 35(11): 1537-1543. (ZHAO Yong, LI Ben-wei, ZHU Fei-xiang, et al. Surrogate Model Optimization of Compressor Characteristics Based on QPSO Algorithm[J]. Journal of Propulsion Technology, 2014, 35(11): 1537-1543.)
(  0) 0) |
| [20] |
贺谦, 李元生, 温志勋, 等. 涡轮叶片多学科可靠性及稳健设计优化[J]. 推进技术, 2010, 31(2): 193-197. (HE Qian, LI Yuan-sheng, WEN Zhi-xun, et al. Multidisciplinary Probabilistic and Robust Design Optimization for Turbine Blade[J]. Journal of Propulsion Technology, 2010, 31(2): 193-197.)
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

