2. 西安航天动力研究所,陕西 西安 710100
2. Xi'an Aerospace Propulsion Institute, Xi'an 710100, China
重复使用运载火箭根据“多次使用,费用均摊”的原则,显著降低单位有效载荷的发射成本,能实现“廉价、快速、机动、可靠”自由进出空间的目标,正成为未来航天运输系统的主要发展方向[1, 2]。
可靠安全回收是运载火箭实现可重复使用的基础。目前火箭回收方式可分为伞降回收、滑翔飞行以及垂直着陆三种。美国SpaceX公司以Merlin 1D系列发动机为动力,开展重复使用飞行器研究,成为世界上第一个成功回收火箭并再次利用的私营公司[3, 4]。以垂直着陆技术实现火箭的子级回收,对运载火箭的动力系统,尤其是单台发动机作为火箭的主动力装置,提出了很高的技术要求,主要包括以液体火箭发动机深度变推力和多次起动为代表的先进技术[5]。对于补燃循环液体火箭发动机而言,不仅需在低入口压力下实现多次可靠点火、快速平稳起动,而且需在大范围变工况下满足高性能和高可靠性的要求。因此发动机大范围变推力技术复杂、研制难度大、创新性强。
变推力液体火箭发动机技术是航天液体动力的重要发展领域。航天运输系统的动力装置采用变推力发动机,可以实现最佳推力控制,从而使运载能力达到最大;载人航天的主动段飞行使用变推力发动机推进,可以严格控制宇航员的过载,确保宇航员的飞行安全;对于空间飞行器的交会对接与轨道机动,变推力发动机可以提高操纵控制的灵活性。如果导弹系统采用变推力发动机进行推进,则可以改善导弹飞行轨道的机动性,从而提高导弹武器的突防能力。由于液体火箭发动机是高密度的能量释放器,尤其对于高压补燃循环发动机而言,对推力进行设计和控制时需要解决诸多技术上的难题,如补燃循环大范围推力稳定调节控制技术、大范围推力调节下燃烧组件稳定燃烧技术、大范围变工况下推力室可靠冷却技术和大变比涡轮泵稳定工作技术等。
美国、俄罗斯等国已经开展了变推力火箭发动机的探索研究和工程实践,研制了以“阿波罗”登月下降级LMDE发动机、RD-862以及RD-191等为代表的变推力液体火箭发动机,并已经获得工程应用。我国研制成功了嫦娥三号探测器7500N变推力挤压式发动机[6],变推比达5:1,是实现月面软着陆的两大关键技术瓶颈之一,在探月二期工程中发挥了关键作用,为探月三期及后续任务奠定了基础。
目前,液氧煤油高压补燃循环发动机已成为我国新一代运载火箭CZ-5,CZ-6及CZ-7的主动力。鉴于可重复使用运载火箭的需要,本文首次提出了发生器燃料路流量调节器调节、主涡轮前燃气分流以及氧化剂主路节流等相结合,并辅助以气体乳化提高喷注器压降的组合深度推力调节方案。国外尚无与此类似的推力组合调节方案,该方案可以深化发动机推力调节技术,提高发动机性能,大幅增强发动机任务扩展能力。
2 发动机系统动力学模型补燃循环发动机系统复杂,参数变化剧烈、耦合性强,技术难度远高于发生器循环发动机,是发动机研制中的核心。
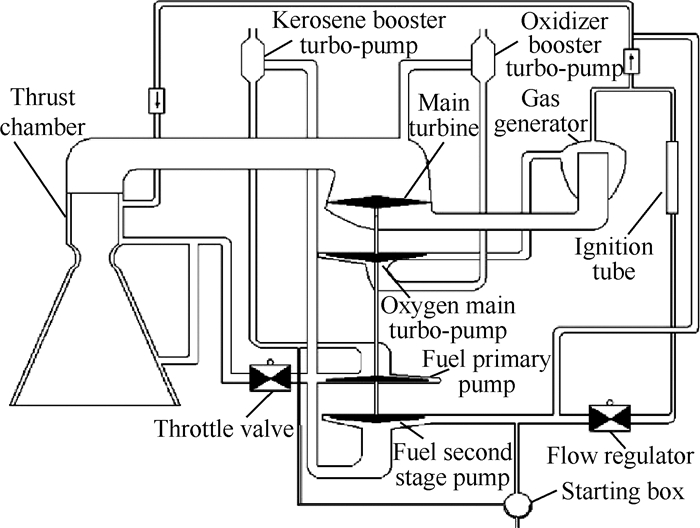
补燃循环发动机主要由氧预压泵、氧主泵、燃料预压泵、燃料一级泵、燃料二级泵、主涡轮、流量调节器、节流阀、燃气发生器、推力室、各种阀门以及相连的液体、气体管路等组成。1200kN液氧煤油补燃循环发动机的系统组成如图 1所示。
|
Fig. 1 System composition of 1200kN LOX/kerosene high pressure staged combustion engine |
建立液氧煤油发动机系统各组件的模型是研究发动机深度变推力的前提和基础。在自身起动机理研究的基础上,建立了流体管路分布参数模型、涡轮泵组件模型、阀门和调节器模型、燃烧组件模型以及气液容腔模型等,涉及到300多个参数,近2000个非线性微分方程[7]。
管道内液体推进剂流动是一维绝热有摩擦的瞬变流动,描述管道内液体瞬变流的基本方程是一对拟线性双曲型偏微分方程[8]
| $ \frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + \frac{{4{\tau _{\rm{w}}}}}{D} + g\cos \theta = 0 $ | (1) |
| $ \frac{{\partial p}}{{\partial t}} + u\frac{{\partial p}}{{\partial x}} + \rho {a^2}\frac{{\partial u}}{{\partial x}} = 0 $ | (2) |
式中p为流体压力;u为流体流速;ρ为流体密度;D为管路内径;g为质量场加速度;θ为管流轴线方向与加速度方向的夹角;a为压力波传播速度;τw为管壁切应力。
根据转动动力学定律,相对于涡轮泵旋转轴的动量矩对时间的导数等于作用在涡轮泵转子上的外力矩
| $ J\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}} = {M_{\rm{t}}}-\sum {{M_{\rm{p}}}} $ | (3) |
式中J,ω,Mt和Mp分别为涡轮泵的转动惯量、角速度、涡轮的扭矩和泵的扭矩。
涡轮产生的扭矩为
| $ {M_{\rm{t}}} = \frac{{{P_{\rm{t}}}}}{\omega } = \frac{{{q_{{\rm{mt}}}}{L_{{\rm{oag}}}}{\eta _{\rm{t}}}}}{{2\pi n/60}} $ | (4) |
式中Pt为涡轮的功率;qmt为涡轮燃气流量;Loag为燃气可用绝热功;ηt为涡轮效率。
泵的扭矩为
| $ {M_{\rm{P}}} = \frac{{{a_{\rm{P}}}{n^3} + {b_{\rm{P}}}{n^2}{q_{\rm{m}}} + {c_{\rm{P}}}nq_{\rm{m}}^2}}{{2\pi n/60}} + {J_{\rm{P}}}\frac{{{\rm{d}}n}}{{{\rm{d}}t}}-{B_{\rm{P}}}\frac{{{\rm{d}}{q_{\rm{m}}}}}{{{\rm{d}}t}} $ | (5) |
式中aP,bP和cP分别为试验确定的功率特性系数;JP和BP分别为泵叶轮中流体的转动及平动阻力系数。
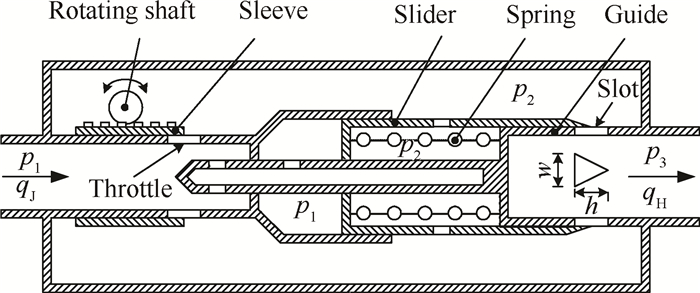
流量调节器是发动机推力调节的控制元件,安装在燃料二级泵与燃气发生器之间,起着控制和稳定进入燃气发生器的燃料流量的作用,其结构如图 2所示[9]。
|
Fig. 2 Structure schematic diagram of the flow regulator |
滑阀受力方程为
| $ m\frac{{{{\rm{d}}^2}{x_{\rm{H}}}}}{{{\rm{d}}t}} = {A_{\rm{P}}}\left( {{P_1}-{P_2}} \right) + {F_{\rm{Y}}}-{F_{{\rm{T0}}}}-{B_{\rm{v}}}v - {K_{{x_{\rm{H}}}}} $ | (6) |
式中xH为滑阀位移;FT0为调节弹簧的初装力;K为调节弹簧的刚度;m为流量调节器中运动件的折算质量;Bv为折算摩擦系数;FY为滑套所受的液动力。
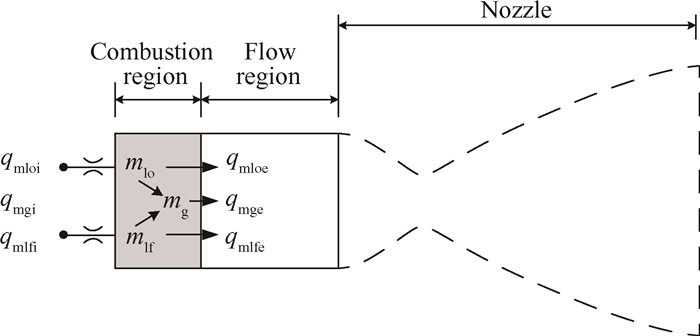
热力组件包括发动机推力室、燃气导管和发生器,其动力学模型是类似的,采用图 3所示的分区模型,将燃烧室分为燃烧区和流动区两个区,作如下假设[10]:进入热力组件中的液相推进剂在经过一个燃烧时滞τ后,瞬时变为气相的燃烧产物;每一瞬时,热力组件中的压力、混合比、温度分布均匀;气相燃烧产物遵循理想气体定律;不考虑波动过程。
|
Fig. 3 Combustion chamber partition diagram of the thermal component |
积存的燃料、氧化剂和燃烧产物表达式为
| $ \frac{{{\rm{d}}{m_{{\rm{lf}}}}}}{{{\rm{d}}t}} = {q_{{\rm{mlfi}}}}-{q_{{\rm{mlfe}}}}-\frac{{{m_{{\rm{lf}}}}}}{{{\tau _{\rm{f}}}}} $ | (7) |
| $ \frac{{{\rm{d}}{m_{{\rm{lo}}}}}}{{{\rm{d}}t}} = {q_{{\rm{mloi}}}}-{q_{{\rm{mloe}}}}-\frac{{{m_{{\rm{lo}}}}}}{{{\tau _{\rm{o}}}}} $ | (8) |
| $ \frac{{{\rm{d}}{m_{\rm{g}}}}}{{{\rm{d}}t}} = {q_{{\rm{mgi}}}}-{q_{{\rm{mag}}}} + \frac{{{m_{{\rm{lf}}}}}}{{{\tau _{\rm{f}}}}} + \frac{{{m_{{\rm{lo}}}}}}{{{\tau _{\rm{o}}}}} $ | (9) |
式中mlf,mlo和mg分别表示热力组件中积存的燃料、氧化剂和燃气质量;qmlfi,qmloi,qmgi,qmlfe,qmloe和qmge分别表示流入流出热力组件的燃料、氧化剂和燃气的质量流量;τf,τo分别表示燃料和氧化剂的转化时间。
推进剂组元混合比为
| $ \frac{{{\rm{d}}{r_{\rm{g}}}}}{{{\rm{d}}t}} = \frac{{{r_{\rm{g}}} + 1}}{{{m_{\rm{g}}}}}\left[{\frac{{{m_{{\rm{lo}}}}}}{{{\tau _{\rm{o}}}}} + \frac{{{r_{\rm{i}}}}}{{{r_{\rm{i}}} + 1}}{q_{{\rm{mgi}}}}-{r_{\rm{g}}}\left( {\frac{{{m_{{\rm{lf}}}}}}{{{\tau _{\rm{f}}}}} + \frac{1}{{{r_{\rm{i}}} + 1}}{q_{{\rm{mgi}}}}} \right)} \right] $ | (10) |
式中ri为热力组件入口处燃气的推进剂组元混合比。
热力组件中压力的变化为
| $ \begin{array}{l} \frac{{{\rm{d}}p}}{{{\rm{d}}t}} = \frac{{RT}}{{V-\frac{{{m_{{\rm{lf}}}}}}{{{\rho _{\rm{f}}}}}-\frac{{{m_{{\rm{lo}}}}}}{{{\rho _{\rm{o}}}}}}}\frac{{{\rm{d}}{m_{\rm{g}}}}}{{{\rm{d}}t}} + \frac{p}{{RT}}\frac{{{\rm{d}}RT}}{{{\rm{d}}t}} + \\ \;\;\;\;\;\;\;\frac{p}{{V-\frac{{{m_{{\rm{lf}}}}}}{{{\rho _{\rm{f}}}}} - \frac{{{m_{{\rm{lo}}}}}}{{{\rho _{\rm{o}}}}}}}\left( {\frac{1}{{{\rho _{\rm{o}}}}}\frac{{{\rm{d}}{m_{{\rm{lo}}}}}}{{{\rm{d}}t}} + \frac{1}{{{\rho _{\rm{f}}}}}\frac{{{\rm{d}}{m_{{\rm{lf}}}}}}{{{\rm{d}}t}}} \right) \end{array} $ | (11) |
式中V为热力组件的容积,ρo和ρf分别为氧化剂和燃料的密度。
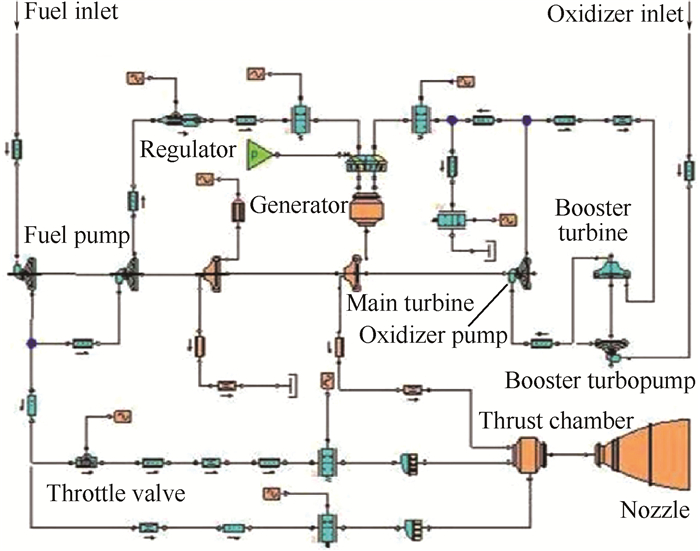
基于多领域统一建模与仿真MWorks平台[11],应用Modelica语言[12, 13],连接发动机系统各模型方程的参数传递接口,建立了液氧煤油高压补燃循环发动机的系统仿真平台,如图 4所示。
|
Fig. 4 System simulation platform of the LOX/kerosene high pressure staged combustion engine |
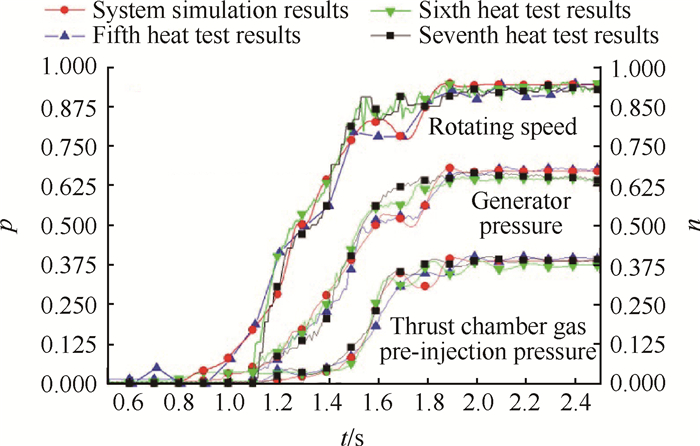
根据图 4建立的发动机系统仿真平台,对液氧煤油补燃循环发动机的起动至额定工况进行了仿真计算,并且与第5~7次整机地面热试车测量参数进行了比较,如图 5所示(压力p和转速n均为无量纲表示)。其中仿真和试车的发动机额定工况为海平面推力1200kN,比冲2942m/s,推力室混合比2.60。
|
Fig. 5 LOX/kerosene engine performance comparison of the system simulation and heat test results |
从图 5中可以看出,发动机主要性能参数的计算值与实测值吻合较好,表明液氧煤油高压补燃循环发动机的系统仿真平台能够准确描述发动机的系统参数特性。
3 液体火箭发动机变推力技术变推力液体火箭发动机能调节火箭主动飞行段的过载,可以实现月球、火星等天体表面软着陆,而且未来可重复使用火箭的回收过程也需进行深度推力调节,因而各航天大国均特别重视变推力发动机的研制。
3.1 国内外变推力发动机技术特点目前,国内外正式应用的具有代表性的变推力液体火箭发动机如表 1和图 6所示[14, 15]。
|
|
Table 1 Technical parameters of variable thrust liquid rocket engine at home and abroad |

|
Fig. 6 Variable thrust liquid rocket engine at home and abroad |
从国内外变推力发动机技术发展可知,变推力发动机具有以下特点:
(1) 挤压式发动机推力调节方案:通过栓式喷注器、可调汽蚀管、线性调节作动器组合技术,直接调节进入燃烧室的流量为主,最大可达到10:1的变推力能力,如LMDE,7500N变推力液体火箭发动机。
(2) 常规推进剂补燃循环发动机推力调节方案:通过多种补燃循环发动机节流措施,达到了10:1变推力能力,如RD-862发动机。
(3) 在液氧煤油高压补燃循环发动机推力调节中,仅通过调节涡轮燃气温度实现变推力的能力较弱,还需进一步采用氧路节流的方式加深推力调节能力,如RD-180,RD-191发动机,目前发动机最大变推比仅为3.7:1。
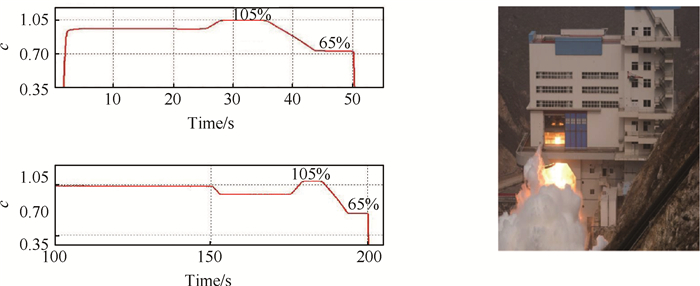
我国研制的1200kN液氧煤油高压补燃循环发动机在燃气发生器燃料路设置流量调节器进行单路推力调节,现地面试验推力调节能力达65%~105%,其地面热试车数据如图 7所示(图中c表示发动机实际推力F与额定推力1200kN之比)。
|
Fig. 7 Ground heat test curve of 1200kN LOX/kerosene engine |
与国外变推力液体火箭发动机相比,1200kN液氧煤油高压补燃循环发动机的推力调节能力仍存在较大的差距,尚不能满足可重复使用运载火箭对发动机的要求,因此需开展液氧煤油补燃循环发动机深度变推力技术研究,为后续变推力补燃循环发动机的工程研制奠定技术基础。
3.2 液氧煤油发动机推力调节途径分析利用图 4所示的发动机仿真平台,对1200kN液氧煤油发动机的推力调节途径进行分析。
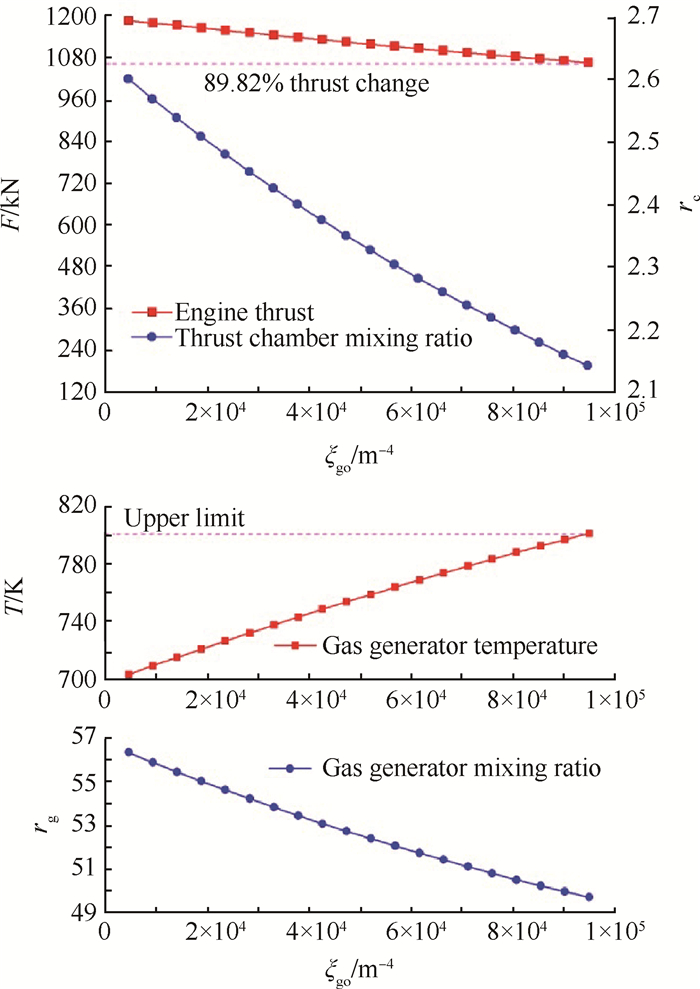
3.2.1 燃气发生器氧化剂路调节分析燃气发生器氧化剂路推力调节的仿真结果如图 8所示,其中F为发动机的推力,rc为推力室的混合比,T为燃气发生器的温度,rg为燃气发生器的混合比。随着燃气发生器氧路流阻系数ξgo的增大,发动机推力变化不大,但燃气发生器的温度明显升高。由于富氧燃气具有强烈的氧化作用,主涡轮在无冷却情况下的燃点温度比常规条件下低很多,其温度极限为800K。因此,燃气发生器氧路单独调节的变推力极限为89.82%。
|
Fig. 8 Variable thrust simulation of oxidizer road for gas generator |
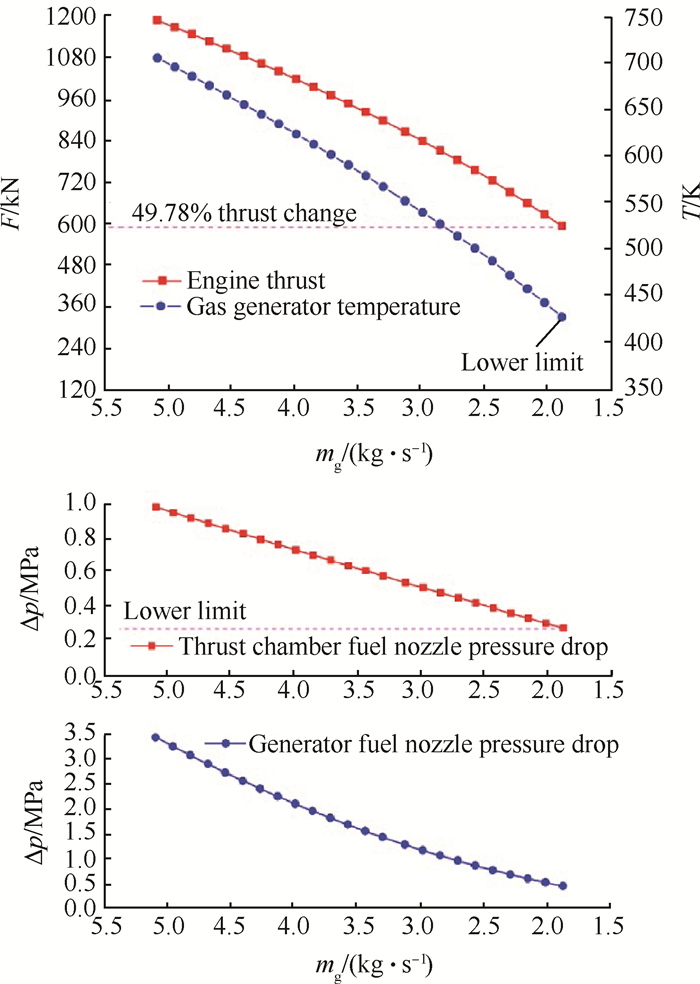
燃气发生器燃料路推力调节的仿真结果如图 9所示。通过调节发生器燃料路流量mg来控制燃气温度,从而控制涡轮输出功率。当推力下降至约49.78%工况时,达到了发生器稳定燃烧温度下限420K,同时推力室燃料喷嘴压降也达到极限值0.3MPa。因此,无法实现50%以上的深度变推力能力。
|
Fig. 9 Variable thrust simulation of fuel road for gas generator |
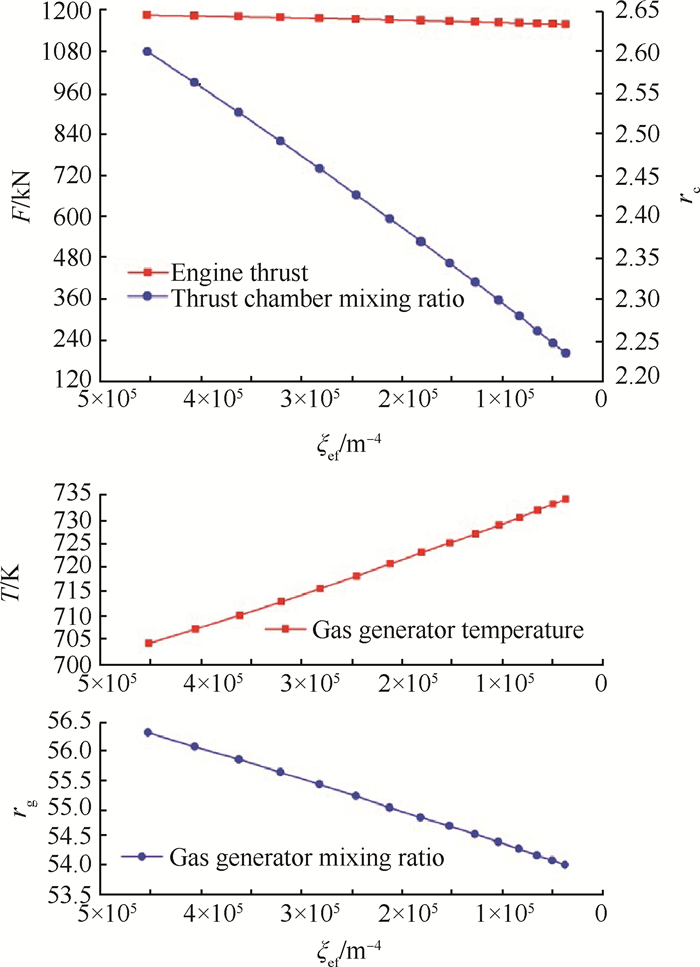
推力室燃料路推力调节的仿真结果如图 10所示。控制进入推力室的燃料流量,如增大节流阀的转角可减小发动机的组元比,但由于减小了燃料路流阻系数ξcf,燃料流量略有增大,同时会使主涡轮泵转速降低,氧流量略微减小,这样可保证推力室总流量基本不变,发动机的推力变化很小,但可以有效控制发动机的混合比。
|
Fig. 10 Variable thrust simulation of fuel road for thrust chamber |
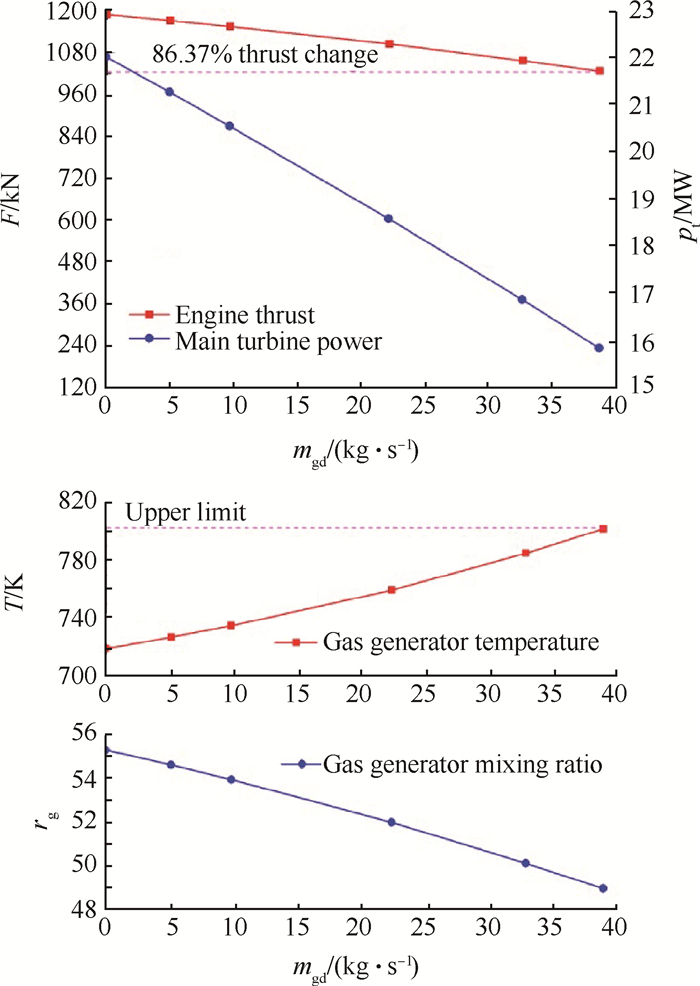
涡轮燃气供应路分流推力调节的仿真结果如图 11所示。旁路引出富氧燃气mgd,减少进入涡轮的燃气总流量,降低涡轮功率,达到降推力的目的。燃气分流阀开度增大时,由于流量调节器的稳流作用,减缓了推力下降程度。涡轮燃气分流与氧路分流相比,由于氧路分流进一步降低了燃气发生器的混合比,大幅提高了涡轮入口的温度,从而可知燃气分流比氧路分流更加可靠。因此,涡轮燃气供应路分流的单独调节变推力极限为86.37%。
|
Fig. 11 Variable thrust simulation of diverting flow of turbine gas supply road |
综合以上分析可知,发生器燃料路单路推力调节可达49.78%,但由于逼近燃气发生器温度下限,推力未能进一步降低;推力室燃料路调节对发动机混合比影响较大,因此可以随动调节混合比,防止大幅偏离造成性能下降;在涡轮燃气分流调节中,由于稳流型流量调节器的作用,发生器的温度上升较快,减缓了推力下降程度;发生器氧路和涡轮燃气分流调节均使发生器的温度上升,可拓宽发生器燃料路流量调节器的调节范围。
因此,在单路调节的基础上,需开展液氧煤油补燃循环发动机的组合推力调节技术研究,满足发动机深度变推力要求。
4 液氧煤油发动机深度变推力技术 4.1 发动机系统方案根据发动机单路调节的仿真结果,在已有1200kN液氧煤油补燃循环发动机系统的基础上进行改进技术研究,建立的1200kN液氧煤油补燃循环发动机深度变推力及多次起动系统如图 12所示。

|
Fig. 12 System composition of deep throttling and multiple starting LOX/kerosene engine |
与图 1所示的发动机原系统相比,主要改进如下:增加了涡轮旁路的燃气分流阀,减少驱动涡轮的燃气流量;液氧主阀具有双工位调节能力,以实现氧路的节流;为实现发动机在低入口压力下起动,设置起动加速阀,其入口与氧主泵出口联通,出口连接氧预压涡轮驱动路;增加点火剂贮箱,实现发动机的多次点火起动;低工况下调整推力室冷却环带阀门流阻,提高冷却可靠性。
4.2 深度变推力系统仿真利用图 4所示的发动机仿真平台,对图 12所示的发动机深度变推力及多次起动系统进行系统仿真,可获得1200kN液氧煤油发动机推力深度调节过程中的参数变化情况,如表 2~表 4所示。
|
|
Table 2 Performance parameters of depth variable thrust of 1200kN LOX/kerosene rocket engine |
|
|
Table 3 Adjusting device parameters of depth variable thrust of 1200kN LOX/kerosene rocket engine |
|
|
Table 4 Component feature parameters of depth variable thrust of 1200kN LOX/kerosene rocket engine |
仿真结果表明:当推力下降到海平面推力的10%时,通过发生器燃料路流量调节器、氧化剂供应路、涡轮燃气供应路分流以及推力室燃料供应路的组合调节,发动机性能高,参数可满足要求。此时,发生器和推力室燃料喷嘴压降仅为96kPa和38kPa,为保证稳定燃烧,在不改变发动机结构的基础上,需采用气体进行乳化以提高喷嘴压降的措施。
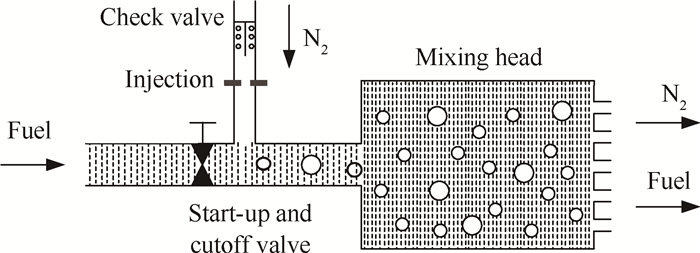
4.3 燃烧组件的气体乳化在1200kN液氧煤油补燃循环发动机深度变推力时,由于燃气发生器和推力室的喷注器压降过低,为改善推进剂组元的雾化效果,在不改变发动机结构的基础上,对发生器和推力室燃料头腔用氮气进行乳化,提高喷注器压降[16],如图 13所示。在补燃发动机研制过程中,也采用氮气吹除燃气发生器的燃料喷注器的方案,主要目的是在发动机起动之前,对煤油起乳化作用,提高喷注器的压降,改善煤油的雾化,其效果较好。
|
Fig. 13 Schematic diagram of generator and thrust chamber gas blowing |
气体乳化模型的假设条件:气体在混合头腔的压缩过程近似为绝热过程;由头腔流出的燃料流量包括气体携带的流量和混合头腔压力作用下流出的流量;假定气体和液体同时流出时所占的喷嘴流通面积的比例取决于头腔的充填程度。
吹除气体的质量流量
| $ {q_{{\rm{mpu}}}} = {C_{\rm{d}}}{A_{{\rm{pu}}}}A\left( k \right)q\left( \lambda \right)\frac{{{p_{{\rm{gv}}}}}}{{\sqrt {{R_{{\rm{pu}}}}{T_{{\rm{pu}}}}} }} $ | (12) |
式中Apu为等效流通面积;k为氮气绝热指数;λ为吹除气体速度系数;pgv为吹除气体压力;qmpu为进入头腔的吹除气体质量流量;q(λ)为吹除气体流量函数。
燃料混合头腔气体容积的变化
| $ \frac{{{\rm{d}}{V_{{\rm{ghf}}}}}}{{{\rm{d}}t}} = \frac{{-\left( {{q_{{\rm{mhfi}}}}-{q_{{\rm{mhfe}}}}} \right)}}{{{\rho _{\rm{f}}}}} $ | (13) |
燃料混合头腔中液体的相对充填量
| $ \bar V = \frac{{{V_{{\rm{hf}}}}-{V_{{\rm{ghf}}}}}}{{{V_{{\rm{hf}}}}}} $ | (14) |
式中Vghf为头腔中气体容积;qmhfi为进入头腔的燃料质量流量;qmhfe为流出头腔的燃料质量流量;ρf为燃料密度;Vhf为燃料头腔容积。
对于均相模型,根据马尔基涅利公式,两相流压降、气体单独流过时的压降与液体单独流过时的压降存在如下关系
| $ {\left( {\Delta {p_{{\rm{hfg}}}}} \right)^{\frac{1}{n}}} = {\left( {\Delta {p_{\rm{g}}}} \right)^{\frac{1}{n}}} + {\left( {\Delta {p_1}} \right)^{\frac{1}{n}}} $ | (15) |
式中Δpg为气体单独流过时的压降;Δpl为液体单独流过时的压降。
式(12)~(15)描述了燃气发生器和推力室燃料头腔的充填过程,模型考虑了气液两相流动,气体的乳化作用对头腔充填和流动的影响。
根据燃烧组件的气体乳化模型,可计算出向发生器和推力室的燃料喷注器乳化的气体参数。根据运载火箭回收的总体要求,气体乳化的时间设为5s,如表 5所示。
|
|
Table 5 Gas parameters of generator and thrust chamber blowing (5s) |
从表 5中可以看出,当推力下降到10%工况时,向发生器和推力室燃料喷嘴分别通入0.890kg/s和2.220kg/s氮气,可满足喷嘴压降不小于0.3MPa的要求。当采用复合材料气瓶时,气体乳化的时间设定为5s,发生器和推力室燃料喷嘴氮气乳化增加的总重量分别为12.91kg和25.82kg。
5 变推力发动机关键技术及解决途径国际上液氧煤油补燃循环发动机的最大推力调节范围为3.7:1 (RD-191),尚未有达到10:1深度节流的先例,研制难度大,不仅需突破深度变推力和多次起动技术,还需突破其他关键技术。
(1) 补燃循环大范围推力稳定调节控制技术
补燃循环发动机系统复杂,参数变化剧烈、耦合性强;低工况时喷注器和调节装置压降低,粗糙燃烧波动引起供应系统的不稳定;而且低工况下调节器及发生器存在低频响应,此时脉动压力大幅增加。因此需通过发动机动静特性仿真,优化调节策略和起动方案,开展变工况系统稳定性研究,建立稳定性系统模型,分析补燃循环发动机系统稳定性机理,提出发动机稳定性保障措施。
(2) 大范围推力调节下燃烧组件稳定燃烧技术
喷注器是组织推进剂喷雾、混合和燃烧的关键组件,对燃烧组件的燃烧稳定性、燃气温度均匀性等具有重要影响。特别是在大范围变工况时,燃烧组件的流量和混合比发生大幅度变化,使得组织稳定燃烧更为困难。开展喷注单元内流场仿真研究,获得低工况下气体乳化吹除对喷嘴内压力场、速度场等分布的影响。
(3) 大范围变工况下推力室可靠冷却技术
进入推力室的燃气温度高,可达3000℃,热流密度大,达到100MW/m2,是现役主发动机的4倍,而且受到煤油结焦温度380℃的限制,因此推力室的热防护面临较大的困难。可结合推力室传热计算结果,优化选取合适的冷却方案和流量调节策略,并通过传热、部组件热试或整机热试车等手段考核,在低工况下调整推力室冷却环带路流阻,增加冷却环带相对流量,保证低工况下冷却可靠性。
(4) 大变比涡轮泵稳定工作技术
1200kN液氧煤油补燃循环发动机的研制经验表明,大变比涡轮泵需解决超宽变工况范围内泵性能稳定性问题、轴向力平衡技术、涡轮端动密封工作可靠性技术、大范围变工况时泵气蚀问题、涡轮材料的抗烧蚀特性等问题。可通过设置具有大范围调节能力的轴向力调节装置,通过介质运转试验确定出合理的密封比压,开展泵结构优化设计、摩擦副材料和密封结构优化选取、涡轮泵仿真系统研究及材料烧蚀试验研究等,解决大范围变工况稳定工作涡轮泵技术。
6 结论在分析国内外变推力液体火箭发动机特点的基础上,针对1200kN液氧煤油补燃循环发动机,首次提出发生器燃料路流量调节器调节、主涡轮前燃气分流以及氧化剂主路节流等相结合,并辅助以气体乳化吹除喷注器的组合深度推力调节方案,调节能力达10:1,实现多次点火起动,具有性能高、调节范围大的优点。
该组合调节方案是在发动机原系统上进行了适应性改进,未对系统特性和组件进行改动,而且涡轮泵、推力室等组件已经通过了低工况下的液流试验,满足大范围变推力的工况要求,因此系统动态特性应满足要求,后续将通过实际地面低工况试车进一步验证。
对低工况下发动机所涉及的补燃循环大范围推力稳定调节控制技术、大范围推力调节下燃烧组件稳定燃烧技术、大范围变工况下推力室可靠冷却技术以及大变比涡轮泵稳定工作技术进行了分析,并提出了相应的解决途径。
| [1] |
Deneu F, Malassigne M, Le-couls O, et al. Promising Solutions for Fully Reusable Two-Stage-to-Orbit Configurations[J]. Acta Astronautica, 2005, 56(8): 729-736. DOI:10.1016/j.actaastro.2004.11.003
(  0) 0) |
| [2] |
冯韶伟, 马忠辉, 吴义田, 等. 国外运载火箭可重复使用关键技术综述[J]. 导弹与航天运载技术, 2014, 335(5): 82-86. (  0) 0) |
| [3] |
郑雄, 杨勇, 姚世东, 等. 法尔肯9可重复使用火箭发展综述[J]. 导弹与航天运载技术, 2016, 344(2): 39-46. (  0) 0) |
| [4] |
李斌, 张小平, 高玉闪. 我国可重复使用液体火箭发动机发展的思考[J]. 火箭推进, 2017, 43(1): 1-7. (  0) 0) |
| [5] |
高朝辉, 刘宇, 肖肖, 等. 垂直着陆重复使用运载火箭对动力技术的挑战[J]. 火箭推进, 2015, 41(3): 1-6. (  0) 0) |
| [6] |
雷娟萍, 兰晓辉, 章荣军, 等. 嫦娥三号探测器7500N变推力发动机研制[J]. 中国科学:技术科学, 2014, 44(6): 569-575. (  0) 0) |
| [7] |
刘红军. 液氧/煤油发动机稳态参数分布特性的仿真[J]. 推进技术, 2004, 25(5): 385-387. (LIU Hong-jun. Monte-Carlo Simulation on Static Characteristics of a Liquid Oxygen/Kerosene Staged Combustion Cycle Engine[J]. Journal of Propulsion Technology, 2004, 25(5): 385-387.)
(  0) 0) |
| [8] |
蔡亦刚. 流体传输管道动力学[M]. 杭州: 浙江大学出版社, 1990.
(  0) 0) |
| [9] |
Jung T. Static Characteristics of a Flow Regulator for a Liquid Rocket Engine[J]. Journal of Spacecraft and Rockets, 2011, 48(3): 541-544. DOI:10.2514/1.52130
(  0) 0) |
| [10] |
Beliaev E N, Chevanov V K, Chervakov V V. Mathematical Modeling of Working Processes of Liquid Propellant Rocket Engines[M]. Moscow: MAI, 2009.
(  0) 0) |
| [11] |
周凡利. 工程系统多领域统一模型编译映射与仿真求解研究[D]. 武汉: 华中科技大学, 2011.
(  0) 0) |
| [12] |
Hubertus Tummescheit. Design and Implementation of Object-Oriented Model Libraries using Modelica[D]. Lund: Lund Institute of Technology, 2002.
(  0) 0) |
| [13] |
陈宏玉, 刘红军, 陈建华, 等. 补燃循环发动机关机过程仿真研究[J]. 推进技术, 2016, 37(12): 2219-2225. (CHEN Hong-yu, LIU Hong-jun, CHEN Jian-hua, et al. Investigation on Shutdown Process of a LOX/Kerosene Staged Combustion Cycle Rocket Engine[J]. Journal of Propulsion Technology, 2016, 37(12): 2219-2225.)
(  0) 0) |
| [14] |
刑继发. 世界导弹与航天发动机大全[M]. 北京: 军事科学出版社, 1999.
(  0) 0) |
| [15] |
毛根旺. 大型液体火箭发动机的最新发展[J]. 推进技术, 1995, 16(1): 1-6. (MAO Gen-wang. The Latest Developments of Large-Scale Liquid Rocket Engine[J]. Journal of Propulsion Technology, 1995, 16(1): 1-6.)
(  0) 0) |
| [16] |
岳春国, 李进贤, 侯晓, 等. 变推力液体火箭发动机综述[J]. 中国科学:技术科学, 2009, 39(3): 464-468. (  0) 0) |
 2018, Vol. 39
2018, Vol. 39


