2. 西安卫星测控中心,陕西 西安 710043
2. Xi'an Satellite Control Center, Xi'an 710043, China
冷气推进系统是一种常用的推进系统,具有结构简单、工作性能稳定、可靠性高、成本低廉、电功耗小、无毒无污染等优点[1]。冷气推进系统一般指的是压缩气体冷气推进系统[2]。压缩气体为高压气体,多选用氮、氦、氖、氙等惰性气体[3]。氮气相对于其它惰性气体而言,其有效比冲较高,应用相对较多[4]。冷气推进系统与其它推进系统相比,其比冲相对较低,应用往往受到一定限制[5]。但得益于MEMS(MicroElectron-Mechanical System,微机电系统)技术发展[6],冷气推进系统目前在微小卫星中获得较为广泛的应用。冷气推进系统的研究多集中在部件小型化[7]、提高可靠性、增加有效比冲等方面。
梁振华等[8]对固体冷气微推力器的推进剂配方进行了研究,给出了两种不同配方,可满足不同需要。李明新等[9]对所设计的微小推力冷气发动机进行高空模拟试验和比冲测量,丙烷和氮气的平均比冲对应为83.5s和75.6s。David H[10]针对微小推力需求,利用光固化成型技术制作了一款集成的微小冷气推进系统,适用于皮纳卫星,但不适合于长期型任务。Hiroyuki K等[11]介绍了一种共用氙气源的电推进与冷气推进复合的推进系统,整个系统质量不到10kg,应用于深空探测任务。汪旭东等[12]针对连续可调小推力问题,设计了一种数据驱动PID(Propor⁃ tion,Integration and Differentiation,比例积分微分)控制器,获得了快速响应的控制效果。李晶等[13]利用随遇平衡原理在重力场中消除了冷气发动机自重及高压供气系统对微小推力测量的影响,实现了冷气发动机稳态小推力的自动、准确测量,可为喷管设计和定型提供实验支持。Kvell U等[14]介绍了一种基于MEMS技术制造的冷气推进系统,用于纳卫星轨道与姿态控制。Joseph C等[15]在某小卫星的冷气推进系统设计与制造、测试中,给出了一种冷气泄漏的评估参考,即在设计寿命期内推进剂泄漏质量一般应不超过20%,在制造技术与工艺提高的前提下一般不超过10%。
以上工作从研制、设计、测量等不同方面进行研究,有助于提升冷气推进系统的工作性能。但对于在轨冷气泄漏的相关资料却相对缺乏,刘展等[16]从被动防隔热、混合控压、主动制冷等方面对国外低温推进剂蒸发量控制方面的研究状况进行了综述,但其研究对象为液体燃料,并非冷气。与冷气贮存相关的检漏文献相对较多(这里不进行列举、赘述),但是相关研究、试验与应用多是在地面进行,缺少在轨数据检验。
徐福祥[17]介绍了卫星在气源耗尽条件下的姿态恢复过程,彭仁军等[18]则报道了另一颗卫星在主贮箱燃料耗尽、备贮箱燃料结冰下的姿态故障抢修与恢复,两者的共同点是:异常处理中无气源可用,主要采用磁控恢复卫星姿态(任务艰巨、历程艰辛)。因此,在卫星姿态发生重大异常时,有无气源可用,其工作难易差别显而易见。对于在轨卫星的长期管理而言,冷气在轨贮存是其发挥姿态或轨道控制作用的前提条件之一,冷气剩余量估计也是遥测诊断[19]与器件健康状态评估的重要内容之一。这里结合某卫星在轨运行实例,针对冷气推进系统进行冷气泄漏率估计与剩余质量预测,应用于航天器长期管理。
2 冷气推进系统的推进剂泄漏近地卫星A运行在晨昏轨道,降交点地方时在06:00 AM左右,轨道偏心率接近于0,初始轨道高度约595km,采用偏置动量控制方式,设计寿命为3y。卫星A上装有冷气推进系统,工质为高压氮气,初始压力接近13MPa,容积60L,配置6个推力器(标称推力1.5N),主要用于入轨时期以及异常情况下的姿态控制。在轨稳态工作模式下,整星采用磁控与轮控结合的控制方式。
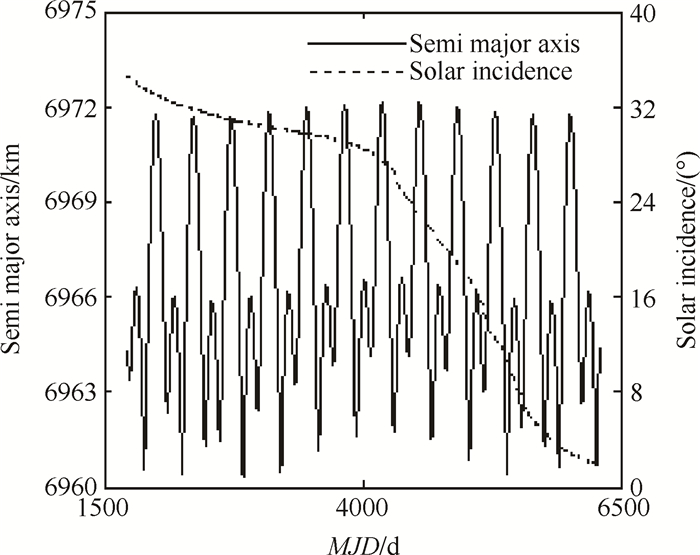
卫星入轨以来的轨道半长轴和光照角变化如图 1所示。
|
Fig. 1 Semi major axis and solar incidence |
图 1中的横轴为约简儒略日,时间起点为UTC(Coordinated Universal Time,世界协调时)时间的2000年1月1日12时,1d的时长为86400s。这里的光照角定义为轨道法线与地日矢量的夹角。
从图 1可以看出,卫星在轨运行期间从未进行过轨道控制,半长轴衰减主要为大气阻力作用下的自然衰减。光照角变化呈双峰值、年周期规律,范围约在0~32°。
如果不考虑空间环境因素影响(例如太阳活动增强),再综合考虑文献[20~22]对整星的热工况的研究结果可以知道,卫星在轨热流变化相对稳定,整星温度在热涂层性能退化的作用下应呈现逐渐升高趋势。
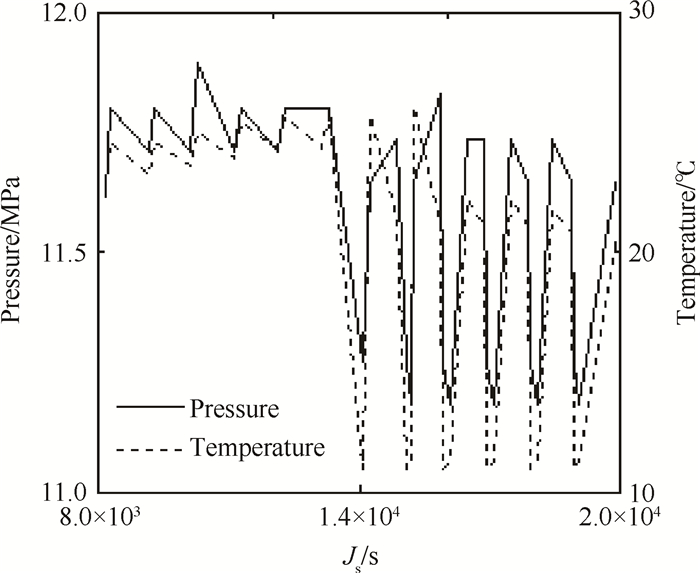
卫星冷气推进系统在入轨初期进行过喷气实施姿态控制以后,从未进行过姿态控制,开关阀一直是关闭状态。冷气罐的温度与压力参数变化如图 2所示。
|
Fig. 2 Temperature and pressure |
图 2中横轴为积秒(起点为每一天的零时,终点为下一天的零时,最大值为86400s),可以看出,在相对较短的时间段内(一天或者数天),温度与压力变化基本同步:温度升则压力升,温度降则压力降。
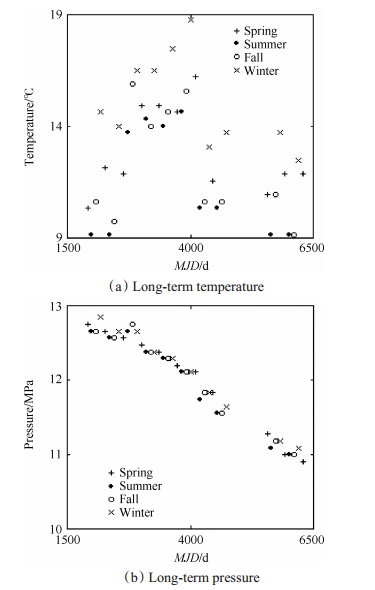
但从较长的时间段来看(数月或者一年),温度具有年周期变化规律,压力呈下降趋势,具体如图 3所示。
|
Fig. 3 Temperature and pressure in long term |
图 3中,为减少数据采样量,仅选取每年的分、至日附近的数据作为表征(截止期为2017年3月21日)。以年为周期来看,冬至前后的温度与压力数值基本上要高于夏至前后的数值,这可能是日地距离变化所致:冬至前后日地距离近,太阳辐照强烈,夏至前后的情形则相反。但从整个在轨时段来看,冷气罐的温度呈现先升后降变化,压力呈现明显的长期下降趋势,前者可能是太阳活动变化与热涂层性能退化综合作用下的结果,后者则可能是推进剂泄漏所致。
3 推进剂泄漏率的估计模型氮气泄漏可能对推进系统的性能造成严重影响,一般分为内泄漏与外泄漏两种,前者主要通过阀门损失,后者则通过其它部位损失。如果阀门的密封性能不好,则可能造成内泄漏,文献[23]即是研究聚四氟乙烯材料密封圈的密封性能的例子。至于外泄漏,一般采用全焊接结构方式来减少损失,再考虑地面的严格检漏测试与筛选,外泄漏一般很少在轨发生。
这里主要利用气态方程[24]对推进剂泄漏率进行估计。气态方程为
| $ pV = nRT $ | (1) |
式中p为压力,MPa;V为体积,m3;n为摩尔量,mol;R为常数,参照Flament N等[25]的数据,取为8.31J·mol-1·K-1;T为温度,K。显然,这里的冷气罐体积基本上不变,可以考虑体积为常数。接下来,对图 3中的温度与压力数据进行归一化处理,得到ak
| $ {a_k} = \frac{{{p_k}}}{{{T_k}}}{T_{\rm{r}}}V,\;\;\;\;k = 0,1,2,3, \cdots $ | (2) |
式中Tr为273.15K,常数;k表示采样数据组的序号,无量纲。
以k=0时的第一组数据为参考,可计算推进剂泄漏率bk为
| $ {b_k} = - \frac{{{a_k} - {a_0}}}{{{t_k} - {t_0}}},\;\;\;\;k = 1,2,3, \cdots $ | (3) |
式中t表示数据对应的采样时刻,s。
同样,利用式(1)可以进行剩余推进剂质量相对于初始质量的比率ck的计算
| $ {c_k} = \frac{{{p_k}}}{{{T_k}}}\frac{{{T_0}}}{{{p_0}}},\;\;\;\;k = 1,2,3, \cdots $ | (4) |
显然,第一组数据是剩余率计算的参考,气体体积也认为是常数、不变。
另外,根据式(3)的泄漏率计算结果,还可以转换成推进剂的质量泄漏率mk为
| $ {m_k} = - \frac{{{a_k} - {a_0}}}{{{t_k} - {t_0}}}\frac{{28}}{{R \cdot {T_{\rm{r}}}}},\;\;\;\;k = 1,2,3, \cdots $ | (5) |
式中28即是氮气的摩尔质量的数值。显然,这里的质量泄漏率的单位是kg/s。
根据质量的泄漏率,可以计算漏气对于姿态扰动的影响。这里仅考虑力臂最大(距y轴力臂最大)情形下的扰动。首先计算扰动力与力矩。
| $ {F_k} = \int_{{t_0}}^{{t_k}} {{m_k}v{\rm{d}}t} ,\;\;\;\;k = 1,2,3, \cdots $ | (6) |
式中Fk为姿态的扰动力,N;v为喷气速度,m/s。则有
| $ {T_k} = d \times {F_k} = \frac{{{\rm{d}}{H_k}}}{{{\rm{d}}t}},\;\;\;\;k = 1,2,3, \cdots $ | (7) |
式中Tk为姿态的扰动力矩,N·m;d为力臂,m;Hk为角动量,N·m·s。角动量Hk还可以表示为
| $ {H_k} = J{\omega _k} = J\frac{{{\rm{d}}\theta }}{{{\rm{d}}t}},\;\;\;\;k = 1,2,3, \cdots $ | (8) |
式中ωk为绕y轴的角速度,rad/s;θ为俯仰角,rad;J为绕y轴的转动惯量,kg·m2。力臂与扰动力正交,力臂的大小为1m,因此可以得到扰动角度为
| $ \theta = \frac{1}{J}\int_{{t_0}}^{{t_k}} {\int_{{t_0}}^{{t_k}} {{m_k}v{\rm{d}}t{\rm{d}}t} } ,\;\;\;\;k = 1,2,3, \cdots $ | (9) |
式中将初始角度取为0。如果将冷气的质量泄漏率、喷气速率均看作参数,有
| $ \theta = \frac{1}{{2J}}{m_k}v{\left( {{t_k} - {t_0}} \right)^2},\;\;\;\;k = 1,2,3, \cdots $ | (10) |
下面针对式(3)和式(4)进行误差分析。这里假定各测量值之间相互独立。
先考虑式(3)的泄漏率计算值的误差
| $ \begin{array}{l} {\rm{d}}{b_k} = \frac{{ - 1}}{{{t_k} - {t_0}}}{\rm{d}}\left( {{a_k} - {a_0}} \right)\\ {\rm{d}}{a_k} = \frac{{{T_k}{\rm{d}}{p_k} - {p_k}{\rm{d}}{T_k}}}{{T_k^2}}{T_{\rm{r}}}V \end{array} $ | (11) |
显然,在式(11)中,将温度Tr,体积V以及时间差均作为常数处理。对于时间差主要是考虑该数值相当大,在107数量级以上,而且时刻确定精度也高(星上时间数据的最小单位一般为1ms,对应的均方差优于1ms,卫星时间同步精度文章可参见文献[26]),因此将该值仅作常数考虑。
一般情况下,压力测量分辨率优于0.1MPa,而温度测量分辨率优于0.1K。这里,假定压力与温度的最小分辨率为0.1MPa与0.1K,误差分布服从均匀分布,则对应的误差分布区间为[-0.05,0.05]MPa与[-0.05,0.05]K。参考唐美燕等[27]的计算方法,对应的均方差为
| $ \begin{array}{l} {\sigma _P} = \sqrt {\frac{1}{{12}}{{\left( { - 0.05 - 0.05} \right)}^2}} = 0.029\\ {\sigma _T} = \sqrt {\frac{1}{{12}}{{\left( { - 0.05 - 0.05} \right)}^2}} = 0.029 \end{array} $ | (12) |
式中前者为压力的均方差,MPa;后者为温度的均方差,K。
进一步,即使假定压力的均方差为1MPa,温度的均方差为1K,初始值对应为10MPa和300K,再考虑冷气罐的体积因素,从式(11)可以知道,泄漏率的计算误差很小;而且随着时间差数值的进一步增大,该值会变得更小。所以,在这里可以不用考虑泄漏率的计算值的误差。
同样地,对于质量泄漏率的误差,亦无需考虑(其分析过程与推进剂泄漏率误差相似)。
对于式(4)的比率计算值误差
| $ \begin{array}{l} {\rm{d}}{c_k} = \frac{{{T_0}}}{{{T_k}}}{\rm{d}}\left( {\frac{{{p_k}}}{{{p_0}}}} \right) + \frac{{{p_k}}}{{{p_0}}}{\rm{d}}\left( {\frac{{{T_0}}}{{{T_k}}}} \right) = \\ \;\;\;\;\;\;\;\;\frac{{{T_0}}}{{{T_k}}}\frac{{{p_0}{\rm{d}}{p_k} - {p_k}{\rm{d}}{p_0}}}{{p_0^2}} + \frac{{{p_k}}}{{{p_0}}}\frac{{{T_k}{\rm{d}}{T_0} - {T_0}{\rm{d}}{T_k}}}{{T_k^2}} \end{array} $ | (13) |
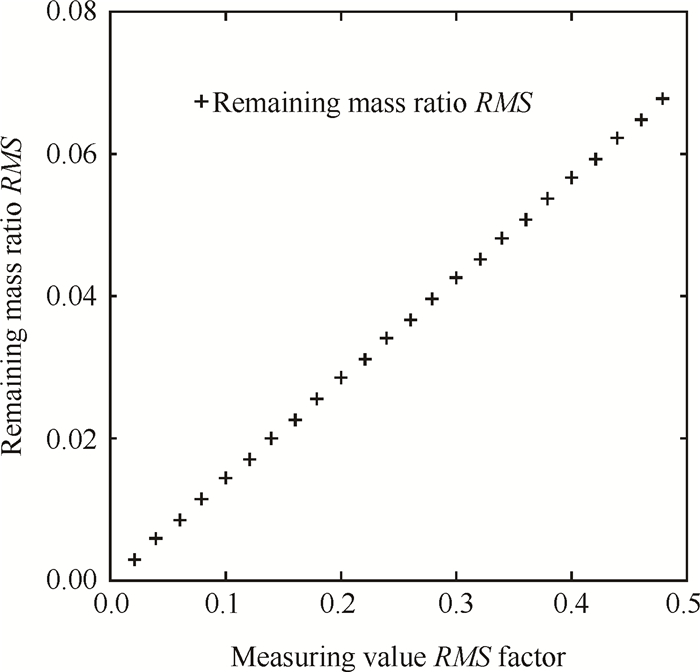
类似地,假定压力数值均为10MPa,均方差为p,单位为MPa;温度数值均为300K,均方差为x,单位为K。这里x定义为测量值均方差系数,无量纲。将x取值为[0,0.5],则对应的式(13)的剩余质量比率均方差如图 4所示。
|
Fig. 4 Root mean square of remaining mass ratio |
图 4中,将剩余质量比率简称为剩余比率,用+表示其均方差。显然,如果将系数取为0.1,则剩余比率均方差将优于2%;如将式(7)的结果代入,即取为0.03,对应结果将优于0.5%。
从以上误差分析来看,式(3)和式(4)的计算精度都比较高。
4 遥测数据分析及讨论根据图 3中的数据,利用式(3)可以得到冷气的泄漏率;式(3)中的计算结果直接取算术平均,作为泄漏率的估计值;结果如图 5所示。
|
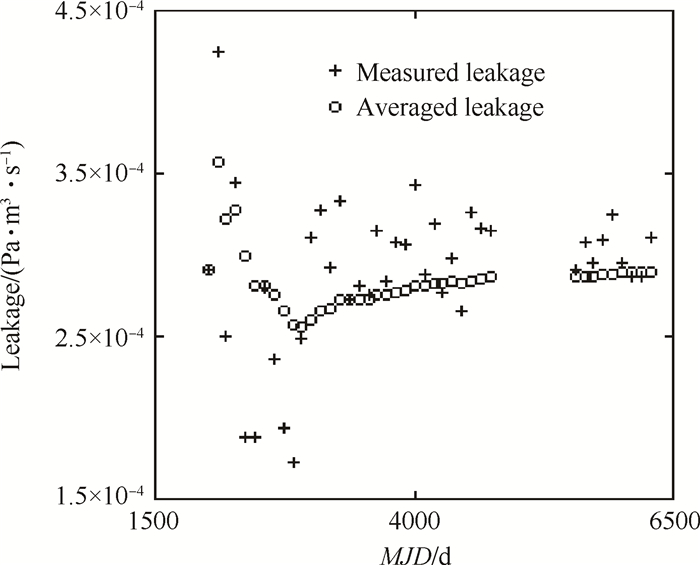
Fig. 5 Cold gas leakage |
图 5中+为计算值(测量值),o为平均值。可以看出,在最初将近5y的时间里,泄漏率呈现振荡变化,范围在150~450Pa·cm3·s-1,中心值约为275Pa·cm3·s-1;随后泄漏率基本稳定在275Pa·cm3·s-1,虽然中间有数据缺失段,但是稳定值的变化很小,基本可以看作不变。
同样,质量泄漏率亦可由式(5)计算得到,或者由图 5中的结果乘以一个系数也可得到。质量泄漏率的稳定值约为3.4μg/s。
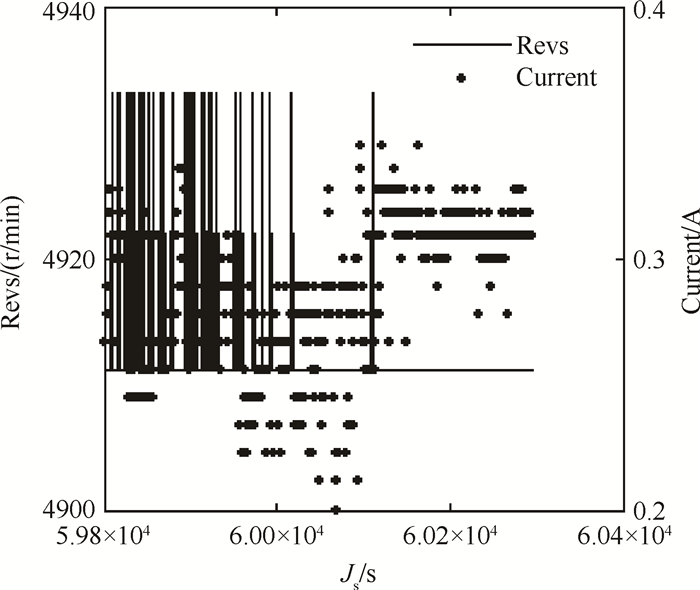
利用质量泄漏率的数值,可以对最大扰动进行估计。这里,取转动惯量为500kg·m2,喷气速率为1km/s(实际速率远小于此),则由式(10)可计算姿态角变化2π需要的时长约为43000s。这说明在将近12h的时间里,漏气扰动会使得y轴旋转360°。这一数值太小,很容易被偏置动量轮吸收,最后由磁力矩器卸载,不会对姿态控制系统造成影响。图 6~8分别给出了卫星的动量轮转速与驱动电流、磁力矩器电流、三轴姿态角的实时遥测数据。
|
Fig. 6 Momentum wheel revs and current |
|
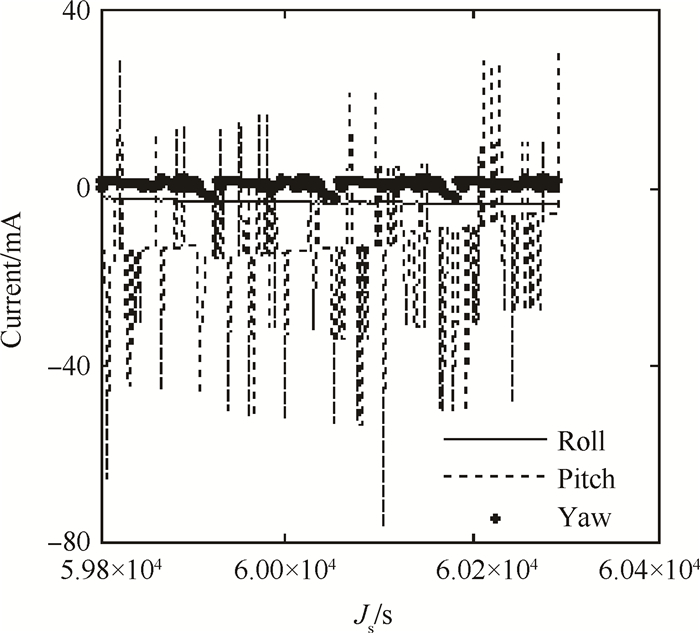
Fig. 7 Magnetic torque current |
|
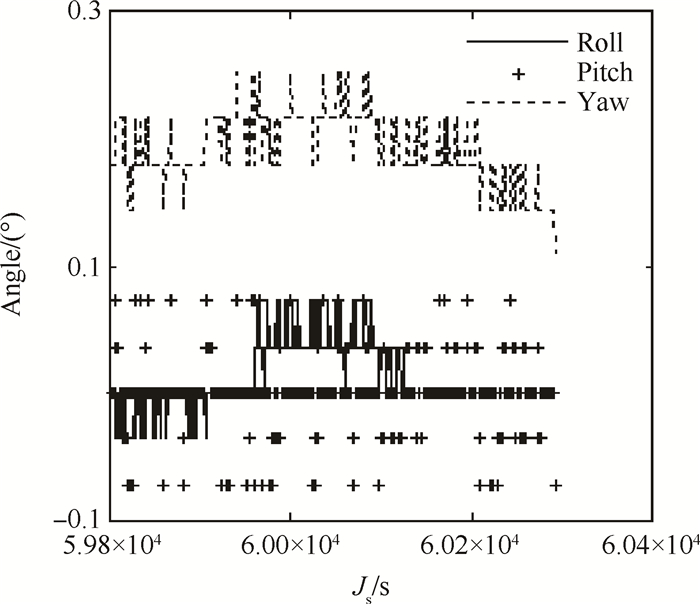
Fig. 8 Attitude Angle |
图 6中,动量轮转速均值为4912r/min,均方差为6r/min;电流为0.287A,均方差为0.029A。
图 7中,统计X轴磁力矩器电流为-3.2mA,均方差为0.4mA;Y轴磁力矩器电流为-13.3mA,均方差为13.5mA;Z轴磁力矩器电流为0.8mA,均方差为1.1mA。
图 8中,滚动角均值为0.0107°,均方差为0.0244°;俯仰角均值为-0.0004°,均方差为0.0265°;偏航角均值为0.1926°,均方差为0.0269°。
以上遥测参数的数值均在遥测诊断的正常值门限之内,姿态角的精度更是优于设计指标。因此,冷气推进剂泄漏没有对姿控系统带来影响,或者说,泄漏造成的影响可以忽略不计。
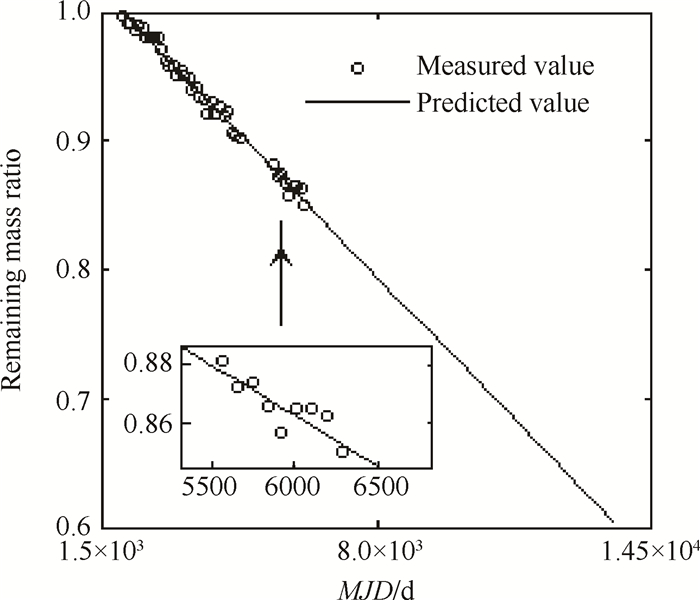
利用图 5中的结果和式(4),计算可以得到冷气推进剂剩余质量相对于初始质量的比率,并可在比率计算值的基础上进行预测,如图 9所示。
|
Fig. 9 Remaining mass ratio prediction |
在图 9中,o为计算值(测量值),实线为预测值。这里的预测是先在计算值的基础上进行线性拟合、然后进行线性预测(文献[28, 29]均给出了具体的线性拟合的例子)。从图 9可以知道,在轨10y时,推进剂泄漏不足15%;从最后一组数据(对应时间为2017年3月21日)向后预测20y,剩余推进剂仍在60%以上。需要说明的是,如果中途出现冷气的应用,则将应用结束点作为新的初始点,再次计算,形成分段计算与估计、预测。
参照Joseph C等[15]关于小卫星冷气推进系统的泄漏标准,再考虑卫星设计寿命为3y,则卫星A的冷气推进系统虽有泄漏,但可以认为满足指标要求。在后续测控中,需要在遥测诊断中持续关注冷气推进剂泄漏情况,为超期服役卫星的测控与管理提供数据支持。
5 结论对于冷气推进系统的推进剂泄漏进行评估,得到以下结论:
(1)冷气罐的温度具有年周期变化规律,冬至前后为高温水平,夏至前后为低温水平,其它时期则介于高温与低温状况之间;冷气罐压力在泄漏前提下,呈现长期下降趋势。
(2)冷气的泄漏率约为275Pa·cm3·s-1,对应的氮气工质的质量泄漏率约为3.4μg/s。
(3)冷气泄漏对卫星姿态扰动非常小,完全可以忽略不计。
(4)卫星在轨的10y时间里,冷气的泄漏质量不足15%;预测在轨30y时,剩余推进剂质量仍在60%以上,满足应用需求。
(5)国产冷气推进型号产品可靠性较高,适合于长寿命低轨卫星的姿态、轨道控制应用。
在冷气泄漏情形下,压力不断变小,下一步可针对相应的推力变化进行建模与估计、预测,并应用于在轨卫星长期测控与管理中的遥测诊断辅助、以及器件健康状态评估。
| [1] |
边炳秀. 卫星推进系统的历史、现状和未来[J]. 控制工程, 2001, 8(5): 28-39. (  0) 0) |
| [2] |
屠善澄. 卫星姿态动力学与控制(4)[M]. 北京: 中国宇航出版社, 2009, 40-69.
(  0) 0) |
| [3] |
王璐, 李国岫, 虞育松, 等. 微小超高压冷气推进系统动态工作性能仿真研究[J]. 上海航天, 2014, 31(6): 52-56. (  0) 0) |
| [4] |
周伟勇, 张育林. 基于有效比冲的小卫星冷气推进系统设计[J]. 宇航学报, 2010, 31(1): 173-178. (  0) 0) |
| [5] |
尤裕荣, 曾维亮. 冷气发动机系统动态特性仿真研究[J]. 火箭推进, 2009, 35(6): 14-18. (  0) 0) |
| [6] |
唐飞, 叶雄英, 周兆英. MEMS冷气推进器的制作及实验研究[J]. 微纳电子技术, 2003, 40(7): 441-444. (  0) 0) |
| [7] |
Ryan P, Christopher T. Design, Test, and Validation of a Refrigerant-Based Cold-Gas Propulsion System for Small Satellites[C]. Logan, Utah: 24th Annual AIAA/USU Conference on Small Satellites, 2010. https://digitalcommons.usu.edu/smallsat/2010/all2010/48/
(  0) 0) |
| [8] |
梁振华, 刘旭辉, 朱朋, 等. 固体冷气推进剂性能初步分析[J]. 推进技术, 2016, 37(1): 181-187. (LIANG Zhen-hua, LIU Xu-hui, ZHU Peng, et al. Preliminary Analysis on Properties of Solid Cool Gas Propellant[J]. Journal of Propulsion Technology, 2016, 37(1): 181-187.)
(  0) 0) |
| [9] |
李明新, 汤海滨, 张尊. 微小推力冷气发动机动静态性能实验研究[J]. 推进技术, 2013, 34(6): 728-733. (LI Ming-xin, TANG Hai-bin, ZHANG Zun. Experimental Investigation on Dynamic and Steady Performance of Cold Gas Micro-Propulsion Thruster[J]. Journal of Propulsion Technology, 2013, 34(6): 728-733.)
(  0) 0) |
| [10] |
David H. A Novel Cold Gas Propulsion System for Nanosatellites and Picosatellites[C]. Logan, Utah: 22nd Annual AIAA/USU Conference on Small Satellites, 2008. https://digitalcommons.usu.edu/smallsat/2008/all2008/44/
(  0) 0) |
| [11] |
Hiroyuki K, Hiroki K, Kazuya Y, et al. On-orbit Performance of a Miniature Propulsion System on a 70 kg Space Probe to Explore Near-Earth Asteroids[C]. Logan, Utah: 29th Annual AIAA/USU Conference on Small Satellites, 2015. https://digitalcommons.usu.edu/smallsat/2015/all2015/113/
(  0) 0) |
| [12] |
汪旭东, 范旭丰, 陈君, 等. 微小冷气比例推力器模块的数据驱动PID控制策略[J]. 信息与控制, 2014, 43(3): 381-384. (  0) 0) |
| [13] |
李晶, 蒋金伟, 赵宝瑞. 冷气发动机小推力测量系统[J]. 宇航计测技术, 2003, 23(6): 14-17. (  0) 0) |
| [14] |
Kvell U, Puusepp M, Kaminski F, et al. Nanosatellite Orbit Control Using MEMS Cold Gas Thrusters[J]. Proceedings of the Estonian Academy of Sciences, 2014, 63(2): 279-285.
(  0) 0) |
| [15] |
Joseph C, Jesus A. Design and Test of an Economical Cold Gas Propulsion System[C]. Logan, Utah: 14th Annual AIAA/USU Conference on Small Satellites, 2000. https://digitalcommons.usu.edu/smallsat/2000/All2000/74/
(  0) 0) |
| [16] |
刘展, 厉彦忠, 王磊, 等. 低温推进剂长期在轨压力管理技术研究进展[J]. 宇航学报, 2014, 35(3): 254-261. (  0) 0) |
| [17] |
徐福祥. 用地球磁场和重力场成果挽救风云一号(B)卫星的控制技术[J]. 宇航学报, 2001, 22(2): 1-11, 17. (  0) 0) |
| [18] |
彭仁军, 马雪阳, 郑科宇, 等. 一颗低轨道卫星在轨故障抢修与恢复[J]. 航天器工程, 2008, 17(1): 24-29. (  0) 0) |
| [19] |
郝培杰, 徐冰霖, 卢晓东, 等. 卫星单粒子闩锁异常的诊断与自动报警[J]. 飞行器测控学报, 2014, 33(6): 512-517. (  0) 0) |
| [20] |
吴文瑞, 黄海. 太阳同步轨道卫星热控分系统分析及优化[J]. 航天器工程, 2012, 21(2): 44-49. (  0) 0) |
| [21] |
过九镕. 两颗通信卫星热控分系统长期在轨性能评述[J]. 中国空间科学技术, 1991, 11(5): 29-33. (  0) 0) |
| [22] |
宋馨, 张有为, 刘自军, 等. 基于卫星在轨温度预示热控涂层性能退化的方法[J]. 中国空间科学技术, 2015, 35(6): 40-47. DOI:10.3780/j.issn.1000-758X.2015.06.005 (  0) 0) |
| [23] |
廖彬, 曾详兵, 潘晓霞, 等. 聚四氟乙烯密封圈密封性能研究[J]. 真空科学与技术学报, 2015, 35(1): 69-73. (  0) 0) |
| [24] |
蔺金贤, 钟志京, 张豫川, 等. 不规则形状容器容积的两种快速标定方法[J]. 真空科学与技术学报, 2015, 35(1): 64-68. (  0) 0) |
| [25] |
Flament N, Williams S, Muller R D, et al. Origin and Evolution of the Deep Thermochemical Structure Beneath Eurasia[J]. Nature Communications, 2017(8): 1-9.
(  0) 0) |
| [26] |
李强, 洪涛, 林乐天. 测控中的星载计算机快速切换[J]. 飞行器测控学报, 2016, 35(2): 125-130. (  0) 0) |
| [27] |
唐美燕, 谢海斌. 均匀分布的四舍五入数据对参数估计的影响[J]. 吉林师范大学学报(自然科学版), 2013, 35(1): 103-107. (  0) 0) |
| [28] |
汤恩义, 周岩, 欧建生, 等. 面向条件判定覆盖的线性拟合制导测试生成[J]. 软件学报, 2016, 27(3): 593-610. (  0) 0) |
| [29] |
杨连乔, 陈伟, 阙秀福, 等. 基于指数拟合的半导体瞬态热学测试分析方法[J]. 仪器仪表学报, 2015, 36(11): 2420-2426. DOI:10.3969/j.issn.0254-3087.2015.11.003 (  0) 0) |
 2018, Vol. 39
2018, Vol. 39

