2. 沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室,辽宁 沈阳 110136
2. Liaoning Key Laboratory of Advanced Measurement and Test Technology for Aviation Propulsion System, Shenyang Aerospace University, Shenyang 110136, China
火箭是运载各种航天器的重要工具,火箭发动机管道系统中的阀门用以接通或切断介质、调节介质流量等,是重要的管道附件,其工作可靠性对整个系统的正常运行起着关键作用[1]。
据国内外统计,阀门故障占液氢液氧火箭发动机故障总数的30%左右,其中拒动与卡滞故障约占阀门各种故障的40%左右[2, 3]。殷谦等[4]通过对液体火箭发动机故障模式进行分析,发现阀门经常出现关闭失效故障。魏国俭等[5, 6]通过对阀门运动副卡滞故障机理进行分析,提出了阀门改进方法,崔景芝等则在阀门产品可靠性评估方法上进行了大量研究[7]。
近年来,在部件单元测试时,多次发生阀门拒动故障,即控制室人员对发生器氧阀发出阀门开、关命令后,阀门却没有执行该动作,即阀门开、关动作失效,给整机的台架试车与实际工作带来严重威胁。如何能够快速、准确判断出阀门开关动作成为一个亟待解决的课题。在液氢液氧火箭发动机阀门实际应用中,由于不允许只因单元测试而改变阀门及管路现有结构,即不能用新加装流量计、压力计测试管路流量、压力等传统方法来判断阀门故障,故在以往的测试中,实验人员主要靠耳听阀门开关动作所产生的冲击响声及用手摸阀体表面的振动来进行判断,这严重依赖于人的实践经验和主观感受,随意性较大,获得的信息不全,容易出现误判,且经验知识传承性差,总结不出特征规律,从而严重制约着整机测试的进度。
针对此类问题,张少博等[8]分析了阀门出现故障时声压幅值范围和声压谱的故障特征信号,利用声学检测方法来检测阀门故障,取得了较好方法。但由于一般实验外场条件恶劣,容易受到外界噪声干扰。阀门开关动作会在阀体的振动信号中有所反映,因此可以采用阀体表面的振动信号作为阀门动作状态的检测信号。目前利用振动信号进行状态检测的方法主要应用于旋转机械系统中[9, 10],而用于阀门的工作状态检测,国内外研究均很少[11, 12]。
本文采用双自寻优小波分析与短时傅里叶分析相结合的方法,对阀门的振动加速度信号进行处理。着重从时域和频域两个角度分析阀门开关动作振动特征,提出了利用“相对瞬时能量”来评价阀门开关状态这一简单易行的评价指标,并给出了其数学描述,基于LabVIEW[13]平台开发出便携式阀门开关动作自动检测系统。
2 短时傅里叶变换与小波分析理论 2.1 短时傅里叶变换传统的傅里叶变换在平稳信号分析和处理中具有重要作用,但由于其是一种全局的变换而没有刻画出特定时间段的特性,缺少时域定位的功能,因此不适用于阀门冲击响应这类时变信号。如果将非平稳过程视为由一系列短时平稳信号组成,则任意一短时信号就可采用传统的傅里叶变换进行分析。1946年,Dennis Gabor提出了加窗傅里叶变换概念[14],用一个在时间上可滑移的时窗进行傅里叶变换,从而实现了在时间域和频率域都具有较好局部性的分析方法,这种方法被称为短时傅里叶变换。
设g(t)是标准时窗函数,通过g(t)所观察到信号x(t)的部分是x(t)g(t)。当g(t)的中心位于τ,由加窗信号x(t)g(t -τ)的傅里叶变换便产生短时傅里叶变换
| $ STF{T_x}\left( {\tau, f} \right) = \int_{-\infty }^{ + \infty } x \left( t \right){g^*}\left( {t-\tau } \right){{\rm e}^{-{\rm{j2 \mathsf{ π} }}ft}}{\rm{d}}t $ | (1) |
式中g(t-τ)ej2πft是STFT的基函数。
根据Heisenberg不确定性原理,时间分辨率Δt和频率分辨率Δf不可能同时任意小,其乘积受到以下限制
| $ \Delta t\Delta f \ge \frac{1}{{4\pi }} $ | (2) |
短时傅里叶变换中存在时间和频率分辨力的矛盾:窗函数时宽越窄,时间分辨力越高,但这时带通滤波器的通带越宽,频率分辨力也就越低;反之亦然。因此,对于短时傅里叶变换,窗函数g(t)的选取是关键。由于高斯函数的傅里叶变换仍然是高斯函数,当且仅当采用高斯窗函数,式(2)等式成立。即最优时间局部化的窗函数是高斯函数,如式(3)所示
| $ {g_{\rm{G}}}\left( t \right) = \frac{1}{{2\sqrt {\pi \alpha } }}{{\rm{e}}^{{\rm{-}}\frac{{{t^2}}}{{4\alpha }}}} $ | (3) |
这里恒有α>0。故本文选取高斯窗函数进行短时傅里叶变换。
2.2 小波分析在实际工程应用中,往往要求对低频信号采用宽时窗,高频信号采用窄时窗,以提高线谱分辨率。为了弥补短时傅里叶变换采用固定的窗函数大小和形状的不足,1984年法国地球物理学家Morlet J在分析处理地球物理勘探资料时提出来了小波变换的概念,其后Grossman A采用平移和伸缩不变性建立了小波变换的理论体系。它的优点在于有一个灵活可变的时间、频率窗,具有良好的时域和频域的局部化性能。
给定一个基本函数ψ(t),令
| $ {\psi _{a, b}}\left( t \right) = \frac{1}{{\sqrt a }}\psi \left( {\frac{{t-b}}{a}} \right) $ | (4) |
式中a, b均为常数,且a>0。若a, b不断地变化,可得到一族函数ψa, b(t)。给定平方可积信号x(t),即x(t)∈ L2(R),则x(t)的小波变换定义为
| $ \begin{array}{l} W{T_x}\left( {a, b} \right) = \frac{1}{{\sqrt a }}\int x {\left( t \right)} {\psi ^*}\left( {\frac{{t-b}}{a}} \right){\rm{d}}t = \\ \int {x\left( t \right)\psi _{a, b}^*} \left( t \right){\rm{d}}t = \left\langle {x\left( t \right), {\psi _{a, b}}\left( t \right)} \right\rangle \end{array} $ | (5) |
式中a为尺度因子,b为时移因子。
通过振动加速度传感器采集到的阀门振动冲击信号中包含各种低频、高频噪声,传统的带通滤波器不适用于非平稳信号滤波,小波技术可将信号无冗余、无疏漏、正交地分解到独立的频带内,而且特别适合于非平稳信号的分析。目前小波去噪的方法主要分为三类:(1)对含有噪声信号进行小波变换后,计算相邻尺度间各点小波系数的相关性大小,根据小波系数类型的不同进行取舍,然后直接进行重构;(2)基于小波变换的模极大值原理,即根据信号和噪声在小波变换各尺度上的不同传播性质,剔除由噪声产生的模极大值点,进而恢复信号;(3)Donoho提出的阈值方法,在降噪过程中,把小波系数绝对值较小的置为零,而对较大的系数保留或收缩,分别对应硬阈值和软阈值方法,然后利用估计小波系数进行信号重构,即达到了去噪的效果[15]。
3 阀门开关动作振动信号分析 3.1 阀门振动信号双自寻优小波去噪方法据前面分析可知,阀门所处工作环境复杂,其冲击激励下的响应经阀体不同结构间传递及耦合作用,均反映在阀体表面,使传感器采集到的振动特征信号中含有大量的噪声,给阀门开关动作状态检测带来了极大的困难,甚至可能发生误判,因此对信号进行去噪处理极为必要。
一个含有噪声的一维模型可表示为
| $ s\left( k \right) = f\left( k \right) + \varepsilon \cdot e\left( k \right), \;\;\;\;k = 0, 1, 2, \cdots, n-1 $ | (6) |
式中s(k)为含有噪声的信号,f (k)为真实信号,e(k)为噪声信号,ε为噪声系数的标准偏差。利用小波去噪的目的就是从s(k)得到真实的信号f (k)。
在小波去噪方法中,目前较常用的为阈值法,其决定去噪效果最为关键的两个因素是阈值和阈值函数的选取,传统方法一般存在两者之间相互选取无法解决耦合性的问题,影响去噪效果。针对此问题,本文应用阈值和阈值函数各自寻优又相互结合的双自寻优小波去噪方法,其目标是所有阈值和所有阈值函数参数都能互相结合,从各种结合中寻找出最优的搭配,去噪效果优于传统方法。具体步骤为:
(1) 确定分解层数及最高分解层的阈值上限TL,当阈值从0逐步增大到某值后,信噪比不会再随阈值的增大而改变,此值即为TL。
(2) 选取阈值函数集,本文采用含有参数的改进阈值函数,其定义为
| $ \eta \left( w \right) = \left\{ \begin{array}{l} w-\alpha \cdot {\mathop{\rm sgn}} \left( w \right) \cdot T\;\;\left| w \right| \ge T\\ \;\;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| w \right| < T \end{array} \right. $ | (7) |
式中参数α的自寻优区间为[0, 1],T为阈值。
(3) 取适当步长,遍历阈值和阈值函数(参数α),得到最优信噪比及其所对应的参数,从而达到最优降噪效果。
3.2 阀门开关动作状态评价指标—相对瞬时能量阀门开关动作过程很短,在开关动作的冲击作用下,其振动信号是非平稳信号。阀门开启和关闭动作的瞬时时间内,信号的频谱有较大的突变。因此,可采用阀体振动信号频谱的瞬时能量来衡量阀门开关动作状态。根据实际工况取某一关心的频带来进行能量分析。
设在时刻tj(0≤j≤M,M为离散的时间个数),关心的频带内离散的频谱幅值为σitj (1≤i≤N,N为该频带内离散的谱线个数)。则在该时刻tj,关心的频带的瞬时能量Etj可以表示为
| $ {E_{{t_j}}} = {\sum\limits_{i = 1}^N {\left( {\sigma _{{t_j}}^i} \right)} ^2} $ | (8) |
为了在应用上通用化,采用归一化的相对瞬时能量来判定阀门的开关动作状态。文中采用按整个离散时间段内瞬时能量的最大值进行归一,可以表示为
| $ {\overline E _{{t_j}}} = \frac{{{E_{{t_j}}}}}{{{E_{\max }}}} $ | (9) |
式中Etj为归一化后的tj时刻的相对瞬时能量,Emax为整个离散时间段内瞬时能量的最大值。
4 阀门开关动作自动检测系统开发与应用 4.1 便携式阀门开关动作自动检测系统开发为了能够方便、快捷、准确地识别出阀门开关动作状态,为实际工程应用提供决策,在以上理论分析的基础上,本文基于LabVIEW平台开发出便携式阀门开关动作自动检测系统,如图 1所示。

|
Fig. 1 Portable automatic monitoring system for the status of switching valve action |
系统硬件包括IEPE加速度传感器、便携式动态数据采集仪和笔记本电脑。软件功能包括数据采集、数据处理及阀门开关动作快速识别等功能,此外还拥有数据库管理、实验报表等功能模块。
4.2 阀门开关动作状态检测系统应用本文利用所开发的阀门开关动作自动检测系统对某类型阀门进行了长时、大量测试。
为了较全面地测试阀体的振动信号,每个阀体上轴向(即沿管路方向)和径向各布置一个振动加速度传感器。该类阀门(菌阀)的工作状态是由初始的关闭状态到打开状态,再关闭,即包括一个打开和一个关闭的动作,通过设置合适的采样时间长度,可以在一次测试过程中包括阀门整个工作过程的所有状态。而且,为了保证测试数据的有效性,对每一个阀门重复测试12次,采样频率设置为10.24kHz。
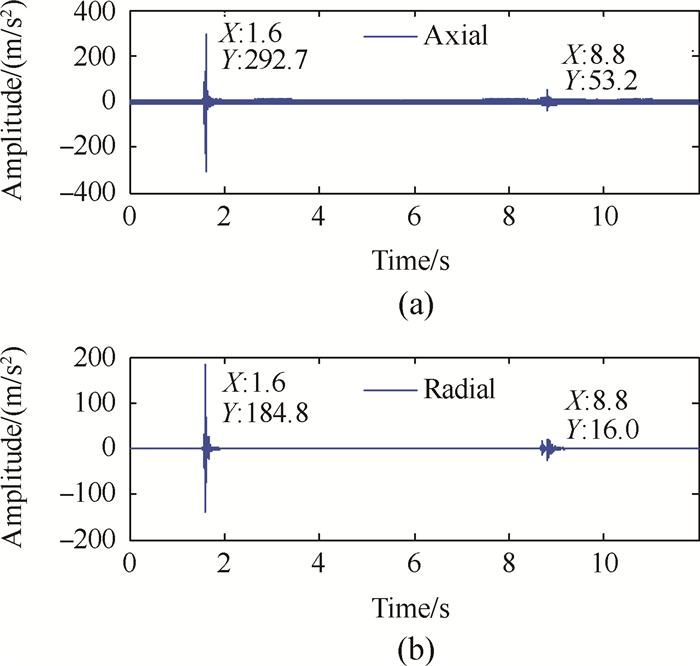
5 测试结果分析 5.1 原始信号时频域分析对上文所述阀门(菌阀)进行开关动作测试,所得时域信号如图 2所示,图 2(a)为阀门轴向振动时域响应,图 2(b)为径向振动时域响应。
|
Fig. 2 Time domain signals of valve vibration response |
从振动响应时域信号中可以看出,在阀门开动作时刻(1.6s)有明显的冲击,加速度信号存在突变。在阀门关动作时刻(8.8s)也有冲击,但由于关的动作冲击能量较小,且阀门有整体晃动,信号中还有一些低、高频噪声,因此冲击特点不突出,不便于进行状态自动识别,容易发生误判,因此必须对其进行降噪处理。
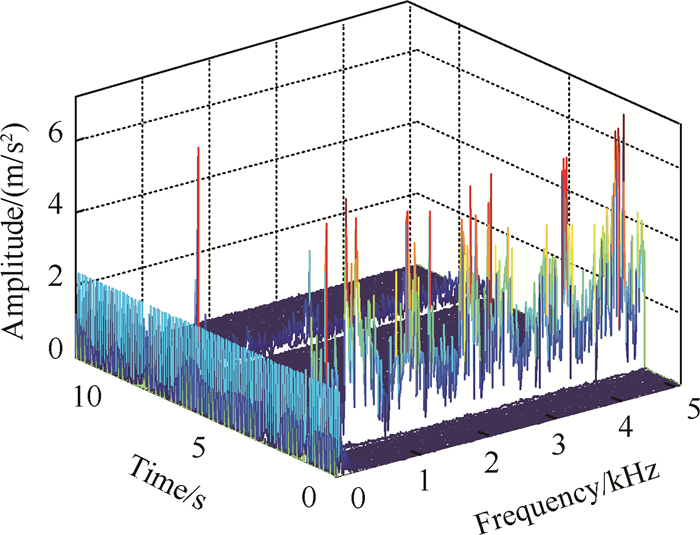
为进一步对阀门振动响应特性进行深入分析,运用短时傅立叶变换对其该非平稳信号进行时频分析,其轴向振动如图 3所示。
|
Fig. 3 3-D waterfall diagram of valve axial vibration response |
从三维时频瀑布图可看出,在1.6s与8.8s左右微小时段存在明显的峰值,与图 2中时域信号特征一致,说明该阀门在开关动作时的时频特性是非常明显的。由于传感器采集到的振动信号为阀体在脉冲激励作用下的响应,是一个宽频带的信号,贯穿整个频带。
由于此阀门两端与管路连接,在冲击作用下存在整体晃动,加上振动传感器与数据采集仪存在少许零漂,因此在测试信号中存在一定的零频、极低频成份。此外由于测试环境较恶劣,测试系统中还存在部分高频电磁噪声,对阀门动作状态识别造成了干扰。
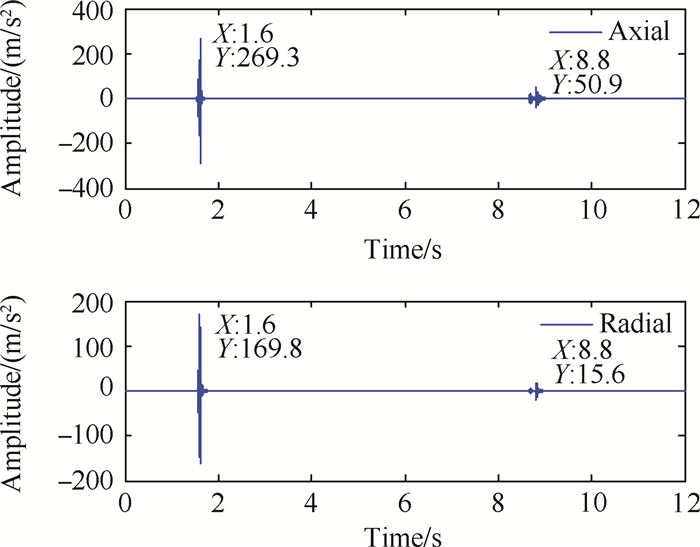
5.2 降噪后信号时频域分析为了消除原始响应信号中的低频、高频噪声干扰,运用双自寻优小波分析方法对其进行降噪,参数α步长取为0.01,在[0, 1]区间进行寻优,阈值步长取为0.05,经计算分析得,当α = 0(硬阈值函数)时,信噪比为31.2dB;当α = 1(软阈值函数)时,信噪比为30.4dB;当α = 0.68时,信噪比最大,为33.8dB,故选取该值所对应的阈值函数。原始信号降噪后时域波形如图 4所示。
|
Fig. 4 Time domain signal of valve vibration response using wavelet denoising technique |
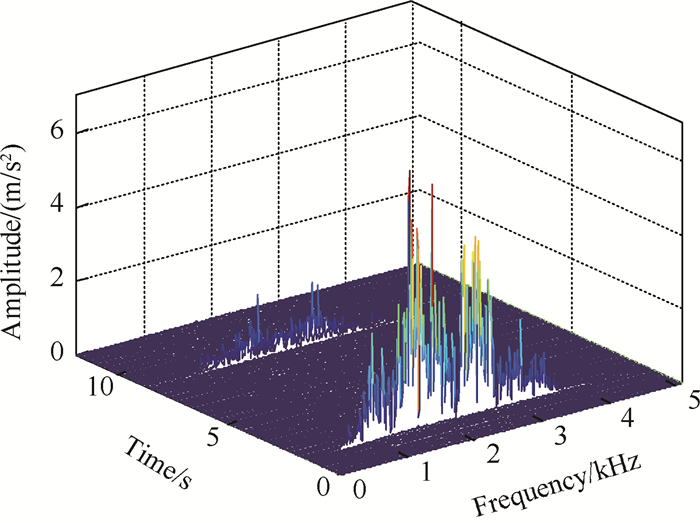
对降噪后的信号进行时频分析,轴向三维谱阵如图 5所示。从经过双自寻优小波降噪后的时域波形与时频瀑布图中可看出,去除了低频与高频噪声成份,降噪效果良好。
|
Fig. 5 3-D waterfall diagram of valve axial vibration response using wavelet denoising technique |
在计算相对瞬时能量前,频带的选取非常重要,通过分析发现,若将原始信号中的所有频率成份包含进去,识别结果不确定性较大;而对小波降噪后所剩余的频段成份进行计算则一致性行很好。按式(9)计算所选频段内的相对瞬时能量,结果如图 6所示。
|
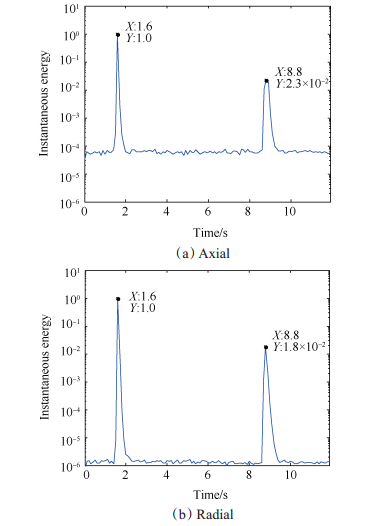
Fig. 6 Relative instantaneous energy of valve vibration response |
由阀门轴向振动响应相对瞬时能量图可看出,该阀门开动作能量最大,相对瞬时能量为1,关动作相对瞬时能量为2.3 × 10-2,而无动作时段相对瞬时能量均在10-4以下,能够非常清晰地识别出开关动作状态及所对应的时刻。
由阀门径向振动响应相对瞬时能量图可看出,该阀门开动作能量最大,相对瞬时能量为1,关动作相对瞬时能量为1.8 × 10-2,而无动作时段相对瞬时能量均在10-5以下,能够非常清晰地识别出开关动作状态。
对12次测试结果(相对瞬时能量)进行统计分析,列取其最大、最小值,结果如表 1所示。由表 1可知,阀门“开”动作能量绝对占优,其相对瞬时能量为1,“关”动作相对瞬时能量在10-2 ~ 10-1,而无动作时相对瞬时能量均在10-4以下,各动作状态相对瞬时能量区分度较大,因此适合应用这一指标来识别阀门开关动作状态。
|
|
Table 1 Statistics of relative instantaneous energy for 12 testing results |
本文采用短时傅里叶分析、小波分析技术对阀门开关动作振动特性进行了分析及信号降噪处理,提出了利用“相对瞬时能量”这一指标来判断阀门的动作状态,得到以下结论:
(1) 对于阀门冲击响应这一非平稳信号,双自寻优小波分析降噪效果良好。
(2) 通过对阀门振动信号进行短时傅里叶变换分析,阀门在开关动作时的时频特性非常明显。
(3) 阀门“开”动作相对瞬时能量为1,“关”动作相对瞬时能量在10-2 ~ 10-1,比无动作时相对瞬时能量大2个数量级,区分度大。运用相对瞬时能量这一指标对阀门开关动作状态进行识别,及时、准确,基于该指标所开发的便携式阀门开关动作自动检测系统易于实现阀门故障快速诊断。
| [1] |
陈林, 王兴松, 张逸芳, 等. 阀门故障诊断技术综述[J]. 流体机械, 2015, 43(9): 36-42. (  0) 0) |
| [2] |
杨波, 王金全, 刘启国. 阀门电动执行机构故障诊断研究[J]. 阀门, 2007(1): 36-38. (  0) 0) |
| [3] |
吴建军, 张育林, 陈启智. 液体火箭发动机故障检测与诊断综述[J]. 推进技术, 1995, 16(6): 45-50. (WU Jian-jun, ZHANG Yu-lin, CHEN Qi-zhi. A Survey on Fault Detection and Diagnosis for Lqiuid Rocket Propulsoin System[J]. Journal of Propulsion Technology, 1995, 16(6): 45-50.)
(  0) 0) |
| [4] |
殷谦, 张金容. 液体火箭发动机故障模式及分析[J]. 推进技术, 1997, 18(2): 22-25. (YIN Qian, ZHANG Jin-rong. Failure Mode and Analyssi for Liquid Propellant Rocket Engines[J]. Journal of Propulsion Technology, 1997, 18(2): 22-25.)
(  0) 0) |
| [5] |
魏国俭, 陶瑞峰, 许健, 等. 航天阀门运动副卡滞故障分析及对策[J]. 航天器环境工程, 2012, 29(1): 7-13. (  0) 0) |
| [6] |
张宗美. 航天故障手册[M]. 北京: 宇航出版社, 1994.
(  0) 0) |
| [7] |
崔景芝, 修建生, 孙法国, 等. 阀门产品的可靠性评估方法[J]. 载人航天, 2011, 17(2): 59-64. (  0) 0) |
| [8] |
张少博, 王乃世, 陈海峰, 等. 基于声压测量的阀门故障检测方法研究[J]. 火箭推进, 2015, 41(4): 100-104. (  0) 0) |
| [9] |
侯敬宏, 黄树红, 申弢, 等. 基于小波分析的旋转机械振动信号定量特征研究[J]. 机械工程学报, 2004, 40(1): 131-135. (  0) 0) |
| [10] |
韩磊, 洪杰, 王冬. 基于小波包分析的航空发动机轴承故障诊断[J]. 推进技术, 2009, 30(3): 328-331. (HAN Lei, HONG Jie, WANG Dong. Fault Diagnosis of Aero-Engine Bearings Based on Wavelet Package Analysis[J]. Journal of Propulsion Technology, 2009, 30(3): 328-331.)
(  0) 0) |
| [11] |
Wang C, Zhang Y, Zhong Z. Fault Diagnosis for Diesel Valve Trains Based on Time-Frequency Images[J]. Mechanical Systems and Signal Processing, 2008, 22(8): 1981-1993. DOI:10.1016/j.ymssp.2008.01.016
(  0) 0) |
| [12] |
Wenbing W, Shuqun Y, Yijian H. Fault Diagnosis of Pressure Relief Valve Based on Power Spectrum[J]. Energy Procedia, 2012, 17, Part B: 1319-1325.
(  0) 0) |
| [13] |
陈树学, 刘萱. Labview宝典[M]. 北京: 电子工业出版社, 2011.
(  0) 0) |
| [14] |
Gabor D. Theory of Communication[J]. Journal of the Institute of Electrical Engineers of Japan, 1946, 93: 429-457.
(  0) 0) |
| [15] |
肖方煜, 汤伟, 傅娜. 自寻优阈值小波去噪方法[J]. 信号处理, 2012, 28(4): 577-586. (  0) 0) |
 2018, Vol. 39
2018, Vol. 39


