2. 北京航空工程技术研究中心,北京 100076
2. Beijing Aeronautical Engineering Technical Research Center, Beijing 100076, China
分布式控制系统中,总线网络的服务质量(Quality of Service,QoS)和控制系统品质(Quality of Performance,QoP)是一对矛盾体,良好的网络QoS必然要求较大的采样周期和较小的数据包容量,然而,这样将导致过多的信息被忽略或舍弃从而影响控制系统QoP[1, 2]。因此针对具有网络调度的航空发动机分布式控制系统,进行网络参数与容错控制器的协同设计具有实际意义。调度协议作用下的总线网络通常被称为通信受限网络[3, 4]。
近年来,国内外学者针对该问题进行了一系列有益的研究,杜明莉等[5]针对具有通信约束的网络控制系统,提出了一种基于TOD调度协议和鲁棒H∞控制器的协同设计方法。李祖欣[6]、谢林柏[7]等则应用通信序列概念将具有通信约束的网络控制系统建模为集成控制和调度的离散周期系统,并给出了可调度条件和控制器设计方法。以上文献虽考虑了网络调度策略,但其建模过程均将网络参数视为恒定已知,侧重于在具有通信约束情况下的控制系统设计,并未将网络参数纳入控制器的设计过程。陈惠英等[8]利用最小二乘支持向量机在线预测下一采样周期内的可用网络带宽,并据此动态调整控制回路优先级和采样周期。将系统建模为变采样系统,实现了分布式控制系统中调度与控制器的协同设计。该方法对采样周期的调整是动态的,能够最大限度地利用网络资源,但该方法要求传感器在任意时刻都能实现变频采样,且要求高精度的传感器同步时钟,若将其应用于航空发动机系统,还需克服恶劣工作环境的影响,给控制系统的传感器设计带来了挑战。
鉴于以上分析,本文选取Maximum error firsttry once discard(MEF-TOD)调度协议对网络资源进行分配,针对主动丢包故障(由调度协议引起的主动数据丢包)提出了一种基于线性矩阵不等式理论的网络参数与保成本容错控制器协同设计方法。首先建立MEF-TOD调度协议作用下,状态变量和控制变量的传输特性;其次分析在通信受限情况下网络诱导时延与网络参数之间的内在联系,将采样周期和数据包容量作为未知量引入航空发动机分布式控制系统的建模过程,得到调度协议约束下的网络参数与控制系统参数联合模型;再次给出联合闭环系统渐进稳定且存在成本函数上界的充分条件;最后针对非线性优化问题难以直接求解的问题,提出一种启发式优化求解方法,并在此基础上给出网络参数与控制器增益的具体求解步骤。
2 通信受限的航空发动机分布式控制系统建模 2.1 系统描述具有通信约束的航空发动机分布式控制系统如图 1所示[9],本文所研究的通信约束为介质访问约束,即由于带宽限制及数据共享传输的特点,总线网络在同一时刻只能允许有限个节点接入并传输数据。各节点必须竞争得到网络访问权才能发送数据[10],为了降低节点冲突,提高数据传输的针对性,便需要采用适当的网络调度策略对变量进行选择,以保证总线网络的服务质量,图中三类时延τsc, τca, τc分别为输出时延、控制时延和计算时延。
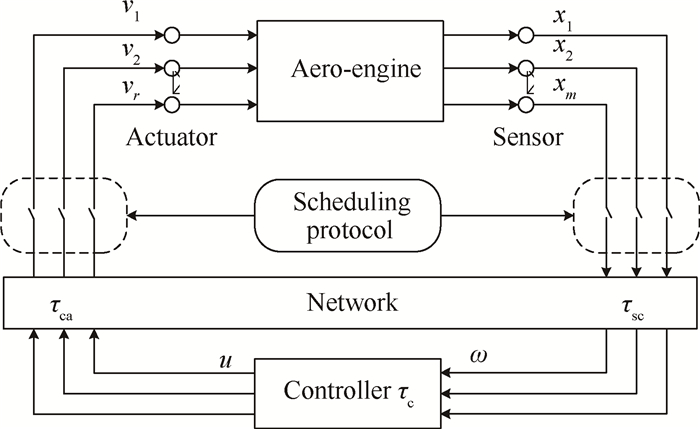
|
Fig. 1 Structure of aero-engine distributed control system with communication protocol restriction |
为简化推证过程,依据带通信约束的航空发动机分布式控制系统网络特性,做如下假设:
假设1:传感器为时间驱动,中央控制器和执行机构为事件驱动。
假设2:数据为单包传输,且无时序错乱。
假设3:由于调度策略的作用,控制时延和传感器输出时延之和τ小于一个采样周期,即τ=τsc+τca<T,且τ为随机变量。
假设4:网络带宽η恒定已知,每个周期内非实时数据宽度θk已知,采样周期T恒定未知,每个周期内传输数据包容量P恒定未知。
基于以上假设,具有通信约束的航空发动机分布式控制系统可描述为如下通用形式
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot x}}\left( t \right) = f\left( {\mathit{\boldsymbol{x}}\left( t \right),\mathit{\boldsymbol{u}}\left( t \right),T,P} \right)\\ \mathit{\boldsymbol{x}}\left( t \right) = \varphi \left( t \right),t \in \left[ { - {\tau _0},0} \right] \end{array} \right. $ | (1) |
式中x(t) ∈ Rm,u(t) ∈ Rr分别为系统状态变量和控制变量,τ0为零时刻分布式控制系统时延,φ(t)为系统初始状态函数。
2.2 MEF-TOD调度策略本文采用Walsh[11]提出的MEF-TOD协议对网络节点的数据传输进行调度。MEF-TOD协议是一种基于最大加权误差的网络调度方法,当多个节点在传输过程中发生冲突时,计算各调度模式本时刻与上一时刻变量的加权误差,最大加权误差中所包含的节点获得传输许可,其余节点竞争失败则放弃本次传输,从而动态分配网络带宽。未获得最新数据的节点由零阶保持器(ZOH)保持前一时刻的值。
定义系统状态变量和控制变量在k时刻的调度矩阵分别为Γ(k)和Δ(k)
| $ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left( k \right) = {\rm{diag}}\left( {{\gamma _1}\left( k \right),{\gamma _2}\left( k \right), \cdots ,{\gamma _m}\left( k \right)} \right) $ | (2) |
| $ \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}\left( k \right) = {\rm{diag}}\left( {{\delta _1}\left( k \right),{\delta _2}\left( k \right), \cdots ,{\delta _r}\left( k \right)} \right) $ | (3) |
式中,γi(k)={0, 1}当xi(k)被成功传输,γi(k)=1,否则γi(k)=0;相同地,δi(k)={1, 0},当ui(k)被成功传输,δi(k)=1,否则δi(k)=0。需要说明的是在γi(k), (i=1, 2, …, m)和δi(k), (i=1, 2, …, r)中,取值为1的变量个数不大于P,存在Cm+rP=(m+r)!/[(m+r-P)!P!]=N种数据传输模式,分别对应N个调度矩阵Ψi (k)=diag(Γ(k), Δ(k)),(i=1, 2, …, N)。由以上分析可知,数据传输模式的选择由状态变量和控制变量的加权误差决定,第i种数据传输模式对应的加权误差ei(k)定义为
| $ \begin{array}{l} {{\mathit{\boldsymbol{\bar e}}}_i}\left( k \right) = {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_i}{\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}^x}{{\left( k \right)}^{\rm{T}}}}&{{\mathit{\boldsymbol{e}}^x}{{\left( {k - 1} \right)}^{\rm{T}}}} \end{array}} \right)^{\rm{T}}} = \\ \;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_i}\left( {\frac{{{x_1}\left( k \right) - {x_1}\left( {k - 1} \right)}}{{{x_i}\left( {k - 1} \right)}}, \cdots \frac{{{x_m}\left( k \right) - {x_m}\left( {k - 1} \right)}}{{{x_m}\left( {k - 1} \right)}},} \right.\\ \;\;\;\;\;\;\;\;\;\;\;{\left. {\frac{{{u_1}\left( {k - 1} \right) - {u_1}\left( {k - 2} \right)}}{{{u_1}\left( {k - 2} \right)}}, \cdots \frac{{{x_r}\left( {k - 1} \right) - {x_r}\left( {k - 2} \right)}}{{{x_r}\left( {k - 2} \right)}}} \right)^{\rm{T}}} \end{array} $ | (4) |
| $ \sigma = \arg \max \left\{ {\left\| {{{\mathit{\boldsymbol{\bar e}}}_1}\left( k \right)} \right\|,\left\| {{{\mathit{\boldsymbol{\bar e}}}_2}\left( k \right)} \right\|, \cdots ,\left\| {{{\mathit{\boldsymbol{\bar e}}}_N}\left( k \right)} \right\|} \right\} $ | (5) |
式中arg为取下标函数,σ为k时刻所选择的数据传输模式。则经过调度的状态变量ω和控制变量v可表示为式
| $ \mathit{\boldsymbol{\omega }}\left( k \right) = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }\left( k \right)\mathit{\boldsymbol{x}}\left( k \right) + \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }\left( k \right)} \right)\mathit{\boldsymbol{\omega }}\left( {k - 1} \right) $ | (6) |
| $ \mathit{\boldsymbol{v}}\left( k \right) = {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }\left( k \right)\mathit{\boldsymbol{u}}\left( k \right) + \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }\left( k \right)} \right)\mathit{\boldsymbol{v}}\left( {k - 1} \right) $ | (7) |
由假设4可知,在影响总线网络QoS的四个因素中,网络带宽η,非实时数据宽度θk已知,采样周期T和数据包容量P未知,为待定的网络参数,若要将参数T,P纳入发动机离散状态空间模型,首先需要得到参数T,P与网络时延τ之间的关系。如果网络可调度且数据包在传输过程中没有非人为损失,则在k时刻式(8)成立[12]。
| $ \left( {k + 1} \right)\bar P + {{\bar \theta }_k} = \left( {kT + \tau \left( k \right)} \right)\eta $ | (8) |
式中P=μP,μ为每个传输变量占用的数据宽度。
| $ \tau \left( k \right) = \frac{{\left( {k + 1} \right)\bar P + {{\bar \theta }_k}}}{\eta } - kT $ | (9) |
忽略噪声干扰,航空发动机分布式控制系统连续状态空间模型可表示为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot x}}\left( t \right) = {\mathit{\boldsymbol{A}}_c}\mathit{\boldsymbol{x}}\left( t \right) + {\mathit{\boldsymbol{B}}_c}\mathit{\boldsymbol{u}}\left( t \right)\\ \mathit{\boldsymbol{y}}\left( t \right) = {\mathit{\boldsymbol{C}}_c}\mathit{\boldsymbol{x}}\left( t \right) + {\mathit{\boldsymbol{D}}_c}\mathit{\boldsymbol{u}}\left( t \right) \end{array} \right. $ | (10) |
按照1.1节所做的假设,对连续状态空间模型离散化,得到
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{Ax}}\left( k \right) + \left( {{\mathit{\boldsymbol{B}}_0} + \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{F}}_k}\mathit{\boldsymbol{E}}} \right)\mathit{\boldsymbol{v}}\left( k \right) + }\\ {\left( {{\mathit{\boldsymbol{B}}_1} - \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{F}}_k}\mathit{\boldsymbol{E}}} \right)\mathit{\boldsymbol{v}}\left( {k - 1} \right)} \end{array} $ | (11) |
式中
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{Ax}}\left( k \right) + \left( {\mathit{\boldsymbol{A}}_c^{ - 1}\left( {\mathit{\boldsymbol{H}} - \mathit{\boldsymbol{I}}} \right) + \beta \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{F}}_k}\mathit{\boldsymbol{E}}} \right)\mathit{\boldsymbol{v}}\left( k \right) + }\\ {\left( {\mathit{\boldsymbol{A}}_c^{ - 1}\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{H}}} \right) - \beta \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{F}}_k}\mathit{\boldsymbol{E}}} \right)v\left( {k - 1} \right)} \end{array} $ | (12) |
假设系统状态完全可测,采用状态反馈控制器v(k)=Kσω(k),综合式(6),式(7),式(12)可得航空发动机分布式控制系统的网络参数与控制系统的联合模型
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{Ax}}\left( k \right) + \left( {\mathit{\boldsymbol{A}}_c^{ - 1}\left( {\mathit{\boldsymbol{H}} - \mathit{\boldsymbol{I}}} \right) + \beta \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{F}}_k}\mathit{\boldsymbol{E}}} \right)\mathit{\boldsymbol{v}}\left( k \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\mathit{\boldsymbol{A}}_c^{ - 1}\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{H}}} \right) + \beta \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{F}}_k}\mathit{\boldsymbol{E}}} \right)\mathit{\boldsymbol{v}}\left( {k - 1} \right)\\ \;\;\;\;\mathit{\boldsymbol{\omega }}\left( k \right) = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }\left( k \right)\mathit{\boldsymbol{x}}\left( k \right) + \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }\left( k \right)} \right)\mathit{\boldsymbol{\omega }}\left( {k - 1} \right)\\ \;\;\;\;\mathit{\boldsymbol{v}}\left( k \right) = {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }\left( k \right)\mathit{\boldsymbol{u}}\left( k \right) + \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }\left( k \right)} \right)\mathit{\boldsymbol{v}}\left( {k - 1} \right)\\ \;\;\;\;\mathit{\boldsymbol{u}}\left( k \right) = {K_\sigma }\omega \left( k \right) \end{array} \right. $ | (13) |
令M0=Ac-1(H-I)+βHFkE,M1=Ac-1(A-H)-βHFkE,则可得到如下联合闭环系统
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{x}}\left( {k + 1} \right) = \left( {\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{M}}_0}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }{\mathit{\boldsymbol{K}}_\sigma }{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right)\mathit{\boldsymbol{x}}\left( k \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{\mathit{\boldsymbol{M}}_0}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }{\mathit{\boldsymbol{K}}_\sigma }\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right)} \right)\mathit{\boldsymbol{\omega }}\left( {k - 1} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{\mathit{\boldsymbol{M}}_0}\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }} \right)\mathit{\boldsymbol{ + }}{\mathit{\boldsymbol{M}}_1}} \right)\mathit{\boldsymbol{v}}\left( {k - 1} \right)\\ \;\;\;\;\mathit{\boldsymbol{\omega }}\left( k \right) = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }\left( k \right)\mathit{\boldsymbol{x}}\left( k \right) + \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }\left( k \right)} \right)\mathit{\boldsymbol{\omega }}\left( {k - 1} \right)\\ \;\;\;\;\mathit{\boldsymbol{v}}\left( k \right) = {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }{\mathit{\boldsymbol{K}}_\sigma }{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }\mathit{\boldsymbol{x}}\left( k \right) + {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }{\mathit{\boldsymbol{K}}_\sigma }\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right)\mathit{\boldsymbol{\omega }}\left( {k - 1} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }} \right)\mathit{\boldsymbol{v}}\left( {k - 1} \right) \end{array} \right. $ | (14) |
对于存在总线网络的航空发动机分布式控制系统而言,网络服务质量与控制器性能是一对矛盾体。控制系统要达到最优的控制效果必然要求较高的采样频率,且要求在每个采样周期内系统状态变量和控制变量都能无损传输。但总线网络存在带宽限制,系统的采样频率和数据包容量不可能无限增大,因此,需要在网络服务质量与控制系统性能之间寻找最佳平衡点,即选择适当的网络参数使控制系统性能达到最优。本文以网络参数与控制系统的联合模型(13)作为被控对象,对网络参数和保成本容错控制器进行协同设计,以成本函数J作为协同设计最优化问题的目标函数,其中R1,R2为成本函数的已知加权矩阵,R1,R2是对称正定的。
| $ J = \sum\limits_{k = 0}^\infty {\mathit{\boldsymbol{x}}{{\left( k \right)}^{\rm{T}}}{\mathit{\boldsymbol{R}}_1}\mathit{\boldsymbol{x}}\left( k \right)} + \mathit{\boldsymbol{u}}{\left( k \right)^{\rm{T}}}{\mathit{\boldsymbol{R}}_2}\mathit{\boldsymbol{u}}\left( k \right) $ | (15) |
网络参数与保成本控制器协同设计目标:对于采用MEF-TOD协议进行调度的航空发动机分布式控制系统(13),设计保成本控制器,使得闭环系统(14)在任意一种数据传输模式下均能保持渐进稳定,成本函数J有上界J*,即J<J*,且保证J*最小。
3.1 联合闭环系统稳定性分析为方便讨论特给出引理1,该引理是针对分布式控制系统存在不确定小时延情况引入的,利用引理1可将不确定小时延转化为区间范围内固定矩阵的乘积形式,为线性矩阵不等式的建立提供了可能。
引理1[13] 对于矩阵W, M, N和F(k),其中W对称,如果F(k)满足F(k)TF(k)≤I,则有W+NTF(k)TMT+MF(k)N<0,当且仅当存在标量ε>0,使得W+ε-1NTN+εMMT<0。
定理1 对于采用MEF-TOD协议进行调度的航空发动机分布式控制系统(13),若当∀σ ∈ {1, 2, …, N}(1~N分别对应某一种数据传输模式)时,存在矩阵Kσ,A,H,对称正定矩阵W,Q,S以及正实数εσ使得线性矩阵不等式(16)成立,则闭环系统(14)渐进稳定,且成本函数J有上界:J<x(0)TWx(0) + ω(-1)TQω(-1)+v(-1)TSv(-1)。
| $ \left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{\bar W}}}&0&0&{\mathit{\boldsymbol{\bar W}}{\mathit{\boldsymbol{A}}^{\rm{T}}}}&{\mathit{\boldsymbol{\bar W \boldsymbol{\varGamma} }}_\sigma ^{\rm{T}}}&0&{\mathit{\boldsymbol{\bar W}}}&0&0&0&{\mathit{\boldsymbol{\bar W \boldsymbol{\varGamma} }}_\sigma ^{\rm{T}}}\\ * &{ - \mathit{\boldsymbol{\bar Q}}}&0&0&{\mathit{\boldsymbol{\bar Q}}{{\left( {1 - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right)}^{\rm{T}}}}&0&0&0&0&0&{\mathit{\boldsymbol{\bar Q}}{{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right)}^{\rm{T}}}}\\ *&* &{ - \mathit{\boldsymbol{\bar S}}}&{\mathit{\boldsymbol{\bar S \boldsymbol{\varOmega} }}_1^{\rm{T}}}&0&{\mathit{\boldsymbol{\bar S}}{{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }} \right)}^{\rm{T}}}}&0&0&{\mathit{\boldsymbol{\bar S}}{{\left( { - \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }} \right)}^{\rm{T}}}}&0&0\\ *&*&* &{{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_3}}&0&0&0&0&0&{{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_2}}&0\\ *&*&*&* &{ - \mathit{\boldsymbol{\bar Q}}}&0&0&0&0&0&0\\ *&*&*&*&* &{ - \mathit{\boldsymbol{\bar S}}}&0&0&0&{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }{\mathit{\boldsymbol{K}}_\sigma }}&0\\ *&*&*&*&*&* &{ - \mathit{\boldsymbol{R}}_1^{ - 1}}&0&0&0&0\\ *&*&*&*&*&*&* &{ - \mathit{\boldsymbol{R}}_2^{ - 1}}&0&{{\mathit{\boldsymbol{K}}_\sigma }}&0\\ *&*&*&*&*&*&*&* &{ - {\varepsilon _\sigma }}&{\mathit{\boldsymbol{E}}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }{\mathit{\boldsymbol{K}}_\sigma }}&0\\ *&*&*&*&*&*&*&*&* &{ - \mathit{\boldsymbol{I}}}&0\\ *&*&*&*&*&*&*&*&*&* &{ - \mathit{\boldsymbol{I}}} \end{array}} \right] < 0 $ | (16) |
式中Ω1=Ac-1((A-I)-(H-I)Δσ),Ω2=Ac-1(H-I)ΔσKσ,Ω3=-W+εσβ2HHT,W=W-1,Q=Q-1,S=S-1。
证明:构造如下Lyapunov函数:
| $ V\left( k \right) = \mathit{\boldsymbol{x}}{\left( k \right)^{\rm{T}}}\mathit{\boldsymbol{Wx}}\left( k \right) + \mathit{\boldsymbol{\omega }}{\left( {k - 1} \right)^{\rm{T}}}\mathit{\boldsymbol{Q\omega }}\left( {k - 1} \right) + \mathit{\boldsymbol{v}}{\left( {k - 1} \right)^{\rm{T}}}\mathit{\boldsymbol{Sv}}\left( {k - 1} \right) $ |
| $ \begin{array}{l} \Delta V\left( k \right) = V\left( {k + 1} \right) - V\left( k \right) = \mathit{\boldsymbol{x}}{\left( {k + 1} \right)^{\rm{T}}}\mathit{\boldsymbol{Wx}}\left( {k + 1} \right) + \mathit{\boldsymbol{\omega }}{\left( k \right)^{\rm{T}}}\mathit{\boldsymbol{Q\omega }}\left( k \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{v}}{\left( k \right)^{\rm{T}}}\mathit{\boldsymbol{Sv}}\left( k \right) - \mathit{\boldsymbol{x}}{\left( k \right)^{\rm{T}}}\mathit{\boldsymbol{Wx}}\left( k \right) + \mathit{\boldsymbol{\omega }}{\left( {k - 1} \right)^{\rm{T}}}\mathit{\boldsymbol{Q\omega }}\left( {k - 1} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{v}}{\left( {k - 1} \right)^{\rm{T}}}\mathit{\boldsymbol{Sv}}\left( {k - 1} \right) \end{array} $ |
为使推导过程简洁,给出如下定义
| $ \begin{array}{l} {\mathit{\boldsymbol{G}}_{1\sigma }} = \mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{M}}_0}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }{\mathit{\boldsymbol{K}}_\sigma }{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma },{\mathit{\boldsymbol{G}}_{2\sigma }} = {\mathit{\boldsymbol{M}}_0}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }{\mathit{\boldsymbol{K}}_\sigma }\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right),{\mathit{\boldsymbol{G}}_{3\sigma }} = \\ {\mathit{\boldsymbol{M}}_0}\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }} \right) + {\mathit{\boldsymbol{M}}_1},{\mathit{\boldsymbol{U}}_{1\sigma }} = {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }{\mathit{\boldsymbol{K}}_\sigma }{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma },{\mathit{\boldsymbol{U}}_{2\sigma }} = {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }{\mathit{\boldsymbol{K}}_\sigma }\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right),z\left( k \right) = \\ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}{{\left( k \right)}^{\rm{T}}}}&{\mathit{\boldsymbol{\omega }}{{\left( {k - 1} \right)}^{\rm{T}}}}&{\mathit{\boldsymbol{v}}{{\left( {k - 1} \right)}^{\rm{T}}}} \end{array}} \right]。\end{array} $ |
则有
| $ \begin{array}{l} \Delta V\left( k \right) = z{\left( k \right)^{\rm{T}}}\left\{ {\left[ \begin{array}{l} \mathit{\boldsymbol{G}}_{1\sigma }^{\rm{T}}\\ \mathit{\boldsymbol{G}}_{2\sigma }^{\rm{T}}\\ \mathit{\boldsymbol{G}}_{3\sigma }^{\rm{T}} \end{array} \right]W{{\left[ \begin{array}{l} \mathit{\boldsymbol{G}}_{1\sigma }^{\rm{T}}\\ \mathit{\boldsymbol{G}}_{2\sigma }^{\rm{T}}\\ \mathit{\boldsymbol{G}}_{3\sigma }^{\rm{T}} \end{array} \right]}^{\rm{T}}} + \left[ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma ^{\rm{T}}\\ {\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right)^{\rm{T}}}\\ 0 \end{array} \right]\mathit{\boldsymbol{Q}}{{\left[ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma ^{\rm{T}}\\ {\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right)^{\rm{T}}}\\ 0 \end{array} \right]}^{\rm{T}}} + } \right.\\ \left[ \begin{array}{l} \mathit{\boldsymbol{U}}_{1\sigma }^{\rm{T}}\\ \mathit{\boldsymbol{U}}_{2\sigma }^{\rm{T}}\\ {\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }} \right)^{\rm{T}}} \end{array} \right]\mathit{\boldsymbol{S}}{\left[ \begin{array}{l} \mathit{\boldsymbol{U}}_{1\sigma }^{\rm{T}}\\ \mathit{\boldsymbol{U}}_{2\sigma }^{\rm{T}}\\ {\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }} \right)^{\rm{T}}} \end{array} \right]^{\rm{T}}} + \left[ \begin{array}{l} {\left( {{\mathit{\boldsymbol{K}}_\sigma }{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right)^{\rm{T}}}\\ {\left( {{\mathit{\boldsymbol{K}}_\sigma }\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right)} \right)^{\rm{T}}}\\ 0 \end{array} \right]{\mathit{\boldsymbol{R}}_2}{\left[ \begin{array}{l} {\left( {{\mathit{\boldsymbol{K}}_\sigma }{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right)^{\rm{T}}}\\ {\left( {{\mathit{\boldsymbol{K}}_\sigma }\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right)} \right)^{\rm{T}}}\\ 0 \end{array} \right]^{\rm{T}}} + \\ \left. {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_1} - \mathit{\boldsymbol{W}}}&0&0\\ 0&{ - \mathit{\boldsymbol{Q}}}&0\\ 0&0&{ - \mathit{\boldsymbol{S}}} \end{array}} \right]} \right\}\mathit{\boldsymbol{z}}\left( k \right) - \left[ {\mathit{\boldsymbol{x}}{{\left( k \right)}^{\rm{T}}}{\mathit{\boldsymbol{R}}_1}\mathit{\boldsymbol{x}}\left( k \right) + \mathit{\boldsymbol{u}}{{\left( k \right)}^{\rm{T}}}{\mathit{\boldsymbol{R}}_2}\mathit{\boldsymbol{u}}\left( k \right)} \right] = \\ z{\left( k \right)^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varTheta} z}}\left( k \right) - \left[ {\mathit{\boldsymbol{x}}{{\left( k \right)}^{\rm{T}}}{\mathit{\boldsymbol{R}}_1}\mathit{\boldsymbol{x}}\left( k \right) + \mathit{\boldsymbol{u}}{{\left( k \right)}^{\rm{T}}}{\mathit{\boldsymbol{R}}_2}\mathit{\boldsymbol{u}}\left( k \right)} \right] \end{array} $ | (17) |
由式(17)可知,若Θ<0则ΔV(k)<0,闭环系统(14)渐进稳定,此时
| $ \mathit{\boldsymbol{x}}{\left( k \right)^{\rm{T}}}{\mathit{\boldsymbol{R}}_1}\mathit{\boldsymbol{x}}\left( k \right) + \mathit{\boldsymbol{u}}{\left( k \right)^{\rm{T}}}{\mathit{\boldsymbol{R}}_2}\mathit{\boldsymbol{u}}\left( k \right) < - \Delta V\left( k \right) $ | (18) |
将式(18)从k=0到k=∞求和,可得J<V(0) -V(∞),由于闭环系统(14)渐进稳定,故V(∞)=0,则有
| $ \begin{array}{l} J < V\left( 0 \right) = x{\left( 0 \right)^{\rm{T}}}\mathit{\boldsymbol{Wx}}\left( 0 \right) + \\ \;\;\;\mathit{\boldsymbol{\omega }}{\left( { - 1} \right)^{\rm{T}}}\mathit{\boldsymbol{Q\omega }}\left( { - 1} \right) + \mathit{\boldsymbol{v}}{\left( { - 1} \right)^{\rm{T}}}\mathit{\boldsymbol{Sv}}\left( { - 1} \right) \end{array} $ | (19) |
根据Schur补性质,Θ<0等价于式(20)
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_1} - \mathit{\boldsymbol{W}}}&0&0&{\mathit{\boldsymbol{G}}_{1\sigma }^{\rm{T}}}&{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma ^{\rm{T}}}&{\mathit{\boldsymbol{U}}_{1\sigma }^{\rm{T}}}&{{{\left( {{\mathit{\boldsymbol{K}}_\sigma }{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right)}^{\rm{T}}}}\\ * &{ - \mathit{\boldsymbol{Q}}}&0&{\mathit{\boldsymbol{G}}_{2\sigma }^{\rm{T}}}&{{{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right)}^{\rm{T}}}}&{\mathit{\boldsymbol{U}}_{2\sigma }^{\rm{T}}}&{{{\left( {{\mathit{\boldsymbol{K}}_\sigma }\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right)} \right)}^{\rm{T}}}}\\ *&* &{ - \mathit{\boldsymbol{S}}}&{\mathit{\boldsymbol{G}}_{3\sigma }^{\rm{T}}}&0&{{{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }} \right)}^{\rm{T}}}}&0\\ *&*&* &{ - {\mathit{\boldsymbol{W}}^{ - 1}}}&0&0&0\\ *&*&*&* &{ - {\mathit{\boldsymbol{Q}}^{ - 1}}}&0&0\\ *&*&*&*&* &{ - {\mathit{\boldsymbol{S}}^{ - 1}}}&0\\ *&*&*&*&*&* &{ - \mathit{\boldsymbol{R}}_2^{ - 1}} \end{array}} \right] < 0 $ | (20) |
根据G1σ,G2σ的定义,采用引理1方法对M0,M1进行拆分,再利用Schur补性质合并拆分项,可得到矩阵不等式(20)的等价形式
| $ \left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{W}}}&0&0&{{\mathit{\boldsymbol{A}}^{\rm{T}}}}&{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma ^{\rm{T}}}&0&\mathit{\boldsymbol{I}}&0&0&0&{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma ^{\rm{T}}}\\ * &{ - \mathit{\boldsymbol{Q}}}&0&0&{{{\left( {1 - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right)}^{\rm{T}}}}&0&0&0&0&0&{{{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\sigma }} \right)}^{\rm{T}}}}\\ *&* &{ - \mathit{\boldsymbol{S}}}&{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1^{\rm{T}}}&0&{{{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }} \right)}^{\rm{T}}}}&0&0&{{{\left( { - \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }} \right)}^{\rm{T}}}}&0&0\\ *&*&* &{{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_3}}&0&0&0&0&0&{{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_2}}&0\\ *&*&*&* &{ - {\mathit{\boldsymbol{Q}}^{ - 1}}}&0&0&0&0&0&0\\ *&*&*&*&* &{ - {\mathit{\boldsymbol{S}}^{ - 1}}}&0&0&0&{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }{\mathit{\boldsymbol{K}}_\sigma }}&0\\ *&*&*&*&*&* &{ - \mathit{\boldsymbol{R}}_1^{ - 1}}&0&0&0&0\\ *&*&*&*&*&*&* &{ - \mathit{\boldsymbol{R}}_2^{ - 1}}&0&{{\mathit{\boldsymbol{K}}_\sigma }}&0\\ *&*&*&*&*&*&*&* &{ - {\mathit{\boldsymbol{\varepsilon }}_\sigma }}&{\mathit{\boldsymbol{E}}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_\sigma }{\mathit{\boldsymbol{K}}_\sigma }}&0\\ *&*&*&*&*&*&*&*&* &{ - \mathit{\boldsymbol{I}}}&0\\ *&*&*&*&*&*&*&*&*&* &{ - \mathit{\boldsymbol{I}}} \end{array}} \right] < 0 $ | (21) |
式中Ω1=Ac-1((A-I)-(H-I)Δσ),Ω2=Ac-1(H-I)ΔσKσ,Ω3=-W-1+εσβ2HHT。为便于使用Matlab中LMI工具箱进行求解,需对式(21)中的矩阵不等式线性化,分别左乘和右乘diag(W-1, Q-1, S-1, I, I, I, I, I, I, I, I),并将W=W-1,Q=Q-1,S=S-1代入,可得线性矩阵不等式(16),证毕。
3.2 网络参数与保成本容错控制器增益求解网络参数与保成本控制器增益求解可通过基于线性矩阵不等式约束的优化设计方法求解,即通过求解约束条件范围内的可行解,并在可行解空间内寻找可使成本性能上界J*最小的最优解,从而获得网络参数和保成本控制器增益。设闭环系统(14)的初始值z(0)=[x(0)T ω(-1)T v(-1)T]T,则网络参数与保成本控制器增益协同设计的优化问题如式(22)所示。
| $ \begin{array}{l} \mathop {\min }\limits_{P,Q,S} \left[ {\mathit{\boldsymbol{x}}{{\left( 0 \right)}^{\rm{T}}}\mathit{\boldsymbol{Wx}}\left( 0 \right) + \mathit{\boldsymbol{\omega }}{{\left( { - 1} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q\omega }}\left( { - 1} \right) + \mathit{\boldsymbol{v}}{{\left( { - 1} \right)}^{\rm{T}}}\mathit{\boldsymbol{Sv}}\left( { - 1} \right)} \right]\\ {\rm{s}}.{\rm{t}}.\left\{ \begin{array}{l} {\rm{LMI}}\left( {6.11} \right),\sigma \in \left\{ {1,2, \cdots ,N} \right\}\\ {\varepsilon _\sigma } > 0\\ \mathit{\boldsymbol{W}} > 0,\mathit{\boldsymbol{Q}} > 0,\mathit{\boldsymbol{S}} > 0\\ \frac{{\mu P}}{\eta } < T < {T_{\max }}\\ P \in \left\{ {1,2, \cdots ,r + m} \right\} \end{array} \right. \end{array} $ | (22) |
由于采样周期T和数据包容量P与线性矩阵不等式(16)之间存在非线性关系,优化问题(22)难以直接求解,若采用穷举法对定义域内的T和P一一列举,随着采样周期的增大将出现组合爆炸的问题,因此,本文提出一种启发式的优化求解方法,对优化问题(22)的求解过程进行简化,具体步骤如下
Step1:给定数据包容量初始值P0=1,则采样周期的初始值为T0=μP0/η,设置采样周期的搜索步长为1ms。
Step2:将T0, P0代入线性凸优化问题(23),求解W, Q, S, εσ, Kσ以及最小成本函数上界J0*,若凸优化问题无可行解,则令T=T0+0.001i, (i=1, 2, …),P=P0,继续本步骤求解,直至求得可行解。
| $ \begin{array}{l} \mathop {\min }\limits_{P,Q,S} \left[ {\mathit{\boldsymbol{x}}{{\left( 0 \right)}^{\rm{T}}}\mathit{\boldsymbol{Wx}}\left( 0 \right) + \mathit{\boldsymbol{\omega }}{{\left( { - 1} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q\omega }}\left( { - 1} \right) + \mathit{\boldsymbol{v}}{{\left( { - 1} \right)}^{\rm{T}}}\mathit{\boldsymbol{Sv}}\left( { - 1} \right)} \right]\\ {\rm{s}}.{\rm{t}}.\left\{ \begin{array}{l} {\rm{LMI}}\left( {6.11} \right),\sigma \in \left\{ {1,2, \cdots ,N} \right\}\\ {\varepsilon _\sigma } > 0\\ \mathit{\boldsymbol{W}} > 0,\mathit{\boldsymbol{Q}} > 0,\mathit{\boldsymbol{S}} > 0 \end{array} \right. \end{array} $ | (23) |
Step3:令T=T+0.001,P=P0,重新求解凸优化问题(23),得到此时的最小成本函数上界J1*,若J1*<J0*,则重复本步骤,直至求得Ji+1*>Ji*,(Ji*和Ji+1*为相邻两次求解所得的最小成本函数上界),Ji*即为P=P0时的最小成本函数上界,记为J*(0),此时T为最佳采样周期。
Step4:令P=P0+j, (j=1, 2, …, r+m-1),重复Step1~Step3,遍历{j=1, 2, …, r+m-1}后停止计算。比较J*(j), (j=0, 1, …r+m-1)得到最小值J*,及其对应的最佳采样周期T,数据包容量P和控制器增益Kσ。
4 仿真及结果分析以双轴发动机在地面条件下(H=0 km, Ma=0)工作于最大状态的小偏离状态空间模型作为被控对象,其数学表达式为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot x}}\left( t \right) = {\mathit{\boldsymbol{A}}_c}\mathit{\boldsymbol{x}}\left( t \right) + {\mathit{\boldsymbol{B}}_c}\mathit{\boldsymbol{u}}\left( t \right)\\ \mathit{\boldsymbol{y}}\left( t \right) = {\mathit{\boldsymbol{C}}_c}\mathit{\boldsymbol{x}}\left( t \right) \end{array} \right. $ | (24) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_c} = \left[ {\begin{array}{*{20}{c}} { - 3.573}&{0.672}\\ {0.337}&{ - 3.492} \end{array}} \right],{\mathit{\boldsymbol{B}}_c} = \left[ {\begin{array}{*{20}{c}} {0.496}&{0.669}\\ {0.636}&{3.604} \end{array}} \right],{\mathit{\boldsymbol{C}}_c} = \left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right]}\\ {\mathit{\boldsymbol{x}} = {{\left[ {\begin{array}{*{20}{c}} {{n_{\rm{H}}}}&{{n_{\rm{L}}}} \end{array}} \right]}^{\rm{T}}},\mathit{\boldsymbol{u}} = {{\left[ {\begin{array}{*{20}{c}} {{m_{\rm{f}}}}&{{A_8}} \end{array}} \right]}^{\rm{T}}},\mathit{\boldsymbol{y}} = {{\left[ {\begin{array}{*{20}{c}} {{n_{\rm{H}}}}&{{n_{\rm{L}}}} \end{array}} \right]}^{\rm{T}}}} \end{array} $ |
状态空间模型(24)的传递函数形式可表示为x(s)=G(s)u(s),其中传递矩阵为
| $ \mathit{\boldsymbol{G}}\left( s \right) = \left[ {\begin{array}{*{20}{c}} {\frac{{0.496s + 2.159}}{{{s^2} + 7.065s + 12.251}}}&{\frac{{0.69s + 4.758}}{{{s^2} + 7.065s + 12.251}}}\\ {\frac{{0.636s + 2.439}}{{{s^2} + 7.065s + 12.251}}}&{\frac{{3.604s + 13.127}}{{{s^2} + 7.065s + 12.251}}} \end{array}} \right] $ | (25) |
对于采用CAN2.0标准的CAN总线,一个完整的数据帧包含110个数据位(bit),即μ=110:帧起始标志占1个数据位,仲裁场占11个数据位,控制场占6个数据位,数据场占8个字节共64个数据位,CRC场占16个数据位,应答场占2个数据位,帧结束占7个数据位。由于数据帧的发送是连续的,因此帧间空间仅占3个数据位[14]。设总线网络带宽η为30kbit/s,非实时数据宽度θk为80bit,各周期内非实时数据的发送概率为30%,由位于[0, 1]内的随机数ς(k)来实现,如式(26)所示。采样周期T和数据包容量P需满足约束条件式(27)。
| $ {\theta _k} = \left\{ \begin{array}{l} 80{\rm{bit,when}}~\varsigma \left( k \right) \le 0.3\\ 0{\rm{bit,when}}~\varsigma \left( k \right) > 0.3 \end{array} \right. $ | (26) |
| $ {\theta _k} + \mu P \le T\eta $ | (27) |
求得分布式控制系统的系统最佳采样周期T=0.016s,总线数据包容量P=3,此时存在4种数据传输模式
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_1} = {\rm{diag}}\left( {1,0,1,1} \right),{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_2} = {\rm{diag}}\left( {0,1,1,1} \right)\\ {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_3} = {\rm{diag}}\left( {1,1,1,0} \right),{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_4} = {\rm{diag}}\left( {1,1,0,1} \right) \end{array} $ |
根据定理1求得分布式控制系统按照上述4种数据传输模式工作时,控制器增益分别为
| $ \begin{array}{l} {\mathit{\boldsymbol{K}}_1} = \left[ {\begin{array}{*{20}{c}} {0.0259}&{0.2223}\\ { - 0.0192}&{ - 0.2826} \end{array}} \right],{\mathit{\boldsymbol{K}}_2} = \left[ {\begin{array}{*{20}{c}} {0.0243}&{0.2198}\\ { - 0.0214}&{ - 0.3071} \end{array}} \right]\\ {\mathit{\boldsymbol{K}}_3} = \left[ {\begin{array}{*{20}{c}} { - 0.1511}&{ - 2.4416}\\ { - 0.0225}&{ - 0.1721} \end{array}} \right],{\mathit{\boldsymbol{K}}_4} = \left[ {\begin{array}{*{20}{c}} { - 0.0308}&{ - 0.4664}\\ { - 0.0357}&{ - 0.5109} \end{array}} \right] \end{array} $ |
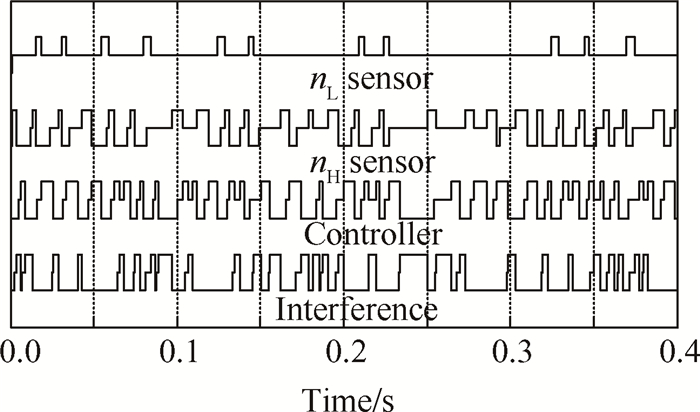
当采样周期T=16ms,数据包容量P=3时,系统在以上控制器作用下,状态变量nL和nH的阶跃响应如图 2所示,纵坐标为归一化处理后的值,即实际转速占最大转速的百分比。从图中可以看出,当选择网络参数T=16ms,P=3时,按照定理1求出的控制器增益能够保证联合闭环系统渐进稳定,且控制器具有较为理想的动态性能。此时分布式控制系统中各节点的网络调度如图 3所示,为便于显示,本文仿真仅给出0~0.4s的网络调度图,图中四条曲线分别为四个节点的数据传输状态,分为低、中、高三类,低为未发送、中为排队等待发送、高为正在发送。
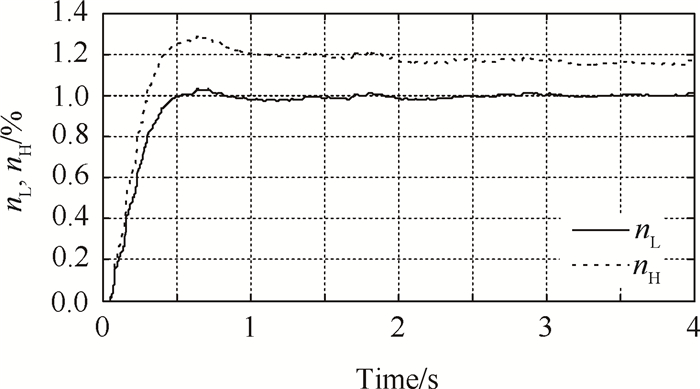
|
Fig. 2 Step response of state variables when T=16ms and P=3 |
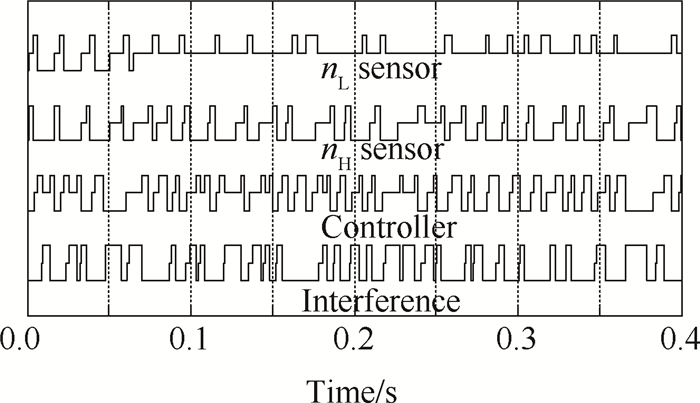
|
Fig. 3 Network scheduling when T=16ms and P=3 |
为检验网络参数与容错控制器增益联合求解方法的有效性,选择满足式(27)的另一组网络参数T=10ms,P=2进行仿真,此时闭环系统的阶跃响应如图 4所示。从图中可以看出,当选择T=10ms,P=2时,得到的控制器增益仍然能够保证联合闭环系统渐进稳定,但响应曲线存在较大幅度的波动,低压转速超调量由0.02%增大为0.1%,参数最大摆动由0.01%增大为0.03%,控制器的动态性能劣于图 2。造成这一现象的原因是:根据2.2节方法求解可知,系统的最佳网络参数为T=16ms,P=3,此时得到的容错控制器增益能够保证成本函数上界J*最小,即控制器动态性能最优。当采样周期变为T=10ms后,虽然单位时间内数据的传输次数增多,但由于网络带宽是固定的,数据包容量必然降低,从而影响了闭环系统的动态性能。图 5给出了当T=10ms,P=2时各节点的网络调度图,从图中亦可证明以上分析的正确性。
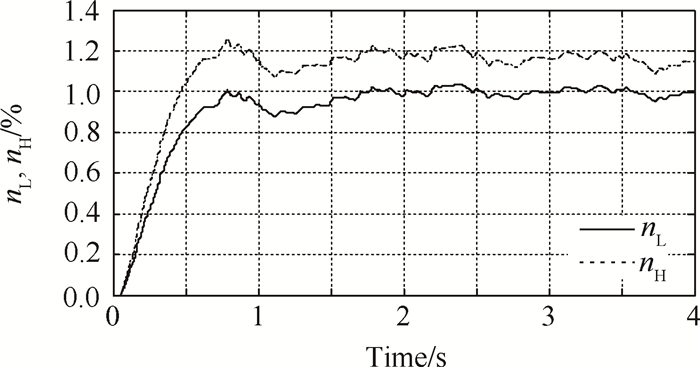
|
Fig. 4 Step response of state variables when T=10ms and P=2 |
|
Fig. 5 Network scheduling when T=10ms and P=2 |
通过本文研究,得到以下结论:
(1)将采样周期和数据包容量引入控制器设计模型后,采用网络参数与保成本控制器参数加权求和的方式设定优化目标,保证了多个优化参数时闭环系统在任意一种数据传输模式下均能保持渐进稳定。
(2)经过协同设计的网络参数和控制器,在保证系统渐进稳定的前提下,低压转子转速超调量由0.1%变为0.02%,降低了80%,参数最大摆动由0.03%变为0.01%,降低了66.7%,有效改善了系统的动态性能。
(3)加入调度协议后,网络时延变为随机跳变的不确定短时延,通过容错设计,控制器弱化了时延不确定性对闭环系统性能的影响,使该控制器对时延具有鲁棒性。
| [1] |
赵维佺, 李迪. 网络控制系统中调度与控制的协同设计[J]. 工业控制计算机, 2007, 20(12): 1-5. DOI:10.3969/j.issn.1001-182X.2007.12.001 (  0) 0) |
| [2] |
宣慧明, 文利燕, 彭晨. 资源受限网络控制系统的信息调度[J]. 南京师范大学学报(工程技术版), 2012, 12(2): 11-17. (  0) 0) |
| [3] |
Yuan G E, LIU Zhen-an, CHEN Qi-gong, et al. Stability of Networked Control Systems with Communication Constraints[J]. Journal of University of Science and Technology of China, 2008, 38(3): 266-271.
(  0) 0) |
| [4] |
王俊波, 胥布工. 资源受限的网络控制系统调度[J]. 控制与决策, 2008, 23(5): 551-559. (  0) 0) |
| [5] |
杜明莉, 周川, 陈庆伟, 等. 具有通信约束的网络控制系统动态调度与H∞控制协同设计[J]. 控制理论与应用, 2012, 29(9): 1132-1138. (  0) 0) |
| [6] |
李祖欣, 王万良, 成新民. 资源约束系统的信息调度及其渐进稳定性[J]. 信息与控制, 2008, 37(5): 593-598. (  0) 0) |
| [7] |
谢林柏, 纪志成, 潘庭龙, 等. 基于信息调度的网络化控制系统[J]. 系统工程与电子技术, 2005, 27(3): 449-452. (  0) 0) |
| [8] |
陈惠英. 资源受限网络控制系统控制与调度方法研究[D]. 杭州: 浙江工业大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10337-2009058020.htm
(  0) 0) |
| [9] |
王磊, 谢寿生, 彭靖波, 等. 航空发动机分布式控制系统不确定性鲁棒H∞容错控制[J]. 推进技术, 2013, 34(6): 836-842. (WANG Lei, XIE Shousheng, PENG Jing-bo, et al. Uncertain Robust H∞ Fault-Tolerant Control for Aero-Engine Distributed Control System[J]. Journal of Propulsion Technology, 2013, 34(6): 836-842.)
(  0) 0) |
| [10] |
李睿超, 郭迎清, 李岩, 等. 基于数据集中器的超燃冲压发动机分布式控制系统通信方案设计[J]. 推进技术, 2016, 37(9): 1766-1773. (LI Rui-chao, GUO Ying-qing, LI Yan, et al. Communication Scheme Design of Distributed Control System for Scram jet Engine Based on Data Concentrators[J]. Journal of Propulsion Technology, 2016, 37(9): 1766-1773.)
(  0) 0) |
| [11] |
Walsh G C, Ye H, Bushnell L G. Stability Analysis of Network Control Systems[J]. IEEE Transaction on Control Systems Technology, 2002, 10(3): 438-446. DOI:10.1109/87.998034
(  0) 0) |
| [12] |
邵奇可, 俞立, 欧林林, 等. 基于网络QoS的控制系统协同设计方法研究[J]. 自动化学报, 2010, 36(9): 1356-1360. (  0) 0) |
| [13] |
郭一楠, 张芹英, 巩敦卫, 等. 一类时变时延网络控制系统的鲁棒容错控制[J]. 控制与决策, 2008, 23(6): 689-692. (  0) 0) |
| [14] |
彭靖波. 基于分布式控制的航空发动机先进控制算法研究[D]. 西安: 空军工程大学, 2009.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

