2. 沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室,辽宁 沈阳 110136
2. Liaoning Key Laboratory of Advanced Measurement and Test Technology for Aviation Propulsion System, Shenyang Aerospace University, Shenyang 110136, China
中介轴承工作于航空发动机高、低压转子之间,内外滚道同时旋转且润滑不良、载荷大、温度高。由于其工作环境恶劣极易出现磨损、剥落和腐蚀发生破坏[1]。中介轴承位于发动机内部,故障源与传感器之间传递路径复杂,故障振动信号很容易被零部件的噪声信号或其它信号所淹没,故障特征很难提取[2, 3]。声发射信号以其信号频率高、特征信号明显、对冲击信号敏感、不受结构和旋转动态振动噪声的影响等优点,被广泛应用到滚动轴承在线监测和故障诊断中[4]。声发射信号采样频率高,一般采样率在1M赫兹以上。因此,中介轴承故障监测过程中声发射信号数据量非常巨大,使得数据分析与处理十分困难。
国内外专家学者针对采集的故障信号数据量大、分析与处理困难的问题开展了大量研究工作,提出了多种数据缩减方法实现故障数据缩减并保留关键故障特征。Qu等[5]基于通讯原理提出一种外差解调方法对齿轮故障声发射信号进行频率缩减,将声发射信号采样率从MHz降低到kHz,大大缩减了数据采集量,并在缩减后的声发射信号中提取出了齿轮故障的特征参数,据此对齿轮故障进行诊断。Van Hecke等[6, 7]提出时域同步采样和谱平均相结合的方法对滚动轴承故障信号进行数据缩减,同样在缩减后数据中提取出多个故障特征参数,实现了滚动轴承的故障诊断。张斌等[8]利用小波分析良好的时—频双局域性特点,结合统计检测理论提出了一种湍流采样数据量缩减算法,该方法保留了与原始数据同等的湍流信息,缺点是该方法的数据缩减率较低。王实等[9]证明了格环境的内部覆盖,并提出了一种新的格子机算法,通过寻找内部覆盖实现数据缩减,但该算法距离工程应用还存在一定差距。Robinson等[10, 11]发明了一种峰值分析方法对齿轮故障的融合信号进行数据缩减,该方法的缺点是降采样频率高于某一频率成分会产生虚假频率,进而影响诊断结果。为了克服峰值分析方法的缺点,Lin等[12]提出了峰值保持降采样方法对轴承故障信号进行数据缩减,在实现数据缩减的同时保留了轴承故障的关键频率信息,但该方法保留的故障特征较微弱。现有数据缩减算法是在高斯信号模型基础上发展的[13],它通过把原数据分割成多段信号片断然后进行统计检测来缩减数据量,其缺点则在于经过缩减的数据会丢失部分信息。
本文针对中介轴承故障声发射信号的周期冲击特征,提出一种峰值保持降采样(PHDS)和谱峭度(SK)算法相结合的中介轴承故障声发射信号数据缩减技术。根据谱峭度准则确定故障声发射信号滤波的最佳中心频率,根据最佳中心频率确定数据缩减率,采用峰值保持降采样方法对故障声发射信号进行数据缩减。实现在保留中介轴承故障冲击特征前提下尽可能地缩减声发射信号数据,提高声发射信号的处理效率。
2 声发射信号数据缩减技术 2.1 峰值保持降采样算法故障诊断中多采用等间隔降采样方法来对数据进行缩减,该方法以固定间隔对信号进行降采样,保留对应采样点的固定值,这样很容易造成中介轴承信号的冲击特征信息丢失。峰值保持降采样算法[12]的基本思路是对于高采样率的原始信号以固定的降采样比对信号进行分段,将每段的峰值作为重采样值。此种方法对于声发射信号的冲击特征保留效果明显。
假设被采集的中介轴承故障声发射信号为s(t)
| $ \mathit{\boldsymbol{s}}\left( t \right) = \left[ {s\left( {{t_0}} \right),s\left( {{t_1}} \right), \cdots ,s\left( {{t_i}} \right) \cdots } \right]\;\;\;\left( {0 \le i \le N - 1} \right) $ | (1) |
首先,将s(t)分为M个数据段,则信号s(t)变换为S(T),S(T)可表示如下
| $ \mathit{\boldsymbol{S}}\left( t \right) = \left[ {S\left( {{T_0}} \right),S\left( {{T_1}} \right), \cdots ,S\left( {{Y_j}} \right) \cdots } \right]\;\;\;\left( {0 \le j \le M - 1} \right) $ | (2) |
式中,M = int(N/r),int表示取整,有
| $ \mathit{\boldsymbol{S}}\left( {{T_j}} \right) = \left[ {s\left( {{t_i}} \right),s\left( {{t_{i + 1}}} \right), \cdots ,s\left( {{T_{i + r}}} \right)} \right] $ |
N为原始故障信号的序列长度。r为降采样率,即数据减缩率。可根据公式(3)求得
| $ r = {f_0}/{f_{\rm{d}}} $ | (3) |
式中f0为原始数据采样频率,fd为降采样频率。
然后,提取序列S(Tj)中数值绝对值的最大值作为保留值代表序列S(Tj)。S(Tj)保留值的符号则根据S(Tj-1)保留值的符号确定。例如,S(Tj)信号最大值和最小值的符号相反,并且S(Tj-1)信号保留值的符号为正,S(Tj)信号的保留值符号为负。峰值保持采样法流程图如图 1所示。
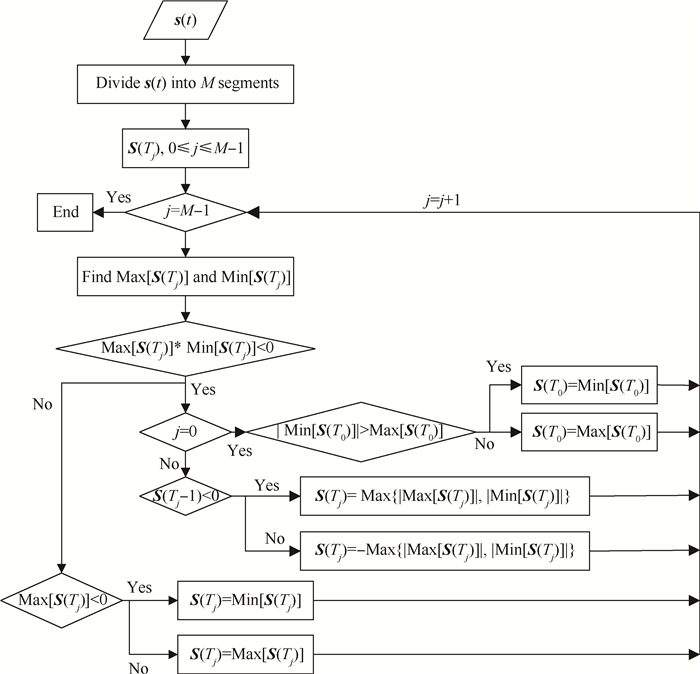
|
Fig. 1 Flow chart of the PHDS algorithm |
谱峭度[14]最初由Dwyer提出,主要是为了检测和描述瞬态信号。其本质是计算每条频率线的峭度,以反映出该频率成分处信号冲击的剧烈程度,能够发现隐藏的非平稳信号,并指出所在的频带。
中介轴承故障声发射信号是典型的非平稳信号,将中介轴承故障的冲击信号X(t)产生的系统响应Y(t)按照Wold-crammer进行频域分解,即
| $ Y\left( t \right) = \int_{ - \infty }^{ + \infty } {{{\rm{e}}^{{\rm{j}}2{\rm{ \mathsf{ π} }}ft}}H\left( {t,f,\bar \omega } \right){\rm{d}}X\left( f \right)} $ | (4) |
式中H(t, f, ω)是依赖于随机变量ω的复包络。
同时,定义Y(t)的四阶谱累积量为
| $ {C_{4Y}}\left( f \right) = {S_{4Y}}\left( f \right) - 2S_{2Y}^2\left( f \right)\;\;\;\left( {f \ne 0} \right) $ | (5) |
式中S2nY(t, f)是2n阶瞬时矩,用来表示复包络在频率f和时间t处的能量强度,表示为
| $ {S_{2nY}}\left( {t,f} \right) = E\left\{ {{{\left| {H\left( {t,f} \right){\rm{d}}X\left( f \right)} \right|}^{2n}}\bar \omega } \right\}/{\rm{d}}f = {\left| {H\left( {t,f} \right)} \right|^{2n}} \cdot {S_{2nX}} $ | (6) |
对于一个给定的随机变量ω,式(6)是时间和频率的函数,采用该式分析具有时频结构的非平稳过程非常有效。但是对于条件性的非平稳过程,需分析集成了多个输出ω的平均的时域结构的特性,因此定义一个谱矩,其表达式
| $ {S_{2nY}}\left( f \right) = E\left\{ {{S_{2nX}}\left( {t,f} \right)} \right\} = E\left\{ {{{\left| {H\left( {t,f} \right){\rm{d}}X\left( f \right)} \right|}^{2n}}} \right\}/{\rm{d}}f $ | (7) |
定义谱峭度为能量归一化累计量表示为
| $ {K_Y}\left( f \right) = \frac{{{C_{4Y}}\left( f \right)}}{{S_{2Y}^2\left( f \right)}} = \frac{{{S_{4Y}}\left( f \right)}}{{S_{2Y}^2\left( f \right)}} - 2\;\;\;\;\left( {f \ne 0} \right) $ | (8) |
系统响应Y(t)在频率f处计算得到的峭度值即为谱峭度。
2.3 PHDS-SK技术为了获得峰值保持降采样的最佳降采样率,基于谱峭度最大准则,采用快速峭度图[15]计算中介轴承故障声发射信号时频图上每个频率的谱峭度值。所得谱峭度值最大的f和Δf就是峰值保持采样法的最佳降采样频率和带宽,可以使得降采样后的信号更加完整地保留中介轴承故障信息。
快速峭度图是将中介轴承声发射信号按照二分/三分交替的方式不断进行分解,然后采用公式(8)计算每层每个频段上的谱峭度值,并用颜色的深浅代表谱峭度值的大小,其频率分辨率为Δf = 2-(k+1)f0,其中f0为采样频率,谱峭度值的最大中心频率fd和带宽Δf就是峰值保持采样法的最佳降采样频率和带宽。获取最佳降采样频率fd后,根据公式(3)确定最佳降采样率。然后采用PHDS方法对中介轴承故障声发射原始信号进行数据缩减。声发射信号对于转速信号不敏感,对于故障的冲击信息较为敏感。而PHDS-SK技术是对采集到故障声发射信号进行缩减,其本质是尽可能保持峰值信息的降采样技术,因此,该方法不受中介轴承的实际转速影响,适用性较强。基于PHDS-SK技术可以实现中介轴承故障声发射信号数据缩减的同时,尽可能多的保存中介轴承的故障信息。
3 中介轴承故障模拟 3.1 中介轴承故障模拟实验为了验证PHDS-SK数据缩减技术的准确性,采用双转子试验台开展中介轴承故障模拟实验,双转子中介轴承模拟实验系统如图 2所示。该实验台模拟了某型发动机的支承传动方案,在该支承方案中4号支点为中介轴承。采用SAEU2S声发射系统进行声发射信号的采集与分析,同时在机匣和轴承座的轴向和径向方向上布置了4个声发射传感器,传感器布置如图 3所示。试验台的中介轴承安装的是SKF nu1004M圆柱滚子轴承。采用线切割的方法在中介轴承的内圈和外圈制造了宽为1mm的矩形槽表面缺陷,缺陷如图 4所示。声发射信号为高频信号,因此,本次实验设置采样频率为1MHz。

|
Fig. 2 Fault simulation system of rolling element bearings |

|
Fig. 3 Acoustic emission sensor locations |

|
Fig. 4 Inter-shaft bearing with fault |
实验过程中高低压转子同向旋转,高压转子设置为1kr/min,低压转子625r/min,实测高压轴为1001r/min,低压轴为624r/min,径向载荷设定为200N。SKF nu1004M轴承的参数如表 1所示。
|
|
Table 1 Parameters of SKF nu1004M bearing |
根据轴承故障频率的理论公式(9),计算轴承内、外圈同向旋转时,中介轴承外圈表面存在缺陷时的故障频率为33.55Hz,2倍频为67.1Hz,3倍频为100.7Hz。
| $ {\omega _{\rm{o}}} = \frac{{\left| {{n_{\rm i}} - {n_{\rm o}}} \right|}}{{2 \times 60}}\left( {1 - \frac{d}{{{D_{\rm{m}}}}}\cos \alpha } \right)Z $ | (9) |
式中ni和no分别为中介轴承内、外圈的转速;Z为轴承滚子个数,d为滚子直径,Dm为轴承节径,α为轴承压力角。
3.2 中介轴承故障数值模拟本文在Hertz接触理论的基础上建立两自由度的局部故障动力学模型,并假设滚子不会发生打滑现象。基于Patil等[16]假设将滚子与滚道的接触简化为非线性的弹簧—质量系统,简化模型如图 5所示。

|
Fig. 5 Simplified model of inter-shaft bearing |
图中第i个滚子与X轴的夹角为θi,H为滚子经过缺陷时的时变位移激励,其变形量δ为
| $ \delta = x\cos {\theta _i} + y\sin {\theta _i} - {C_{\rm{r}}} - H $ | (10) |
本文根据Patil假设理论建立轴承动力学模型,将接触刚度、阻尼、Hertz接触力、时变位移和恒定径向载荷W带入动力学方程。所建立的中介轴承动力学方程为
| $ \left\{ \begin{array}{l} M\ddot x + c\dot x + K\sum\limits_{i = 1}^Z {\lambda {\delta ^{10 - 9}}\cos {\theta _i}} = W\\ M\ddot x + c\dot x + K\sum\limits_{i = 1}^Z {\lambda {\delta ^{10/9}}\sin {\theta _i}} = 0 \end{array} \right. $ | (11) |
式中Z为轴承滚子个数,K为内、外圈与滚动体之间的接触刚度。λ为滚子与滚道是否接触的开关量,表示为
| $ \lambda = \left\{ \begin{array}{l} 1\;\;\;\;\left( {\delta > 0} \right)\\ 0\;\;\;\;\left( {\delta \le 0} \right) \end{array} \right. $ | (12) |
本文采用改进的Newmark-β法对建立的运动微分方程进行动力学求解。获取中介轴承外圈故障声发射模拟信号。
4 数据缩减技术验证 4.1 实验验证通过对中介轴承外圈故障模拟与声发射信号采集,得到了中介轴承外圈故障的声发射信号。采集的原始声发射信号的时域信号和包络谱如图 6和图 7所示。
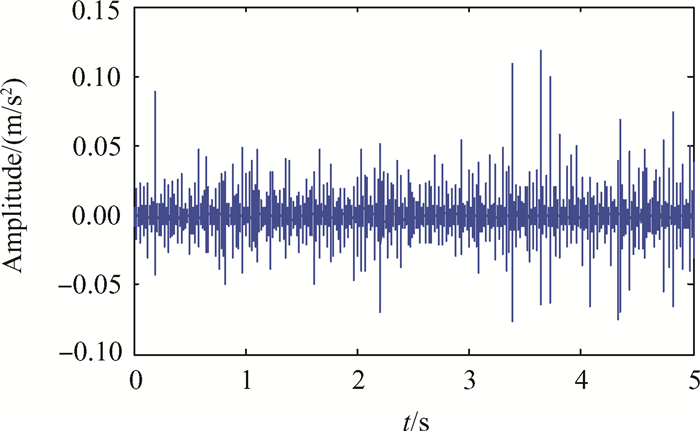
|
Fig. 6 Acoustic emission signals of inter-shaft bearing with outer ring fault |
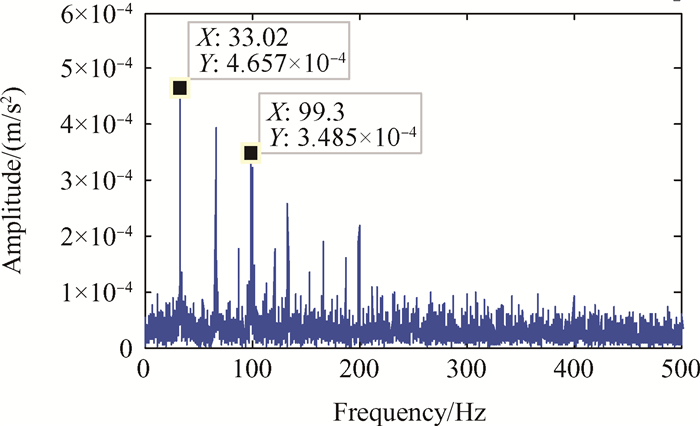
|
Fig. 7 Envelope spectra of inter-shaft bearing fault acoustic emission signals |
从图 6可以看出,中介轴承外圈存在缺陷时,其时域信号存在明显的冲击成分,且冲击脉冲的强度存在周期性的变化,周期成分为滚动体经过缺陷的冲击信号受到轴的转频或保持架转频调制的原因。从图 7中可以清晰地看出,滚动体通过外滚道的通过频率为33.02Hz,该频率与理论值相比存在误差,这是由于在实验过程中轴承存在打滑现象。图中同时存在通过频率的2倍频和3倍频。
采用PHDS-SK数据缩减技术对中介轴承外圈故障声发射信号进行处理。首先,采用快速峭度图对声发射信号按照二分/三分交替的方式进行分解,然计算每层每个频段上的谱峭度值,计算结果如图 8所示。从图中可以看出中心频率为781.25Hz,带宽为312.5Hz的频带内的谱峭度值最大。峭度对于轴承故障的冲击特征十分敏感,峭度较大的频带内冲击特征较为明显,故障信息丰富。对快速峭度图计算结果向上取整确定出最佳的降采样频率为800Hz。实验设置的声发射采样频率为1MHz,可知数据量缩减为原始数据的1/1250。

|
Fig. 8 Fast kurtogram of inter-shaft bearing fault acoustic emission signals |
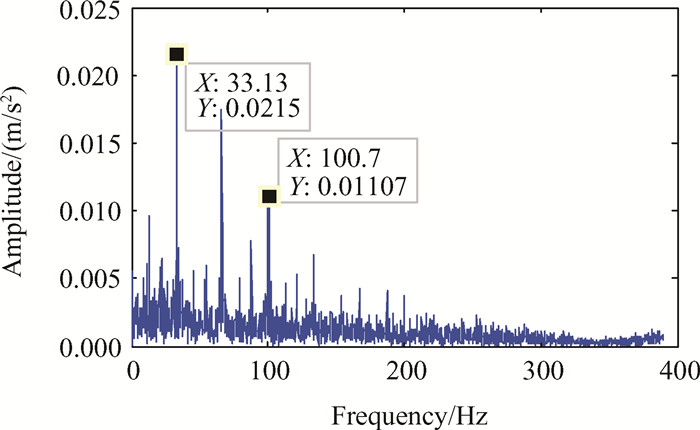
根据确定的最佳降采样频率,采用峰值保持采样算法对声发射信号进行数据缩减。数据缩减后故障信号时域图和包络谱图如图 9和图 10所示。从时域图中可以看出基于PHDS-SK技术缩减的数据保留了声发射信号的冲击特征。通过对缩减后数据进行包络分析,可以提取出中介轴承外圈故障特征频率。该频率相对于原始信号所提取的故障频率更加接近计算值33.55Hz,说明该方法具有一定的降噪和提高信噪比的作用。
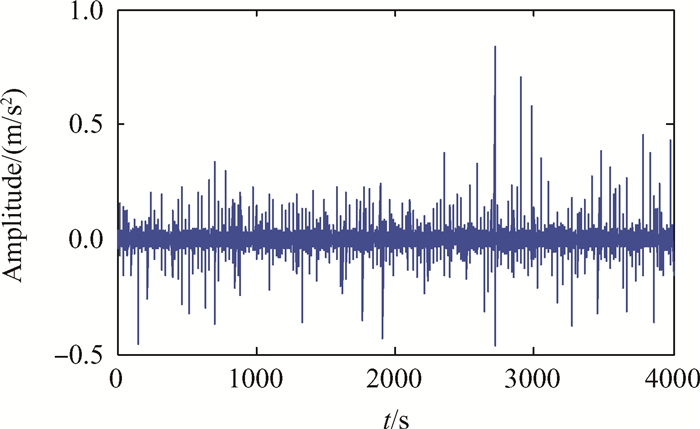
|
Fig. 9 Acoustic emission PHDS-SK signals of inter-shaft bearing with outer ring fault |
|
Fig. 10 PHDS-SK envelope spectra of inter-shaft bearing outer ring fault acoustic emission signal |
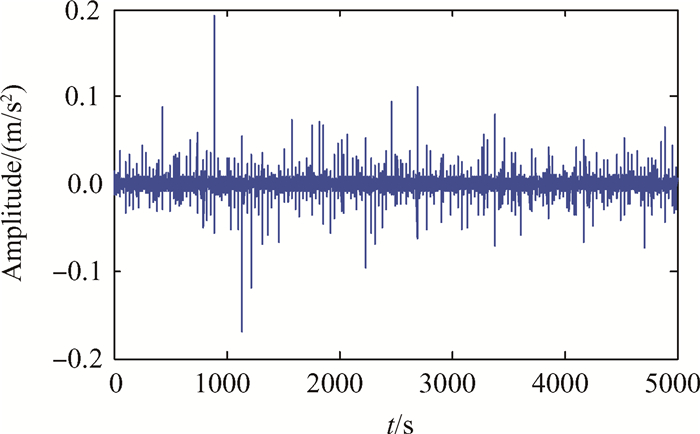
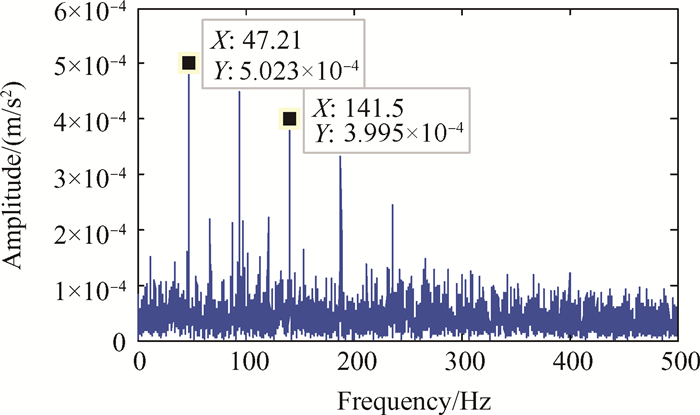
采用PHDS-SK数据缩减技术对中介轴承内圈故障声发射信号进行处理。采用快速峭度谱计算出最佳采样频率为937.25,因此向上取整确定出最佳的降采样频率为1kHz。根据确定的最佳降采样频率采用PHDS算法对信号进行数据缩减。数据缩减后故障信号时域图和包络谱图如图 11和图 12所示。从时域图中同样可以看出缩减的数据保留了故障信号的冲击特征。缩减后数据的包络谱分析可以提取出中介轴承内圈故障特征频率47.21Hz及其倍频,该值与经验公式计算出的内圈故障频率47.17Hz十分接近。实验设置的声发射采样频率为1MHz,可知数据量缩减为原始数据的1/1000。再次验证了本文提出的PHDS-SK数据缩减技术的有效性。
|
Fig. 11 Acoustic emission PHDS-SK signals of inter-shaft bearing with inner ring fault |
|
Fig. 12 PHDS-SK envelope spectra of inter-shaft bearing inner ring fault acoustic emission signal |
当采集的声发射信号包含较强背景噪声时,可能造成故障频率不明显或者故障数据中峰值较多,针对此种情况可以采用时域同步平均技术进行采样,以提高信号的信噪比。本技术中的谱峭度算法可以选取故障特征明显最优降采样频率,以提高峰值保持采样算法对故障峰值的最大限度的保留。
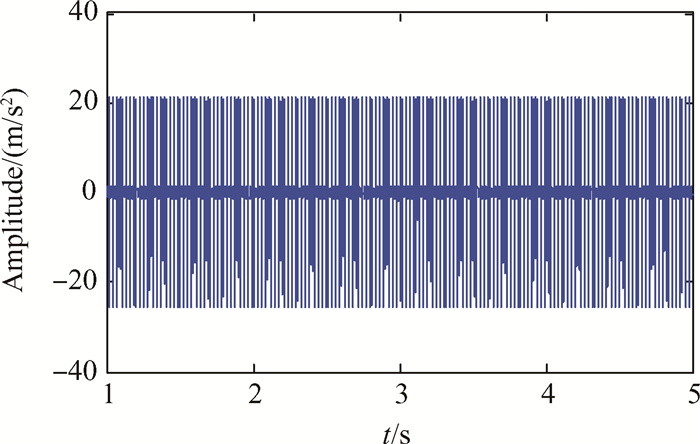
4.2 仿真结果验证当缺陷位于中介轴承外滚道时,通过本文建立的动力学模型仿真求得的时域信号和包络谱如图 13和14所示。
|
Fig. 13 Simulated signal of inter-shaft bearing with outer ring fault |
|
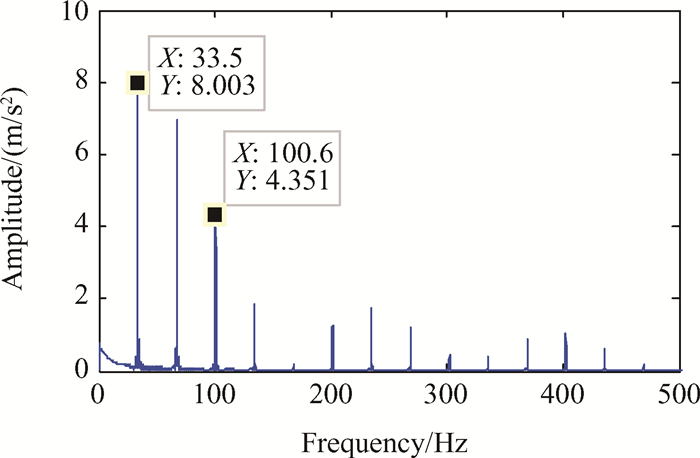
Fig. 14 Envelope spectra of inter-shaft bearing fault simulated signals |
从图 13中可以看出,中介轴承故障仿真的时域信号存在明显的周期冲击成分。从图 14中可以看出,本文建立模型仿真出来的包络谱与实验包络谱图的结果基本相似,同时出现了通过频率1至4倍频,且频率依次递减。模型求得的通过频率为33.57Hz,与理论计算的频率33.55基本相同。
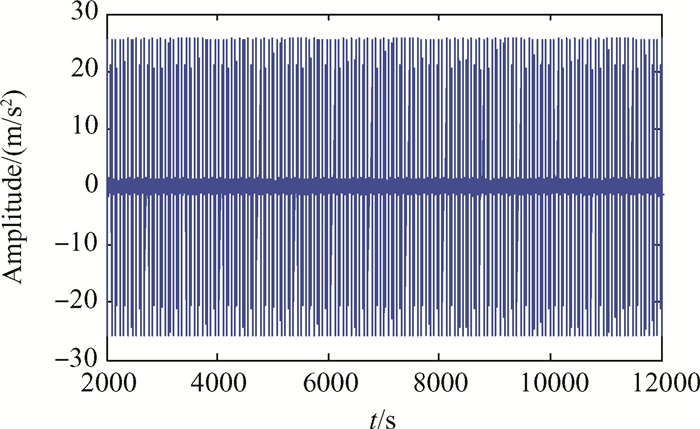
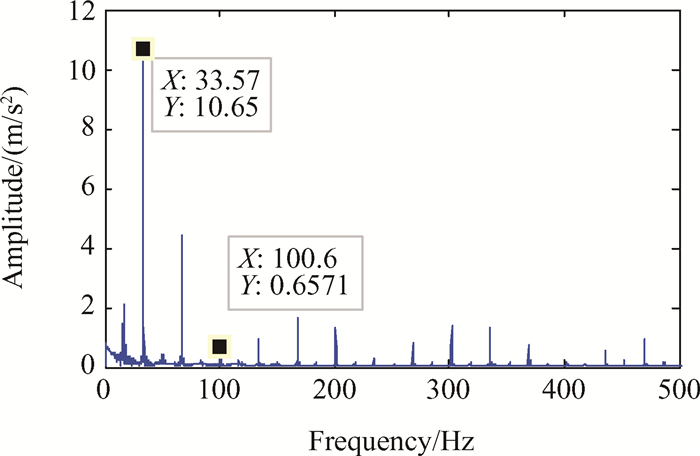
采用PHDS-SK数据缩减技术对数值仿真的中介轴承外圈故障信号进行处理。首先,采用快速峭度图对模拟信号进行谱峭度值计算。根据快速峭度图计算结果可以取整确定出最佳的降采样频率为2500Hz。数值模拟设置的采样频率为1MHz,数据量缩减为原始数据的1/400。根据确定的最佳降采样频率采用峰值保持采样算法对声发射信号进行数据缩减。数据缩减后故障信号时域图和包络谱图如图 15和图 16所示。从时域图中可以看出基于PHDS-SK技术缩减的数据保留了外圈故障信号的冲击特征。通过对缩减后数据进行包络分析可以提取出中介轴承外圈故障特征频率,提取到的频率数值与计算结果一致。
|
Fig. 15 PHDS-SK simulated signal of inter-shaft bearing with outer ring fault |
|
Fig. 16 PHDS-SK envelope spectra of inter-shaft bearing fault simulated signal |
(1)本文针对中介轴承故障声发射信号数据量大,分析处理困难的问题,提出一种峰值保持降采样(PHDS)和谱峭度(SK)算法相结合的轴承故障声发射信号数据缩减技术。该技术能够在保留中介轴承外圈故障冲击特征前提下缩减声发射信号数据,提高声发射信号的处理效率。
(2)采用PHDS-SK数据缩减技术分别对中介轴承外圈故障的实验模拟和动力学仿真结果进行数据缩减,数据量分别缩减为原始数据的1/1250和1/400。该技术能够在大量缩减故障信号数据量的同时,保存中介轴承外圈故障的周期冲击特征,并准确提取出外圈故障频率。
| [1] |
廖明夫, 马振国, 刘永泉, 等. 航空发动机中介轴承的故障特征与诊断方法[J]. 航空动力学报, 2013, 28(12): 2752-2758. (  0) 0) |
| [2] |
艾延廷, 陈潮龙, 田晶, 等. 基于信息熵距和FSVM隶属度的转子振动状态评估方法[J]. 推进技术, 2013, 34(11): 1543-1548. (AI Yan-ting, CHEN Chao-long, TIAN Jing., et al. Studies on Assessing Method of Rotor Vibration State Based on Information Entropy Distance and FSVM Membership[J]. Journal of Propulsion Technology, 2013, 34(11): 1543-1548.)
(  0) 0) |
| [3] |
费成巍, 白广忱, 李晓颖. 基于过程功率谱熵SVM的转子振动故障诊断方法[J]. 推进技术, 2012, 33(2): 293-298. (FEI Cheng-wei, BAI Guang-chen, LI Xiaoying. Method of Rotor Vibration Fault Diagnosis from Process Power Spectrum Entropy and SVM[J]. Journal of Propulsion Technology, 2012, 33(2): 293-298.)
(  0) 0) |
| [4] |
郝如江, 褚福磊, 张新明. 基于小波变换的滚动轴承故障声发射信号提纯技术[J]. 振动与冲击, 2006, 8(25): 335-337. (  0) 0) |
| [5] |
Qu Y, He D, Yoon J, et al. Gearbox Tooth Cut Fault Diagnostics Using Acoustic Emission and Vibration Sensors-a Comparative Study[J]. Sensors, 2014, 14(1): 1372-1393.
(  0) 0) |
| [6] |
Hecke B V, Qu Y, He D, et al. A New Spectral Average-Based Bearing Fault Diagnostic Approach[J]. Journal of Failure Analysis and Prevention, 2014, 14(3): 354-362.
(  0) 0) |
| [7] |
Hecke B V, Yoon J, He D. Low Speed Bearing Fault Diagnosis Using Acoustic Emission Sensors[J]. Applied Acoustics, 2016, 105: 35-44. DOI:10.1016/j.apacoust.2015.10.028
(  0) 0) |
| [8] |
张斌, 王彤, 谷传纲, 等. 基于小波分析的湍流采样数据量缩减算法[J]. 上海交通大学学报, 2008, 42(11): 1896-1899. DOI:10.3321/j.issn:1006-2467.2008.11.032 (  0) 0) |
| [9] |
王实, 王晖, 高文. 格子机数据挖掘方法[J]. 计算机学报, 2000, 23(6): 570-575. (  0) 0) |
| [10] |
Robinson J C, Vanvoorhis B, Miller W. Machine Fault Detection Using Vibration Signal Peak Detector[P]. US: 5895857A, 1999. http://www.freepatentsonline.com/5895857.html
(  0) 0) |
| [11] |
Robinson J C, Piety K R. PeakVue Analysis, New Methodology for Bearing Fault Detection[J]. Sound and Vibration, 1996, 30: 22-25.
(  0) 0) |
| [12] |
Lin T R, Kim E, Tan A C. A Practical Signal Processing Approach for Condition Monitoring of Low Speed Machinery Using Peak-Hold-Down-Sample Algorithm[J]. Mechanical Systems and Signal Processing, 2013, 36(2): 256-270. DOI:10.1016/j.ymssp.2012.11.003
(  0) 0) |
| [13] |
刘国华. 声发射信号处理关键技术研究[D]. 杭州: 浙江大学, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1255622
(  0) 0) |
| [14] |
Dwyer R. Detection of non-Gaussian Signals by Frequency Domain Kurtosis Estimation[C]. USA: IEEE International Conference on Acoustics, Speech, and Signal Processing, 2003. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1172264
(  0) 0) |
| [15] |
Antoni J. Fast Computation of the Kurtogram for the Detection of Transient Faults[J]. Mechanical Systems and Signal Processing, 2007, 21(1): 108-124. DOI:10.1016/j.ymssp.2005.12.002
(  0) 0) |
| [16] |
Patil M S, Mathew J, Rajendrakumar P K, et al. A Theoretical Model to Predict the Effect of Localized Defect on Vibrations Associated with Ball Bearing[J]. International Journal of Mechanical Sciences, 2010, 52(9): 1193-1201. DOI:10.1016/j.ijmecsci.2010.05.005
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

