固体火箭冲压发动机具有结构简单、比冲高、维护方便以及可靠性良好等优点, 成为了新一代高性能导弹系统的首选。而在高空环境中, 发动机会因为燃料消耗过多使比冲骤降。为了使导弹能在大空域、较宽的马赫数范围内作战, 要求导弹的动力装置必须能够对燃气流量进行有效地调节[1, 2]。美国、德国、俄罗斯、日本等各个军事强国对燃气流量调节技术均产生了足够重视[3, 4]。我国各个航空航天研究所、西北工业大学、北京理工大学、哈尔滨工业大学等高校也对流量调节技术积极地展开研究[5]。控制燃气流量的方法主要有变喉面式、非壅塞式和固定流量式等[6]。国内外对变喉面式研究的较多, 控制效果也是最理想的, 其原理是通过机械传动机构调节燃气发生器的喉道面积进而改变推进剂的燃速, 达到控制流量的目的[7]。常用的机械阀门有柱塞阀、滑盘阀、锥阀、旋转调节阀。美国著名的丛林狼超声速掠海飞行靶弹通过电机带动柱塞阀改变喉部面积从而实现燃气流量的调节。欧洲MBDA研制的“流星”导弹应用滑盘阀来调节燃气流量, 最大调节比可达12:1。锥阀因自身的形状特征使其处于顺气流高速流, 并且抗沉淀性能与另外几种阀门相比有明显的优势, 因此被应用于俄罗斯的R-77M-PD超视距空空导弹, 调节比也能达到9:1。近年来日本的固冲发动机技术取得了较大的突破, 并采用了GAP推进剂和旋转调节阀控制燃气流量, 调节比为5:1[8~10]。
由于燃气发生器在工作过程中, 不可避免地会出现阀体烧蚀和燃气中固体颗粒沉积现象, 造成了喉部面积变化的非线性;推进剂不断的燃烧使得燃气发生器的自由容积不断变化, 造成了系统的时变性[11~13]。因被控对象具有很强的非线性和时变性, 压强闭环控制系统的算法设计起来相当复杂, 关于控制算法的文献更是少见。聂聆聪等曾提出模糊积分算法进行压力闭环控制[14], 使燃气发生器在长时间工作下仍具有良好的动态性能, 但因缺少比例系数自整定作用导致系统响应时间较长。刘源翔等设计了一种前馈自适应PID算法[15], 可以有效地克服系统参数摄动对控制的影响, 但该自适应控制器需通过反馈得到不易测量的自由容积, 难以应用到实际过程中。
经典的PID控制器因具有算法简单、稳点性强等优点被广泛应用于闭环控制系统, 但其最大的缺点是不适用于被控对象参数变化、非线性严重的系统[16]。这使得经典的PID控制器难以在燃气发生器上取得较好的控制效果。模糊控制以人的操作经验为基础, 并不依赖系统精确的数学模型, 将自然语言表述成控制策略, 成为了人类解决复杂系统的重要手段。然而模糊控制缺少积分作用, 在平衡点附近的稳态精度较差, 难以达到较高的控制精度[17]。为弥补上述缺陷, 本文提出模糊控制器和PI控制器相结合, 充分发挥各自的优点, 使控制效果更佳完美, 改善固体火箭冲压发动机的高空作战性能。
燃气流量调节系统具有强时变性的主要因素是喉道面积时变性和自由容积时变性。文中研究的系统采用的是钨铜合金制成的锥阀和喷管, 实验证明钨铜合金具有非常强的耐烧蚀性。因此忽略了喉道与锥阀的烧蚀带来的时变性对控制系统的影响, 着重讨论自由容积时变性的影响。
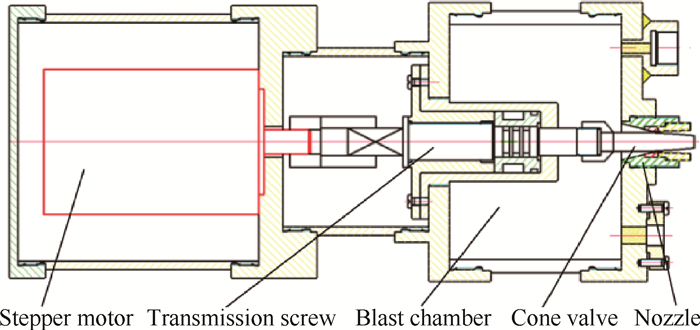
2 燃气发生器结构和系统数学模型 2.1 燃气发生器的结构及工作原理如图 1所示, 燃气发生器由执行机构、燃烧室、喷管组成。执行机构包括步进电机、联轴器、传动螺杆以及锥阀等。工作原理如下, 推进剂在燃烧室内迅速燃烧产生大量的燃气, 燃气通过带有锥阀调节的喷管排出;测压传感器实时采集燃气发生器内的压强并传递给控制器, 控制器根据理想压强与实际压强的偏差控制步进电机的转向和步数, 从而使传动螺杆和锥阀沿轴向移动, 让喷管的喉部面积发生变化, 燃气发生器内的压强亦随之改变。
|
Fig. 1 Flow adjustable gas generator |
若要对系统进行控制, 须先建立燃气发生器的数学模型。由质量守恒定律可知燃烧室内的燃气质量随时间的变化率
| $ {\dot m_{\rm{g}}} = {\dot m_{\rm{b}}}-\dot m $ | (1) |
| $ {\dot m_{\rm{g}}} = {\rm{d}}\left( {{\rho _{\rm{g}}}{V_{\rm{r}}}} \right)/{\rm{d}}t $ | (2) |
| $ {\dot m_{\rm{b}}} = {\rho _{\rm{p}}}{A_{{\rm{br}}}}\alpha p_{_{\rm{r}}}^n $ | (3) |
| $ \dot m = \frac{{{p_{\rm{r}}}{A_{{\rm{rt}}}}}}{{{C^*}}} $ | (4) |
根据上式推导出火箭发动机的零维内弹道微分方程为
| $ \frac{{{V_{\rm{r}}}}}{{R{T_{\rm{r}}}}}\frac{{{\rm{d}}{p_{\rm{r}}}}}{{{\rm{d}}t}} = {\rho _{\rm{p}}}{A_{{\rm{br}}}}\alpha p_{\rm{r}}^n-\frac{{{p_{\rm{r}}}{A_{{\rm{rt}}}}}}{{{C^*}}}-\frac{1}{{R{T_{\rm{r}}}}}{A_{{\rm{br}}}}\alpha p_{\rm{r}}^{n + 1} $ | (5) |
将式(5)在某一平衡点处进行小扰动线性化后得到燃气发生器内压强与喷管喉部面积之间的传递函数, 即系统的动态模型
| $ {G_{\rm{p}}}\left( s \right) = \frac{{\Delta p\left( s \right)}}{{\Delta {A_{{\rm{rt}}}}\left( s \right)}} = \frac{K}{{Ts + 1}} $ | (6) |
| $ \begin{array}{l} K = \frac{{{p_0}R{T_{\rm{r}}}}}{{{A_{{\rm{rt}}}}R{T_{\rm{r}}} + \left( {n + 1} \right){A_{{\rm{br}}}}\alpha p_0^n{C^*}-n{\rho _{\rm{p}}}{A_{{\rm{br}}}}\alpha p_0^{n-1}R{T_{\rm{r}}}{C^*}}}\\ T = \frac{{{V_{{\rm{r0}}}}{C^*}}}{{{A_{{\rm{rt}}}}RT + \left( {n + 1} \right){A_{{\rm{br}}}}\alpha p_0^n{C^*}-n{\rho _{\rm{p}}}{A_{{\rm{br}}}}\alpha p_0^{n - 1}R{T_{\rm{r}}}{C^*}}} \end{array} $ |
式中p0和Vr0分别为燃气发生器工作时的压强和自由容积;RTr为推进剂的火药力;Art为喷管的喉部面积;Abr为推进剂的燃面面积;ρg为燃气的密度;α和n分别为推进剂的燃速系数和燃速压强指数;ρp和C*分别为推进剂的密度和特征速度。
系统的执行机构是步进电机, 步进电机通过接收到的脉冲步数来改变喷管的喉部面积, 因此整个控制系统的传递函数是燃气发生器内的压强和步进电机步数之间的关系
| $ {G_n}\left( s \right) = \frac{{\Delta p\left( s \right)}}{{\Delta N\left( s \right)}} = \frac{{\Delta p\left( s \right)}}{{\Delta {A_{{\rm{rt}}}}\left( s \right)}} \cdot \frac{{\Delta {A_{{\rm{rt}}}}\left( s \right)}}{{\Delta S\left( s \right)}} \cdot \frac{{\Delta S\left( s \right)}}{{\Delta N\left( s \right)}} $ | (7) |
式中ΔArt(s)/ΔS(s)是平衡点处喉部面积和锥阀位移的传递函数, ΔS(s)/ΔN(s)是锥阀位移与步进电机步数的传递函数, 它们是根据锥阀与喷管的结构关系建立的数学模型得到。对于本文研究的系统, 在确定锥阀初始位置后, ΔArt(s) ΔN(s) = 8.959 × 10-9。故由式(7)可知本文研究的系统是一个增益和时间常数均随时间变化的一阶时变系统, 因此在设计控制器时不考虑微分作用, 只需要比例和积分作用即可满足控制要求。
3 Fuzzy-PI双模控制器设计 3.1 模糊控制器经典的PI控制器只适应于数学模型精确的特定系统, 随着被控对象的复杂性、非线性、滞后性和耦合性的增加, 想要使用PI控制器精确控制的可能性逐渐减小。因此对于本文研究的具有较强非线性和时变性的系统来说, 经典的PI控制器显然难以达到期望的效果。而模糊控制器在处理非线性和时变性问题上展现了优势, 它以模糊集合论, 模糊语言变量及模糊逻辑推理为基础, 模拟人的近似推理与决策过程, 具有很强的灵活性和适应性。
参考被控对象的数学模型, 设计一个二维输入一维输出的Mamdani型模糊控制器。以压强的偏差e和偏差变化率ec作为控制器的两个输入, 步进电机的步数u作为控制器的输出。输入和输出的模糊论域均为{-3, -2, -1, 0, 1, 2, 3}, 对应于语言变量的模糊子集为{NB, NM, NS, ZO, PS, PM, PB};输入输出变量的隶属函数均为三角形分布;采用面积中心法将输出量去模糊化;根据控制理论和经验得出如表 1所示的“IF-THEN”形式的模糊规则表。以If e=PB and ec=ZO THEN u=NB为例, 压强的偏差为正大且偏差变化率为零, 说明燃气发生器内压强远达不到理想值并且偏差没有减小的趋势, 则此时应加大控制量, 即u应该为负大(这里负代表步进电机反转)。模糊控制器的系统框图如图 2所示。控制器将偏差e和偏差变化率ec经过量化因子ke和kec量化为模糊变量, 经过模糊推理、模糊决策, 再经过比例因子ku去模糊化后得到输出值的清晰量, 使步进电机按照期望值改变喉部面积, 从而实现控制压强的目的。
|
|
Table 1 Fuzzy rules of u |

|
Fig. 2 Assumption diagram fuzzy controller |
模糊控制因缺少积分作用导致其稳态控制精度较差, 在平衡点附近存在控制盲区, 这是模糊控制器固有性质决定的。下面以离散论域上的模糊控制器为例, 证明在平衡点附近存在盲区[19]:
设偏差信号e的物理论域E=[-a, a], 模糊论域N= {-nj, -nj-1, ..., -1, 0, 1, ..., nj-1, nj}, 则量化因子k=nj/a, 将e的清晰值模糊化时, 在|k∙e|<nj情况下, n由取整公式n = int(|k∙e|+0.5)计算得到。如果在平衡点附近, 即n=0时, 此时的输入量e的值并不一定等于零。由此可知只要系统偏差量满足式(8)时, 模糊控制器就将系统偏差视为零, 因此模糊控制器无法消除绝对值为0.5a/nj时的稳态误差。
| $ \left| e \right| < 0.5/k = 0.5a/{n_j} $ | (8) |
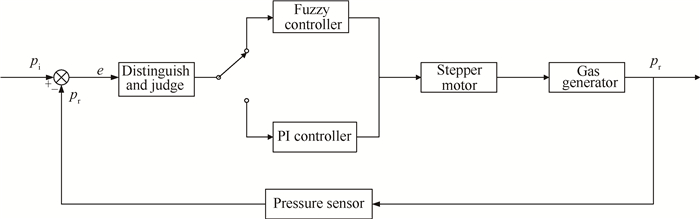
PI控制器具有积分作用, 可以消除系统的稳态误差, 提高控制精度。因此本文提出将模糊控制器与PI控制器相结合的策略, 让二者发挥各自的优点。控制器在工作时对偏差信号e进行识别判断, 在偏差大的情况下采用模糊控制器, 使系统的响应速度得到提高;在偏差小的情况下采用PI控制器, 消除模糊控制器的盲区, 使系统的稳态精度得到提高[20]。在模态切换过程中, 为了防止输出量的突变或波动对系统动态性能造成不利影响, 要求控制器的输出量必须连续, 即切换点处PI控制器的初始输出量必须等于模糊控制器的输出量。对于燃气发生器来说, 最大工作压强一般在10MPa以上, 通常认为偏差e的绝对值为2MPa以上均为大偏差, 因此本次研究将e的物理论域定义在[-2 × 106, 2 × 106], 那么由式(8)可得模态切换的阈值为0.333MPa, 即偏差值大于阈值时使用模糊控制, 不大于阈值时切换到PI控制。整个控制过程如图 3所示。
|
Fig. 3 Schematic diagram of Fuzzy-PI dual mode controller |
为了验证Fuzzy-PI双模控制器能够提高系统的控制精度、改善系统的动态性能, 针对控制系统时变性和非线性的特点, 在不同自由容积条件下对Fuzzy-PI控制与传统的PI控制算法下压强的时域动态响应进行仿真。工作点设计在平衡压强为12MPa处, 整定控制器的参数。
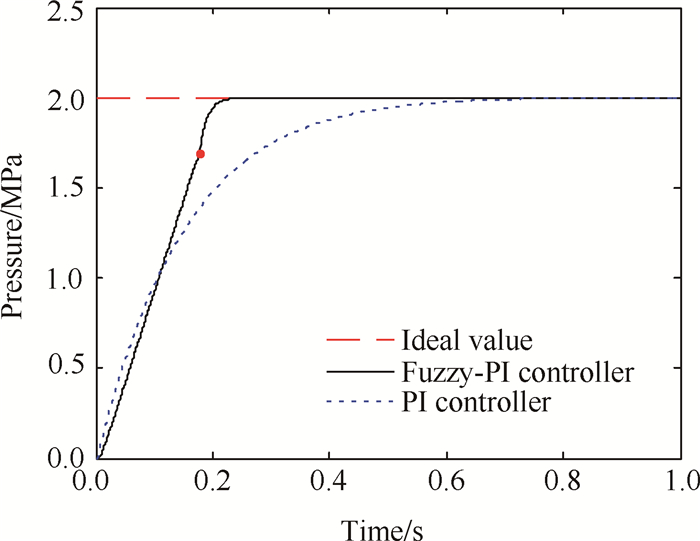
4.1 系统线性模型仿真当系统的自由容积恒定时, 两种控制器对压强的阶跃响应如图 4所示。容易看出, 两种控制器在1倍自由容积下均能使燃气发生器内的压强调节到理想值, 并且没有产生超调现象。然而Fuzzy-PI双模控制器较经典PI控制器在对阶跃信号的响应时间方面明显占优。另外, 在Fuzzy-PI控制的曲线上可以观察到一个明显的转折点, 此时达到偏差阈值, 由模糊控制转向PI控制, 系统输出逐渐上升到给定值并且无超调现象, 取得了较好的控制效果。
|
Fig. 4 Control results of two kinds of controller with no free volume change |
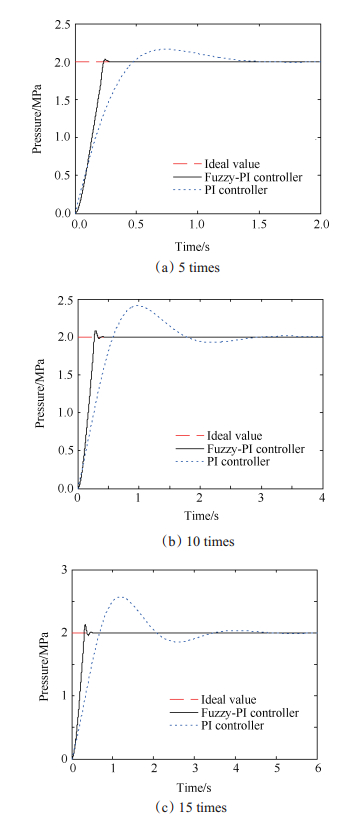
前面已经分析系统具有时变性的主要因素是自由容积的时变性, 因此下面针对自由容积变化时的系统进行仿真研究。图 5(a), (b), (c)分别为自由容积变化5倍, 10倍, 15倍时两种控制器对压强的阶跃响应。响应结果由表 2给出。从图中可以得到, 随着自由容积的增大, 两种控制算法均出现超调, 并且响应时间都有所增加。做进一步的对比分析, 在自由容积变化5~15倍时, 经典的PI控制器超调量的增加非常明显, 分别为8.15%, 20.65%和28.45%;而Fuzzy-PI双模控制器在控制超调量方面则显示了巨大优势, 三种自由容积下的超调量分别为1.50%, 4.35%和6.35%。在响应速度方面, 经典的PI控制器显得不尽人意, 最长的响应时间达到了4.89s, 显然不适合应用在需要较快响应速度的燃气发生器上;而Fuzzy-PI双模控制器可以将不同工况下的系统响应时间控制在1s之内, 展现出了该控制器响应速度快的优势。因此Fuzzy-PI双模控制对系统参数变化不太敏感, 体现出较强的鲁棒性。
|
Fig. 5 Control results of two kinds of controller with 5~15 times free volume change |
|
|
表 2 Response result with different free volume |
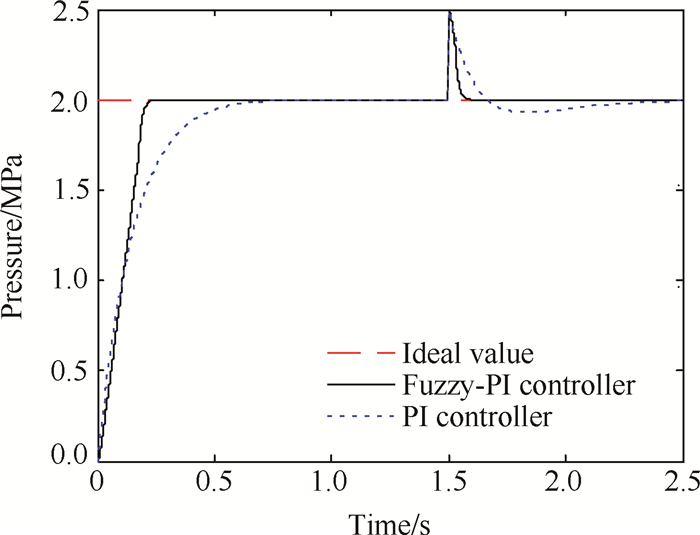
在燃气发生器实际的工作过程中, 有时会因为推进剂的燃烧不充分导致燃烧产物中附带大量的高温固体颗粒, 在喷管的喉道处沉积造成喷管堵塞, 使燃气发生器内压强突然升高, 造成了系统的不稳定。为了比较Fuzzy-PI双模控制器和经典的PI控制器对干扰信号的抵抗能力, 模拟在自由容积恒定的工况下工作时间达到1.5s时, 燃气中附带某些颗粒较大的固体, 将喷管部分堵住, 使燃气发生器内压强迅速上升的情况, 其结果如图 6所示。通过比较可以发现, Fuzzy-PI双模控制器对干扰信号的调整时间比经典的PI控制器短得多, 说明Fuzzy-PI双模控制器的抗干扰能力更强一些。
|
Fig. 6 Control results of two kinds of controller with disturbance |
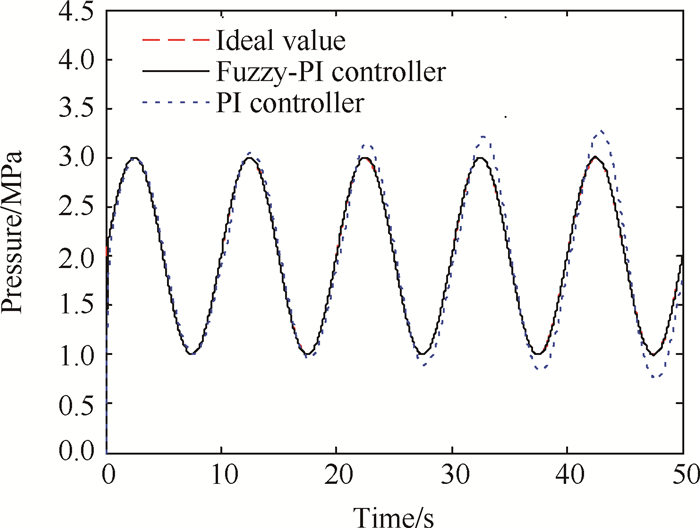
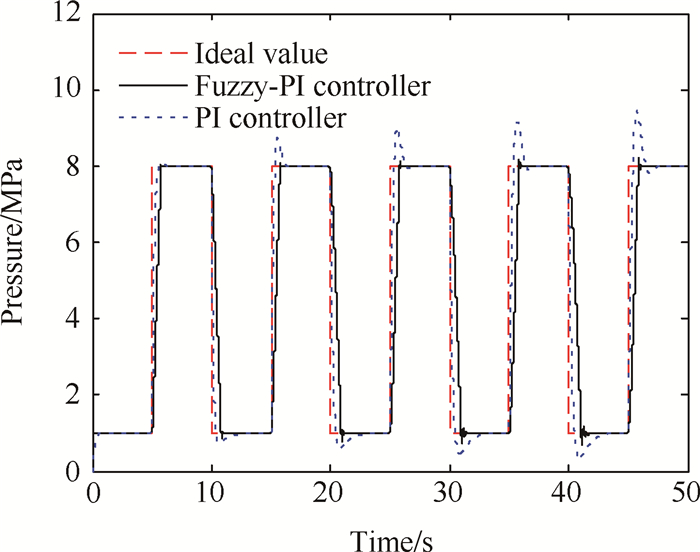
以上分析均针对的是燃气流量调节控制系统的线性模型, 考虑到系统具有较强非线性的特点, 系统参数会随着推进剂燃烧而不断变化, 故根据式(5)对系统在长时间工作下的非线性模型进行仿真。压力指令信号分别为正弦波和方波, 响应结果如图 7, 8所示。可以看出, Fuzzy-PI双模控制器跟随正弦信号的能力依旧远远优于PI控制器, 滞后时间和超调量非常小, 表明该控制器适用在固冲发动机飞行中需要得到连续可调推力的情况。由图 8可知随着工作时间的逐渐增大, Fuzzy-PI双模控制器的超调量有所增大, 但与PI控制器相比仍具有很大优势, 且在方波指令作用下, Fuzzy-PI双模控制器反复切换模态, 其控制效果并没有降低, 证明Fuzzy-PI双模控制器稳定且可行。
|
Fig. 7 Control results of two kinds of controller with sine instruction signal |
|
Fig. 8 Control results of two kinds of controller with square wave instruction signal |
(1)流量可调的燃气发生器经过数学建模得到的是参数随时间变化的一阶时变性系统, 因此可不考虑微分环节, 使用PI控制器对系统进行控制。
(2)基于Fuzzy-PI双模控制器的压强闭环控制系统与经典PI控制器的系统相比, 在不同工况下依然保持着良好的动态性能。当自由容积变化1~15倍时, 超调量能被控制在6.35%以下, 相比经典PI控制器减少了约4.5倍;响应时间也均在1s以内, 最高可缩短4.11s。并且, 该控制器的鲁棒性及抗干扰能力相对较强, 非常适合解决燃气发生器由非线性和时变性带来的不易精确控制的难题。
模糊控制器的关键在于模糊规则表的建立, 而模糊规则毕竟是由人的经验确定的, 会带有主观性。为了弥补本文的不足, 还需要通过大量的实验总结数据, 修改模糊规则表, 或考虑使用遗传算法对模糊规则进行优化, 使控制精度进一步提高。
| [1] |
BAO W, LI B, CHANG J. Switching Control of Thrust Regulation and Inlet Buzz Protection for Ducted Rocket[J]. Acta Astronautica, 2010, 67(7-8): 764-773. DOI:10.1016/j.actaastro.2010.04.022
(  0) 0) |
| [2] |
Ronald S Fry. A Century of Ramjet Propulsion Technology Evolution[J]. Journal of Propulsion and Power, 2004, 20(1): 27-57. DOI:10.2514/1.9178
(  0) 0) |
| [3] |
霍东兴, 闫大庆, 高波. 可变流量固体冲压发动机技术研究进展与展望[J]. 固体火箭技术, 2017, 40(1): 7-15. (  0) 0) |
| [4] |
张玲翔. 美国弹用冲压发动机技术的进展[J]. 飞航导弹, 1998(11): 39-44. (  0) 0) |
| [5] |
龚晰, 何保成, 刘志明. 固体火箭冲压发动机发展与流量调节现状[J]. 飞航导弹, 2015(2): 74-78. (  0) 0) |
| [6] |
牛文玉. 燃气流量可调的固体火箭冲压发动机控制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10213-2011015943.htm
(  0) 0) |
| [7] |
马立坤. 燃气流量可调固体火箭冲压发动机动态响应过程研究[D]. 长沙: 国防科学技术大学, 2011. http://cdmd.cnki.com.cn/article/cdmd-90002-1012020511.htm
(  0) 0) |
| [8] |
周建军. 固体火箭冲压发动机燃气流量调节技术与实验研究[J]. 弹箭与制导学报, 2005, 25(4): 558-560. (  0) 0) |
| [9] |
王起飞, 苗永强. 流星空空导弹战术技术性能分析[J]. 航空兵器, 2004(5): 5-8. (  0) 0) |
| [10] |
杨石林. 可变燃气流量固冲发动机控制系统研究进展[C]. 西安: 中国航天第三专业信息网第三十七届技术交流会暨第一届空天动力联合会议, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10007-1015801412.htm
(  0) 0) |
| [11] |
何勇攀, 陈玉春, 于守志, 等. 固体火箭冲压发动机燃气发生器动态特性影响分析[J]. 航空动力学报, 2017, 32(1): 227-232. (  0) 0) |
| [12] |
聂聆聪, 张政伟, 李岩. 燃气发生器压力闭环波动描述函数分析方法研究[J]. 推进技术, 2016, 37(3): 540-545. (NIE Ling-cong, ZHANG Zheng-wei, LI Yan. Research of Describing Function Method on Gas Generator Pressure Closed-Loop Oscillation[J]. Journal of Propulsion Technology, 2016, 37(3): 540-545.)
(  0) 0) |
| [13] |
刘源翔, 聂聆聪, 张皎, 等. 基于线性自抗扰控制器的燃气流量可调发生器压强控制算法研究[J]. 推进技术, 2015, 36(12): 1768-1773. (LIU Yuanxiang, NIE Ling-cong, ZHANG Jiao, et al. Research on Pressure Control Algorithm of a Flow Adjustable Gas Generator Based on Linear Active Disturbance Rejection Control[J]. Journal of Propulsion Technology, 2015, 36(12): 1768-1773.)
(  0) 0) |
| [14] |
聂聆聪, 刘志明, 刘源翔. 流量可调燃气发生器压力闭环模糊控制算法[J]. 推进技术, 2013, 34(4). (NIE Ling-cong, LIU Zhi-ming, LIU Yuan-xiang. Pressure Close Loop Fuzzy Control Method of a Flow Adjustable Gas Generator[J]. Journal of Propulsion Technology, 2013, 34(4).)
(  0) 0) |
| [15] |
刘源翔, 姚晓先, 聂聆聪, 等. 一种流量可调燃气发生器压强控制算法的研究[J]. 固体火箭技术, 2014, 37(1). (  0) 0) |
| [16] |
杨劲松. Fuzzy-PI双模模糊张力控制系统仿真[J]. 计算机仿真, 2010, 27(6): 216-220. (  0) 0) |
| [17] |
席爱民. 模糊控制技术[M]. 西安: 西安电子科技大学出版社, 2008, 186-190.
(  0) 0) |
| [18] |
武晓松, 陈军, 王栋. 固体火箭发动机原理[M]. 北京: 兵器工业出版社, 2010, 236-239.
(  0) 0) |
| [19] |
石辛民, 郝整清. 模糊控制及其MATLAB仿真[M]. 北京: 清华大学出版社, 2008, 121-123.
(  0) 0) |
| [20] |
张省伟, 林辉. 一种模糊-PI双模控制系统的仿真与设计[J]. 电子设计工程, 2011, 19(2): 37-39. (  0) 0) |
 2018, Vol. 39
2018, Vol. 39

