转子是水轮机、汽轮机、航空发动机等大型旋转机械的关键组件,作为重要的负载与传动结构,其运行状态直接影响整个系统的安全性与稳定性。近些年,旋转机械的复杂程度与自动化程度不断提高,增大了转子故障发生概率,探究可行的转子故障诊断方法具有重要的工程意义[1]。
常见的转子故障类型主要包括转静碰摩、油膜涡动、油膜振荡、不对中、不平衡、裂纹等。已有研究表明转子故障振动信号通常为多分量信号,信号成分主要包括现场噪声、转频及转频谐波分量[2, 3]。不同故障模式的转子振动信号呈现不同的故障特征。因而基于振动信号分析的转子故障诊断方法受到了国内外学者的广泛关注,并因其有效性而被广泛采纳[4]。目前对于转子故障诊断主要包括以下几个途径:(1)恒定转速下的高信噪比转子故障振动信号可直接由幅值谱方法提取谐波频率[5]。(2)通过基于键相信号的计算阶比跟踪方法处理变转速转子故障诊断问题[6]。(3)利用STFT(Short time Fourier transform)、小波变换、WVD(Wigner-valle distribution)、希尔伯特黄变换(Hilbert Huang transform,HHT)等时频分析方检测转子振动信号各频率成分随时间的变化,依据时频谱中的故障特征信息判断转子的故障类型[7, 8]。但已有的转子故障诊断方法存在一定不足。如:幅值谱分析方法不适于分析信噪比较低的转子故障信号,且分析变转速转子故障振动信号时会产生“频谱涂抹”问题。基于键相信号的计算阶比跟踪方法需要安装键相测量装置,增加了故障诊断成本,且易受现场条件制约。诸多时频分析方法中,STFT时频窗固定,小波分析效果受母函数选取影响很大,WVD需克服交叉项干扰,HHT通过经验模态分解(Empirical mode decomposition,EMD)方法将原信号分解成各个本征模态函数(Intrinsic mode function,IMF)分量,并利用希尔伯特变换计算IMF分量的瞬时频率,具有较强的自适应性,但EMD算法存在模态混叠、包络拟合失真等问题,无法保证分解精度[9]。为了改善EMD方法的分解效果,相关学者在其基础上提出了集成经验模态分解[10]、局部均值分解[11]、本征时间尺度分解[12]、局部特征尺度分解[13]等信号分解方法。但此类方法都是基于极值点拟合的递归分离方法,当信噪比较低时,分解效果较差。近些年,形态分量分析[14]、经验小波变换[15]、变分模态分解[16]等非递归式的信号分解方法也被提出,虽然在一定程度上抑制了噪声影响,遗憾的是形态分量分析、经验小波变换和变分模态分解都属于参数化分解方法,分解过程中需要解决复杂的参数选取问题。
实际工作过程中,转子需要面对升、降速等变转速工况,此时的转子振动信号表现出强烈的非平稳特性,故障特征难以被识别。为解决变转速转子故障诊断这一难点问题,笔者将一种新的无参数自适应信号分解方法—奇异谱分解(Singular spectrum decomposition,SSD)引入到转子振动信号分析中,以提高对转子振动信号的分解精度。同时受HHT原理启发,将SSD与希尔伯特变换(Hilbert transform,HT)结合,利用SSD-HT时频谱提取转子的时频故障信息。最后融合适于分析变转速信号的阶比跟踪方法,提出基于SSD-HT的时频阶比跟踪故障诊断方法,在不使用键相测量装置的条件下,精确提取变转速转子故障振动信号的阶次特征。应用仿真分析与实验分析验证了所述方法的有效性。
2 奇异谱分解原理简介SSD是一种可将多分量非平稳信号自适应分解为一系列由高频到低频次序排列的奇异谱分量(Singular spectrum component,SSC)的新的分解方法。算法实现过程如下[17]。
(1)构造轨迹矩阵。对于数据长度为N的时间序列x(n),设定嵌入维数为M,可构建出一个M×N的矩阵X,矩阵的第i行为xi =[x(i), …, x(N), x(1), …, x(i-1)],分别取i=1,…,M,即矩阵X =[x1T, x2T, …, xMT]T。以x(n) ={1, 2, 3, 4, 5}为例,若M取3,则构造的矩阵X为
| $ \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} 1&2&3&4&5\\ 2&3&4&5&1\\ 3&4&5&1&2 \end{array}} \right] $ | (1) |
式中X的虚线部分为奇异谱分析中的轨迹矩阵。SSD在传统轨迹矩阵基础上提出一种新的轨迹矩阵,利用轨迹矩阵对角线平均实现分量提取,将X右下方3个元素移至左上方,形成新的矩阵
| $ \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {}&{}&1&{}&{}\\ {}&1&2&{}&{}\\ 1&2&3&4&5\\ 2&3&4&5&{}\\ 3&4&5&{}&{} \end{array}} \right] $ | (2) |
此矩阵的交叉对角线的元素相同且数目相等,拾取X的虚线部分构成SSD的新轨迹矩阵。
(2)自适应确定嵌入维数M的大小。嵌入维数M的选取对于分析效果具有重要影响,为此SSD方法根据文献[18],采用一种自适应准则来选取第j次迭代时采用的M的数值,从而克服传统SSA方法依据经验选取M的缺陷。令第j次迭代时残余分量rj(n)的表达式为
| $ {\mathit{\boldsymbol{r}}_j}\left( n \right) = x\left( n \right) - \sum\nolimits_{k = 1}^{j - 1} {{\mathit{\boldsymbol{r}}_k}\left( n \right)} ,\;\;\;{r_0}\left( n \right) = x\left( n \right) $ | (3) |
首先,计算第rj(n)的功率谱密度(Power spectral density,PSD)。然后,找出PSD的最大峰值频率fmax,第1次迭代过程中,若fmax/fs < 10-3(其中fs为采样频率,10-3为设定阈值),则残余项视作一个大趋势分1136推进技术2018年量,将M设置为N/3。否则,需要多次迭代,嵌入维数设置成M=1.2(fs/fmax)。
(3)按高频至低频的顺序依次重构第j个信号分量。具体步骤如下:第1次迭代中,若检测出存在大趋势项,则利用第1个左右特征向量得到g(1)(n),这样X1 = σ1u1v1T,g(1)(n)通过对X1进行对角平均获得。反之,迭代次数j>1,g(j)(n)作为一个待提取的具有物理意义的时间尺度分量,其频率成分集中于频带[fmax-Δf, fmax + Δf]上,这里Δf表示余量信号rj(n)的PSD主峰带宽的一半。将此频带内所有具有突出谱峰并对所选模态分量的主峰能量贡献最大的左特征向量建立一个子集Ij(Ij ={i1, …, ip}),然后对应的信号分量通过矩阵XIj= Xi1+… + Xip对角平均获得。
为实现Δf的精确估计,通过高斯函数叠加方式定义一个谱模型来描述PSD的轮廓。此模型由三个高斯函数叠加而成,且每个高斯函数代表一个谱峰,即
| $ \gamma \left( {f,\mathit{\boldsymbol{\theta }}} \right) = \sum\limits_{i = 1}^3 {{A_i}\exp \left( { - \frac{{{{\left( {f - {u_i}} \right)}^2}}}{{2\sigma _i^2}}} \right)} $ | (4) |
式中Ai,ui,σi分别表示高斯函数的幅值、位置和带宽。θ =[A, σ]T为参数向量,其中A =[A1, A2, A3],σ =[σ1, σ2, σ3]。第1个高斯函用于数描述主谱峰,第2个高斯函数用于描述次谱峰,第3个高斯函数用于描述两个主要谱峰之间的部分。因此模型限定各高斯函数的位置中心
| $ {u_1} = {f_{\max }},\;\;{u_2} = {f_2},\;\;{u_3} = \left( {{f_{\max }} + {f_2}} \right)/2 $ | (5) |
模型参数通过所观测PSD的模型加权最小二乘拟合获得,设定模型参数初始值
| $ \left\{ \begin{array}{l} A_1^{\left( 0 \right)} = \frac{1}{2}{\rm{PSD}}\left( {{f_{\max }}} \right),\sigma _1^{\left( 0 \right)} = f:{\rm{PSD}}\left( f \right) = \frac{2}{3}{\rm{PSD}}\left( {{f_{\max }}} \right)\\ A_2^{\left( 0 \right)} = \frac{1}{2}{\rm{PSD}}\left( {{f_2}} \right),\sigma _2^{\left( 0 \right)} = f:{\rm{PSD}}\left( f \right) = \frac{2}{3}{\rm{PSD}}\left( {{f_{\max }}} \right)\\ A_3^{\left( 0 \right)} = \frac{1}{4}{\rm{PSD}}\left( {{f_3}} \right),\sigma _3^{\left( 0 \right)} = 4\left| {{f_{\max }} - {f_2}} \right| \end{array} \right. $ | (6) |
采用Levenberg-Marquardt优化算法确定模型参数的最优值。对于给定σ1的估计值,Δf = 2.5σ1,选择系数2.5可使得主峰带宽包含主峰99%左右的面积,同时排除基线噪声。为了获得有效的时间尺度分量,每个分量提取过程中通常需要进行多次迭代,为保证算法的收敛性,利用尺度因子
| $ \hat a = \mathop {\min }\limits_a \left\| {{\mathit{\boldsymbol{v}}^{\left( j \right)}}\left( n \right) - a{{\mathit{\boldsymbol{\tilde g}}}^{\left( j \right)}}\left( n \right)} \right\|_2^2 $ | (7) |
式中
(4)设定分解停止条件。分解过程中得到估计信号分量
| $ NMS{E^{\left( j \right)}} = \frac{{\sum\nolimits_{i = 1}^N {{{\left( {{\mathit{\boldsymbol{r}}^{\left( {j + 1} \right)}}\left( i \right)} \right)}^2}} }}{{\sum\nolimits_{i = 1}^N {{{\left( {\mathit{\boldsymbol{x}}\left( i \right)} \right)}^2}} }} $ | (8) |
当归一化均方差小于给定阈值(这里设定为1%)时,分解过程结束。否则,余量信号将作为原信号重复上述分解过程,直到满足分解停止条件,最后的分解结果表示为
| $ \mathit{\boldsymbol{x}}\left( n \right) = \sum\limits_{k = 1}^m {{{\mathit{\boldsymbol{\tilde g}}}^{\left( k \right)}}\left( n \right)} + {\mathit{\boldsymbol{r}}^{\left( {m + 1} \right)}}\left( n \right) $ | (9) |
式中m表示奇异谱分量个数。
SSD的数学表达式推导及算法收敛证明详见文献[17]。
3 基于SSD-HT的时频阶比跟踪对转子故障振动信号进行奇异谱分解可得到若干个蕴含故障信息的奇异谱分量,其优越的信号分解能力,使之具备了时频分析的基础。对每个奇异谱分量SSCi(t)进行希尔伯特变换[19]
| $ H\left[ {SS{C_i}\left( t \right)} \right] = \frac{1}{{\rm{ \mathsf{ π} }}}\int_{ - \infty }^{ + \infty } {\frac{{SS{C_i}\left( \tau \right)}}{{t - \tau }}{\rm{d}}\tau } $ | (10) |
则SSCi(t)的解析信号可表示为
| $ {z_i}\left( t \right) = SS{C_i}\left( t \right) + {\rm{j}}H\left[ {SS{C_i}\left( t \right)} \right] = {a_i}\left( t \right){{\rm{e}}^{{\rm{j}}{\phi _i}\left( t \right)}} $ | (11) |
式中ai(t),φi(t)分别为SSCi(t)的幅值函数与相位函数,记为
| $ {a_i}\left( t \right) = \sqrt {SSC_i^2\left( t \right) + {H^2}\left[ {SS{C_i}\left( t \right)} \right]} $ | (12) |
| $ {\phi _i}\left( t \right) = \arctan \frac{{H\left[ {SS{C_i}\left( t \right)} \right]}}{{SS{C_i}\left( t \right)}} $ | (13) |
对相位函数利用式(14)计算SSCi(t)的瞬时频率
| $ {\omega _i}\left( t \right) = \frac{{{\rm{d}}{\phi _i}\left( t \right)}}{{{\rm{d}}t}} $ | (14) |
根据各个奇异谱分量的瞬时幅值和瞬时频率信息可得到完整的时频表示,即SSD-HT时频谱
| $ H\left( {\omega ,t} \right) = \mathit{Re}\sum\limits_{i = 1}^k {{a_i}\left( t \right)\exp \left( {{\rm{j}}\int {{\omega _i}\left( t \right){\rm{d}}t} } \right)} $ | (15) |
转子故障振动信号一般由转子转频及其谐波分量构成,虽然变转速条件下的各频率成分随时间变化,但同转频的阶次比不变。求得转子故障信号的时频分布以后,可根据现场运行状况和预知信息识别出转频fr(t),并利用转频信息对原信号进行阶比跟踪分析,提取转子故障信号的特征阶次,具体步骤如下[20]。
(1)根据转频信息求得累积转角,并产生相应的键向时标
| $ 2{\rm{ \mathsf{ π} }}\int_{{T_0}}^{{T_n}} {{f_r}\left( t \right){\rm{d}}t} = n\Delta \theta \;\;\;\;\;n = 1,2,3 \cdots $ | (16) |
式中n表示采样时刻序列号,Δθ为等角度增量,且Δθ = 2π/Omax,Omax为最大分析阶比。旋转机械升、降速运行阶段,fr(t)通常满足光滑连续条件,在较小范围内可用多项式进行高精度逼近,表达式为fr(t) =at2 + bt + c,代入式(16)得
| $ \frac{{aT_n^3}}{3} + \frac{{bT_n^2}}{2} + c{T_n} = \frac{n}{{2{O_{\max }}}} - \frac{{aT_0^3}}{3} + \frac{{bT_0^2}}{2} + c{T_0} $ | (17) |
求出次方程的数值解,便可得到等角度采样键相时标Tn(n=1,2,3…,N),N为角域重采样信号长度。
(2)利用键相时标Tn对原信号运用Langrange插值求得角域重采样信号y(Tn)
| $ y\left( {{T_n}} \right) = x\left( {{t_i}} \right) + \frac{{x\left( {{t_{i + 1}}} \right) - x\left( {{t_i}} \right)}}{{{t_{i + 1}} - {t_i}}}\left( {{T_n} - {t_i}} \right)\;\;\;\left( {{t_i} \le {T_n} < {t_{i + 1}}} \right) $ | (18) |
(3)对角域重采样信号y(Tn)进行傅里叶变换得到阶次谱,识别出各分量相对于转频的阶次,从而对故障模式进行判别。
4 仿真分析通过一个3分量的时变非平稳信号x(t)进行仿真验证,其表达式为
| $ \left\{ \begin{array}{l} x\left( t \right) = {x_1}\left( t \right) + {x_2}\left( t \right) + n\left( t \right)\\ {x_1}\left( t \right) = \cos \left[ {2{\rm{ \mathsf{ π} }}{f_r}\left( t \right)t} \right]\\ {x_2}\left( t \right) = 0.5\cos \left[ {6{\rm{ \mathsf{ π} }}{f_r}\left( t \right)t} \right]\\ n\left( t \right) = 0.15{\rm{rand}}\left( {1,N} \right) \end{array} \right. $ | (19) |
式中x1(t)的瞬时频率fr(t) =20+40t,x2(t)的瞬时频率为3fr(t),即原信号包含转频及转频3倍频谐波,n(t)模拟随机噪声信号。
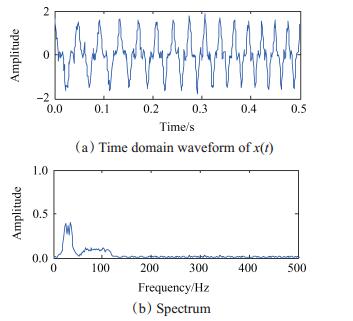
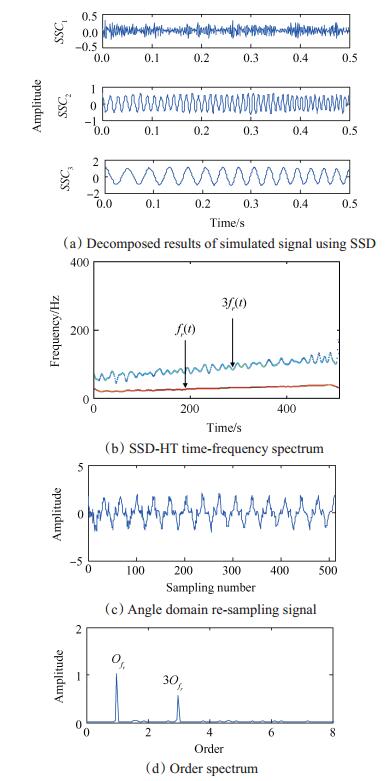
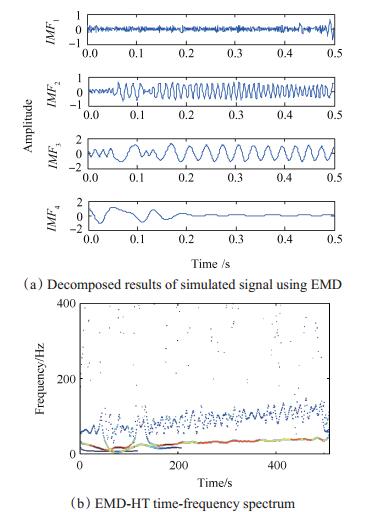
图 1为仿真信号的时域波形与幅值谱。由于仿真信号各分量的瞬时频率随时间变化,所以幅值谱出现了频率模糊现象,无法反映原信号的频率成分。对仿真信号进行SSD分解,产生3个奇异谱分量如图 2(a)所示,其中SSC1为噪声分量,SSC2和SSC3为x(t)的有效奇异谱分量,分别对应原信号的x2(t)和x1(t)。对SSC2和SSC3进行希尔伯特变换,得到图 2(b)所示的SSD-HT时频谱,该谱图反映了x(t)的频率成分随时间变化情况。根据时频谱中的转频fr(t),进行阶比跟踪分析得到角域重采样信号及其阶次谱,如2(c)、(d)。阶次谱显示的阶次分别为转频的1倍频和3倍频,成功提取了仿真信号的阶次成分。图 3为仿真信号的希尔伯特黄变换对比分析结果,EMD方法将仿真信号分解为4个IMF分量,其中IMF2和IMF3为仿真信号的有用分量,但二者都出现了频率混叠现象,对各本征模态分量进行希尔伯特变换得到的EMD-HT时频谱也说明各IMF分量存在频率混叠现象,HHT方法未能实现仿真信号的分量分解与时频信息提取。仿真分析表明SSD方法对于时变非平稳信号具备更强的分解能力,本文方法可有效提取时变非平稳信号的阶次特征。
|
Fig. 1 Time domain waveform and spectrum of x(t) |
|
Fig. 2 Analysis results of simulated signal using the proposed method |
|
Fig. 3 Analysis results of simulated signal using the HHT method |
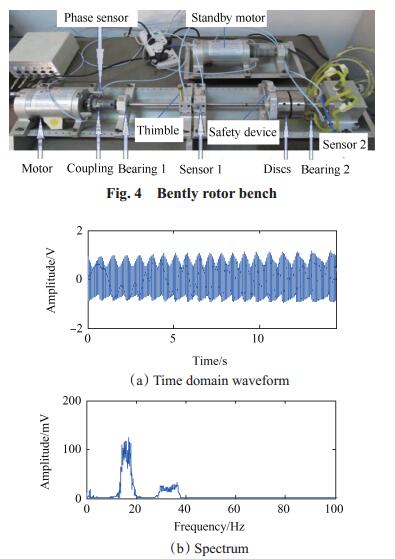
在图 4所示的Bently转子故障模拟实验台上模拟了变转速条件下的油膜涡动和碰摩故障。实验台由电机、联轴器、转子圆盘系统、滑动轴承、转速调节控制器、供油系统、支架等部件构成。电机输出端处安装一个键相传感器为转速调节器提供反馈信号,通过转速调节控制器可实现0~10kr/min转速范围内的无级调速。在滑动轴承与转轴末端分别装有一对电涡流传感器对振动信号进行测量,并通过Zonic-Book/618E信号采集系统采集数据,采样频率fs = 1.28kHz。

|
Fig. 4 Bently rotor bench |
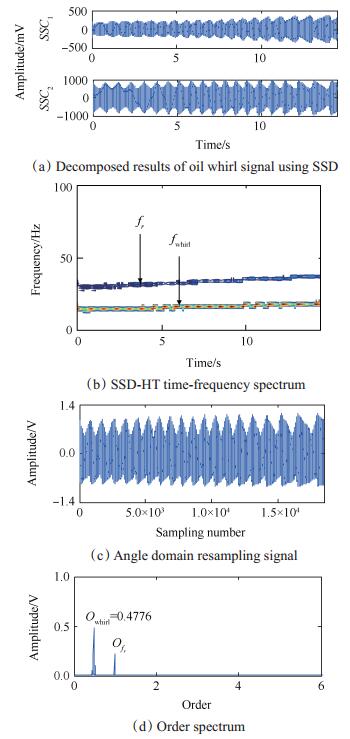
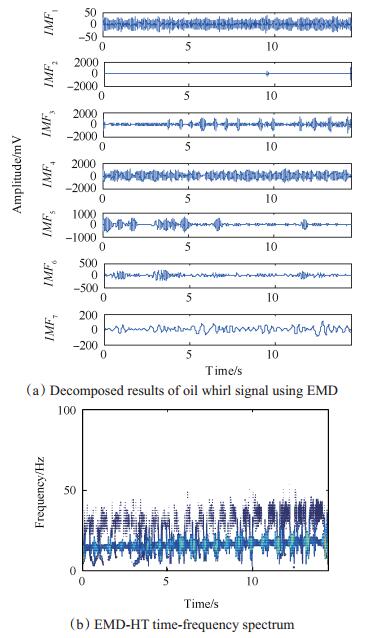
由转子动力学原理可知转子转速在运行至临界转速附近时会发生油膜失稳故障。前期油膜失稳故障表现为油膜涡动,振动信号含转频及涡动频率,因涡动频率fwhirl约等于1/2fr,油膜涡动又称半频涡动。当转速继续升高至2倍临界转速以上时,油膜涡动会演变为油膜振荡,此时转子系统振幅骤增,破坏性极大,因而对于早期油膜涡动故障诊断具有重要现实意义。本实验台一阶临界转速在1.9kr/min左右,油膜涡动故障模拟实验中转速由零逐渐升高,但最高转速不超过3.8kr/min。取1.8~2.4kr/min升速过程的转子径向振动信号进行分析,此段信号的时域波形及幅值谱如图 5所示。幅值谱由于发生严重的频率模糊现象,不能识别油膜涡动的频率特征。对1138推进技术2018年故障信号进行奇异谱分解,产生两个奇异谱分量,如图 6(a)所示。图 6(b)为SSD-HT时频谱,谱图中存在两个频率成分,分别为转频和涡动频率。利用转频信息对油膜涡动故障信号进行阶比跟踪分析,得到角域重采样信号及其阶次谱,分别如图 6(c)、(d)所示。阶次谱在0.4776和1这两个阶次处具有峰值,分别对应涡动频率阶次与转频自身阶次,本文方法准确识别出油膜涡动故障特征。图 7为HHT方法的对比分析结果,应用EMD方法对油膜涡动信号进行分解后产生了很多无意义分量,并且频率混叠问题严重,EMD-HT时频谱的频率成分存在交叉现象,无法精确识故障特征。
|
Fig. 5 Time domain waveform and spectrum of oil whirl fault signal |
|
Fig. 6 Analysis results of oil whirl signal using the proposed method |
|
Fig. 7 Analysis results of oil whirl signal using the HHT method |
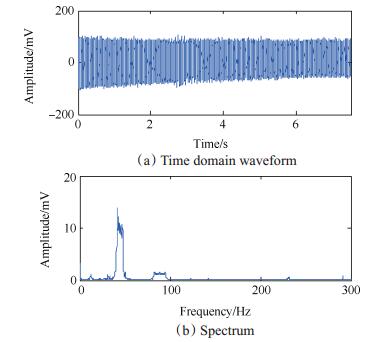
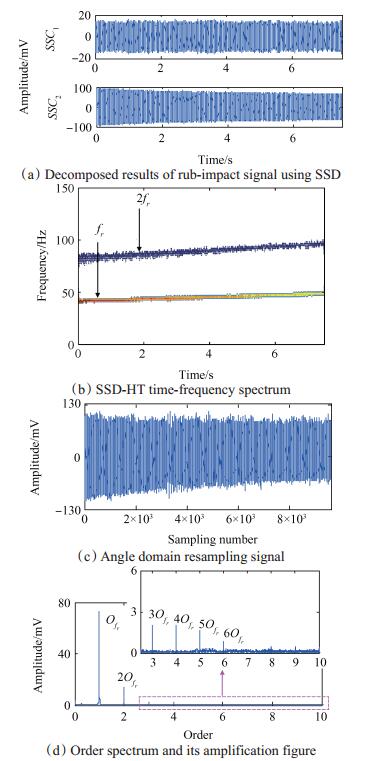
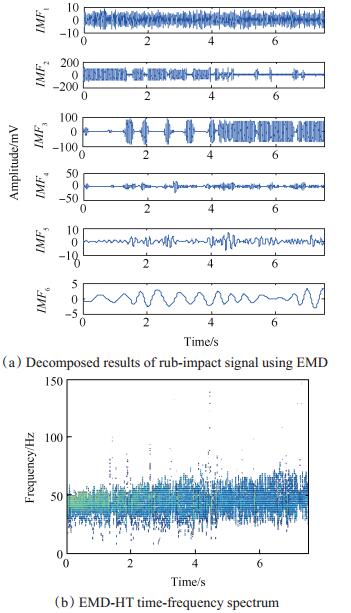
转子在运行过程中,动子与静子之间可能相互接触,发生碰摩故障。已有文献中的研究表明:恒定转速下,转子发生碰摩故障时,振动信号的幅值谱特征频率由转频及其倍频组成。变转速条件下碰摩故障信号的阶次成分则表现为转频1阶及其倍数阶次。本文通过变转速碰摩实验分析,进一步来验证所述方法的有效性。图 8为碰摩发生示意图,转子运行过程中通过调节铜棒与转盘之间的距离控制碰摩的发生。截取2.4~3.0kr/min升速阶段的转子碰摩信号进行分析,图 9为此段信号的时域波形及幅值谱,幅值谱方法因频率模糊问题对于变转速碰摩故障信号分析失效。图 10(a)、(b)分别为碰摩故障信号的SSD分量图、SSD-HT时频谱,可知两个分量分别为转频信号及其2倍频谐波。利用转频信息对碰摩故障信号进行阶比分析,得到角域重采样信号如图 10(c)所示。10(d)为角域重采样信号的阶次谱及其局部放大图,在转频的1~6倍频阶次处具有突出峰值,充分说明转子发生碰摩故障。由于转频的3~6倍频谐波分量幅值较小,原信号经SSD分析时未能成功分离出这些信号分量,通过阶比分析很好地弥补了SSD的缺陷。图 11为HHT方法的对比分析结果,HHT方法未能实现变转速碰摩故障信号的分量分离与时频特征提取。

|
Fig. 8 Rubbing diagram |
|
Fig. 9 Time domain waveform and spectrum of rub-impact signal |
|
Fig. 10 Analysis results of rub-impact signal using the proposed method |
|
Fig. 11 Analysis results of rub-impact signal using the HHT method |
传统的故障诊断方法难以提取转子在变转速工况下的故障特征,为此本文提出了基于SSD-HT时频阶比跟踪的转子故障诊断方法,得到以下结论:
(1)SSD方法可克服EMD方法的频率混叠问题,实现对转子故障振动信号各信号分量的分离。
(2)SSD-HT的时频分析精度高于HHT方法,通过SSD-HT时频谱可提取转子故障振动信号的时频信息。
(3)本文方法能够在无键相测量装置条件下,精确提取变转速工况转子故障振动信号的特征阶次,在保证分析可靠性的同时降低了故障诊断成本。
| [1] |
Aijun Hu, Lanlan Hou, Ling Xiang. Dynamic Simulation and Experimental Study of An Asymmetric DoubleDisk Rotor-Bearing System with Rub-Impact and OilFilm Instability[J]. Nonlinear Dynamics, 2016, 84: 641-659. DOI:10.1007/s11071-015-2513-3
(  0) 0) |
| [2] |
费成巍, 白光忱. 基于WCFSE-FSVM的转子振动故障诊断方法[J]. 推进技术, 2013, 34(9): 1266-1271. (FEI Cheng-wei, BAI Guang-chen. Rotor Vibration Fault Diagnosis Method Based on WCFSE-FSVM[J]. Journal of Propulsion Technology, 2013, 34(9): 1266-1271.)
(  0) 0) |
| [3] |
陈向民, 于德介, 李蓉. 基于信号共振稀疏分解与重分配小波尺度谱的转子碰摩故障诊断方法[J]. 振动与冲击, 2013, 32(13): 27-33. DOI:10.3969/j.issn.1000-3835.2013.13.006 (  0) 0) |
| [4] |
陶海亮, 左志涛, 高庆, 等. 基于时频分析的裂纹转子碰摩故障特征研究[J]. 推进技术, 2013, 34(4): 520-528. (TAO Hai-liang, ZUO Zhi-tao, GAO Qing, et al. Fault Analysis of Rotor with Rub-Impact and Crack Based on Time-Frequency Analysis[J]. Journal of Propulsion Technology, 2013, 34(4): 520-528.)
(  0) 0) |
| [5] |
Costa C D, Kashiwagi M, Mathias M H. Rotor Failure Detection of Induction Motors by Wavelet Transform and Fourier Transform in Non-Stationary Condition[J]. Case Studies in Mechanical Systems & Signal Processing, 2015(1): 15-26.
(  0) 0) |
| [6] |
Dogruer T, Akar M. Broken Rotor Bar Fault Diagnosis in Induction Motors using Resampling Based Order Tracking Analysis Method[J]. Journal of New Results in Science, 2016, 5(12): 111-125.
(  0) 0) |
| [7] |
任立通, 谢寿生, 胡金海, 等. 基于稳定约束的自适应随机共振转子故障检测方法[J]. 推进技术, 2013, 34(10): 1398-1405. (REN Li-tong, XIE Shou-sheng, HU Jin-hai, et al. Adaptive Stochastic Resonance Rotor Fault Detection Algorithm Based on Stability Constraint[J]. Journal of Propulsion Technology, 2013, 34(10): 1398-1405.)
(  0) 0) |
| [8] |
Harish Chandra N, Sekhar A S. Fault Detection in Rotor Bearing Systems Using Time Frequency Techniques[J]. Mechanical System and Signal Processing, 2016, 72-73: 105-133. DOI:10.1016/j.ymssp.2015.11.013
(  0) 0) |
| [9] |
唐贵基, 庞彬. 基于改进希尔伯特振动分解的机械故障诊断方法研究[J]. 振动与冲击, 2015, 34(3): 167-171. (  0) 0) |
| [10] |
Yaguo Lei, Zhengjia He, Yanyang Zi. Application of EEMD Method to Rotor Fault Diagnosis of Rotating Machinery[J]. Mechanical System and Signal Processing, 2009, 23: 1327-1338. DOI:10.1016/j.ymssp.2008.11.005
(  0) 0) |
| [11] |
向玲, 鄢小安. 汽轮机转子故障振动中LMD法和EMD法性能对比研究[J]. 动力工程学报, 2014, 34(2): 945-951. (  0) 0) |
| [12] |
Mark G Frei. Intrinsic Time-Scale Decomposition: Time-Frequency-Energy Analysis and Real-Time Filtering of Non-Stationary Signals[J]. Proceedings Mathematical Physical & Engineering Sciences, 2007, 463(2078): 321-342.
(  0) 0) |
| [13] |
郑近德, 程军圣, 聂永红, 等. 完备总体平均局部特征尺度分解及其在转子故障诊断中的应用[J]. 振动工程学报, 2014, 27(4): 637-646. (  0) 0) |
| [14] |
陈向民, 于德介, 李星, 等. 形态分量分析在转子早期碰摩故障诊断中的应用[J]. 振动工程学报, 2014, 27(3): 466-472. (  0) 0) |
| [15] |
Gilles J. Empirical Wavelet Transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010. DOI:10.1109/TSP.2013.2265222
(  0) 0) |
| [16] |
Dragomiretskiy K, Zosso D. Variational Mode Decomposition[J]. IEEE Transactions on Signal Processing, 2014, 63(3): 531-544.
(  0) 0) |
| [17] |
Bonizzi P, Karel Jhm, Meste O. Singular Spectrum Decomposition: A New Method for Time Series Decomposition[J]. Advances in Adaptive Data Analysis, 2014, 6(4): 1-34.
(  0) 0) |
| [18] |
Corino V D A, Mainardi L T, Stridh M, et al. Improved Time-Frequency Analysis of Atrial Fibrillation Signals Using Spectral Modeling[J]. IEEE Transactions on Biomedical Engineering, 2008, 55(12): 2723-2730. DOI:10.1109/TBME.2008.2002158
(  0) 0) |
| [19] |
Huang N E, Wu M, Qu W, et al. Application of Hilbert-Huang Transform to Non-Stationary Financial Time Series Analysis[J]. Applied Stochastic Models in Business and Industry, 2003, 19(3): 245-268. DOI:10.1002/(ISSN)1526-4025
(  0) 0) |
| [20] |
郭瑜, 秦树人, 汤宝平, 等. 基于瞬时频率估计的旋转机械阶比跟踪[J]. 机械工程学报, 2003, 39(3): 32-36. (  0) 0) |
 2018, Vol. 39
2018, Vol. 39

