2. 北京航空航天大学 能源与动力工程学院,北京 100191;
3. 先进航空发动机协同创新中心,北京 100191
2. School of Energy and Power Engineering, Beihang University, Beijing 100191, China;
3. Collaborative Innovation Center of Advanced Aero-Engine, Beijing 100191, China
航空发动机在运转过程中除承受一般的准静态载荷之外,还可能承受多种形式的动态载荷,因此在进行结构动力学设计时,需要依据设计层次的不同采取不同的设计手段和设计准则。其中,对于整机系统以及整机下一级的子系统,需要进行结构完整性和安全性设计,在常规载荷作用下保证系统结构的完整,在极端恶劣的载荷下保证发动机乃至飞机及人员的安全。
叶片丢失是适航认证的关键环节,国际各航空安全管理机构对航空发动机叶片丢失均有明确要求,美国联邦航空管理局[1]要求高涵道比涡扇发动机必须通过叶片丢失的整机试验。而航空发动机中转子系统的安全性设计主要考虑转静子系统瞬态动力特性和转子系统的持续生存能力。对于该问题,在对象上,包含了复杂的转子和承力系统机构;在载荷特征上,加载时间短,载荷强度高,为典型的冲击载荷;在响应特征上,具有整体耦合性、高度非线性和严重的破坏性,是危及整机系统安全性的重要问题。
由于涉及对象广、结构特征多样、载荷作用规律复杂,叶片丢失激励下整机系统的动力学行为研究十分困难,涉及结构动力学、转子动力学、冲击动力学等学科领域。早期的研究主要是通过严酷的整机试验验证,但是由于其耗资巨大,近年的研究趋势是在设计初期尽量避免或减少整机的试验,尽可能通过分析和模拟的手段验证结构的动力响应规律和特征。从力学机理角度,Genta[2]针对简单转子开展突加不平衡振动响应研究,表明瞬态振动响应与转子的工作状态有关,超临界状态运转的柔性转子瞬态振动响应更剧烈。Dzenan[3]考虑了转子的刚度分布,采用简化模型预估了突加不平衡响应。Sinha[4]进一步考虑复杂转子的结构和力学特征等效,进行了叶片丢失过程中突加不平衡和碰摩等载荷激励下的响应分析,获得了一些动力学特征。国内外航空发动机设计部门采用的主要手段是基于有限元程序的数值仿真方法,大多针对叶片丢失瞬时的动力响应,而对其产生的破坏性危害和提高安全性的策略方法则鲜有涉及[5~10]。转子系统在风车状态下的持续生存能力,是近年新兴的一个研究方向,主要体现于转静件间的持续碰摩,这种碰摩与常见的旋转机械碰摩程度不同,碰摩深度更强,能量转移转化过程更加剧烈。
在现有研究中,在方法上以线性分析为主,对于强冲击载荷作用下的大载荷、大变形非线性问题研究不足,分析模型无法实现完整的结构与动力学等效,以至于动力学响应的研究结果难以指导整机系统的结构设计和提高系统的安全性。本文建立结构力学特征等效的转子系统模型,基于开展冲击载荷激励下的转子结构系统动力响应分析,提出提高整机安全性的设计策略和设计方法,并将其应用于实际的高涵道比涡扇发动机进行验证分析。
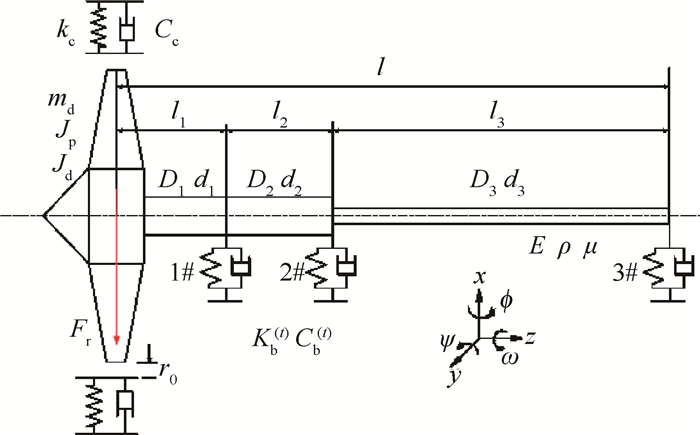
2 冲击激励下柔性转子动力学响应机理 2.1 高速柔性悬臂转子模型在叶片丢失的冲击激励下柔性转子将经历瞬态冲击、大不平衡响应、叶片与机匣持续碰摩等复杂的物理过程。高涵道比涡扇发动机的低压转子为柔性转子系统,建立既能反映柔性转子结构力学特征、又能等效载荷的力学分析模型如图 1所示。模型满足刚度分布特征等效、载荷传递特征等效、转子工作状态等效和转静件间耦合特征的要求。
|
Fig. 1 Model of high speed flexible cantilever rotor |
(1)转子系统的动力学方程一般形式为
| $ \mathit{\boldsymbol{M\ddot q + }}\left( {\mathit{\boldsymbol{C + G}}} \right)\mathit{\boldsymbol{\dot q + Kq = Q}} $ | (1) |
式中q为广义自由度,M为质量惯性矩阵,C为阻尼矩阵,G为陀螺矩阵,K为刚度矩阵,Q为载荷向量。
(2)当考虑不平衡载荷突变时,转子系统的动力学方程中包含时变载荷向量
| $ \mathit{\boldsymbol{Q}}\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {{{\left\{ {0\;\;\;\;0\;\;\;\;0\;\;\;0} \right\}}^{\text{T}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}&{t < {t_1}} \\ { {{m_{\text{d}}}r{\omega ^2}\left\{ {\cos \;\omega t\;\;\;\sin \;\omega t\;\;\;\;\;0\;\;\;\;\;0} \right\}}^{\text{T}}}&{t \geqslant {t_1}} \end{array}} \right. $ | (2) |
(3)存在持续冲击碰摩时
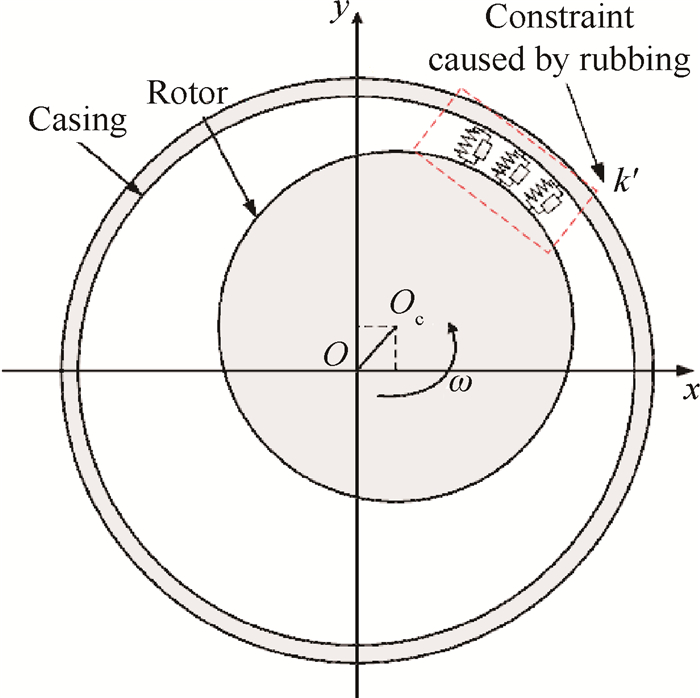
持续冲击碰摩是柔性转子最为常见碰摩形式,此时转子将受到重复的径向冲击作用[11],对转子的横向位移产生约束,改变转子系统的刚度,类似于附加支承,导致转子系统的固有特性发生改变,进而影响其响应特性,如图 2所示。
|
Fig. 2 Model of rotor system with continuous Rub-Impact |
当转子振幅超过间隙(|qk| > r0)发生持续碰摩时,转子受到附加刚度记为Kr,此时转子的运动方程变为
| $ \mathit{\boldsymbol{M\ddot q + }}\left( {\mathit{\boldsymbol{C + G}}} \right)\mathit{\boldsymbol{\dot q + }}\left[{{\mathit{\boldsymbol{K}}_{\text{s}}} + {\mathit{\boldsymbol{K}}_{\text{r}}}\left( t \right)} \right]\mathit{\boldsymbol{q = Q}}\left( t \right) $ | (3) |
| $ k' = {k_{\text{c}}}\left( {1 + j\;{\text{sign}}\left( {\mathit{\Omega} \left| {{q_{\text{k}}}} \right| + \omega r} \right)\mu } \right)\left( {1 - \frac{{{r_0}}}{{\left| {{q_{\text{k}}}} \right|}}} \right) $ | (4) |
式中kc为碰摩接触刚度,Ω为转子涡动角速度,ω为自转角速度,μ为转静件摩擦系数。
2.2 突加不平衡转子响应特征根据上文所建立模型,对突加不平衡激励下高速柔性转子模型响应特征进行分析。转子一阶临界转速ωn为2886r/min,选取1.4ωn(4040r/min)作为工作转速,假设突加不平衡量为1.5kg·m(3kg的叶片在半径为0.5m处丢失),施加载荷时刻为0.5s,采用Newmark直接积分方法求解方程(2),计算转子的振动响应。
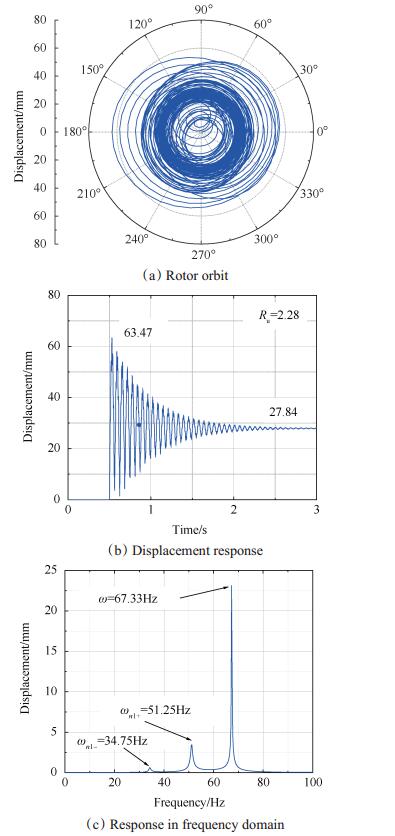
突加不平衡激励下,转子振动响应特征如图 3所示,可知:(1)转子的瞬态振动响应轨迹呈现椭圆形轨迹;(2)振动响应幅值在突加不平衡时刻增大,之后振荡并衰减至稳态;(3)频域成分中包含转速频率、转子第一阶正进动频率及反进动频率,说明突加不平衡载荷可以激起转子的低阶正进动和反进动。
|
Fig. 3 Response of sudden unbalance rotor |
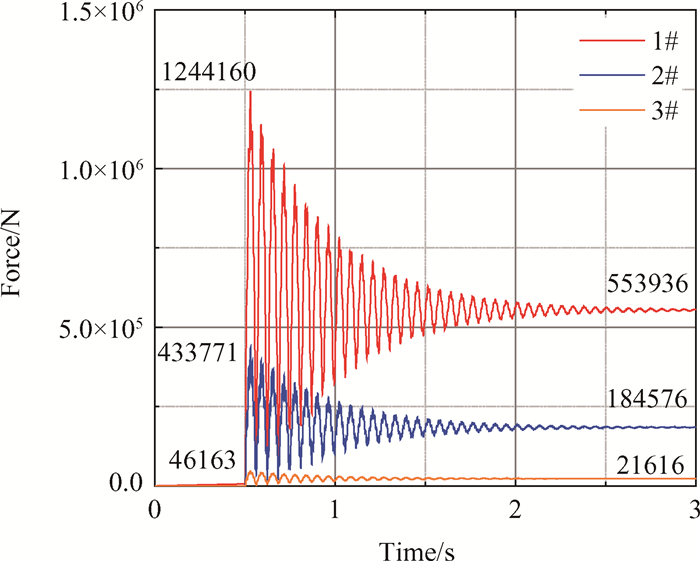
提取突加不平衡载荷激励下三个支点的支反力,见表 1和图 4,结果表明:(1)支反力响应特征与转子振动响应特征基本一致,在突加不平衡瞬时突增,之后振荡并衰减至稳态,瞬态峰值远大于稳态值;(2)三个支点的支反力响应由近至远(距轮盘位置)依次降低,靠近轮盘的1#支点反力最大,远远高于2#,3#支点支反力,对该支点轴承和承力结构的安全性提出了严峻考验。
|
|
Table 1 Reaction force response and impact factor |
|
Fig. 4 Reaction force response of sudden unbalance rotor |
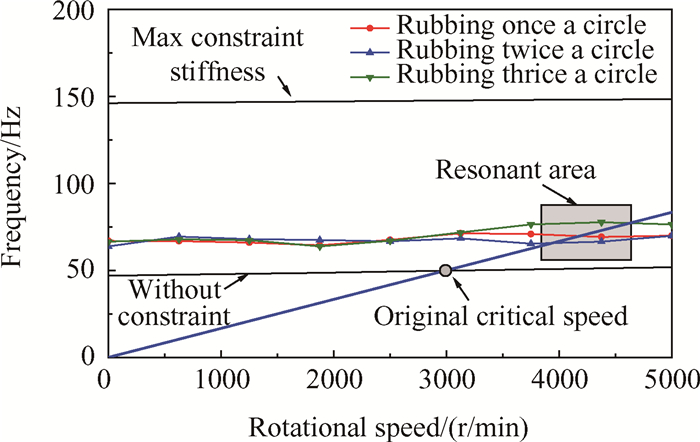
风扇叶片丢失后,处于超大不平衡状态运转的转静子之间发生持续的冲击碰摩。根据2.1节机理1114推进技术2018年模型与式(3)、式(4),采用Hill无穷行列式法对持续冲击碰摩转子的模态频率进行求解[14],计算中假设碰摩接触刚度与支承刚度相等,碰摩时间占比α = 0.8,得到不同碰摩频率下转子系统的动频线和临界转速,如图 5所示。
|
Fig. 5 Critical speed of rotor with continuous Rub-Impact |
结果表明持续冲击碰摩转子由于附加约束刚度,其模态频率提高,位于无附加约束的初始状态和最大附加约束刚度所对应的频率范围之间。转子系统的临界转速增大,由2886r/min升高至[3902 ,4619]r/min。
对持续冲击碰摩转子系统振动响应和支反力响应进行分析,计算转速取为0.6ωn(1732r/min),不平衡量为1.5kg·m,转静件初始间隙为2mm。
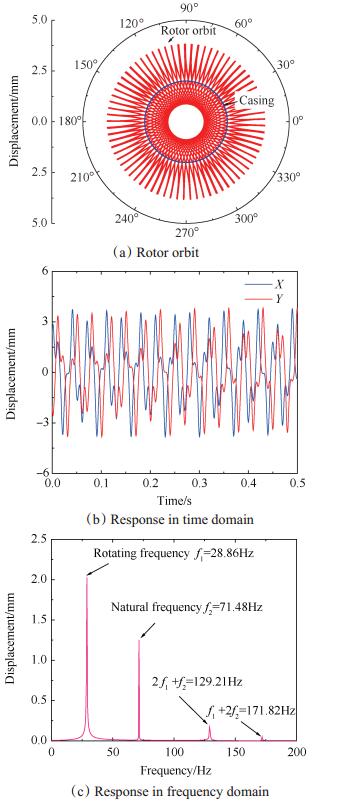
持续冲击碰摩转子振动响应计算结果如图 6所示,由轴心轨迹和时域响应可见,转子在大不平衡载荷作用下的振幅超过了初始间隙,出现持续冲击碰摩作用;在频域响应中,转子包含四个频率成分,即转速频率、衰减振动频率及二者的组合,进一步说明碰摩过程中转子系统的固有特性受到约束作用而产生的改变。
|
Fig. 6 Vibration response of rotor system with continuous Rub-Impact |
表 2为各支点的支反力,结果表明:(1)轴承支反力在一定范围内变化,碰摩中轴承承受交变的支反力载荷;(2)相比无碰摩转子,轴承的支反力响应降低,其中1#支点较显著,支反力由136747N降至67022N,表明机匣约束转子振动响应的同时也会降低轴承的支反力水平,有助于改善转子系统的安全水平。
|
|
Table 2 Reaction force response amplitude of rotor system with continuous Rub-Impact |
依据前文的分析建立了一套悬臂转子-支承系统试验器,对突加不平衡激励下的转子动力响应进行试验验证。
(1)突加不平衡试验装置
装置包含了完整的“转子-支承-机匣”系统,如图 7所示,转子为悬臂支承的单盘转子,两个支承分别为刚性支承和弹性支承,弹性支承位置的载荷沿“鼠笼-机匣内环-支板-机匣外环-安装边”路线外传,轮盘上设计有用于施加突加不平衡载荷的飞脱螺栓。

|
Fig. 7 Sudden unbalance rotor system |
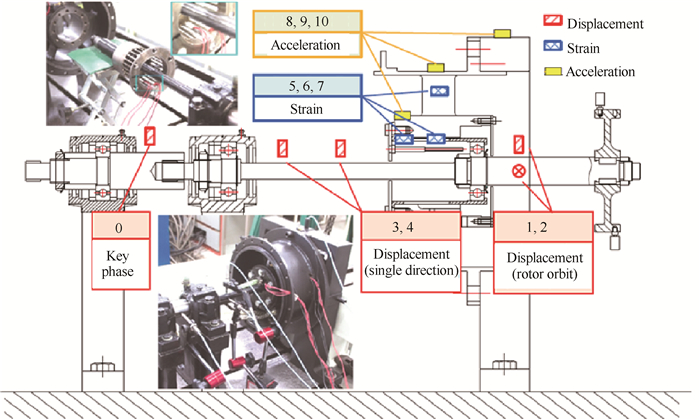
试验系统测点布置如图 8所示,采用电涡流传感器、电阻应变片和加速度传感器采集振动信号。在转子上布置5个电涡流位移传感器,其中0#测点为转速的键相信号,1~4#测点测量不同位置轴段的位移;5~7#测点为电阻应变片,5#和6#位于鼠笼笼条上,7#位于支承框架支板上。
|
Fig. 8 Measuring points of the testing system |
(2)持续冲击碰摩试验装置
持续冲击碰摩试验装置如图 9所示,包括转子-支承系统和碰摩约束装置,其中转子-支承系统与突加不平衡试验相同,通过转轴与碰摩约束装置之间的碰摩实现对持续冲击碰摩的模拟。

|
Fig. 9 Rotor system with continuous Rub-Impact |
碰摩约束装置如图 9中右侧上下小图所示,刚性碰摩环和弹性约束环串联布置,刚性碰摩环与转子接触并发生碰摩;弹性约束环材料为金属橡胶,可通过改变金属橡胶密度实现多种约束刚度。
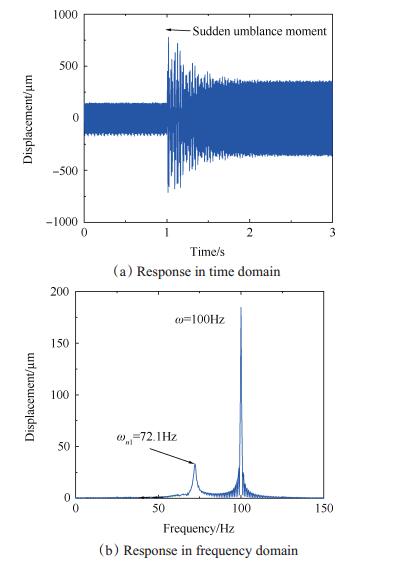
3.2 突加不平衡实验对转速状态(6kr/min)的转子系统进行突加不平衡试验(10g·cm)。试验转子系统响应特征如图 10所示,转子在突加不平衡载荷瞬时振动响应突增,随后响应幅值衰减直至稳态,与计算响应特征相近;由频域响应可知,其包含转速频率成份和转子第一阶进动频率。
|
Fig. 10 Vibration response of rotor in horizontal direction |
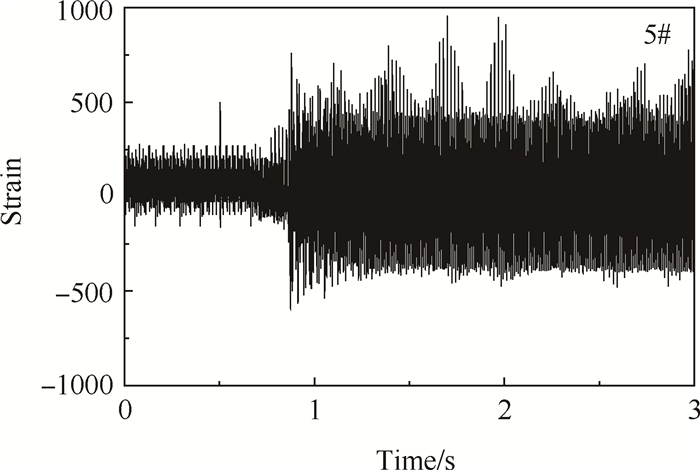
图 11为鼠笼上的应变信号(5#),突加不平衡载荷后的振动响应显著提高,说明其在不平衡量增大时,外传载荷随之增大,支点轴承的载荷状况更加恶劣。
|
Fig. 11 Load response characteristics of support |
对转子施加不平衡量10.5g·cm,碰摩约束装置选取三种弹性材料,材料阻尼比相同,约为0.13;径向刚度分别为2.79×105,4.54×105,1.2×106N/m,模拟不同约束程度。
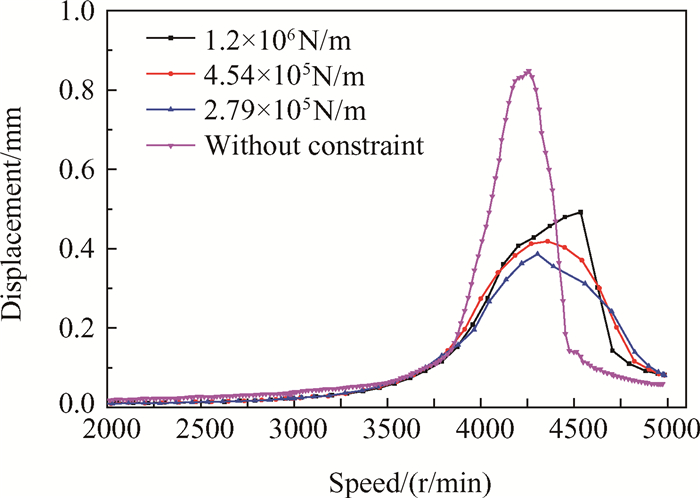
图 12为试验测得转子在升速过程中的幅值-转速曲线,与计算结果一致,当转子运转过程中存在持续冲击碰摩时,共振转速提高,同时共振转速范围增大。表 3中列出了不同碰摩状态下转子共振转速,结果表明,约束程度越强,共振转速提高越多。
|
Fig. 12 Restraint stiffness influence on the inherent characteristics of the rotor(1# point) |
|
|
表 3 Resonance speed with different constraint stiffness |
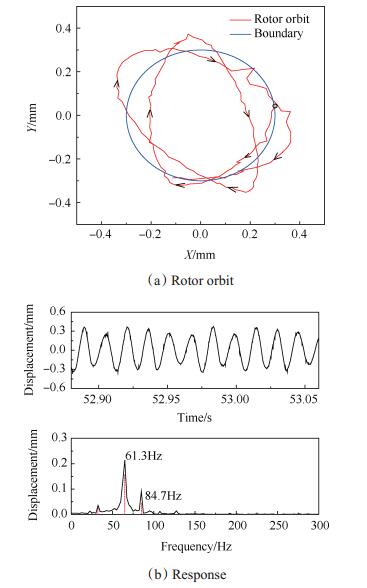
以弹性刚度为5×107N/m试验为例,转子发生持续冲击碰摩,转子轴心轨迹图及其对应时/频域响应图 13(a)所示,与计算结果一致,结果表明此时转子轴心轨迹发生弹跳,转子与约束环间出现持续的接触-分离,产生约束,转子响应幅值减小;持续冲击碰摩下,转子响应频域成分中非转速一倍频成分明显。
|
Fig. 13 Vibration response of rotor with continuous Rub-Impact |
上文的理论分析和实验结果证明,在叶片丢失引起的突加不平衡激励下,振动瞬态响应幅值增大,1#支点的瞬态支反力显著增大;并且在随后的持续冲击碰摩状态下,转子系统受到附加约束作用,临界转速提高[15],发动机慢车转速可能临近临界转速,引发共振或共振裕度降低,导致整机系统难以维持安全的运转。因而需要采取必要的结构和动力学设计来提高整机系统的安全性。
4 叶片丢失整机动力学仿真与安全性设计 4.1 整机动力学分析模型高涵道比涡扇发动机风扇转子叶片丢失时,风扇转子受到突加的超大不平衡激励,出现持续冲击碰摩作用,可采用高速柔性悬臂转子模型对其进行响应分析。
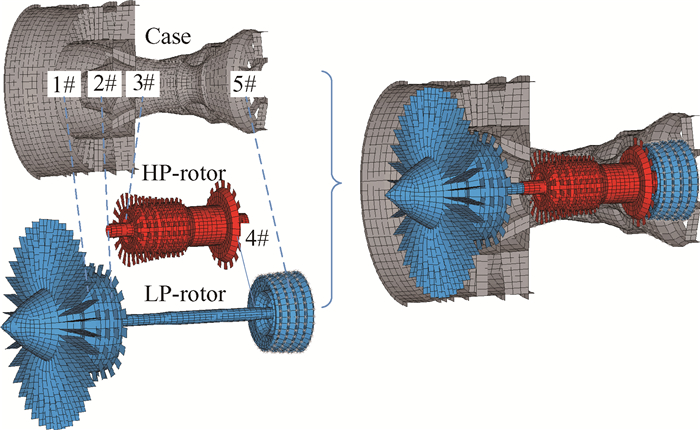
采用简化等效的原则[16, 17],基于ANSYS/ LS-DYNA平台建立整机壳单元有限元分析模型,模型由静子机匣、高压转子和低压转子三个部分组成,如图 14所示。经过将模型的质量分布、转动惯量分布、模态特性等与实际数据进行对比和校核后,确认该模型能够满足计算需求。
|
Fig. 14 Finite element model for the analysis of transient dynamic characteristics |
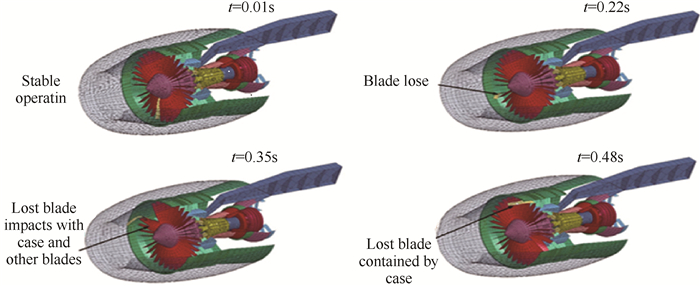
对叶片丢失全过程进行动力学仿真计算,如图 15所示,包括:风扇叶片丢失前转子稳态运转—叶片瞬时断裂飞出—飞出的叶片与尾随叶片和机匣撞击—叶片被机匣包容。丢失叶片轨迹为螺旋线,轮盘上剩余的叶片受到丢失叶片的撞击以及机匣的约束作用(碰摩),说明本文建立的仿真方法能够实现叶片丢失过程的完整模拟。
|
Fig. 15 Simulation of blade loss process |
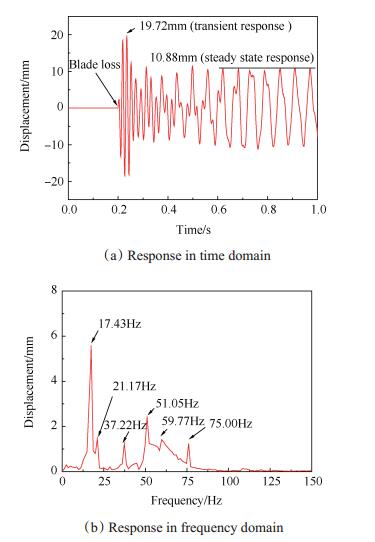
风扇轮盘位置的时域振动响应结果如图 16(a)所示,当叶片丢失发生后,转子振动响应突增,在0.233s时达到峰值,为19.72mm;随后振动响应衰减,并在0.5s时趋于稳定,稳态振幅为10.88mm;稳定振动阶段,转子振动响应为非规则正弦曲线,主要是由于转子与机匣间持续的碰摩作用。
|
Fig. 16 Vibration response of fan-disk |
图 16(b)为叶片丢失过程中频域响应特征,频率成分复杂,其中75.34Hz对应转子的转速频率;37.22Hz为转速频率的1/2,来自于碰摩激励产生的分频;17.43Hz,21.17Hz,51.05Hz和59.77Hz为冲击载荷激起的转子系统进动频率,分别对应于第一阶(16.83Hz,整机俯仰振型)和第二阶模态(48.72Hz,风扇俯仰型振型)的正进动和反进动频率。
风扇盘位移响应中同时出现了瞬态冲击特征(振荡衰减、激起正反进动)和持续碰摩造成的固有特性变化(共振频率增大),与2,3节机理和实验的结果一致。
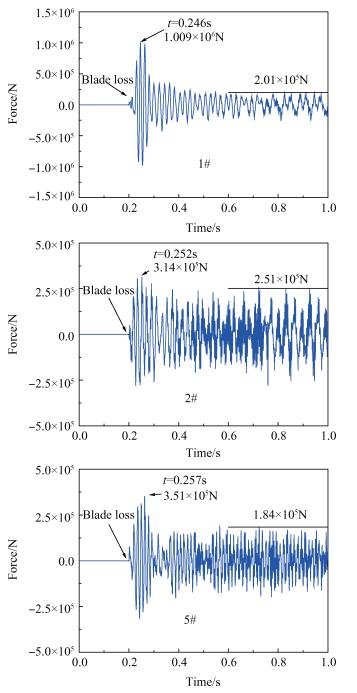
4.2.2 支承结构载荷响应在风扇叶片丢失激励下,高涵道比涡扇发动机低压转子的各支点支反力时域响应如图 17所示,提取峰值响应时间、瞬态峰值、稳态幅值,如表 4所示。
|
Fig. 17 Response of support reaction force in time domain |
|
|
Table 4 Support reaction force of rotor system |
由整机仿真计算结果可知:
(1)在叶片丢失发生时,由于突加不平衡载荷的作用,各支点均会产生明显的冲击效果,即支反力瞬时突增,随后衰减到稳定的振动幅值;其中靠近风扇的1#支点的支反力最大,达10.09×105N(约100吨力)。
(2)在支反力响应衰减后,支反力幅值也不是稳定的,原因在于转子系统在大不平衡载荷作用下与机匣产生持续冲击碰摩,转子不断受到径向冲击力和轴向摩擦力激励,支反力也随之呈现非稳态的特征。
4.3 安全性设计由4.2节分析结果可知,发生叶片丢失时,1#支点载荷状态最恶劣,支反力达到近百吨,可能导致滚珠破碎、抱轴等严重的后果;转子系统响应幅值较大,稳态响应幅值达10.88mm。故有必要采取安全性设计措施以保护轴承和转子系统。
4.3.1 设计策略1#支点具有最大支反力,降低1#支点支承刚度,可降低其支反力,实现对危险支点轴承的保护。综合考虑,可采用降低1#支点支承刚度的策略,减小转子系统临界转速同时降低1#支点支反力。
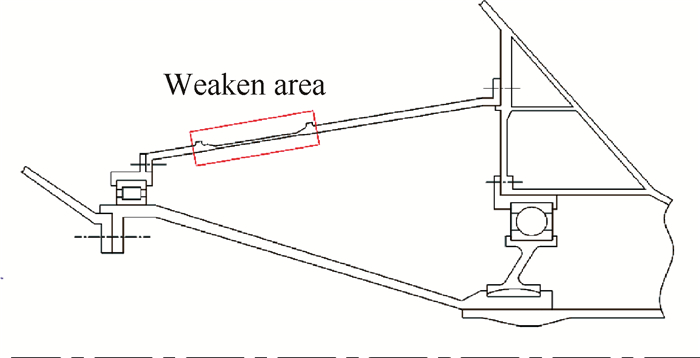
可以通过结构设计实现变支承刚度,实际中主要结构设计手段为易断件设计,如图 18所示,即在支承鼓筒上设计局部薄弱段,使其在大冲击载荷下变形断裂。有些设计在支承鼓筒连接位置采用易断螺栓结构,螺栓被削弱部分在大冲击载荷下瞬时断裂。
|
Fig. 18 Design of easily broken part of support structure |
通过易断结构设计可以实现变支承刚度,使支承结构在特定冲击载荷条件下完全丧失刚度或部分丧失刚度。
因此可通过1#支点主动失效(当量刚度大幅下降至小于0.01),大幅降低转子临界转速[18, 19],优化转子动力响应,从而避免产生二次故障,提高转子系统的生存能力。
4.3.2 安全性设计下的转子动力响应采用变支承刚度策略,通过在ANSYS中的*CONSTRAINED_JOINT_SPHERICAL_ID_FAILURE关键字定义1#支点轴承的失效,触发轴承失效的载荷阈值设置为5×105N。
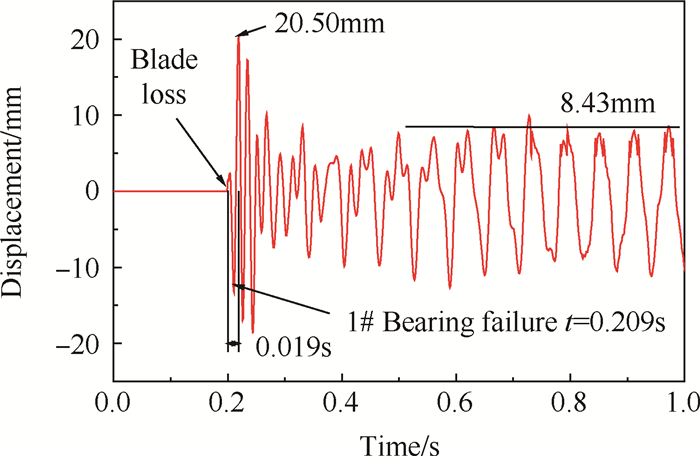
1#支点采用安全性设计后,发生风扇叶片丢失时,风扇轮盘位置振动响应如图 19所示,将其与图 16进行对比,得到转子系统振动响应特征如下:
|
Fig. 19 Vibration response of fan-disk in time domain |
(1)1#支点失效后,瞬态峰值略有增加,说明虽然系统的刚度降低,但是由于机匣的约束,瞬态振动响应峰值变化不大。
(2)稳态响应幅值降低,原因在于,切断支承使转子系统的动力特性发生改变,转子系统模态频率和临界转速降低,发生叶片丢失时工作转速距新的临界转速值变远,各位置稳态幅值随之降低。
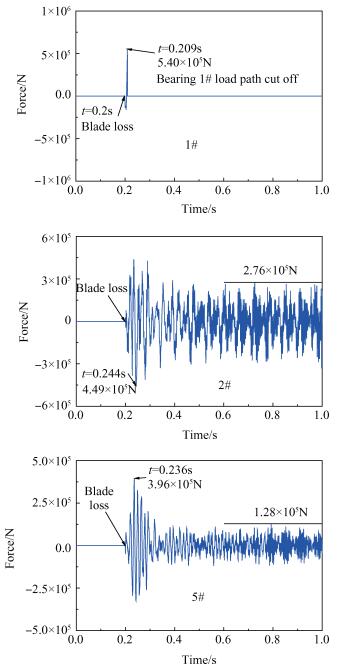
4.3.3 支承结构载荷响应特征风扇转子支点(1#,2#和5#)的支反力响应曲线如图 20所示,提取响应峰值时间、瞬态峰值、稳态幅值于表 5中。
|
Fig. 20 Response of support reaction force in time domain (with safety design) |
|
|
Table 5 Support reaction force of rotor system(with safety design) |
对比分析图 20和图 17,以及表 4和表 5,得到如下结论:
(1)1#支点在反力超过5×105N后,支承结构剪断,而不再受载,反力变为0。
(2)对于除1#支点外各支点,支反力瞬态峰值提高约10%~20%,说明在突加不平衡和支点刚度突变双重激励下,支点反力水平提高。
(3)采用变刚度支承后,最大支反力值为5.4 × 105N,远低于采用安全策略前最大支反力值(1.0 × 106N),峰值载荷降低46%,说明采用安全性策略可有效降低支点最大支反力值。
5 结论本文针对冲击激励下转子结构系统的动力响应特征进行了理论分析和试验研究,并针对其引发的航空发动机安全性问题开展了动力学设计策略、结构设计方法以及整机动力响应的仿真,得到的主要结论如下:
(1)建立了高速柔性悬臂转子系统动力学模型,通过与实验数据对比,验证了该模型可以有效地计算冲击载荷作用下的转子动力响应,支撑安全性设计的机理分析研究。机理分析表明,冲击载荷下会激起转子系统的低阶正、反进动,冲击引发的持续碰摩会改变转子共振转速,降低响应幅值。
(2)冲击载荷对转子系统的安全性带来严重影响,一方面,突加不平衡冲击载荷使系统的瞬态振动加剧,临近的支点轴承反力可能超过轴承的承载能力,引发轴承滚子破碎等恶劣后果;另一方面,风车状态中,超大不平衡转子受到持续的冲击碰摩作用,转子系统受到附加约束作用,临界转速提高,发动机慢车转速可能临近临界转速,引发共振或者共振裕度降低,导致整机系统难以维持安全的运转。
(3)提出了的变支承刚度设计策略,在达到设定的轴承外传载荷失效阈值时,通过切断传力路线以保持轴承完整性、避免抱轴卡滞。算例表明,该策略使得支点所承受的峰值载荷降低46%。持续冲击碰摩过程中的附加约束作用,虽然可以抑制转子的振动响应,但也扩宽了转子共振范围,使系统偏于危险,而降低支承刚度也恰恰解决了这一问题,使得风车状态远离系统共振区,进一步改善了系统的安全性。
| [1] |
Federal Aviation Regulations. 14 CFR Part 33 Airworthiness Standards: Aircraft Engines[S]. US: Federal Aviation Administration, 1993: 81-99. http://commdocs.house.gov/committees/Trans/hpw104-37.000/hpw104-37_0f.htm
(  0) 0) |
| [2] |
Genta G. Dynamics of Rotating Systems[M]. Germany: Springer-Verlag, 2005.
(  0) 0) |
| [3] |
Dzenan H. Mechanical Loads on a Turbofan Engine Structure at Blade-Off[D]. Sweden: Lulea University of Technology, 2009. http://ltu.diva-portal.org/smash/record.jsf?pid=diva2:1030140
(  0) 0) |
| [4] |
Sinha S K. Rotordynamic Analysis of Asymmetric Turbofan Rotor Due to Fan Blade-Loss Event with ContactImpact Rub Loads[J]. Journal of Sound and Vibration, 2013, 332(9): 2253-2283. DOI:10.1016/j.jsv.2012.11.033
(  0) 0) |
| [5] |
Verrier P, Martinal H, Kohli-Lynch S. Blade Loss Sim ulations of Bending Vibrations Applied to a 1750mW Turbo Generator Set[C]. Korea: 8th IFToMM International Conference on Rotor Dynamics, 2010: 725-730.
(  0) 0) |
| [6] |
Ortiz R, Herran M, Chalons H. Blade Loss Studies in Low-Pressure Turbines from Blade Containment to Controlled Blade-Shedding[C]. Portugal: Computational Methods and Experimental Measurements, 2009: 412-422. https://www.researchgate.net/publication/267934477_Blade_loss_studies_in_low-pressure_turbines_-_From_blade_containment_to_controlled_blade-shedding
(  0) 0) |
| [7] |
Cosme N, Chevrolet D, Bonini J, et al. Prediction of Transient Engine Loads and Damage due to Hollow Fan Blade-Off[J]. European Journal of Computational Mechanics, 2002, 11(5): 651-666.
(  0) 0) |
| [8] |
Jain R. Prediction of Transient Loads and Perforation of Engine Casing during Blade-Off Event of Fan Rotor Assembly[C]. Rhode Island: Proceedings of the IMPLAST 2010 Conference, 2010: 1-10. https://www.sciencedirect.com/science/article/pii/S1270963812000211
(  0) 0) |
| [9] |
Sinha S K. Dynamic Characteristics of a Flexible Bladed-Rotor with Coulomb Damping Due to Tip-Rub[J]. Journal of Sound and Vibration, 2004, 273(4-5): 875-919. DOI:10.1016/S0022-460X(03)00647-3
(  0) 0) |
| [10] |
Husband J B. Developing an Efficient FEM Structural Simulation of a Fan Blade-Off Test in a Turbofan Jet Engine[D]. Canada: University of Saskatchewan, 2007. http://ecommons.usask.ca/handle/10388/etd-10292007-111221
(  0) 0) |
| [11] |
王海飞, 陈果. 考虑多叶片-机匣多点变形转静碰摩模型的机匣响应特征与验证[J]. 推进技术, 2016, 37(1): 128-145. (WANG Hai-fei, CHEN Guo. Casing Response Characteristics and Its Verification Considering Multiple Blades-Casing Multiple Point Deformation Rotor-Stator Rubbing Model[J]. Journal of Propulsion Technology, 2016, 37(1): 128-145.)
(  0) 0) |
| [12] |
张思进. 机械碰撞运动中的非光滑动力学[M]. 长沙: 湖南大学出版社, 2008.
(  0) 0) |
| [13] |
张华彪. 航空发动机转子系统碰摩的非线性动力学研究[D]. 哈尔滨: 哈尔滨工业大学, 2012. https://www.wenkuxiazai.com/doc/154d7ecbf8c75fbfc77db273-2.html
(  0) 0) |
| [14] |
Meng M W, Jun W J, Zhi W. Frequency and Stability Analysis Method of Asymmetric Anisotropic Rotor-Bearing System Based on Three-Dimensional Solid Finite Element Method[J]. Journal of Engineering for Gas Turbines and Power, 2015, 137(10).
(  0) 0) |
| [15] |
邓旺群, 聂卫健. 高速柔性转子临界转速随支承刚度的变化规律[C]. 大连: 第11届全国转子动力学学术讨论会, 2014. http://www.cnki.com.cn/Article/CJFDTotal-ZSZK201503022.htm
(  0) 0) |
| [16] |
陈萌, 马艳红, 刘书国, 等. 航空发动机整机有限元模型转子动力学分析[J]. 北京航空航天大学学报, 2007, 33(9): 1013-1016. (  0) 0) |
| [17] |
高金海, 洪杰. 航空发动机整机动力特性建模技术研究[J]. 战术导弹技术, 2006, 27(3): 29-35. (  0) 0) |
| [18] |
张力. 高涵道比涡扇发动机转子系统动力特性及安全性设计理论方法[D]. 北京: 北京航空航天大学, 2015.
(  0) 0) |
| [19] |
张大义, 刘烨辉, 洪杰, 等. 航空发动机整机动力学模型建立与振动特性分析[J]. 推进技术, 2015, 36(5): 768-773. (ZHANG Da-yi, LIU Ye-hui, HONG Jie, et al. Investigation on Dynamical Modeling and Vibration Characteristics for Aero Engine[J]. Journal of Propulsion Technology, 2015, 36(5): 768-773.)
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


