2. 先进航空发动机协同创新中心,北京 100083
2. Co-Innovation Center for Advanced Aero-Engine, Beijing 100083, China
粉末高温合金在高温环境下强度远高于传统高温合金[1],且微观组织结构更为均匀、疲劳性能更为优异[2]。作为一种典型粉末高温合金,FGH97的优点主要为其持久强度较高、有较高的抗蠕变能力,且能够在700~800℃高温条件下正常工作[3]。针对FGH97的疲劳与断裂性能,国内外已经从试验和数值模拟角度进行了研究。张莹等[4]研究了FGH97试样低周疲劳断口特征,并揭示了缺陷等因素影响其低周疲劳寿命的微观机理。佴启亮等[5]测定了650℃时晶粒大小对FGH97裂纹扩展速率的影响,并与FGH95,FGH96进行对比,发现FGH97的疲劳断裂性能较为优异,主要体现为其能够较好地抵抗裂纹萌生且裂纹萌生后扩展速率相对较低。袁善虎等[6]则用FGH97光滑试样进行了多种力学性能试验,根据Chaboche本构方程拟合试验结果并得到了相关参数,并进一步在缺口试样力学性能分析中得到了应用。刘浩等[7]研究了保载时间和应力强度因子范围对FGH97试样微观断口的影响,提出了一种裂纹扩展模型以考虑时间因素。
在Elber[8]之后,许多学者对裂纹闭合进行了研究且广泛采用有限元法。基于大量试验数据,Newman [9]给出了中心裂纹在拉伸载荷作用下裂纹张开应力的表达式,并引入了约束因子以考虑三维效应。Dougherty[10]提出了一种通用的有限元方法来模拟塑性致闭现象,提高了裂纹闭合的计算效率和准确性。Solanki等[11]对网格划分、裂纹扩展模式和几何效应等因素对于裂纹闭合的影响进行了分析。Antunes等[12]认为有限元模拟裂纹闭合中某些参数的选取上存在一些难以避免的自身不确定性,据此提出了一种数值模型。李亚智、李学峰等[13, 14]研究了有限元模拟裂纹闭合的理论基础,模拟了含中心裂纹试件的裂纹扩展,并考虑了裂纹闭合接触方式、二维受力假设以及变载对闭合比影响。左平等[15]研究了FGH95的紧凑拉伸(CT)试样的裂纹闭合,计算了裂纹扩展寿命且误差仅为7.43%。这些研究成果值得肯定,但仍存在一定不足。目前大部分计算均采用简单本构模型如理想弹塑性模型,其难以描述裂纹尖端在循环载荷下的应力应变,可以定性地反映裂纹闭合规律,但无法准确计算闭合比。同时对于裂纹闭合时裂纹尖端压缩应力的研究仍较为不足,需要进一步补充。
综上所述,有必要在粉末高温合金裂纹闭合和扩展方面进行更为细致的研究。本文主要从塑性致闭角度研究FGH97裂纹扩展规律,采用有限元方法分析裂纹尖端单元尺寸、本构模型及节点释放周期的影响,同时探讨裂纹尖端压缩应力与裂纹闭合的关系;提出修正有效应力强度因子范围的概念,并据此计算裂纹扩展寿命。
2 塑性致闭的有限元模型参照《金属材料疲劳裂纹扩展速率试验方法》(GB/T 6398 2000),ASTM E647-1995a以及《金属材料高温疲劳裂纹扩展速率试验方法》(HB 7680-2000),进行了FGH97的CT试样裂纹扩展试验,试样如图 1所示,相关参数[16]见表 1。
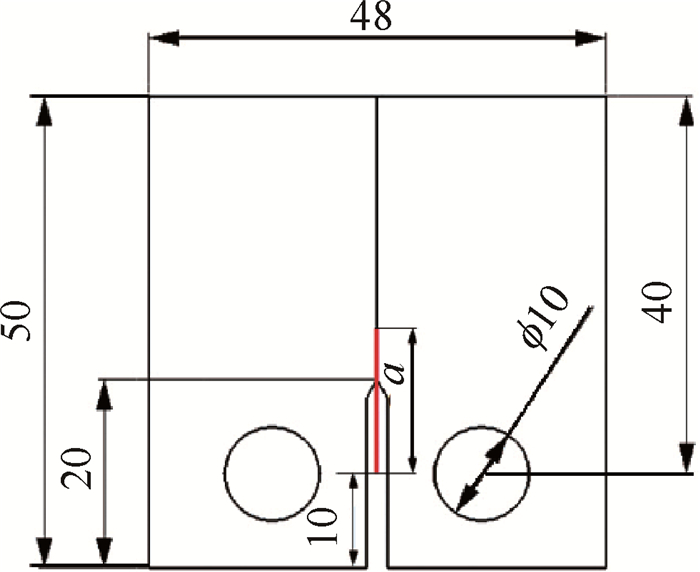
|
Fig. 1 FGH97 compact tension specimen(mm) |
|
|
Table 1 Crack propagation tests parameter |
由于试样存在对称面,仅取其一侧进行建模,单元类型为CPS4即平面应力状态四边形单元,对X方向上(即裂纹扩展方向)进行网格细分,对称面未开裂处施加对称约束,有限元模型见图 2。

|
Fig. 2 Finite element model |
采用刚性线法模拟裂纹面的相互接触:建立一条刚性线作为主接触面,设置试样对称表面为从接触面,两者建立接触对;刚性线不能被穿透,从而防止裂纹面相互渗透。采用节点释放法(Debond technique)模拟裂纹的连续扩展:主从接触面通过节点粘连在一起,特定时刻裂纹尖端节点会被释放,下一个节点成为新的裂纹尖端节点并更新主从接触面实现裂纹扩展,节点释放法见图 3。
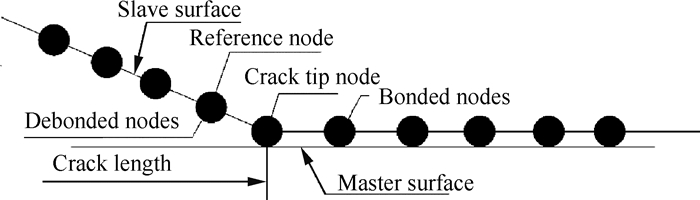
|
Fig. 3 Debond technique |
选择节点释放时刻涉及到两个问题,一是在一个载荷循环内何时释放[17],本文指定在最大载荷时刻;二是每次节点释放需要间隔几个循环载荷(后文中称为节点释放周期),除特别说明外均采用每两周期释放一个节点。本文根据节点位移[18]判断裂纹是否闭合:取裂纹尖端后的第一个节点作为参考节点,当参考节点的张开位移减小至0时认为发生了闭合,反之认为裂纹张开。
3 有限元结果分析 3.1 单元尺寸的影响裂纹尖端处应力梯度大且载荷复杂,因此单元尺寸应足够小。为了考察单元尺寸的影响,划分了五套网格,具体参数见表 2,本构模型均采用双线性随动硬化模型。
|
|
Table 2 Meshing scheme |
定义Smax,Smin和Sop分别为最大外载、最小外载和裂纹张开外载,闭合比U = Sop/Smax。计算得到五套网格下U随裂纹长度a的变化,结果见图 4。从3μm的计算结果可以看出,当裂纹较短时U较小;随着裂纹扩展,U迅速提高;扩展至一定长度后U趋于稳定。随着单元尺寸从40μm细化至3μm,U逐渐增大,这是因为单元尺寸越小,参考节点距离裂纹尖端越近;单元尺寸过大时,闭合比无法收敛。Roychowdhury[19]指出塑性区应含有3个以上单元,Solanki等[20]提出若节点Mises应力大于0.95倍屈服极限就认为处于塑性区,经验证3μm和5μm的单元尺寸均满足要求;同时可以看出3μm和5μm的结果几乎重合,说明进一步细分网格对结果精度提升有限且极大增加计算时间,寿命预测结果也验证了5μm的计算结果已经足够精确,所以后续均采用5μm单元尺寸。
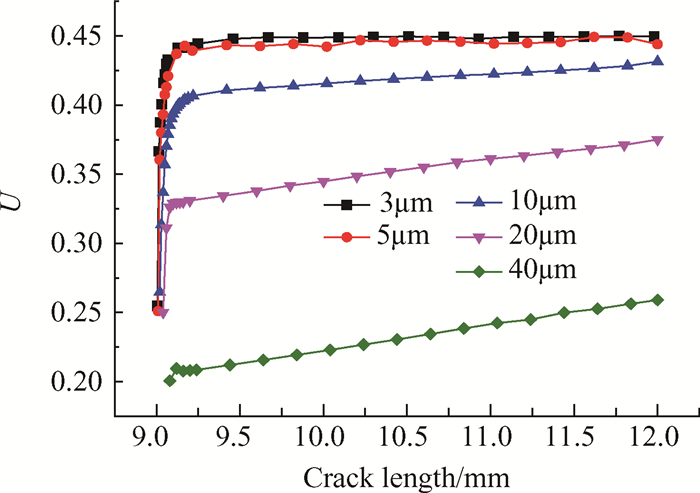
|
Fig. 4 Crack closure ratio of different element size |
裂纹闭合的一个重要现象是裂纹尖端会产生压缩应力[21],因此可以从压缩应力区域的演变解释闭合比的变化。给出了五种网格下裂纹长度9.4mm时(从图 4看出,9.4mm时闭合比已稳定)裂纹尖端压缩应力区域,结果见图 5(a)。结果显示,压缩应力区域随着单元尺寸的细化而扩大直至收敛,3μm和5μm的区域几乎重合;单元尺寸为20μm和40μm时由于节点应力计算误差较大,压缩应力区域呈现不规则形状。对于5μm单元尺寸,给出了压缩应力区域随裂纹长度的变化,结果见图 5(b)。结果显示,随着裂纹扩展压缩应力区域不断扩大且最终趋于稳定。图 5(a)和图 5(b)说明可以用裂纹尖端压缩应力区域的演变反映闭合比的变化,压缩应力区域尺寸越大,对应的闭合比也越大。
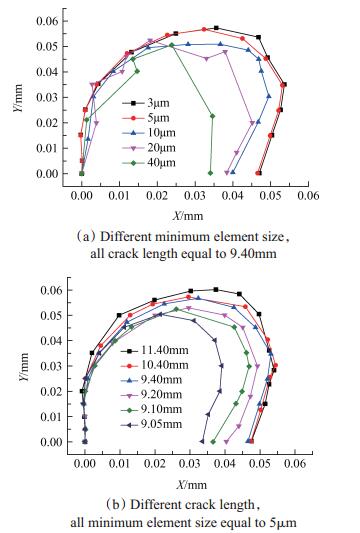
|
Fig. 5 Compressive stress zone around crack tip |
有限元模拟裂纹闭合的一个重点就是采用合适的本构模型以描述裂纹尖端在循环载荷下的应力应变。采用5μm单元尺寸讨论了多线性各向同性硬化(MLISO)模型、双线性随动硬化(BLKINE)模型和Chaboche模型的裂纹闭合差异。其中Chaboche模型本构方程为
| $ \dot \varepsilon _{ij}^{{\text{in}}} = \frac{3}{2}{\left[{\frac{{J\left( {{\sigma _{ij}}-{X_{ij}}} \right)-R-k}}{K}} \right]^n}\frac{{\left( {\sigma {'_{ij}} - X{'_{ij}}} \right)}}{{\left( {{\sigma _{ij}} - {X_{ij}}} \right)}} $ | (1) |
| $ \dot R = b\left( {Q - R} \right)\dot P $ | (2) |
| $ {{\dot X}_{ij}} = \frac{2}{3}ca\dot \varepsilon _{ij}^{{\text{in}}} - c{X_{ij}}\dot P - \beta {\left| {J\left( {{X_{ij}}} \right)} \right|^{r - 1}}{X_{ij}} $ | (3) |
式中
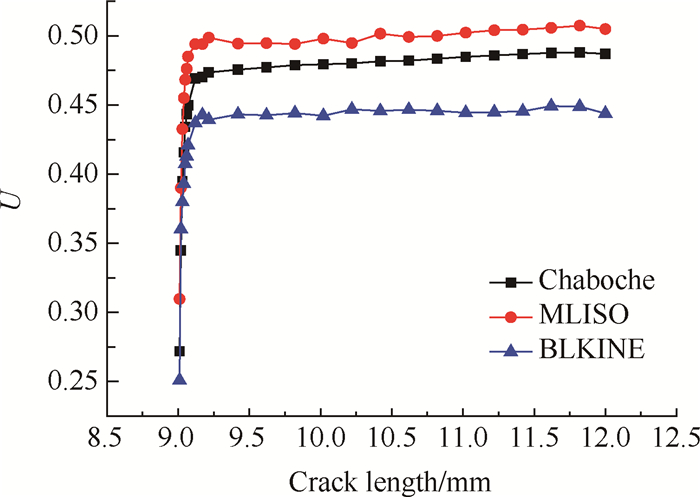
不同本构模型的闭合比随裂纹长度变化计算结果见图 6,可以看出MLISO模型的闭合比最大,BLKINE模型的闭合比最小,由于Chaboche模型可以更好地描述材料的循环变形特性,且后续寿命预测结果误差最小,因此认为其计算结果更为准确。
|
Fig. 6 Crack closure ratio of different constitutive model |
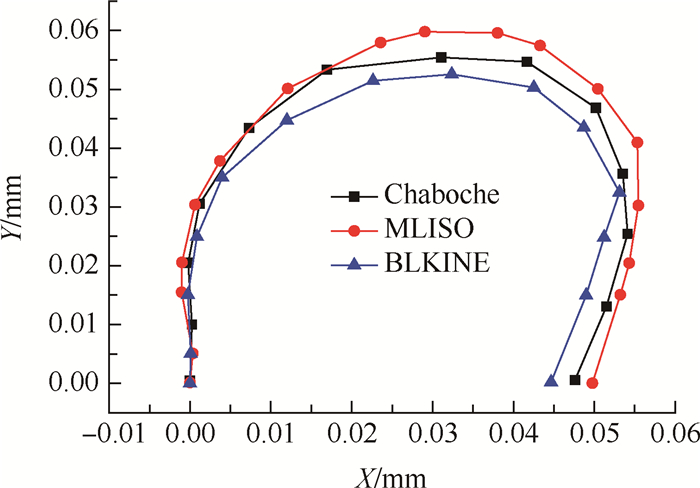
可以用压缩应力区域反映不同本构模型的闭合比,给出了单元尺寸5μm,裂纹长度9.4mm时三种本构模型压缩应力区域大小,见图 7。结果与图 6规律相符,MLISO模型的压缩应力区域最大,BLKINE模型的压缩应力区域最小,Chaboche模型的压缩应力区域介于两者之间。
|
Fig. 7 Compressive stress zone around crack tip of different constitutive model |
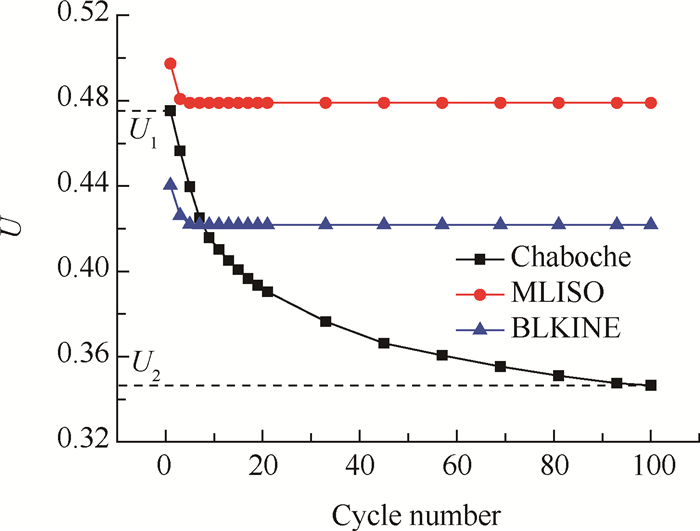
前述计算均是每两周期释放一个节点即节点释放周期为2,有限元模拟中单元尺寸与节点释放周期的比值即为裂纹扩展速率,以5μm单元尺寸且两周期释放一个节点为例,裂纹扩展速率为2.5μm/cycle,而试验测得的裂纹扩展速率仅为10-5mm/cycle量级。对于确定的有限元模型,两者的差别主要体现在节点释放周期。采用5μm单元尺寸进行计算:分别取三种本构模型,采用每两周期释放一个节点,但当裂纹扩展至9.4mm时,间隔100个周期(此时对应的有限元裂纹扩展速率为5×10-5mm/cycle,与试验吻合)再释放下一个节点从而得到闭合比随周期的变化,结果见图 8。结果显示,对于MLISO模型和BLKINE模型,当周期数从1增加到3时,闭合比会发生明显的下降,随后几乎保持不变;而对于Chaboche模型,闭合比随着周期数的增加不断降低,100周期时近似收敛。
|
Fig. 8 Crack closure ratio as a function of cycle number |
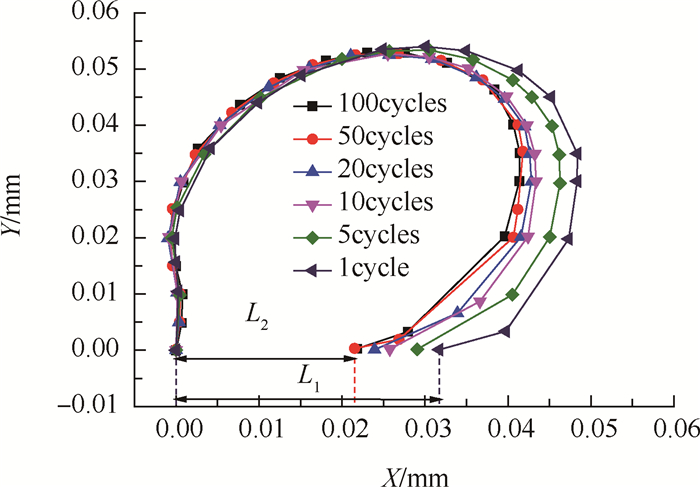
同时计算了Chaboche模型压缩应力区域随周期数的变化,结果见图 9,随着周期的增加,压缩应力区域也是逐渐变小至收敛。
|
Fig. 9 Compressive stress zone as a function of cycle numbers |
上述研究表明,使用MLISO模型和BLKINE模型,或虽然使用Chaboche模型但节点释放周期小于100,计算得到的闭合比会偏大。因此针对Chaboche模型进行闭合比修正:用某一循环的压缩应力区域尺寸L2与第一次循环的压缩应力区域尺寸L1的比值来定义修正系数
| $ \alpha = \frac{{{L_2}}}{{{L_1}}} $ | (4) |
对于本文模型,取第100个循环(此时有限元和试验的裂纹扩展速率互相吻合)对应的L作为L2。
根据图 9由长度比值定义的修正系数与根据图 8直接用闭合比比值定义的修正系数符合良好,即
| $ {U_{{\text{cor}}}} = {U_1} \times \alpha $ | (5) |
由于
| $ \Delta {K_{{\text{eff}}}} = {K_{\max }} - {K_{{\text{op}}}} $ | (6) |
考虑修正系数之后可以得到修正裂纹张开应力强度因子Kop, cor和修正有效应力强度因子范围ΔKeff, cor,并以ΔKeff, cor作为裂纹扩展驱动力进行裂纹扩展速率计算和寿命预测。
| $ {K_{{\text{op, cor}}}} = {U_{{\text{cor}}}} \times {K_{\max }} = \alpha \times U \times {K_{\max }} = \alpha \times {K_{{\text{op}}}} $ | (7) |
| $ \Delta {K_{{\text{eff, cor}}}} = {K_{\max }} - {K_{{\text{op, cor}}}} = {K_{\max }} - \alpha \times {K_{{\text{op}}}} $ | (8) |
采用工程中广泛应用的Paris公式计算裂纹扩展速率,修正后的形式见下式,其中a和N分别为裂纹长度和载荷循环数,c,m参数由试验获得[16]
| $ \frac{{{\text{d}}a}}{{{\text{d}}N}} = c\Delta {K_{{\text{eff, cor}}}}^m $ | (9) |
使用5μm单元尺寸的计算结果,拟合得到ΔKeff, cor与a的关系,再通过数值积分即可得到裂纹扩展寿命。为了验证修正的合理性,同时在另外三种条件下进行了寿命预测,即未考虑裂纹闭合、考虑了裂纹闭合但未进行修正和Paris提出的局部裂纹闭合假设,Paris推荐使用如下公式估计有效应力强度因子范围[23],其中ΔKeff, upp和ΔKeff, low分别为有效应力强度因子范围的上限和下限
| $ \Delta {K_{{\text{eff}}}} \leqslant {K_{\max }} - \frac{2}{π }{K_{{\text{op}}}} = {K_{{\text{eff, upp}}}} $ | (10) |
| $ \Delta {K_{{\text{eff}}}} \geqslant {K_{\max }} - \frac{2}{π}{K_{{\text{op}}}} - \left( {1 - \frac{2}{π }} \right){K_{\min }} = \Delta {K_{{\text{eff, low}}}} $ | (11) |
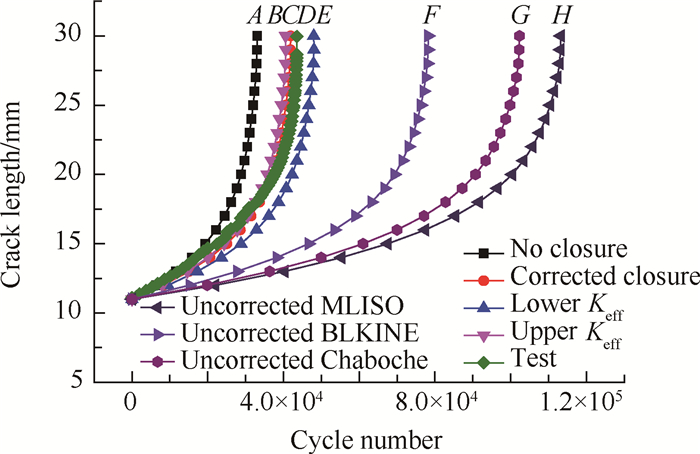
寿命预测结果见图 10,试验过程中从11mm开始记录数据,以此作为裂纹扩展起始点,并规定对应循环数为0。其中A曲线代表未考虑裂纹闭合,与试验曲线D相比偏于保守且偏差为24.11%;曲线F,G,H分别表示BLKINE,Chaboche和MLISO模型考虑裂纹闭合但未修正,与曲线D相比寿命预测过于乐观,偏差分别为79.50%,134.76%和159.80%,说明未经修正的闭合比偏大;式(10)和式(11)得到的结果分别为B和E,分别代表预测寿命的下限和上限;进行修正之后得到的曲线为C,其与曲线D相比偏差为3.86%,且介于B和E之间,因此可以认为修正是合理的,提高了寿命预测的准确性。
|
Fig. 10 Life prediction |
本文采用有限元方法模拟了FGH97的CT试样裂纹闭合效应,分析了影响闭合比的几个因素,得到如下结论:
(1)对于不同裂纹尖端单元尺寸、裂纹长度和本构模型,均可以用裂纹尖端压缩应力区域尺寸反映闭合比大小。
(2)随着裂纹扩展,闭合比先从较小值迅速增加,随后变化速率降低直至稳定;裂纹尖端单元尺寸从40μm减小至3μm,闭合比也不断增大直至稳定。
(3)单元尺寸为5μm时,各向同性硬化模型的闭合比约为0.51,随动硬化模型的闭合比约为0.44,Chaboche模型的闭合比约为0.48。
(4)对于Chaboche模型,随着周期数的增加,压缩应力区域尺寸和闭合比都逐渐降低;可以通过选择适当的周期数以得到闭合比修正系数和修正有效应力强度因子范围。
(4)对闭合比和有效应力强度因子范围进行修正之后,寿命预测的精度明显提高,与试验结果偏差仅为3.86%。
| [1] |
魏大盛, 王延荣. 粉末冶金涡轮盘裂纹扩展寿命分析[J]. 推进技术, 2008, 29(6): 753-758. (WEI Dasheng, WANG Yan-rong. Lifing Methodology of Crack Propagation in Powder Metallurgy Turbine Disk[J]. Journal of Propulsion Technology, 2008, 29(6): 753-758.)
(  0) 0) |
| [2] |
刘德林, 李影, 姜涛, 等. FGH97粉末高温合金的断裂特征[J]. 机械工程材料, 2013, 37(11): 49-54. (  0) 0) |
| [3] |
张义文, 刘建涛. 粉末高温合金研究进展[J]. 中国材料进展, 2013, 32(1): 1-11. (  0) 0) |
| [4] |
张莹, 张义文, 张娜, 等. 粉末冶金高温合金FGH97的低周疲劳断裂特征[J]. 金属学报, 2010, 46(4): 444-450. (  0) 0) |
| [5] |
佴启亮, 董建新, 张麦仓, 等. 粉末高温合金FGH97疲劳裂纹扩展行为[J]. 工程科学学报, 2016, 38(2): 248-256. (  0) 0) |
| [6] |
袁善虎, 魏大盛, 王延荣. FGH97缺口试样基于黏塑性本构的弹塑性响应分析[J]. 航空动力学报, 2012, 27(10): 2348-2355. (  0) 0) |
| [7] |
刘浩, 鲍蕊, 岳晨阳, 等. 应力强度因子变程相关的FGH97蠕变-疲劳裂纹扩展主导因素[J]. 航空动力学报, 2016, 31(6): 1400-1407. (  0) 0) |
| [8] |
Elber W. Fatigue Crack Closure under Cyclic Tension[J]. Engineering Fracture Mechanics, 1970, 2(1): 37-44. DOI:10.1016/0013-7944(70)90028-7
(  0) 0) |
| [9] |
Newman J C Jr. A Crack Opening Stress Equation for Fatigue Crack Growth[J]. International Journal of Fracture, 1984, 24(4): 131-135. DOI:10.1007/BF00020751
(  0) 0) |
| [10] |
Dougherty J D. Fatigue Crack Propagation and Closure Behavior of Modified 1070 Steel: Finite Element Study[J]. Engineering Fracture Mechanics, 1997, 56(2): 189-212. DOI:10.1016/S0013-7944(96)00104-X
(  0) 0) |
| [11] |
Solanki Kiran J C, Newman Newman Jr. Finite Element Analysis of Plasticity-Induced Fatigue Crack Closure: an Overview[J]. Engineering Fracture Mechanics, 2004, 71(2): 149-171. DOI:10.1016/S0013-7944(03)00099-7
(  0) 0) |
| [12] |
Antunes F V, Rodrigues D M. Numerical Simulation of Plasticity Induced Crack Closure: Identification and Discussion of Parameters[J]. Engineering Fracture Mechanics, 2008, 75(10): 3101-3120. DOI:10.1016/j.engfracmech.2007.12.009
(  0) 0) |
| [13] |
李亚智, 李学峰. 疲劳裂纹闭合的数值模拟方法[J]. 机械科学与技术, 2006, 25(10): 1233-1237. DOI:10.3321/j.issn:1003-8728.2006.10.028 (  0) 0) |
| [14] |
李学峰. 疲劳裂纹闭合效应数值模拟方法研究[D]. 西安: 西北工业大学, 2005. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y711760
(  0) 0) |
| [15] |
左平, 魏大盛, 王延荣. FGH95粉末高温合金裂纹闭合效应及裂纹扩展特性研究[J]. 材料工程, 2015, 43(8): 56-61. DOI:10.11868/j.issn.1001-4381.2015.08.010 (  0) 0) |
| [16] |
袁善虎. 粉末冶金材料及结构的力学行为试验与数模模拟[D]. 北京: 北京航空航天大学, 2014. http://jme.biam.ac.cn/CN/10.11868/j.issn.1001-4381.2015.08.010
(  0) 0) |
| [17] |
Pommier S. A Study of the Relationship Between Variable Level Fatigue Crack Growth and the Cyclic Constitutive Behavior of Steel[J]. International Journal of Fatigue, 2001, 23(Supplement1): S111-S118.
(  0) 0) |
| [18] |
McClung R C, Sehitoglu H. On the Finite Element Analysis of Fatigue Crack Closure-1. Basic Modeling Issues[J]. Engineering Fracture Mechanics, 1983, 33(2): 237-252.
(  0) 0) |
| [19] |
Roychowdhury S. A Numerical Investigation of 3D Small-Scale Yielding Fatigue Crack Growth[J]. Engineering Fracture Mechanics, 2003, 70(17): 2363-2383. DOI:10.1016/S0013-7944(03)00003-1
(  0) 0) |
| [20] |
Solanki Kiran J C. Newman Jr. Finite Element Modeling of Plasticity-Induced Crack Closure with Emphasis on Geometry and Mesh Refinement Effects[J]. Engineering Fracture Mechanics, 2003, 70(12): 1475-1489. DOI:10.1016/S0013-7944(02)00168-6
(  0) 0) |
| [21] |
陈亚龙, 杨晓光, 石多奇. 带保载平面应变塑性诱发裂纹闭合效应[J]. 航空动力学报, 2010, 25(9): 2030-2035. (  0) 0) |
| [22] |
袁善虎, 王延荣, 魏大盛. 考虑应力松弛的缺口疲劳寿命预测方法[J]. 推进技术, 2014, 35(5): 681-687. (YUAN Shan-hu, WANG Yan-rong, WEI Dasheng. Method for Fatigue Life Prediction of Notched Specimen with Considered Stress Relaxation[J]. Journal of Propulsion Technology, 2014, 35(5): 681-687.)
(  0) 0) |
| [23] |
Paris P C, Hiroshi Tada, Donald J K. Service Load Fatigue Damage-a Historical Perspective[J]. International Journal of Fatigue, 1999, 21(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


