静压推力轴承是重型数控装备的关键部件,在高速重载工况运行过程中由于油膜剪切和挤压共同作用,旋转工作台和底座产生不均匀变形,静压承载能力下降,严重时就会发生干摩擦,因此需要寻求一种补偿静压损失的措施,来提高极端工况下静压推力轴承高精度稳定运行。
陈燕生[1]将扇形多垫平面推力轴承的油垫简化为矩形,求得其承载力、刚度等计算公式,但未涉及承载力损失及补偿问题。王少力等[2]恒流供油扇形静压推力轴承承载力的计算,推导了计入离心力因素的恒流供油扇形静压推力轴承承载力解析计算公式,设计了重型液体静压转台实验系统,并进行实验研究,但未提及静压损失问题。Xiong Wanli等[3]分析并模拟了高精密数控机床主轴的动静压结合支撑方式,研究了在这一支撑方式下主轴的变形,以及油膜的润滑等性能,但此类支承为径向轴承。赵明等[4]总结预载恒流静压导轨的重型数控立车的工作台静压计算时必须考虑结构变形对油膜厚度的影响,因此该计算问题为静压-结构耦合问题,提出一种计算刚性位移的方法,但未探讨极端工况时静压支承的承载力损失问题。Johnson Robert E等[5]使用ABAQUS软件模拟仿真了闭式支承的承载表面变形对静压支撑的油腔内流量,液压油的承载能力,以及油腔内的压力分布,最终表明承载的平面为凹平面时静压推力轴承承载力能力较大。Osterie J F等和Kapur V K等研究了圆形油腔平面推力轴承的承载力[6~8]。Osterie J F等[7]研究了流体惯性力对静压止推轴承性能影响以及气穴现象,指出惯性力对静压止推轴承的承载力影响显著;Kapur V K等[8]研究流体热效应和惯性力共同作用对液体静压推力轴承性能影响,得到了绝热条件下油膜承载力表达式和压力分布图。韩东江和钟冲等研究了静压推力轴承的润滑特性,得到了一些有意义的结论,指导了静压推力轴承的优化设计,解决了工程实际中的具体问题[9~14]。于晓东研究了高速重载对静压推力轴承油膜厚度的影响,发现随着旋转工作台转速升高和承载增大,惯性流量、剪切和挤压热增大,润滑油粘度下降,致使油膜厚度变薄,局部出现油膜破裂和干摩擦,导致静压支承摩擦失效[15]。于晓东等采用流固耦合方法对圆形腔静压支承摩擦副的温度分布规律及其速度特性进行了分析,间隙油膜在挤压和剪切以及泵功耗联合作用下产生的热,通过流固耦合方式传递给静压导轨和油垫,进而扩散到整个旋转工作台和底座。间隙油膜接触处摩擦副温度最高,向四周扩散温度逐渐降低。随着旋转工作台转速增加,油膜温度上升,工作台上表面和侧面温度下降,并趋于平缓,底座侧面温度从下到上先升高后降低[16]。
根据国内外参考文献综述发现,上述研究均未深入分析推力轴承承载力降低的原因及补偿的办法。针对恒流供油双矩形腔静压推力轴承极端工况运行过程中承载力降低问题,推导了其静压性能损失解析计算公式,设计了新型油垫可倾式静压支承结构,并提出了静压损失动压补偿的想法,达到了增加极端工况静压推力轴承运行精度和稳定性的效果。
2 油垫可倾式静压推力轴承结构及动压形成机理 2.1 油垫可倾式静压推力轴承结构油垫可倾式静压推力轴承主要由旋转工作台、动静压油垫和机床底座三部分组成[17~19]。该静压推力轴承为开式恒流支承结构,并用回油槽隔开,底座上均匀分布十二个可倾式静压油垫,可倾式油垫下方为一块窄矩形凸台,与底座采用双销间隙配合连接,即为可倾式静压油垫,使油垫实现周向和径向可倾,其结构如图 1和图 2所示。构造合理有效的动静压油垫,利用动压补偿静压损失,以改善动静压推力轴承在工作过程中的静压失效问题。
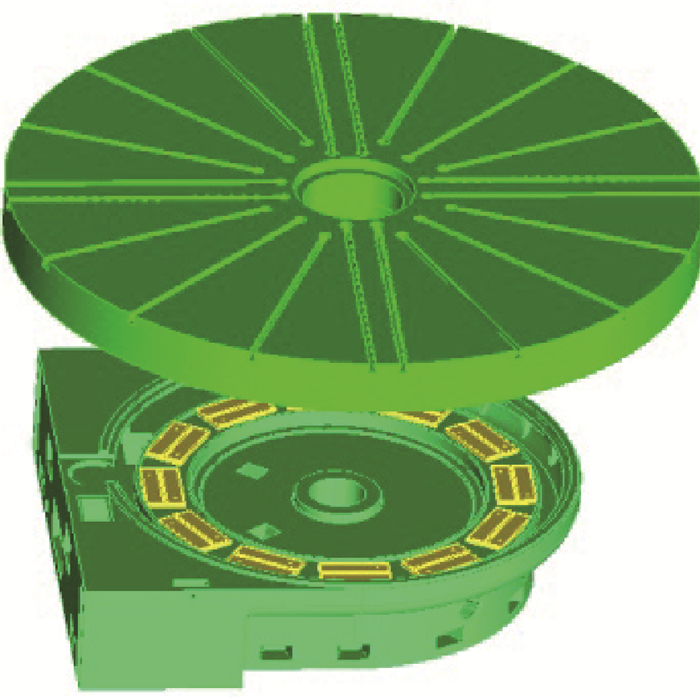
|
Fig. 1 Geometry structure of the hydrodynamic thrust bearing |

|
Fig. 2 Structure of tilting type hydrostatic oil pad |
油垫可倾式静压推力轴承运行过程中,由于受力作用,油垫发生周向和径向倾斜,两个相对运动的摩擦副表面间形成楔形间隙,两相对运动表面间具有一定的相对滑动速度,且速度方向使润滑油从楔形大口流进,小口流出,间隙油膜具有一定粘度,且充分供油,符合动压形成原理,产生动压,实际应用结构如图 3所示。

|
图 3 Instance of tilting type hydrostatic oil pad |
双矩形腔静压推力轴承油腔结构尺寸如图 4所示。
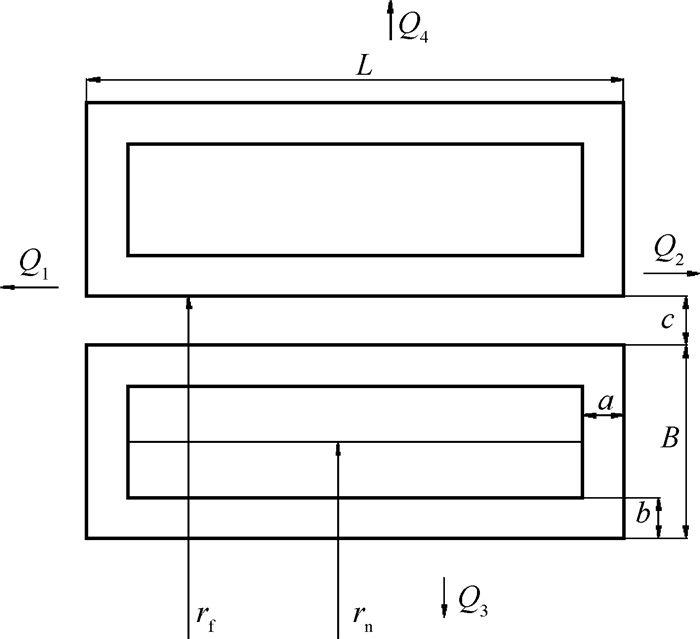
|
Fig. 4 Oil cavity structure size of double rectangular hydro static thrust bearing |
顺流流量
| $ {Q_1} = \frac{{{h^3}\Delta p\left( {B - b} \right)}}{{6\mu a}} - \frac{{\mu h}}{2}\left( {B - b} \right)w{R_{{\text{ne}}}} $ | (1) |
式中Δp为中心油腔压力;rn为旋转中心到第一个油腔中心的距离,rf为旋转中心到第二个油腔中心的距离。
逆流流量
| $ {Q_2} = \frac{{{h^3}\Delta p\left( {B - b} \right)}}{{6\mu a}} + \frac{1}{2}\left( {B - b} \right)w{R_{{\text{ne}}}} $ | (2) |
式中
| $ {Q_3} = \frac{{{h_3}{l_{{\text{ne}}}}\Delta p}}{{12\mu b}} - \frac{{\text{π }}}{{20\mu }}\rho {h^3}{w^2}{\left( {{r_{\text{n}}} + \frac{b}{2}} \right)^2}{r_{{\text{n1}}}}^2 $ | (3) |
离心力下内圆弧封油边流量
| $ {Q_4} = \frac{{{h^3}{l_{{\text{ne}}}}\Delta p}}{{12\mu b}} + \frac{{\text{π }}}{{20\mu }}\rho {h^3}{w^2}{\left( {{r_{\text{n}}} + B - \frac{b}{2}} \right)^2}{r_{{\text{n2}}}}^2 $ | (4) |
式中
供油流量
| $ \begin{gathered} {Q_0} = {Q_1} + {Q_2} + {Q_3} + {Q_4} = \hfill \\ \frac{{{h^3}{b_{{\text{ne}}}}\Delta p}}{{3\mu a}} + \frac{{{h^3}{l_{{\text{ne}}}}\Delta p}}{{6\mu b}} + \frac{{{\text{π }}\rho {h^2}{w^2}\left( {{r_{{\text{n2}}}}^2 - {r_{{\text{n1}}}}^2} \right)}}{{20\mu }} \hfill \\ \end{gathered} $ | (5) |
令
| $ \begin{gathered} {b_{{\text{ne}}}} = B - b, {b_{{\text{fe}}}} = B - b, {l_{{\text{ne}}}} = L - a, \hfill \\ {k_{{\text{n1}}}} = \frac{{{b_{{\text{ne}}}}}}{{3a}}, {k_{{\text{n2}}}} = \frac{{{l_{{\text{ne}}}}}}{{6b}}, {k_{{\text{n3}}}} = \frac{{{\text{π }}\rho }}{{20}} \hfill \\ \end{gathered} $ |
上式简化为
| $ {Q_0} = {k_{{\text{n1}}}}\frac{{{h^3}\Delta p}}{\mu } + {k_{{\text{n2}}}}\frac{{{h^3}\Delta p}}{\mu } + {k_{{\text{n3}}}}\frac{{{h^3}{w^2}\left( {{r_{{\text{f2}}}}^2 - {r_{{\text{f1}}}}^2} \right)}}{\mu } $ | (6) |
单个油腔压力
| $ \Delta {p_{\text{n}}}=\frac{{\mu {Q_0} - {k_{{\text{n3}}}}{h^3}{w^2}\left( {{r_{{\text{n2}}}}^2 - {r_{{\text{n1}}}}^2} \right)}}{{\left( {{k_{{\text{n1}}}} + {k_{{\text{n2}}}}} \right){h^3}}} $ | (7) |
单个油腔静压承载力
| $ W = \Delta {p_{\text{n}}}{A_{\text{e}}} $ | (8) |
| $ W = \frac{{\mu {Q_0}{A_{\text{e}}}}}{{\left( {{k_{{\text{n1}}}} + {k_{{\text{n2}}}}} \right){h^3}}} - \frac{{{k_{{\text{n3}}}}{h^3}{w^2}\left( {{r_{{\text{n1}}}}^2 - {r_{{\text{n2}}}}^2} \right){A_{\text{e}}}}}{{\left( {{k_{{\text{n1}}}} + {k_{{\text{n2}}}}} \right){h^3}}} $ | (9) |
式(9)中第一项为离心力引起的承载力变化量,即为静压承载力的损失量
| $ {Q_{\text{s}}} = \frac{{\mu {Q_0}{A_{\text{e}}}}}{{\left( {{k_{{\text{n1}}}} + {k_{{\text{n2}}}}} \right){h^3}}} $ | (10) |
当静压推力轴承在高速重载极端状况下运行时,热力耦合作用下的摩擦副变形不均匀,导致支承油膜厚度减小且不均匀,出现静压承载力不足,支承摩擦副直接接触失效[20, 21]。需要通过动压改善间隙油膜厚度的均匀性,弥补静压承载力的不足,动压的增加量能有效补偿静压的损失量,从而达到增加极端工况静压推力轴承运行精度和稳定性的效果。
4 矩形凸台宽度对动压效应影响及补偿设旋转工作台与油膜接触面对称中心线上导轨内外侧两点A和B,油垫对称中心线上内外侧两点C和D,如图 5所示。

|
Fig. 5 A, B, C and D point of hydrostatic bearing friction pairs |
为了限制油垫的最大变形,在极端工况35t,160r/min条件下,取凸台长度为油垫长度,凸台高度为1.5mm,研究凸台宽度5~55mm时油垫总变形。限于篇幅仅给出分析结果如图 6所示,不同凸台宽度与油垫最大变形关系如图 7所示。油垫对称中心线上内外侧两点C和D的Z向变形与凸台宽度的关系如表 1所示。

|
Fig. 6 Deformation of oil pad with different convex platform width |
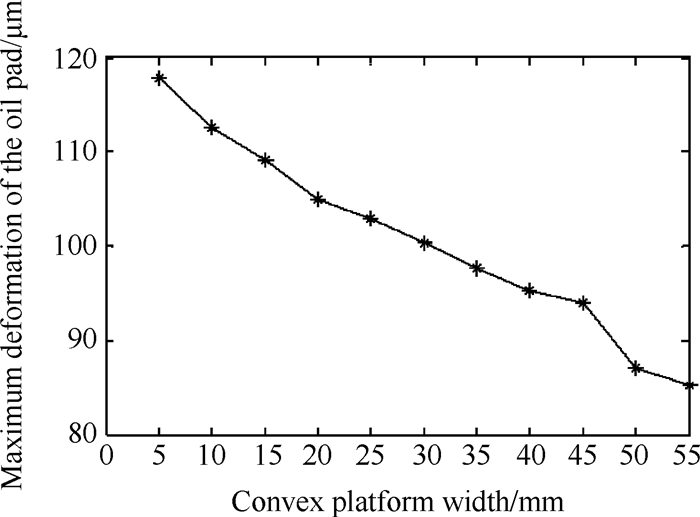
|
Fig. 7 Relationship between the maximum deformation of the oil pad and convex platform width |
|
|
Table 1 Z direction deformation of D, C point in the oil pad with different convex platform width |
由图 6可以发现:不同凸台宽度时油垫总变形随着旋转半径的增加而增加,并且增长速率逐渐增大,变形呈上翘趋势,这说明油膜下表面变形也呈现上翘趋势。由于施加在旋转工作台上的温度场与压力场不变,所以旋转工作台导轨变形不发生变化,油膜上表面与油膜下表面变形均呈上翘趋势,表明凸台宽度变化所形成的动压对油膜变形起均化作用,即油垫变形能够适应导轨变形,达到补偿静压损失的效果。
由表 1与图 6数据可知油垫变形在凸台宽度为5~55mm呈逐渐减小趋势,主要由于凸台宽度为零时,相当于静压支承,没有动压产生,凸台宽度为5mm,动压产生,而且较大,补偿静压损失比较多,油膜变形量小,油膜厚度变化少,随着宽度增大,动压作用逐渐减弱,补偿静压损失较小,油膜变形进一步加大,与无凸台油垫相比油膜变形量小,油膜厚度也能够相对稳定,当凸台宽度增加到油垫宽度时,动压为零,不能起到补偿静压损失的作用,油膜变形无改善。由表 1又可发现油垫D点与C点Z向变形随着凸台宽度增大而减小,且其变形值均为正值,由旋转工作台导轨变形不变,所以A,B点变形不变,通过每种工况下C,D点的变形即可得到油膜的预测模型图,凸台宽度35mm时油膜预测模型如图 8所示,油膜形状由初始设计油膜厚度155μm平行间隙变为一端152.1μm另一端为159.4μm的楔形间隙。
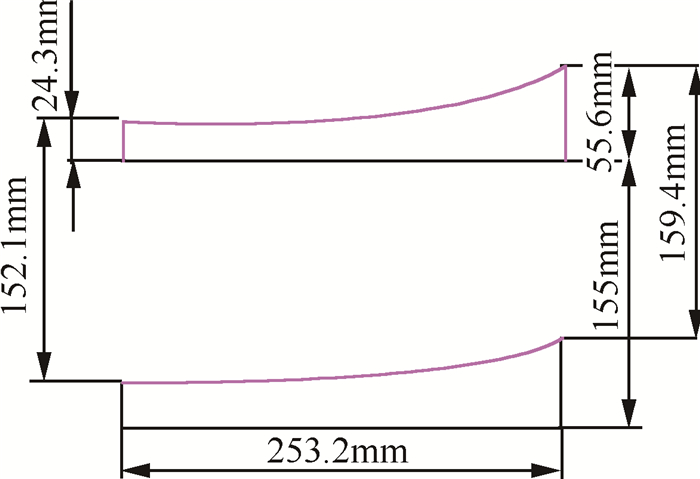
|
Fig. 8 Prediction model of oil film with convex platform width 35mm |
为了保证静压推力轴承稳定运转,尽量使油膜厚度保持相对恒定,从油膜预测模型图中可以看出在凸台宽度为35mm时油膜最大变形与油膜最小变形都是最接近于155μm,所以当凸台宽度为35mm时能够使油膜保持相对稳定。
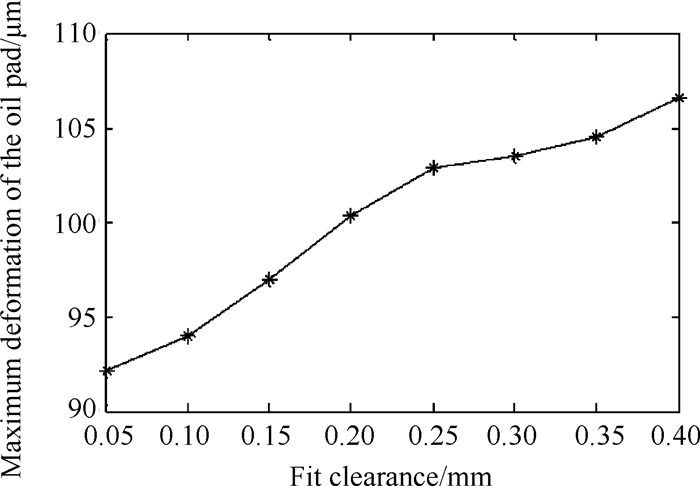
5 销连接配合间隙对动压效应影响及补偿在凸台宽度为35mm,高度为1.5mm和长度为油垫长度结构参数此基础上,进一步调整油垫与底座双销连接配合间隙使油垫周向可倾。模拟销与底座配合间隙为0.05~0.4mm时油垫总变形,配合间隙与油垫最大变形关系如图 9。油垫对称中心线上内外侧两点C和D的Z向变形与配合间隙的关系如表 2所示。
|
Fig. 9 Relationship between the maximum deformation of the oil pad and fit clearance |
|
|
Table 2 D, C point Z to deformation of the oil pad under different fit clearance |
凸台长度为油垫长度,宽度为35mm,高度为1.5mm,双销与底座配合间隙为0.25mm油膜预测模型如图 10所示,由表 2可知配合间隙为0.25mm时,油膜均化作用被进一步调整,油膜厚度能够保持较好的稳定值,约0.155mm左右,油膜厚度均化效果最好,动压很好地补偿静压损失。
通过调整凸台宽度、高度及双销连接配合间隙,使油膜厚度能够保持相对的稳定值0.155mm,仿真结果表明凸台宽度为35mm,高度为1.5mm,长度为油垫长度,配合间隙为0.25mm时,动压效应相对较好,动压增量能够明显补偿静压损失量。

|
Fig. 10 Prediction model of oil film with fit clearance 0.25mm |
实验选用46号液压油,工作载荷35t,工作台转速160r/min,可倾油垫底部支承宽度15mm,35mm,55mm,高度1.5mm,油垫底部与静压支承底座采用配合间隙为0.25mm。用点温仪测量润滑油出口温度,以控制油温,保证润滑油粘度在工作范围内。通过液压泵供油,限定油膜厚度为0.155mm,油膜初始厚度变化由油膜厚度测量表监测,保证动静压推力轴承正常工作。通过位移传感器示值监测油膜厚度变化,将位移传感器放在油膜下表面与油垫接触处油垫的D点与C点,分别为位移传感器1和位移传感器2,记录动静压推力轴承不同工况下稳定运行时BD,AC相对位移实验数据,即油垫变形。实验装置、数据采集系统和位移传感器如图 11~13所示。

|
Fig. 11 Test device |

|
Fig. 12 Data acquisition system |

|
Fig. 13 Displacement transducer |
通过数据采集系统采集两个位移传感器读数,测得如下数据如表 3所示,并与仿真BD和AC油膜厚度对比。
|
|
Table 3 Comparison of experimental and simulation oil film thickness with different convex platform width |
由表 3实验数据可以发现BD和AC间油膜厚度随着其宽度增加而增加,总体BD间油膜厚度大于AC间油膜厚度,表明油膜内侧的变形要小于外侧变形,在凸台宽度为35mm时,两侧油膜厚度较为接近0.155mm。
在凸台宽度为35mm,高度1.5mm,油垫与底座双销连接配合间隙为0.25mm时,BD和AC间的油膜厚度与仿真值一致性较好,油膜厚度接近0.155mm初始油膜厚度,误差为5.2%。
7 结论通过本文研究,得到结论如下:
(1)推导了极端工况条件下双矩形腔静压推力轴承静压承载性能损失量理论计算公式,设计了一种新型可倾式油垫结构,油垫底部由矩形凸台支承,矩形凸台与底座采用双销间隙连接结构,实现了油垫周向及径向可倾。
(2)确定了支承凸台长度为油垫长度,宽度为35mm,高度为1.5mm,油垫与底座双销连接配合间隙为0.25mm可倾油垫最佳结构参数和装配关系。
(3)该结构参数时动压效应较为明显,油膜均化效果较好,动压增量能够很好地补偿静压损失量,油膜变形相对较小,油膜能够保持相对稳定厚度,油膜形状为一端152.8μm另一端为154.6μm的楔形间隙,更接近初始设计油膜厚度155μm平行间隙,实验与仿真数据对比误差为5.2%,起到产生动压并补偿静压损失的作用。
| [1] |
陈燕生. 液体静压支承原理和设计[M]. 北京: 国防工业出版社, 1980.
(  0) 0) |
| [2] |
王少力, 熊万里, 孟曙光. 离心力对恒流供油扇形静压推力轴承承载力的影响分析[J]. 机械强度, 2014, 36(5): 716-722. (  0) 0) |
| [3] |
Xiong Wanli, Yang Xuebing, Lv Lang, et al. Review on Key Technology of Hydrodynamic and Hydrostatic High-Frequency Motor Spindles[J]. Journal of Mechanical Engineering, 2009, 45(9): 1-18. DOI:10.3901/JME.2009.09.001
(  0) 0) |
| [4] |
赵明, 黄正东, 王书婷, 等. 重型数控立车工作台静压计算[J]. 机械工程学报, 2009, 45(9): 120-125. (  0) 0) |
| [5] |
Johnson Robert E, Manring Noah D. Translating Circular Thrust Bearings[J]. Journal of Fluid Mechanics, 2005, 530: 197-212. DOI:10.1017/S0022112005003782
(  0) 0) |
| [6] |
Osterle J F, Hughes W F. The Effect of Lubricant Inertia in Hydrostatic Thrust Bearing Lubrication[J]. Wear, 1957, 6(1): 465-471.
(  0) 0) |
| [7] |
Osterle J F, Hughes W F. Inertia-Induced Cavitation in Hydrostatic Thrust Bearings[J]. Wear, 1961, 4(3): 228-233. DOI:10.1016/0043-1648(61)90124-7
(  0) 0) |
| [8] |
Kapur V K, Kamlesh Verma. The Simultaneous Effects of Inertia and Temperature on the Performance of a Hydrostatic Thrust Bearing[J]. Wear, 1979(54): 113-122.
(  0) 0) |
| [9] |
韩东江, 杨金福, 陈昌婷, 等. 轴承供气压力对静压气体轴承-转子系统动力学特性影响的实验[J]. 推进技术, 2014, 35(9): 1265-1270. (HAN Dong-jiang, YANG Jin-fu, CHEN Chang-ting, et al. Experimental Research for Effects of Bearing Supply Gas Pressure on Aerostatic Bearing-Rotor System Dynamic Characteristics[J]. Journal of Propulsion Technology, 2014, 35(9): 1265-1270.)
(  0) 0) |
| [10] |
钟冲, 刘振侠, 胡剑平, 等. 轴承腔壁面油膜厚度超声测量实验研究[J]. 推进技术, 2014, 35(8): 1110-1115. (ZHONG Chong, LIU Zhen-xia, HU Jianping, et al. Experimental Study of Ultrasonic Measurement of Oil Film Thickness in Bearing Chamber Wall[J]. Journal of Propulsion Technology, 2014, 35(8): 1110-1115.)
(  0) 0) |
| [11] |
Zhang Yan-Qin, Fan Li-Guo. Simulation and Experimental Analysis on Supporting Characteristics of Multiple Oil Pad Hydrostatic Bearing Disk[J]. Journal of Hydrodynamics, 2013, 25(2): 236-241. DOI:10.1016/S1001-6058(13)60358-3
(  0) 0) |
| [12] |
Yanqin Zhang, Weiwei Li, Zeyang Yu. Flow Criterion Research on Fluid in Hydrostatic Bearing from Laminar to Turbulent Transition[J]. International Journal of Hybrid Information Technology, 2014, 7(3): 369-374.
(  0) 0) |
| [13] |
Yanqin Zhang, Yao Chen, Zeyang Yu. Influence of Strengthening Rib Location on Temperature Distribution of Heavy Vertical Lathe Worktable[J]. International Journal of u-and e-Service, Science and Technology, 2014, 7(1): 65-71.
(  0) 0) |
| [14] |
Yan Qin Zhang, Wei Wei Li, Li Guo Fan. Simulation and Experimental Analysis of Influence of Inlet Flow on Heavy Hydrostatic Bearing Temperature Field[J]. Asian Journal of Chemistry, 2014, 26(17): 5478-5482.
(  0) 0) |
| [15] |
于晓东, 孙丹丹, 吴晓刚, 等. 环形腔多油垫静压推力轴承膜厚高速重载特性[J]. 推进技术, 2016, 37(7): 1350-1355. (YU Xiao-dong, SUN Dan-dan, WU Xiao-gang, et al. High Speed and Heavy Load Characteristic on Oil Film Thickness of Annular Recess MultiPad Hydrostatic Thrust Bearing[J]. Journal of Propulsion Technology, 2016, 37(7): 1350-1355.)
(  0) 0) |
| [16] |
于晓东, 吴晓刚, 隋甲龙, 等. 环形腔多油垫静压推力轴承膜厚高速重载特性[J]. 推进技术, 2016, 37(10): 1350-1355. (YU Xiao-dong, WU Xiao-gang, SUI Jia-long, et al. Numerical and Experimental Study on Temperature Field of Hydrostatic Bearing Friction Pairs[J]. Journal of Propulsion Technology, 2016, 37(7): 1350-1355.)
(  0) 0) |
| [17] |
庞志成. 液体气体静压技术[M]. 哈尔滨: 黑龙江人民出版社, 1981.
(  0) 0) |
| [18] |
丁振坤. 液体静压支承设计[M]. 上海: 上海科学技术出版社, 1986.
(  0) 0) |
| [19] |
陈伯贤. 流体润滑理论及其应用[M]. 北京: 机械工业出版社, 1991.
(  0) 0) |
| [20] |
韩占忠, 王敬, 兰小平. FLUENT流体工程仿真计算实例与应用[M]. 北京: 北京理工大学出版社, 2004.
(  0) 0) |
| [21] |
王福军. 计算流体动力学分析—FLUENT软件原理与应用[M]. 北京: 北京清华大学出版社, 2004.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

