2. 中国航发湖南动力机械研究所,湖南 株洲 412002
2. AECC Hunan Aviation Powerplant Research Institute, Zhuzhou 412002, China
随着现代涡轮发动机技术的发展,涡轮前温度逐渐提高,涡轮叶片的热负荷逐渐增加,因此需要先进的冷却方式来保证发动机热端部件的正常工作[1]。典型的涡轮叶片外部冷却方式为气膜冷却,即在涡轮叶片表面及端壁附近布置一排或多排离散气膜孔以达到冷却的目的。目前,大部分的气膜冷却设计中都采用圆柱型气膜孔的冷却方式,但是根据学者们[2, 3]的研究发现,圆柱型气膜孔由于存在射流动量集中、穿透性较强、覆盖性较弱的缺点,射流冷气的利用率较低。因此,在圆柱型气膜孔的基础上对几何结构进行优化改进成为了气膜冷却研究中的重要分支。
气膜孔结构的改进主要从两个方面进行:(1)改进气膜孔的形状(异形气膜孔),包括气膜孔进口及出口形状的改进;(2)在圆柱型气膜孔的基础上设置扰流或整流结构,包括突片、突脊、凹坑等[4~6]。Gold-stein等[7]最早开始对异形气膜孔进行研究,他们研究了扇形气膜孔(在圆柱型气膜孔的基础上出口进行流向、展向扩张)的气膜冷却效率,结果表明扇形孔的气膜覆盖范围相比于圆柱型气膜孔有较大提升,同时气膜冷却效率也有较大提高。Hyams等[8]研究了五种异形气膜孔结构的气膜冷却效果,结果表明,在气膜孔出口进行展向扩张能够有效提高气膜冷却效率。对扇形孔影响较大的几种几何结构参数,学者们进行了进一步的分析研究[9~12],包括孔的长径比、进出口面积比、孔间距、气膜孔倾角等。结果表明,对扇形孔的流动及换热特性影响较大的参数为气膜孔间距及气膜孔流向倾角。学者们在扇形孔的基础上进一步发展,Makki等[13]通过实验研究了前倾扇形孔(簸箕形孔)的冷却特性,结果表明相比于圆柱型气膜孔,簸箕形气膜孔的冷却效率有20%左右的提升。Lee等[14]提出了一种新型类扇形气膜孔并与扇形孔等其他孔型进行了对比,结果表明新型气膜孔能够有效提高气膜冷却效率。Issakhanian等[15]提出了一种椭圆形气膜孔并通过实验研究了该新型气膜孔的冷却效率,结果表明,通过气膜孔型的改进气膜冷却效率有较大提高。Sargison等[16, 17]提出了一种收缩扩张型气膜孔,其基本结构为展向扩张、流向收缩、出口面积减小的结构。该结构的冷却效率及换热系数均高于扇形气膜孔,且其引起的叶栅气动损失远比扇形孔小。国内学者对气膜孔的改进同样进行了研究[18~21]。李广超等[18]研究了圆柱孔和不同出口宽度双向扩张孔气膜冷却特性。刘聪等[19]通过实验研究了单排簸箕型气膜孔的冷却效率并分析了多个气动参数对其分布规律的影响。Bai等[20]采用数值计算和实验结合的方式研究了双扇形孔的气膜冷却效果,研究中动量比I=0.5,1和2,湍流度为Tu= 2%。结果表明:在研究动量比范围内,双扇形孔相比圆柱形孔有更大的流量系数;双扇形孔有更好的气膜冷却效果,展向覆盖更好。Yang等[21]通过数值模拟比较了圆柱形孔、豆形孔、三叶草形孔和雪花形孔,结果表明在吹风比为0.5时三种新孔型与圆柱形孔有相同的气膜冷却效果,然而随着吹风比增加,三种新孔型的冷却效果更好,并且从总体冷却效果来说,豆形孔是最佳孔形。
从气膜冷却孔的研究进展来看,气膜孔型的变化主要就是为了通过孔型的不断改进以达到改善其流场特性及换热特性、提高气膜冷却效率的目的。本文在前人研究的基础上,研究了一种新型的边倒圆型气膜孔,并通过实验及计算验证了新型孔的冷却效率、换热系数以及流量系数的特性规律,发现研究的边倒圆孔在这三项指标上都有改善,丰富了气膜冷却孔型方面的相关内容,为此类孔形的进一步研究奠定基础。
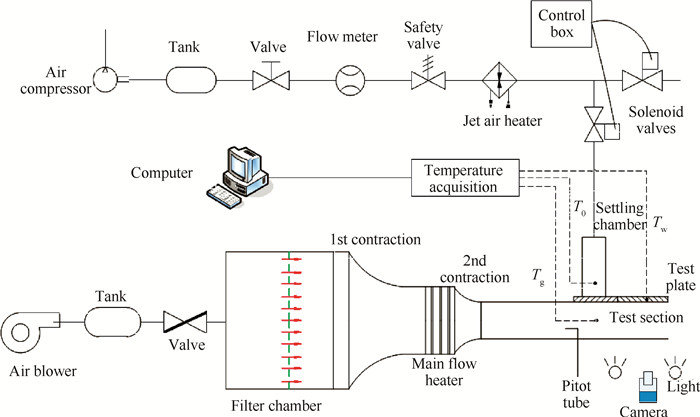
2 实验装置及测量方法 2.1 实验装置本实验系统是一低速回流风洞系统,由风机、管道、主流通道、二次流通道和测量段组成,如图 1所示。主流由鼓风机供气,经储气罐和管道后,由蝶阀控制进入主流通道,实验时可以通过控制蝶阀的开度来控制主流流量。然后主流进入稳流段,稳流段内布置了阻尼网,能够使得主流较均匀地进入到收缩段。阻尼网后还有一过滤网,可以滤掉空气中的杂质,进一步起到整流的作用。收缩段按照维托辛斯基曲线设计。主流经过收缩段后均匀地经过快速加热器,快速加热器为多层金属网状加热器,具有加热均匀、响应快的特点,该加热器连接到直流电源上,由电脑端的控制系统控制。可以通过控制输入电流改变主流的温度。二次流由螺杆式空气压缩机供气,经过管道、手动阀门、流量计和加热器进入气膜孔。二次流的流量大小通过下方的控制阀门调节。之后经过二次流加热器,二次流温度通过调节电压大小控制。经过加热器后的二次流由电磁阀控制流向:实验开始前,二次流排向室内环境中;实验开始时,关闭控制气流通向室内的电磁阀,打开控制气流通向二次流腔的电磁阀,二次流经二次流腔后通过气膜孔进入主流通道。在二次流腔有机玻璃板上靠近气膜孔位置布置有两个热电偶,用来测量二次流温度。
|
Fig. 1 Schematic of experimental setup |
实验测量段由主流通道,气膜孔板,实验测量板共同组成。为了让主流边界层重新发展,实验测量段距离气膜孔19倍孔径处设置30°倾角的劈缝结构。实验中采用模块化设计,通过更换不同的气膜孔板来实现对不同气膜孔型的实验测量。实验中应用热电偶测量主流以及二次流的来流温度。在热电偶前布置皮托管测量主流速度。
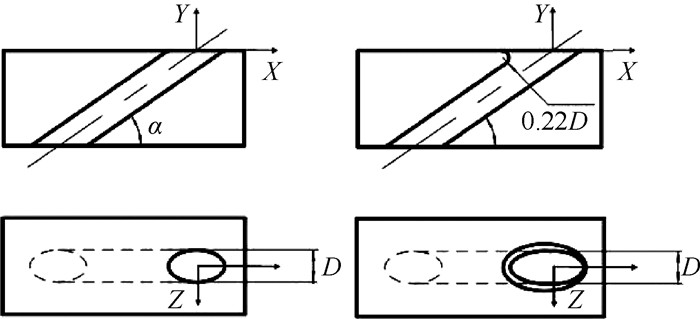
实验中研究的边倒圆型气膜孔与圆柱型气膜孔的结构简图如图 2所示。圆柱型气膜孔孔径D= 10mm,长径比L/D=5.2,气膜孔倾角α=30°,气膜孔板厚度为30mm。边倒圆型气膜孔为一种在圆柱型气膜孔基础上进行改进的气膜孔型,其基本特征为在气膜孔出口上游处进行边倒圆处理,边倒圆半径R= 0.22D。实验中圆柱型气膜孔采用机械加工而成,边倒圆型气膜孔采用光固化快速成型(3D打印)工艺加工而成,叶片材料为光敏树脂,加工误差在±0.1 mm以内。实验平板布置7排气膜孔,气膜孔间距P/D= 3。实验测量板如图 3所示。
|
Fig. 2 Schematic of test plate and hole shape |

|
Fig. 3 Photo of test plate |
实验中采用热色液晶测量的方法,应用瞬态导热理论对气膜测量平板表面进行全表面测量。刘存良[22]对瞬态传热测量理论及热色液晶的测量原理详细进行了介绍。实验中通过K型热电偶及9046温度采集模块对主流腔及二次流腔的温度进行测量。叶片表面温度通过SONY HDR-CX350E型彩色摄像机进行记录,测量频率为25帧/秒。气膜孔的流动特性通过压力扫描阀测量二次流腔与主流腔内的静压得到。
2.3 实验误差分析实验中主流与二次流温度通过K型热电偶测量,其测量误差约为ΔTTC = ±0.2K,涡轮叶片表面温度通过热色液晶测量,其测量误差约为ΔTIR = ±1K。时间测量误差为Δt = ±0.1s。根据误差传递公式[23],可以算出冷却效率的实验误差约为6.7%~13.3%,换热系数的不确定度为8.3%~16.7%。流量系数通过压力扫描阀测量得到,流量系数的不确定度约为3%。
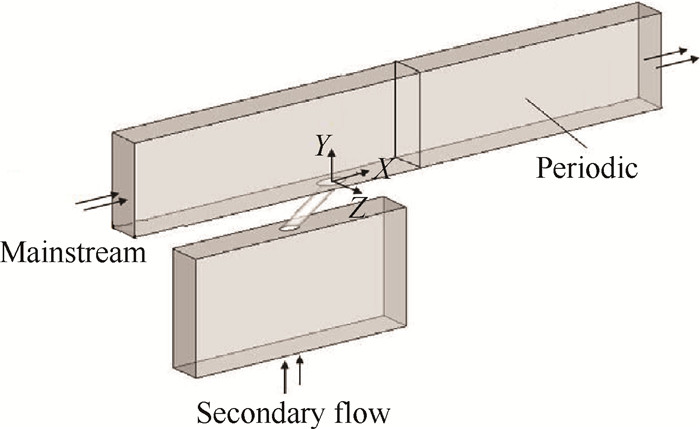
3 计算模型及网格参数 3.1 物理模型为了分析新型气膜孔的流动及换热规律,本文采用了数值模拟方法对相应的实验工况进行了计算研究。计算的几何模型如图 4所示。计算模型中主要由主流腔、二次流供气腔及气膜孔三部分组成。主流腔入口距气膜孔中心20D,主流腔出口距气膜孔中心30D,主流腔高8D,二次流腔高度10D。计算模型中气膜孔展向方向只取一个周期单元,主流及二次流腔宽度为3D。主流及二次流腔两侧边界区域定义为周期性边界条件。图中为圆柱型气膜孔的几何模型,边倒圆型气膜孔的几何模型与之类似。
|
Fig. 4 Computational domain |
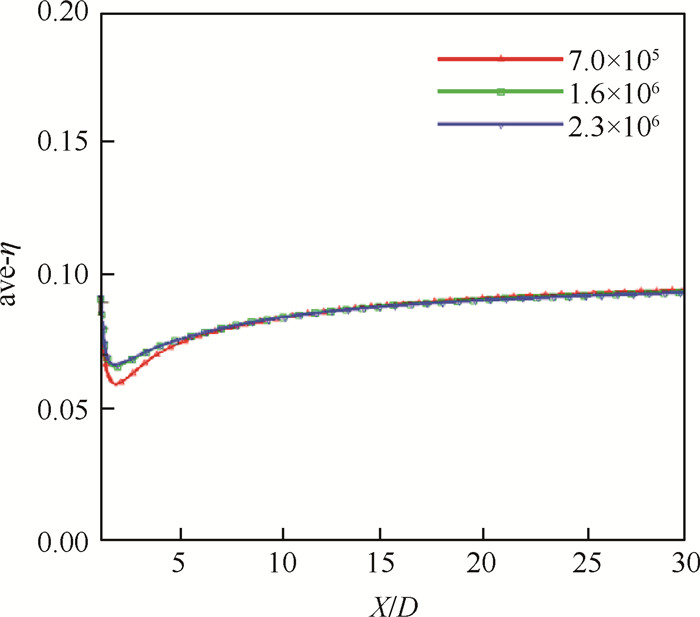
本计算中网格均采用ICEM CFD 13.0生成。为了准确计算边界层内的速度和温度分布,对于增强壁面函数,要求临近壁面的y+ < 1,并且在近壁区至少布置10层网格,因此各计算模型在气膜孔内以及临近壁面处的网格均进行了加密处理,计算结果y+均符合要求。图 5为数值计算中气膜孔附近的网格示意图。为保证计算中网格的无关性,对不同数量的网格(7.0×105,1.6×106,2.3×106)进行验证如图 6,网格数量1.6×106时,计算结果无明显变化,因此最终各计算模型的网格均在1.6×106左右。

|
Fig. 5 Computational mesh grid |
|
Fig. 6 Comparison of three kinds of grid |
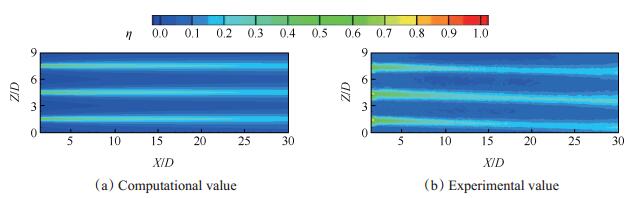
本研究中将数值计算结果与实验结果进行了对比,如图 7所示。比较了两种研究方法下动量比I=1时圆柱孔下游壁面的冷却效率分布,可以观察到数值计算的结果与实验测量相比偏低,但在气膜孔下游气膜的流向及展向分布变化趋势是相似的,可以应用数值计算对气膜流动机理进行分析。
|
Fig. 7 Contour of effectiveness on the wall surface |
本文通过实验研究了圆柱型气膜孔及边倒圆型气膜孔在动量比I=0.5,1.0,2.0,4.0条件下的流动及换热特性。其中动量比定义为
| $ I = {\rho _{\rm{c}}}U_{\rm{c}}^2/{\rho _{\rm{g}}}U_{\rm{g}}^2 $ | (1) |
式中Ug,ρg为主流速度及主流密度,Uc,ρc为气膜孔入口平均速度及二次流密度。
无量纲温度定义为
| $ \theta = \frac{{{T_{\rm{g}}}-T}}{{{T_{\rm{g}}}-{T_{\rm{c}}}}} $ | (2) |
式中Tg为主流温度,Tc为二次流温度,T为当地温度。
气膜冷却效率定义为
| $ \eta = \frac{{{T_{\rm{g}}}-{T_{{\rm{aw}}}}}}{{{T_{\rm{g}}}-{T_{\rm{c}}}}} $ | (3) |
式中Tg为主流温度,Tc为二次流温度,Taw为绝热壁面温度。
换热系数定义为
| $ h = q/\left( {{T_{{\rm{aw}}}}-{T_{\rm{w}}}} \right) $ | (4) |
式中q为壁面换热的热流密度。
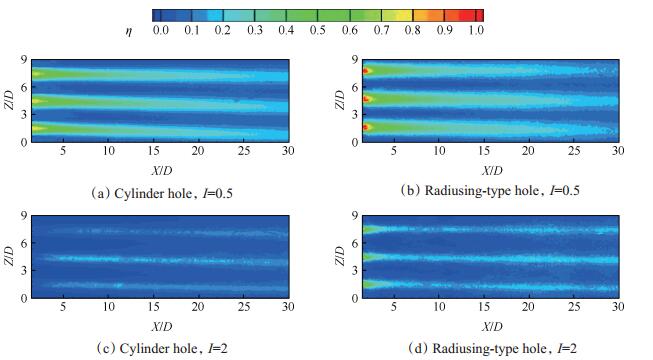
4.2 边倒圆孔冷却效率及换热系数结果分析中,冷却效率及换热系数分析采用实验结果,并通过数值模拟对孔的流动机理进行分析。本实验研究中选择圆柱型气膜孔下游表面冷却效率作为基准,与边倒圆型气膜孔的气膜冷却效率进行比较。同时为了减小实验边界的影响,只选择中间三个气膜孔下游的气膜冷却效率作比较。图 8为两种动量比两种气膜孔形下游气膜冷却效率实验结果分布云图。从图中可以看出:小动量比条件下两种孔形均呈现中心线上冷却效率高,气膜孔两侧效率较低的特点。且随着流动逐渐发展,气膜冷却效率逐渐降低。从图中能够明显地观察到边倒圆型气膜孔出口处近孔下游区域存在很高的冷却效率区域,之后随着流动发展两种气膜孔的冷却效率分布情况基本类似。随着动量比增加,在动量比I=2时,圆柱孔的气膜在孔出口附近的吹脱现象明显,气膜孔出口附近冷却效率较低,而后气膜在主流的作用下再次附着于表面,气膜冷却效率有所提升。而边倒圆型气膜孔在孔出口近下游仍然有很高的冷却效率,而且在下游中心线上的冷却效率更高,气膜展向扩张仍较好,气膜孔间处的冷却效率相比圆柱孔也较高。相比于圆柱型气膜孔,出口进行边倒圆处理能够明显改善气膜冷却效率。
|
Fig. 8 Contour of experimental effectiveness on the wall surface |
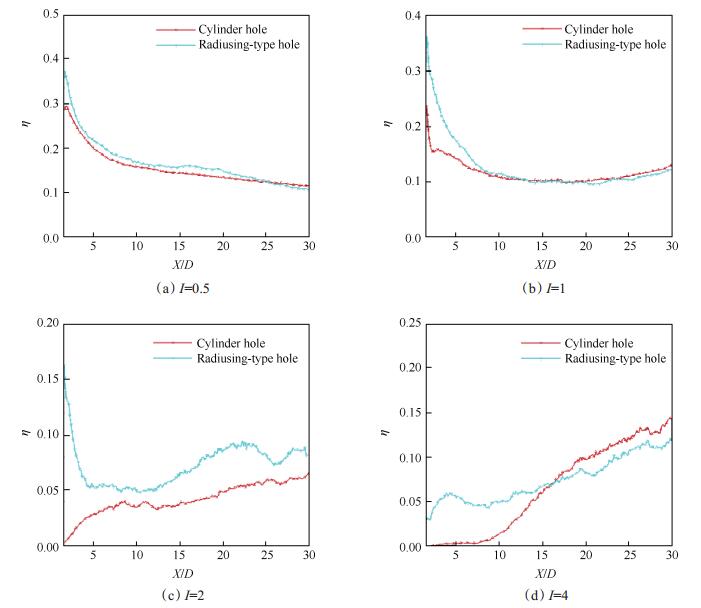
图 9给出了四个动量比条件下的圆柱型气膜孔和边倒圆型气膜孔的展向平均气膜冷却效率实验平均曲线图。小吹风比条件(I=0.5,I=1)时,气膜孔出口附近处,边倒圆型气膜孔的气膜冷却效率相比于圆柱型气膜孔较高;随着流动逐渐发展,气膜冷却效率逐渐降低,两种气膜孔的冷却效率较为接近。大吹风比条件下(I=2,I=4)时,两种孔型的气膜均存在吹脱再附着现象,这与冷却效率云图相对应。动量比I=2时,边倒圆型气膜孔的气膜冷却效率整体比圆柱型气膜冷却效率高。但在动量比I=4时,气膜孔下游前半段边倒圆型气膜孔的平均冷却效率更高,而后半段圆柱孔冷却效果更好。综合来看通过气膜孔出口形状的改进,边倒圆型气膜孔的冷却效率在整体上有所提升。
|
Fig. 9 Laterally averaged effectiveness at different momentum ratios |
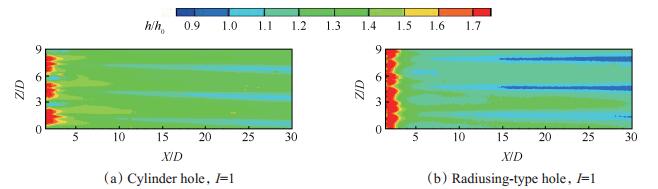
图 10给出了动量比I=1的实验工况下,圆柱孔和边倒圆型气膜孔的换热系数比分布图。图中h0为无气膜存在时壁面换热系数。两种气膜孔出口附近均存在高换热区域,而向下游流动的过程中,中心线换热系数降低两侧升高,总体上换热系数是降低的。边倒圆型气膜孔与圆柱孔相比,近孔处换热系数更高,远孔下游处换热系数更低。这是因为边倒圆型气膜孔前缘处主流与冷气射流掺混更剧烈,具有较强扰动的掺混气体流出后会显著增强该区域的换热系数;但在较远的下游处,由于边倒圆孔气膜的覆盖性较高,且二次流抗掺混能力较强,因此换热系数较低。
|
Fig. 10 Contour of experimental heat transfer coefficient on the wall surface |
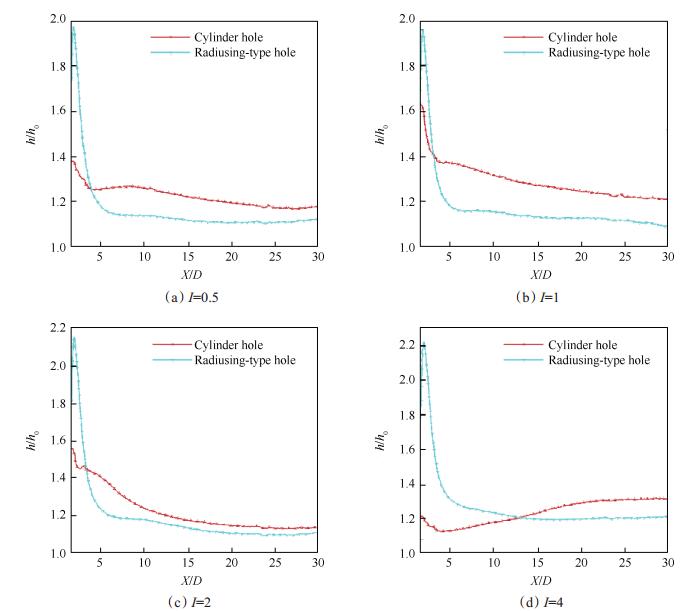
四种动量比条件下的两种孔下游的展向平均换热系数与实验值的比值如图 11所示。可以看出,边倒圆孔在不同工况下换热系数比均比较稳定,基本在1.2~2内,而且变化趋势非常相似。在大约X/D < 4范围内换热系数比有比较剧烈的变化,下降非常迅速,也正是在这段区域边倒圆孔换热系数明显大于圆柱孔换热系数,而在较远下游处新孔形的换热系数比圆柱孔约小15%,但在I=4时远孔区域(X/D>13后)圆柱型气膜孔的换热系数较高。
|
Fig. 11 Laterally averaged heat transfer coefficient at different momentum ratios |
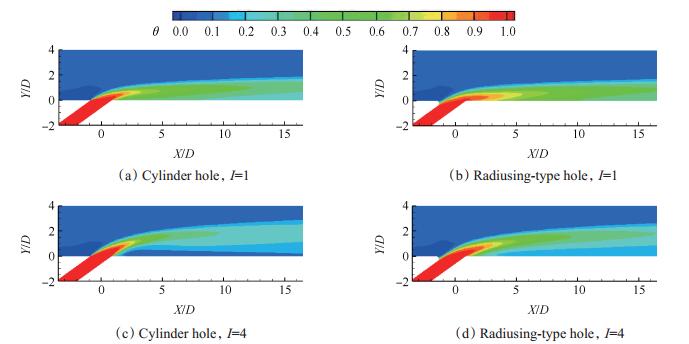
通过数值模拟中的流场结构,可以对上节中边倒圆型气膜孔的冷却效率以及换热系数实验结果进行分析。图 12为两种动量比下两种气膜孔Z=0截面上的无量纲温度云图。对比小动量比(I=1)条件下的两种孔型的无量纲温度云图,可以观察到边倒圆型气膜孔的冷气射流从气膜孔内流出后的贴壁性较强,气膜穿透能力有所下降,因此在气膜孔下游区域具有很好的气膜覆盖效果,这能大大提高气膜冷却效率。随着动量比增大到I=4时,冷气射流自气膜孔喷出后,圆柱型孔的射流有先喷出再附着的流动趋势,且再附着点位置比较靠后,而边倒圆型气膜孔的冷气几乎一直贴附在壁面,没有明显的气膜吹脱现象。这是由于新型气膜孔在出口处进行了边倒圆的扩张型处理,在小动量比条件下冷气射流在气膜孔出口处更易扩张膨胀并受到主流的挤压作用,不仅气膜展向覆盖范围较大,而且冷气更贴近壁面(在近孔下游区域更加明显)。大动量比下冷气射流动量较大且较集中,穿透性较强,此时主流的挤压作用比小动量比下的影响小。但是在边倒圆孔的出口扩张及主流挤压作用相比于圆柱型气膜孔仍较强,气膜覆盖性能相对较好。
|
Fig. 12 Computational value of dimensionless temperature field on Z=0 section |
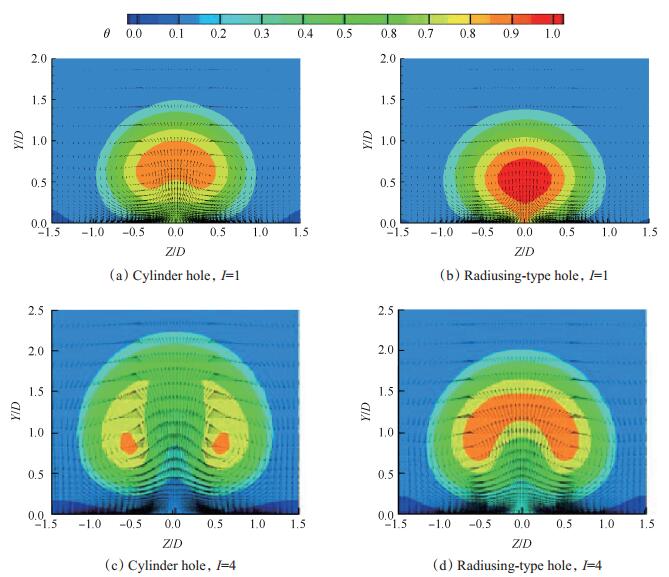
图 13给出了两种气膜孔垂直主流通道X/D=6截面上的无量纲温度云图。可以观察到,I=1时的小动量比下,边倒圆型气膜孔的射流核心较靠近壁面,且中心区域无量纲温度较高,这说明新型孔的射流与主流间扩散作用较弱,射流较集中,这种现象有利于提高气膜冷却效率。当动量比增加到I=4时,冷气量增多,此时射流逐渐脱离壁面。圆柱型气膜孔的射流冷气核心已经远离壁面,且射流的扩张较明显,涡中心区域无量纲温度较低。由于边倒圆型气膜孔的出口扩张作用,新孔型的射流法向速度相对较小,气膜贴壁性也更强,而且射流与主流间的掺和较弱,涡中心区域无量纲温度较高。通过图 10与图 11可以清楚地观察到边倒圆型气膜孔射流的发展规律,由于边倒圆型孔气膜覆盖性强,射流与主流掺混弱的特点能够有效提高气膜冷却效率。
|
Fig. 13 Computational value of dimensionless temperature field on X/D=6 section |
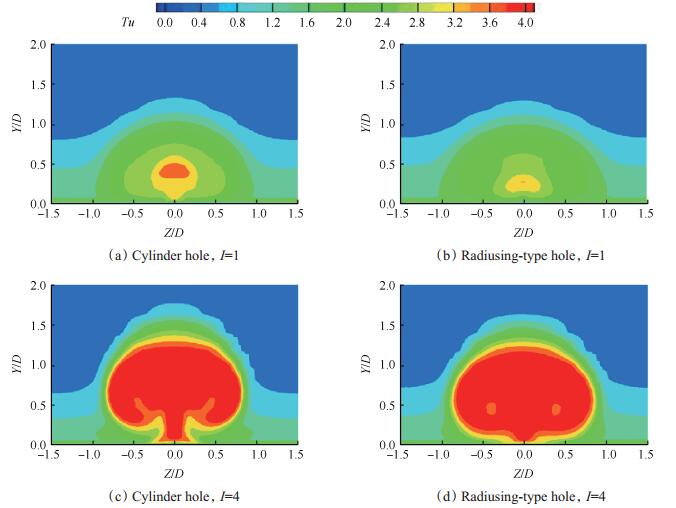
图 14给出了两种气膜孔下游截面的湍流度云图。小动量比I=1条件下,边倒圆型气膜孔后湍流度最小,并且湍流中心区域贴近壁面,能够有效地减弱主流和二次流的掺混,冷气射流能够长时间保持较低的温度,从而提高气膜冷却效果;大动量比I=2条件下,两种气膜孔后湍流度分布差别减小,但边倒圆孔高湍流区域相比于圆孔仍然更贴近壁面。通过孔型的改变,射流法向扩散减弱,气膜贴附性增强,能够有效提高冷却效率。
|
Fig. 14 Computational value of turbulence field on X/D=6 section |
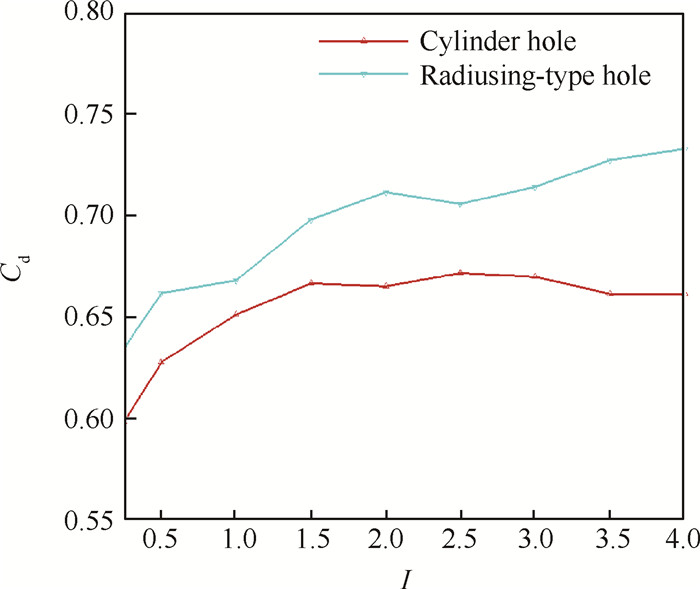
图 15为实验条件下边倒圆型气膜孔与圆柱型气膜孔在不同动量比下的流量系数对比。从图中可以看出,两种孔型的流量系数均随着动量比的增大而增加,且增长趋势逐渐减缓。各个吹风比下的边倒圆型气膜孔的流量系数均高于圆柱型气膜孔,流量系数平均高约5%。这说明由于气膜孔出口进行边倒圆扩张的改进,使得边倒圆型气膜孔的流通能力大幅提高,流动损失明显减小。
|
Fig. 15 Discharge coefficient at different momentum ratios |
本文应用瞬态导热测量理论,并采用热色液晶测量技术对边倒圆型气膜孔的流动及换热特性进行了实验研究,并应用数值模拟的方法对其流动机理进行了分析。主要结论如下:
(1)边倒圆型气膜孔的出口扩张作用使得二次流法向动量降低,展向动量变大,气膜贴附性较强。边倒圆型气膜孔的主流通道内反转肾型对涡强度较小,与主流间的扩散作用较弱,射流相对集中。
(2)边倒圆型气膜孔的近孔下游区域气膜贴壁性较好,气膜展向覆盖面积也更大,气膜冷却效率较高,换热系数较大。而气膜孔下游较远处冷却效率提升有所减弱,换热系数较低。
(3)边倒圆型气膜孔压力损失较小,流量系数比圆柱孔约高5%,气膜孔具有较强的流通能力。
| [1] |
葛绍岩, 刘登瀛, 徐靖中, 等. 气膜冷却[M]. 北京: 科学出版社, 1985.
(  0) 0) |
| [2] |
Pedersen D R, Eckert E R G, Goldstein R J. Film Cool-ing with Large Density Differences between the Main-stream and the Secondary Fluid Measured by the HeatMass Transfer Analogy[J]. Journal of Heat Transfer, 1977, 99(4): 620-627. DOI:10.1115/1.3450752
(  0) 0) |
| [3] |
Sinha A K. Film-Cooling Effectiveness Downstream of a Single Row of Holes with Variable Density Ratio[J]. Journal of Turbomachinery, 1991, 113(3): 442-449. DOI:10.1115/1.2927894
(  0) 0) |
| [4] |
Zaman K. Reduction of Jet Penetration in a Cross-Flow by Using Tabs[R]. AIAA 98-3276.
(  0) 0) |
| [5] |
杨成凤, 张靖周, 陈利强, 等. 前缘突脊倾斜气膜冷却效果的实验[J]. 工程热物理学报, 2008, 29(7): 1174-1176. (  0) 0) |
| [6] |
Lu Y, Dhungel A, Ekkad S V. Film Cooling Measure-ments for Cratered Cylindrical Inclined Holes[R]. ASME GT 2007-27386.
(  0) 0) |
| [7] |
Goldstein R J, Eckert E R G, Burggraf F. Effects of Hole Geometry and Density on Three-Dimensional Film Cooling[J]. International Journal of Heat & Mass Trans-fer, 1974, 17(5): 595-607.
(  0) 0) |
| [8] |
Hyams D G, Leylek J H. A Detailed Analysis of Film Cooling Physics, Part Ⅲ: Streamwise Injection with Shaped Holes[J]. Journal of Turbomachinery, 1997, 122(1): 122-132.
(  0) 0) |
| [9] |
Dittmar J, Schulz A, Wittig S. Assessment of Various Film-Cooling Configurations Including Shaped and Com -pound Angle Holes Based on Large-Scale Experiments[J]. Journal of Turbomachinery, 2003, 125(1): 57-64. DOI:10.1115/1.1515337
(  0) 0) |
| [10] |
Saumweber C, Schulz A, Wittig S. Free-Stream Turbu-lence Effects on Film Cooling with Shaped Holes[J]. Journal of Turbomachinery, 2003, 125(1): 65-73. DOI:10.1115/1.1515336
(  0) 0) |
| [11] |
Gritsch M, Colban W, SchäR H, et al. Effect of Hole Geometry on the Thermal Performance of Fan-Shaped Film Cooling Holes[J]. Journal of Turbomachinery, 2005, 127(4): 718-725.
(  0) 0) |
| [12] |
Saumweber C, Schulz A. Effect of Geometry Variations on the Cooling Performance of Fan-Shaped Cooling Holes[J]. Journal of Turbomachinery, 2012, 134(6).
(  0) 0) |
| [13] |
Makki Y, Jakubowski G. An Experimental Study of Film Cooling from Diffused Trapezoidal Shaped Holes[R]. AIAA 86-1326
(  0) 0) |
| [14] |
Lee K D, Kim S M, Kim K Y. Numerical Analysis of Film-Cooling Performance and Optimization for a Novel Shaped Film-Cooling Hole[R]. ASME GT 2012-68529.
(  0) 0) |
| [15] |
Issakhanian E, Elkins C J, Eaton J K. Film Cooling Ef-fectiveness Improvements Using a Non-Diffusing Oval Hole[R]. ASME GT 2015-42243.
(  0) 0) |
| [16] |
Sargison J E, Guo S M, Oldfield M L G, et al. A Con-verging Slot-Hole Film-Cooling Geometry, Part 1: LowSpeed Flat-Plate Heat Transfer and Loss[J]. Journal of Turbomachinery, 2002, 124(3): 453-460. DOI:10.1115/1.1459735
(  0) 0) |
| [17] |
Sargison J E, Guo S M, Oldfield M L G, et al. A Con-verging Slot-Hole Film-Cooling Geometry, Part 2: Tran-sonic Nozzle Guide Vane Heat Transfer and Loss[J]. Journal of Turbomachinery, 2002, 124(3): 461-471. DOI:10.1115/1.1459736
(  0) 0) |
| [18] |
李广超, 付建, 张魏, 等. 双向扩张孔出口宽度对气膜冷却特性影响[J]. 推进技术, 2016, 37(11): 2088-2096. (LI Guang-chao, FU Jian, ZHANG Wei, et al. Effects of Exit Width on Film Cooling Characteris-tics[J]. Journal of Propulsion Technology, 2016, 37(11): 2088-2096.)
(  0) 0) |
| [19] |
刘聪, 朱惠人, 付仲议, 等. 涡轮导叶吸力面簸箕型孔气膜冷却特性实验研究[J]. 推进技术, 2016, 37(6): 1142-1150. (LIU Cong, ZHU Hui-ren, FU Zhong-yi, et al. Experimental Study of Film Cooling Characteristics for Dust-Pan Shaped Holes on Suction Side in Turbine Guide Vane[J]. Journal of Propulsion Technology, 2016, 37(6): 1142-1150.)
(  0) 0) |
| [20] |
Bai J T, Zhu H R, Liu C L. Film Cooling Characteristic of Double-Fan-Shaped Film Cooling Holes[R]. ASME GT 2009-59318.
(  0) 0) |
| [21] |
Yang X, Liu Z, Feng Z P. Numerical Evaluation of Nov-el Shaped Holes for Enhancing Film Cooling Perfor-mance[J]. Journal of Heat Transfer, 2015, 137(7): 071701. DOI:10.1115/1.4029817
(  0) 0) |
| [22] |
刘存良. 新型高效气膜孔冷却特性研究[D]. 西安: 西北工业大学, 2009.
(  0) 0) |
| [23] |
Moffat R J. Describing the Uncertainties in Experimen-tal Results[J]. Experimental Thermal and Fluid Sci-ence, 1988, 1(1): 3-17. DOI:10.1016/0894-1777(88)90043-X
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


