2. 中国科学院 工程热物理研究所,北京 100190
2. Institute of Engineering Thermophysics, Chinese Academy of Sciences, Beijing 100190, China
多级轴流压气机作为航空发动机三大核心部件之一,其性能水平在很大程度上决定了发动机的整体性能。压气机的级负荷越高,对其稳定工作裕度的要求也更加苛刻,追求更高级压比与提高压气机稳定工作裕度之间存在着一定的矛盾。
高负荷多级轴流压气机的稳定性问题一直是限制高水平航空发动机发展的一大瓶颈[1]。如何使压气机在飞行速度和高度包络线内以及各种进气畸变和其他不稳定来流条件下稳定工作,一直是压气机设计中努力追求的目标。通常,对于军用航空发动机而言,要求其风扇/压气机留有15%~25%的失速裕度。目前,随着叶片三维设计技术的发展,压气机级负荷能力得到不断提高,但却使设计点更加接近失稳边界,导致失速裕度不足。国外设计的某高负荷跨声速转子采用“复合后掠”技术,失速裕度仅为0~6%[2]。
当压气机面临稳定裕度不足问题时,通常需要采用稳定性控制技术来拓宽工作范围。俄罗斯研究者[3]对一台三级轴流压气机分别在海平面和巡航高度开展了多转速下的性能测试,结果表明当转速降至80%设计转速时,压气机的稳定裕度迅速下降;进一步下降至60%设计转速时,压气机稳定裕度无法达标。巡航高度的试验测量结果更为严峻。通过实施缝式机匣处理后,部分转速稳定裕度达到指标。我国某型发动机曾出现高转速下停车故障,实验结果表明停车是由多级轴流压气机后面级喘振引起的。经过在后面级采用机匣处理大幅度提高了稳定裕度[4]。有的发动机曾遇到在中低转速稳定裕度不足的问题,经过对多种稳定性控制技术的筛选,最终确定了一种机匣处理方案解决了失速裕度不足问题[5]。可见,作为被实践检验的有效扩稳途径之一,机匣处理具有理论和工程上的双重竞争力。
多级轴流压气机高速旋转与狭小空间给内部流动结构研究造成了极大困难。直至今天,深入到机匣处理内部包括定常(时均意义上)和非定常流动的实验数据仍然匮乏。因此,失速机理尚未得到根本统一的解释,机匣处理设计也就难以形成普适方法。针对特定压气机设计时,往往需要大量计算和试验来建立数据库,时间成本高昂。虽然经过几十年的探索,研究者对于压气机失速机理的认识已经从早期的Emmons堵塞模型[6]发展到了非定常观点[7~9],同时也对机匣处理的设计积累了一定的经验,但现阶段机匣处理的设计仍需依靠大量的实验以建立完备的数据库,研制时间和成本相对较高。同时,利用数值计算预测机匣处理的扩稳效果也面临压气机失速边界准确模拟这一高难挑战[10]。
为降低机匣处理设计周期与成本,作者所在课题组针对叶顶先失速的一类压气机主流/泄漏流交界面自转子叶片前缘溢出触发失速的机理[11],提出决定主流/泄漏流交界面位置的动力学内因是叶顶端区轴向动量的分布[12]。通过控制体积分,将叶顶端区轴向动量沿轴向依次累加得到分布曲线,即钟形曲线。此方法的特点在于,不需要计算出加入机匣处理后的整条压气机特性线,仅通过对比光壁机匣近失速流量下各方案叶顶端区轴向动量分布曲线,便可以快速预测机匣处理的扩稳效果。目前,这一方法已经成功应用到指导周向槽机匣处理设计上[13]。
实践经验表明,相对于周向槽,轴向缝类机匣处理通常具有更强的扩稳能力[14]。因此,国际上对轴向缝扩稳机理进行了大量研究。Takata等[15]在低速压气机上开展详实的实验研究,发现轴向缝内流动增强了叶顶端区流体的轴向动量。Crook等[16]通过数值模拟对轴向缝下的叶顶流场分析发现,泄漏流的动量得到了提升,泄漏涡轨迹向通道下游移动。Wilke等[17]对轴向缝与动叶端区之间的相互作用进行了数值模拟,结果表明主流与泄漏流交界面向通道下游移动。可见,轴向缝通过改变叶顶端区轴向动量分布,从而推迟主流/泄漏流交界面从前缘溢出,与其扩稳效果密切相关。
然而,轴向缝方案的选择和优化过程通常不可避免地需要三维非定常CFD程序来计算完整的压气机特性线,以期准确捕捉采用轴向缝后的失速边界,进而对不同方案的扩稳效果进行比较,从中筛选出最优方案。这一过程十分耗时,并且针对如何准确捕捉压气机失速过程这一国际性难题,对数值方案具有很高的要求。本研究从轴向缝改变动叶端区轴向动量分布的角度出发,以轴向动量为关键参数,采用钟形曲线方法对缝类机匣处理的扩稳效果进行评估与验证,对此类在工程中广泛应用的机匣处理的初始方案选择和优化具有重要实际意义。
本研究采用低速大尺寸模型压气机为实验平台原因有两点:一方面,对于探索高负荷多级轴流压气机内部流动规律这一类高难度问题,采用低速大尺寸模型以规避直接进行原型实验的风险和难度是国际上普遍做法。另一方面,无论在高转速还是中低转速下,多级压气机失稳位置即后面级(高转速)或前面级(中低转速)动叶叶尖通常处于高亚声速流动状态,此时采用低速模型可以有效反演高速原型(无激波)内部流动特点。因此,本文将借助实验室自有的低速大尺寸压气机试验台,开展钟形曲线法的实验验证。本文针对一台低速大尺寸轴流压气机设计三种轴向缝式机匣处理,并对光壁机匣和各轴向缝方案进行数值模拟。采用控制体法量化各方案叶顶端区轴向动量分布曲线,即钟形曲线。在对曲线物理意义进行阐明的基础上,通过比较轴向缝方案的钟形曲线对各自扩稳效果进行快速预测。在低速大尺寸压气机上通过试验验证钟形曲线方法的预测结果。
2 研究示例 2.1 低速大尺寸轴流压气机本文使用的低速大尺寸压气机实验台(LSRC,Low-Speed Large Scale Research Compressor)是作者在借鉴多级轴流压气机后面级低速模化方法[18]的基础上,对模化相似准则进行修正,针对跨声速压气机中低转速工况(无激波)自主设计的一台具有相似叶顶流动特性的低速大尺寸模型压气机。
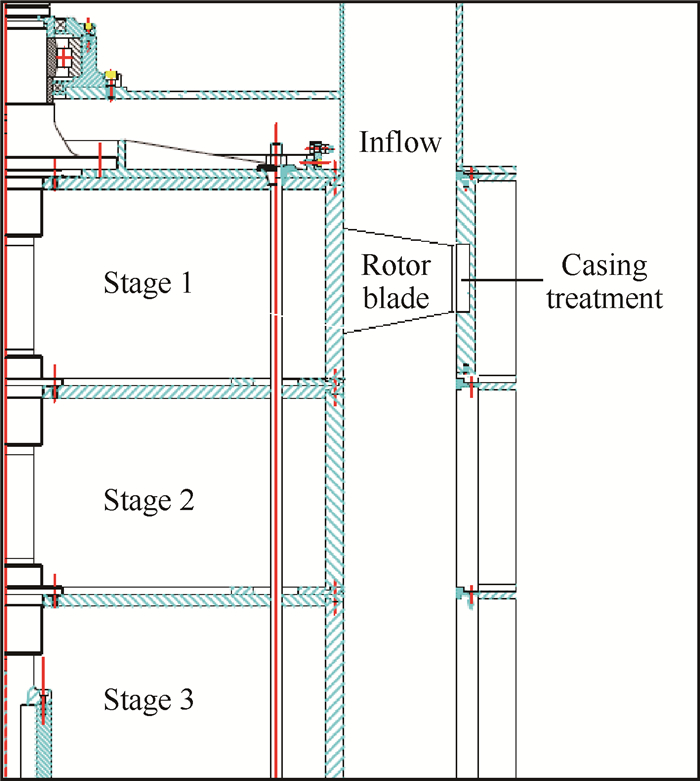
实验台总体结构如图 1所示,采用立式布局容易保证叶顶间隙均匀。压气机最多可以安装三级叶片,由一台直流电机驱动,转速从900~1300r/min可调,精度为±1r/min。气流先后经过进气段、试验段和排气段最终回到室外大气。本研究选取单转子作为研究对象,主要参数在表 1中给出,具体设计参数可参见文献[19]。
|
Fig. 1 Cross-section view of LSRC |
|
|
Table 1 Primary parameters of LSRC rotor |
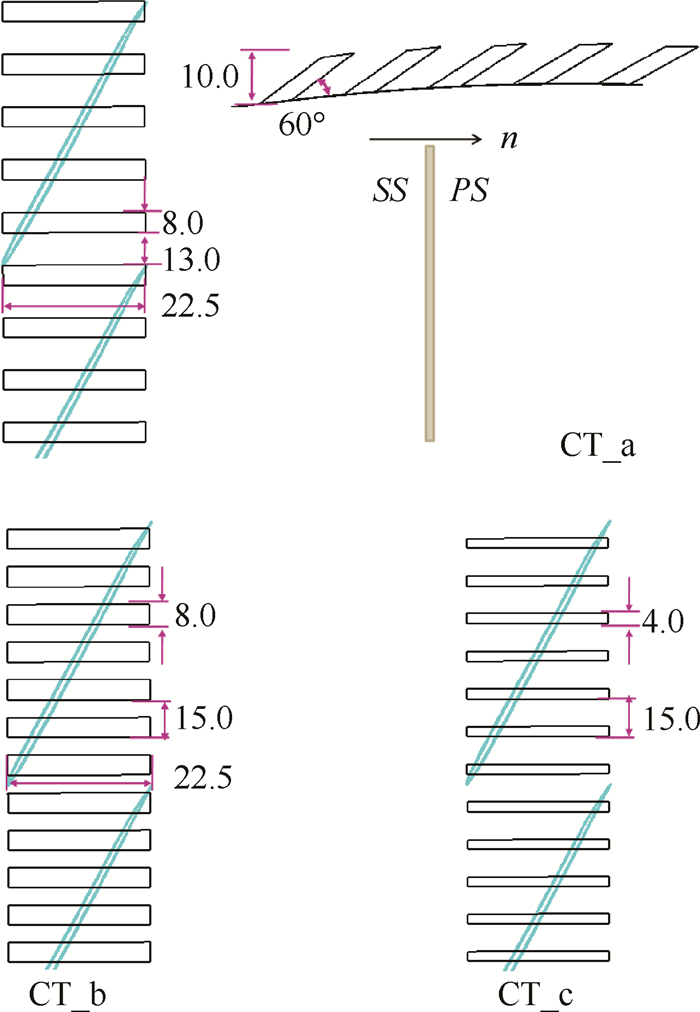
研究表明,机匣处理对动叶端区轴向动量分布的改变是其扩稳的动力学内因,而开口面上的轴向动量输运是影响端区轴向动量的主要原因[20, 21]。因此,本研究设计了三种不同开口率(即缝开口面积与光壁机匣面积之比)的轴向缝来验证钟形曲线快速判断轴向缝类机匣处理扩稳能力的可靠性。本文设计均采用具有较好扩稳能力的轴向倾斜缝式结构,所有缝向叶片旋转方向倾斜60°,如图 2所示,三种斜缝径向深度均为10mm,分别命名为CT_a,CT_b和CT_c。这三种轴向缝是经过对缝数、缝宽和缝深进行参数化研究之后筛选的具有较好扩稳效果的方案,具体结果请参见文献[19]。其中a方案和b方案缝宽均为8mm,b方案在a方案基础上每通道缝数由5增加为7,而c方案在b方案基础上保持缝数不变,缝宽降为4mm,三个方案的开口率分别为36%,50%和25%。
|
Fig. 2 Geometries of axial-slots(mm) |
本文采用单通道URANS数值模拟。虽然单通道模拟在捕捉叶片失速过程中跨通道扰动的传播过程有所缺陷,但考虑到本文的研究目的是基于在光壁转子濒临失稳的状况下,判断在此时加入轴向缝机匣处理的压气机是否可保持流动稳定,或不同轴向缝处理后对压气机流动的稳定性的改善程度,不需要精确分析压气机的旋转失速过程。综合衡量计算精度和计算时间仍选定单通道数值模拟方法,并将通过详细的网格独立性和湍流模型的验证获得最佳数值计算方案。
计算采用EURANUS求解器对相对坐标系下的雷诺时均N-S方程进行全三维求解。选用Spalart-Allmaras湍流模型封闭控制方程,该湍流模型被证实在低速大尺寸压气机环境下具有良好的湍流模拟表现[22]。通过控制壁面第一层网格厚度Ywall保证壁面无量纲雷诺数Y+~1。因实验特性线均折合至标准大气状况,进口条件设定为总温总压,出口边界给定平均静压,壁面采用无滑移无传热边界条件。
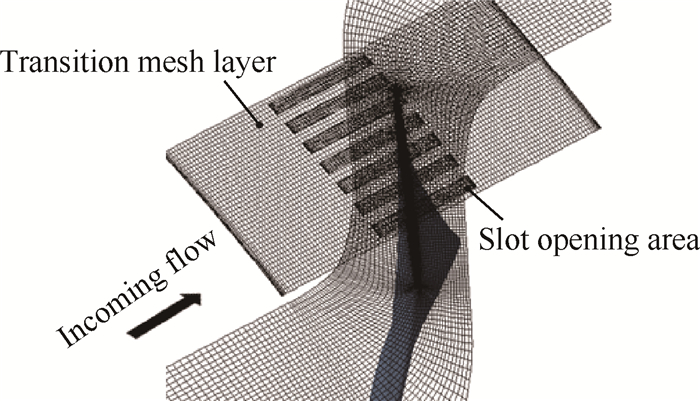
为合理捕捉转子扫略过轴向缝的固有非定常流动现象,在机匣壁面与轴向缝之间引入了滑移面网格,即设置一个薄层衔接在相对系下的转子通道和绝对系下的轴向缝,如图 3所示。该方法被证实对压气机特性线的失速点影响较小[19, 23]。非定常计算采用隐式双时间法,每个通道内设置40个物理时间步长,每一物理时间步下的虚拟时间步数为20,此时间步长的设置被证明可达到合理捕捉叶顶泄漏流非定常波动的要求[11]。
|
Fig. 3 Treatment for the sliding interface |
对于光壁机匣,经过网格独立性验证后,最终确定网格点总数为150万,周向、轴向和径向网格数分别为41、209和113,其中叶顶间隙内径向网格数为25。对于机匣处理方案,选取CT_a作为示例开展了缝内网格数的独立性验证。最终,所有缝内轴向和径向网格数均设置为61和33,CT_a和CT_b方案的周向网格数为17,CT_c方案周向网格数为9。
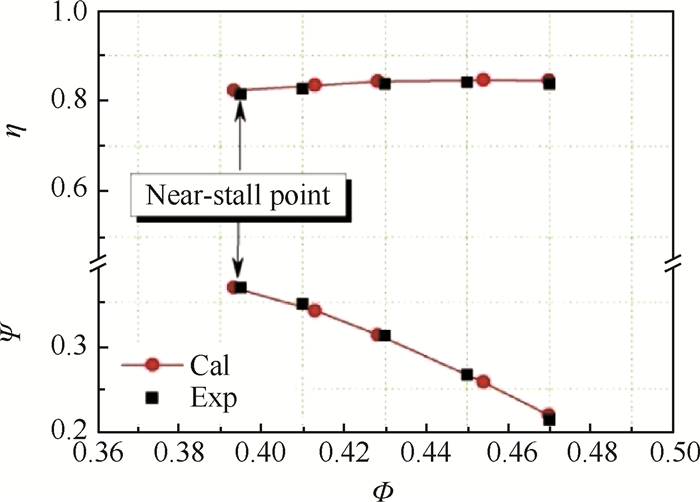
图 4给出了光壁机匣特性线的计算与实验结果,图中横坐标为流量系数,纵坐标分别为静压升系数和等熵滞止效率,各参数具体定义见式(1)~(3)。
| $ \mathit{\Phi }\rm{=}\frac{{{\mathit{V}}_{\mathit{z}}}}{{{\mathit{U}}_{\rm{m}}}} $ | (1) |
| $ \mathit{\Psi }\rm{=}\frac{{{\mathit{p}}_{\rm{2}}}\rm{-}\mathit{p}_{1}^{*}}{\frac{1}{2}\mathit{\rho U}_{\rm{m}}^{\rm{2}}} $ | (2) |
| $ \mathit{\eta }\rm{=}\frac{{{({{\mathit{\pi }}^{\rm{*}}})}^{{}^{\mathit{k}\rm{-1}} \diagup {}_{\mathit{k}}\;}}\ \rm{-1}}{\frac{\mathit{T}_{\rm{2}}^{\rm{*}}}{\mathit{T}_{\rm{1}}^{\rm{*}}}\rm{-1}} $ | (3) |
|
Fig. 4 Calculated and experimental characteristic curves of smooth casing |
式中Vz为进口平均轴向速度,Um为叶中线速度,p2和p1*分别为出口静压和进口总压的平均值,ρ为进口平均密度,π*是压气机转子总压比,k是气体绝热指数,T1*和T2*分别为进出口总温。
从图中可以看出,整个流量范围内,计算特性点与实验测试得到的特性吻合良好。实验测得光壁的近失速点流量系数Φ=0.395,而数值模拟预测的近失速点流量系数为Φ=0.393,相对误差为0.5%。考虑到实验中流量系数的测量误差为0.8%,认为本文采用的数值手段可以合理地反映出该低速转子的特性。
图 5进一步给出了流量系数为0.47工况下,转子进出口的轴向速度和相对气流角沿径向的分布情况。出于安全因素的考虑,实验测量的径向范围取为35%~100%叶高。计算数据点位置与实验测点实际位置相同,详细测量方法及探针标定过程见文献[19]。可以看出,计算结果较好地预测了转子叶片进出口流动参数的径向分布规律。在90%叶高以上的区域,计算偏差略高可能受两方面因素影响:一方面,计算域进气段相对实验台实际情况选取较短,造成叶顶边界层厚度略低,因此计算的叶顶轴向速度更大;另一方面,实验时探针沿径向动作,其与机匣开孔处之间的缝隙存在轻微漏气现象,也可能会对叶顶附近测量造成一定影响。不过总体来看,本文采用的数值模拟手段可以认为合理可信。
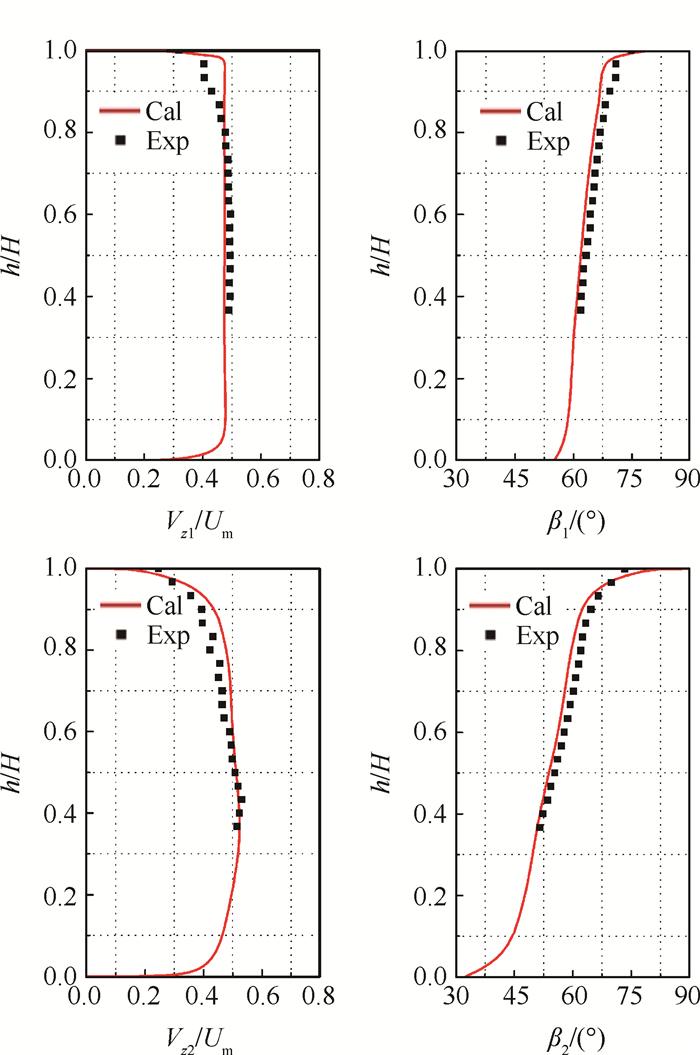
|
Fig. 5 Comparison between the calculated and measured axial velocity and relative flow angle for smooth casing |
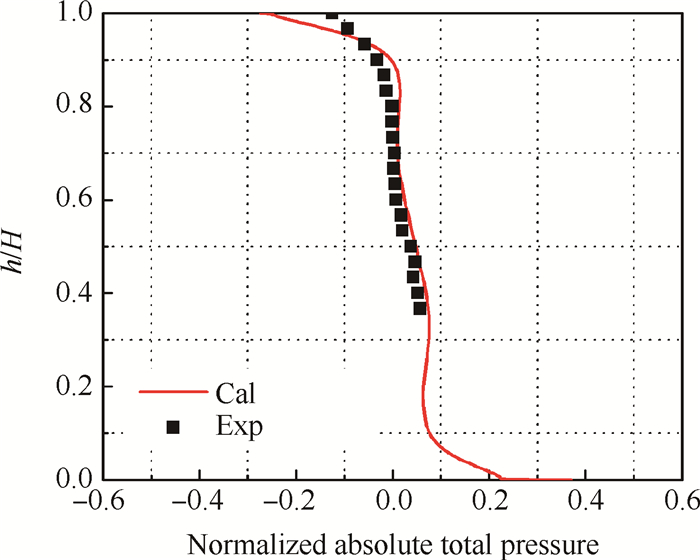
为了验证轴向缝数值方案的可靠性,图 6给出了CT_b方案下转子出口绝对总压径向分布的数值与实验结果,绝对总压采用了无量纲形式,定义见公式(4)。可以看出,计算结果对90%叶高以上范围的总压略微高估,这也与上述两点因素有关。沿整个叶高来看,数值模拟结果与测量结果总体趋势吻合较好,表明轴向缝数值方案的确定是合理的。
| $ {{{\mathit{\tilde{p}}}}^{\rm{*}}}\rm{=}\frac{{{\mathit{p}}^{\rm{*}}}\rm{-}\mathit{p}_{\rm{m}}^{\rm{*}}}{\frac{1}{2}\mathit{\rho U}_{\rm{m}}^{\rm{2}}} $ | (4) |
|
Fig. 6 Comparison between the calculated and measured absolute total pressure for CT_b case |
大量研究表明,绝大多数现代轴流压气机的失速先兆率先发生在叶顶区域。Vo等[24]提出了突尖型失速先兆的两个必要条件,其一就是来流与叶顶泄漏流的交界面自转子前缘溢出。林峰等[11]在低速压气机的实验和数值计算中观察到了这一现象,并提出了突尖形失速先兆的形成过程。Bennington等[25]观测了跨声速压气机中该界面在机匣壁面的投影,发现该界面在节流过程中不断前移,直至与转子前缘平齐时失速发生。进一步,他建立了叶顶间隙内流动的一维简化模型,得出该交界面的位置由主流和泄漏流的轴向动量比决定。本团队杜娟[26]在数值模拟中提取出了主流和泄漏流的轴向动量,验证了该结论。可见,叶顶区域的流动稳定性与端区轴向动量平衡有着密切联系。因此,合理评估主流与泄漏流交界面的位置对准确预测压气机流动稳定性至关重要。对于主流/泄漏流交界面位置评估最常见的方法就是根据叶顶某展向截面上的二维流场信息进行判断,如静压云图、熵云图等。然而,由于主流/泄漏流交界面本质上是空间中一个复杂的三维流面,难以量化其位置,因此采用二维流场信息往往不能较为精确的预测压气机的流动稳定性[27]。
基于此,本文将采用钟形曲线法,在叶顶沿轴向建立一系列离散的控制体单元,用以获取主流/泄漏流动量抗衡在动叶端区的时空平均效果。为合理得到主流/叶顶泄漏流的轴向动量分布,动叶端区控制体的设置应满足:(1)描述轴向动量沿轴向的变化;(2)包含泄漏流的主要流动结构。图 7给出了低速大尺寸压气机转子的动叶端区控制体划分示意图,图中SC代表光壁机匣(Smooth Casing)。在叶顶沿轴向从前缘至尾缘划分了21个控制体单元,周向延伸一个叶片通道。径向需要涵盖光壁机匣和机匣处理下泄漏流影响的叶顶区域范围,这里拟取为机匣面至80%叶高范围,下一节展开分析。

|
Fig. 7 Sketch of the control volumes in the tip region |
由于控制体的两个周向面满足周期性边界条件,因此在每一个控制体单元上应用动量方程可得到如下公式
| $ \begin{align} & \sum{{{\mathit{M}}_{\mathit{Z}}}}\rm{=}\int_{\mathit{Z}\rm{-}}{\mathit{\rho }{{\mathit{V}}_{\mathit{Z}}}\rm{(}\mathit{\boldsymbol{V}}\cdot \mathit{\boldsymbol{n}}\rm{)d}{{\mathit{A}}_{\mathit{Z}\rm{-}}}}\rm{+}\int_{\mathit{Z}\rm{+}}{\mathit{\rho }{{\mathit{V}}_{\mathit{Z}}}\rm{(}\mathit{\boldsymbol{V}}\cdot \mathit{\boldsymbol{n}}\rm{)d}{{\mathit{A}}_{\mathit{Z}\rm{+}}}} +\\ & \int_{\mathit{BT}}{\mathit{\rho }{{\mathit{V}}_{\mathit{Z}}}\rm{(}\mathit{\boldsymbol{V}}\cdot \mathit{\boldsymbol{n}}\rm{)d}{{\mathit{A}}_{\mathit{BT}}}}\rm{+}\int_{\mathit{CS}}{\mathit{\rho }{{\mathit{V}}_{\mathit{Z}}}\rm{(}\mathit{\boldsymbol{V}}\cdot \mathit{\boldsymbol{n}}\rm{)d}{{\mathit{A}}_{\mathit{CS}}}} \\ \end{align} $ | (5) |
式中下标Z-和Z+分别为控制体的上游和下游轴向控制面,CS和BT分别代表径向的上、下控制面。
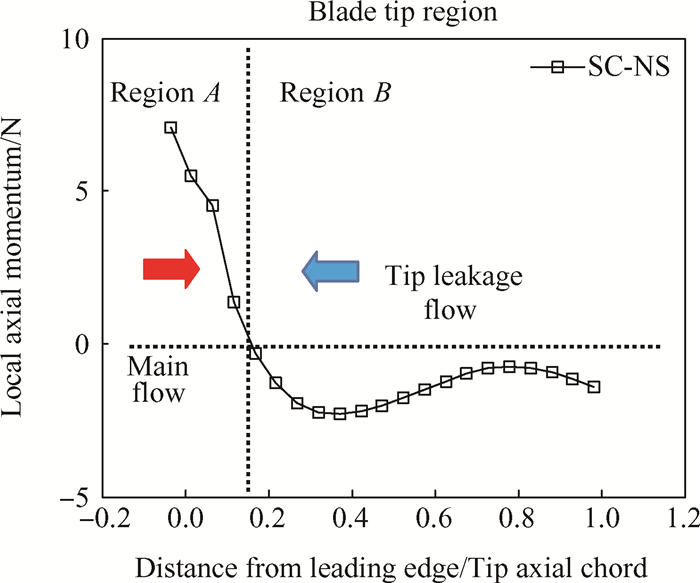
根据式(5),图 8给出了光壁SC近失速工况NS点(Near Stall Point at Φ=0.39)的叶顶端区当地轴向动量沿轴向的分布曲线。图中横坐标为无量纲轴向坐标,0和1分别代表转子叶顶前缘和尾缘。纵坐标由式(5)可知,积分是单位时间通过控制面的动量,因此单位是力的量纲N。从图中可以看出,叶顶区域根据轴向动量正负可以分为两部分A和B,叶顶轴向动量从前缘开始首先为正,说明流体具有从上游流向下游的趋势,可认为当地控制体位于主流主导区。此后,轴向动量在大约20%轴向弦长处变为负值,说明流体具有逆主流流动的趋势,此时认为其位于叶顶泄漏流占据主导的区域。可见,轴向动量为0的点,可以视为叶顶端区主流主导区(A区)和泄漏流主导区(B区)空间平均后的分界点,表征了主流与泄漏流之间的空间作用效果。
|
Fig. 8 Local axial momentum distribution(Φ=0.39) |
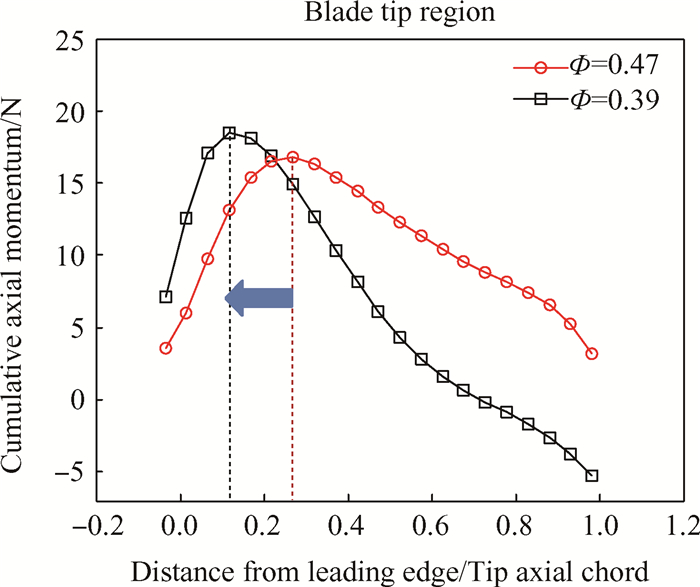
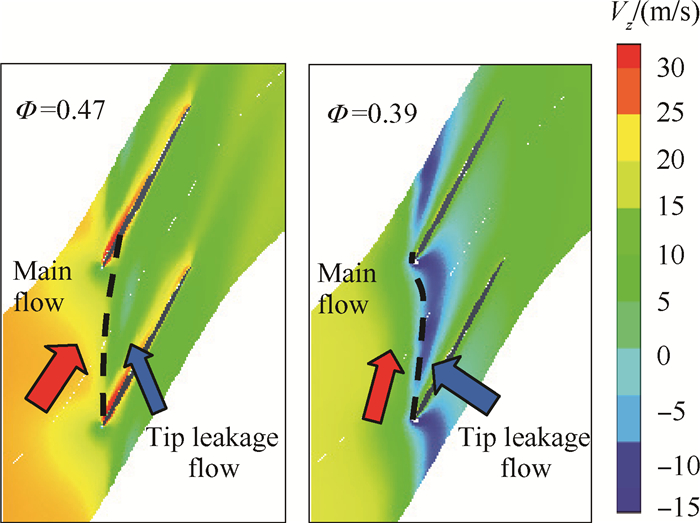
进一步,将每一个控制体上的轴向动量依次累加,得到一条累加轴向动量(Cumulative axial momentum)曲线,如图 9所示。该曲线形似钟形,简称钟形曲线。钟形曲线上每一点的值代表从叶顶前缘至当地轴向范围内的总轴向动量。这样观察的优点是,累加轴向动量曲线不受控制体单元轴向宽度选取引起的误差所影响,曲线上每一点都可看作是基于第一个控制体轴向动量的相对变化。以钟形曲线顶点为分界(对应图 8动量为0的点),左半支斜率为正,说明这一范围内的每个控制体单元上的轴向动量均为正值(对应区域A),累加动量不断增加;右半支斜率为负,说明控制体上的轴向动量为负(对应区域B),累加动量不断降低。图 10给出低速大尺寸压气机流量系数为0.47和0.39(NS Point)时,叶顶98%截面轴向速度云图。结合图 9和10可以看出,随着流量系数减小,主流/泄漏流交界面(图 10黑色虚线)不断前移,相对应的钟形曲线的顶点也向上游移动。
|
Fig. 9 Bell-shaped curves |
|
Fig. 10 Axial velocity contours at 98% span |
由此可见,在压气机节流过程中,钟形曲线顶点的轴向位置不断前移,揭示了这一过程中叶顶负载不断增加导致主流正向轴向动量降低、泄漏流负向轴向动量增加的物理机制。因此,钟形曲线顶点位置代表了主流主导区和泄漏流主导区分界面的空间平均效果,可以当作判断压气机流动稳定程度的关键参数。
4.2 控制体径向深度对钟形曲线的影响钟形曲线法是基于控制体方法对叶顶区域的轴向动量进行量化的,因此控制体范围的合理选取对量化结果显得尤为重要。对控制体轴向和周向范围选取比较直观、容易理解,下文将着重对控制体径向范围的选取进行探讨。
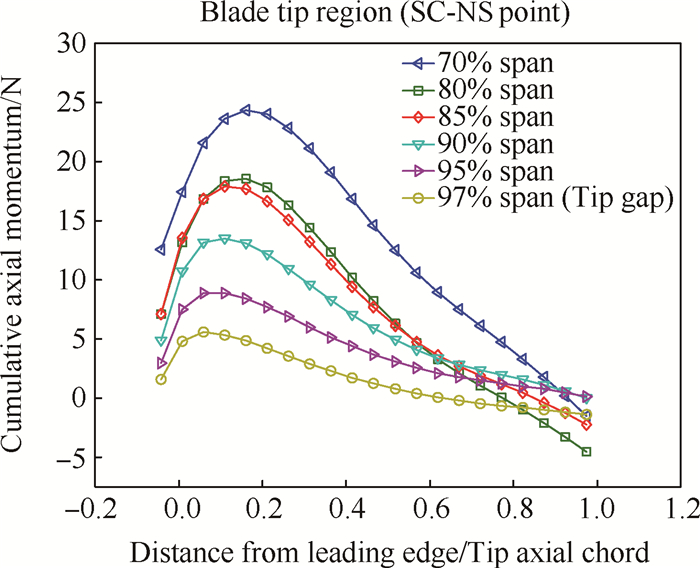
控制体径向范围选取的原则是保证控制体涵盖叶顶端区主流与泄漏流相互作用的主要区域,准确反映二者相互作用的空间平均效果,因此针对不同控制体径向范围对钟形曲线顶点位置的影响进行了分析。图 11为在光壁机匣近失速流量下(Φ=0.39),控制体上边界取为机匣面,下边界分别选取在不同径向位置时钟形曲线对比情况。结果表明:(1)随着控制体径向范围扩大,钟形曲线顶点位置总体呈现向下游移动的趋势;(2)在某些控制体径向深度区间内,钟形曲线顶点位置保持不变。由此可见,控制体径向范围的选取并不是任意的,要尽量准确反映叶顶泄漏流产生的影响,则控制体下边界需要选取在合理的叶高范围内。
|
Fig. 11 Effects of radial depth of control volume on bellshaped curves(Φ=0.39) |
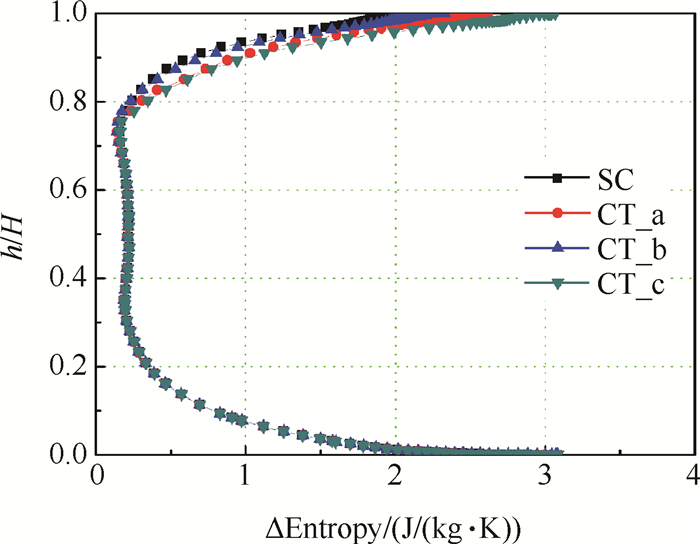
为了获得合理的控制体径向范围,准确量化叶顶端区的钟形曲线,进而预测不同轴向缝的扩稳效果,结合数值流场参数来确定控制体下边界位置。图 12给出了光壁机匣和轴向缝方案下,叶片出口熵增沿径向分布情况。结果表明,在采用机匣处理后叶顶区域熵增变化主要集中在80%叶高以上,说明在轴向缝作用下主流与泄漏流的相互作用主要在这一区域内发生了变化。因此,将选取80%叶高截面作为控制体径向下边界来量化钟形曲线,以评估不同轴向缝的扩稳效果。
|
Fig. 12 Entropy increase distributions at outlet for smooth casing and casing treatments(Φ=0.39) |
在对钟形曲线的物理本质和控制体范围进行分析后,将采用控制体方法获得三个轴向缝方案的叶顶端区轴向动量曲线,并对它们的扩稳效果进行预测与验证。
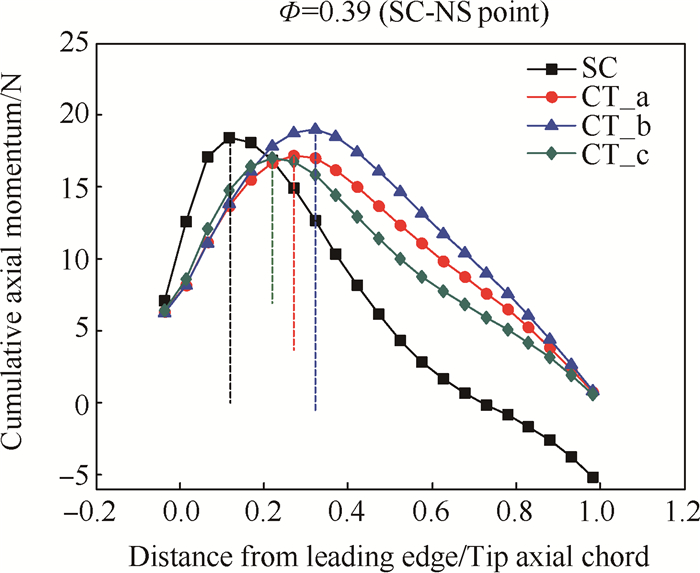
采用前述的控制体划分方法,图 13给出了光壁机匣和三种轴向缝方案下Φ=0.39时,即光壁机匣对应的近失速流量系数下,叶顶端区的钟形曲线。需要说明的是,图中所有曲线均为非定常计算的时间平均结果,并且为所有通道求和后的全圆周动量分布。根据钟形曲线的物理意义判断,设计的这三种轴向缝结构均具有扩稳能力。其中,CT_b方案的扩稳效果最佳,其顶点位置最靠下游,约为32%轴向弦长;CT_a的扩稳效果次之,其顶点位置约为26%轴向弦长;CT_c方案的扩稳效果最弱,其顶点位置最靠近上游,约为21%轴向弦长。
|
Fig. 13 Bell-shaped curves of smooth casing and three axial-slot casing treatments |
为验证钟形曲线对评估缝式机匣处理扩稳能力的可靠性,在低速大尺寸压气机上开展了实验验证。在实验过程中,通过间隙调节机构保证每组实验中转子的叶顶间隙相同。实验中特性线的采集方法是通过控制出口阀门关闭进行连续节流,直到压气机失速为止。保证每一机匣处理下的压气机进口条件和出口节流过程相同,特性点均折合至标准大气条件,得到的实验特性线如图 14,其中黑色曲线为光壁机匣特性线。

|
Fig. 14 Characteristic curves of smooth casing and three axial-slot casing treatments |
由于本文采用低速压气机开展研究,出口总压比非常低,因此对轴向缝扩稳效果的评估方法是通过对比特性线失速点流量系数相对光壁机匣的减少量,定义为SMI(Stall Margin Improvement),其具体公式如下,式中SC和CT分别代表光壁机匣和轴向缝机匣处理。
| $ \mathit{SMI}\rm{=}\frac{{{{\mathit{\dot{m}}}}_{\rm{SC, NS}}}\rm{-}{{{\mathit{\dot{m}}}}_{\rm{CT, NS}}}}{{{{\mathit{\dot{m}}}}_{\rm{CT, NS}}}} $ | (6) |
按照上述定义,CT_a,CT_b和CT_c三种方案的SMI分别为6.33%,9.11%和1.77%,表明通过实验测得的三种轴向缝扩稳能力强弱与采用控制体方法进行预测的结果是一致的,即CT_b>CT_a>CT_c,验证了钟形曲线法快速判断轴向缝扩稳效果的可靠性。
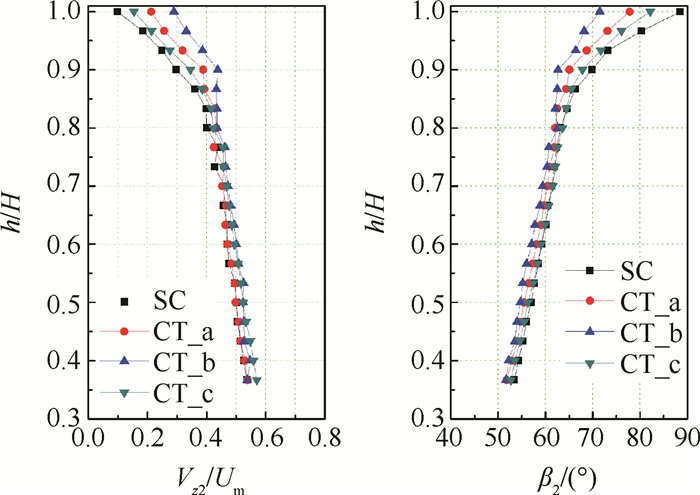
为了进一步分析轴向缝对叶顶端区流动产生的影响,图 15给出了光壁机匣近失速工况(Φ=0.39)以及对应流量下三种轴向缝机匣处理下的出口轴向速度和相对气流角沿径向分布情况。由图中信息可知:(1)在三种轴向缝作用下,出口轴向速度和气流角均在约80%叶高以上的叶顶端区发生了变化,表明控制体径向范围的选取是比较合理的;(2)采用轴向缝后,出口轴向速度均得到了提高,相对气流角相应降低,即流动方向更加靠近吸力面;(3)结合图 13,轴向缝对叶顶区域轴向速度和相对气流角的影响程度与钟形曲线顶点位置向下游推移的程度是一致的。可见,轴向缝的扩稳效果与其对叶顶端区轴向动量的改善程度密不可分,这进一步证明了采用钟形曲线法对扩稳效果进行快速评估是可靠的。
|
Fig. 15 Outlet velocities and flow angles of smooth casing and three axial-slot casing treatments(Φ=0.39) |
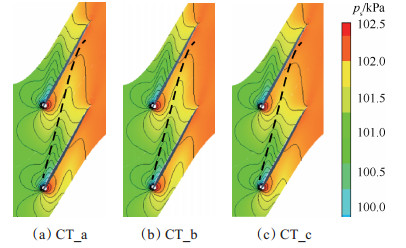
前文已述,主流/泄漏流交界面可表征叶尖敏感型压气机濒临失速的程度。多种文献中曾通过观察熵或静压云图来界定主流/泄漏流交界面在通道中的位置。然而,主流与泄漏流是在叶顶端区的三维空间内相互作用,基于二维流场信息可能无法准确反映主流/泄漏流作用的空间效果,导致此方法有时不具备分辨不同机匣处理扩稳能力的精度要求[27]。如图 16,给出了三种轴向缝在光壁近失速流量下98%叶高截面上的静压云图。根据图中黑色虚线所代表的泄漏涡涡核轨迹,发现难以判断三种方案下泄漏流轨迹的差别,也就无法准确评估三种轴向缝的扩稳能力。
|
Fig. 16 Static pressure contours of 98% span of three axialslot configurations at Φ=0.39 |
相比之下,钟形曲线法在评估扩稳效果上则具有较好的精度优势。首先,通过合理选取控制体范围来涵盖主流/泄漏流主要作用区域,更接近真实地反映了叶顶端区三维流动特征;其次,采用控制体积分法量化得到的钟形曲线代表了控制范围内所有二维截面上主流/泄漏流抗衡的综合效果,提高了叶顶端区主流/泄漏流交界面的空间辨识率。由此可见,与传统的二维流场参数云图相比,钟形曲线法可以更精确地反映叶顶端区主流/泄漏流交界面的变化,因此对判断机匣处理扩稳效果更具精度优势。
4.4.2 时间优势轴向缝与叶顶端区之间存在固有的非定常效应,对于这类机匣处理问题需要开展非定常数值模拟。在本研究的网格量级和数值方案下,采用课题组自行搭建的并行计算服务器,单节点6核并行收敛一个非定常工况点需要物理步长12000步,CPU时间约40h。当工况点接近失速时,所需收敛的物理步数更多,CPU时间更长。对于本研究采用的轴向缝方案而言,计算一条完整的特性线一般至少需要240h。采用钟形曲线预测方法,只需要对各轴向缝方案在光壁近失速流量下的单一工况进行求解即可,CPU时间将缩短为60h左右。
可见,采用钟形曲线方法对轴向缝扩稳效果进行预测,相对于获取完整特性线计算的时间成本大幅度降低。这很好地体现了钟形曲线方法快速的特点,对于需要海量前期筛选工作的机匣处理设计具有很好的工程应用前景。
需要指出的是,钟形曲线方法并不仅局限于低速亚音环境或轴向缝机匣处理,文献[12]曾在以NASA Rotor 67为代表的三台跨声速压气机(叶顶相对马赫数分别为1.38,0.85和1.27)上针对周向槽类机匣处理开展了钟形曲线研究。结果表明,这三台跨声速压气机都是叶尖敏感型压气机,失速都起始于动叶叶顶端区。虽然叶顶都出现激波,但其主流/泄漏流交界面仍会随流量降低而最终从前缘溢出,相应钟形曲线顶点位置也随着压气机节流过程而向上游移动。在此基础上,针对三台跨声速压气机采用了不同周向槽方案进行了扩稳效果判断并获得试验验证。因此,只要压气机失速过程是由主流/泄漏流交界面自叶顶前缘溢出这一流动机理主导,这一方法即可广泛用于快速评估高速和低速压气机稳定程度以及预测机匣处理、叶顶喷气、自循环引气-喷气等扩稳策略的扩稳能力。
5 结论本文提出以轴向动量为关键参数,采用一种快速评估机匣处理扩稳能力的钟形曲线法预测了三种轴向缝的扩稳能力并完成实验验证,得到结论如下:
(1) 基于动叶叶顶先失速的一类压气机主流/泄漏流交界面自转子前缘溢出的触发机制,提出在叶顶端区沿轴向建立一系列离散控制体单元,通过在控制面积分量化各控制体的轴向动量并逐次累加,获得叶顶端区内的钟形曲线。钟形曲线代表了叶顶主流与泄漏流之间轴向动量相抗衡的结果。曲线顶点的轴向位置即为主流与泄漏流交界面的空间平均位置,可用于表征压气机内部流动稳定程度。
(2) 采用钟形曲线法,建立的控制体需要涵盖叶顶端区主流与泄漏流相互作用的主要区域。钟形曲线顶点位置依赖于控制体的径向范围,因此需要结合流场对控制体下边界进行确定。
(3) 设计了三种轴向缝机匣处理,通过对比它们在光壁近失速流量工况下的钟形曲线顶点位置,预测了三种方案的扩稳效果并进行了实验验证,结果证明了控制体径向范围选取的合理性和钟形曲线法用于评估轴向缝扩稳能力的可靠性。
(4) 钟形曲线法用于预测扩稳效果的优点表现为对于叶顶端区主流/泄漏流交界面空间位置捕捉的精度优势和对扩稳效果预测的时间优势,对于需要海量前期筛选工作的机匣处理设计具有很好的工程应用前景。
本研究后续还需要开展以下工作:
(1) 在低速大尺寸压气机实验台上充分利用其测量优势,探究轴向缝内部流动机理。
(2) 验证钟形曲线法预测低速模型压气机轴向缝的扩稳效果在高速原型机上的相似性。
(3) 开展多通道或全圆周数值计算,以考虑压气机临近失速时旋转不稳定现象的影响。
(4) 对网格自动生成、控制体范围及钟形曲线参数化进行研究,构建机匣处理自动寻优设计平台。
| [1] |
李孝堂. 燃气轮机的发展及中国的困局[J]. 航空发动机, 2011, 37(3): 1-7. (  0) 0) |
| [2] |
Creason T L, Baghdadi S. Design and Test of Low Aspect Ratio Fan Stage[R]. AIAA 88-2816.
(  0) 0) |
| [3] |
Pankov S V, Mileshin V I, Korzhnev V N. Numerical and Experimental Investigations Bypass-Flow Fans for an Advanced Civil Aircraft Engine[C]. USA: 29th Congress of the International Council of the Aeronautical Sciences, 2014.
(  0) 0) |
| [4] |
高耀林, 李克明. 后面级"机匣处理"对多级轴流压气机性能的影响[J]. 工程热物理学报, 1982, 3(2): 131-134. (  0) 0) |
| [5] |
蒋世亮, 王绿江, 郝树成. 多级轴流压气机在中低转速下扩稳装置的研究[J]. 航空发动机, 2000, 2: 1-6. (  0) 0) |
| [6] |
Emmons H W, Pearson C E, Grant H P. Compressor Surge and Stall Propagation[J]. Journal of Turbomachinery, 1955, 77(4): 455-469.
(  0) 0) |
| [7] |
Jiang Huabing, Lu Yajun, Yuan Wei, et al. An Experimental Investigation on the Unsteady Excitation Effect of Casing Treatment on a Low Speed Axial Compressor [R]. ASME GT 2007-27571.
(  0) 0) |
| [8] |
孙大坤, 孙晓峰. 非定常机匣处理对失速先兆波的抑制作用实验研究[J]. 航空动力学报, 2008, 23(4): 671-679. (  0) 0) |
| [9] |
Du Juan, Lin Feng, Zhang Hongwu, et al. Numerical Investigation on the Self-Induced Unsteadiness in Tip Leakage Flow for a Transonic Fan Rotor[J]. Journal of Turbomachinery, 2010, 132(2): 1-9.
(  0) 0) |
| [10] |
Houghton T, Day I. Enhancing the Stability of Subsonic Compressors Using Casing Grooves[R]. ASME GT 2009-59210.
(  0) 0) |
| [11] |
Lin Feng, Zhang Jingxuan, Chen Jingyi, et al. Flow Structure of Short Length Scale Disturbance in an Axial Flow Compressor[J]. Journal of Propulsion and Power, 2008, 24(6): 1301-1308. DOI:10.2514/1.36525
(  0) 0) |
| [12] |
南希. 动叶端区轴向动量控制体分析方法及其在周向槽机匣处理中的应用[D]. 北京: 中国科学院工程热物理研究所, 2014. http://cdmd.cnki.com.cn/Article/CDMD-80135-1014320144.htm
(  0) 0) |
| [13] |
Nan Xi, Ma Ning, Li Jichao, et al. Evaluation of the Effectiveness of Typical Casing Treatments for a Low-Speed Compressor by an Integral Method[J]. Journal of Aerospace Science and Technology, 2016, 52: 234-242. DOI:10.1016/j.ast.2016.03.001
(  0) 0) |
| [14] |
Hathaway M D. Passive Endwall Treatments for Enhancing Stability[R]. NASA TM-2007-214409.
(  0) 0) |
| [15] |
Takata H, Tsukuda Y. Stall Margin Improvement by Casing Treatment—Its Mechanism and Effectiveness[J]. Journal of Engineering for Power, 1977, 99(1): 121-133. DOI:10.1115/1.3446241
(  0) 0) |
| [16] |
Crook A J, Greitzer E M, Tan C S, et al. Numerical Simulation of Compressor Endwall and Casing Treatment Flow Phenomena[J]. Journal of Turbomachinery, 1993, 115(3): 501-512. DOI:10.1115/1.2929280
(  0) 0) |
| [17] |
Wilke I, Kau H P. A Numerical Investigation of the Influence of Casing Treatments on the Tip Leakage Flow in a HPC Front Stage[R]. ASME GT 2002-30642.
(  0) 0) |
| [18] |
Wisler D C. Loss Reduction in Axial-Flow Compressor through Low-Speed Model Testing[J]. Journal of Engineering for Gas Turbines and Power, 1985, 107: 354-363. DOI:10.1115/1.3239730
(  0) 0) |
| [19] |
马宁. 高速压气机低速模化相似准则及轴向缝机匣处理流动机理研究[D]. 北京: 中国科学院工程热物理研究所, 2016. http://cdmd.cnki.com.cn/Article/CDMD-80135-1016206137.htm
(  0) 0) |
| [20] |
Legras G, Trébinjac I, Gourdain N, et al. A Novel Approach to Evaluate the Benefits of Casing Treatment in Axial Compressors[J]. International Journal of Rotating Machinery, 2012, 18.
(  0) 0) |
| [21] |
Liu Le, Li Jichao, Nan Xi, et al. The Stall Inceptions in an Axial Compressor with Single Circumferential Groove Casing Treatment at Different Axial Locations[J]. Journal of Aerospace Science and Technology, 2016, 59: 145-154. DOI:10.1016/j.ast.2016.10.014
(  0) 0) |
| [22] |
Liu Yangwei, Yu Xianjun, Liu Baojie. Turbulence Models Assessment for Large-Scale Tip Vortex in Axial Compressor Rotor[J]. Journal of Propulsion and Power, 2008, 24(1): 15-25. DOI:10.2514/1.26134
(  0) 0) |
| [23] |
姚刚. 跨声速风扇机匣处理非定常流动分析及某进气道数值计算[D]. 南京: 南京航空航天大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10287-2009053869.htm
(  0) 0) |
| [24] |
Vo H D, Tan C S, Greitzer E M. Criteria for Spike Initiated Rotating Stall[J]. Journal of Turbomachinery, 2008, 130(1): 1-9.
(  0) 0) |
| [25] |
Bennington M A, Ross M H, Cameron J D, et al. An Experimental and Computational Investigation of Tip Clearance Flow and Its Impact on Stall Inception[R]. ASME GT 2010-23516.
(  0) 0) |
| [26] |
杜娟. 跨音压气机/风扇转子叶顶泄漏流的非定常机制研究[D]. 北京: 中国科学院工程热物理研究所, 2010. http://cdmd.cnki.com.cn/Article/CDMD-80135-2010088116.htm
(  0) 0) |
| [27] |
Cevik M, Vo H D, Yu H. Casing Treatment for Desensitization of Compressor Performance and Stability to Tip Clearance[J]. Journal of Turbomachinery, 2016, 138(12): 1-16.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

