高超声速飞行器具有速度快、突防能力强等特点,可迅速打击数千或上万公里外的军事目标,实现“全球快速打击”,具有重要的战略意义,其研究越来越受到各个大国的重视[1, 2]。高超声速飞行器外部流场以及壁面热流的准确预测对于飞行器的设计与研发起到了至关重要的作用[3]。相比实验,数值模拟可以大大缩短研发周期,同时,也可以避免地面试验的天地换算中带来的误差。计算流体力学(Computational Fluid Dynamics,CFD)作为数值模拟手段参与到飞行器的设计、研发过程中,为高超声速飞行器的设计提供必要的数据与参数。对于复杂外形的高超声速飞行器的模拟,非结构网格或者混合网格在网格前处理、并行计算、网格自适应等方面表现出了比结构化网格更强大的优势[4, 5]。然而,传统的非结构网格在高超声速热流计算中存在不足[6, 7],Gnoffo等分析其原因在于对流通量的计算未考虑多维效应,Gnoffo提出了一种可以解决四面体非结构网格在计算热流不准的多维对流通量方法[8, 9]。
Levy等[10]将迎风型数值方法分为四类:(1)网格相关法;(2)旋转方法;(3)旋转/插值方法;(4)真实多维格式。网格相关有限体积法是把多维方程投影到坐标轴方向或者控制体界面的法线方向,并在计算通量的过程中认为这些方向流动是一维的,然后通过求解扩张一维Riemann问题得到控制体界面上的通量,这种方法在计算中取得了很好的效果且相对简单。但是这种网格相关的有限体积法有时不能正确反映多维效应的影响[11, 12],非结构四面体网格采用网格相关法计算得到的热流存在严重问题[7],而真实多维格式十分复杂、计算量非常大[13],并且其三维条件下的收敛性一直是存在的问题[14, 15],很难应用于工程实际。“旋转方法”是基于Euler方程的旋转不变性,在控制体界面上将法向向量按照一定规则分解,并在每个方向上求解Riemann问题,进而得到控制体界面上的通量。孙宇涛[12]、任玉新[12, 14]使用结构网格对旋转迎风格式进行了分析与讨论,发现旋转Roe格式的旋转方向取为控制体界面两侧速度差矢量的方向时,能够完全消除激波不稳定或者“红玉”现象。雷国东等[11]将旋转近似Riemann求解器的二阶精度迎风型有限体积法推广到格心型非结构有限体积法。张帆等[16]基于格心型非结构有限体积法,讨论分析了旋转迎风格式中旋转角度在一阶格式下对激波不稳定性以及接触间断的影响,并提出了一种基于压力函数的激波指示器,用来控制旋转角度,以达到激波稳定并且边界层计算精度不变的效果。
非结构网格处理高超声速气动热问题时,网格相关法得到的壁面热流依赖于网格分布,并且得到的结果与实际情况并不相符,这就需要在变量及通量重构中考虑多维效应。Gnoffo提出的多维对流通量重构方法[8, 9]其实属于“旋转/插值”方法,将原先格点型非结构有限体积法基于边的处理方式[17]换成了基于单元的处理方式。该重构方法简单而有效,该格式有效地解决了四面体网格热流计算不准确的问题,并推广到了高温热化学非平衡气体条件下飞行器的热流预测[18]。“旋转/插值”方法在变量重构上需要考虑旋转的方向以及网格的拓扑关系,对于格点型非结构有限体积法而言,“旋转方向”体现在三角形/四面体单元中多维对流通量重构所依赖的主方向的确定。文献[8, 9]中选择密度梯度作为单元内多维对流重构的主方向。对于Gnoffo提出的“旋转/插值”方法,单元中主方向的选择对于流场计算影响尚未进行过讨论研究,本文使用不同的主方向对圆柱绕流问题进行计算,针对结果中出现的“红玉”现象以及压力场非物理曲折现象进行了分析,在此基础上提出一种确定主方向的混合方式,并与其他几种单一方式计算结果进行比较。
2 计算方法 2.1 控制方程控制方程选用基于Euler坐标描述的无源项的三维可压缩Navier-Stokes方程,其守恒型积分形式具体可以写为
| $ \iiint {\frac{{\partial Q}}{{\partial t}} {\rm{d}}\mathit{\Omega }} + \iint {\left( {\mathit{\boldsymbol{f}} - \mathit{\boldsymbol{h}}} \right){\rm{d}}\sigma } = 0 $ | (1) |
式中Ω为控制体,σ为控制体单元面,Q是守恒变量,f和h分别为对流通量与粘性通量,具体表达式为
| $ \mathit{\boldsymbol{Q}} = \left[ \begin{array}{l} \rho \\ \rho u\\ \rho v\\ \rho w\\ \rho E \end{array} \right],\mathit{\boldsymbol{f}} = \left[ \begin{array}{l} \rho U\\ \rho Uu + p{n_x}\\ \rho Uv + p{n_y}\\ \rho Uw + p{n_z}\\ \rho UH \end{array} \right] $ | (2) |
| $ \mathit{\boldsymbol{h}} = \left[ \begin{array}{l} 0\\ {n_x}{\tau _{xx}} + {n_y}{\tau _{xy}} + {n_z}{\tau _{xz}}\\ {n_x}{\tau _{yx}} + {n_y}{\tau _{yy}} + {n_z}{\tau _{yz}}\\ {n_x}{\tau _{zx}} + {n_y}{\tau _{zy}} + {n_z}{\tau _{zz}}\\ {n_x}{\mathit{\Theta }_x} + {n_y}{\mathit{\Theta }_y} + {n_z}{\mathit{\Theta }_z} \end{array} \right] $ | (3) |
式中ρ为气体的密度,u, v, w分别为x, y, z三个方向上的速度分量,E为单位质量单位体积内的总能量,U为控制体面上的法向速度,p为压强,H为单位质量单位体积内的总焓,τij表示应力张量的9个分量,nx, ny, nz表示控制体面上法向矢量的三个分量,其它变量的表达式为
| $ \begin{array}{l} {\mathit{\Theta }_x} = u{\tau _{xx}} + v{\tau _{xy}} + w{\tau _{xz}} + \eta \frac{{\partial T}}{{\partial x}}\\ {\mathit{\Theta }_y} = u{\tau _{yx}} + v{\tau _{yy}} + w{\tau _{yz}} + \eta \frac{{\partial T}}{{\partial y}}\\ {\mathit{\Theta }_z} = u{\tau _{zx}} + v{\tau _{zy}} + w{\tau _{zz}} + \eta \frac{{\partial T}}{{\partial z}} \end{array} $ | (4) |
式中T表示空气的温度,η是空气热传导系数。本文的研究对象为量热气体,因而使用理想气体状态方程p=ρRT,其中R为气体常数;气体的动力黏性系数使用Sutherland公式进行计算[17];对于空气等各向同性流体,导热系数η无方向性,仅为温度和压力的函数,一般引入Prandtl数Pr确定如下
| $ \eta = \frac{{\mu {C_p}}}{{\mathit{Pr}}} $ | (5) |
式中Cp为气体的定压比热容,对于层流状态下的空气,Pr=0.72。
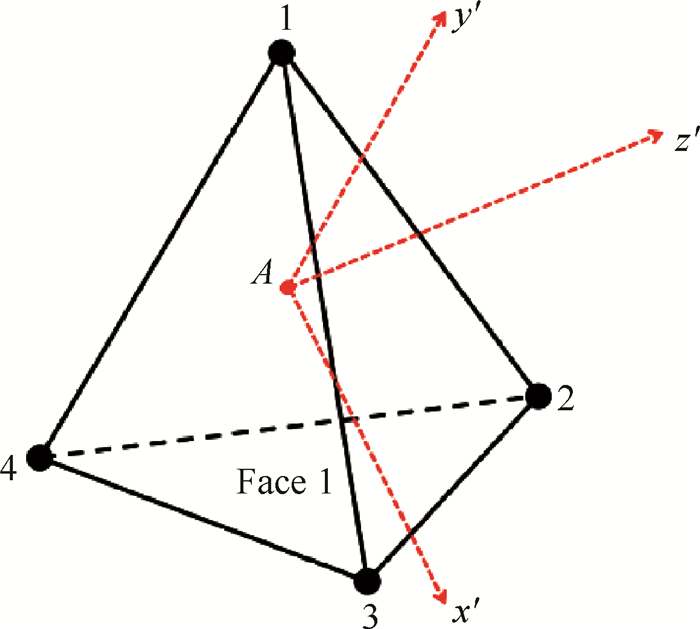
2.2 空间离散格式本文使用的是格点型非结构有限体积法,二维情况下控制体如图 1中阴影所示。对流通量的离散采用的是文献[8]中的多维(Multi-dimensional)通量重构方式,变量以及通量在单元中沿主方向x′以及垂直于x′的方向进行重构。在单元A中(二维情况下如图 1中的三角形Δ023,三维情况下如图 2中所示的四面体),通量依据Green-Gauss公式可写为
| $ \frac{{\partial {f_A}}}{{\partial x'}} = \frac{1}{{{\mathit{\Omega }_A}}}\sum\limits_{k = {\rm{faces}}} {{{\bar f}_k}{A_k}{n_{k,x'}}} $ | (6) |

|
Fig. 1 Schematic diagram of control volume(2D) |
|
Fig. 2 Schematic diagram of tetrahedral element |
式中k表示单元A中节点k相对的那个面;fk是单元A中k面上所有节点通量的平均值;ΩA表示的是单元A的体积;nk, x′表示k面法向矢量在x′方向上的投影。
三维情况下,式(6)具体可以写成如下形式
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{f}}_{x',A}}}}{{\partial x'}} = {\alpha _{3,x'}}\left( {{\mathit{\boldsymbol{f}}_{4,x'}} + {\mathit{\boldsymbol{f}}_{2,x'}} + {\mathit{\boldsymbol{f}}_{1,x'}}} \right) + {\alpha _{1,x'}}\left( {{\mathit{\boldsymbol{f}}_{4,x'}} + {\mathit{\boldsymbol{f}}_{3,x'}} + {\mathit{\boldsymbol{f}}_{2,x'}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;{\alpha _{2,x'}}\left( {{\mathit{\boldsymbol{f}}_{1,x'}} + {\mathit{\boldsymbol{f}}_{3,x'}} + {\mathit{\boldsymbol{f}}_{4,x'}}} \right) + {\alpha _{4,x'}}\left( {{\mathit{\boldsymbol{f}}_{1,x'}} + {\mathit{\boldsymbol{f}}_{2,x'}} + {\mathit{\boldsymbol{f}}_{3,x'}}} \right) \end{array} $ | (7) |
其中
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{f}}_{x',A}}}}{{\partial x'}} = \left( {{\alpha _{2,x'}} + {\alpha _{3,x'}} + {\alpha _{4,x'}}} \right){\mathit{\boldsymbol{f}}_1} + \left( {{\alpha _{1,x'}} + {\alpha _{3,x'}} + {\alpha _{4,x'}}} \right){\mathit{\boldsymbol{f}}_2} + \\ \;\;\;\;\;\;\;\;\;\;\;\left( {{\alpha _{1,x'}} + {\alpha _{2,x'}} + {\alpha _{4,x'}}} \right){\mathit{\boldsymbol{f}}_3} + \left( {{\alpha _{1,x'}} + {\alpha _{2,x'}} + {\alpha _{3,x'}}} \right){\mathit{\boldsymbol{f}}_4} = \\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{{\Delta x'}}\left[ {{\beta _{1,x'}}{\mathit{\boldsymbol{f}}_1} + {\beta _{2,x'}}{\mathit{\boldsymbol{f}}_2} + {\beta _{3,x'}}{\mathit{\boldsymbol{f}}_3}} \right] \end{array} $ | (8) |
式中的Δx′可以理解为是单元A穿过x′方向上的距离,定义为
| $ \frac{2}{{\Delta x'}} = \sum\limits_{n = {\rm{nodes}}} {\left( {\left| {{\alpha _{n - 1,x'}} + {\alpha _{n + 1,x'}}} \right|} \right)} $ | (9) |
式中下标n=nodes表示对单元A中所有节点循环。由此,βn, x′的表达式可以写为
| $ {\beta _{n,x'}} = \Delta x'\left( {{\alpha _{n - 1,x'}} + {\alpha _{n + 1,x'}}} \right) $ | (10) |
需要说明的是,式(9),式(10)对二维以及三维问题均成立,区别在于,二维情况下是对三角形三个节点(图 1中节点012)循环,而三维情况下是是对四面体四个节点(图 2中节点1234)进行循环。
2.3 重构方法本文所使用重构方法与文献[14, 16]的不同在于,原始变量重构时考虑了旋转方向因素,重构是在单元主方向以及垂直于主方向的平面上进行的。在四面体单元中,变量以及通量的重构是在如图 2中所示的x′,y′以及z′上分别进行的。三个方向上重构是类似的,这里主要介绍主方向x′上对流通量的重构方法。
首先需要计算x′方向上左右两侧物理量。本文采用的格式为格点型有限体积法,控制体内的物理量的值存放在四面体的节点上。因而,在四面体单元内,通过对四个节点上原始变量的值可以得到x′上两个虚点值,计算公式为
| $ {\mathit{\boldsymbol{q}}_{R,x'}} = \frac{1}{2}\sum\limits_{n = {\rm{nodes}}} {\left( {\left| {{\beta _{n,x'}}} \right| + {\beta _{n,x'}}} \right){\mathit{\boldsymbol{q}}_n}} $ | (11) |
| $ {\mathit{\boldsymbol{q}}_{L,x'}} = \frac{1}{2}\sum\limits_{n = {\rm{nodes}}} {\left( {\left| {{\beta _{n,x'}}} \right| - {\beta _{n,x'}}} \right){\mathit{\boldsymbol{q}}_n}} $ | (12) |
式中qR, x′与qL, x′是四面体单元内主方向x′两侧物理量左右状态值。
在此基础上,利用qR, x′与qL, x′,使用二阶STVD格式计算x′方向上的对流通量fx′为
| $ {\mathit{\boldsymbol{f}}_{x'}} = \frac{1}{2}\left[ {\mathit{\boldsymbol{f}}{{\left( \mathit{\boldsymbol{q}} \right)}_{L,x'}} + \mathit{\boldsymbol{f}}{{\left( \mathit{\boldsymbol{q}} \right)}_{R,x'}} - \mathit{\boldsymbol{R}}_{x'}^{ - 1}\left| {{\mathit{\Lambda }_{\lim ,x'}}} \right|\left( {{\rm{d}}{{\mathit{\boldsymbol{\tilde q}}}_{x'}} - {\rm{d}}{{\mathit{\boldsymbol{\tilde q}}}_{x',\lim }}} \right)} \right] $ | (13) |
式中Rx′与Λlim, x′是使用Roe平均后变量值计算的;
| $ {\rm{d}}{{\mathit{\boldsymbol{\tilde q}}}_{x'}} = {\mathit{\boldsymbol{R}}_{x'}}\left( {{\mathit{\boldsymbol{q}}_{R,x'}} - {\mathit{\boldsymbol{q}}_{L,x'}}} \right) = {\mathit{\boldsymbol{R}}_{x'}}\sum\limits_{n = {\rm{nodes}}} {{\beta _{n,x'}}{\mathit{\boldsymbol{q}}_n}} $ | (14) |
| $ {\rm{d}}{{\mathit{\boldsymbol{\tilde q}}}_{R,x'}} = \Delta x'{\mathit{\boldsymbol{R}}_{x'}}\sum\limits_{n = {\rm{nodes}}} {\left( {\left| {{\beta _{n,x'}}} \right| + {\beta _{n,x'}}} \right)\nabla {\mathit{\boldsymbol{q}}_{n,GG}}{\mathit{\boldsymbol{n}}_{x'}}} $ | (15) |
| $ {\rm{d}}{{\mathit{\boldsymbol{\tilde q}}}_{L,x'}} = \Delta x'{\mathit{\boldsymbol{R}}_{x'}}\sum\limits_{n = {\rm{nodes}}} {\left( {\left| {{\beta _{n,x'}}} \right| - {\beta _{n,x'}}} \right)\nabla {\mathit{\boldsymbol{q}}_{n,GG}}{\mathit{\boldsymbol{n}}_{x'}}} $ | (16) |
| $ {\rm{d}}{{\mathit{\boldsymbol{\tilde q}}}_{x',\lim }} = \mathit{\Phi }\min \bmod \left[ {2{\rm{d}}{{\mathit{\boldsymbol{\tilde q}}}_{R,x'}},2{\rm{d}}{{\mathit{\boldsymbol{\tilde q}}}_{x'}},2{\rm{d}}{{\mathit{\boldsymbol{\tilde q}}}_{L,x'}},\frac{1}{2}\left( {{\rm{d}}{{\mathit{\boldsymbol{\tilde q}}}_{R,x'}}, + {\rm{d}}{{\mathit{\boldsymbol{\tilde q}}}_{L,x'}}} \right)} \right] $ | (17) |
式中Φ(0≤Φ≤1)是限制因子,具体见文献[8]中描述。
三维条件下,按照式(12)~式(17)的方法可以计算得到其他两个方向上的通量,进而可以通过通量重组得到控制体面An上的通量,表示如下
| $ {\mathit{\boldsymbol{f}}_{An}} = {n_{An,x'}}{\mathit{\boldsymbol{f}}_{x'}} + {n_{An,y'}}{\mathit{\boldsymbol{f}}_{y'}} + {n_{An,z'}}{\mathit{\boldsymbol{f}}_{z'}} $ | (18) |
式中nAn, x′,nAn, y′以及nAn, z′分别表示An面上法向矢量与x′,y′以及z′方向的夹角。
2.4 熵修正为了避免出现Carbuncle(红玉)现象,在Roe方法中要使用熵修正。本文使用Harten型熵修正函数
| $ {\lambda _{\lim }} = \left\{ \begin{array}{l} \frac{{{\lambda ^2}}}{{4{\lambda _{\min }}}} + {\lambda _{\min }}\;\;\;\;\;\lambda < 2\lambda_{\min} \\ \lambda \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\lambda \ge 2\lambda_{\min} \end{array} \right. $ | (19) |
非结构网格中,网格的固有性质使得边与边界层之间没有必然的关系,需要根据流动的局部特征来定义λmin。对于标准的基于边的重构方式,λmin除了在激波区域外,其值必须要小。基于压力的赋值限制器Φ用来定义λmin
| $ {\lambda _{\min }} = \delta \left( {1 - \mathit{\Phi }} \right)\left( {V + c} \right) $ | (20) |
式中c为声速;V为控制体面元上的法向速度;Φ为限制器,具体表达式可参照文献[8]中的相关公式;δ为参数,取值一般为0.01~1.0。
2.5 主方向nx′的确定从空间重构以及通量计算中可以发现,首先要解决的问题是确定nx′,ny′以及nz′,在文献[8, 9]中,选择单元内密度梯度作为nx′方向,当单元内梯度为0的时则选择当地速度矢量作为nx′方向;因为原始变量的重构也考虑了旋转方向以及多维效应,所以无法像文献[16]中公式(33)那样通过一个角度α来控制旋转方向,使得其在激波附近使用旋转迎风格式,而在连续区域内使用的是网格相关的一维迎风格式。文献[14]则选用控制面两侧的速度矢量差作为旋转的方向。
在后面的算例中会给出利用文献[8, 9]中nx′的确定方法计算得到的压力场存在非物理解,因而本文提出了一种使用压力函数作为激波指示器来确定nx′的方法,如公式(24)所示。该方法的主要思想是通过压力函数使得在激波附近使用压力梯度来确定nx′方向,在压力梯度小的区域使用笛卡尔坐标系来确定nx′方向,而在过渡区域使用基于压力的函数Φ进行加权平均确定nx′方向以保证方法的连续过渡。对比式(21)与式(24),可以发现PD4即是PD1与PD3的混合方法,通过函数Φ来实现两种方法的过渡。
为了对比不同nx′方向的计算结果,本文选择以下四种nx′确定方式:
(1) PD1(Principle Direction 1):选择固定的笛卡尔坐标系方向作为nx′
| $ \begin{array}{l} {\mathit{\boldsymbol{n}}_{x'}} = {\left( {1,0,0} \right)^{\rm{T}}}\\ {\mathit{\boldsymbol{n}}_{y'}} = {\left( {0,1,0} \right)^{\rm{T}}}\\ {\mathit{\boldsymbol{n}}_{z'}} = {\left( {0,0,1} \right)^{\rm{T}}} \end{array} $ | (21) |
(2) PD2(Principle Direction 2):文献[8, 9]中给出的密度梯度方向作为n
| $ {\mathit{\boldsymbol{n}}_{x'}} = \left\{ \begin{array}{l} \nabla \rho \;\;\;\;\;\left| {\nabla \rho } \right| \ne 0\\ {\mathit{\boldsymbol{V}}_{{\rm{local}}}}\;\;\;\;\left| {\nabla \rho } \right| = 0 \end{array} \right. $ | (22) |
(3) PD3(Principle Direction 3):选择压力梯度方向作为nx′
| $ {\mathit{\boldsymbol{n}}_{x'}} = \left\{ \begin{array}{l} \nabla \rho \;\;\;\;\;\left| {\nabla p} \right| \ne 0\\ {\mathit{\boldsymbol{V}}_{{\rm{local}}}}\;\;\;\;\left| {\nabla p} \right| = 0 \end{array} \right. $ | (23) |
(4) PD4(Principle Direction 4):选择压力梯度作为nx′,并使用限制因子Φ进行控制
| $ \begin{array}{l} {\mathit{\boldsymbol{n}}_{x',x}} = 1.0 + \frac{{1 - \mathit{\Phi }}}{{\left| {\nabla p} \right|}}\frac{{\partial p}}{{\partial x}}\\ {\mathit{\boldsymbol{n}}_{y,x'}} = \frac{{1 - \mathit{\Phi }}}{{\left| {\nabla p} \right|}}\frac{{\partial p}}{{\partial y}}\\ {\mathit{\boldsymbol{n}}_{z,x'}} = \frac{{1 - \mathit{\Phi }}}{{\left| {\nabla p} \right|}}\frac{{\partial p}}{{\partial z}} \end{array} $ | (24) |
式(17),式(20),式(24)中都有一个基于压力函数的限制器,其作用是使基于压力的函数对压力梯度大的强间断区域与连续区域进行不同的处理。文献[8, 16]中给出了不同形式的压力函数作为流场中的激波指示器。式(17),式(20),式(24)中的Φ采用与为了与文献[8]中的压力限制器一致。
在任意四面体内,四个节点上的压力满足
| $ \begin{array}{*{20}{c}} {\phi = {p_{\max }}/{p_{\min }},{p_{\max }} = \max \left( {{p_1},{p_2},{p_3},{p_4}} \right),{p_{\min }} = \min \left( {{p_1},{p_2},{p_3},{p_4}} \right)}\\ {\hat \phi = \min \left[ {1,\max \left( {0,\frac{{{\phi _{\max }} - \phi }}{{{\phi _{\max }} - {\phi _{\min }}}}} \right)} \right]} \end{array} $ | (25) |
| $ \mathit{\Phi } = \frac{{1 - \cos \left( {\hat \phi {\rm{ \mathsf{ π} }}} \right)}}{2} $ | (26) |
式中ϕmax=3, ϕmin=2。
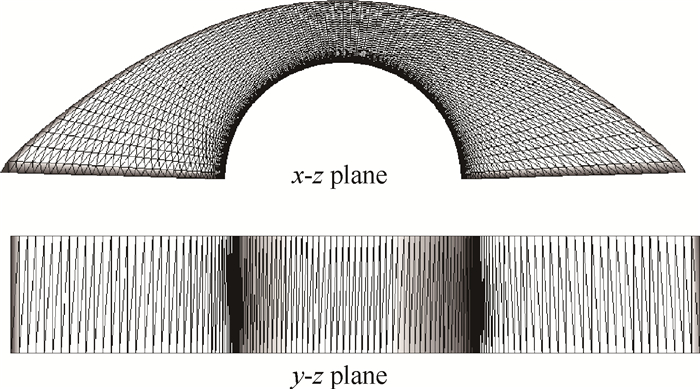
3 算例分析 3.1 单层圆柱高超声速绕流问题高超声速飞行器的翼前缘、舵面等受热严重的区域可以近似为圆柱面。选择半径为1m的圆柱,来流条件与文献[8]中圆柱算例一致,自由来流速度为V∞=5000m/s,密度为ρ∞=0.001kg/m3,温度为T∞ =200K,攻角为0°。采用四面体网格计算,网格如图 3所示,需要说明的是图 3中的网格左右两侧是不对称的。本算例的目的是为了探究主方向对于高超声速条件下弓形激波计算稳定性的影响,为了不受限制器以及重构方式的干扰,在x′,y′,z′三个方向上均选择一阶STVD格式进行计算;同样地,为了避免受熵修正参数的干扰,算例中均不考虑熵修正。各个算例中的nx′确定方法见表 1。
|
Fig. 3 Monolayer tetrahedral mesh for cylinder |
|
|
Table 1 List of cases |
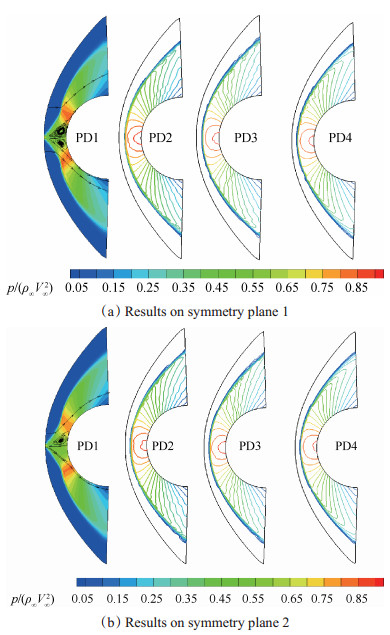
表 1中四个算例计算得到的圆柱绕流的无量纲压力等值线云图如图 4所示,需要说明的是图中p/(ρ∞V∞2)表示的是无量纲压力,具体来说是压力使用自由来流的密度以及速度进行无量纲化,图 4分别表示y方向上两个对称面上的计算结果。Case 1使用PD1方法确定主方向,方向向量如式(21)所示,从图 4中第一个云图可以看出,Case 1结果出现“Carbuncle”现象,通过观察发现,在驻点附近区域出现了非物理分离涡,这是“Carbuncle”现象的典型特征。与Case1不一样的是,其他三个算例都没有出现“Carbuncle”现象,这说明主方向的选择对于激波数值稳定性有一定的作用。从图 4所示的压力等值线云图中可以看出,Case2与Case3计算得到的压力等值线在弓形激波后呈现“zigzag”外形,这样的结果是非物理的;很明显,Case4算例的压力等值线云图中并没有出现“zigzag”型的压力曲线。
|
Fig. 4 Contours on symmetry planes for 1st order results |
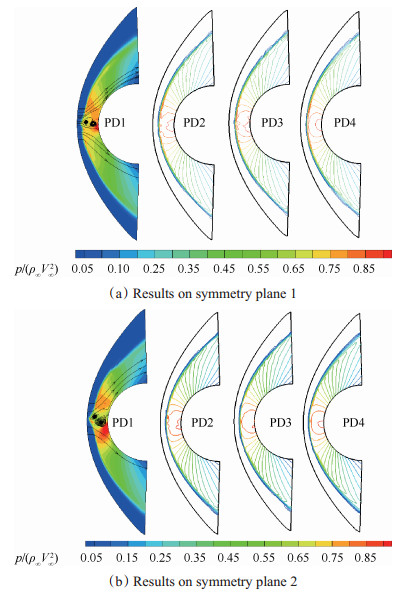
前面已经提到,为了不受限制器以及重构方式的干扰,图 4中结果是x′,y′,z′三个方向上均为一阶STVD格式进行计算的结果。现分别在x′,y′,z′三个方向上按照式(13)~式(17)进行二阶重构,各个方向上不考虑熵修正,同样按照表 1中算例安排进行计算,得到的结果如图 5所示。对比图 4与图 5计算结果,可以发现Case 1结果仍然有典型的红玉现象出现;对于Case 2,Case 3与Case 4三个算例的压力场结果,可以看出仅在激波附近有很小的抖动,并不像图 4中那样呈现出“zigzag”外形,但是Case 2与Case 3在驻点附近的压力等值线存在明显的褶皱,并不像Case 4那样光顺。
|
Fig. 5 Contours on symmetry planes for 2nd order results |
为了检验图 4,5中Case2与Case3的结果是否与网格疏密有关,将图 3中所示的网格在激波以及波后区域进行加密,对称面上的网格如图 6所示。分别使用PD2,PD3以及PD4主方向确定方式进行计算,图 7是加密网格后得到的压力分布等值线图,可以清楚地看出,由于激波处网格加密使得捕捉到的激波间断更加明显;网格加密后,PD2与PD3计算得到的结果尽管相比于稀疏网格结果有所改善,但是波后的压力等值线仍然存在“zigzag”型曲线。从该算例可以看出,在没有熵修正的情况下,使用一阶格式计算高超声速圆柱绕流问题,PD4主方向确定方式不仅没有出现红玉现象,而且消除了强弓形激波后压力等值线非物理曲折的现象。

|
Fig. 6 Refined mesh |
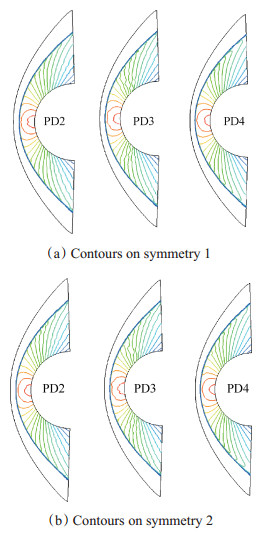
|
Fig. 7 Pressure contours of refined mesh for 1st order results |
从图 5中可以看出,各个主方向二阶计算结果的差别体现在驻点区域以及靠近激波附近的抖动与不光顺现象。采用图 6所示的加密网格进行计算,在三个方向上均采用二阶STVD格式进行计算,计算结果如图 8所示。对比图 7与图 8中等值线云图可以发现,在图 8中PD2与PD3计算结果中不存在激波后“zigzag”型曲线,并且与图 5中结果对比可以发现,由于激波处以及波后流场区域网格加密,在驻点附近的压力等值线并没有出现像图 5所示的抖动与不光顺。由此可以看出,PD4主方向确定方式在各方向采用二阶格式时,在网格较为稀疏的情况下可以得到激波波后更为准确的压力场结果。
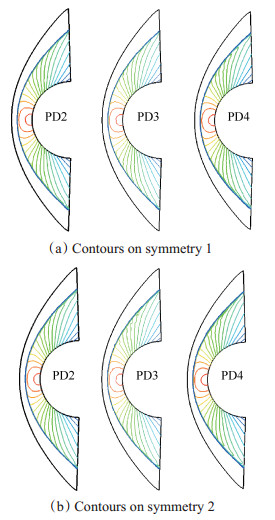
|
Fig. 8 Pressure contours of refined mesh for 2nd order results |
前面的算例中圆柱在展向只有一层网格,并且网格量无论稀疏都采用的是规则四面体网格。为了研究展向网格以及非规则网格对于计算的影响,本算例选择三套不同的网格进行计算,分别为非对称规则四面体网格Grid_1、对称规则四面体网格Grid_2、不规则四面体网格Grid_3,三套网格整体以及局部细节见图 9所示,图 9(d)展示的即是展向网格分布,它们的展向网格都有十层,并且这三套网格全部是四面体网格。
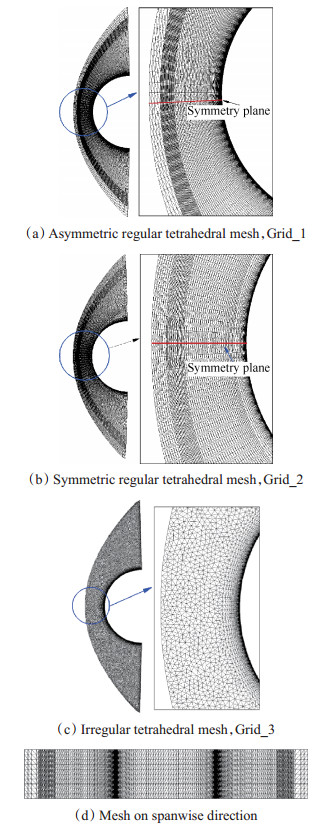
|
Fig. 9 Global and local mesh for different grids |
本节中所有计算均采用Harten型熵修正,并且系数均取为δ=0.60,使用图 9中三种不同的网格进行计算,自由来流条件与上一小节一样,并且同样使用一阶格式进行计算。在上一小节没有熵修正的情况下,Case 2与Case 3得到的流场中压力等值线存在非物理的“zigzag”现象,而Case 4中并未出现这样的异常现象。考虑到Case 2与Case 3的结果具有一致性,讨论网格对计算影响时选用PD2方式进行研究,在本节算例中计算分析的算例如表 2所示。
|
|
Table 2 List of cases for ten spanwise cells |
Case 5计算得到的结果如图 10(a)所示,图中曲折的等值面呈现“zigzag”形状,并且“前后左右”并不对称;图 10(b)中展示的是两个边界对称面上的压力等值线,“zigzag”形状出现在对称面1的下部的Zone1区域与对称面2上部的Zone2区域。这种现象说明网格的非对称性对于出现的压力等值线非物理抖动有一定的影响。
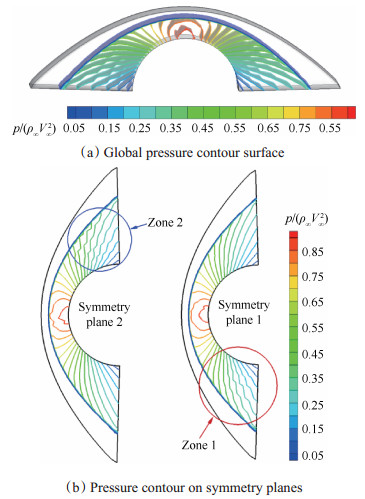
|
Fig. 10 Results of Case 5 |
Grid_2网格是完全上下对称的,采用PD2方式计算得到的结果如图 11所示。相比较于图 10(b)中所示,在对称面1上,非物理的“zigzag”现象完全消失了;在对称面2的上,不仅上半部分Zone2区域出现“zigzag”压力等值线,而且在下半部分同样出现了“zigzag”压力等值线。换句话说,Grid_2上下对称的网格改善了Grid_1计算中上下不对称的情况,但是对于压力等值线的非物理分布并没有改善。可以这样认为,对称规则四面体网格上下对称性并不能改变等压力线非物理曲折现象,激波波后的非物理扰动在展向也有传播。规则网格不论对称与否,激波后产生的非物理的扰动会在一个方向上传播而不停止。

|
Fig. 11 Results of Case 6 |
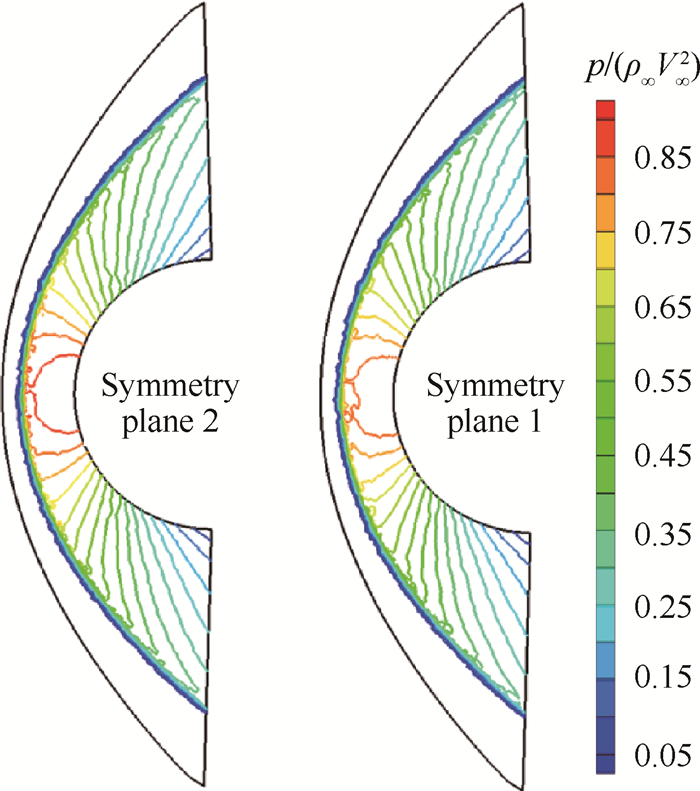
Case 7计算结果如图 12所示,可以清楚地看出,不规则网格计算得到的压力场有非常大的改善,并没有出现像图 10,图 11那样的“zigzag”现象。这说明不规则排列的四面体网格使得激波后的压力的非物理扰动没有按照特定的方向进行传播,或者可以这样认为,是因为不规则的排列使得这种扰动不能顺利传播。
|
Fig. 12 Results of Case 7 |
对采用PD2方式计算结果的分析可以看出,网格加密对于规则四面体网格下压力等值线出现的异常的情况并没有改善,同时也可以看出,对于PD2方式而言,不规则四面体网格对波后非物理的“zigzag”现象有明显的抑制作用。
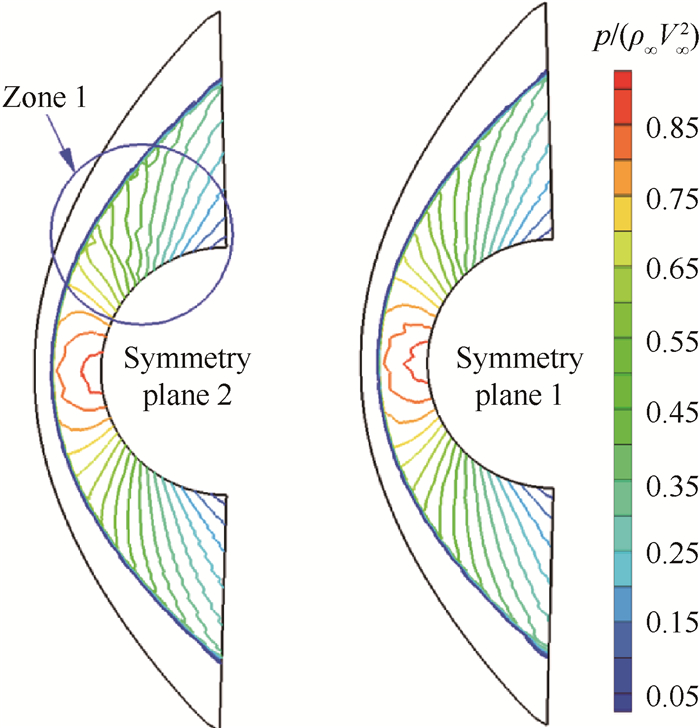
Case 5,Case 8以及Case 9使用Grid_1的计算结果可以反映主方向nx′对激波后压力非物理扰动传播的影响。图 13是Case 8计算得到的结果,与图 10(b)结果相比较,换用压力梯度作nx′的方向得到的结果仍然不是很好,这个可以从图 11中Zone 1区域中可以清楚地看出。一阶格式耗散大,得到的压力场应该更光滑才对,可是Case 5与Case 8的结果不但不光滑反而产生了非物理的曲折。从图 10与图 13的结果可以分析出,单纯使用密度或压力梯度作为nx′方向对于压力场的模拟始终存在非物理“zigzag”现象。本文提出的混合方式PD4在激波附近使用压力梯度作为主方向,而在压力梯度小的地方使用PD1方式作为主方向,在过渡区域使用压力函数加权作为连续过渡。
|
Fig. 13 Results of Case 8 |
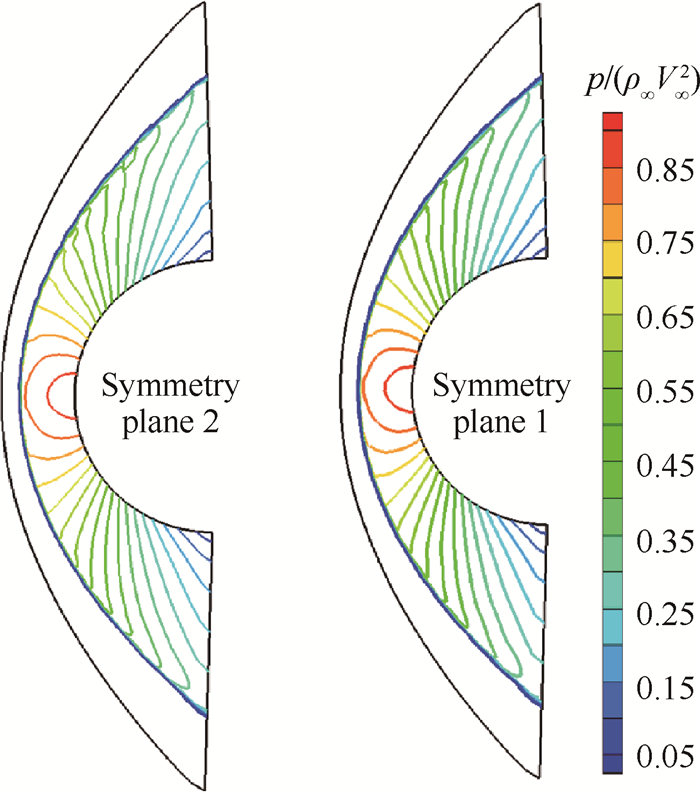
图 14是Case 9计算得到的压力等值线图,对比于图 12,13,不仅Zone1与Zone2中的“zigzag”型的压力线不复存在,而且对于驻点区域压力有明显的改善,这说明PD4方式可以有效地消除激波后“zigzag”型的压力分布,并且能够整体改善压力场的结果。
|
Fig. 14 Results of Case 9 |
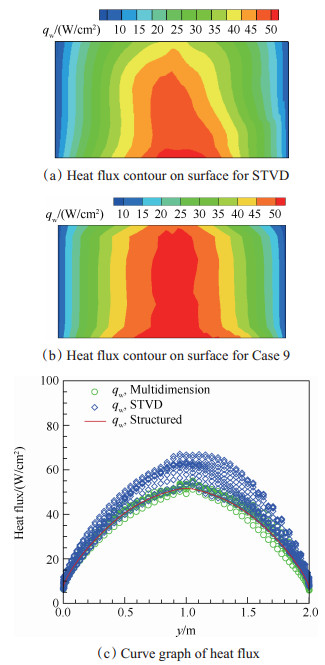
本文提出的混合方式PD4有效地改善了压力场的计算,抑制了激波后非物理扰动的传播。图 15给出了Case 9壁面上热流结果以及网格相关的STVD算法得到的结果的比较。从图中可以看出,在对称面附近热流等值线有些许偏折,这样的偏折在文献[8]中也同样存在。
|
Fig. 15 Comparison of heat flux on surface |
为了对壁面热流计算结果进行定量分析,采用结构化网格程序AHEAT对该问题进行计算,该程序的正确性已经在文献[2, 19]中得到了验证。图 15(c)中红线所表示的即是结构网格程序计算结果。选取图中y=0处热流进行比较,计算得到与结构网格计算结果的相对误差:STVD格式的相对误差约为29.2%,多维通量格式的相对误差为4.0%。
由此可以看出,与结构网格计算结果相比较,本文所提改进方法计算壁面热流结果除了在对称边界处有少许偏差外,其余区域计算结果与结构网格计算结果吻合较好,这说明本文提出的主方向混合确定方式可以有效计算壁面热流。
4 结论通过本文研究,得到以下结论:
(1) PD1方式在计算中存在激波不稳定现象,PD2与PD3两种方式对网格严重依赖,在强激波后压力场存在非物理“zigzag”现象。
(2) 本文提出的混合方式可以同时消除红玉现象以及压力场等值线曲折的非物理现象,并且驻点区域压力场计算得更好。
(3) 本文提出的混合方式计算得到的驻点热流相对误差由STVD格式的29.2%降到了4.0%,说明该方法计算得到的热流是合理的。
| [1] |
刘健, 原志超, 杨恺, 等. 高超声速飞行器多层复杂热防护结构气-固耦合快速热分析方法[J]. 推进技术, 2016, 37(2): 227-234. (LIU Jian, YUAN Zhi-chao, YANG Kai, et al. Fast Algorithm of Coupled Flow-Thermal for Multi-Layered Complex TPS of Hypersonic Aircraft[J]. Journal of Propulsion Technology, 2016, 37(2): 227-234.)
(  0) 0) |
| [2] |
杨恺, 原志超, 朱强华, 等. 高超声速热化学非平衡钝体绕流数值模拟[J]. 推进技术, 2014, 35(12): 1585-1591. (YANG Kai, YUAN Zhi-chao, ZHU Qiang-hua, et al. Numerial Simulation of Huypersonic Thermochemical Nonequilibrium Blunt Body Flows[J]. Journal of Propulsion Technology, 2014, 35(12): 1585-1591.)
(  0) 0) |
| [3] |
彭治雨, 石义雷, 龚红明, 等. 高超声速气动热预测技术及发展趋势[J]. 航空学报, 2015(1): 325-345. (  0) 0) |
| [4] |
张来平, 贺立新, 刘伟, 等. 基于非结构/混合网格的高阶精度格式研究进展[J]. 力学进展, 2013(2): 202-236. (  0) 0) |
| [5] |
伍贻兆, 田书玲, 夏健. 基于非结构动网格的非定常流数值模拟方法[J]. 航空学报, 2011(1): 15-26. (  0) 0) |
| [6] |
Nompelis I, Drayna T, Candler G. Development of a Hybrid Unstructured Implicit Solver for the Simulation of Reacting Flows over Complex Geometries[R]. AIAA 2004-2227.
(  0) 0) |
| [7] |
Gnoffo P. Simulation of Stagnation Region Heating in Hypersonic Flow on Tetrahedral Grids (Invited)[R]. AIAA 2007-3960.
(  0) 0) |
| [8] |
Gnoffo P. Updates to Multi-Dimensional Flux Reconstruction for Hypersonic Simulations on Tetrahedral Grids[R]. AIAA 2010-1271.
(  0) 0) |
| [9] |
Gnoffo P. Multi-Dimensional Inviscid Flux Reconstruction for Simulation of Hypersonic Heating on Tetrahedral Grids[R]. AIAA 2009-599.
(  0) 0) |
| [10] |
Levy D W, Powell K G, van Leer B. Use of a Rotated Riemann Solver for the Two-Dimensional Euler Equations[J]. Journal of Computational Physics, 1993, 106(2): 201-214. DOI:10.1016/S0021-9991(83)71103-4
(  0) 0) |
| [11] |
雷国东, 任玉新. 求解多维欧拉方程的二阶非结构网格混合旋转Riemann求解器[J]. 计算物理, 2009(6): 799-805. (  0) 0) |
| [12] |
孙宇涛, 任玉新. 求解多维欧拉方程的二阶旋转输运格式[J]. 空气动力学学报, 2005(3): 326-329. (  0) 0) |
| [13] |
Mazaheri A R, Nishikawa H. High-Order Hyperbolic Residual-Distribution Schemes on Arbitrary Triangular Grids[R]. AIAA 2015-2445.
(  0) 0) |
| [14] |
Ren Y. A Robust Shock-Capturing Scheme Based on Rotated Riemann Solvers[J]. Computers & Fluids, 2003, 32(10): 1379-1403.
(  0) 0) |
| [15] |
Capdeville G. A High-Order Multi-Dimensional HLL-Riemann Solver for Non-Linear Euler Equations[J]. Journal of Computational Physics, 2011, 230(8): 2915-2951. DOI:10.1016/j.jcp.2010.12.043
(  0) 0) |
| [16] |
Zhang F, Liu J, Chen B, et al. Evaluation of Rotated Upwind Schemes for Contact Discontinuity and Strong Shock[J]. Computers & Fluids, 2016, 134-135: 11-22.
(  0) 0) |
| [17] |
Blazek J. Computational Fluid Dynamics: Principles and Applications[M]. Oxford: Butterworth-Heinemann, 2015.
(  0) 0) |
| [18] |
Gnoffo P A, Wood W A, Kleb B, et al. Functional Equivalence Acceptance Testing of FUN3D for Entry, Descent, and Landing Applications[R]. AIAA 2013-2558.
(  0) 0) |
| [19] |
Zhichao Y, Shizhang H, Xiaowei G, et al. Effects of Surface-Catalysis Efficiency on Aeroheating Characteristics in Hypersonic Flow[J]. Journal of Aerospace Engineering, 2017, 30(3).
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


